Нейросети — это просто (Часть 17): Понижение размерности

Содержание

• Введение
• 1. Понимание задачи понижения размерности
• 2. Метод анализа главных компонент (PCA)
• 3. Реализация PCA средствами MQL5
• 4. Тестирование
• Заключение
• Ссылки
• Программы, используемые в статье

Введение

Продолжаем погружение в изучение моделей и алгоритмов обучения без учителя. Мы уже рассмотрели алгоритмы кластеризации данных. И в данной статье я хочу предложить Вам познакомиться с решением задачи понижения размерности. По существу, это определенные алгоритмы сжатия данных, которые широко используются на практике. Давайте познакомимся с реализацией одного из таких алгоритмов и возможностью его применения в построении нашей модели для трейдинга.

1. Понимание задачи понижения размерности

Каждый новый день, каждый новый час и каждый новый миг даёт нам огромное количество информации во всех сферах жизнедеятельности человечества. В наш мир информационных технологий люди ходят сохранить и обработать как можно больше этой информации. А для хранения больших объемов информации требуются ёмкие хранилища данных. В то же время для обработки больших объемов данных требуются соответствующие вычислительные ресурсы. И, вполне естественно, что возникает желание найти способ записать имеющуюся информацию в более сжатом виде. При этом если сжатый вид несет полный контекст информации, то потребуется и меньше ресурсов на его обработку.

К примеру, мы занимаемся задачей распознавания образов на изображении размером 200*200 пикселей и каждый пиксель записан в формате color, который в памяти занимает 4 байта. Возможность представления каждого пикселя в одном из 16.5 млн цветов явно избыточная для решения нашей задачи. И в большинстве случаев, качество работы нашей модели не пострадает если мы уменьшим градацию, скажем, до 16 или 32 цветов. В таком случае для записи номера цвета каждого пикселя нам будет достаточно 1-го байта. Конечно, нам потребуется одноразовые затраты на запись нашей матрицы цветов, 64 байта для 16 цветов и 128 байта для 32 цветов. Согласитесь, это не большая плата за сжатие всех наших изображений в 4 раза. Если подумать, то подобную задачу можно решить и уже известным нам методом кластеризации данных. Хотя это и не самый эффективный способ.

Ещё одна область использования методов понижения размерности — это визуализация данных. К примеру, у Вас есть данные описания состояний некой системы, представленные 10 параметрами. И Вам необходимо найти способ визуализировать эти данные. Для восприятия человеком наиболее предпочтительными являются 2-х и 3-мерные изображения. Конечно, можно сделать несколько слайдов с различными вариациями 2-3 параметров. Но это не даст полного представления о картине состояний системы. И в большинстве случаев различные состояния в различных слайдах будут сливаться в одну точку. И не всегда это будут одни и те же состояния.

Поэтому, нам бы хотелось найти такой алгоритм, который помог бы нам перевести все наши состояния системы из 10 параметров в 2-х или 3-мерное пространство. И при этом максимально возможно разделил бы наши состояния системы с сохранением их взаимного расположения. И конечно, при этом с минимальной потерей информации.

Возможно, Вы скажете: "Это все конечно интересно, но какая практическая польза в трейдинге?" А давайте посмотрим в наш терминал. Какое количество индикаторов он нам предоставляет. Да, многие из них имеют корреляцию данных в той или иной степени. Но каждый из них даёт нам как минимум одно значения описания нашей рыночной ситуации. А если это умножить на количество торговых инструментов. А различные вариации параметров индикаторов и анализируемых таймфреймов способны до бесконечности увеличивать число параметров описания текущего состояния рынка.

Без сомнения, мы не будем в одной модели сразу изучать все инструменты и все возможные индикаторы. Но тем не менее, в поисках наиболее подходящей их комбинации мы можем использовать довольно большое их число. А это усложнит нашу модель и время её обучения. Поэтому снижение размерности исходных данных с сохранением максимума информации прямой путь как к сокращению затрат на обучение модели, так и сокращению времени принятия решения. А значит реакция на поведения рынка будет молниеносной. И сделки будут совершаться по максимально выгодной цене.

И надо ещё сказать, что алгоритмы понижения размерности всегда используются лишь для предварительной обработки данных. Так как возвращают лишь сжатую форму исходных данных. Которые затем сохраняются или передаются для последующей обработки. Это может быть визуализация данных или обработка какой-либо другой моделью.

Таким образом, для построения своей торговой системы мы можем взять максимум необходимой информации для описания текущего состояния рынка. Сжать её с помощью одного из алгоритмов понижения размерности. При этом мы надеемся, что в процессе сжатия будет отсеяна часть шума и коррелирующихся данных. И сжатые данные подадим на вход нашей модели принятия торговых решений.

Надеюсь, идея понятна. А для её реализации в качестве алгоритма понижения размерности я предлагаю взять один из наиболее распространённых метод анализа главных компонент. Данный алгоритм хорошо зарекомендовал себя при решении различных задач и может тиражироваться на новые данные. Что позволяет проводить сжатие поступающих данных и передавать их в модель принятия решений для генерации торговых решений в режиме реального времени.

2. Метод анализа главных компонент (PCA)

Метод анализа главных компонент был изобретён английским математиком Карлом Пирсоном ещё в 1901 году. С тех пор он успешно применяется во многих областях науки.

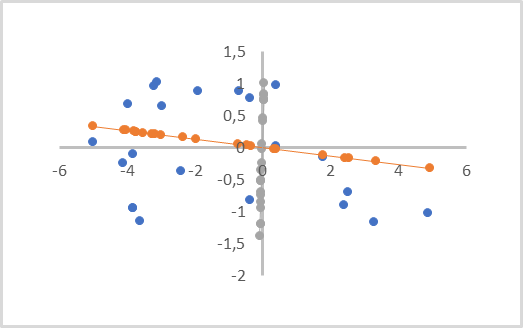
Для понимания сути самого метода предлагаю взять упрощенную задачу понижения размерности 2-мерного массива данных до вектора. С геометрической точки зрения это можно представить как проекция точек некой плоскости на прямую.

На рисунке ниже исходные данные представлены синими точками и сделаны две проекции на оранжевую и серую линию с точками соответствующего цвета. Как можно заметить, среднее расстояние от исходных точек до их оранжевых проекций будет меньше аналогичных расстояний до серых проекций. При этом среди серых проекций можно заметить наложение проекций точек друг на друга. Следовательно, оранжевая проекция для нас более предпочтительна, так как разделяет все отдельные точки и обладает меньшей потерей данных при понижении размерности (расстояние от точек до их проекций).

Такая линия называется главной компонентой. Отсюда и название метода — анализ главных компонент.

С математической точки зрения, каждая главная компонента является числовым вектором с размером, равным размерности исходных данных. Произведение вектора исходных данных описания одного состояния системы на соответствующий вектор главной компоненты и даёт точку проекции анализируемого состояния на прямой.

В зависимости от размерности исходных данных и требований к сжатию данных таких главных компонент может быть несколько, но не более размерности исходных данных. При визуализации объемной проекции их будет 3. А при сжатии данных исходят из допустимой погрешности обычно берется потеря до 1% данных.

Наверное, следует обратить внимание, что это визуально как бы похоже на линейную регрессию. Но это абсолютно разные методы и дают различные результаты.

При построении линейной регрессии выводится линейная зависимость значения одной переменной от другой. И минимизируются расстояния до линии перпендикулярно осям координат. Такая линия может проходить в любой части плоскости.

При анализе главных компонент значения по всем осям абсолютно независимы и равнозначны. Минимизируются расстояния, перпендикулярные самой линии, а не осям координат. И линия главной компоненты обязательно проходит через начало координат. Поэтому все исходные данные перед применением метода должны быть нормализованы. Или, как минимум, центрированы относительно начала координат. Иными словами, нам нужно в каждом измерении центрировать данные относительно «0». 

Ещё одной важной особенность метода анализа главных компонент является то, что в результате его применения мы получаем матрицу ортогональных векторов главных компонент. То есть между всеми векторами главных компонент полностью отсутствует корреляция. Этот факт оказывает положительное влияние на весь процесс обучения последующей модели принятия решения, которая получает на вход сжатые данные.

С математической точки зрения метод анализа главных компонент можно представить в виде спектрального разложения ковариационной матрицы исходных данных. А ковариационную матрицу легко найти по формуле.

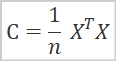
где

• C - ковариационная матрица,
• X - матрица исходных данных,
• n - количество элементов в исходных данных.

В результате данной операции мы получим квадратную матрицу ковариации. Размер которой равен количеству признаков описания состояния системы. По главной диагонали данной матрицы будут располагаться дисперсии признаков. А остальные элементы матрицы представляют степень ковариации соответствующих пар признаков.

На следующем этапе нам предстоит осуществить сингулярное разложение полученной ковариационной матрицы. Само по себе сингулярное разложение матрицы довольно сложный математический процесс. Но введение матриц и матричных операций в язык MQL5 сильно упростило нам этот процесс. Так как данная операция уже реализована для матриц. Поэтому разберем сразу результаты сингулярного разложения.

В результате сингулярного разложения матрицы мы получаем 3 матрицы, произведение которых равно исходной матрице. Средняя матрица ∑ представляет собой диагональную матрицу размером равную исходной матрицы. По главной диагонали этой матрицы лежат сингулярные числа, представляющие дисперсию значений по осям сингулярных векторов. Сингулярные числа не отрицательные и расположены в порядке убывания. Все остальные элементы матрицы равны «0». Поэтому, её часто представляют в виде вектора.

U и V унитарные квадратные матрицы, содержащие левые и правые сингулярные вектора, соответственно. Размер матрицы U равен количеству строк в исходной матрице, а размер матрицы V — количеству столбцов в исходной матрице.

В нашем частном случае, когда мы осуществляем сингулярное разложение квадратной матрицы ковариации, матрицы U и V имеют одинаковый размер.

Для целей понижения размерности данных мы будем использовать матрицу U. Так как сингулярные числа расположены в порядке убывания, то нам достаточно взять необходимое количество первых столбцов матрицы U. Новую матрицу обозначим как матрицу UR . Чтобы понизить размерность нам достаточно умножить матрицу исходных данных на созданную нами матрицу UR.

И тут возникает вопрос, до какого значения оптимально понижать размерность. Если перед нами стоит задача визуализации данных, то такого вопроса не будет. Так как выбор размерности от 1 до 3 зависит от создаваемой проекции. Но мы планируем сжимать данные с минимальной потерей информации для последующей передачи в другую модель принятия решения. Поэтому, основным критерием для нас является объем утраченной информации.

Оптимальным вариантом определения объема сохраненной информации является подсчет доли сингулярных значений, соответствующих используемым сингулярным векторам.

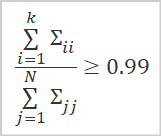
где

• k — количество используемых векторов,
• N — общее количество сингулярных значений.

На практике обычно выбирают такое количество столбцов k, при котором значение выше приведенного отношения составляет не менее 0.99. Что соответствует сохранению 99% информации.

Теперь, когда мы познакомились с общими теоретическими аспектами, можно переходить к реализации метода.

3. Реализация PCA средствами MQL5

Для реализации алгоритма метода анализа главных компонент мы создадим новый класс CPCA наследником базового класса CObject. Весь код нового класса мы сохраним в файл "pca.mqh".

Надо сказать, что в реализации данного класса мы будем использовать матричные операции. Поэтому, результат обучения нашей модели, а точнее матрицу UR мы сохраним в матрице m_Ureduce.

Кроме того, объявим ещё 3 локальных переменных. Прежде всего, это флаг статуса обучения модели b_Studied. А также 2 вектора v_Means и v_STDs, в которые мы сохраним значения средних арифметических и среднеквадратичных отклонений для последующей нормализации данных.

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDы;

В конструкторе класса мы укажем значение false в флаге состояния обучения модели b_Studied и инициализируем матрицу m_Ureduce с нулевым размером. Деструктор класса оставим пустым, так как внутри класса мы не создаём никаких вложенных объектов.

CPCA::CPCA()   :  b_Studied(false)
  {
   m_Ureduce.Init(0, 0);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPCA::~CPCA()
  {
  }

Следующим мы воссоздадим метод обучения модели Study. В параметрах метод получает матрицу исходных данных. А возвращает логический результат выполнения операций.

Как уже было сказано выше, для проведения анализа главных компонент необходимо использовать нормализованные данные. Поэтому, прежде чем приступить к реализации основного алгоритма метода, мы проведем нормализацию исходных данных по формуле, приведенной ниже. 

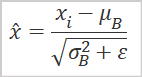
Использование матричных операций нам упрощает и эту задачу. Теперь нам не требуется создавать системы циклов. Для нахождения средних арифметических значений по всем признакам нам достаточно воспользоваться методом Mean матричных операций с указанием измерения для подсчета значений. В результате выполнения операции мы получаем сразу вектор, в котором содержатся средние арифметические значения по всем признакам.

В знаменателе нашей формулы нормализации данных мы видим квадратный корень из дисперсии, который соответствует среднеквадратическому отклонению. И здесь нам помогут матричные операции. Метод STD возвращает вектор среднеквадратичных отклонений по указанному измерению. Нам остается добавить лишь небольшую константу для исключения ошибки деления на ноль.

Полученные вектора мы сохраним в соответствующие переменные v_Means и v_STDs. Ведь аналогичную нормализацию исходных данных нам необходимо выполнять как на стадии обучения модели, так и на стадии промышленной эксплуатации.

Далее мы проведем непосредственно нормализацию данных. Для этого мы подготовим матрицу X размером равным размеру исходных данных. И организуем цикл с числом итераций равным количеству строк в матрице исходных данных.

В теле цикла мы осуществим нормализацию исходных данных и результат операций сохраним в предварительно созданной матрице X. Использование векторных операций и тут нам поможет избавиться от необходимости создания вложенного цикла.

bool CPCA::Study(matrix &data)
  {
   matrix X;
   ulong total = data.Rows();
   if(!X.Init(total,data.Cols())
      return false;
   v_Means = data.Mean(0);
   v_STDs = data.STD(0) + 1e-8;
   for(ulong i = 0; i < total; i++)
     {
      vector temp = data.Row(i) - v_Means;
      temp /= v_STDs;
      X = X.Row(temp, i);
     }

После нормализации исходных данных мы переходим непосредственно к реализации алгоритма метода анализа главных компонент. Как было сказано выше, на первом этапе нам предстоит посчитать ковариационную матрицу. Благодаря использованию матричных операций это легко укладывается в одну строчку кода. Чтобы не создавать излишних объектов, результат операций я перезаписываю в нашу матрицу X.

   X = X.Transpose().MatMul(X / total);

Согласно выше приведенному алгоритму, следующей операцией должно быть сингулярное разложение матрицы ковариации. В результате данной операции мы ожидаем получить 3 матрицы: левых сингулярных векторов, сингулярных значений и правых сингулярных векторов. Как Вы помните, элементы матрицы сингулярных значений только по главной диагонали могут иметь не нулевые значения. Поэтому, для экономии ресурсов в реализации MQL5 вместо матрицы возвращается вектор сингулярных значений.

Перед вызовом функции мы объявим 2 матрицы и 1 вектор для получения результатов. И лишь затем вызовем матричный метод сингулярного разложения SVD. В параметрах методу передадим матрицы и вектор для записи результатов операции.

   matrix U, V;
   vector S;
   if(!X.SVD(U, V, S))
      return false;

Теперь, когда мы получили ортогональные матрицы сингулярных векторов, нам необходимо определить до какого уровня мы будем понижать размерность исходных данных. В соответствии с общей практикой мы будем сохранять не менее 99% информации, содержащейся в исходных данных.

Следуя выше указанной логике, мы сначала определяем общую сумму всех элементов вектора сингулярных значений. При этом обязательно проверим, чтобы полученное значение было больше «0». Отрицательным оно не может быть по определению, так как сингулярные числа не отрицательные. Кроме того, мы должны исключить ошибку деления на «0».

После этого посчитаем накопительные суммы значений вектора сингулярных значений и разделим полученный вектор на общую сумму сингулярных значений.

В результате мы получим вектор возрастающих значений с максимумом равным «1».

Теперь, для определения количества необходимых столбцов нам остаётся найти в векторе позицию первого элемента большего или равного пороговому значения сохранения информации. В приведенном примере указано значение 0.99. Что обеспечивает сохранения 99% исходной информации. 

   double sum_total = S.Sum();
   if(sum_total<=0)
      return false;
   S = S.CumSum() / sum_total;
   int k = 0;
   while(S[k] < 0.99)
      k++;

Нам остается лишь изменить размер матрицы и перенести её содержимое в матрицу нашего класса. После этого изменяем флаг обучения модели и выходим из метода.

   if(!U.Resize(U.Rows(), k + 1))
      return false;
//---
   m_Ureduce = U;
   b_Studied = true;
   return true;
  }

После того, как мы создали метод обучения модели, а точнее определения матрицы понижения размерности исходных данных. Мы также можем создать метод понижения размерности поступающих данных ReduceM. Который получает в параметрах исходные данные и возвращает матрицу пониженной размерности.

Разумеется, исходные данные должны быть сопоставимы с данными, используемыми при обучении модели. Здесь мы говорим о количестве и качестве признаков описания состояния системы, а не количестве наблюдений.

В начале метода мы создаем блок контролей, в котором проверяем флаг обучения модели и равенство количества столбцов в матрице исходных данных (количество признаков) с количеством строк в нашей понижающей матрице m_Ureduce. При не выполнении любого из условий выходим из метода и возвращаем матрицу нулевого размера.

matrix CPCA::ReduceM(matrix &data)
  {
   matrix result;
   if(!b_Studied || data.Cols() != m_Ureduce.Rows())
      return result.Init(0, 0);

После успешного прохождения блока контролей до осуществления понижения размерности нам необходимо нормализовать исходные данные. Алгоритм нормализации будет аналогичным рассмотренному выше при обучении модели. Только на это раз мы не будем рассчитывать среднее арифметическое значение и среднеквадратичное отклонение. А воспользуемся соответствующими векторами, сохраненными при обучении. Таким образом мы обеспечим сопоставимость новых результатов и полученными при обучении.

   ulong total = data.Rows();
   if(!X.Init(total,data.Cols()))
      return false;
   for(ulong r = 0; r < total; r++)
     {
      vector temp = data.Row(r) - v_Means;
      temp /= v_STDs;
      result = result.Row(temp, r);
     }

До завершения алгоритма метода нам остаётся умножить матрицу нормализованных значений на понижающую матрицу и вернуть результат операции вызывающей программе.

   return result.MatMul(m_Ureduce);
  }

Вот мы и построили методы обучения модели понижения размерности исходных данных. Благодаря использованию матричных операций код получился довольно кратким и без погружения в математические тонкости. Но давайте вспомним, что это первый код в нашей библиотеке с использованием матричных операций. А до этого мы использовали динамические массивы в объектах CBufferDouble. Поэтому, для организации совместимости наших объектов необходимо создать интерфейс переноса данных из динамического буфера в матрицу и обратно.

Для организации данного процесса мы создадим два метода FromBuffer и FromMatrix. Первый метод будет принимать в параметрах динамический буфер данных и размер вектора описания одного состояния системы. А возвращать будет матрицу, в которую будет перенесено содержимое буфера.

В теле метода сначала мы организуем блок контролей. В котором сначала проверим действительность указателя на объект буфера исходных данных. А затем проверим кратность размера буфера размеру вектора описания одного состояния анализируемой системы.

matrix CPCA::FromBuffer(CBufferDouble *data, ulong vector_size)
  {
   matrix result;
   if(CheckPointer(data) == POINTER_INVALID)
     {
      result.Init(0, 0);
      return result;
     }
//---
   if((data.Total() % vector_size) != 0)
     {
      result.Init(0, 0);
      return result;
     }

После успешного прохождения всех проверок мы определим количество строк в матрице и инициализируем матрицу результатов.

   ulong rows = data.Total() / vector_size;
   if(!result.Init(rows, vector_size))
     {
      result.Init(0, 0);
      return result;
     }

Далее мы организуем систему вложенных циклов, в которой перенесем все содержимое динамического буфера в матрицу.

   for(ulong r = 0; r < rows; r++)
     {
      ulong shift = r * vector_size;
      for(ulong c = 0; c < vector_size; c++)
         result[r, c] = data[(int)(shift + c)];
     }
//---
   return result;
  }

По завершению системы циклов мы выходим из метода и вернем вызывающей программе созданную матрицу.

Второй метод  FromMatrix выполняет обратную операцию. В параметрах методу мы передаём матрицу с данными, а на выходе получаем динамический буфер данных.

В теле метода мы сначала создаём новый объект динамического массива и сразу проверяем результат выполнения операции.

CBufferDouble *CPCA::FromMatrix(matrix &data)
  {
   CBufferDouble *result = new CBufferDouble();
   if(CheckPointer(result) == POINTER_INVALID)
      return result;

Затем резервируем размер динамического массива, достаточный для записи всего содержимого матрицы.

   ulong rows = data.Rows();
   ulong cols = data.Cols();
   if(!result.Reserve((int)(rows * cols)))
     {
      delete result;
      return result;
     }

Далее нам остается лишь перенести содержимое матрицы в динамический массив. Данная операция выполняется в системы двух вложенных циклов.

   for(ulong r = 0; r < rows; r++)
      for(ulong c = 0; c < cols; c++)
         if(!result.Add(data[r, c]))
           {
            delete result;
            return result;
           }
//---
   return result;
  }

После успешного выполнения всех операций цикла мы выходим из метода и возвращаем созданный объект буфера данных вызывающей программе.

Здесь надо сказать, что мы не сохраняем указатель на созданный объект. Поэтому, вся работа по отслеживанию его состояния и удаления из памяти после завершения работы должна быть организована на стороне вызывающей программы.

Для работы с векторами создадим аналогичные методы. Переносить данные из буфера в вектор мы будем перегруженным методом FromBuffer. А обратную операцию организуем в методе FromVector. Алгоритмы построения методов аналогичны приведенным выше. А с полным кодом методов можно ознакомиться во вложении.

После создания методов переноса данных мы можем создать перегрузку метода обучения модели, которая в параметрах будет получать динамический буфер данных и размер вектора описания одного состояния системы. Алгоритм построения такого метода довольно прост. Мы сначала переносим данные из динамического буфера в матрицу с использованием выше рассмотренного метода FromBuffer. А затем вызываем ранее рассмотренный метод обучения модели, передав в него полученную матрицу.

bool CPCA::Study(CBufferDouble *data, int vector_size)
  {
   matrix d = FromBuffer(data, vector_size);
   return Study(d);
  }

Аналогичную перегрузку создадим и для метода понижения размерности ReduceM. Только в отличии от рассмотренной перегрузки метода обучения, в параметрах данного метода мы передаем только буфер исходных данных без указания размера вектора описания одного состояния анализируемой системы. Это связано с тем, что на данный момент модель уже должна быть обучена и размер вектора описания состояния системы должен быть равен количеству строк в понижающей матрице.

Еще одно отличие данного метода состоит в том, что для предотвращения излишнего переноса данных мы сначала проверяем обучена ли модель и кратность размера буфера размеру вектора описания состояния системы. И только после успешного прохождения контролей вызываем метод переноса данных.

matrix CPCA::ReduceM(CBufferDouble *data)
  {
   matrix result;
   result.Init(0, 0);
   if(!b_Studied || (data.Total() % m_Ureduce.Rows()) != 0)
      return result;
   result = FromBuffer(data, m_Ureduce.Rows());
//---
   return ReduceM(result);
  }

Для получения матрицы пониженной размерности в виде динамического буфера данных создадим ещё 2 перегруженных метода Reduce. Один в параметрах будет получать динамический буфер данных исходных данных. А второй — матрицу. Их код приведен ниже. 

CBufferDouble *CPCA::Reduce(CBufferDouble *data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

CBufferDouble *CPCA::Reduce(matrix &data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

Может показаться странным, но несмотря на различие в параметрах методов, их содержимое абсолютно одинаковое. Но это легко объясняется использованием выше описанных перегрузок метода ReduceM.

С функциональностью класса мы разобрались. Теперь нам остаётся лишь создать методы работы с файлами. Мы ведь помним, что у любой однажды обученной модели должна быть возможность быстро восстановить свою работу для последующего использования. И, как всегда, начнём мы с метода сохранения данных Save.

Но прежде, чем приступить к построению алгоритма метода сохранения данных давайте посмотрим на структуру нашего класса и подумаем, что мы должны сохранить в файл.

Среди частных переменных класса мы видим один флаг обучения модели b_Studied, матрицу понижения размерности m_Ureduce и 2 вектора со средними арифметическими v_Means и среднеквадратическим отклонением v_STDs. И для полного восстановления работоспособности модели нам потребуется сохранить все эти элементы.

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDs;
   //---
   CBufferDouble     *FromMatrix(matrix &data);
   CBufferDouble     *FromVector(vector &data);
   matrix            FromBuffer(CBufferDouble *data, ulong vector_size);
   vector            FromBuffer(CBufferDouble *data);

public:
                     CPCA();
                    ~CPCA();
   //---
   bool              Study(CBufferDouble *data, int vector_size);
   bool              Study(matrix &data);
   CBufferDouble     *Reduce(CBufferDouble *data);
   CBufferDouble     *Reduce(matrix &data);
   matrix            ReduceM(CBufferDouble *data);
   matrix            ReduceM(matrix &data);
   //---
   bool              Studied(void)  {  return b_Studied; }
   ulong             VectorSize(void)  {  return m_Ureduce.Cols();}
   ulong             Inputs(void)   {  return m_Ureduce.Rows();   }
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedPCA; }
  };

При построении различных моделей все ранее рассмотренные методы сохранения данных в параметрах получали хендл файла для записи данных. Аналогичный метод этого класса не является исключением. И в теле метода мы сразу проверяем действительность полученного хендла.

bool CPCA::Save(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

Далее мы сохраняем значение флага обучения модели. Ведь именно его состояния определяет необходимость сохранения остальных данных. Если модель ещё не обучена, то нет необходимости сохранять пустые вектора и матрицу. Мы просто завершаем работу метода.

   if(FileWriteInteger(file_handle, (int)b_Studied) < INT_VALUE)
      return false;
   if(!b_Studied)
      return true;

Если же модель обучена мы переходим к сохранению остальных элементов. Сначала мы сохраним понижающую матрицу. Для матриц в языке MQL5 ещё не реализована функция сохранения данных. Но у нас есть метод записи в файл буфера данных. Почему бы нам этим не воспользоваться?

Сначала мы перенесем данные из матрицы в динамический буфер данных. Затем сохраним количество столбцов матрицы. И вызовем метод сохранения нашего буфера данных. И здесь надо вспомнить, что в методе переноса данных из матрицы в буфер мы не сохраняли указатель на объект. И выше я уже указывал, что вся работа по очистке памяти такого объекта лежит на вызывающей программе. Поэтому, после завершения операций сохранения данных мы должны удалить созданный объект.

   CBufferDouble *temp = FromMatrix(m_Ureduce);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(FileWriteLong(file_handle, (long)m_Ureduce.Cols()) <= 0)
     {
      delete temp;
      return false;
     }
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

Аналогичным алгоритмом воспользуемся и для сохранения данных векторов.

   temp = FromVector(v_Means);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

   temp = FromVector(v_STDs);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;
//---
   return true;
  }

После успешного выполнения всех операций выходим из метода с результатом true.

Восстановление данных из файла осуществляется в методе Load в том же порядке. Сначала мы осуществляем проверку действительности хендла файла для загрузки данных.

bool CPCA::Load(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

Затем мы считываем состояние флага обучения модели. И если модель ещё не обучена, то выходим из метода с положительным результатом. Нам нет необходимости осуществлять какую-либо работу с понижающей матрицей и векторами, так как они будут переписаны в процессе обучения модели. А при попытке выполнить понижения размерности данных до обучения будет проверено состояния флага обучения и завершен метод с негативным результатом.

   b_Studied = (bool)FileReadInteger(file_handle);
   if(!b_Studied)
      return true;

Для обученной модели мы сначала создадим объект динамического буфера. Потом считаем количество столбцов в понижающей матрице. И загрузим содержимое понижающей матрицы в буфер данных.

После успешной загрузки данных, мы просто переносим содержимое динамического буфера в нашу матрицу.

   CBufferDouble *temp = new CBufferDouble();
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   long cols = FileReadLong(file_handle);
   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   m_Ureduce = FromBuffer(temp, cols);

С помощью аналогичного алгоритма загрузим содержимое векторов.

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_Means = FromBuffer(temp);

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_STDs = FromBuffer(temp);

После успешной загрузки всех данных мы удаляем объект динамического буфера данных и выходим из метода с положительным результатом.

   delete temp;
//---
   return true;
  }

На этом мы заканчиваем работу над нашим классом метода анализа главных компонент. А с полным кодом всех методов и функций можно ознакомиться во вложении.

4. Тестирование

Тестирование работы нашего класса метода анализа главных компонент я осуществлял в 2 этапа. В первом тесте я произвел обучение модели. Для этого я создал советник "pca.mq5" на базе эксперта из предыдущей статьи "kmeans.mq5". Изменения коснулись лишь объекта используемой модели и функции обучения модели Train.

В начале процедуры мы, как и прежде, определим дату начала периода обучения.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

 Затем загрузим котировки и значения используемых индикаторов.

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
      return;
   if(!ArraySetAsSeries(Rates, true))
      return;
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

После этого мы сгруппируем полученные данные в одну матрицу. 

   int total = bars - (int)HistoryBars;
   matrix data;
   if(!data.Init(total, 8 * HistoryBars))
     {
      ExpertRemove();
      return;
     }
//---
   for(int i = 0; i < total; i++)
     {
      Comment(StringFormat("Create data: %d of %d", i, total));
      for(int b = 0; b < (int)HistoryBars; b++)
        {
         int bar = i + b;
         int shift = b * 8;
         double open = Rates[bar]
                       .open;
         data[i, shift] = open - Rates[bar].low;
         data[i, shift + 1] = Rates[bar].high - open;
         data[i, shift + 2] = Rates[bar].close - open;
         data[i, shift + 3] = RSI.GetData(MAIN_LINE, bar);
         data[i, shift + 4] = CCI.GetData(MAIN_LINE, bar);
         data[i, shift + 5] = ATR.GetData(MAIN_LINE, bar);
         data[i, shift + 6] = MACD.GetData(MAIN_LINE, bar);
         data[i, shift + 7] = MACD.GetData(SIGNAL_LINE, bar);
        }
     }

И вызовем метод обучения нашей модели.

   ResetLastError();
   if(!PCA.Study(data))
     {
      printf("Ошибка выполнения %d", GetLastError());
      return;
     }

После успешного обучения сохраним модель в файл и вызовем завершение работы советника.

   int handl = FileOpen("pca.net", FILE_WRITE | FILE_BIN);
   if(handl != INVALID_HANDLE)
     {
      PCA.Save(handl);
      FileClose(handl);
     }
//---
   Comment("");
   ExpertRemove();
  }

С полным кодом советника можно ознакомиться во вложении.

В результате выполнения данного советника на исторических данных за последние 15 лет удалось снизить размерность исходных данных со 160 элементов до 68. То есть сокращение размера исходных данных почти в 2.4 раза с риском потери всего 1% информации.

На следующем этапе тестирования мы взяли уже обученную модель анализа главных компонент. И после понижения размерности исходных данных подали результат работы нашего класса на вход полносвязного перцептрона. Для этого теста мы создали советник "pca_net.mq5" на базе аналогичного эксперта из предыдущей статьи "kmeans_net.mq5". Обучение перцептрона осуществлялось на исторических данных за 2 последних года.

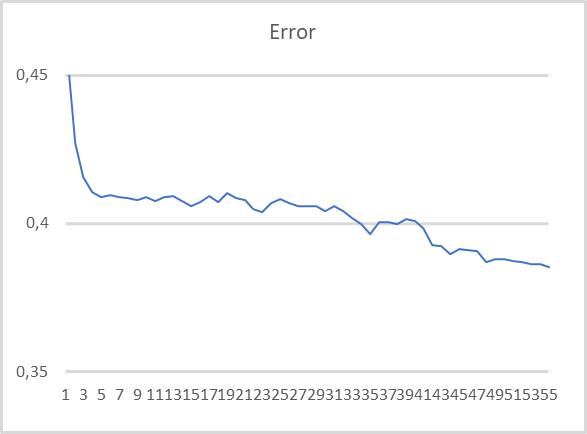
Как видно на представленном графике, при обучении модели на сжатых данных наблюдается довольно стабильная тенденция к понижению ошибки. После 55 эпох обучения размер ошибки ещё не стабилизировался. А значит возможно дальнейшее снижение ошибки при продолжении обучения.

Заключение

В данной статье мы рассмотрели решение ещё одного типа задач с использованием алгоритмов обучения без учителя — понижение размерности. Для решения подобных задач нами был создан класс CPCA, в котором реализован алгоритм метода анализа главных компонент. Это довольно эффективный метод сжатия данных с прогнозируемым порогом потери информации.

При тестировании созданного класса нам удалось сжать исходные данные почти в 2.4 раза с риском потери всего 1% информации. Что, согласитесь, является довольно неплохим результатом и позволяет повысить эффективность модели, обучаемой на сжатых данных.

Кроме того, одной из особенностей метода главных компонент является использование ортогональной матрицы для понижения размерности. Что практически сводит к «0» корреляцию между признаками в сжатых данных. Данное свойство также повышает эффективность последующего обучения модели на сжатых данных. И это подтверждают результаты второго теста.

В то же время следует предостеречь читателя от использования метода главных компонент в попытке борьбы с переобучением модели. Это довольно плохая практика. В таких случаях лучше все же использовать методы регуляризации.

И ещё одно наблюдение из общей практики. Несмотря на то, что в процессе сжатия данных теряется не значительная доля информации. Это все же происходит. Поэтому использование методов понижения размерности рекомендуется использовать только если обучение моделей без его использования не дало ожидаемых результатов.

Плюс мы познакомились с матричными операциями. За их появление в языке MQL5 отдельное спасибо компании MetaQuotes. Использование матричных операций значительно упрощает написание кода при создании рассматриваемых нами моделей для решения задач искусственного интеллекта.

Ссылки

1. Нейросети — это просто (Часть 14): Кластеризация данных
2. Нейросети — это просто (Часть 15): Кластеризации данных средствами MQL5
3. Нейросети — это просто (Часть 16): Практическое использование кластеризации

Программы, используемые в статье

#	Имя	Тип	Описание
1	pca.mq5	Советник	Советник для обучения модели
2	pca_net.mq5	Советник	Советник тестирования передачи данных 2-ой модели
3	pсa.mqh	Библиотека класса	Библиотека для организации метода анализа главных компонент
4	kmeans.mqh	Библиотека класса	Библиотека для организации метода k-средних
5	unsupervised.cl	Библиотека	Библиотека кода программы OpenCL  для организации метода k-средних
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL