ニューラルネットワークが簡単に（第18部）：アソシエーションルール

内容

• はじめに
• 1.アソシエーションルール
• 2.アプリオリアルゴリズム
• 3.FP成長アルゴリズム
• 結論
• 参考文献リスト

はじめに

分析対象データ量の増加に伴い、教師なし学習法への関心が高まっています。これまでの数回で、教師なし学習に属するクラスタリングや次元削減のアルゴリズムについて見てきました。今回は、教師なし学習法について引き続き勉強します。今回は、これらの手法で対応可能なもう1つのタイプの問題であるアソシエーションルールマイニングについて考えてみることにします。この問題タイプはスーパーマーケットでの買い物のマーケティングに端を発しており、最も頻繁に遭遇する商品セットを見つける目的で、市場のバスケットを分析するために使用されていました。現在では、これらの問題を解決するアルゴリズムが様々な分野で広く利用されています。このようなアルゴリズムが、取引にどのように利用できるかを見ていきます。

1.アソシエーションルール

アソシエーションルールの解析問題は、データマイニングの応用問題に属します。さらに、大規模なデータベースにおいて、データ間の興味深い関係を特定することができるため、基本的なものの1つです。

この種の問題は、小売店でのショッピングで初めて定式化され、定義されました。マーケティング担当者は、POSシステムに登録された膨大な取引データを分析することで、どのようなビジネス効果が得られるかという問題に直面しました。従来は総販売量のみで分析していました。お客様のレシートを分析することで、お客様が購入した特定の商品群を分析することができ、新たな地平が開けました。

最初のアルゴリズムは、1993年にIBMの開発者グループによって作られました。この時、大原則が策定され、それがアルゴリズム群の基礎となったのです。

まず、アルゴリズムが検出するルールは、頻繁に遭遇するものです。つまり、ランダムであってはならず、分析されたデータベースで一定回数以上繰り返されなければなりません。つまり、確認する必要があるということです。統計学の観点からは、このような規則を含む取引の標本は代表的なものであるべきです。この要件を満たすため、アソシエーションルールを決定するために使用されるすべてのアルゴリズムには、最小支持パラメータMinSupがあり、これは、分析サンプル内のトランザクション総数に対するルール発生頻度の比率を「1」の端数で示します。

組合せの法則によれば、要素の位置を考慮せずにA、B、Cの3つの項目のセットがあるとすると、これらの1〜3個を含むセットは7つ得ることができます。項目の数が増えれば、可能な組み合わせの数も増えます。データベースの容量を考えると、各集合の頻度を直接再計算することは、かなりリソースを消費する作業となります。このような再計算は不可能な場合が多いです。そこで、著者らは反単調性の性質を利用しました。

データベースにおいて、項目Aがすべての可能性の中から1セットだけ遭遇した場合、その出現頻度はAそのものの出現頻度と等しくなります。遭遇するセットの数が多ければ、分析したサンプル中のそれらの出現回数の合計はAの出現回数に等しくなるので、その頻度は小さくなるしかありません。したがって、ある項目の出現頻度がMinSupより小さければ、この項目を含む集合のすべての可能な変種の出現頻度もMinSupより小さくなることになります。各項目の出現頻度を計算することで、実用的価値のないランダムセットのかなりの部分を排除することができるということです。

このように、アソシエーションルールの検索アルゴリズムは、これまで考えられてきたものとは全く異なるものです。以前は、入手可能なすべてのデータを最大限に活用することを心がけていました。これに対し、アソシエーションルールのマイニングアルゴリズムはランダム（ノイズ）な項目を即座に排除します。

すべてのアソシエーションルールアルゴリズムで使用される2つ目のパラメータは、最小信頼度MinConfで、これもまた、1の端数で指定します。このパラメータを説明するには、各ルールが前提部と結論部の2つの部分から構成されていることを知る必要があります。前提部と結論部は、1つの項目で構成されることも、複数の項目で構成されることもあります。一般的には、「前提部が真であれば、かなりの確率で結論部も真になる」という法則があります。

前提部の発生後に結論部が発生する確率は100％ではありません。一方、結論部の発生確率の最小値はMinConfパラメータで設定されます。このパラメータを満たしたルールは有効とみなされ、ルールの配列に保存されます。これは、ルール実行頻度と前提部の頻度の比として定義されます。

2.アプリオリアルゴリズム

アソシエーションルールを見つけるための最も有名なアルゴリズムの1つは、おそらくRakesh AgrawalとRamakrishnan Srikantが1994年に提案したアプリオリアルゴリズムです。このアルゴリズムは、データベースの中から最も頻度の高いパターンを探し出すという反復処理に基づいています。その後、選択されたパターンからルールが抽出されます。

よりよく理解するために、5つの項目で10回の取引をおこなうという小さな例でのアルゴリズムの動作を見てみましょう。

取引ID	内容
T1	BCDE
T2	BCD
T3	B
T4	BCD
T5	D
T6	ACD
T7	BCDE
T8	BCE
T9	CDE
T10	AD

問題に、最小支持度0.3と最小信頼度0.7（それぞれ30%と70%）の定数を導入してみよう。

すべてのアソシエーションルールのアルゴリズムは、バイナリ配列で動作します。そこで、手始めに、上記のデータを2進数の表として提示してみます。

取引ID	A	B	C	D	E
T1	0	1	1	1	1
T2	0	1	1	1	0
T3	0	1	0	0	0
T4	0	1	1	1	0
T5	0	0	0	1	0
T6	1	0	1	1	0
T7	0	1	1	1	1
T8	0	1	1	1	0
T9	0	0	1	1	1
T10	1	0	0	1	0

この表から、項目Aは2回しか出現せず、その支持度は0.2、つまり20％に相当することが容易に計算できます。同様に、他の項目の支持度も計算してみます。B — 0.6, C — 0.7, D — 0.8, E — 0.4です。ご覧の通り、Aのみは最低限必要な支持条件を満たしていません。そこで、反単調性の性質に従って、それ以降の処理から除外します。

残った要素から、頻出パターンの候補を作成します。前のステップでは頻出項目を決定しました。このアルゴリズムに従って、候補を2つの項目の集合に決定します。BC, BD, BE, CD, CE, DEです。

あとは、データベース全体を処理して、選ばれた各候補の支持度を割り出します。

取引ID	BC	BD	BE	CD	CE	DE
T1	1	1	1	1	1	1
T2	1	1	0	1	0	0
T3	0	0	0	0	0	0
T4	1	1	0	1	0	0
T5	0	0	0	0	0	0
T6	0	0	0	1	0	0
T7	1	1	1	1	1	1
T8	1	0	1	0	1	0
T9	0	0	0	1	1	1
T10	0	0	0	0	0	0

今回は、すべての候補の支持度が最低支持度の条件を満たしています。 BC — 0.5, BD — 0.4, BE — 0.3, CD — 0.6, CE — 0.4, DE — 0.3です。ただし、いつもこうなるとは限りません。実用的な問題を解く場合、後方によってはより排除されやすくなります。

次に、反復作業を続けます。今回は、3項目の候補セットを作ってみましょう。そのために、前回の反復で選択された頻出パターンを取り出し、1つの要素だけが異なるペアを結合します。4つの候補を決定することができます。BCD、BCE、BDE、CDEです。

アプリオリアルゴリズムによれば、すべての新しい候補の支持度を決定するために、もう一度データベース全体を調べなければなりません。

取引ID	BCD	BCE	BDE	CDE
T1	1	1	1	1
T2	1	0	0	0
T3	0	0	0	0
T4	1	0	0	0
T5	0	0	0	0
T6	0	0	0	0
T7	1	1	1	1
T8	0	1	0	0
T9	0	0	0	1
T10	0	0	0	0

その結果得られた候補の支持値は、BCD — 0.4、BCE — 0.3、BDE — 0.2、CDE — 0.3です。今回の反復では、BDE項目セットは、支持が最低限必要な条件を満たさないため、除外しています。それ以外の候補は、頻出パターンとして考えます。

次の反復では、4つの項目の候補セットをコンパイルします。前の反復で選択されたパターンに基づいて、BCDEの候補を1つだけ作ることができます。ただし、この候補の支持度を計算する前に、その構成要素であるBDEに注目しましょう。この候補は、最低限必要な支持が0.3であるのに対し、支持が0.2しかなかったため、前回の反復で削除されました。したがって、反単調性規則に従い、BCDE候補は0.2より大きい支持を持つことはできませんが、これは最低支持度を下回っています。

他に候補がないため、頻出パターン探索のプロセスを停止し、次のサブプロセスである選択された頻出パターンに基づくルールの決定に移ります。ります。そのために、選択されたパターンを前提部と結論部に分割します。その後、各ルールの信頼度を決定し、必要最小限の信頼度と比較することができます。

集合から各項目について、順次ルールを構築していきます。最初の段階で、Aを使ったパターンをすべて排除した（その支持がMinSup以下）ので、Bを使ったルールの決定を始めます。

選択されたパターンから、分析した項目を含むものをすべて判定してみましょう。パターンから項目Bを抜き出して結論部とし、残りの部分を前提部とします。また、作成された各ルールの信頼度を決定します。

ルール信頼度は、前提部が形成されたときに、どの程度の確率で結論部が出現するかを示すものです。それを判断するために、データベース全体を再確認する必要はありません。頻出パターン選択段階であらかじめ計算しておいた前提部の支持度に、フルパターンの支持度を割り当てるだけです。

パターン	前提部	支持	ルール
BC (0.5)	C (0.7)	0.71	C -> B
BD (0.4)	D (0.8)	0.50	D -> B
BE (0.3)	E (0.4)	0.75	E -> B
BCD (0.4)	CD (0.6)	0.67	CD -> B
BCE (0.3)	CE (0.4)	0.75	CE -> B

ルールD→B、ルールCD→Bは最低支持度の0.7を満たしていないため、除外しました。

他のルールも同様に決定します。

パターン	前提部	支持	ルール
BC (0.5)	B(0.6)	0.83	B -> C
CD (0.6)	D (0.8)	0.75	D -> C
CE (0.4)	E (0.4)	1.00	E -> C
BCD (0.4)	BD (0.4)	1.00	BD -> C
BCE (0.3)	BE (0.3)	1.00	BE -> C
CDE(0.3)	DE(0.3)	1.00	DE->C
CD (0.6)	C (0.7)	0.86	C -> D
DE(0.3)	E (0.4)	0.75	E->D
BCD (0.4)	BC (0.5)	0.80	BC -> D
CDE(0.3)	CE (0.4)	0.75	CE -> D

我々は、アソシエーションルールのマイニングのための最も有名なアルゴリズムの11つであるアプリオリを見てきました。しかし、その簡便さと人気の高さにもかかわらず、実際にはほとんど使われていません。これは、検討した手法のボトルネックが、頻出パターン候補の支持度を評価するために必要なデータベースの多重反復処理であるためです。分析対象となるデータベースの量が増えれば増えるほど、これは問題になってきます。この問題は、次のアルゴリズムで効率的に解決されます。任意の容量、任意の数の分析項目があるデータベースに対して、わずか数回の反復処理しか必要としません。

3.FP-Growthアルゴリズム

ここで、アソシエーションルールを見つけるための最速アルゴリズムの一つを例に、上記の問題の解決方法を考えてみます。FP-Growth(FrequentPattern-Growth)。アルゴリズムの構造上、訓練標本の全要素の完全な反復は、その実行過程でわずか2回しかおこなわれません。この2回を除いて、アルゴリズムは訓練標本を呼び出すことはありません。

先に検討したアソシエーションルールマイニングアルゴリズムと同様に、FP-Growthは条件付きで2つのサブ問題に分割することが可能です。

1. 頻出パターンを見つけます。この例では、この段階をFP木の構築と呼んでいます。
2. タスクの特定

アルゴリズムは、まずランダムな項目を排除することから始まります。そのために、前のアルゴリズムと同様に、訓練セット全体に対して最初のパスを実行し、各項目の支持度を計算します。その後、頻度がMinSupより小さいものをすべて削除します。

残りの項目は、支持度の高い順に並んでいます。上記の例では、以下のようなシリーズになります。

D (0.8) -> C (0.7) -> B (0.6) -> E(0.4) 

次に、FP-treeを成長させます。そのためには、訓練標本に対して2回目のパスを実行します。各トランザクションでは、支持度の降順に並べられた頻出項目のみを取り出し、木に経路を構築します。したがって、支持度の最も高いノードは木の根に、最も低いノードは葉になります。また、各ノードに対してカウンタを作成します。最初の反復では，カウンタ値を1（または1/N，Nは訓練標本の大きさ）に等しくします。

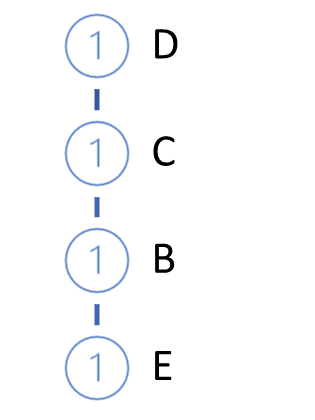
そして、データベースから次のトランザクションを取得します。同じように経路を作り、私たちの木に追加します。そのために、木の根から、すでに枝が存在する経路を確認します。根からの経路を繰り返す場合は、既存のノードのカウンタを増やすだけです。新しい部分には、枝を作成します。

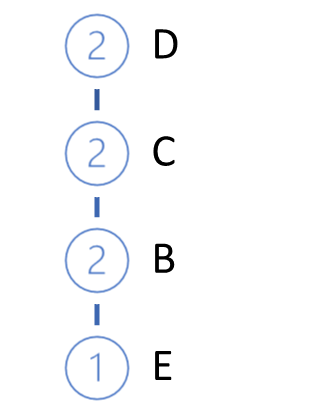
この反復のサイクルは、訓練セット全体の反復が完了するまで繰り返されます。上記の例では、以下のようなFP-treeが得られます。

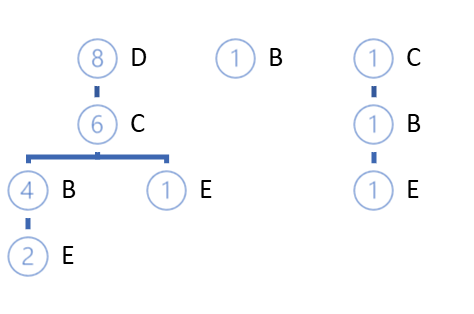
高い確率で、根そのものとは異なる経路を見つけることができます。2つのオプションが考えられます。

• 森をつくる
• 選択範囲全体を束ねる、ある種の根ノードを作成します。

当然ながら、FP木の成長プロセスの初期には、ほとんどの場合、新しいノードが作成されることになる。しかし、訓練標本に沿って移動する過程で、新しい枝を作らずに既存のノードのカウンタを増やすことに行き着きます。このアルゴリズムの具体的な特徴は、木を構築する過程で、学習サンプルを、データベースにアクセスすることなく、コンピュータのRAM内で簡単に操作できるサイズに圧縮できることです。

さらに、ルールの定義に関連する作業は、元のデータベースを使用せずに、FP木のみを使用して行われます。

ルールは、すべての項目に対して、支持度の高い順に構築されます。

最初の段階で、指定された頻度より低い頻度の項目はすでに排除されており、現在、木には頻繁に出現する項目のみが含まれています。また、木を構成する際に、降順に並び替えています。支持度の低い項目は葉になります。

そこで、支持度の低いものから順にルールを決めていくために、葉から根へと移動していきます。ここでは、まだ明示されていない因果関係をたどることができます。このアルゴリズムでは、支持度の低い項目は、支持度の高い特徴の組み合わせの結果として現れると仮定しています。

ただし、ルール定義のアルゴリズムに話を戻しましょう。最下位の支持項目を取り上げ、この項目につながるFP-treeの全経路を決定します。経路を選択する際には、まず、経路の項目からパターンを形成する際に、目的の項目の出現頻度に注目します。経路選択の基準は、前ノードの支持に対する項目の支持の比率です。この比率は、ルールの最小信頼度より小さくなってはなりません。

上記の例では、最も低い支持度をEで示しました。FP-treeの3つの経路がそれにつながります。DCBE（0.2）、DCE（0.1）、CBE（0.1）です。どの経路も最低限必要な支持度を満たしていません。そのうち2つは最低信頼度の要件を満たしていません。したがって、Eに関するルールを作成することはできません。なお、このことはアプリオリアルゴリズムで得られた結果でも確認されています。 

Eの葉を削除して、次のようなFP-treeの表示を得ることができます。

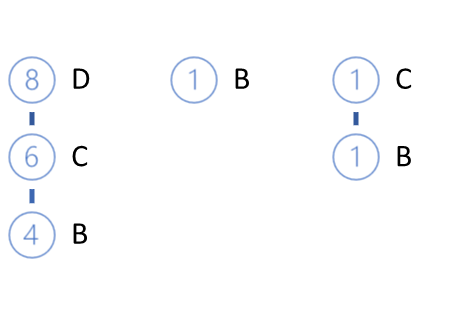
次に分析するのはB要素です。左派の中では最も低い支持度です。3つの経路があります。DCB（0.4）、B（0.1）、CB（0.1）です。

選択された支持経路において、分析された項目の前の各項目は、与えられた経路において分析された項目の支持が割り当てられます。

選択された経路をもとに、参加項目のリストを形成し、それぞれの支持度を決定します。なお、支持度は、元の訓練データセットのレコード総数に対する、選択された経路における項目出現数の比率として決定されます。したがって、各項目の新たな支持度は、初期項目の支持度や（ルールを決定している）分析項目の支持度を超えることはできません。

ここでも、支持度が最低限に満たないものは削除しています。残りの項目を支持度の高い順に並べます。

この例では、C（0.5）、D（0.4）となっています。

なお、今回は選択した経路のみでの計算をおこなったため、当初とはかなり異なる結果になる可能性があります。この要因の結果、いくつかの項目が削除され、新しい階層での順序が変更されることがあります。

さらに、新しい階層にしたがって、選択した経路を用いて新しいプライベートな木を構築します。木構築のアルゴリズムはFP-treeの構築と変わりません。

構築されたプライベート木の枝は、ルールの前提部となり、その結果、分析項目の結論部となります。

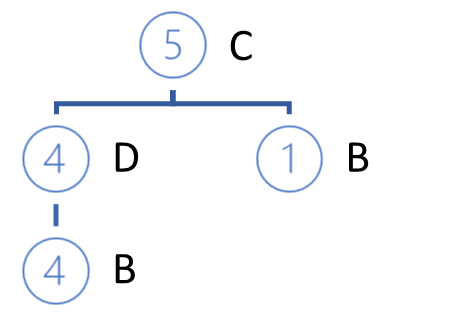
プライベート木を構築した後、元のFP木から分析対象項目のノードを削除します。その仕掛けは、最小限の支持で項目を分析したことです。つまり、この項目を含むすべてのノードがFP-treeの葉となります。したがって、それらを削除しても、他の項目の経路には影響しません（少し前に、因果関係を述べました）。

また、分析した特徴を徐々に削除していくことで、のFP木を徐々に減らしていきます。これにより、他の項目の分析において、さらに検索するためのデータ量を減らすことができます。これは、アルゴリズム全体の性能に影響します。

同様に、FP木の元の階層にある各項目に対してルールを構築します。

FP木に少なくとも1つの根ノードが存在する項目についてのみ、ルールを構築できることに留意されたい。前提部として使うものがないため、根のルールを作ることはできません。もちろん、潜在的な顧客がスーパーマーケットを訪れる場合は別です。スーパーマーケットに来たのだから、何か買うでしょう。おそらく、これがベストセラーのひとつになるのでしょう。ただし、これは今回検討しているアルゴリズムの範囲を超えています。

結論

今回は、教師なし学習法で解くもう1つのタイプの問題であるアソシエーションルールマイニングについて考えました。これまで、2つのアソシエーションルールマイニングアルゴリズムについて述べてきました。アプリオリとFP-Growthです。ただし、他にも様々なアルゴリズムがあります。残念ながら、1回の記事ですべてをカバーすることはできません。しかも、理論的な側面しか提供されていません。次回は、MQL5を用いたアソシエーションルールマイニングアルゴリズムの実用的な構築について考えてみたいとおもいます。また、実用的な取引タスクに適用してその効率を評価します。

参考文献リスト

1. ニューラルネットワークが簡単に（第14部）：データクラスタリング
2. ニューラルネットワークが簡単に（第15部）：MQL5によるデータクラスタリング
3. ニューラルネットワークが簡単に（第16部）：クラスタリングの実用化
4. ニューラルネットワークが簡単に（第17部）：次元削減
5. アソシエーションルールのマイニングアルゴリズム
6. 候補を生成しない頻出パターン