Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal

Sumário

• Introdução
• Analisando a aplicabilidade dos fractais ao trading
• Base teórica para a construção de um fractal universal
• Escrevendo código para implementar um fractal universal
• Estabelecendo a primeira fórmula com base num fractal simétrico
• Avaliando o desempenho da fórmula criada para todos os argumentos positivos e reais
• Fractal avançado como resultante do fractal universal
• Resumindo os resultados
• Conclusão
• Links

Introdução

No último artigo, vimos os fundamentos da teoria da probabilidade. Esta nos ajudará a entender melhor as peculiaridades do uso de funções fractais para resolver tarefas relacionadas com o trading. Por isso, hoje mostrarei algumas funções fractais autossuficientes capazes de descrever os processos de precificação de que precisamos. Como resultado, conseguiremos generalizar, simplificar o material estudado anteriormente e plantear algumas fórmulas que nos ajudarão a encontrar respostas claras a questões carentes de avaliações quantitativas. 

Analisando a aplicabilidade dos fractais ao trading

Continuarei com a ideia de generalizar os resultados obtidos no artigo anterior e de apresentar o seguinte material da maneira mais compacta e universal possível. Se tomarmos o exemplo de como construir um fractal visto no último artigo, será de pouca utilidade em termos práticos, o que nos importa, acima de tudo, é quais regras para construir essas estruturas nós somos capazes de determinar. Como se viu, essas regras se mantêm inalteradas para três tipos de fractais:

1. Fractal com bordas simétricas
2. Fractal com bordas assimétricas
3. Fractal com borda superior ou inferior

Se organizarmos nossas ideias, fica claro que esses fractais podem ser usados para descrever os seguintes processos:

• Simulação acelerada de negociação com capacidade de avaliar a probabilidade de surgimento de diferentes cenários, considerando as restrições de depósito (uma vez que a borda inferior pode representar o nível do depósito em que continuar a negociar será impossível)
• Estimativa do número médio de etapas dentro do fractal (por exemplo, pode-se estimar quantas ordens ocorrerão em média antes de obtermos o lucro ou a perda desejados)
• Estimativa dos valores médios totais para cada etapa (por exemplo, pode-se calcular o tempo médio que a posição estará colocada, com base nas estatísticas para uma posição menor, o processo reverso também é possível; além disso, o valor se refere ao tamanho dos stops em pontos ou em diferença de preço )
• Estimativa da rentabilidade das opções com base num fractal com uma única borda
• Possibilidades não consideradas

Base teórica para a construção de um fractal universal

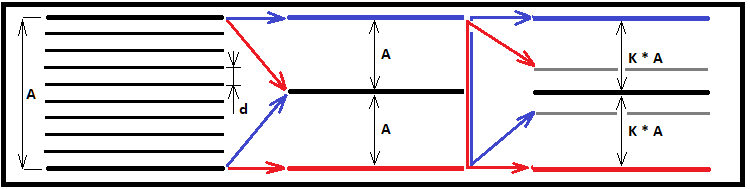
Começaremos pegando as regras de construção que estabeleci no artigo anterior e complementando-as para compreender plenamente como é construído um fractal. Adicionalmente, convém mencionar que notei um pequeno erro, nas minhas fórmulas, que não permitia conseguir a assimetria das bordas tanto para cima quanto para baixo. Porém, deduzi as fórmulas de forma correta e elas funcionam para qualquer fractal. E, na verdade, consegui obter uma função para a implementação de qualquer fractal. Todos os fractais possíveis são um caso especial de um fractal geral. Se tomarmos os três tipos de fractais que defini acima, verifica-se que as condições do fractal geral para a implementação destes três casos especiais assumirão a forma:

1. m = n & [ m > s & n > s ]
2. ( m > n || n > m )  & [ m > s & n > s ]
3. ( m > S && n <= S ) || ( n > S && m <= S )

Esses três tipos de fractais podem ser representados como um esquema:

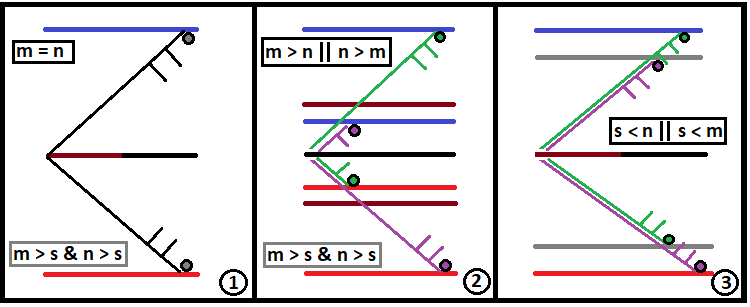
Idealmente, "S" deve tender para o infinito. Não descrevi as variáveis a seguir no artigo anterior, mas vou fazer isso aqui para obter uma visão ampla de como usar a fórmula geral para obter casos especiais. Um fractal é uma função que opera com base no princípio de reação em cadeia, como acontece com uma bomba atômica. Se definirmos uma reação em cadeia com muita profundidade, o computador poderá não ser capaz de lidar com os cálculos, no melhor dos casos, ele simplesmente ficará processando tais cálculos por um longo tempo, quer em questão de minutos, horas ou até dias. Com isso em mente, para iniciar adequadamente uma reação em cadeia no fractal, é necessário encontrar dois valores fundamentais:

• Half - metade da largura do canal
• Middle - valor "U" que corresponde à linha do meio

O valor "Half" para todos os três casos, que determinamos no artigo anterior, é calculado de forma muito simples usando a média aritmética de "m" e "n":

• Half = ( n + m ) / 2

Para obter o segundo valor, já são necessárias três opções lógicas, sendo que a primeira e a segunda podem ser combinadas, logo precisamos considerar apenas duas opções:

1. n >= m
2. n < m

Além disso, dado que o eixo "U" está direcionado "para cima", o valor "n" é a parte superior do canal e o valor "m" é a parte mais baixa; obtemos duas relações para ambos os possíveis casos de definição de "m" e "n":

1. Middle = Half - m
2. Middle = - ( Half - n )

Esses valores serão passados para a própria função fractal, pois sem eles é impossível implementar a lógica de ramificação interna, que descrevi no artigo anterior. O protótipo desta função ficará assim:

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Como se pode ver, para a inicialização correta do fractal, é necessário passar cinco valores obrigatórios:

1. Half - metade da largura do canal
   
2. Middle - valor "U" que corresponde à linha do meio
   
3. m - número de etapas até a borda inferior
4. n - número de etapas até a borda superior
5. s - número máximo permitido de etapas em qualquer direção para uma única cadeia

Os outros valores são nomeados em letras maiúsculas para deixar claro que são dinâmicas e serão completamente diferentes em cada nível fractal individual. Antes de tudo, vamos defini-los:

• S - número de etapas que se acumularam na atual cadeia de probabilidades para transferência para o próximo nível fractal
• U - remoção de final-de-cadeia do ponto-inicial-de-cadeia para transferência para o próximo nível fractal
• P - produto total das probabilidades de toda a cadeia com base no esquema de Bernoulli, para transferência para o próximo nível fractal

A partir disso, fica claro que para executar o fractal, precisaremos passar os valores corretos para a função:

• S = 0 (dado que é o início e ainda não houve nenhuma etapa)
• U = 0 (pelo mesmo motivo, porque estamos no início da cadeia)
• P = 1 (dado que é o elo zero e todas as cadeias que saem dele devem constituir um grupo completo)

Vamos terminar de formular as regras gerais para fractais que simulam precificação ou negociação, para isso reescrevemos brevemente as regras que foram obtidas no artigo anterior. Essas regras são necessárias para as partes internas do fractal. As regras são baseadas em algumas fórmulas indispensáveis para etapas iguais:

• f = u + d  — este valor, neste caso, é o número de etapas da futura árvore de combinação (o tamanho é determinado pela distância até a borda mais próxima do corredor fractal)
• s = u - d  — número de etapas finais para cima, expresso em termos de segmentos decrescentes e crescentes

Acabamos de determinar o que integraremos num loop ao longo de "u". Além disso, usaremos o valor "s" como um novo "u" que passaremos para o próximo nível fractal, se o número de etapas restantes permitir. Para fazer isso, teremos que definir uma fórmula para "u" que não contenha "d". Isso pode ser feito facilmente expressando "d" da primeira equação e substituindo-o na segunda:

• s = 2*u - f

Mas esse número poderia ser aceito como um novo valor "U" para transferência posterior se o "U" atual fosse igual a zero, portanto, esse "s" deve ser adicionado a "U" e, assim, obteremos um novo valor para transmissão posterior:

• NewU = s + U  - nosso novo "U" para transferência para o próximo nível fractal

Conforme já definido no último artigo, esta expressão assume três valores com base nos possíveis valores de "f". Peguei o diagrama do artigo anterior e o retrabalhei para que ninguém mais tivesse dúvidas:

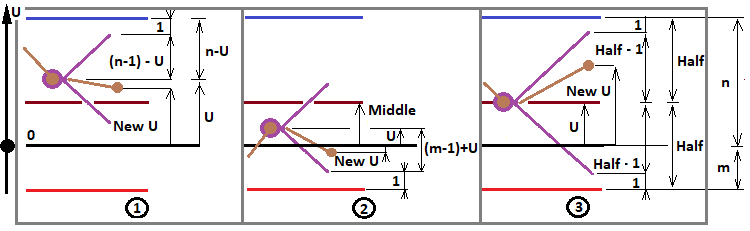
Este diagrama é muito apropriado neste caso, uma vez que agora estamos empenhados em determinar todas as configurações fractais possíveis que podem ser úteis para resolver a maioria dos nossos problemas. Com base neste diagrama, definimos três casos para "f":

1. f = ( n - 1 ) - U
2. f = ( m - 1 ) + U
3. f = Half - 1

Esses três casos surgem quando são atendidas as condições apropriadas:

1. U > Middle
2. U < Middle
3. U = Middle

Resta apenas descrever os dois últimos valores para transferência para o próximo nível fractal e esclarecer separadamente as questões de coleta de números dentro do fractal. Tais valores são calculados da seguinte forma:

• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i)  — nossa nova probabilidade de cadeia "P" para transferência para o próximo nível fractal
• NewS = S + f = S + (floor(Mid) - 1) — nosso novo "S" para transferência para o próximo nível fractal

Antes de começar a coletar números numa variável comum, precisamos entender que a coleta de números deve ocorrer num bloco semelhante, mas com a única diferença de que ocorre apenas uma etapa e, portanto, o esquema de Bernoulli não é mais necessário. A ordem dos operadores não é importante, eles apenas precisam estar no mesmo bloco. A coleta de números só é possível nas situações "1" e "2", mas com alguns esclarecimentos:

1. U = n - 1
2. U = - ( m - 1 )

Para o primeiro caso, os três valores anteriores serão calculados muito mais facilmente, já que damos apenas uma etapa:

• NewU = U - 1
• NewP = P * p
• NewS = S + 1

Para o segundo caso tudo é semelhante, com algumas ressalvas:

• NewU = U + 1
• NewP = P * ( 1 - p )
• NewS = S + 1

Também é muito importante dizer que após generalizar os fractais, cada um deles é dividido em 2 tipos:

• Fractal de cálculo da probabilidade total de cruzar a borda superior do corredor
• Fractal de cálculo da probabilidade total de cruzar a borda inferior do corredor

Por sua vez, cada um deles corresponde a outro tipo vinculado ao fractal de partida:

• Fractal para calcular o número médio de etapas para cruzar a borda superior
• Fractal para calcular o número médio de etapas para cruzar a borda inferior

Na verdade, todos esses quatro tipos de fractais diferem apenas na forma dos números somados. No caso de coleta de probabilidades, apenas podem ser somados "P*p" e "P*(1-p)". Para considerar os outros dois fractais, precisamos de variáveis adicionais para transferência para os próximos níveis fractais. A questão é que, em tais fractais, usamos etapas do mesmo tamanho, mas na direção oposta, e suas probabilidades são "p" ou "1-p" por causa da integridade do grupo. Mas, nos casos em que "p" não é igual a "0,5", esse fato significa automaticamente que se trata de dois eventos completamente diferentes, que podem ter características completamente diferentes. Por características, quero dizer um conjunto de algumas variáveis aleatórias que correspondem a um determinado evento. Uma desses valores é a "vida útil da posição". Pode haver quantos forem necessários e, se necessário, podemos considerá-los da mesma forma que o tempo. O mais interessante é que ao considerarmos um número simples de etapas podemos simplificar o estudo de todos esses valores. Nesse caso, os números somados ficarão assim:

1.  P * p * NewS
2.  P * ( 1 - p ) * NewS

Pode-se ver que as probabilidades são multiplicadas pelo próprio número de etapas nesta cadeia de etapas terminal; e esta é uma fórmula para casos em que as etapas para cima e para baixo são igualmente prováveis. Em casos alternativos, teremos que descrever as etapas para cima e para baixo com dois fractais diferentes ou fornecer uma estrutura para armazenar os dois números. No segundo caso, a função fractal retornará não um número, mas, sim, um contêiner com dados. O contêiner é independente e não requer expansão. Fui um pouco além e preparei um contêiner desse tipo que nos permite armazenar todos os parâmetros necessários de que possamos precisar e, a esse respeito, não precisaremos descrever várias funções com o mesmo tipo de código. Em vez disso, combinei todas essas funções numa única que pode descrever todos os parâmetros de que podemos precisar. O tipo de fractal e a tarefa que ele resolve dependerão diretamente dos parâmetros de entrada da função. Para expandir essa abordagem, precisamos substituir a variável "S" e seu equivalente "NewS" pelos seguintes valores:

1. SU - todas as etapas para cima tomadas da cadeia de probabilidade selecionada
2. SD - todas as etapas para baixo tomadas da cadeia de probabilidade selecionada
3. NewSU e NewSD - para transferência para o próximo nível fractal
4. SU + SD = S

Esses valores precisam ser determinados da mesma forma que definimos "S". Para o caso quando "U > Middle":

• NewSU = SU
• NewSD = SD + 1

Para o caso quando "U < Middle":

• NewSU = SU + 1
• NewSD = SD

Além disso, para a atualização final do fractal em si, precisamos de seis valores:

1. UpperMidSDown - número médio provável total de etapas para baixo antes de atingir a borda superior
2. UpperMidSUp -  número médio provável total de etapas para cima antes de atingir a borda superior
3. UpperSummProbability - probabilidade de cruzar a borda superior
4. LowerMidSDown - número médio provável total de etapas para baixo antes de atingir a borda inferior
5. LowerMidSUp - número médio provável total de etapas para cima antes de atingir a borda inferior
6. LowerSummProbability - probabilidade de cruzar a borda inferior

Os valores "1", "2", "4", "5" refletem a soma dos produtos do número correspondente de etapas e sua probabilidade. Esses valores não têm sentido por si só, pois eles são componentes de fórmulas cujos valores são mais úteis e que serão discutidos a seguir. Os valores "3", "6" são as probabilidades das hipóteses de cruzar duas bordas que formam um grupo completo. Juntas, todos esses valores tornam possível determinar muitas coisas.

Escrevendo código para implementar um fractal universal

Para a inicialização correta do fractal, precisamos de uma função que execute todas as operações preparatórias. Criei a implementação deste algoritmo ao estilo MQL5:

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Depois de calcular o fractal, a função retorna nosso contêiner com todos os dados de que podemos precisar:

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

Este contêiner fornece uma sobrecarga do operador "+ =" para mesclar duas estruturas iguais, isso é útil para a função principal. Bem, eis a função fractal:

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

O código foi testado no MetaTrader 5 e funciona muito bem. Esta lógica pode ser expandida se desejarmos, pois ainda existem muitas possibilidades adicionais, mas neste caso não gerei os parâmetros de entrada desta função, porque existe código suficiente para meus propósitos. Estude seu código cuidadosamente e verá que os princípios matemáticos descritos acima são totalmente atendidos. Como se pode ver, mesmo um pequeno trecho de código pode fazer maravilhas. Sempre aderi ao fato de que o código deve conter o máximo de lógica e matemática possível, isso é exatamente o que será útil, apenas fazer código por fazer código não faz nenhum sentido, mesmo um bonito é inútil se não puder ser usado para o fim a que se destina. Nosso objetivo principal é que seja útil ao negociar. Como prova, vou mostrar o log:

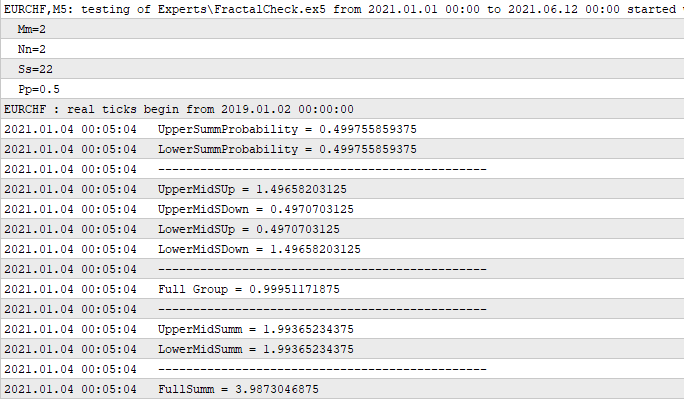
Neste caso, pode-se ver que criei um Expert Advisor simples que calcula todo o fractal no primeiro tick recebido. Isso acontece apenas uma vez, já que não precisamos de cálculos repetidos, pois eles darão o mesmo resultado. Os primeiros seis números são parte do contêiner e os demais são derivados deles. Não formulei todas as derivadas, mas apenas as mais importantes, o que será útil para entender que com a ajuda dessas seis variáveis podemos obter todos os outros dados que serão de nosso interesse. Por exemplo, vamos dar uma olhada em "Full Group". Não é à toa que tem esse nome, porque a soma das probabilidades de duas hipóteses incompatíveis de cruzar uma das fronteiras de acordo com nossos cálculos anteriores deve ser igual a um, o que nosso código confirma com sucesso. A seguir estão dois números idênticos, que são a soma de "1", "2" e "3", "4". E o último número já é a soma dos dois penúltimos números e representa o número médio de etapas que a cadeia percorrerá. Não foi à toa que defini exatamente esses parâmetros de entrada para a função de início, onde "m" e "n" são iguais e simétricos, e o porquê ficará claro a seguir.

Estabelecendo a primeira fórmula com base num fractal simétrico

Se você olhar de perto o resultado do log, podemos ver que o número médio de etapas pelas quais a cadeia passará tende para o valor "4". Além disso, é claro que dobramos o corredor em relação a uma única etapa. Teremos uma etapa única se definirmos "n" e "m" igual a um. Em outras palavras, se quisermos calcular o número médio de etapas num corredor que é composto de corredores menores, de modo que um número inteiro de corredores menores cabem num novo corredor e este último também é simétrico, então podemos assumir que:

• P[n] = P[n-1] * 2  - expressão recursiva para a largura em etapas do novo corredor, com base na largura do antigo corredor menor do qual é composto o novo corredor
• S[n] = S[n-1] * 4 - expressão recursiva para calcular o número médio de etapas num novo corredor, expresso em termos do número médio de etapas num corredor menor

Se aceitarmos "P[0]=1" e "S[0]=1" e, logo, iniciarmos a numeração dessa recursão a partir do índice "0", será fácil adivinhar que essa recursão pode ser representada como duas séries muito semelhantes:

• P[n] = 2^n , n = 0 ... + infinity
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

Se olharmos atentamente para a primeira série e transformarmos corretamente a segunda série, verifica-se que a segunda série pode ser expressa por meio dos elementos da primeira. Em outras palavras, é formada a dependência S = S(P) = P^2. Até agora, ela só era verdadeira para dobrar recursivamente a largura do corredor. Pessoalmente, quando vi essa fórmula, surgiu a ideia de verificar se ela era importante para qualquer número arbitrariamente grande de "n" e "m". Este é um segundo passo lógico para tomar aquele "n=3", "m=3" e calcular os mesmos valores. Ao verificar este fato, descobrimos que para esses parâmetros de entrada verifica-se que o número médio de passos tende para o número "9". A propósito, você também pode verificar tudo isso usando o código que dei acima ou os programas MathCad 15 que também irei anexar ao artigo. É fácil adivinhar que podemos compor exatamente a mesma série para esses parâmetros e fazer as mesmas coisas:

• P[n] = 3^n , n = 0 ... + infinity
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Como se pode ver nos resultados, obtivemos a mesma relação "S=S(P)=P^2". Podemos fazer as mesmas coisas para todos os outros possíveis cenários para dividir o intervalo, mas isso não é necessário. Isso significa que, se sabemos, por exemplo, a vida útil média de um preço num corredor simétrico, podemos calcular a vida útil média de um preço em qualquer outro corredor. Podemos calculá-lo assim:

• S = S0 * K^2 - número médio de etapas no novo corredor
• T = S * T0 - vida útil média do novo corredor
• T = T0 * K^2- vida útil média do novo corredor expressa em termos do tempo médio de outro corredor (obtemos considerando S0 = 1 )
• S0 - número médio de etapas no corredor antigo
• T0 - tempo médio de uma etapa do corredor antigo
• P = K * P0  --> K = P/P0 - número de vezes que o novo corredor é maior que o antigo
• P - largura do novo corredor
• P0 - largura do antigo corredor

Agora podemos testar essa hipótese usando o MathCad 15. Primeiro, vamos verificar nossas suposições sobre a dependência quadrática:

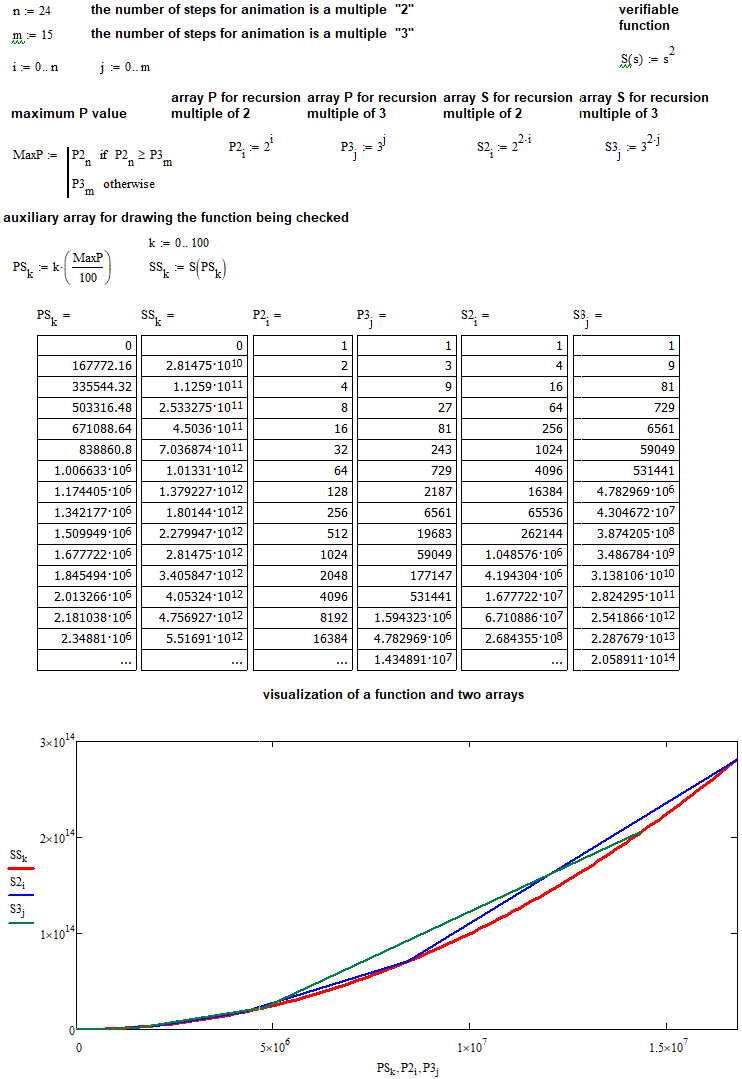
Agora, eu acho, tudo está muito claro e fácil de entender.

Avaliando o desempenho da fórmula criada para todos os argumentos positivos e reais

Acontece que a fórmula funciona para todos os inteiros "P", mas não está claro se ela pode ser usada para o caso de "K" fracionário. Para ter um "K" fracionário, devemos mostrar esperteza. Imagine que temos um corredor de preços com um tempo médio de vida conhecido e existe outro corredor em que ele cabe "N" vezes, mas o tempo médio de vida deste último ainda é desconhecido. Mas abaixo podemos encontrá-lo usando a mesma fórmula. Segundo essa lógica, verifica-se que:

• T = T0 * N^2 ---> T0 = T / N^2
• T - tempo do nosso corredor e cujo tempo médio é conhecido
• T0 - tempo médio do corredor menor a partir do qual é feito nosso corredor

Ou seja, verifica-se que podemos encontrar o tempo de um corredor menor, e vamos precisar dele para calcular o tempo do terceiro corredor com um fator de aumento fracionário. Uma vez que encontramos o tempo médio do corredor menor, agora podemos encontrar sua largura em pontos:

• d = P / N

Depois disso, podemos saber quantos desses corredores inteiros cabem no corredor ampliado por meio da seguinte proporção:

• Smin = MathFloor( K * P / d ) = MathFloor( K * N )
• Lim( N --> +infinity ) [ K * N/MathFloor( K * N ) ] = 1

Percebe-se que a largura do corredor é reduzida e não afeta o resultado. A segunda linha contém uma proporção muito importante que permitirá saber o que fazer a seguir. Ela indica que ao dividir o corredor original em tantos segmentos quanto possível, podemos esquecer a parte fracionária que é descartada como resultado da execução da função "MathFloor". O limite que tende à unidade nos sugere isso. Se ficarmos confusos com essa imprecisão, podemos encontrar outro valor:

• Smax = MathFloor( K * P / d ) + 1 =  MathFloor( K * N ) + 1 = Smin + 1

Agora está claro que o verdadeiro valor "K * N" se encontra entre os valores "Smin" e "Smax", e quando "N" tende ao infinito, teremos dois corredores demasiado semelhantes e seus tempos médios também tenderão um para o outro, já que seus tamanhos diferem em apenas 1 segmento. A partir disso, conclui-se que o tempo médio do corredor de que precisamos será determinado com mais precisão pela média aritmética do tempo médio desses corredores:

• T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 =  T0 *( Smin^2 + Smax^2 ) / 2
• T1 - tempo médio do corredor que precisamos determinar

Para ilustrar, criei o seguinte:

Agora, tendo formulado uma expressão alternativa para o cálculo do tempo de vida do corredor, podemos comparar o resultado com o valor da função para inteiros "K", substituindo o "K" fracionário. Se os números na saída de duas expressões coincidirem, concluiremos que a função encontrada para inteiros "K" é viável para absolutamente quaisquer inteiros e números fracionários no intervalo "0 ... +infinity". Vamos fazer a primeira verificação com "N = 1000", acho que essa divisão será suficiente para ver a identidade de dois números, se for o caso:

Como se pode ver, os dois números são quase idênticos, e essa identidade, em teoria, deveria ser maior quanto maior o valor de "N" que usamos. Isso também pode ser provado assumindo o seguinte:

• Lim( N --> +infinity ) [  (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 )  ] = 1

No numerador desse limite está nossa expressão aproximada para o cálculo do tempo médio do novo corredor, já no denominador está uma expressão que presumivelmente descreve com precisão o mesmo valor. Fiz uma função simples que realiza todos os mesmos cálculos que foram feitos na imagem anterior, apenas para toda a faixa do número "N", começando com o número "1". Agora podemos ver o resultado deste programa:

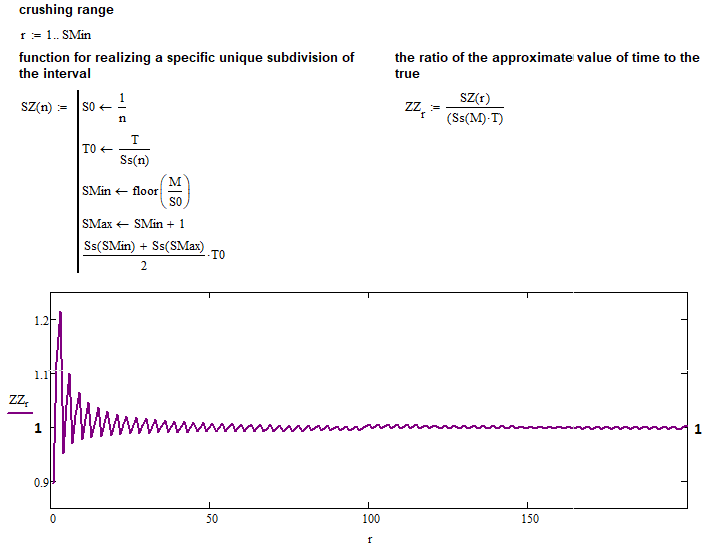
Como se pode ver, todas as suposições estão totalmente confirmadas e a função que encontramos para todo "K" é absolutamente viável para qualquer "K" positivo. Agora temos apenas uma fórmula única, mas muito útil, sobre a qual podemos construir muitas coisas, incluindo mais matemática para uma descrição completa de todo o fractal universal.

Fractal avançado como resultante do fractal universal

Para exemplificar como implementar um fractal universal, podemos tomar um com apenas uma borda, pegando, digamos, "n=1", "m ---> +infinity", "s = m+1", "p=0.5". Até agora, estamos considerando fractais com etapas igualmente prováveis em ambas as direções, o que é aplicável apenas ao passeio aleatório, mas este fractal fornece todas as possibilidades. Para avançar para uma análise mais profunda de uma estrutura tão complexa, é necessário primeiro considerar os fundamentos que nos ajudarão com isso, além disso, já nesta fase temos fórmulas muito úteis e interessantes e conclusões fundamentais sobre esses processos fractais. Tendo executado este fractal com diferentes valores de "s", obtive os seguintes dados:

• s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
• s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
• s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
• s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882

Um novo aumento no número de etapas permitidas tem efeitos no tempo de computação, ou seja, o tempo de computação aumenta tanto que podemos esperar horas e dias, isso certamente não é surpreendente, mas se olharmos para a velocidade à qual a probabilidade média total aumenta, podemos ver que a convergência desta série não é possível usando este tipo de fractal. Mas acontece que, com base na fórmula que definimos acima, já será possível estimar essa convergência usando uma forma de fractal completamente diferente, mas muito útil, que nos dará uma resposta a essa pergunta. Além disso, como se verá, este tipo de fractal poderá nos ajudar a calcular o tempo para a estratégia "Carry trade". Primeiro, mostrarei uma ilustração e, em seguida, contarei o que há nela:

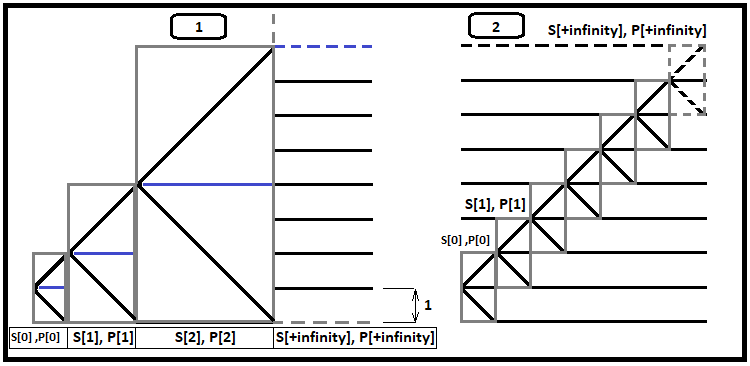
Imagine que o processo de precificação comece a uma etapa de distância da borda, não importa onde ela esteja, para cima ou para baixo. Na figura, peguei o exemplo com a borda inferior, porque é melhor percebido. Vamos dar uma olhada no primeiro fractal. Cada caixa cinza contém dois cenários para o desenvolvimento de eventos:

1. Borda superior do retângulo atingido
2. Parte inferior do retângulo atingido

Também podemos ver que, quando é alcançada a borda superior do corredor, neste mesmo ponto é iniciado automaticamente um novo fractal maior e assim por diante até o infinito. Se considerarmos este processo da mesma forma que num fractal universal, não veremos nada mais do que as mesmas cadeias de probabilidades, mas agora temos uma fórmula que diz qual o número médio de etapas que ocorrerá num determinado corredor simétrico com base na quantidade de etapas que cabem nele (agora entendemos que consideramos como uma etapa apenas um corredor menor que pode ser aninhado no de origem).

Acontece que agora não precisamos considerar todo o fractal para calcular o número médio de etapas, mas apenas precisamos aplicar a fórmula derivada a cada um desses fractais e considerar como uma etapa não o mesmo valor, mas, sim, o atingimento da borda superior ou inferior do próximo fractal aninhado. Deste modo, podem ser elaboradas cadeias probabilísticas - o que será muito simples. A probabilidade de atingir a borda no primeiro fractal "P[0]" será igual a "0,5", acho que isso é óbvio - isso significa que houve um segundo caso em que tivemos que criar o próximo fractal, e em que também esperamos que o preço chegue à borda. Pode-se ver que esses eventos estão aninhados mutuamente, e todas essas cadeias também formam um grupo completo.

Acontece que a probabilidade de atingir a borda no segundo fractal "P[1]" é igual ao anterior, mas multiplicada pelo mesmo "0,5", verifica-se que este processo pode ser continuado indefinidamente, e, também podemos determinar o número médio de etapas iniciais, com base na fórmula derivada e as probabilidades dessas cadeias. Para fazer isso, primeiro definimos uma fórmula para a probabilidade de cada cadeia individual, levando em consideração que o número médio de etapas para cruzar as bordas superior e inferior do fractal é idêntico. Acontece que:

• PUp = PDown = P - razão que mostra que a probabilidade de tocar as bordas superior e inferior de um fractal é igualmente provável para todos os limites de todos os fractais aninhados
• P[j] = 0.5^(j+1) , j = 0 ... + infinity- probabilidade de que aconteça a cadeia "j"
• S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ),  i = 1... + infinity - fórmula recorrente para calcular a probabilidade média total de etapas para todos os níveis fractais (com  S[0] = 1*0.5 = 0.5)
• F(K) = K^2 - nossa fórmula para calcular o número médio de etapas
• D(i) = 2^i - número de etapas que se encaixam no próximo nível fractal
• S[i-1]/P[i-1] - número médio de etapas no ramo não considerado remanescente, desde que o ramo atual tenha ocorrido (afinal, devemos levar em consideração aquelas etapas que estiveram antes disso, além do fractal aninhado atual)
  

O segundo fractal é na verdade idêntico ao primeiro, no sentido de que as probabilidades de cadeias são idênticas, ou seja, a matriz "P[]". E por que é necessário? Imagine que temos a estratégia "Carry Trade". Acontece que, para avaliar a rentabilidade, precisamos entender que temos duas contas, uma swap e outra livre de swap para travar posições com um swap positivo. Além disso, precisaremos de uma fórmula para calcular o tempo médio de manutenção de posição lucrativa, e esse tempo médio é uma consequência direta da fórmula do número médio de etapas. Não vou abordar esse assunto muito profundamente neste artigo, mas quero apenas algumas pessoas comecem a compreender a importância por trás dessa matemática. Vou cobrir esse problema em detalhes em meu ramo com swaps um pouco mais tarde. Agora vamos definir a fórmula para as probabilidades médias totais das etapas para o segundo fractal:

• S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) -  fórmula recorrente para calcular a probabilidade média total das etapas para todos os níveis fractais (com  S[0] = 1*0.5 = 0.5)

Neste caso, esta fórmula é apenas um caso especial da anterior, pois no segundo fractal "K=1" é absolutamente sempre, para todos os níveis do fractal. Vamos descobrir quais são os limites das somas desses valores para ambos os fractais:

Como se pode ver, a primeira linha diverge, o que indica que na ausência de um limite superior, com negociação indefinida, teremos um tempo médio igual ao mesmo infinito, mas no segundo caso, obteremos uma borda bem definida igual a "2". Isso significa que se abrirmos uma posição com um swap positivo, em média teremos que fechar essa posição após duas etapas (consequentemente, o tempo médio de manutenção de uma posição será 2*T, onde "T" é o tempo médio de manutenção, desde que fechemos a posição quando atingirmos uma das bordas). No segundo e mais simples caso, simplesmente fechamos ambas as posições em ambas as contas, mesmo se a conta swap tiver um lucro. É claro que a primeira opção é muito mais atraente, mas sua implementação exigirá um saque e depósito rápido e suave de fundos em ambas as contas. Se não houver essa opção, teremos que usar a variação clássica, que não é tão lucrativa, mas estável.

Resumindo os resultados

Na segunda parte do ciclo, alcançamos resultados muito interessantes, inclusive para uso prático em negociações, mas o mais importante, ficou claro que isso está longe de ser tudo o que pode ser feito usando fractais. Se definirmos claramente o que foi feito neste artigo:

• Definidas regras matemáticas claras para a construção de um fractal universal
• Criado um código funcional ao estilo MQL5 com base nos princípios matemáticos declarados
• Graças à duas plataformas MetaTrader 5 e MathCad 15 que são diferentes, todos os princípios matemáticos declarados foram testados com sucesso
• Graças aos algoritmos obtidos, foi gerada a primeira fórmula para calcular o tempo de vida de um corredor arbitrário
• A fórmula foi testada e validada usando programação para todos os casos possíveis
• Com base na fórmula obtida, foi gerado um novo tipo de fractal mais rápido
• O fractal resultante tornou possível acelerar os cálculos e determinar o que estava além do poder do fractal universal
• Considerado superficialmente um caso especial de uso de um fractal avançado para problemas de negociação de swap
• Obtidas ferramentas para um maior desenvolvimento da teoria

Além disso, quero ressaltar que minha caixa de ferramentas se expandiu muito e agora posso começar a analisar fractais com etapas de diferente probabilidade (situações de tendência e situações relacionadas à análise de estatísticas de negociação). Mais uma vez, quero esclarecer que neste artigo foram investigados apenas os casos em que "p = 1 - p = q = 0.5". Essa suposição significa que até agora todos os cálculos são aplicáveis apenas a situações que descrevem um passeio aleatório, mas acho que você entende que ainda há muitas possibilidades e isso não é nem a metade.

Separadamente, gostaria de mostrar mais uma vez de forma simples e rápida a fórmula que foi obtida como resultado do estudo do fractal. Suspeito que muitos podem não ter entendido isso e, para evitar isso, descreverei brevemente novamente o que e por quê:

1. S = K^2 - número médio de etapas no novo corredor, com base no fato de que a etapa é outro corredor
2. T = S * T0 =  T0 * K^2- vida útil média de um corredor desconhecido
3. T0 - vida útil média de um corredor conhecido
4. P = K * P0  --> K = P/P0 - quantas vezes o corredor conhecido é maior que o desconhecido
5. P - largura do corredor cuja vida útil média é desconhecida
6. P0 - largura do corredor conhecido

Substituindo "4" por "1", podemos expressar o número médio de etapas que estarão no corredor desconhecido por meio dos valores conhecidos, e substituindo "1" por "2" obtemos a vida útil média deste corredor que é calculada com base nos valores conhecidos:

• T0, P0, P

Também quero responder algo que preocupou muitos no processo de leitura deste artigo:

• Por que precisamos usar fórmulas se podemos coletar estatísticas de negociação no testador de estratégia MetaTrader 5?

Resposta:

• Sim, você pode fazer isso, mas não sempre que seja possível coletar essas estatísticas, uma vez que nem todos os instrumentos têm um histórico de negociação suficiente para coletar uma quantidade arbitrariamente significativa de dados para tais avaliações. Para corredores grandes, isso será impossível, pois você pode escolher um corredor que ao longo de todos os seu histórico nunca cruzou suas bordas ou selecionar corredores de largura menor para esta fórmula e obter dados que não podem ser obtidos nas estatísticas. Além disso, esse tipo de matemática oferece precisão e flexibilidade incomparáveis. Essas não são todas as vantagens.

Conclusão

Neste artigo, tentei descrever toda a lógica a partir da qual você pode construir pesquisas adicionais sobre processos de precificação. Até agora isso não é suficiente para a aplicação prática, mas estou cem por cento certo de que é possível investigar todas as variedades de um fractal universal e obter com base nelas todas as fórmulas possíveis para descrever, incluindo corredores de preços assimétricos e corredores com uma borda arbitrária. No próximo artigo, continuarei a estudar o fractal universal e tentarei simplificar os resultados em fórmulas, e veremos também uma nova matemática muito interessante que permitirá usar as fórmulas não só para processos de formação de valores, mas também para descrever backtests e sinais de negociação. Graças a isso, poderemos analisar com absoluta precisão qualquer estratégia em termos de tempo e probabilidades, e isso, no final, é tudo o que nos pode preocupar em relação à negociação.

Links

• Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos