Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle

Sommaire

• Introduction
• Évaluation des possibilités d'utilisation des fractales dans le trading
• Base théorique pour la construction d'une fractale universelle
• Écrire le code pour mettre en œuvre une fractale universelle
• Dérivation de la première formule sur la base d'une fractale symétrique
• Évaluation de la performance de la formule dérivée pour tous les arguments positifs et réels
• Fractale avancée développée à partir de la fractale universelle
• Synthèse des résultats
• Conclusion
• Références

Introduction

Dans l'article précédent, nous avons abordé les bases de la théorie des probabilités qui nous aideront à comprendre les caractéristiques spécifiques de l'utilisation des fonctions fractales pour les opérations de trading. Dans le prolongement de ce sujet, je montrerai quelques fonctions fractales autosuffisantes qui peuvent décrire tous les processus de calcul des prix requis. Nous essaierons de les généraliser et de les simplifier, ainsi que de créer des formules pour répondre à diverses questions qui manquent d'estimations quantitatives claires et de réponses sans ambiguïté. 

Évaluation des possibilités d'utilisation des fractales dans le trading

Poursuivons le sujet en résumant les résultats de l'article précédent et en présentant le matériel sous une forme plus compacte et universelle. Vous souvenez-vous de l'exemple de construction d'une fractale présenté dans l'article précédent ? Une telle fractale n'a guère d'utilité pratique. Mais dans le cas présent, nous nous intéressons principalement aux règles de construction de la structure que nous avons déterminées. Il s'est avéré que ces règles peuvent être appliquées à 3 types de fractales :

1. Fractale avec bords symétriques
2. Fractale avec bordures asymétriques
3. Fractale avec bordure supérieure ou inférieure

Ces fractales peuvent être utilisées pour décrire les processus suivants :

• Imitation accélérée des transactions avec la possibilité d'évaluer les probabilités de différents scénarios, en tenant compte des restrictions de dépôt (puisque la bordure inférieure peut symboliser le niveau de dépôt à partir duquel il est impossible de poursuivre les transactions).
• Estimation du nombre moyen de pas à l'intérieur d'une fractale (par exemple, vous pouvez estimer le nombre d’ordres que nous avons en moyenne avant d'obtenir le profit ou la perte souhaités).
• Estimation des valeurs moyennes totales pour chaque étape (par exemple, vous pouvez calculer le temps moyen de maintien de la position, sur la base des statistiques d'une position plus petite, c'est-à-dire une position avec des niveaux d'arrêt plus petits en points ou en différence de prix).
• Évaluation de la rentabilité des options basées sur une fractale à bord unique
• Autres capacités

Base théorique pour la construction d'une fractale universelle

Utilisons les règles de construction que nous avons dérivées dans l'article précédent, et complétons-les pour comprendre comment une fractale est construite. J'ai également trouvé une petite erreur dans mes formules, à cause de laquelle l'asymétrie des frontières vers le bas ou vers le haut était impossible. Les formules dérivées se sont avérées correctes et fonctionnent donc pour n'importe quelle fractale. En fait, il s'agit d'une fonction permettant d'implémenter n'importe quelle fractale. Toutes les fractales possibles sont un cas particulier d'une fractale générale. Si nous prenons les trois types de fractales définis ci-dessus, les conditions de la fractale générale pour la mise en œuvre de ces 3 cas particuliers seront les suivantes :

1. m = n & [ m > s & n > s ]
2. ( m > n || n > m )  & [ m > s & n > s ]
3. ( m > S && n <= S ) || ( n > S && m <= S )

Schématiquement, ces 3 types de fractales se présentent comme suit :

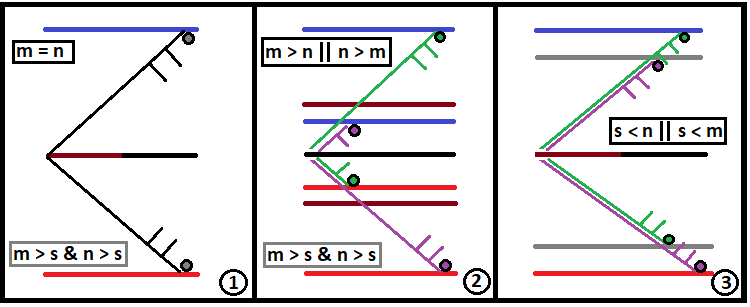
Idéalement, "S" devrait tendre vers l'infini. Les variables suivantes n'ont pas été décrites dans mon article précédent. Je fournirai ici les descriptions afin d'obtenir une image complète de la manière d'utiliser la formule générale pour obtenir les cas particuliers. Une fractale est une fonction qui fonctionne sur le principe d'une réaction en chaîne, comme dans une bombe atomique. Si la réaction en chaîne est trop profonde, l'ordinateur risque de ne pas pouvoir faire face à des calculs aussi importants. Si le cas n'est pas particulièrement critique, elle prendra simplement un temps très long - des minutes, des heures, voire des jours. Pour lancer correctement une réaction en chaîne dans une fractale, il faut trouver 2 valeurs fondamentales :

• Half — la moitié de la largeur du canal
• Middle — la valeur "U" qui correspond à la ligne médiane

La demi-valeur peut être facilement calculée pour les 3 cas que nous avons déterminés dans l'article précédent : il s'agit de la moyenne arithmétique de m et n :

• Half = ( n + m ) / 2

Pour implémenter la deuxième valeur, nous devrons utiliser 3 variantes logiques. Toutefois, la première et la deuxième variantes peuvent être combinées en une seule. Nous avons donc 2 variantes :

1. n >= m
2. n < m

Ensuite, étant donné que l'axe "U" est dirigé vers le haut et que la valeur n est la partie supérieure des canaux, tandis que m est la partie inférieure, nous obtenons 2 rapports pour 2 cas avec m et n possibles :

1. Middle = Half - m
2. Middle = - ( Half - n )

Ces valeurs seront transmises à la fonction fractale pour un usage interne, car la logique de branchement interne décrite dans l'article précédent ne peut être mise en œuvre sans elles. Le prototype de la fonction est le suivant :

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Nous devons donc transmettre 3 valeurs obligatoires pour que la fractale démarre correctement :

1. Half — la moitié de la largeur du canal
   
2. Middle — la valeur "U" qui correspond à la ligne médiane
   
3. m — le nombre de pas vers le bord inférieur
4. n — le nombre de pas vers le bord supérieur
5. s — le nombre maximum autorisé de pas dans n'importe quelle direction pour une seule chaîne

D'autres valeurs sont indiquées par des lettres majuscules pour montrer que ces valeurs sont dynamiques et qu'elles seront différentes à différents niveaux fractals. Voici leur définition :

• S — le nombre de pas accumulés dans la chaîne de probabilités actuelle ; à passer au niveau fractal suivant
• U — la distance actuelle entre le point de départ de la chaîne et son extrémité ; à transmettre au niveau fractal suivant
• P — le produit cumulé des probabilités de l'ensemble de la chaîne sur la base du schéma de Bernoulli ; à transmettre au niveau fractal suivant

Ainsi, pour que la fractale démarre correctement, nous devons entrer les valeurs suivantes dans la fonction :

• S = 0 (puisqu'il s'agit d'un début, donc il n'y a pas encore eu d'étapes)
• U = 0 (pour la même raison)
• P = 1 (puisqu'il s'agit d'une chaîne zéro et que toutes les étapes suivantes doivent constituer un groupe complet)

Pour terminer le développement des règles générales pour les fractales qui simulent la fixation des prix ou le trading, réécrivons brièvement les règles qui ont été obtenues dans l'article précédent. Ces règles sont utilisées à l'intérieur de la fractale. Les règles sont basées sur plusieurs formules pour les mêmes étapes :

• f = u + d — c'est le nombre de pas de l'arbre des combinaisons futures (la distance est déterminée par la distance à la frontière la plus proche de la plage fractale)
• s = u - d — le nombre d'étapes finales, exprimé en termes de segments descendants et ascendants

Nous avons décidé de passer par "u". Nous utiliserons aussi la valeur "s" comme nouveau "U", qui sera transmis au niveau fractal suivant, si le nombre d'étapes restantes le permet. Pour ce faire, nous devons définir une formule pour "u" qui ne contienne pas "d". Pour cela, exprimez "d" de la première équation et substituez-le dans la seconde :

• s = 2*u - f

Cette valeur pourrait également être utilisée comme nouvelle valeur de "U" pour passer plus loin si la valeur actuelle était égale à zéro. Nous devons donc ajouter ce "s" à "U" pour obtenir la valeur qui doit être transmise ultérieurement :

• NewU = s + U — notre nouveau "U" pour passer au niveau fractal suivant

Comme déjà défini dans l'article précédent, cette expression prend 3 valeurs possibles, basées sur les 3 valeurs possibles du nombre "f". J'ai révisé un diagramme de l'article précédent pour illustrer l'idée :

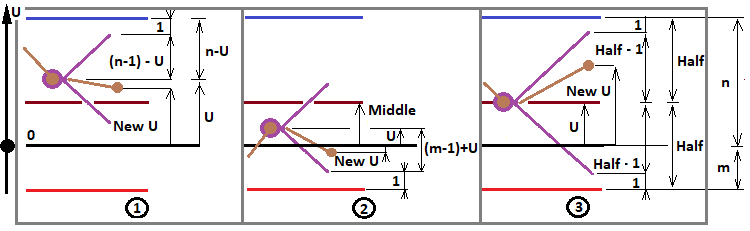
Ce diagramme est très approprié ici, puisque nous déterminons maintenant toutes les configurations fractales possibles qui peuvent nous être utiles pour résoudre la plupart des problèmes. Selon ce schéma, nous définissons 3 cas pour "f" :

1. f = ( n - 1 ) - U
2. f = ( m - 1 ) + U
3. f = Half - 1

Ces 3 cas apparaissent lorsque les conditions suivantes sont remplies :

1. U > Middle
2. U < Middle
3. U = Middle

Nous devons maintenant décrire les 2 dernières valeurs à transmettre au niveau fractal suivant et examiner comment les nombres sont collectés dans la fractale. Les 2 dernières valeurs sont calculées comme suit :

• NewP = P * C(f, i) * Pow(p, i) * Pow(1-p, f-i ) — notre nouvelle probabilité de chaîne "P" à transmettre au niveau fractal suivant
• NewS = S + f = S +(floor(Mid) - 1) — notre nouveau "S" à transmettre au niveau fractal suivant

Avant de commencer à rassembler les nombres dans une variable commune, il faut savoir que les nombres doivent être rassemblés dans un bloc similaire. Mais dans ce cas, nous ne faisons qu'une seule étape, et nous n'avons donc pas besoin du schéma de Bernoulli. L'ordre des déclarations n'est pas important ; elles doivent simplement se trouver dans le même bloc. Les chiffres ne peuvent être collectés que dans les cas "1" et "2", avec quelques précisions :

1. U = n - 1
2. U = - ( m - 1 )

Dans le premier cas, les 3 valeurs précédentes sont plus faciles à calculer car nous n'avons qu'une seule étape :

• NewU = U - 1
• NewP = P * p
• NewS = S + 1

Dans le second cas, il y a une différence mineure :

• NewU = U + 1
• NewP = P * ( 1 - p )
• NewS = S + 1

Sur la base de la généralisation de toutes les fractales, chacune de ces fractales est divisée en 2 types :

• Fractale calculant la probabilité totale de franchir la limite supérieure du canal
• Fractale calculant la probabilité totale de franchir la limite inférieure du canal

Chacun de ces types correspond à un autre type de fractale, qui s'ajoute à l'original :

• Fractale calculant le nombre moyen de pas pour franchir la bordure supérieure
• Fractale calculant le nombre moyen de pas pour franchir la bordure inférieure

Ces 4 types de fractales diffèrent par la forme des nombres additionnés. Lorsque l'on rassemble les probabilités, on ne peut ajouter que "P*p" et "P*(1-p)". Pour les deux autres fractales, nous avons besoin de variables supplémentaires pour passer aux niveaux fractals suivants. Dans ces fractales, nous utilisons des pas de taille égale qui sont de directions opposées, de sorte que leurs probabilités sont soit "p", soit "1-p". Mais lorsque "p" n'est pas égal à 0,5, cela signifie qu'il s'agit de deux événements différents, pouvant avoir des caractéristiques différentes. Par caractéristiques, j'entends un ensemble de variables aléatoires correspondant à un événement donné. L'une de ces valeurs est la durée de vie de la position. Il peut y avoir un nombre quelconque de ces valeurs, et nous pouvons les considérer comme du temps si nécessaire. Cette partie peut être simplifiée en suivant quelques étapes simples. Les nombres à additionner auront la forme suivante :

1.  P * p * NewS
2.  P * ( 1 - p ) * NewS

Comme vous pouvez le constater, les probabilités sont multipliées par le nombre d'étapes de cette chaîne d'étapes. Mais cette formule ne s'applique que lorsque la probabilité d'une hausse ou d’une baisse est la même. Dans d'autres cas, nous devrons utiliser deux structures différentes pour décrire les pas en avant et les pas en arrière, ou fournir une structure pour stocker les deux nombres. Dans le second cas, la fonction fractale ne renvoie pas un nombre, mais un conteneur de données. Le conteneur ne nécessite pas d'extension. J'ai également fourni un conteneur qui peut stocker tous les paramètres requis, de sorte qu'il n'est pas nécessaire de décrire plusieurs fonctions avec un code similaire. Au lieu de cela, j'ai combiné toutes les fonctions en une seule, qui peut décrire tous les paramètres requis. Le type de fractale et la tâche qu'elle permet de résoudre dépendent directement des paramètres d'entrée de la fonction. Pour étendre le concept, le premier "S" et son équivalent "NewS" doivent être remplacés par les valeurs suivantes :

1. SU — les dernières étapes à la hausse de la chaîne de probabilité sélectionnée
2. SD — les dernières étapes à la baisse de la chaîne de probabilité sélectionnée
3. NewSU et NewSD — les valeurs à transmettre au niveau fractal suivant
4. SU + SD = S

Ces valeurs doivent être définies de manière similaire à la définition de "S". Lorsque "U > Middle" :

• NewSU = SU
• NewSD = SD + 1

Quand "U < Middle" :

• NewSU = SU + 1
• NewSD = SD

Six autres valeurs sont nécessaires pour l'amélioration finale de la fractale :

1. UpperMidSDown — le nombre total moyen probable de pas vers le bas avant d'atteindre la limite supérieure.
2. UpperMidSUp — le nombre total moyen probable de pas vers le haut avant d'atteindre la limite supérieure.
3. UpperSummProbability — la probabilité de franchir la bordure supérieure
4. LowerMidSDown — le nombre total moyen probable de pas vers le bas avant d'atteindre la limite inférieure.
5. LowerMidSUp — le nombre total moyen probable de pas vers le haut avant d'atteindre la limite inférieure.
6. LowerSummProbability — la probabilité de franchir la bordure inférieure

Les valeurs "1", "2", "4", "5" indiquent la somme des produits du nombre d'étapes correspondant et leur probabilité. Ces valeurs n'ont pas de sens en l'état, mais elles sont des composantes de formules de valeurs utiles dont nous parlerons plus loin. Les valeurs "3" et "6" sont les probabilités d'hypothèse de franchissement de deux limites qui forment un groupe complet. Grâce à ces valeurs, nous pouvons déterminer une multitude d'autres choses.

Écrire le code pour mettre en œuvre une fractale universelle

Pour lancer correctement la fractale, nous avons besoin d'une fonction qui exécute toutes les opérations préparatoires avant le lancement de la fractale. Après quoi elle lancera correctement la fractale sur la base de règles prédéfinies. J'ai préparé une implémentation de cet algorithme dans le style MQL5 :

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Après le calcul de la fractale, la fonction renvoie notre conteneur avec toutes les données nécessaires :

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

Ce conteneur comprend une surcharge de l'opérateur "+=", qui permet de combiner deux structures identiques. Cette partie sera utilisée pour la fonction principale. Voici la fonction fractale :

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

Le code a été vérifié dans MetaTrader 5 - il fonctionne assez bien. Cette logique peut encore être développée, si nécessaire, et il existe encore de nombreuses possibilités avancées. Mais j'ai décidé de ne pas allonger la liste des paramètres d'entrée de la fonction pour l'instant, car la fonctionnalité mise en œuvre est tout à fait suffisante pour nos besoins. En étudiant attentivement le code, vous constaterez qu'il est parfaitement conforme aux principes mathématiques énoncés ci-dessus. Bien que court, ce bout de code peut faire des merveilles. Je pense que le code doit contenir autant de logique et de mathématiques que possible. C'est ce dont nous aurons besoin en fin de compte. Même un beau code est inutile s'il ne peut pas être utilisé dans le but pour lequel il a été conçu. Dans notre cas, l'objectif visé est de l’appliquer au trading. Voici le journal en guise de confirmation :

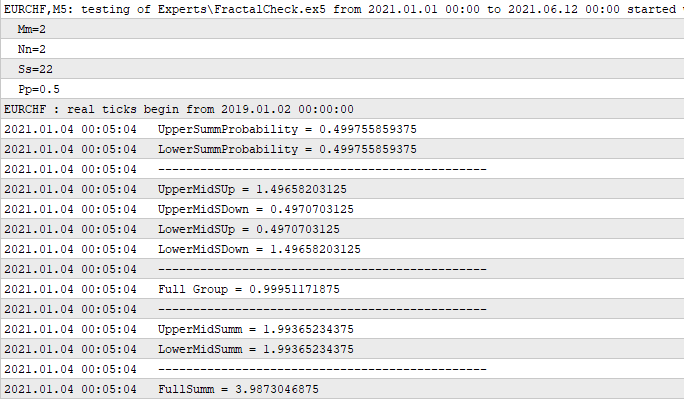
Dans ce cas, j'ai créé un Expert Advisor simple, qui calcule la fractale entière au premier tick reçu. Ce calcul est effectué une seule fois, il n'est donc pas nécessaire d'effectuer d'autres calculs. Les six premiers chiffres font partie du conteneur, et les autres en sont dérivés. Je ne montre ici que les dérivés les plus importants, ce qui peut aider à comprendre que ces 6 variables permettent de recevoir toutes les autres variables dont nous pourrions avoir besoin. Prenons l'exemple du "Full Group". Il est appelé ainsi parce que la somme des probabilités de deux hypothèses non superposées d'un des passages de frontière selon le calcul précédent doit être égale à un. Notre code le confirme. Suivent deux nombres identiques qui sont la somme de "1", "2" et "3", "4". Ce dernier chiffre est la somme des avant-derniers chiffres - il s'agit du nombre moyen d'étapes que la chaîne franchira. La raison pour laquelle j'ai défini ces paramètres d'entrée de la fonction set, où "m" et "n" sont égaux et symétriques, sera expliquée plus loin.

Dérivation de la première formule sur la base d'une fractale symétrique

D'après le résultat du journal, le nombre moyen d'étapes par lesquelles la chaîne passera tend vers "4". Le canal est doublé par rapport à un pas d'unité. On parle de pas d'unité si "n" et "m" sont égaux à 1. En d'autres termes, si nous voulons calculer le nombre moyen de pas dans un canal composé de canaux plus petits (dans ce cas, un nombre entier de petits canaux s'insèrent dans un plus grand et le nouveau canal est également symétrique), nous pouvons supposer que :

• P[n] = P[n-1] * 2 — est l'expression récursive de la largeur du nouveau canal en pas, basée sur la largeur du canal précédent, plus petit, à partir duquel le nouveau canal est composé.
• S[n] = S[n-1] * 4 — est l'expression récursive pour calculer le nombre moyen de pas du nouveau canal, exprimé par la valeur moyenne d'un canal plus petit.

Si l'on admet que "P[0]=1" et "S[0]=1", et si l'on commence la numérotation de la récursion à partir de l'indice "0", cette récursion peut être représentée par 2 séries très similaires :

• P[n] = 2^n , n = 0 ... + infini
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

Si l'on examine attentivement la première série et que l'on transforme correctement la deuxième série, il s'avère que la deuxième série peut être exprimée à l'aide des éléments de la première série. En d'autres termes, nous obtenons la dépendance suivante : S = S(P) = P^2. Cette dépendance n'est vraie que pour le doublement récursif de la largeur du canal. Lorsque j'ai vu cette formule, j'ai décidé de vérifier son applicabilité pour n'importe quel grand nombre arbitraire "n" et "m". Logiquement, dans la deuxième étape, nous fixons "n=3", "m=3" et calculons les mêmes variables. Avec ces paramètres d'entrée, le nombre moyen de pas tend vers le chiffre "9". Vous pouvez vérifier cette partie vous-même, en utilisant le code ci-dessus ou en utilisant les programmes MathCad 15 joints ci-dessous. La même série peut être fournie pour ces paramètres :

• P[n] = 3^n , n = 0 ... + infini
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Comme vous pouvez le constater, nous obtenons la même relation "S=S(P)=P^2". Nous pourrions répéter la même chose pour tous les autres scénarios possibles liés à la division de l'intervalle, mais ce n'est pas nécessaire. Cela signifie que si nous connaissons, par exemple, la durée de vie moyenne d'un prix à l'intérieur d'un canal symétrique, nous pouvons calculer la durée de vie moyenne d'un prix à l'intérieur de n'importe quel autre canal. Elle peut être calculée comme suit :

• S = S0 * K^2 — le nombre moyen de pas d'un nouveau canal
• T = S * T0 — la durée de vie moyenne du nouveau canal
• T = T0 * K^2 — la durée de vie moyenne du nouveau canal exprimée en termes de durée de vie moyenne d'un autre canal (à condition que S0 = 1 )
• S0 — le nombre moyen de pas de l'ancien canal
• T0 — la durée de vie moyenne d'une étape de l'ancien canal
• P = K * P0 --> K = P/P0 — combien de fois le nouveau canal est plus grand que l'ancien.
• P — la largeur du nouveau canal
• P0 — la largeur de l'ancien canal

Nous pouvons maintenant tester l'hypothèse à l'aide de MathCad 15. Tout d'abord, testons les hypothèses concernant la relation quadratique :

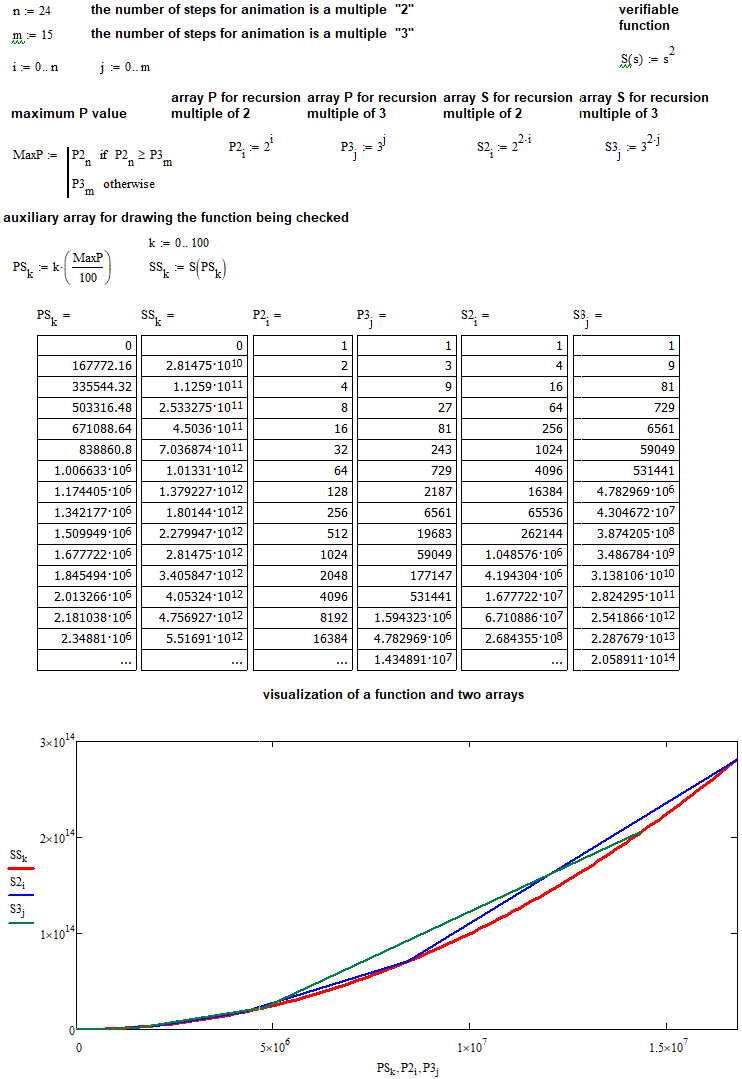
Cela devrait être très clair.

Évaluation de la performance de la formule dérivée pour tous les arguments positifs et réels

La formule fonctionne pour tous les entiers "P". Mais peut-il être utilisé pour un décimal "K" ? Nous devons mettre en œuvre une astuce pour fournir un nombre flottant "K". Supposons que nous ayons un canal de prix dont la durée de vie moyenne est connue, et que nous ayons un canal qui s'insère "N" fois dans notre canal, mais dont nous ne connaissons pas encore la durée de vie moyenne. Nous le trouverons également en utilisant la même formule. Selon cette logique :

• T = T0 * N^2 ---> T0 = T / N^2
• T — la durée de vie de notre canal, dont nous connaissons la durée de vie moyenne
• T0 — est la durée de vie moyenne d'un canal plus petit, dont notre canal est constitué.

Cela signifie que nous pouvons trouver la durée de vie d'un canal plus petit, dont nous avons besoin pour calculer la durée de vie du troisième canal avec un facteur d'augmentation fractionnaire. Maintenant que nous avons trouvé la durée de vie du plus petit canal, nous pouvons trouver sa largeur en points :

• d = P / N

Nous pouvons ensuite calculer le nombre de ces canaux dans un canal élargi, en utilisant le ratio suivant :

• Smin = MathFloor( K * P / d ) = MathFloor( K * N )
• Lim( N --> +infini ) [ K * N/MathFloor( K * N ) ] = 1

Comme vous pouvez le constater, la largeur du canal se réduit, et cela n'affecte pas le résultat. La deuxième ligne indique un ratio très important qui aidera à comprendre ce qu'il faut faire ensuite. Il montre que lorsque nous divisons le canal source en autant de segments que possible, nous pouvons négliger la partie fractionnaire qui est rejetée à la suite de l'utilisation de la fonction MathFloor. Ceci est démontré par la limite qui tend vers l'unité. Si cette imprécision est déroutante, nous pouvons trouver une autre valeur :

• Smax = MathFloor( K * P / d ) + 1 = MathFloor( K * N ) + 1 = Smin + 1

Il est maintenant clair que la valeur réelle de "K * N" se situe entre "Smin" et "Smax". Si "N" tend vers l'infini, nous obtenons 2 couloirs très similaires et leur durée de vie moyenne tendra à être égale, puisque leurs tailles ne diffèrent que d'un segment. Ainsi, la durée de vie moyenne du canal nécessaire sera plus précisément déterminée par la moyenne arithmétique de la durée de vie moyenne de ces canaux :

• T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 =  T0 *( Smin^2 + Smax^2 ) / 2
• T1 — la durée de vie moyenne du canal que nous devons déterminer

La figure suivante illustre mes idées :

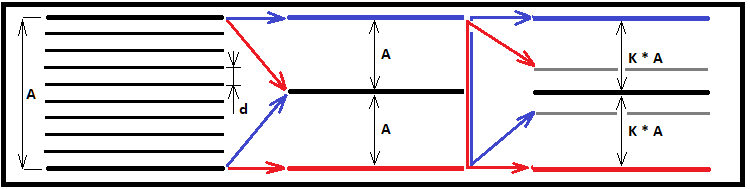
Maintenant que nous avons trouvé une expression alternative pour calculer la durée de vie du couloir, nous pouvons comparer son résultat avec la valeur de la fonction pour l'entier "K", en remplaçant le flottant "K". Si les valeurs résultantes des 2 expressions sont identiques, nous pouvons conclure que la fonction trouvée pour les valeurs entières "K" est absolument applicable pour tous les entiers et les flottants dans l'intervalle "0 ... +infini". Effectuons la première vérification pour "N = 1000". Je pense que cette division sera suffisante pour voir l'identité de 2 nombres s'il y en a :

Comme vous pouvez le constater, les 2 chiffres sont pratiquement identiques. Logiquement, ils devraient être plus identiques pour des valeurs "N" plus élevées. Ceci peut également être prouvé en supposant ce qui suit :

• Lim( N --> +infini ) [  (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 )  ] = 1

Le numérateur de cette limite est notre expression approximative pour calculer la durée de vie moyenne du nouveau couloir, et le dénominateur est une expression qui décrit vraisemblablement avec précision la même valeur. J'ai créé une fonction simple qui effectue les mêmes calculs que dans la capture d'écran précédente. Mais cette fois-ci, elle s'applique à l'ensemble de la plage du nombre "N" commençant par "1". Voyons maintenant le résultat de l'exécution du programme :

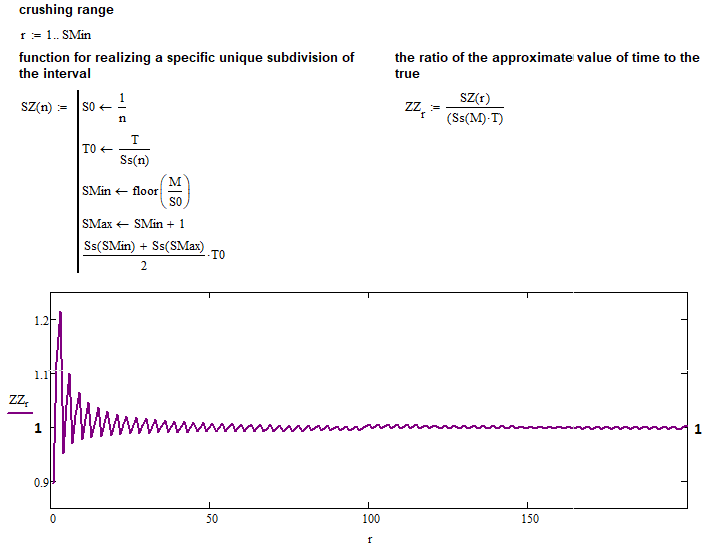
Toutes les hypothèses sont entièrement confirmées : la fonction que nous avons trouvée pour un nombre entier "K" est absolument applicable pour tout "K" positif. Nous disposons à présent d'une fonction unique et très utile qui peut être utilisée comme base pour d'autres actions, par exemple comme base pour d'autres mathématiques visant à décrire l'ensemble de la fractale universelle.

Fractale avancée développée à partir de la fractale universelle

Comme exemple utile et supplémentaire d'application d'une fractale universelle, nous pouvons prendre une fractale à une bordure, avec, disons, "n=1", "m ---> +infini", "s = m+1", "p=0,5". Jusqu'à présent, nous avons considéré des fractales avec des pas de probabilité égale dans les deux directions, ce qui n'est applicable qu'à la marche aléatoire. Mais cette fractale offre toutes les possibilités. Afin de procéder à une analyse plus approfondie d'une structure aussi complexe, il convient tout d'abord d'en examiner les fondements. Cette étape initiale nous permet également d'obtenir des formules utiles et de tirer des conclusions fondamentales concernant ces processus fractals. J'ai testé la fractale avec différentes valeurs de "s" et j'ai obtenu les données suivantes :

• s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
• s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
• s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
• s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882

Une augmentation supplémentaire du nombre d'étapes autorisées conduit à la singularité du temps de calcul, c'est-à-dire que le temps de calcul augmente tellement qu'il nécessiterait des heures, voire des jours. Mais si l'on observe la vitesse à laquelle la somme moyenne des probabilités augmente, on constate qu'il n'est pas possible d'évaluer la convergence de cette série à l'aide de ce type de fractale. Mais sur la base de la formule dérivée précédemment, nous pouvons évaluer la convergence à l'aide d'un type de fractale différent mais très utile. Cette fractale peut également aider à calculer le temps d'une stratégie très populaire et rentable appelée "Carry trade". Je montrerai d'abord une figure, puis je l'expliquerai :

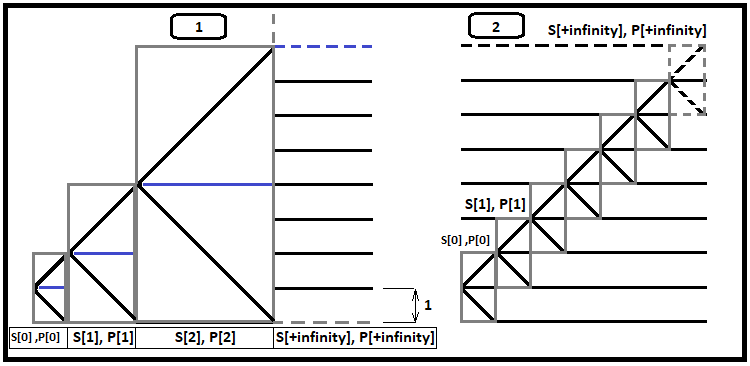
Imaginons que le processus de calcul des prix commence à une étape de la bordure, quel que soit l'endroit où elle se trouve, vers le haut ou vers le bas. La figure ci-dessus montre un exemple avec une bordure plus basse, car elle est plus facile à percevoir. Regardez de plus près la première fractale. Chaque case grise contient deux scénarios pour la suite des événements :

1. Le prix atteint le bord supérieur de la boîte
2. Le prix atteint le bord inférieur de la boîte

Lorsque le prix atteint la limite supérieure du canal, une nouvelle fractale plus grande commence automatiquement à ce point, et ainsi de suite. Si nous considérons ce processus de la même manière que dans la fractale universelle, nous verrons à nouveau les chaînes de probabilité. Mais notre formule indique maintenant le nombre de marches qui seront faites dans un couloir symétrique, en fonction du nombre de marches qui entrent dans le canal (nous voyons maintenant qu'une marche est un couloir plus petit qui entre dans le couloir original).

Il n'est pas nécessaire de considérer l'ensemble de la fractale pour calculer le nombre moyen de pas. Au lieu de cela, appliquez la formule dérivée à chacune des fractales. Le pas ici n'est pas la même valeur, mais il est fait lorsque nous atteignons la limite supérieure ou inférieure de la fractale imbriquée suivante. En partant de cela, nous pouvons créer des chaînes de probabilité très simples. La probabilité d'atteindre la bordure au niveau de la toute première fractale P[0] est égale à 0,5. Cela signifie qu'il existe un deuxième cas possible où nous devons créer la fractale suivante en espérant que le prix atteindra la limite. Tous ces événements sont imbriqués les uns dans les autres et toutes ces chaînes forment un groupe complet.

La probabilité d'atteindre la limite de la deuxième fractale P[1] est égale à la probabilité précédente multipliée par 0,5. Ce processus peut être poursuivi indéfiniment. Le nombre moyen d'étapes peut être déterminé à l'aide de la formule dérivée et des probabilités de chaîne. Pour cela, nous définissons d'abord une formule pour la probabilité de chaque chaîne individuelle, en tenant compte du fait que le nombre moyen d'étapes pour franchir la limite supérieure et pour franchir la limite inférieure est égal. Il s'avère que :

• PUp = PDown = P — le rapport montrant que les probabilités de toucher les limites supérieures et inférieures d'une fractale sont identiques pour toutes les limites de toutes les fractales imbriquées.
• P[j] = 0,5^(j+1), j = 0 ... + infini- — la probabilité que la chaîne j se produise
• S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ), i = 1... + infini — une formule récurrente pour calculer le nombre total d'étapes moyennement probables pour tous les niveaux fractals (avec S[0] = 1*0,5 = 0,5)
• F(K) = K^2 — notre formule dérivée pour calculer le nombre moyen de pas
• D(i) = 2^i — combien de pas correspondent au niveau fractal suivant
• S[i-1]/P[i-1] — le nombre moyen d'étapes dans la branche restante non comptabilisée, à condition que la branche actuelle ait eu lieu (parce qu'en plus de la fractale imbriquée actuelle, il est nécessaire de prendre en compte toutes les étapes qui se sont produites auparavant)
  

La seconde fractale est en fait identique à la première, c'est-à-dire que les probabilités de leurs chaînes (le tableau P[]) sont identiques. Pourquoi en avons-nous besoin ? Supposons que nous ayons la stratégie "Carry Trade". Nous disposons de 2 comptes : un compte avec swap et un compte sans swap pour verrouiller les positions avec un swap positif. Nous avons également besoin d'une formule pour calculer la durée moyenne de maintien d'une position rentable. Ce temps d'attente moyen découle directement de la formule du nombre moyen d'étapes. Je n'aborderai pas cette question en détail dans cet article. Je veux juste montrer l'importance des mathématiques. Ce sujet sera abordé en détail ultérieurement. Définissons maintenant une formule pour les pas de probabilité moyens pour la deuxième fractale :

• S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) — une formule récurrente pour calculer le nombre total de pas moyennement probable pour tous les niveaux fractals (alors que S[0] = 1*0,5 = 0,5)

Dans ce cas, cette formule n'est qu'un cas particulier de la formule précieuse car dans la seconde fractale K=1, toujours, pour tous les niveaux fractals. Cherchons à connaître les limites des sommes de ces quantités pour les 2 fractales :

La première série diverge, ce qui signifie que lorsqu'il n'y a pas de limite supérieure et que le trading est sans fin, le temps moyen est égal à l'infini. Dans le second cas, nous obtenons une limite claire égale à 2. Cela signifie que si nous ouvrons une position avec un swap positif, nous devrons en moyenne fermer cette position après deux étapes (le temps moyen de maintien de la position sera donc égal à 2*T, où T est le temps moyen de maintien de la position à condition que nous fermions la position lorsqu'elle atteint l'une des bornes). Dans le deuxième cas, le plus simple, nous clôturons simplement les 2 positions sur les 2 comptes, même si le compte avec swap affiche un nombre positif. La première option est évidemment beaucoup plus attrayante, mais sa mise en œuvre nécessiterait un retrait et un dépôt rapides sur les deux comptes. Si cette option n'est pas possible, nous devrons recourir à une option classique, qui génère moins de bénéfices mais présente une plus grande stabilité.

Synthèse des résultats

Dans la deuxième partie de la série d'articles, nous avons obtenu des résultats très intéressants, y compris des résultats pour une application pratique dans le trading. Plus important encore, il est désormais clair que le champ d'application possible des fractales est immense. Ce que nous avons fait dans l'article :

• Définition de règles mathématiques claires pour la construction d'une fractale universelle
• Création d'un code fonctionnel de type MQL5 basé sur les principes mathématiques énoncés
• Les principes ont été vérifiés avec succès en utilisant deux plateformes, MetaTrader 5 et MathCad 15.
• En utilisant les algorithmes, nous avons obtenu la première formule pour calculer la durée de vie d'un canal arbitraire.
• Test et validation de la formule à l'aide de la programmation pour tous les cas possibles
• Obtention d'un nouveau type de fractale plus rapide, sur la base de la formule obtenue
• Le résultat nous a permis d'accélérer les calculs et de déterminer ce qui ne pouvait pas être déterminé par une fractale universelle
• Un cas particulier d'utilisation d'une fractale avancée pour des problèmes de trading de swaps a été abordé.
• Obtention d'outils pour le développement ultérieur de la théorie

Je tiens également à souligner que ma boîte à outils s'est considérablement élargie. Nous pouvons maintenant analyser des fractales avec des étapes de probabilité différentes (situations de tendance et situations liées à l'analyse des statistiques de trading). Une fois de plus, veuillez noter que dans cet article, nous n'avons considéré que les cas où "p = 1 - p = q = 0,5". Cela signifie que tous les calculs ne s'appliquent qu'aux situations qui décrivent une marche aléatoire. Les possibilités sont donc beaucoup plus nombreuses.

Voici la formule qui a été obtenue après l'étude de la fractale. Une fois de plus, je vais l'expliquer brièvement :

1. S = K^2 — le nombre moyen de pas du nouveau couloir, basé sur le fait qu'un pas est égal à un autre couloir
2. T = S * T0 =  T0 * K^2 — la durée de vie moyenne d'un couloir inconnu
3. T0 — la durée de vie moyenne d'un couloir connu
4. P = K * P0  --> K = P/P0 — combien de fois le couloir connu est plus grand que le couloir inconnu.
5. P — la largeur du couloir dont la durée de vie est inconnue
6. P0 — la largeur du couloir connu

En substituant 4 à 1, nous pouvons exprimer le nombre moyen de pas qui se trouveront dans le couloir inconnu grâce aux valeurs connues, et en substituant 1 à 2, nous obtenons la durée de vie moyenne de ce couloir, qui est calculée sur la base des valeurs connues :

• T0, P0, P

J'ajouterai également une réponse à une question que les lecteurs pourraient se poser au début de cet article :

• Pourquoi avons-nous besoin de formules si nous pouvons collecter des statistiques de trading à partir du testeur de stratégie MetaTrader 5 ?

Réponse :

• Il n'est pas toujours possible de collecter des statistiques, car tous les symboles financiers n'ont pas un historique de transactions suffisant pour permettre de telles évaluations. C'est impossible pour les grands canaux, car on pourrait sélectionner un canal qui n'a jamais franchi ses frontières. En utilisant des couloirs de moindre largeur et la formule, nous pouvons obtenir des données qui ne peuvent pas être obtenues à partir de statistiques. Ce type de calcul vous offre également une précision et une flexibilité inégalées. Il y a bien d'autres avantages.

Conclusion

Dans cet article, j'ai essayé de décrire la logique de calcul, qui peut être utilisée pour mener des recherches plus approfondies sur les processus de calcul des prix. Jusqu'à présent, il n'y a pas beaucoup d'applications pratiques. Mais je suis sûr que nous pouvons étudier toutes les variétés de la fractale universelle et obtenir des formules possibles pour décrire les couloirs de prix asymétriques et à une limite. Dans le prochain article, je poursuivrai mes recherches sur la fractale universelle et j'essaierai de présenter tous les résultats sous forme de formules simples. J'inclurai également de nouvelles mathématiques très intéressantes qui permettront d'utiliser les formules obtenues non seulement pour les processus de fixation des prix, mais aussi pour décrire les backtests et les signaux de trading. Cela nous permettra d'analyser avec une précision absolue toute stratégie en termes de temps et de probabilités, ce qui est en fin de compte l'aspect le plus important du trading.

Références

• Combinatoire et théorie des probabilités pour le trading (Partie I) : L'essentiel