Algoritmo de recompra: Simulação de negociação em várias moedas

Conteúdo

• Introdução
• Explicando a necessidade de simulação de negociação
• Modelo matemático de simulação de preços usando lógica de discretização
• Teste do modelo
• Expert Advisor de teste
• Considerações finais

Introdução

No artigo anterior, mostrei a você muitos recursos úteis que provavelmente você não conhecia, mas o mais interessante está por vir - pesquisa ou simulação de negociação. Então, o que é isso e por que essa complexidade? Às vezes, um testador de estratégias não é suficiente. Embora essa seja uma ferramenta muito conveniente para conhecer o mercado, isso é apenas o primeiro passo. Se você leu atentamente o artigo anterior, provavelmente já sabe o motivo. Para o restante de vocês, recomendo que leiam o material anterior para entender do que se trata. Apesar de tudo isso, tento fazer com que o artigo seja legível, independentemente de quem esteja interessado e venha a lê-lo, e um determinado artigo terá peso máximo para o leitor mesmo sem ter aprendido o anterior.

Explicando a necessidade de simulação de negociação

A razão para a simulação de negociação está diretamente no fato de que a quantidade de dados históricos de quaisquer instrumentos de negociação é limitada. Na verdade, eu suavizei bastante a questão aqui. Essa questão só pode ser compreendida se você entender o material que forneci no artigo anterior ou de alguma outra maneira alternativa. Tenho certeza de que ainda haverá pessoas que consigam fazer isso. 

A essência do problema é que um simples histórico de cotações nem sempre é suficiente, pois esse histórico é formado na interseção de muitos eventos mundiais aleatórios e não aleatórios, e há inúmeros cenários para o desenrolar do evento. Atualmente, estou tentando descrever as coisas da maneira mais simples possível, mas se avançarmos para a linguagem da teoria da probabilidade e ao mesmo tempo usarmos as conquistas do artigo anterior, entendemos que o histórico de cotações de todos os instrumentos que conhecemos poderia ter se desenvolvido de maneira diferente.

Esse fato é óbvio, se você assistiu ao filme "De Volta para o Futuro". Ele tem muitos erros e inconsistências engraçadas do ponto de vista científico, mas, no entanto, esse filme transmite a ideia principal da mensagem fornecida aqui. A essência da mensagem é que uma única versão dos eventos que se desenrolam não é suficiente para nós, e devemos considerar o máximo deles. A história nos oferece apenas uma versão, e seu tamanho às vezes pode ser insuficiente para uma avaliação objetiva. Por exemplo, não faz muito tempo que muitas corretoras obtiveram alguns dos símbolos de criptomoedas mais populares. Isso é muito bom em termos de possibilidade de testar e negociar esses símbolos. Mas a desvantagem é que não há dados históricos suficientes para desenvolver sistemas de negociação sustentáveis para Expert Advisors que operam em barras.

A simulação permitirá criar instrumentos artificiais e gerar suas cotações a cada vez de maneira completamente diferente. Isso nos fornecerá o quadro mais amplo possível para estudar o modelo matemático de recompra e outros princípios matemáticos importantes dos quais falei no artigo anterior. Outra vantagem importante é que seremos capazes de simular um número ilimitado de instrumentos independentes para negociação paralela. Em última análise, não teremos mais limitação na duração dos testes e no número de instrumentos negociados de forma independente. Claro, essas não serão cotações reais, mas elas não diferirão de nenhuma maneira das reais em termos de leis de precificação.

Modelo matemático de simulação de preços usando lógica de discretização

No contexto de nossa tarefa, o uso da abordagem de "discretização arbitrária" é mais do que suficiente, porque uma discretização forte apenas aumentará a eficiência de nosso algoritmo, apenas porque esses sistemas automaticamente resistem mais eficazmente aos spreads. No entanto, construí um algoritmo que permite a simulação de ticks também. Afinal, um tick é o menor intervalo de tempo. O tempo entre a chegada dos ticks é muito diferente, mas se você calcular o tempo médio entre os ticks, poderá imitar os ticks como uma primeira aproximação.

Por uma barra, neste caso, entendemos um período fixo de tempo, que é conveniente para nós perceber visualmente. Mas isso é conveniente apenas porque disseram a você que é conveniente, e você não pode escapar disso, porque todos os terminais de negociação são adaptados especificamente para essa paradigma. No entanto, isso está longe de ser a melhor maneira de discretizar a precificação. Acredito que muitos de vocês estejam familiarizados com "renko". Essa abordagem para discretização de preços é destinada apenas a uma coisa - se afastar do tempo. O valor dessa abordagem pode ser completamente diferente para abordagens e traders diferentes. Tudo isso é individual. No entanto, uso esse exemplo apenas para mostrar uma das formas alternativas de discretizar séries de preços. Esse exemplo, em minha compreensão, deve mostrar que, no contexto de nossa tarefa, usaremos uma lógica de discretização completamente diferente e desconhecida, mas que nos permitirá modelar preços de maneira muito simples e eficiente, sem custos computacionais excessivos.

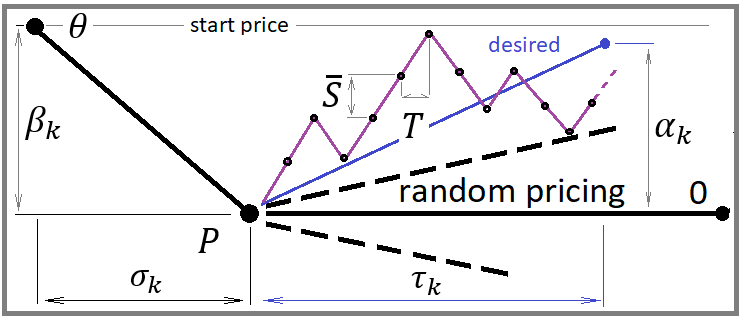
Para a construção correta de um paradigma eficiente e econômico em termos de potência de computação, dê uma olhada na seguinte imagem:

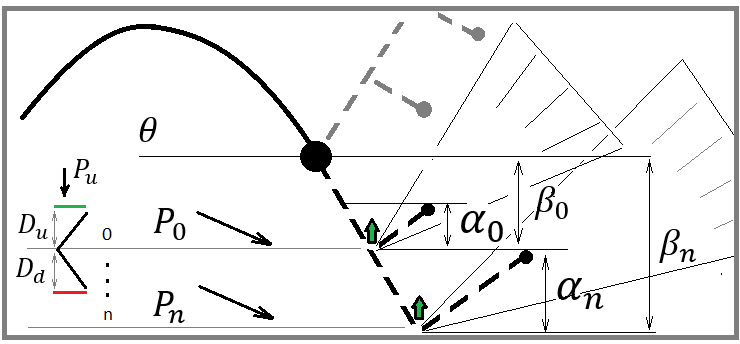
A imagem mostra alguns possíveis cenários de reversões de preços. Essas duas reversões para mim denotam dois pontos arbitrários que podem ser escolhidos de absolutamente qualquer maneira, e o método de escolha não tem importância. O importante é que podemos escolher arbitrariamente qualquer ponto que possa ser considerado como um ponto provável de reversão.

A palavra "provável" deve imediatamente dizer a todo matemático que em um determinado ponto há alguma probabilidade de algum evento desejado. Em nosso caso, podemos dizer que um evento dado pode ser arbitrário. O evento de reversão é caracterizado pelos limites superior e inferior do incremento de preço. A probabilidade desse evento pode ser calculada da seguinte maneira:

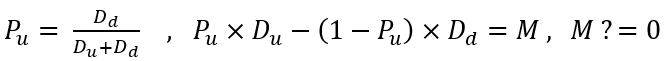
Aqui está a probabilidade de atingir o limite superior e a equação da qual esta fórmula é derivada. A equação caracteriza a expectativa matemática do incremento de preço se não houver momento preditivo. A falta de momento preditivo se traduz em uma expectativa zero, mas em nossa simulação quero ser capaz de ajustar os parâmetros de momento preditivo para que possamos aumentar ou enfraquecer convenientemente as características planas de nossos preços simulados. Por fim, você verá como isso afeta o algoritmo de recompra e obterá um modelo matemático funcional para negociação diversificada usando o algoritmo de recompra. Mas primeiro, quero lhe apresentar toda a matemática por trás de tudo isso.

Atualmente, podemos ver que todas essas equações são bonitas e aparentemente úteis, mas até agora não há um algoritmo conveniente para ajustar a planicidade (reversão) do instrumento. Para desenvolver tal algoritmo, precisamos introduzir os seguintes valores:

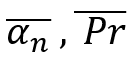
O primeiro valor é na verdade o valor médio de "alfa". Também podemos chamá-lo de expectativa matemática do valor de reversão do preço após um movimento descendente arbitrário. O segundo valor é a expectativa matemática da porcentagem de reversão expressa como um valor relativo ao seu movimento anterior. A essência dessas quantidades é a mesma, com a única exceção:

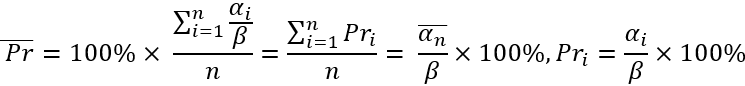
Aqui estou apenas mostrando como essas quantidades estão relacionadas e como são calculadas. Em nosso modelo, regularemos a reversão média definindo sua porcentagem média e inverteremos a lógica usando-a para determinar a reversão média de preço. Você deve admitir que a porcentagem média de reversão é muito conveniente como um valor regulatório para o parâmetro de planicidade do mercado. Se essa porcentagem for definida como zero, então na verdade requeremos uma precificação aleatória (isso é apenas um exemplo). A única coisa que quero observar é que todas as reversões de preço são consideradas em relação ao ponto "theta". Espero que você me perdoe as liberdades em minha notação, porque este material é completamente meu e não há um traço de trabalho de outra pessoa aqui. Essas equações são necessárias para entender o que farei a seguir.

Outra característica importante de qualquer precificação é a volatilidade (taxa de mudança de preço). Esse parâmetro está associado ao tempo, e precisamos encontrar uma maneira extremamente conveniente de definir esse valor. Isso deve nos permitir controlar facilmente e efetivamente a taxa de precificação, além de calcular corretamente o tempo dos ciclos de negociação. Atualmente, tudo isso pode parecer muito complicado, mas ficará muito mais claro quando eu começar a praticar e mostrar como funciona. Vamos lidar primeiro com a volatilidade.

Na interpretação clássica, a volatilidade é um pouco diferente, mais precisamente, o grau de possível movimento relativo de preço de um mínimo para um máximo e vice-versa, de um máximo para um mínimo. Essa é uma maneira muito inconveniente de definir a taxa de movimento de preços. Existe uma maneira muito mais conveniente, que envolve medir o movimento médio de preços ao longo de um período de tempo fixo. Temos esses segmentos. Eles são chamados de barras. Na verdade, temos a lei de distribuição de uma variável aleatória do módulo de mudança de preço por barra. Quanto maior esse valor, maior a volatilidade do preço (taxa de mudança). Introduzimos as seguintes configurações:

Quanto à questão de se a distribuição aleatória do valor "S" deve ser simulada, posso dizer que não é necessário. A única coisa que você precisa saber é que a precificação real será diferente do método que usaremos no modelo matemático. Proponho fixar o valor "S" no nível de seu valor médio. Uma vez que o tempo de cada etapa já está fixado, obtemos tanto o tamanho da etapa quanto a sua duração no tempo. Isso nos permitirá avaliar posteriormente a rentabilidade anual do sistema de negociação, bem como medir o tempo médio do ciclo de negociação. Agora, vejamos a seguinte imagem para avançar:

Uma vez que teremos que simular a precificação para cada etapa, é óbvio que a etapa pode ser para baixo ou para cima. Se definirmos uma etapa equiprovável em ambas as direções, obteremos uma precificação aleatória. Isso significa que, para regular a planicidade, devemos alterar essas probabilidades de etapa. Isso será o fornecimento de algum tipo de "gravidade" ao ponto de partida do preço, a partir do qual o preço começou a subir ou descer. Em nosso caso, precisaremos realizar o seguinte:  

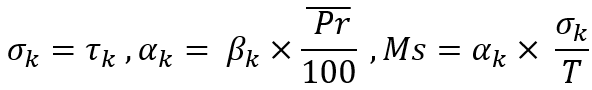
Neste caso, para simplificar o modelo, assumi que a reversão média do preço escolhida exige exatamente o mesmo tempo que foi gasto na alta ou queda de preço anterior. O objetivo desses cálculos é determinar a expectativa instantânea para uma única etapa, a fim de calcular a probabilidade de que a etapa ocorra para cima. Com essa probabilidade, a simulação da nova etapa é ajustada. Esse valor é recalculado após cada etapa para cada instrumento de negociação individual.

Aqui está um ponto muito importante: se descrevermos cada instrumento separadamente, então teremos que criar uma matriz com dados sobre a mudança média de preço para cada um deles. Mas dentro do contexto da minha tarefa, todos os instrumentos são iguais, e portanto é possível introduzir uma característica geral e mais conveniente para descrever uma etapa na forma de uma porcentagem média de mudança de preço:

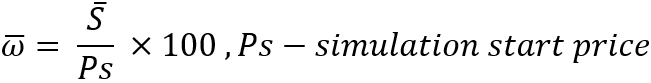
A vantagem dessa característica é que ela é invariante em relação a qualquer preço atual. Além disso, se considerarmos instrumentos ideais, então não importa em qual preço a simulação comece, porque isso não afetará o lucro ou a perda durante os testes. Depois de entendermos isso, então podemos iniciar com segurança a negociação paralela para nosso algoritmo de recompra a partir de um preço, digamos, igual a 1. Após determinar esse valor, já é possível calcular o valor da etapa em si:

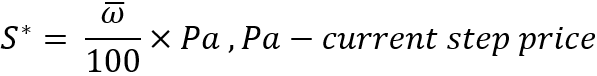
Agora, conhecendo a etapa, podemos afirmar que coletamos todos os dados necessários para calcular a probabilidade de haver uma etapa para cima. Para fazer isso, usamos nossa fórmula original para a expectativa matemática de uma etapa com algumas substituições:

Após essa substituição, podemos resolver essa equação para a probabilidade de uma etapa ascendente e, finalmente, obter a probabilidade faltante:

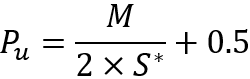
A única coisa que vale a pena observar é que essas equações são válidas para o caso em que o preço da simulação cai abaixo do ponto de partida. Mas o que fazer quando o preço subiu? Tudo é muito simples. Apenas precisamos considerar o gráfico espelhado. Isso pode ser feito porque estamos considerando instrumentos perfeitos. Se imaginarmos que o gráfico de preços pode ser descrito por uma certa expressão "P = P(t)", então a reversão do instrumento parecerá assim:

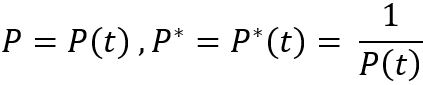
Essa reversão manterá as equações funcionando para a situação em que o preço ultrapassou o ponto de partida. A única coisa que precisamos entender é que todas as quantidades em nossas expressões que são calculadas usando preços (por exemplo, deltas) devem usar o preço já convertido elevado à potência menos um.

Vamos construir agora um modelo de negociação. Eu o criei de forma unidirecional, pois foi originalmente destinado à negociação à vista de criptomoedas. No entanto, esse modelo de negociação também é adequado para pares de moedas forex. A questão é que, se o modelo funcionar, por exemplo, apenas no caso de recompra, ele funcionará igualmente bem para revenda. A única diferença é que, durante o teste, pularemos as meias ondas superiores e trabalharemos apenas nas inferiores. Para gerenciar o modelo de negociação, introduzi as seguintes características:

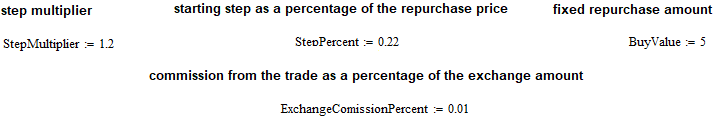
A compra inicial começa a partir do preço "1 - Percentual da Etapa/100", e a etapa de recompra será igual a "Percentual da Etapa/100". Na verdade, ainda deve haver uma multiplicação pelo preço inicial, mas como tomamos esse preço igual a um, o cálculo da etapa é muito simplificado. Além disso, foi introduzida a possibilidade de aumento recorrente da etapa. Por exemplo, podemos aumentar cada etapa subsequente de recompra em relação à anterior em N vezes, ou diminuí-la da mesma forma. Tudo isso depende do valor do coeficiente correspondente. A etapa de recompra é medida na moeda inferior do instrumento (não a moeda base). Essa regra também vale para criptomoedas.

Para simplificar o modelo, assume-se que os instrumentos de negociação aplicados neste caso são aproximadamente os seguintes: EURUSD, GBPUSD, NZDUSD e assim por diante, ou seja, a moeda inferior do instrumento negociado para todos os instrumentos negociados deve ser a mesma. Isso simplifica um modelo já muito complexo, mas é totalmente suficiente tanto para testar os princípios matemáticos do último artigo quanto para otimizar algoritmos de recompra. O spread, em nosso caso, é levado em consideração na forma de uma comissão, que é a mesma coisa. Em geral, os parâmetros são suficientes para o protótipo do modelo matemático. Vamos dar uma olhada no processo de recompra:

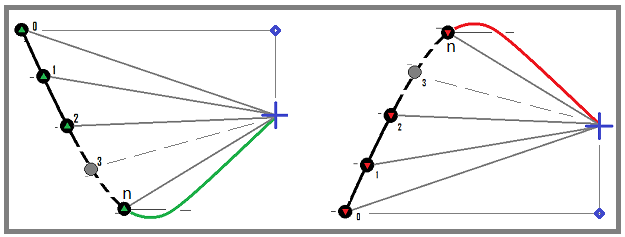
Vamos usar a primeira opção (com o movimento de retorno verde). Isso na verdade é comprar a moeda base e depois vendê-la no ponto azul. Com essa abordagem, qualquer ciclo de negociação concluído será lucrativo. O mesmo se aplica ao ciclo de venda com um movimento de retorno vermelho, mas vamos ignorá-los, como eu disse, para que o modelo seja o mais multifuncional possível e adequado tanto para a negociação no mercado forex quanto para a negociação à vista em bolsas de criptomoedas.

O modelo é feito de tal forma que a alavancagem de negociação não desempenha um papel. Acredito que lhe forneci informações teóricas suficientes para que você possa entender melhor a parte prática, e isso pode ajudar alguém a construir seu próprio modelo usando minhas conquistas.

Teste do modelo

Vamos começar nosso teste com diferentes variações de geração de cotações. Para mostrar visualmente a diferença na geração de cotações, vamos primeiro configurar o modelo da seguinte forma:

Com essa configuração, alcançaremos uma precificação aleatória. Vamos dar uma olhada em um par de cotações geradas a partir desse ponto de vista:

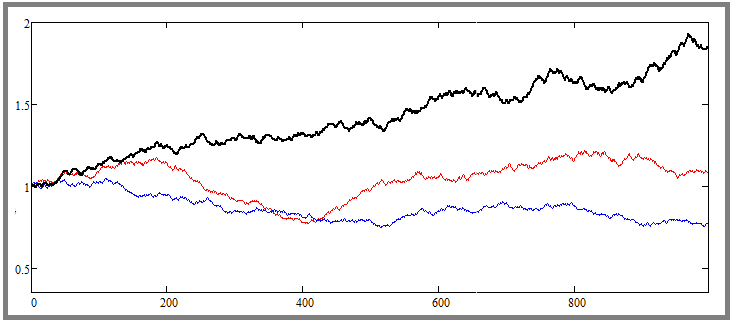
Este é um gráfico de um modelo matemático, que mostra duas cotações escolhidas aleatoriamente do baralho e outra curva adicional, que tem o maior desvio em relação ao preço de partida. No modelo matemático, é possível definir o número necessário de instrumentos a serem simulados em paralelo, e é natural que haja muitos deles, e sempre haverá um que é o menos simétrico e mais volátil. Mas espero que você entenda que esse é apenas o resultado de processos probabilísticos. Agora, vamos colocar o parâmetro em uma posição diferente:

Como você já deve ter entendido, esse passo cria uma gravidade de retorno do preço ao ponto de partida. O resultado é o seguinte:

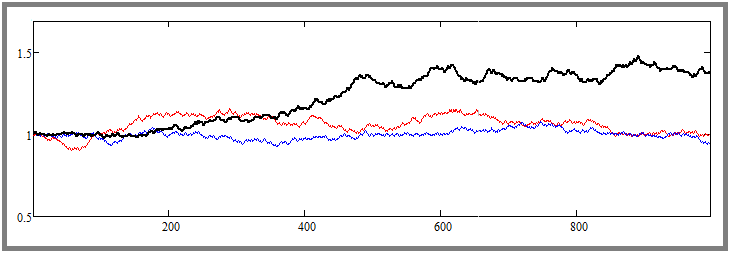
Observe a diferença entre a imagem anterior e a atual. Aqui já forçamos o ajuste da planicidade na direção desejada. Podemos ver que as curvas estão fortemente pressionadas contra o preço de partida - o mesmo aconteceu com a cotação mais volátil colorida de preto. Ambos os exemplos simulam exatamente mil etapas para cada ferramenta. Mais tarde, aumentarei esses números e brincarei com eles para entender como tudo funciona e quais parâmetros são exatamente afetados.

Agora é necessário determinar quais parâmetros devem ser usados para testar a negociação artificial e como ela deve ser testada. Vamos rapidamente relembrar as perguntas que eu respondi no artigo anterior. De forma mais simples e compreensível, elas soaram da seguinte maneira:

1. Condição de rentabilidade dos sistemas de negociação com recompra.
2. A linha de lucro tende a ser uma linha reta perfeita quando se negocia indefinidamente com instrumentos de negociação ideais?
3. A linha de lucro tende a ser uma linha reta perfeita à medida que o número de instrumentos aumenta até o infinito com um período fixo de negociação?

Vamos descobrir a condição de lucratividade. Para fazer isso, primeiro realizaremos negociações paralelas usando preços aleatórios e veremos o resultado. Ele terá uma aparência aproximadamente assim:

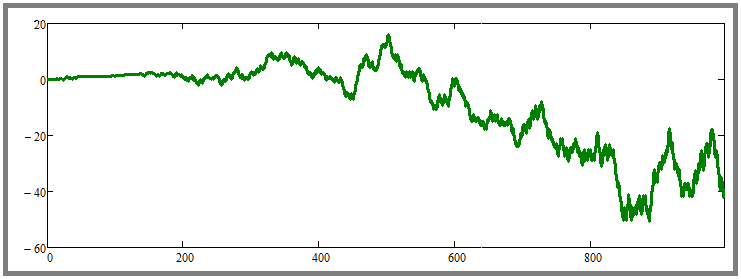
Em diferentes gerações, foram obtidas curvas tanto lucrativas quanto não lucrativas. Ainda não está claro, mas a confirmação da inutilidade das recompras em caso de preços aleatórios pode ser um aumento extremo no número de instrumentos negociados em paralelo. Vamos ver o que acontece se aumentarmos o número para, digamos, cem, e ao mesmo tempo aumentarmos o número de etapas de simulação para cada instrumento para 10.000:

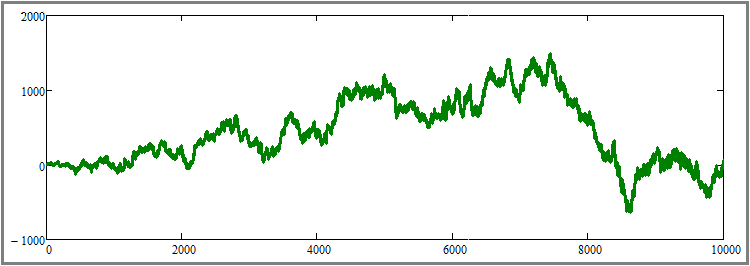
Como você pode ver, nem o aumento no número de instrumentos negociados em paralelo, nem o aumento na duração dos testes tiveram algum efeito visível. Provavelmente, isso confirma o fato matematicamente comprovado do artigo anterior de que qualquer sistema de negociação, incluindo o algoritmo de recompra, drena a conta em caso de precificação completamente aleatória e sem um momento preditivo. Nesta etapa, considero o ponto 1 teoricamente e praticamente comprovado. Agora, passemos ao segundo ponto e configuremos a seguinte configuração:

De acordo com meus testes, a gravidade de retorno se mostrou bastante suficiente para a possibilidade de uma avaliação visual do efeito para qualquer leitor. Claro, podemos definir uma porcentagem menor, mas o efeito não será tão pronunciado. Redefini o número de etapas de simulação para o valor original de mil etapas. Agora, vejamos o resultado:

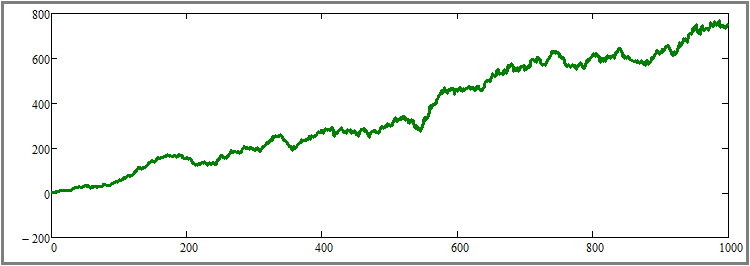
Acredito que não será difícil entender que esse gráfico, entre outras coisas, é uma adição à prova do parágrafo anterior, mas, ao mesmo tempo, também é um ponto de partida para a prova do próximo subparágrafo. A próxima etapa em meu plano é aumentar a duração de todos os segmentos de teste sem alterar nenhum outro parâmetro. Para maior clareza, aumentei o número de etapas de simulação para cada instrumento cinquenta vezes - de 1000 para 50.000. Este é um aumento bastante grande, mas é a única maneira de sentir visualmente esse efeito sem vários testes e média dos resultados. Vejamos o resultado:

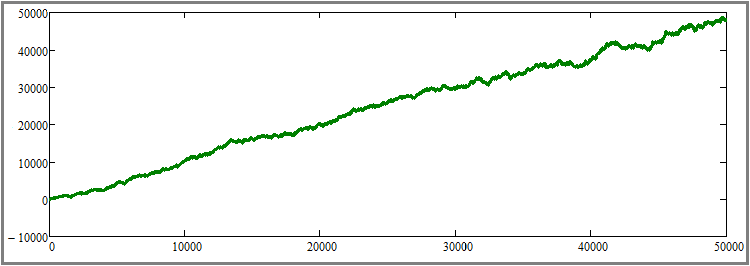
Como podemos ver, a curva ficou muito mais suave e se aproxima de uma linha reta, o que significa que o segundo princípio de aumentar o fator de linearidade (beleza do gráfico) com a duração do teste funciona exatamente como previsto. Claro, isso é verdade apenas com a suposição de que se sabe que a estratégia escolhida é lucrativa. Nesta etapa, considero o segundo subparágrafo teoricamente e praticamente comprovado.

Agora, vamos retornar o número de etapas de simulação ao nível inicial de mil etapas e, inversamente, aumentar o número de instrumentos negociados em paralelo em dez vezes, até o valor de 1000. De acordo com a lenda, devemos obter um aumento visível na beleza do gráfico. Vamos ver se isso é verdade:

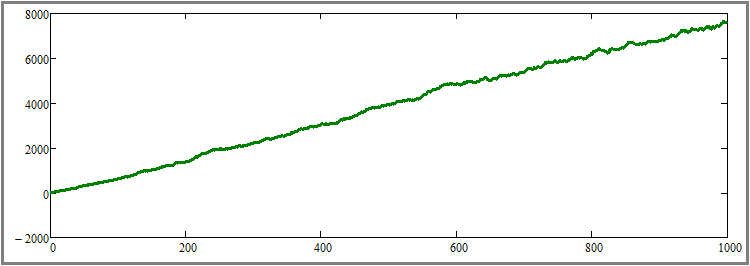
Como podemos ver, essa hipótese foi confirmada, e o efeito é extremamente pronunciado. Nesta fase, acredito que todas as três hipóteses estejam teoricamente e praticamente comprovadas. Os resultados são os seguintes:

1. A condição para a rentabilidade de qualquer sistema de negociação é a presença de um momento preditivo.
2. Com o aumento da duração da negociação ou backtesting, qualquer curva de um sistema de negociação lucrativo se torna mais bonita e reta (sem lote automático) + [sujeito ao ponto 1].
3. Com um aumento no número de pares de moedas negociados para um sistema de negociação multimoedas ou um aumento no número de sistemas negociados simultaneamente, a curva de rentabilidade do sistema de negociação se torna mais bonita e mais reta + [sujeito ao ponto 1 para cada um destes sistemas].

Expert Advisor de teste

Descobrimos como usar sistemas de negociação corretamente, incluindo o algoritmo de recompra, para ganhar dinheiro de maneira eficiente e segura tanto com negociações automáticas quanto manuais. O cálculo de gerenciamento de dinheiro e outras situações variadas para a combinação correta de sistemas de negociação merecem um artigo separado que vou escrever um pouco mais tarde.

Adicionei esta seção para que você possa ver claramente o fato de que o algoritmo de recompra é uma estratégia funcional. Para isso, criei um EA de teste que replica nosso modelo matemático, com a única diferença de que ele também processa as meias ondas superiores (ciclos de negociação de venda). Encontrei algumas configurações que comprovam a possibilidade de criar um sistema de negociação semelhante para o MetaTrader 5. Aqui está uma delas:

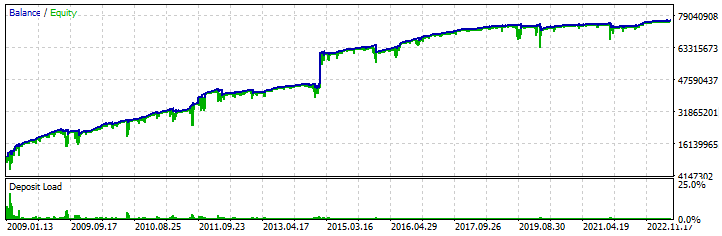
Os testes foram realizados no período de 2009 a 2023, utilizando testes paralelos de todos os "28" pares de moedas semelhantes ao nosso modelo matemático. Utilizei o modelo multibot que descrevi em um dos artigos anteriores para construir o algoritmo de teste. Claro, a curva de lucro está longe de ser ideal, e o depósito inicial para esse tipo de negociação deve ser enorme, mas, no entanto, minha tarefa neste artigo não é lhe dar um robô pronto, mas demonstrar a proximidade ao modelo matemático. O mais importante que você deve entender é que, com certas modificações, esse algoritmo será muito mais seguro, eficiente e viável. Sugiro que você descubra a essência das melhorias por si mesmo. Acredito que será justo, considerando que estou mostrando coisas que geralmente estão escondidas.

O EA, juntamente com o conjunto, bem como o próprio modelo matemático, estão anexados ao artigo como um arquivo, e você pode, se desejar, estudar sua estrutura com mais detalhes e, talvez, desenvolver ainda mais a ideia. Na verdade, há muito mais utilidade em meu modelo matemático do que descrevi aqui. Ele calcula muitas características de negociação importantes graças ao seu próprio conjunto de parâmetros de saída após o backtest. Claro, sua funcionalidade é muito limitada, mas é suficiente para a prova e estimativas aproximadas.

Considerações finais

Neste artigo, concluí a parte prática da comprovação de que o princípio da diversificação funciona e deve ser usado. Mais importante ainda, em combinação com o artigo anterior, provei teoricamente e praticamente muitas coisas importantes que permitem, no mínimo, aumentar a eficiência de suas negociações. Além disso, a sobrevivência do algoritmo de recompra por mais de uma década foi comprovada com a ajuda do EA criado.

Considerando isso, obtivemos a confirmação da teoria das ondas de precificação, ou da planicidade do mercado. Aconselho que você preste atenção neste artigo como uma confirmação adicional. Nele, o autor dedica a máxima atenção exatamente ao mesmo algoritmo que descrevi em meu artigo. A partir daí, você pode obter conhecimento adicional sobre como usar esses efeitos para melhorar meu EA de teste ou desenvolver o seu próprio.