Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal

Contenido

• Introducción
• Valorando las posibilidades de aplicación de los fractales en el trading
• Fundamentos teóricos de la construcción del fractal universal
• Escribiendo el código de implementación del fractal universal
• Mostrando la primera fórmula basada en el fractal simétrico
• Evaluando el rendimiento de la fórmula mostrada para todos argumentos positivos y válidos
• El fractal avanzado como consecuencia del fractal universal
• Generalizando los resultados
• Conclusión
• Enlaces

Introducción

En el último artículo, nos familiarizamos con los fundamentos de la teoría de probabilidad que nos ayudarán a comprender mejor las características del uso de funciones fractales para las tareas comerciales. Prosiguiendo con el tema iniciado en el último artículo, mostraremos varias funciones fractales autosuficientes capaces de describir todos los procesos de fijación de precios que necesitamos, que eventualmente podemos generalizar, simplificar e incluso usar para elaborar algunas fórmulas que nos ayudarán a encontrar respuestas a una variedad de preguntas en las que nos faltan evaluaciones cuantitativas claras y respuestas inequívocas. 

Valorando las posibilidades de aplicación de los fractales en el trading

Vamos a contiuar con nuestra idea resumiendo los resultados del artículo anterior y reduciendo el material a unas dimensiones más compactas y universales. Si tomamos como ejemplo la construcción del fractal del último artículo, está claro que dicho fractal nos resultará de poca utilidad en la práctica; no obstante, el fractal en sí no es tan importante para nosotros como las reglas que podemos definir a la hora de construir estas estructuras. Al final, resulta que estas reglas prácticamente no han cambiado para tres tipos de fractales:

1. Fractal con límites simétricos
2. Fractal con límites asimétricos
3. Fractal con límite superior o inferior

Si lo pensamos, queda claro que tales fractales pueden utilizarse para describir los siguientes procesos:

• Imitación acelerada del comercio con capacidad de evaluar las probabilidades de varios escenarios, considerando la presencia de restricciones en el depósito (ya que el límite inferior puede simbolizar el nivel del depósito con el que será imposible realizar más transacciones).
• Estimación del número promedio de saltos dentro de un fractal (por ejemplo, podemos evaluar cuántas órdenes de media se darán antes de que obtengamos el beneficio o las pérdidas que deseamos)
• Estimación de los valores promedio totales para cada salto (por ejemplo, podemos calcular el tiempo promedio que la posición permanecerá pendiente basándonos en las estadísticas para una posición más pequeña (como tamaño, se indica el tamaño de sus stops en puntos o diferencia de precio), el proceso inverso también es posible)
• Valoración de la rentabilidad de las opciones basadas en un fractal con un solo límite
• Oportunidades no contabilizadas

Fundamentos teóricos de la construcción del fractal universal

Comenzaremos tomando las reglas de construcción que obtuvimos en el artículo anterior y completándolas para lograr una comprensión completa de cómo se construye un fractal. Además, hemos localizado un pequeño error en nuestras fórmulas que impedía la asimetría de los límites tanto hacia arriba como hacia abajo. Resulta que hemos obtenido las fórmulas de manera absolutamente correcta, y funcionan para absolutamente cualquier fractal. De hecho, el resultado es una función que permite implementar absolutamente cualquier fractal. Todos los posibles fractales suponen un caso especial de un fractal general. Si tomamos los tres tipos de fractales que hemos definido anteriormente, resultará que las condiciones del fractal general para la implementación de estos tres casos especiales tomarán la forma:

1. m = n & [ m > s & n > s ]
2. ( m > n || n > m )  & [ m > s & n > s ]
3. ( m > S && n <= S ) || ( n > S && m <= S )

Esquemáticamente, estos tres tipos de fractal tienen el aspecto siguiente:

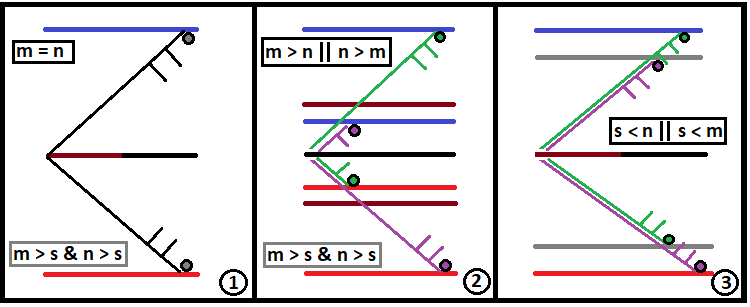
De forma ideal, obviamente, "S" debería tender al infinito. No hemos descrito las siguientes variables en el artículo anterior, pero las describiremos aquí para obtener una imagen completa sobre el uso de la fórmula general para obtener casos especiales. Un fractal es una función que opera según el principio de reacción en cadena, como en una bomba atómica. Si configuramos una reacción en cadena demasiado profunda, es posible que la computadora no pueda acometer los cálculos; en casos no particularmente críticos, simplemente calculará durante mucho tiempo, a veces minutos, a veces horas, e incluso un día completo. Para iniciar correctamente una reacción en cadena en un fractal, deberemos encontrar dos magnitudes fundamentales:

• Half - mitad de la anchura del canal
• Middle - magnitud "U" que se corresponde con la línea media

El valor "Half" para los tres casos que definimos en el artículo anterior, se calcula de forma muy sencilla: se trata de la media aritmética de "m" y "n":

• Half = ( n + m ) / 2

Para implementar la segunda magnitud, necesitaremos las tres variantes de la lógica, pero la primera y la segunda se podrán combinar en una; entonces resultará que debemos considerar solo dos variantes:

1. n >= m
2. n < m

Además, como el eje "U" está dirigido "hacia arriba" y el valor "n" también constituye la parte superior del canal, mientras que el valor "m" es el inferior, obtendremos las dos relaciones para ambos casos posibles de la configuración "m" y "n":

1. Middle = Half - m
2. Middle = - ( Half - n )

Estos valores se transmitirán a la propia función fractal para su uso interno, ya que sin ellos será imposible implementar la lógica de ramificación interna que describimos en el artículo anterior. El prototipo de esta función tendrá el aspecto que sigue:

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Como podemos ver, para iniciar correctamente un fractal, deberemos transmitir cinco magnitudes imprescindibles:

1. Half - mitad de la anchura del canal
   
2. Middle - magnitud "U" que se corresponde con la línea media
   
3. m - número de saltos hasta el límite inferior
4. n - número de saltos hasta el límite superior
5. s - número máximo permitido de saltos en cualquier dirección para una sola cadena

El resto de las cantidades se denominarán en mayúsculas para dejar en claro que estas magnitudes son dinámicas y resultarán completamente distintas en cada nivel fractal individual. Vamos a definir estas en primer lugar:

• S - número de saltos acumulados en la cadena de probabilidades actual,  para ser transmitidos al siguiente nivel fractal
• U - eliminación actual del final de la cadena desde el punto de inicio de la misma, para la transmisión al siguiente nivel fractal
• P - producto recopilado de las probabilidades de toda la cadena usando como base el esquema de Bernoulli,  para la transferencia al siguiente nivel fractal

Partiendo de esto, queda claro que para ejecutar el fractal deberemos transmitir los valores correctos a la función:

• S = 0 (ya que este es el comienzo y aún no ha habido saltos)
• U = 0 (por la misma razón, porque estamos al inicio de la cadena)
• P = 1 (ya que este es el eslabón cero y todas las cadenas que parten de él deben formar un grupo completo)

Vamos a terminar de construir las reglas generales para los fractales que simulan el precio o el comercio reescribiendo brevemente las reglas que se obtuvimos en el artículo anterior. Necesitamos estas reglas para las partes internas del fractal. Las reglas se basan en varias fórmulas básicas para los mismos saltos:

• f = u + d  — en este caso, dicho valor supone el número de saltos del futuro árbol de combinaciones (el tamaño se determina usando la distancia hasta el límite más cercano del corredor fractal)
• s = u - d  — número de saltos ascendentes totales, expresado como segmentos descendentes y ascendentes

Hemos determinado que iteraremos en un ciclo por "u". Además, utilizaremos el valor de "s" como una nueva "U" que transmitiremos al siguiente nivel fractal si el número de saltos que nos quedan nos lo permite. Para ello, tendremos que definir una fórmula para "u" que no contenga "d". Podemos conseguirlo fácilmente expresando "d" de la primera ecuación y sustituyéndola en la segunda:

• s = 2*u - f

Pero esta cifra podría aceptarse como un nuevo valor "U" para la transmisión adicional si la "U" actual fuera igual a cero, por lo que esta "s" deberá añadirse a "U", obteniendo así un nuevo valor para la posterior transmisión:

• NewU = s + U  - nuestra nueva "U" para la transmisión al siguiente nivel fractal

Como ya determinamos en el último artículo, esta expresión adopta tres posibles valores basados ​​en los tres posibles valores del número "f". Hemos tomado el diagrama del último artículo y lo hemos modificado para dispersar cualquier duda:

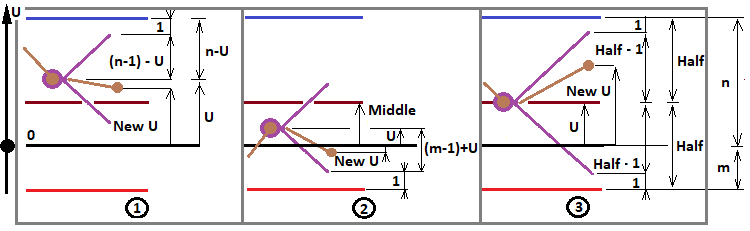
Este diagrama resulta muy apropiado aquí, ya que ahora nos ocupamos de determinar todas las posibles configuraciones fractales que nos puedan resultar útiles para resolver la mayoría de los problemas. Usando este diagrama como base, definiremos los tres casos para "f":

1. f = ( n - 1 ) - U
2. f = ( m - 1 ) + U
3. f = Half - 1

Estos tres casos aparecen cuando se cumplen las condiciones correspondientes:

1. U > Middle
2. U < Middle
3. U = Middle

Solo nos queda describir las dos últimas magnitudes para la transmisión al siguiente nivel fractal y resaltar por separado las cuestiones relacionadas con la recopilación de los números en un fractal. Las dos magnitudes restantes se calculan de la forma siguiente:

• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i)  — nuestra nueva probabilidad de la cadena "P" para la transmisión al siguiente nivel de fractal
• NewS = S + f = S + (floor(Mid) - 1) — nuestra nueva "S" para la transmisión al siguiente nivel de fractal

Antes de iniciar la recopilación de los números en una variable común, tenemos que comprender que la recopilación de estos se deberá realizar en un bloque similar, con la única diferencia de que solo realizaremos un salto y, en consecuencia, el esquema de Bernoulli ya no será necesario. El orden de las declaraciones no es importante, solo tienen que encontrarse en el mismo bloque. La recopilación de los números solo es posible en las situaciones "1" y "2", pero con algunas aclaraciones:

1. U = n - 1
2. U = - ( m - 1 )

Para el primer caso, los tres valores anteriores serán mucho más fáciles de calcular, ya que solo realizamos un salto:

• NewU = U - 1
• NewP = P * p
• NewS = S + 1

Obviamente, para el segundo caso todo resulta parecido, con alguna pequeña diferencia:

• NewU = U + 1
• NewP = P * ( 1 - p )
• NewS = S + 1

También debemos decir que, usando como base la generalización de todos los fractales, cada uno de estos fractales se divide en 2 tipos:

• Fractal para calcular la probabilidad total de cruzamiento del límite superior del corredor.
• Fractal para calcular la probabilidad total de cruzamiento del límite inferior del corredor.

A su vez, cada uno de estos tipos se corresponde con un tipo más de fractal, que se relaciona con el original:

• Fractal para calcular el número promedio de saltos para cruzar el límite superior
• Fractal para calcular el número promedio de saltos para cruzar el límite inferior

Estos cuatro tipos de fractales en realidad se distinguen solo en el tipo de los números sumados. En el caso de la recopilación de probabilidades, solo podemos sumar "P*p" y "P*(1-p). Para analizar los otros dos fractales, necesitaremos variables adicionales para la transmisión a los siguientes niveles fractales. El asunto es que en tales fractales utilizamos saltos del mismo tamaño pero en dirección opuesta, y sus probabilidades son "p" o "1-p" debido a la integridad del grupo. Pero en aquellos casos en los que "p" no es igual a "0.5", este hecho indica automáticamente que son dos eventos completamente distintos que pueden tener características completamente diferentes. Entendemos por características un conjunto de algunas variables aleatorias que se corresponden con un evento dado. Uno de esos valores es la "vida útil de la posición". Puede haber tantas magnitudes como queramos y, si fuera necesario, podremos considerarlas de la misma manera que el tiempo. Lo más interesante es que el análisis de todas estas cantidades se puede simplificar después de considerar un simple número de saltos. En este caso, los números sumados adoptarán la forma que sigue:

1.  P * p * NewS
2.  P * ( 1 - p ) * NewS

Como podemos ver, solo hay que multiplicar las probabilidades por el propio número de saltos en esta cadena completa, salvo que esta es una fórmula para los casos en que los saltos ascendentes y descendentes tienen las mismas probabilidades. En los casos alternativos, deberemos describir los saltos ascendentes y hacia abajo con dos fractales distintos, o bien ofrecer una estructura para guardar ambos números en su interior. En el segundo caso, la función fractal retornará no un número, sino un contenedor con datos. El contenedor es autónomo y no requiere expansión. Hemos ido un poco más allá, ofreciendo un contenedor que nos permita guardar todos los parámetros que podamos requerir; en este sentido, no necesitaremos describir varias funciones con el mismo tipo de código. En su lugar, hemos combinado todas estas funciones en una única función capaz de describir todos los parámetros que podríamos necesitar. El tipo de fractal y la tarea que resuelve dependerán directamente de los parámetros de entrada de la función. Para ampliar el concepto, necesitaremos reemplazar la variable "S" y su equivalente "NewS" con los siguientes valores:

1. SU - saltos totales de la cadena de probabilidad elegida
2. SD - saltos descendentes totales de la cadena de probabilidad elegida
3. NewSU y NewSD - para la transmisión al siguiente nivel fractal
4. SU + SD = S

Debemos determinar los datos de la magnitud de la misma manera que hemos determinado "S". Para cuando "U > Middle":

• NewSU = SU
• NewSD = SD + 1

Para cuando "U < Middle":

• NewSU = SU + 1
• NewSD = SD

Además, para la actualización final del propio fractal, necesitaremos seis valores:

1. UpperMidSDown - número promedio total probable de saltos descendentes antes de alcanzar el límite superior
2. UpperMidSUp - número promedio total probable de saltos ascendentes antes de alcanzar el límite superior
3. UpperSummProbability - probabilidad de cruzar el límite superior
4. LowerMidSDown - número promedio total probable de saltos descendentes antes de alcanzar el límite inferior
5. LowerMidSUp - número promedio total probable de saltos hasta alcanzar el límite inferior
6. LowerSummProbability - probabilidad de cruzar el límite inferior

Los valores "1", "2", "4", "5" muestran la suma de los productos del número correspondiente de saltos y su probabilidad. Estos valores no tienen sentido por sí mismos, pero constituyen parte de las fórmulas de las magnitudes más útiles, que discutiremos más adelante. Los valores "3", "6" representan las probabilidades de las hipótesis de cruzar los dos límites, que forman un grupo completo. Juntas, todas estas magnitudes permiten determinar muchas cosas.

Escribiendo el código de implementación del fractal universal

Para iniciar correctamente el fractal, necesitaremos una función que realice todas las operaciones preparatorias antes del proceso, y luego inicie correctamente el propio fractal usando como base las reglas que hemos definido. Hemos implementado este algoritmo al estilo MQL5:

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Después de calcular el fractal, la función retornará nuestro contenedor con todos los datos que podamos necesitar:

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

En este contenedor se prevé una sobrecarga del operador "+ =" para fusionar dos estructuras idénticas; esto nos resultará útil para la función principal. Aquí tenemos la propia función de fractal:

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

Hemos puesto a prueba el código en MetaTrader 5, y funciona muy bien. Si lo deseamos, podemos ampliar esta lógica: todavía existen muchas posibilidades adicionales. No obstante, en este caso, no hemos generado los parámetros de entrada de esta función, porque hasta ahora el código de este tipo resulta suficiente para nuestros propósitos. Recomendamos al lector que estudie su código con detenimiento: podrá convencerse por sí mismo de que los principios matemáticos descritos anteriormente se cumplen al cien por cien. Como podemos ver, incluso un fragmento de código tan pequeño puede hacer maravillas. Siempre hemos pensado que el código debe contener tanta lógica y matemáticas como sea posible, pues esto será exactamente lo que nos resultará útil al final: el código por sí mismo no tiene razón de ser, incluso un código hermoso será inútil si no podemos usarlo para el propósito previsto. Para nosotros, el propósito directo es su utilidad en el trading. Como prueba, mostraremos el log:

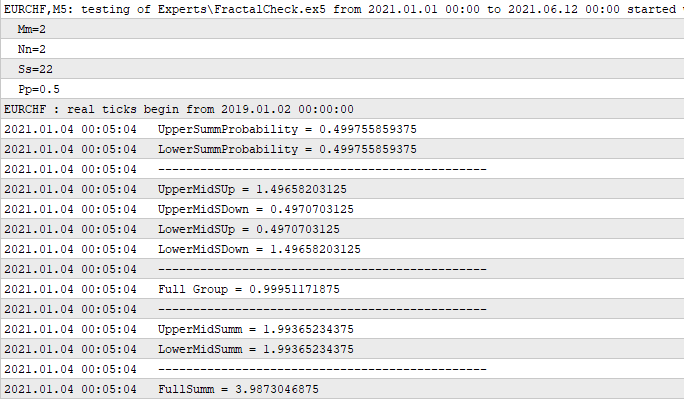
En este caso, podemos ver que hemos creado un asesor simple capaz de calcular el fractal completo en el primer tick recibido; esto ocurre solo una vez, ya que no necesitamos que los cálculos se repitan: darían el mismo resultado. Los primeros seis números forman parte del contenedor y el resto son derivados de estos. No hemos mostrado todas las derivadas, sino solo las más importantes, que nos resultarán útiles para comprender que con la ayuda de estas seis variables podemos obtener los demás datos que nos interesan. Por ejemplo, vamos a analizar "Full Group". No se llama así por casualidad, ya que, según nuestros cálculos anteriores, la suma de las probabilidades de dos hipótesis incompatibles de cruzar uno de los límites debería ser igual a uno, extremo que nuestro código confirma con éxito. Después vienen dos números idénticos, que son la suma de "1", "2" y "3", "4". El último número ya es la suma de los dos penúltimos, y representa el número promedio de saltos por los que pasará la cadena. No en vano hemos configurado exactamente estos parámetros de entrada en la función de inicio, donde "m" y "n" son iguales y simétricas; aclararemos los motivos a continuación.

Mostrando la primera fórmula basada en el fractal simétrico

Si observamos de cerca el resultado del log, podemos ver que el número promedio de saltos por los que pasará la cadena tiende al número "4". En este caso, además, queda claro que hemos duplicado el tamaño del corredor en relación con un solo salto. Tendremos un salto unitario si establecemos "n" y "m" iguales a uno. En otras palabras, si queremos calcular el número promedio de saltos en un corredor formado por corredores más pequeños, de manera que un número entero de corredores más pequeños quepan en el nuevo corredor y el nuevo corredor también resulte simétrico, entonces podemos suponer que:

• P[n] = P[n-1] * 2  - expresión recursiva para la anchura en saltos del nuevo corredor, basada en la anchura del corredor antiguo (más pequeño) a partir del cual se compone el nuevo corredor
• S [n] = S [n-1] * 4 - expresión recursiva para calcular el número promedio de saltos en el corredor nuevo, expresado como el número promedio de saltos en un corredor más pequeño

Si aceptamos "P[0]=1" y "S[0]=1", y en consecuencia comenzamos la numeración de esta recursividad desde el índice "0", resultará fácil adivinar que esta recursividad se puede representar como dos series muy similares:

• P[n] = 2^n , n = 0 ... + infinity
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

Si observamos de cerca la primera fila y transformamos correctamente la segunda, resultará que la segunda fila se puede expresar usando los elementos de la primera. En otras palabras, surge la dependencia S = S(P) = P^2. Hasta ahora, esta dependencia solo era cierta a la hora de duplicar de forma recursiva la anchura del corredor. A nuestro juicio, al ver esta fórmula, surge inmediatamente la idea de comprobar la importancia de esta fórmula para cualquier número aleatoriamente grande de "n" y "m". Resulta lógico como segundo salto adoptar "n=3", "m=3" y calcular los mismos valores. Al comprobar este hecho, resultó que para estos parámetros de entrada el número promedio de saltos tiende al número "9". Por cierto, también podemos verificar todo esto por nosotros mismos usando el código que ofrecimos anteriormente, o bien los programas MathCad 15 que también adjuntaremos al artículo. Resulta sencillo adivinar que podemos componer exactamente la misma serie para estos parámetros y realizar las mismas manipulaciones:

• P[n] = 3^n , n = 0 ... + infinity
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Como podemos ver en los resultados, hemos obtenido la misma relación "S=S(P)=P^2". Obviamente, podemos hacer lo mismo para todos los demás escenarios posibles para dividir el intervalo, pero esto no será necesario. Esto significa que si conocemos, por ejemplo, la vida media de un precio dentro de un corredor simétrico, podremos calcular la vida media de un precio en cualquier otro corredor. Podemos calcularlo así:

• S = S0 * K^2 - número medio de saltos del nuevo corredor
• T = S * T0 - tiempo medio de vida del nuevo corredor
• T = T0 * K^2- tiempo medio de vida del nuevo corredor expresado como el tiempo medio de otro corredor (lo obtenemos adoptando S0 = 1)
• S0 - número medio de saltos del corredor antiguo
• T0 - tiempo medio de un salto del corredor antiguo
• P = K * P0  --> K = P/P0 - cuantás veces mayor es el nuevo corredor respecto al antiguo
• P - anchura del nuevo corredor
• P0 - anchura del corredor antiguo

Ahora podemos comprobar esta hipótesis usando MathCad 15. Primero, revisaremos nuestras suposiciones sobre la dependencia cuadrática:

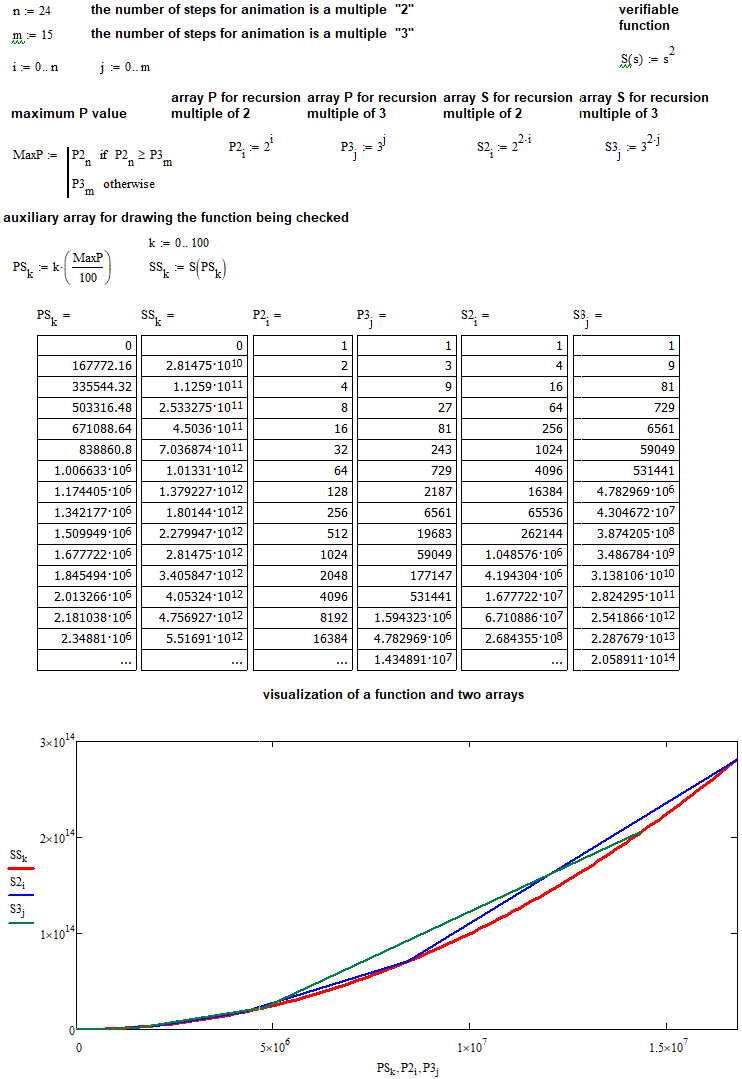
A nuestro juicio, ahora todo queda completalmente claro.

Evaluando el rendimiento de la fórmula mostrada para todos argumentos positivos y válidos

Resulta que la fórmula funciona para todos los números enteros "P", pero no está claro si podemos usarla para el caso de la fracción "K". Para conseguir una "K" fraccionaria, deberemos inventar un truco. Imaginemos que tenemos un corredor de precios con un tiempo promedio de vida conocido, y digamos que también tenemos un corredor que encaja "N" veces en nuestro corredor, pero que desconocemos su tiempo promedio de vida. No obstante, podremos encontrarlo un poco más abajo usando la misma fórmula. Según esta lógica, resultará que:

• T = T0 * N^2 ---> T0 = T / N^2
• T - tiempo de nuestro corredor; tiempo medio del que se conoce
• T0 - tiempo promedio del corredor más pequeño del que se compone nuestro corredor

Es decir, podemos encontrar el tiempo del corredor más pequeño: lo necesitaremos para calcular el tiempo del tercer corredor con un factor de incremento fraccionario. Una vez que encontremos el tiempo promedio del corredor más pequeño, podremos encontrar su anchura en puntos:

• d = P / N

Después de ello, podemos encontrar cuántos de estos corredores completos caben en el corredor ampliado usando la siguiente relación:

• Smin = MathFloor( K * P / d ) = MathFloor( K * N )
• Lim( N --> +infinity ) [ K * N/MathFloor( K * N ) ] = 1

Podemos ver que la anchura del corredor se está reduciendo y no afecta al resultado. La segunda línea contiene una proporción muy importante que nos permitirá comprender qué hacer a continuación. Esta indica que, al dividir el corredor original en tantos segmentos como sea posible, podríamos descuidar la parte fraccionaria descartada como resultado de la ejecución de la función "MathFloor". Precisamente el límite que tiende a la unidad nos indica esto. Si dicha inexactitud nos confunde, podemos encontrar otra cantidad:

• Smax = MathFloor( K * P / d ) + 1 =  MathFloor( K * N ) + 1 = Smin + 1

Ahora está claro que el valor real "K * N" se encuentra exactamente entre los valores "Smin" y "Smax", y que cuando el valor de "N" tiende a infinito, obtenemos dos corredores similares al máximo; su tiempo promedio de vida también tenderá entre sí, ya que sus tamaños difieren solo en 1 segmento. De ello resulta que el tiempo promedio del corredor que necesitamos se determinará con mayor precisión usando la media aritmética del tiempo promedio de estos corredores:

• T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 =  T0 *( Smin^2 + Smax^2 ) / 2
• T1 - tiempo promedio del corredor que necesitamos determinar

Para dar forma a nuestras reflexiones, hemos creado la siguiente ilustración gráfica:

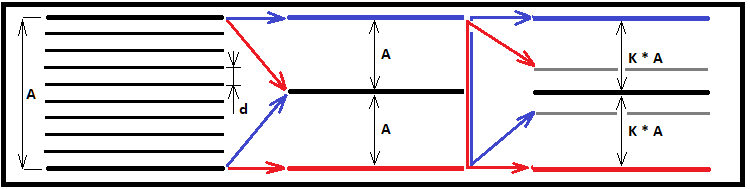
Ahora, tras calcular una expresión alternativa para el cálculo de la vida útil del corredor, podemos comparar su resultado con el valor de la función para los números enteros "K", sustituyendo allí la "K" fraccionaria. Si los números en la salida de las dos expresiones coinciden, concluiremos que la función encontrada para los enteros "K" es totalmente viable para cualquier número entero y fraccionario en el rango "0 ... +infinity". Haremos la primera verificación con "N = 1000"; esta división será suficiente para ver la identidad de los dos números, si es así:

Como podemos ver, los dos números son casi idénticos, y esta identidad, en teoría, debería resultar mayor cuanto mayor sea el valor de "N" que usamos. Esto también se puede probar asumiendo lo siguiente:

• Lim( N --> +infinity ) [  (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 )  ] = 1

En el numerador de este límite, se encuentra nuestra expresión aproximada para calcular el tiempo promedio del nuevo corredor, y en el denominador, una expresión que presumiblemente describe con precisión el mismo valor. Hemos creado una función simple que realiza los mismos cálculos efectuados en la captura de pantalla anterior, salvo para todo el rango del número "N", comenzando por el número "1". Ahora, podemos ver el resultado del funcionamiento de este programa:

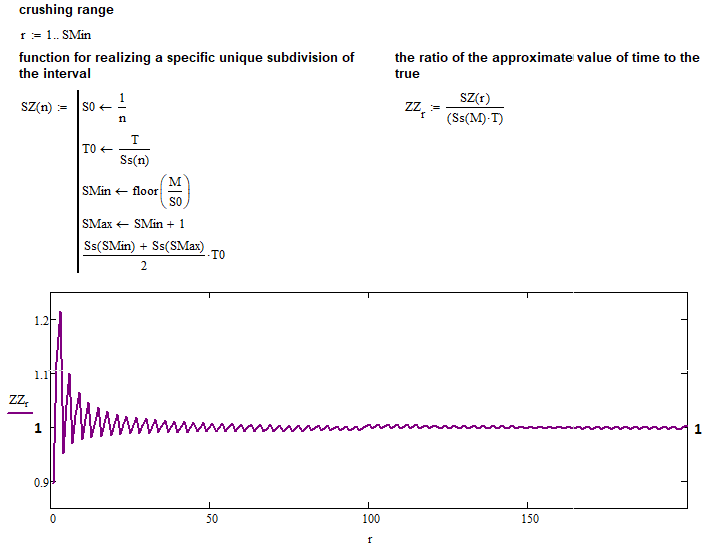
Como podemos ver, todas las suposiciones están completamente confirmadas, y la función que encontramos para la "K" completa es absolutamente viable para cualquier "K" positiva. Ahora solo tenemos una fórmula única, pero muy útil, sobre la que podemos construir muchas cosas, incluidas las matemáticas posteriores para una descripción completa de todo el fractal universal.

El fractal avanzado como consecuencia del fractal universal

Como ejemplo útil de la aplicación posterior de un fractal universal, podemos coger un fractal con un solo límite, tomando, digamos, "n=1", "m ---> +infinity", "s = m+1", "p=0.5". Hasta ahora, estamos analizado fractales con saltos de probabilidad iguales en ambas direcciones, lo cual es aplicable solo al paseo aleatorio; pero este fractal brinda todas las posibilidades. Solo para pasar a un análisis más profundo de una estructura tan compleja, primero deberemos considerar los conceptos básicos que nos ayudarán a realizar un análisis más profundo de la misma; además, ya en esta etapa obtenemos fórmulas muy útiles e interesantes, así como conclusiones fundamentales sobre estos procesos fractales. Tras ejecutar este fractal con diferentes valores de "s", hemos obtenido los siguientes datos:

• s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
• s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
• s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
• s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882

Un aumento adicional en el número de saltos permitidos provoca una singularidad en el tiempo de cálculo: en otras palabras, el tiempo de cálculo aumenta de una forma tan brutal, que podríamos esperar horas y días; ciertamente, esto no resulta sorprendente, pero si observamos la velocidad con la que aumenta la suma de probabilidad promedio, podemos ver que resulta imposible valorar la convergencia de esta serie cuando usamos este tipo de fractal. No obstante, resulta que a partir de la fórmula que hemos mostrado anteriormente, ya sí que resultará posible valorar esta convergencia usando una forma de fractal completamente distinta pero muy útil, que nos ofrecerá una respuesta a esta pregunta. Además, como el lector podrá ver, este tipo de fractal nos ayudará a calcular el tiempo para "Carry trade", una estrategia rentable y muy familiar para todos. En primer lugar, veremos una ilustración gráfica, y luego analizaremos lo que hay en ella:

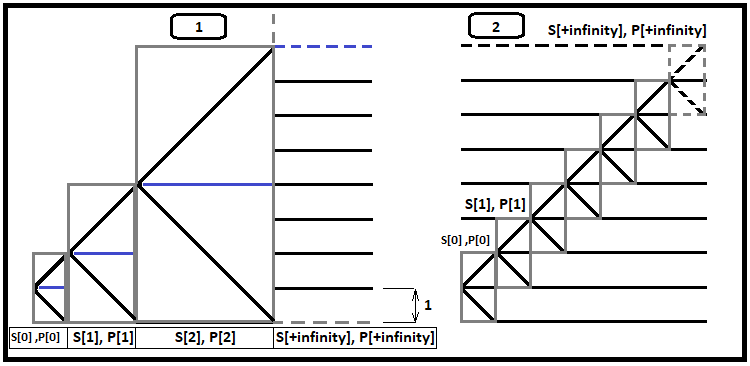
Vamos a imaginar que el proceso de fijación de precios comienza a un salto del límite, sin importar dónde se encuentre este: hacia arriba o hacia abajo. En la imagen, tomaremos el ejemplo con el límite inferior, porque se percibe mejor. Echemos un vistazo más de cerca al primer fractal. Cada rectángulo gris contiene dos posibles desarrollos de eventos:

1. El alcance del límite superior del rectángulo
2. El alcance del límite inferior del rectángulo

También podemos ver que cuando se alcanza el límite superior del corredor, un nuevo fractal de mayor tamaño se inicia automáticamente en el mismo punto, y así sucesivamente hasta el infinito. Si consideramos este proceso de la misma forma que en un fractal universal, no veremos nada más que las mismas cadenas de probabilidades; pero ahora tenemos una fórmula que dice cuál es el número promedio de saltos que se realizarán en un corredor simétrico dado, usando como base cuántos saltos caben en él (ahora entendemos que solo consideramos como un salto un corredor más pequeño que se puede insertar en el original).

Resulta que ahora no necesitamos considerar el fractal completo para calcular el número promedio de saltos, solo necesitamos aplicar la fórmula derivada a cada uno de estos fractales y considerar como salto no la magnitud propia, sino el alcance del límite superior o inferior del siguiente fractal anidado. Sobre esta base, podremos elaborar cadenas probabilísticas que serán muy sencillas. La probabilidad de alcanzar el límite del primer fractal "P[0]" será igual a "0.5": esto resulta obvio para todos, pero significa que hay un segundo caso en el que hemos tenido que crear el siguiente fractal, y también esperar que el precio llegue al límite. Podemos ver que estos eventos están anidados entre sí, y todas estas cadenas también forman un grupo completo.

Resulta que la probabilidad de llegar al límite del segundo fractal "P[1]" es igual a la anterior, pero multiplicada por el mismo "0.5"; por eso, este proceso se puede continuar indefinidamente, y, por supuesto, también podemos determinar el número promedio de saltos iniciales basándonos en la fórmula derivada y las probabilidades de estas cadenas. Para lograrlo, primero tenemos que definir la fórmula para la probabilidad de cada cadena individual, considerando que el número promedio de saltos para cruzar los límites superior e inferior del fractal es idéntico. Resulta que:

• PUp = PDown = P - proporción que muestra que la probabilidad de alcanzar los límites superior e inferior de un fractal es igualmente probable para todos los límites de todos los fractales anidados
• P[j] = 0.5^(j+1) , j = 0 ... + infinity- probabilidad de que tenga lugar precisamente la cadena "j"
• S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ),  i = 1... + infinity - fórmula recursiva para calcular el número promedio de saltos de probabilidad total para todos los niveles fractales (con S[0] = 1*0.5 = 0.5 )
• F(K) = K^2 - nuestra fórmula derivada para calcular el número promedio de saltos
• D(i) = 2^i - número de saltos que caben en el siguiente nivel fractal
• S[i-1]/P[i-1] - número promedio de saltos en la rama no contabilizada restante, siempre que haya tenido lugar la rama actual (después de todo, debemos considerar los saltos que han sucedido antes de esto, aparte del fractal anidado actual)
  

El segundo fractal es en realidad idéntico al primero, en el sentido de que las probabilidades de sus cadenas son idénticas, en otras palabras, la matriz "P[]". ¿Y por qué lo necesitamos? Vamos a imaginar que tenemos una estrategia de "Carry Trade". Resulta que para valorar la rentabilidad, deberemos entender que tenemos dos cuentas, una de swap y otra libre de swap para bloquear una posición con un swap positivo. Además, necesitaremos una fórmula para calcular el tiempo promedio de mantenimiento de una posición rentable; este tiempo promedio será una consecuencia directa de la fórmula del número promedio de saltos. No vamos a abarcar este tema con demasiada profundidad en el presente artículo: solo queremos que al menos algunos lectores comiencen a comprender la importancia de estas matemáticas. Trabajaremos este problema con detalle en una rama con swaps propia un poco más adelante. Por ahora, vamos a definir la fórmula para los saltos de probabilidad promedio para el segundo fractal:

• S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) - fórmula recursiva para calcular el número promedio de saltos de probabilidad total para todos los niveles fractales (con  S[0] = 1*0.5 = 0.5 )

En este caso, esta fórmula solo supondrá un caso especial de la anterior, porque en el segundo fractal, "K=1" se da absolutamente siempre para todos los niveles fractales. Vamos a averiguar a qué son iguales los límites de las sumas de estas magnitudes para ambos fractales:

Como podemos ver, la primera fila diverge, indicándonos que en ausencia de un límite superior, si comerciamos sin fin, obtendremos un tiempo promedio igual al propio infinito; sin embargo, en el segundo caso, obtendremos un límite claro igual a "2". Esto significa que si abrimos una posición con un swap positivo, entonces, de promedio, tendremos que cerrar esta posición después de dos saltos (en consecuencia, el tiempo promedio de mantenimiento de una posición será 2*T, donde "T" es el tiempo promedio de mantenimiento, siempre que cerremos la posición cuando llegue a uno de los límites). En el segundo (y más simple) de los casos, solo tendremos que cerrar ambas posiciones en ambas cuentas, incluso si la cuenta de swap está en positivo. Obviamente, la primera opción es mucho más atractiva, pero su implementación requerirá retirar y depositar los fondos de forma rápida y fluida en ambas cuentas. Si no existe tal opción, tendremos que usar la opción clásica, que no resulta tan rentable, pero que sí es estable.

Generalizando los resultados

En la segunda parte del ciclo, hemos conseguido resultados muy interesantes, incluso para el uso práctico en el comercio, pero lo más importante es que ha quedado claro que esto no es ni mucho menos todo lo que podemos hacer con fractales. Vamos a recapitular lo que hemos hecho en este artículo:

• Hemos definido reglas matemáticas claras para construir un fractal universal.
• Hemos creado un código de trabajo en el estilo MQL5, basado en los principios matemáticos establecidos
• Gracias a las dos plataformas diferentes (MetaTrader 5 y MathCad 15), todos los principios matemáticos establecidos han sido probados con éxito
• Gracias a los algoritmos obtenidos, hemos conseguido la primera fórmula para calcular la vida útil de un corredor arbitrario
• La fórmula ha sido probada y validada con la ayuda de programación para todos los casos posibles
• Usando como base la fórmula obtenida, hemos conseguido un nuevo tipo de fractal más rápido
• El fractal resultante ha hecho posible acelerar los cálculos y determinar qué se encuentra más allá del poder de un fractal universal
• Hemos analizado superficialmente un caso especial sobre el uso de un fractal avanzado para tareas de comercio con swaps
• Hemos conseguido herramientas para un mayor desarrollo de la teoría

Además, querríamos señalar que nuestro instumental se ha expandido enormemente, y ahora podemos comenzar a analizar fractales con diferentes saltos de probabilidad (situaciones de tendencia y situaciones relacionadas con el análisis de estadísticas comerciales). Una vez más, queremos aclarar que en este artículo solo se han investigado los casos en los que "p = 1 - p = q = 0.5". Esta suposición implica que hasta ahora todos los cálculos son aplicables solo a situaciones que describen un paseo aleatorio, pero creo que el lector entenderá que todavía hay muchas posibilidades aquí, y que esto que hemos visto no es aún ni la mitad.

Aparte, queremos mostrar una vez más de forma simple y rápida la fórmula que hemos obtenido como resultado del análisis del fractal. Es posible que muchos de los lectores no hayan entendido esto, y para enmendar la situación, describiremos de nuevo brevemente el qué y el por qué:

1. S = K^2 - número promedio de saltos del nuevo corredor, basado en el hecho de que el salto es otro corredor
2. T = S * T0 =  T0 * K^2- vida media de un corredor desconocido
3. T0 - vida media de un corredor conocido
4. P = K * P0  --> K = P/P0 - cuántas veces el corredor conocido es más grande que el desconocido
5. P - anchura del corredor, cuya vida media se desconoce
6. P0 - anchura del corredor conocido

Sustituyendo "4" por "1", podemos expresar el número medio de saltos que se darán en un corredor desconocido a través de los valores conocidos, y sustituyendo "1" por "2", obtendremos la vida media de este corredor, que se calcula usando como base los valores conocidos:

• T0, P0, P

También querríamos añadir la respuesta a una pregunta que ha preocupado a muchos mientras leían este artículo:

• ¿Por qué necesitamos usar fórmulas si podemos recopilar estadísticas comerciales en el simulador de estrategias de MetaTrader 5?

Respuesta:

• Sí, podemos hacer esto, pero no en todas partes resulta posible recopilar estas estadísticas, ya que no todos los instrumentos tienen una historia comercial suficiente para recopilar una cantidad de datos aleatoriamente significativa para tales valoraciones. Para los grandes brókeres, esto resultará imposible, ya que podríamos elegir un corredor que nunca haya cruzado sus límites en toda la historia, y usando brókeres de menor anchura, podemos usar esta fórmula para obtener datos que no se pueden obtener de las estadísticas. Además, este tipo de matemáticas nos ofrecen una precisión y flexibilidad incomparables. Y estas no son, ni mucho menos, todas las ventajas.

Conclusión

En este artículo, hemos tratado de describir una lógica completa sobre la que construir investigaciones posteriores sobre los procesos de fijación de precios. Sí, hasta ahora esto resulta insuficiente para una aplicación práctica, pero estamos seguros al cien por cien de que será posible investigar todas las variedades del fractal universal y obtener sobre su base todas las fórmulas de descripción posibles, incluyendo los corredores de precios asimétricos y los corredores con un límite libre. En el próximo artículo, seguiremos investigando el fractal universal, y también intentaremos convertir todos los resultados en fórmulas simples. Asimismo, comenzaremos una nueva matemática muy interesante que nos permitirá usar las fórmulas obtenidas no solo en los procesos de formación de los precios, sino también para describir backtests y señales comerciales. Gracias a esto, podremos analizar con absoluta precisión cualquier estrategia en términos de tiempo y probabilidad, y precisamente esto, al final, es todo lo que nos puede preocupar en relación al trading.

Enlaces

• Combinatoria y teoría de la probabilidad en el trading (Parte I): Fundamentos