Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal

İçindekiler

• Giriş
• Ticarette fraktalları kullanma olanaklarının değerlendirilmesi
• Evrensel bir fraktal oluşturmak için teorik temel
• Evrensel bir fraktal uygulamak için kod yazma
• Simetrik bir fraktala dayalı ilk formülün türetilmesi
• Tüm pozitif ve reel argümanlar için türetilmiş formülün performansının değerlendirilmesi
• Evrensel fraktaldan geliştirilen gelişmiş fraktal
• Sonuçların özetlenmesi
• Sonuç
• Referanslar

Giriş

Bir önceki makalede, ticaret görevleri için fraktal fonksiyonlarını kullanmanın belirli özelliklerini anlamamıza yardımcı olacak olasılık teorisinin temellerini tartıştık. Bu konunun devamı olarak, gerekli tüm fiyatlandırma süreçlerini tanımlayabilen bazı kendi kendine yeterli fraktal fonksiyonlarını göstereceğim. Bunları genelleştirmeye ve basitleştirmeye çalışacağız, ayrıca net nicel tahminler ve kesin cevaplar içermeyen çeşitli soruları yanıtlamak için formüller oluşturacağız. 

Ticarette fraktalları kullanma olanaklarının değerlendirilmesi

Bir önceki makalenin sonuçlarını özetleyerek ve materyali daha kompakt ve evrensel bir biçimde sunarak konuya devam edelim. Bir önceki makaledeki fraktal oluşturma örneğini hatırlıyor musunuz? Böyle bir fraktalın pratikte pek bir faydası yoktur, ancak bu durumda biz esas olarak belirlediğimiz yapı oluşturma kurallarıyla ilgileniyoruz. Anlaşıldığı üzere, bu kurallar üç tür fraktala uygulanabilir:

1. Simetrik sınırlara sahip fraktal
2. Asimetrik sınırlara sahip fraktal
3. Üst veya alt sınırlı fraktal

Bu tür fraktallar aşağıdaki süreçleri tanımlamak için uygulanabilir:

• Bakiye kısıtlamalarını dikkate alarak çeşitli senaryoların olasılıklarını değerlendirme yeteneği ile ticaretin hızlandırılmış taklidi (alt sınır, daha fazla ticaretin imkansız olacağı bakiye seviyesini sembolize edebilir)
• Bir fraktal içindeki ortalama adım sayısının tahmini (örneğin, istenen kârı veya zararı elde etmeden önce ortalama kaç emrimiz olduğunu tahmin edebilirsiniz)
• Her adım için toplam ortalama değerlerin tahmini [örneğin, daha küçük bir pozisyon (yani puan veya fiyat farkı cinsinden daha küçük durma seviyelerine sahip bir pozisyon) için istatistiklere dayanarak ortalama pozisyon tutma süresini hesaplayabilirsiniz]
• Tek sınırlı bir fraktala dayalı seçeneklerin kârlılığının değerlendirilmesi
• Diğer olanaklar

Evrensel bir fraktal oluşturmak için teorik temel

Bir önceki makalede türettiğimiz yapı kurallarını kullanalım ve bir fraktalın nasıl inşa edildiğini anlamak için onları tamamlayalım. Buna ek olarak, formüllerimde küçük bir hata buldum, bu nedenle sınırların aşağı veya yukarı doğru asimetrikleştirilmesi imkansızdı. Türetilen formüllerin doğru olduğu ortaya çıktı ve bu nedenle kesinlikle herhangi bir fraktal için çalışıyorlar. Aslında, bu kesinlikle herhangi bir fraktal uygulamak için bir fonksiyondur. Tüm olası fraktallar, genel bir fraktalın özel bir durumudur. Yukarıda tanımlanan üç fraktal tipini ele alırsak, bu üç özel durumun uygulanması için genel fraktalın koşulları aşağıdaki gibi olacaktır:

1. m = n & [m>s & n>s]
2. (m>n || n>m ) & [m>s & n>s]
3. (m>S && n<=S) || (n>S && m<=S)

Şematik olarak, bu üç fraktal türü şu şekilde görünür:

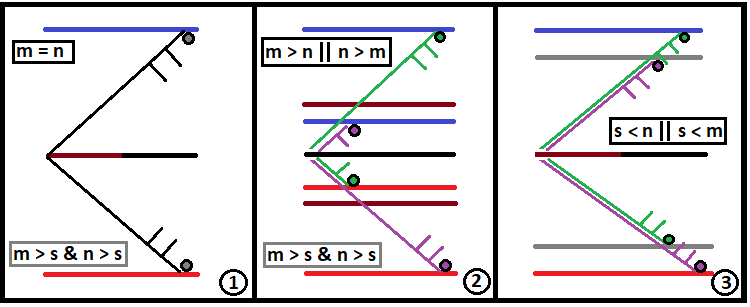
İdeal olarak, "S" sonsuza doğru gitmelidir. Aşağıdaki değişkenler önceki makalemde açıklanmamıştı. Özel durumları elde etmek için genel formülün nasıl kullanılacağına dair tam bir resim elde etmek adına burada ilgili açıklamaları sunacağım. Fraktal, atom bombasında olduğu gibi zincirleme reaksiyon prensibine göre çalışan bir fonksiyondur. Ayarlanan zincirleme reaksiyon çok derinse, bilgisayar bu kadar büyük hesaplamalarla başa çıkamayabilir. Eğer durum özellikle kritik değilse, dakikalar, saatler ve hatta günler gibi çok uzun bir süre hesaplama yapılacaktır. Bir fraktalda zincirleme reaksiyonu doğru bir şekilde başlatmak için iki temel değer bulmalıyız:

• Half - kanal genişliğinin yarısı
• Middle - orta çizgiye karşılık gelen "U" değeri

Half değeri, bir önceki makalede belirlediğimiz üç durum için de kolayca hesaplanabilir: m ve n'nin aritmetik ortalamasıdır:

• Half = (n+m)/2

İkinci değeri uygulamak için üç mantık seçeneği kullanmamız gerekecektir. Bununla birlikte, birinci ve ikinci seçenekler tek bir seçenek halinde birleştirilebilir. Dolayısıyla, elimizde iki seçenek bulunmaktadır:

1. n >= m
2. n < m

Ardından, "U" ekseninin yukarı yönlü olduğu ve n değerinin kanalların üst kısmı, m değerinin ise alt kısmı olduğu göz önüne alındığında, olası m ve n değerlerine sahip iki durum için iki oran elde ederiz:

1. Middle = Half-m
2. Middle = -(Half-n)

Bu değerler dahili kullanım için fraktal fonksiyonuna aktarılacaktır, çünkü önceki makalede açıklanan dahili dallanma mantığı bunlar olmadan uygulanamaz. Fonksiyon prototipi aşağıdaki gibidir:

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Bu nedenle, doğru fraktal başlangıcı için beş zorunlu değeri geçmemiz gerekir:

1. Half - kanal genişliğinin yarısı
   
2. Middle - orta çizgiye karşılık gelen "U" değeri
   
3. m - alt sınıra olan adım sayısı
4. n - üst sınıra olan adım sayısı
5. s - tek bir zincir için herhangi bir yönde izin verilen maksimum adım sayısı

Diğer değerler, bu değerlerin dinamik olduğunu ve farklı fraktal seviyelerinde farklı olacağını göstermek için büyük harflerle belirtilmiştir. İşte onların tanımı:

• S - mevcut olasılıklar zincirinde biriken adım sayısı; bir sonraki fraktal seviyesine geçecektir
• U - zincir başlangıç noktası ile sonu arasındaki mevcut mesafe; bir sonraki fraktal seviyesine geçecektir
• P - Bernoulli şemasına dayalı olarak tüm zincirin olasılıklarının birikmiş çarpımı; bir sonraki fraktal seviyesine geçecektir

Bu nedenle, fraktalın doğru bir şekilde başlatılması için aşağıdaki değerleri fonksiyona girmeliyiz:

• S = 0 (başlangıç olduğu için henüz adım yok)
• U = 0 (aynı sebepten dolayı)
• P = 1 (sıfır zinciri olduğundan ve sonraki tüm adımların bir tam grup oluşturması gerektiğinden)

Fiyatlandırmayı veya ticareti simüle eden fraktallar için genel kuralları geliştirmeyi bitirmek için, bir önceki makalede elde edilen kuralları kısaca yeniden yazalım. Bu kurallar fraktalın içinde kullanılır. Kurallar, aynı adımlar için çeşitli formüllere dayanmaktadır:

• f = u+d - gelecekteki kombinasyon ağacının adım sayısı (mesafe, fraktal aralığının en yakın sınırına olan mesafe ile belirlenir)
• s = u-d - düşen ve yükselen segmentler cinsinden ifade edilen nihai adım sayısı

"u" üzerinden döngü yapacağımızı belirledik. Buna ek olarak, "s" değerini yeni "U" olarak kullanacağız ve kalan adım sayısı destekliyorsa bir sonraki fraktal seviyesine ileteceğiz. Bu amaçla, "u" için "d" içermeyen bir formül tanımlamamız gerekiyor. Bunu yapmak için, ilk denklemdeki "d"yi ifade edelim ve ikinci denklemde yerine koyalım:

• s = 2*u-f

Bu değer, mevcut değerin sıfıra eşit olması durumunda daha ileri iletmek için "U"nun yeni değeri olarak da kullanılabilir. Dolayısıyla, daha sonra aktarılması gereken değeri elde etmek için bu "s"yi "U"ya eklememiz gerekir:

• NewU = s+U - bir sonraki fraktal seviyesine geçecek yeni "U"

Önceki makalede tanımlandığı gibi, bu ifade "f" sayısının üç olası değerine bağlı olarak üç olası değer alır. Fikri açıklamak için bir önceki makalede yer alan bir diyagramı revize ettim:

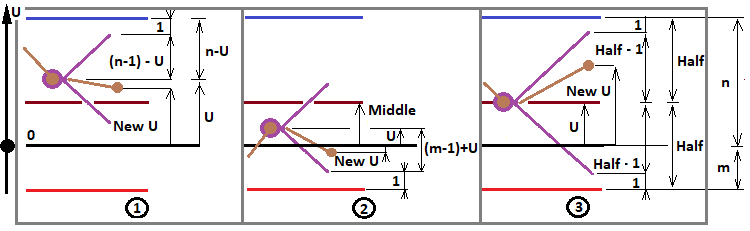
Bu diyagram burada çok uygundur, çünkü şimdi problemlerin çoğunu çözmek için bize yararlı olabilecek tüm olası fraktal konfigürasyonları belirliyoruz. Bu diyagrama göre, "f" için üç durum tanımlıyoruz:

1. f = (n-1)-U
2. f = (m-1)+U
3. f = Half-1

Bu üç durum aşağıdaki koşullar karşılandığında ortaya çıkar:

1. U > Middle
2. U < Middle
3. U = Middle

Şimdi bir sonraki fraktal seviyesine geçecek son iki değeri tanımlamamız ve sayıların fraktalda nasıl birleştirildiğini düşünmemiz gerekiyor. Son iki değer aşağıdaki gibi hesaplanır:

• NewP = P*C(f, i)*Pow(p, i)*Pow(1-p, f-i) - bir sonraki fraktal seviyesine geçecek yeni "P" zinciri olasılığımız
• NewS = S+f = S+(floor(Mid)-1) - bir sonraki fraktal seviyesine geçecek yeni "S"

Sayıları ortak bir değişkende birleştirmeye başlamadan önce, sayıların benzer bir blokta birleştirilmesi gerektiğine dikkat edin - ancak bu durumda yalnızca bir adım atıyoruz, bu nedenle Bernoulli şemasına ihtiyacımız yok. İfadelerin sırası önemli değildir; sadece aynı blok içerisinde olmalıdırlar. Sayılar sadece "1" ve "2" durumlarında, bazı netleştirmelerle birlikte birleştirilebilir:

1. U = n-1
2. U = -(m-1)

İlk durum için, sadece bir adımımız olduğundan önceki üç değeri hesaplamak daha kolaydır:

• NewU = U-1
• NewP = P*p
• NewS = S+1

İkinci durum için küçük bir fark vardır:

• NewU = U+1
• NewP = P*(1-p)
• NewS = S+1

Tüm fraktalların genelleştirilmesine dayanarak, bu fraktalların her biri 2 türe ayrılır:

• Koridorun üst sınırını geçmenin toplam olasılığını hesaplayan fraktal
• Koridorun alt sınırını geçmenin toplam olasılığını hesaplayan fraktal

Bu türlerin her biri, orijinaliyle bağlantılı olan bir başka fraktal türüne karşılık gelir:

• Üst sınırı geçmek için ortalama adım sayısını hesaplayan fraktal
• Alt sınırı geçmek için ortalama adım sayısını hesaplayan fraktal

Bu dört fraktal türü, toplanan sayıların biçimine göre farklılık gösterir. Olasılıkları birleştirirken sadece "P*p" ve "P*(1-p)" ekleyebiliriz. Diğer iki fraktal için, bir sonraki fraktal seviyelerine iletmek için ek değişkenlere ihtiyacımız var. Bu fraktallarda, yönleri zıt olan eşit büyüklükte adımlar kullanırız, bu nedenle olasılıkları ya "p" ya da "1-p"dir. Ancak "p" 0.5'e eşit olmadığında, bu gerçek, bunların farklı özelliklere sahip olabilecek iki farklı olay olduğu anlamına gelir. Özellikler derken, belirli bir olaya karşılık gelen bazı rastgele değişkenler kümesini kastediyorum. Bu değerlerden biri de pozisyon ömrüdür. Bu tür değerlerden istenilen sayıda olabilir ve gerekirse bunları zaman olarak kabul edebiliriz. Bu kısım birkaç kolay adımdan sonra basitleştirilebilir. Toplanacak sayılar aşağıdaki forma sahip olacaktır:

1.  P*p*NewS
2.  P*(1-p)*NewS

Gördüğünüz gibi, olasılıklar bu tamamlanmış adım zincirindeki adım sayısı ile çarpılmaktadır. Ancak bu formül yalnızca yukarı ve aşağı adımların eşit olasılıkta olduğu durumlarda geçerlidir. Alternatif durumlarda, yukarı ve aşağı adımları tanımlamak için iki farklı yapı kullanmamız veya her iki sayıyı da saklamak için bir yapı sağlamamız gerekecektir. İkinci durumda, fraktal fonksiyonu bir sayı değil, bir veri deposu (container) geri döndürecektir. Depo kendi kendine yeterlidir ve genişletilmesi gerekmez. Ayrıca, gerekli tüm parametreleri saklayabilen bir depo sağladım, böylece benzer bir koda sahip birkaç fonksiyonu tanımlamaya gerek kalmadı. Bunun yerine, tüm fonksiyonları gerekli tüm parametreleri tanımlayabilen tek bir fonksiyonda birleştirdim. Fraktalın türü ve çözdüğü görev doğrudan fonksiyonun girdi parametrelerine bağlı olacaktır. Kavramı genişletmek için, ilk "S" ve eşdeğeri "NewS" aşağıdaki değerlerle değiştirilmelidir:

1. SU - seçilen olasılık zincirinden yukarıya doğru nihai adım sayısı
2. SD - seçilen olasılık zincirinden aşağıya doğru nihai adım sayısı
3. NewSU ve NewSD - bir sonraki fraktal seviyesine geçecek değerler
4. SU+SD = S

Bu değerler "S" tanımına benzer şekilde tanımlanmalıdır. "U > Middle" olduğunda:

• NewSU = SU
• NewSD = SD+1

"U < Middle" olduğunda:

• NewSU = SU+1
• NewSD = SD

Fraktalın nihai yükseltmesi için altı değere daha ihtiyaç vardır:

1. UpperMidSDown - üst sınıra ulaşmadan önce aşağıya doğru atılacak toplam ortalama olası adım sayısı
2. UpperMidSUp - üst sınıra ulaşmadan önce yukarıya doğru atılacak toplam ortalama olası adım sayısı
3. UpperSummProbability - üst sınırı geçme olasılığı
4. LowerMidSDown - alt sınıra ulaşmadan önce aşağıya doğru atılacak toplam ortalama olası adım sayısı
5. LowerMidSUp - alt sınıra ulaşmadan önce yukarıya doğru atılacak toplam ortalama olası adım sayısı
6. LowerSummProbability - alt sınırı geçme olasılığı

"1", "2", "4", "5" değerleri, karşılık gelen adım sayısı ve olasılıklarının çarpımlarının toplamını gösterir. Bu değerler bu haliyle anlamsızdır, ancak daha sonra tartışacağımız yararlı değerlerin formüllerinin bileşenleridir. "3" ve "6" değerleri, bir tam grup oluşturan iki sınırı geçme hipotezinin olasılıklarıdır. Bu değerleri kullanarak çok sayıda başka şeyi belirleyebiliriz.

Evrensel bir fraktal uygulamak için kod yazma

Fraktalın doğru şekilde başlatılması için, fraktal başlatılmadan önce tüm hazırlık işlemlerini yürüten ve ardından önceden tanımlanmış kurallara göre fraktalın doğru şekilde başlatılmasını sağlayan bir fonksiyona ihtiyacımız var. Bu algoritmanın MQL5 tarzı bir uygulamasını hazırladım:

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Fraktal hesaplamasından sonra, fonksiyon depomuzu gerekli tüm verilerle birlikte geri döndürür:

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

Bu depo, iki özdeş yapıyı birleştirmek için "+=" operatörünün aşırı yükünü içerir. Bu kısım ana fonksiyon için kullanılacaktır. İşte fraktal fonksiyonu:

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

Kod MetaTrader 5'te kontrol edildi - oldukça iyi çalışıyor. Gerekirse bu mantık daha da genişletilebilir ve hala pek çok gelişmiş olasılık mevcuttur. Ancak fonksiyonun girdi parametrelerinin listesini şimdilik kısa tutmaya karar verdim, çünkü uygulanan işlevsellik amaçlarımız için oldukça yeterli. Kodu dikkatle incelediğinizde, yukarıda özetlenen matematiksel ilkelere tamamen uygun olduğunu göreceksiniz. Kısa olmasına rağmen, bu kod parçası harikalar yaratabilir. Kodun mümkün olduğunca fazla mantık ve matematik içermesi gerektiğine inanıyorum. Nihayetinde ihtiyacımız olan şey bu. Güzel bir kod bile amacına uygun olarak kullanılamazsa bir işe yaramaz. Bizim durumumuzda, amaçlanan hedef ticaret için uygulanabilirliktir. İşte onay olarak günlük:

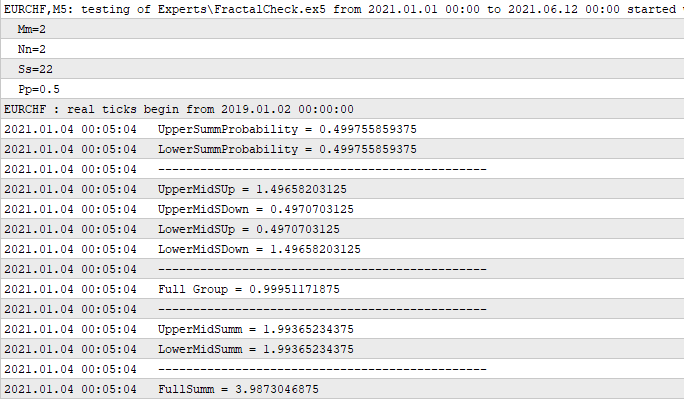
Bu durumda, ilk alınan tikte tüm fraktalı hesaplayan basit bir Uzman Danışman oluşturdum. Bu hesaplama bir kez yapılır, bu nedenle başka bir yeniden hesaplamaya gerek yoktur. İlk altı sayı deponun bir parçasıdır, geri kalanı ise bunlardan türetilmiştir. Burada sadece en önemli türetilmiş ifadeleri gösteriyorum, bu da bu altı değişkenin ihtiyaç duyabileceğimiz diğer tüm değişkenleri almaya izin verdiğini anlamamıza yardımcı olabilir. Örneğin, "Full Group"a göz atalım. Bu şekilde adlandırılmıştır çünkü önceki hesaplamaya göre sınır geçişlerinden birinin örtüşmeyen iki hipotezinin olasılıklarının toplamı bire eşit olmalıdır. Kodumuz tarafından onaylanmıştır. Bunu "1", "2" ve "3", "4" toplamları olan iki özdeş sayı takip eder. Son sayı, sondan bir önceki sayıların toplamıdır - bu, zincirin geçeceği ortalama adım sayısıdır. "m" ve "n"nin eşit ve simetrik olduğu başlangıç fonksiyonunun bu girdi parametrelerini ayarlamamın nedeni daha sonra gösterilecektir.

Simetrik bir fraktala dayalı ilk formülün türetilmesi

Günlük sonucuna göre, zincirin geçeceği ortalama adım sayısı "4" olma eğilimindedir. Koridor, bir birim adıma göre iki katına çıkarılır. Birim adım, "n" ve "m" değerlerinin bire ayarlanmasıdır. Başka bir deyişle, daha küçük koridorlardan oluşan bir koridordaki ortalama adım sayısını hesaplamak istiyorsak (bu durumda tam sayıdaki küçük koridorlar daha büyük bir koridora sığar ve yeni koridor da simetriktir), o zaman şunu varsayabiliriz:

• P[n] = P[n-1]*2 - yeni koridorun oluşturulduğu önceki, daha küçük koridorun genişliğine dayalı olarak, adımlar cinsinden yeni koridor genişliği için yinelemeli ifade
• S[n] = S[n-1]*4 - yeni koridorun ortalama adım sayısını hesaplamak için yinelemeli ifade (daha küçük koridorun ortalama değeri ile ifade edilir)

"P[0] = 1" ve "S[0] = 1" olduğunu kabul edersek ve özyineleme numaralandırmasını "0" indeksinden başlatırsak, bu özyineleme çok benzer iki seri olarak gösterilebilir:

• P[n] = 2^n, n = 0...+sonsuz
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

İlk seriye yakından bakarsanız ve ikinci seriyi doğru bir şekilde dönüştürürseniz, ikinci serinin ilk serinin elemanları kullanılarak ifade edilebileceği ortaya çıkar. Başka bir deyişle, aşağıdaki bağımlılığı elde ederiz: S = S(P) = P^2 Şimdi bu bağımlılık sadece kanal genişliğinin yinelemeli olarak ikiye katlanması için geçerlidir. Bu formülü gördüğümde, herhangi bir rastgele büyük "n" ve "m" sayısı için uygulanabilirliğini kontrol etmeye karar verdim. Mantıksal olarak, ikinci adımda "n = 3", "m = 3" olarak ayarlanır ve aynı değişkenler hesaplanır. Bu girdi parametreleriyle, ortalama adım sayısı "9" sayısına eğilim gösterir. Bu kısmı yukarıdaki kodu kullanarak veya aşağıda ekli MathCad 15 programlarını kullanarak kendiniz kontrol edebilirsiniz. Aynı seriler bu parametreler için de sağlanabilir:

• P[n] = 3^n, n = 0...+sonsuz
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Gördüğünüz gibi, aynı "S = S(P) = P^2" ilişkisini elde ettik. Aralık bölme ile ilgili diğer tüm olası senaryolar için de aynı şeyi tekrarlayabiliriz, ancak bu gerekli değildir. Bu gerçek, diyelim ki simetrik bir kanal içindeki bir fiyatın ortalama ömrünü biliyorsak, başka herhangi bir kanal içindeki bir fiyatın ortalama ömrünü hesaplayabileceğimiz anlamına gelir. Aşağıdaki şekilde hesaplanabilir:

• S = S0*K^2 - yeni koridorun ortalama adım sayısı
• T = S*T0 - yeni koridorun ortalama ömrü
• T = T0*K^2- başka bir koridorun ortalama ömrü cinsinden ifade edilen yeni koridorun ortalama ömrü (S0 = 1 olması koşuluyla)
• S0 - eski koridorun ortalama adım sayısı
• T0 - eski koridorun bir adımının ortalama ömrü
• P = K*P0 --> K = P/P0 - yeni koridorun eskisinden kaç kez daha büyük olduğu
• P - yeni koridorun genişliği
• P0 - eski koridorun genişliği

Şimdi, MathCad 15’i kullanarak hipotezi test edebiliriz. İlk olarak, ikinci dereceden ilişkiye dair varsayımları test edelim:

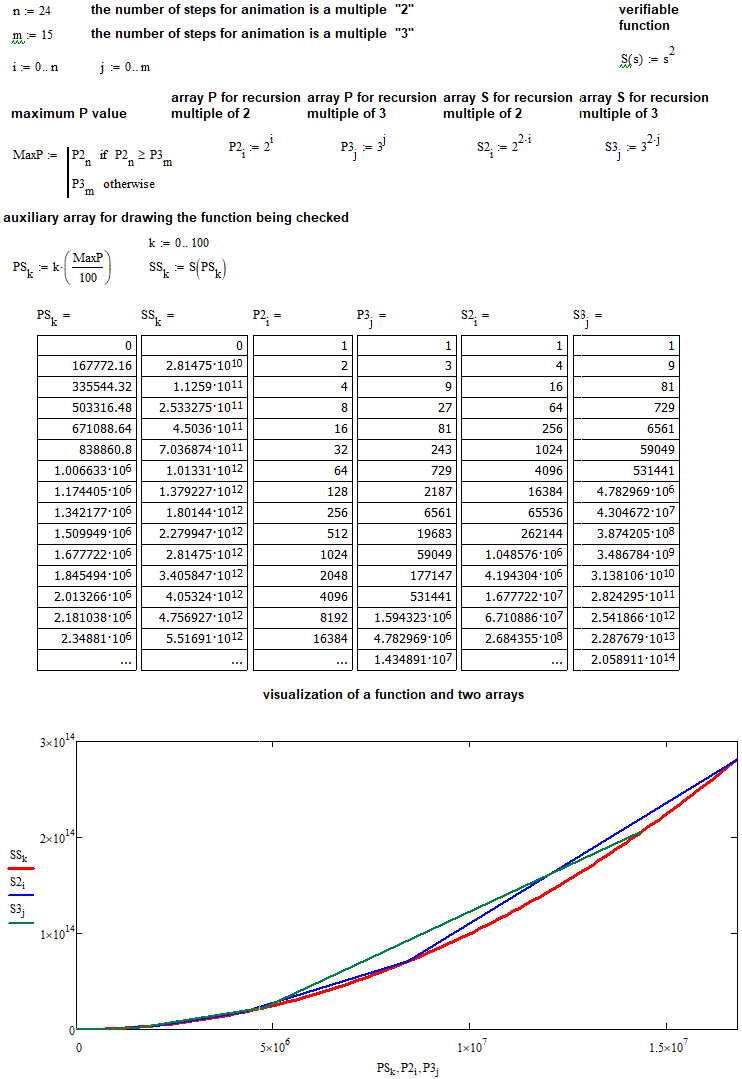
Şimdi, her şeyin çok açık ve anlaşılır olduğunu düşünüyorum.

Tüm pozitif ve reel argümanlar için türetilmiş formülün performansının değerlendirilmesi

Formül tüm "P" tam sayıları için çalışır. Ancak bir ondalıklı "K" için kullanılabilir mi? Bir ondalıklı "K" sağlamak için bir trick uygulamamız gerekiyor. Diyelim ki ortalama ömrü bilinen bir fiyat koridorumuz var ve koridorumuzun içine "N" kez sığan bir koridorumuz var, ancak ortalama ömrünü henüz bilmiyoruz. Aynı formülü kullanarak bulacağız. Bu mantığa göre:

• T = T0*N^2 ---> T0 = T/N^2
• T - ortalama ömrünü bildiğimiz koridorumuzun ömrü
• T0 - koridorumuzu oluşturan daha küçük koridorun ortalama ömrü

Bu, kesirli bir artış faktörü ile üçüncü koridorun ömrünü hesaplamak için ihtiyacımız olan daha küçük bir koridorun ömrünü bulabileceğimiz anlamına gelir. Artık en küçük koridorun ömrünü bulduğumuza göre, puan cinsinden genişliğini bulabiliriz:

• d = P/N

Daha sonra, aşağıdaki oranı kullanarak genişletilmiş bir koridora bu türden kaç koridorun sığacağını hesaplayabiliriz:

• Smin = MathFloor(K*P/d) = MathFloor(K*N)
• Lim(N --> +sonsuz)[K*N/MathFloor(K*N)] = 1

Gördüğünüz gibi, koridor genişliği azalıyor ve sonucu etkilemiyor. İkinci satır, bundan sonra ne yapılacağını anlamaya yardımcı olacak çok önemli bir oranı göstermektedir. Kaynak koridoru mümkün olduğunca çok segmente böldüğümüzde, MathFloor fonksiyonunun sonucu olarak atılan ondalıklı kısmı ihmal edebileceğimizi göstermektedir. Bire eğilimli limit bize tam olarak bunu söylüyor. Bu tutarsızlık kafa karıştırıcıysa, başka bir değer bulabiliriz:

• Smax = MathFloor(K*P/d)+1 = MathFloor(K*N)+1 = Smin+1

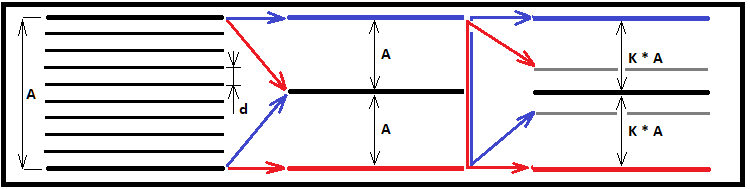
Artık "K*N"nin gerçek değerinin "Smin" ile "Smax" arasında olduğu açıktır. "N" sonsuza giderse, birbirine çok benzeyen iki koridor elde ederiz ve boyutları sadece bir segment farklı olduğundan ortalama ömürleri eşit olma eğiliminde olacaktır. Böylece, gerekli koridorun ortalama ömrü, bu koridorların ortalama ömürlerinin aritmetik ortalaması ile daha doğru bir şekilde belirlenecektir:

• T1 = (T0*Smin^2+T0*Smax^2)/2 = T0*(Smin^2+Smax^2)/2
• T1 - belirlememiz gereken koridorun ortalama ömrü

Aşağıdaki şekil fikirlerimi göstermektedir:

Artık koridorun ömrünü hesaplamak için alternatif bir ifade bulduğumuza göre, bunun sonucunu yerine ondalıklı "K" koyarak tam sayı "K" için fonksiyonun değeriyle karşılaştırabiliriz. İki ifadenin sonuç değerleri aynıysa, tam sayı "K" değerleri için bulunan fonksiyonun "0...+sonsuz" aralığındaki tüm tam sayılar ve ondalıklı sayılar için kesinlikle uygulanabilir olduğu sonucuna varabiliriz. İlk kontrolü "N = 1000" için gerçekleştirelim. Sanırım bu bölme, eğer varsa iki sayının özdeşliğini görmek için yeterli olacaktır:

Gördüğünüz gibi, iki sayı neredeyse aynı. Mantıksal olarak, daha büyük "N" değerleri için daha özdeş olmalıdırlar. Bu aynı zamanda aşağıdaki varsayımla da kanıtlanabilir:

• Lim(N --> +sonsuz)[(T0*(Smin^2+Smax^2)/ 2)/(T*K^2)] = 1

Bu limitin payı, yeni koridorun ortalama ömrünü hesaplamak için kullandığımız yaklaşık ifadedir ve payda da muhtemelen aynı değeri doğru bir şekilde tanımlayan bir ifadedir. Önceki görüntüde olduğu gibi aynı hesaplamaları yapan basit bir fonksiyon oluşturdum. Ancak bu kez "1" ile başlayan "N" sayısının tüm aralığına uygulanır. Şimdi program yürütme sonucunu görelim:

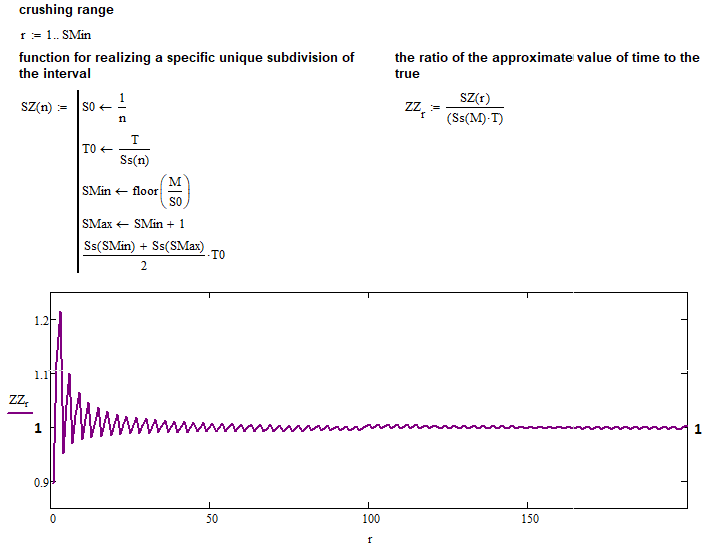
Tüm varsayımlar tamamen doğrulanmıştır: tamsayı "K" için bulduğumuz fonksiyon, herhangi bir pozitif "K" için kesinlikle geçerlidir. Artık elimizde, örneğin tüm evrensel fraktalın tanımlanmasına yönelik daha ileri matematiğin dayanağı olarak, başka eylemler için temel olarak kullanılabilecek tek ve çok kullanışlı bir fonksiyon vardır.

Evrensel fraktaldan geliştirilen gelişmiş fraktal

Evrensel fraktalın ileri uygulamalarına faydalı ve ek bir örnek olarak, "n = 1", "m ---> +sonsuz", "s = m+1", "p = 0.5" olan tek sınır fraktalını ele alabiliriz. Şimdiye kadar, her iki yönde de eşit olasılıklı adımlara sahip fraktalları ele aldık, ki bu sadece rastgele yürüyüş için geçerlidir. Ama bu fraktal tüm olasılıkları sunmaktadır. Böylesine karmaşık bir yapının daha derin bir analizine geçmek için öncelikle temelleri ele almak gerekir. Ayrıca, bu ilk adımda faydalı formüller elde edebilir ve bu fraktal süreçleriyle ilgili temel sonuçlar çıkarabiliriz. Fraktalı farklı "s" değerleri ile test ettim ve aşağıdaki verileri elde ettim:

• s = 22, FullSumm = 2.868, UpperSummProbability = 0.831
• s = 32, FullSumm = 3.618, UpperSummProbability = 0.860
• s = 42, FullSumm = 4.262, UpperSummProbability = 0.877
• s = 45, FullSumm = 4.499, UpperSummProbability = 0.882

İzin verilen adım sayısındaki daha fazla artış, hesaplama süresi tekilliğine yol açar; başka bir deyişle, hesaplama süresi saatler hatta günler gerektirecek kadar artar. Ancak ortalama olasılık toplamının artış hızına bakarsanız, bu serinin yakınsamasını bu tür bir fraktal kullanarak değerlendirmenin mümkün olmadığını görebilirsiniz. Ancak daha önce türetilen formüle dayanarak, yakınsamayı farklı ama çok kullanışlı bir fraktal türü kullanarak değerlendirebiliriz. Bu fraktal, çok popüler ve kârlı bir strateji olan "carry trade" için zamanın hesaplanmasına da yardımcı olabilir. Önce bir şekil göstereceğim, sonra da bunu açıklayacağım:

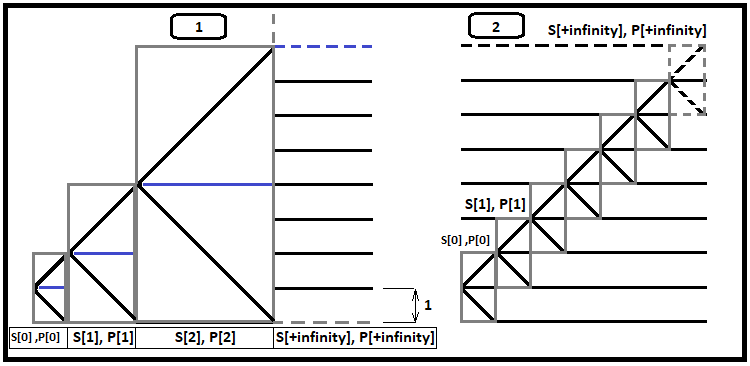
Fiyatlandırma sürecinin, sınır nerede olursa olsun, üst veya alt, sınırdan bir adım sonra başladığını düşünün. Yukarıdaki şekilde, algılanması daha kolay olduğu için alt sınırlı bir örnek gösterilmektedir. İlk fraktala daha yakından bakalım. Her gri kutu, diğer olaylar için iki senaryo içerir:

1. Fiyat kutunun üst kenarına ulaşır
2. Fiyat kutunun alt kenarına ulaşır

Fiyat koridorun üst sınırına ulaştığında, bu noktada otomatik olarak daha büyük yeni bir fraktal başlar ve bu böyle devam eder. Bu süreci evrensel fraktalda olduğu gibi ele alırsak, yine olasılık zincirlerini görürüz. Ancak şimdi formülümüz, simetrik bir koridorda kaç adım atılacağını, koridora kaç adım sığdığına bağlı olarak söylüyor (şimdi bir adımın orijinal koridora sığan daha küçük bir koridor olduğunu görüyoruz).

Şimdi, ortalama adım sayısını hesaplamak için fraktalın tamamını göz önünde bulundurmamız gerekmez. Bunun yerine, türetilen formülü fraktalların her birine uygularız. Buradaki adım aynı değer değildir, ancak bir sonraki iç içe geçmiş fraktalın üst veya alt sınırına ulaştığımızda yapılır. Buna dayanarak, çok basit olacak olasılık zincirleri oluşturabiliriz. İlk fraktal P[0]'da sınıra ulaşma olasılığı 0.5'e eşittir. Bu, fiyatın sınıra ulaşacağını umarak bir sonraki fraktalı oluşturmamız gereken ikinci bir olası durum olduğu anlamına gelir. Tüm bu olaylar iç içe geçmiştir ve tüm bu zincirler bir tam grup oluşturur.

İkinci fraktal P[1]'de sınıra ulaşma olasılığı, önceki olasılığın 0.5 ile çarpımına eşittir. Bu süreç sonsuza kadar devam ettirilebilir. Ortalama adım sayısı, türetilen formül ve zincir olasılıkları kullanılarak belirlenebilir. Bunu yapmak için öncelikle, üst sınırı geçmek için gereken ortalama adım sayısı ile alt sınırı geçmek için gereken ortalama adım sayısının eşit olduğunu dikkate alarak her bir zincirin olasılığı için bir formül tanımlıyoruz. Şunlar ortayı çıktı:

• PUp = PDown = P - bir fraktalın üst ve alt sınırlarına dokunma olasılıklarının, iç içe geçmiş tüm fraktalların tüm sınırları için eşit olasılıkta olduğunu gösteren oran
• P[j] = 0.5^(j+1), j = 0...+sonsuz - j zincirinin gerçekleşme olasılığı
• S[i] = S[i-1]+P[i]*(S[i-1]/P[i-1]+F(D[i])),  i = 1...+sonsuz - tüm fraktal seviyeleri için toplam ortalama olası adım sayısını hesaplamak için yinelemeli formül (S[0] = 1*0.5 = 0.5 iken)
• F(K) = K^2 - ortalama adım sayısını hesaplamak için türetilmiş formülümüz
• D(i) = 2^i - bir sonraki fraktal seviyesine kaç adım sığar
• S[i-1]/P[i-1] - mevcut dalın gerçekleşmiş olması koşuluyla, kalan hesaplanmamış daldaki ortalama adım sayısı (çünkü mevcut iç içe geçmiş fraktala ek olarak, daha önce gerçekleşen tüm adımları hesaba katmak gerekir)
  

İkinci fraktal aslında birincisiyle aynıdır, yani zincirlerinin olasılıkları (P[] dizisi) aynıdır. Neden buna ihtiyacımız var? "Carry trade" stratejisine sahip olduğumuzu varsayalım. İki hesabımız var: pozitif swapla pozisyonları kilitlemek için bir swaplı hesap ve bir swapsız hesap. Ayrıca ortalama kârlı pozisyon tutma süresini hesaplamak için bir formüle ihtiyacımız var. Bu ortalama tutma süresi doğrudan ortalama adım sayısı formülünden kaynaklanır. Bu makalede bu konuyu ayrıntılı olarak ele almayacağım. Ben sadece matematiğin önemini göstermek istiyorum. Bu konu daha sonra ayrıntılı olarak ele alınacaktır. Şimdi, ikinci fraktal için ortalama olasılık adımları için bir formül tanımlayalım:

• S[j] = S[j-1]+P[j]*(S[i-1]/P[i-1]+F(1)) - tüm fraktal seviyeleri için toplam ortalama olası adım sayısını hesaplamak için yinelemeli formül (S[0] = 1*0.5 = 0.5 iken)

Bu durumda, bu formül sadece bir öncekinin özel bir durumudur çünkü ikinci fraktalda “K = 1”dir (her zaman, tüm fraktal seviyeleri için). Her iki fraktal için bu büyüklüklerin toplamlarının limitlerinin neye eşit olduğunu bulalım:

İlk seri ıraksar, yani üst sınır olmadığında ve ticaret sonsuz olduğunda ortalama süre sonsuza eşittir. İkinci durumda 2'ye eşit net bir limit elde ederiz. Bu, pozitif bir swapla bir pozisyon açarsak, ortalama olarak bu pozisyonu iki adım sonra kapatmamız gerekeceği anlamına gelir (böylece ortalama pozisyon tutma süresi 2*T'ye eşit olacaktır, burada T, sınırlardan birine ulaştığında pozisyonu kapatmamız koşuluyla ortalama pozisyon tutma süresidir). İkinci ve en basit durumda, swaplı hesap pozitif bir sayı gösterse bile, her iki hesaptaki her iki pozisyonu da kapatırız. Açıkçası, ilk seçenek çok daha caziptir, ancak uygulanması her iki hesapta da hızlı ve sorunsuz bir para çekme ve yatırma işlemi gerektirecektir. Bu seçenek mümkün değilse, daha az kâr getiren ancak daha fazla istikrara sahip olan klasik bir seçenek kullanmamız gerekecektir.

Sonuçların özetlenmesi

Makale serisinin ikinci bölümünde, ticarette pratik uygulama sonuçları da dahil olmak üzere çok ilginç sonuçlar elde ettik. Daha da önemlisi, fraktalların olası uygulama alanının çok büyük olduğu artık açıktır. Makalede ne yaptık:

• Evrensel bir fraktal oluşturmak için net matematiksel kurallar tanımlandı
• Belirtilen matematiksel ilkelere dayalı olarak çalışan bir MQL5 tarzı kod oluşturuldu
• MetaTrader 5 ve MathCad 15 olmak üzere iki platform kullanılarak ilkeler başarıyla kontrol edildi
• Algoritmalar kullanılarak, rastgele bir koridorun ömrünü hesaplamak için ilk formül elde edildi
• Programlama kullanılarak tüm olası durumlar için formül test edildi ve doğrulandı
• Elde edilen formüle dayanarak yeni bir hızlı fraktal türü elde edildi
• Elde edilen sonuç, hesaplamaları hızlandırmamızı ve evrensel bir fraktal tarafından belirlenemeyenleri belirlememizi sağladı
• Swap problemleri için gelişmiş bir fraktal kullanımının özel bir durumuna değinildi
• Teorinin daha da geliştirilmesi için araçlar elde edildi

Ayrıca alet çantamın büyük ölçüde genişlediğini de belirtmek isterim. Artık fraktalları farklı olasılık adımlarıyla analiz edebiliriz (trend durumları ve ticaret istatistik analizi ile ilgili durumlar). Bir kez daha, bu makalede sadece "p = 1-p = q = 0.5" durumlarını dikkate aldığımızı lütfen unutmayın. Bu, tüm hesaplamaların yalnızca rastgele yürüyüşü tanımlayan durumlar için geçerli olduğu anlamına gelir. Dolayısıyla, çok daha fazla potansiyel olasılık söz konusudur.

Fraktal üzerinde çalışıldıktan sonra elde edilen formül aşağıdadır. Bir kez daha kısaca açıklayacağım:

1. S = K^2 - bir adımın başka bir koridora eşit olduğu gerçeğine dayalı olarak yeni koridorun ortalama adım sayısı
2. T = S*T0 = T0*K^2- bilinmeyen bir koridorun ortalama ömrü
3. T0 - bilinen bir koridorun ortalama ömrü
4. P = K*P0 --> K = P/P0 - bilinen koridorun bilinmeyen koridordan kaç kat daha büyük olduğu
5. P - bilinmeyen bir ömre sahip koridorun genişliği
6. P0 - bilinen koridorun genişliği

4'ü 1'in yerine koyarak bilinmeyen koridorda yer alacak ortalama adım sayısını bilinen değerler üzerinden ifade edebiliriz ve 1'i 2'nin yerine koyarak bu koridorun bilinen değerlere göre hesaplanan ortalama ömrünü elde ederiz:

• T0, P0, P

Bu makalenin başında okuyucuların aklına gelebilecek bir soruya da yanıt ekleyeceğim:

• MetaTrader 5 strateji sınayıcısından ticaret istatistiklerini toplayabiliyorsak neden formüllere ihtiyacımız var?

Cevap:

• Tüm finansal semboller bu tür değerlendirmeler için gerekli olan yeterli işlem geçmişine sahip olmadığından istatistik toplamak her zaman mümkün değildir. Büyük koridorlar için bu mümkün değildir, çünkü sınırları hiç geçmemiş bir koridor seçilebilir. Daha küçük genişliğe sahip koridorları ve formülü kullanarak, istatistiklerden elde edilemeyen verileri elde edebiliriz. Ayrıca, bu tür bir matematik size rakipsiz bir doğruluk ve esneklik sağlar. Çok daha başka avantajlar da vardır.

Sonuç

Bu makalede, fiyatlandırma süreçleriyle ilgili daha fazla araştırma yapmak için kullanılabilecek hesaplama mantığını açıklamaya çalıştım. Şimdiye kadar pratik uygulama için fazla bir şey yok. Ancak evrensel fraktalın tüm çeşitlerini inceleyebileceğimizden ve asimetrik ve tek sınırlı fiyat koridorlarını tanımlamak için olası formüller elde edebileceğimizden eminim. Bir sonraki makalede evrensel fraktal araştırmasına devam edeceğim ve tüm sonuçları basit formüller halinde sunmaya çalışacağım. Ayrıca, elde edilen formüllerin sadece fiyatlandırma süreçleri için değil, aynı zamanda geriye dönük testleri ve ticaret sinyallerini tanımlamak için kullanılmasına izin verecek yeni, çok ilginç matematiği de dahil edeceğim. Bu, herhangi bir stratejiyi zaman ve olasılıklar açısından kesinlikle doğru bir şekilde analiz etmemizi sağlayacaktır, ki bu da nihayetinde ticaretin en önemli yönüdür.

Referanslar

• Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler