Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale

Contenuto

• Introduzione
• Valutare le possibilità di utilizzo dei frattali nel trading
• Basi teoriche per la costruzione di un frattale universale
• Scrivere il codice per implementare un frattale universale
• Derivazione della prima formula basata su un frattale simmetrico
• Valutazione delle prestazioni della formula derivata per tutti gli argomenti positivi e reali
• Frattale avanzato sviluppato dal frattale universale
• Riassunto dei risultati
• Conclusioni
• Riferimenti

Introduzione

Nell'articolo precedente abbiamo discusso le basi della teoria della probabilità, che ci aiuteranno a comprendere le caratteristiche specifiche dell'utilizzo delle funzioni frattali per le attività di trading. Come continuazione di questo argomento, mostrerò alcune funzioni frattali autosufficienti che possono descrivere tutti i processi di determinazione dei prezzi richiesti. Cercheremo di generalizzarli e semplificarli, come creare formule per rispondere a varie domande che non hanno stime quantitative chiare e risposte univoche. 

Valutare le possibilità di utilizzo dei frattali nel trading

Proseguiamo l'argomento riassumendo i risultati dell'articolo precedente e presentando il materiale in una forma più compatta e universale. Ricordate l'esempio di costruzione di un frattale dell'articolo precedente? Un frattale di questo tipo è di scarsa utilità pratica, ma in questo caso siamo principalmente interessati alle regole di costruzione della struttura che abbiamo determinato. Si è scoperto che queste regole possono essere applicate a tre tipi di frattali:

1. Frattale con bordi simmetrici
2. Frattale con bordi asimmetrici
3. Frattale con bordo superiore o inferiore

Tali frattali possono essere applicati per descrivere i seguenti processi:

• Imitazione accelerata del trading con la possibilità di valutare le probabilità di vari scenari, tenendo conto delle limitazioni di deposito (poiché il confine inferiore può simboleggiare il livello di deposito al quale non è possibile effettuare ulteriori operazioni di trading).
• Stima del numero medio di passi all'interno di un frattale (ad esempio, si può stimare quanti ordini abbiamo in media prima di ottenere il profitto o la perdita desiderati)
• Stima dei valori medi totali per ogni fase (ad esempio, è possibile calcolare il tempo medio di mantenimento della posizione, basandosi sulle statistiche di una posizione più piccola, cioè una posizione con livelli di stop più piccoli in punti o in differenza di prezzo).
• Valutazione della redditività delle opzioni basate su un singolo bordo frattale
• Altre capacità

Basi teoriche per la costruzione di un frattale universale

Utilizziamo le regole di costruzione derivate nell'articolo precedente e integriamole per capire come si costruisce un frattale. Inoltre, ho trovato un piccolo errore nelle mie formule, a causa del quale l'asimmetria dei bordi verso il basso o verso l'alto era impossibile. Le formule derivate si sono rivelate corrette e quindi funzionano per qualsiasi frattale. In realtà, si tratta di una funzione per implementare qualsiasi frattale. Tutti i frattali possibili sono un caso speciale di un frattale generale. Se prendiamo i tre tipi di frattali definiti sopra, le condizioni del frattale generale per l'implementazione di questi tre casi speciali saranno le seguenti:

1. m = n & [ m > s & n > s ]
2. ( m > n || n > m )  & [ m > s & n > s ]
3. ( m > S && n <= S ) || ( n > S && m <= S )

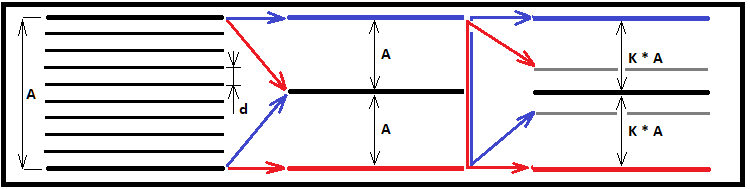
Schematicamente, questi tre tipi di frattali si presentano come segue:

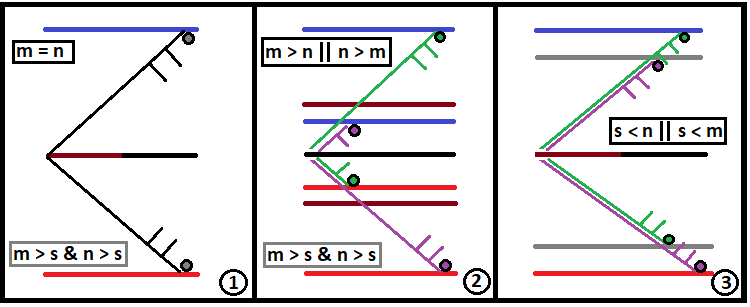
Idealmente, "S" dovrebbe tendere all'infinito. Le seguenti variabili non sono state descritte nel mio precedente articolo. Fornirò qui le descrizioni pertinenti per avere un quadro completo di come utilizzare la formula generale per ottenere i casi speciali. Un frattale è una funzione che funziona secondo il principio della reazione a catena, come in una bomba atomica. Se la reazione a catena impostata è troppo profonda, il computer potrebbe non riuscire a gestire calcoli così massicci. Se il caso non è particolarmente critico, si tratterà semplicemente di un tempo molto lungo — minuti, ore o addirittura giorni. Per avviare correttamente una reazione a catena in un frattale, dovremmo trovare due valori fondamentali:

• Half - la metà della larghezza del canale
• Middle - il valore "U" che corrisponde alla linea centrale

Il valore di Half può essere facilmente calcolato per tutti e tre i casi che abbiamo determinato nell'articolo precedente: è la media aritmetica di m e di n:

• Half = ( n + m ) / 2

Per implementare il secondo valore, dovremo utilizzare tre varianti logiche. Tuttavia, la prima e la seconda variante possono essere combinate in una sola. Abbiamo quindi due varianti:

1. n >= m
2. n < m

Quindi, dato che l'asse "U" è diretto verso l'alto e il valore n è la parte superiore dei canali, mentre m è la parte inferiore, otteniamo due rapporti per due casi possibili con m e n:

1. Middle = Half - m
2. Middle = - ( Half - n )

Questi valori saranno passati alla funzione frattale per uso interno, perché la logica di ramificazione interna descritta nell'articolo precedente non può essere implementata senza di essi. Il prototipo della funzione è il seguente:

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Pertanto, è necessario passare tre valori obbligatori per il corretto avvio del frattale:

1. Half - la metà della larghezza del canale
   
2. Middle - il valore di "U" che corrisponde alla linea centrale
   
3. m - il numero di passi verso il bordo inferiore
4. n - il numero di passi verso il bordo superiore
5. s - il numero massimo consentito di passi in qualsiasi direzione per una singola catena

Altri valori sono indicati con lettere maiuscole per mostrare che questi valori sono dinamici e che saranno differenti su diversi livelli frattali. Ecco la loro definizione:

• S - il numero di passi accumulati nella catena di probabilità corrente; da passare al livello frattale successivo
• U - distanza attuale tra il punto di inizio della catena e la sua fine; da passare al livello frattale successivo
• P - prodotto cumulativo delle probabilità dell'intera catena basato sullo schema di Bernoulli; da passare al livello frattale successivo

Quindi, per un corretto avvio del frattale, dovremmo inserire nella funzione i seguenti valori:

• S = 0 (poiché si tratta di un inizio, quindi non ci sono stati ancora passi)
• U = 0 (per lo stesso motivo)
• P = 1 (poiché si tratta di una catena zero e tutti i passi successivi dovrebbero costituire un gruppo completo)

Per concludere lo sviluppo delle regole generali per i frattali che simulano i prezzi o il trading, riscriviamo brevemente le regole ottenute nell'articolo precedente. Queste regole vengono utilizzate all'interno del frattale. Le regole si basano su diverse formule per le stesse fasi:

• f = u + d — è il numero di passi dell'albero delle combinazioni future (la distanza è determinata dalla distanza dal confine più vicino dell'intervallo frattale)
• s = u - d — il numero di passi finali, espresso in termini di segmenti discendenti e ascendenti

Abbiamo stabilito che cicleremo attraverso "u". Inoltre, utilizzeremo il valore "s" come nuova "U", che verrà passata al livello frattale successivo, se il numero di passi rimanenti lo consente. A tale scopo, è necessario definire una formula per "u" che non contenga "d". Per fare ciò, formulare "d" dalla prima equazione e sostituirla alla seconda:

• s = 2*u - f

Questo valore potrebbe anche essere usato come nuovo valore di "U" da passare in seguito, se il valore attuale fosse uguale a zero. Quindi, dobbiamo aggiungere questa "s" a "U" per ottenere il valore da passare più avanti:

• NewU = s + U - la nostra nuova "U" da passare al livello frattale successivo

Come già definito nell'articolo precedente, questa espressione assume tre possibili valori, basati sui tre possibili valori del numero "f". Ho rielaborato un diagramma dell'articolo precedente per illustrare l'idea:

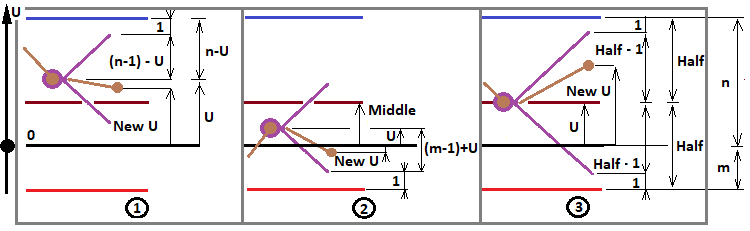
Questo diagramma è davvero appropriato in questo caso, poiché ora determiniamo tutte le possibili configurazioni frattali che possono essere utili per risolvere la maggior parte dei problemi. In base a questo diagramma, definiamo tre casi per "f":

1. f = ( n - 1 ) - U
2. f = ( m - 1 ) + U
3. f = Half - 1

Questi tre casi si presentano quando vengono soddisfatte le seguenti condizioni:

1. U > Middle
2. U < Middle
3. U = Middle

Ora dobbiamo descrivere gli ultimi due valori da passare al livello frattale successivo e considerare come i numeri vengono raccolti nel frattale. Gli ultimi due valori sono calcolati come segue:

• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) — la nostra nuova catena di probabilità "P" da passare al livello frattale successivo
• NewS = S + f = S +(floor(Mid) - 1) — la nostra nuova "S" da passare al livello frattale successivo

Prima di iniziare a raccogliere i numeri in una variabile comune, prestate attenzione al fatto che i numeri dovrebbero essere raccolti in un blocco simile - ma in questo caso facciamo solo un passo, quindi non abbiamo bisogno dello schema di Bernoulli. L'ordine delle dichiarazioni non è importante; dovrebbero essere nello stesso blocco. I numeri possono essere raccolti solo nei casi "1" e "2", con alcune precisazioni:

1. U = n - 1
2. U = - ( m - 1 )

Per il primo caso, i tre valori precedenti sono più facili da calcolare, poiché si tratta di un solo passo:

• NewU = U - 1
• NewP = P * p
• NewS = S + 1

Nel secondo caso, c'è una piccola differenza:

• NewU = U + 1
• NewP = P * ( 1 - p )
• NewS = S + 1

Sulla base della generalizzazione di tutti i frattali, ognuno di essi viene suddiviso in 2 tipi:

• Frattale che calcola la probabilità totale di attraversamento del confine superiore del corridoio
• Frattale che calcola la probabilità totale di attraversamento del confine inferiore del corridoio

A ciascuno di questi tipi corrisponde un altro tipo di frattale, che si affianca all'originale:

• Frattale che calcola il numero medio di passi per attraversare il confine superiore
• Frattale che calcola il numero medio di passi per attraversare il confine inferiore

Questi quattro tipi di frattali si differenziano per la forma dei numeri sommati. Quando si raccolgono le probabilità, possiamo aggiungere solo "P*p" e "P*(1-p)". Per gli altri due frattali, abbiamo bisogno di variabili aggiuntive per passare ai livelli frattali successivi. In questi frattali, utilizziamo passi di dimensioni uguali e di direzione opposta, per cui le loro probabilità sono "p" o "1-p". Ma quando "p" non è uguale a 0,5, questo fatto significa che si tratta di due eventi diversi che possono avere caratteristiche differenti. Per caratteristiche intendo un insieme di alcune variabili casuali che corrispondono a un determinato evento. Uno di questi valori è la durata della posizione. Ci può essere qualsiasi numero richiesto di tali valori, e possiamo considerarli come tempo, se necessario. Questa parte può essere semplificata con pochi semplici passaggi. I numeri da sommare avranno la seguente forma:

1.  P * p * NewS
2.  P * ( 1 - p ) * NewS

Come si può notare, le probabilità sono moltiplicate per il numero di passi di questa catena di passi completata. Ma questa formula si applica solo quando i passi verso l'alto e verso il basso sono ugualmente probabili. In casi alternativi, sarà necessario utilizzare due strutture diverse per descrivere i passi verso l’alto e quelli verso il basso, oppure fornire una struttura per memorizzare entrambi i numeri. Nel secondo caso, la funzione frattale non restituirà un numero, ma un contenitore di dati. Il contenitore non necessita di estensione. Inoltre, ho fornito un contenitore che può memorizzare tutti i parametri richiesti, in modo che non sia necessario descrivere diverse funzioni con un codice simile. Invece, ho combinato tutte le funzioni in una, che può descrivere tutti i parametri richiesti. Il tipo di frattale e il compito da esso risolto dipenderanno direttamente dai parametri di ingresso della funzione. Per estendere il concetto, la prima "S" e il suo equivalente "NewS" devono essere sostituiti con i seguenti valori:

1. SU - gli ultimi passi verso l'alto della catena di probabilità selezionata
2. SD - gli ultimi passi verso il basso della catena di probabilità selezionata
3. NewSU e NewSD - i valori da passare al livello frattale successivo.
4. SU + SD = S

Questi valori devono essere definiti in modo simile alla definizione di "S". Quando "U > Middle":

• NewSU = SU
• NewSD = SD + 1

Quando "U < Middle":

• NewSU = SU + 1
• NewSD = SD

Per l'aggiornamento finale del frattale sono necessari altri sei valori:

1. UpperMidSDown - il numero totale medio probabile di passi verso il basso prima di raggiungere il confine superiore
2. UpperMidSUp - il numero totale medio probabile di passi verso l’alto prima di raggiungere il confine superiore
3. UpperSummProbability - la probabilità di attraversare il confine superiore
4. LowerMidSDown - il numero totale medio probabile di passi verso il basso prima di raggiungere il confine inferiore
5. LowerMidSUp - il numero totale medio probabile di passi verso l’alto prima di raggiungere il confine inferiore
6. LowerSummProbability - la probabilità di superare il confine inferiore

I valori "1", "2", "4", "5" indicano la somma dei prodotti del numero di passi corrispondenti e della loro probabilità. Questi valori sono privi di significato in quanto tali, ma sono componenti di formule di valori utili di cui parleremo più avanti. I valori "3" e "6" sono le probabilità dell'ipotesi di attraversamento dei due bordi che formano un gruppo completo. Utilizzando questi valori, possiamo determinare un'infinità di altre cose.

Scrivere il codice per implementare un frattale universale

Per lanciare correttamente il frattale, abbiamo bisogno di una funzione che esegua tutte le operazioni preliminari prima del lancio del frattale, dopodiché lancia correttamente il frattale in base a regole predefinite. Ho preparato un'implementazione di questo algoritmo in stile MQL5:

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Dopo il calcolo del frattale, la funzione restituisce il nostro contenitore con tutti i dati richiesti:

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

Questo contenitore include un sovraccarico dell'operatore "+=", per combinare due strutture identiche. Questa parte verrà utilizzata per la funzione principale. Ecco la funzione frattale:

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

Il codice è stato verificato in MetaTrader 5 e funziona abbastanza bene. Questa logica può essere ulteriormente ampliata, se necessario, mentre ci sono ancora molte possibilità avanzate. Ma ho deciso di mantenere breve l'elenco dei parametri di ingresso della funzione, perché la funzionalità implementata è sufficiente per i nostri scopi. Studiando attentamente il codice, vedrai che è pienamente conforme ai principi matematici sopra esposti. Anche se breve, questo pezzo di codice può fare miracoli. Credo che il codice debba contenere quanta più logica e matematica possibile. Questo è ciò di cui avremo bisogno alla fine. Anche un bel codice è inutile se non può essere utilizzato per lo scopo per cui è stato creato. Nel nostro caso, lo scopo previsto è l'applicabilità al trading. Ecco il log come conferma:

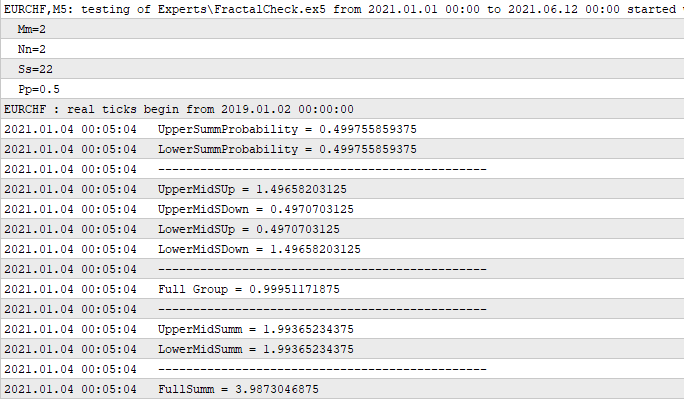
In questo caso, ho creato un semplice Expert Advisor che calcola l'intero frattale al primo tick ricevuto. Questo calcolo viene eseguito una volta sola, quindi non sono necessari ulteriori ricalcoli. I primi sei numeri fanno parte del contenitore, mentre gli altri sono derivati da essi. Riporto qui solo le derivate più importanti, che possono aiutare a capire che queste sei variabili permettono di ricevere tutte le altre variabili di cui possiamo avere bisogno. Ad esempio, date un'occhiata a "Full Group". Si chiama così perché la somma delle probabilità di due ipotesi non sovrapposte di uno degli attraversamenti di confine secondo il calcolo precedente deve essere uguale a uno. È confermato dal nostro codice. Seguono due numeri identici che sono la somma di "1", "2" e "3", "4". Quest'ultimo numero è la somma dei penultimi numeri - si tratta del numero medio di passi che la catena attraverserà. Il motivo per cui ho impostato questi parametri di ingresso della funzione di impostazione, dove "m" e "n" sono uguali e simmetrici, sarà illustrato più avanti.

Derivazione della prima formula basata su un frattale simmetrico

In base al risultato del log, il numero medio di passaggi che la catena attraverserà tende a "4". Il corridoio viene raddoppiato rispetto a un passo unitario. Un passo unitario si ha se "n" e "m" sono impostati su uno. In altre parole, se vogliamo calcolare il numero medio di passi in un corridoio che consiste di corridoi più piccoli (nel qual caso un numero intero di corridoi più piccoli si inserisce in uno più grande e il nuovo corridoio è anche simmetrico), possiamo assumere che:

• P[n] = P[n-1] * 2 - è l'espressione ricorsiva per la larghezza del nuovo corridoio in passi, in base alla larghezza del corridoio precedente, più piccolo, da cui il nuovo corridoio è composto
• S[n] = S[n-1] * 4 - è l'espressione ricorsiva per calcolare il numero medio di passi del nuovo corridoio, espresso attraverso il valore medio di un corridoio più piccolo

se accettiamo che "P[0]=1" e "S[0]=1", e se iniziamo la numerazione della ricorsione dall'indice "0", allora questa ricorsione può essere rappresentata come due serie molto simili:

• P[n] = 2^n , n = 0 ... + infinity
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

Se si osserva attentamente la prima serie e si trasforma correttamente la seconda, si scopre che la seconda serie può essere espressa utilizzando gli elementi della prima. In altre parole, si ottiene la seguente dipendenza: S = S(P) = P^2. Questa dipendenza è vera solo per il raddoppio ricorsivo della larghezza del canale. Quando ho visto questa formula, ho deciso di verificarne l'applicabilità per qualsiasi numero grande arbitrario "n" e "m". Logicamente, nel secondo passo impostiamo "n=3", "m=3" e calcoliamo le stesse variabili. Con questi parametri di ingresso, il numero medio di passi tende al numero "9". È possibile verificare questa parte da soli, utilizzando il codice sopra riportato o i programmi MathCad 15 allegati di seguito. La stessa serie può essere fornita per questi parametri:

• P[n] = 3^n , n = 0 ... + infinity
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Come si può vedere, si ottiene la stessa relazione "S=S(P)=P^2". Potremmo ripetere la stessa cosa per tutti gli altri possibili scenari relativi alla suddivisione dell'intervallo, ma non è necessario. Questo fatto significa che se conosciamo, ad esempio, la durata media di un prezzo all'interno di un canale simmetrico, possiamo calcolare la durata media di un prezzo all'interno di qualsiasi altro canale. Può essere calcolato come segue:

• S = S0 * K^2 - il numero medio di passi di un nuovo corridoio
• T = S * T0 - la durata media del nuovo corridoio
• T = T0 * K^2 - la durata media del nuovo corridoio espressa in termini di durata media di un altro corridoio (a condizione che S0 = 1 )
• S0 - il numero medio di passi del vecchio corridoio
• T0 - la durata media di un passo del vecchio corridoio
• P = K * P0 --> K = P/P0 - quante volte il nuovo corridoio è più grande di quello vecchio
• P - la larghezza del nuovo corridoio
• P0 - la larghezza del vecchio corridoio

Ora possiamo verificare l'ipotesi utilizzando MathCad 15. Innanzitutto, verifichiamo le ipotesi relative alla relazione quadratica:

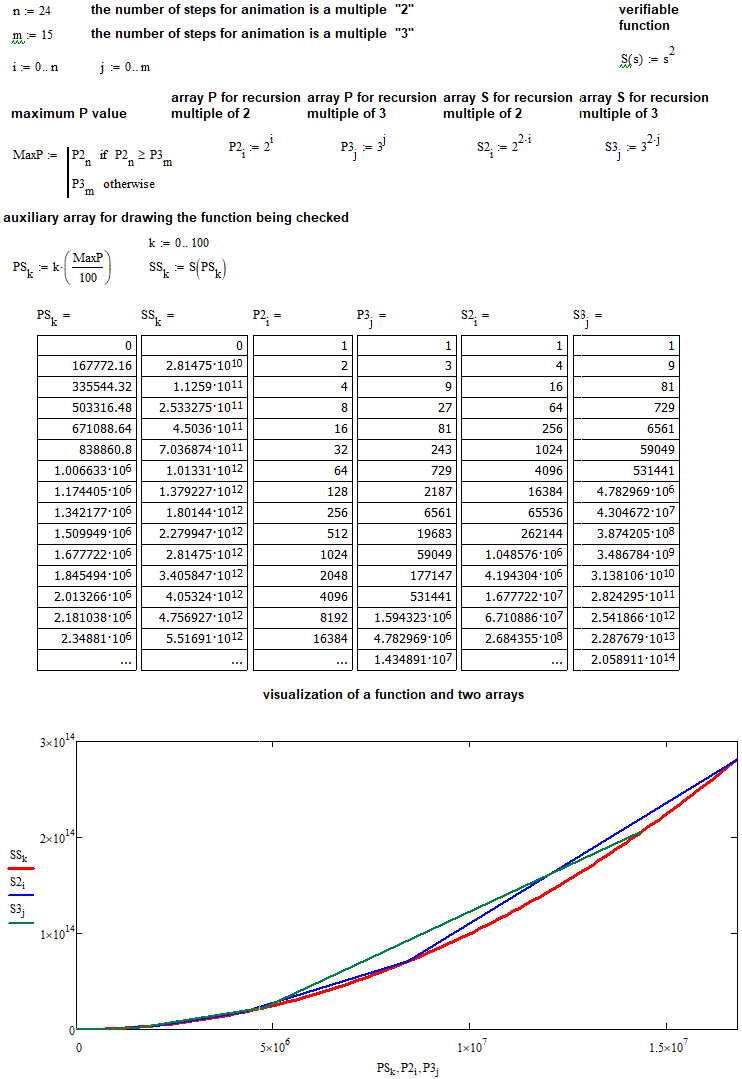
Ora dovrebbe essere molto chiaro.

Valutazione delle prestazioni della formula derivata per tutti gli argomenti positivi e reali

La formula funziona per tutti i numeri "P" interi. Ma può essere utilizzata per un numero "K" in virgola mobile? È necessario implementare un trucco per fornire un "K" in virgola mobile. Supponiamo di avere un corridoio di prezzi con una durata media nota e di avere un corridoio che si inserisce nel nostro corridoio "N" volte, ma non conosciamo ancora la sua durata media. In seguito, la troveremo utilizzando la stessa formula. Secondo questa logica:

• T = T0 * N^2 ---> T0 = T / N^2
• T - è la durata del nostro corridoio, di cui conosciamo la durata media
• T0 - è la durata media di un corridoio più piccolo, di cui il nostro corridoio è composto

Ciò significa che possiamo trovare la durata di un corridoio più piccolo, che ci serve per calcolare la durata del terzo corridoio con un fattore di incremento frazionario. Ora che abbiamo trovato la durata del corridoio più piccolo, possiamo trovare la sua larghezza in punti:

• d = P / N

Quindi, possiamo calcolare quanti corridoi di questo tipo rientrano in un corridoio allargato, utilizzando il seguente rapporto:

• Smin = MathFloor( K * P / d ) = MathFloor( K * N )
• Lim( N --> +infinity ) [ K * N/MathFloor( K * N ) ] = 1

Come si può notare, la larghezza del corridoio si riduce e non influisce sul risultato. La seconda riga mostra un rapporto molto importante che aiuterà a capire cosa fare in seguito. Dimostra che quando si divide il corridoio sorgente nel maggior numero possibile di segmenti, si può trascurare la parte frazionaria che viene scartata come risultato della funzione MathFloor. Ciò è dimostrato dal limite che tende all'unità. Se questa imprecisione confonde, possiamo trovare un altro valore:

• Smax = MathFloor( K * P / d ) + 1 = MathFloor( K * N ) + 1 = Smin + 1

Ora è chiaro che il vero valore di "K * N"è proprio tra "Smin" e "Smax". Se "N" tende all'infinito, si ottengono due corridoi molto simili e la loro durata media tenderà ad essere uguale, poiché le loro dimensioni differiscono solo di un segmento. Pertanto, la durata media del corridoio necessario sarà determinata più accuratamente dalla media aritmetica della durata media di questi corridoi:

• T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 =  T0 *( Smin^2 + Smax^2 ) / 2
• T1 - la durata media del corridoio che dobbiamo determinare

La figura seguente illustra le mie idee:

Ora che abbiamo trovato un'espressione alternativa per calcolare la durata del corridoio, possiamo confrontare il suo risultato con il valore della funzione per il numero intero "K", sostituendolo invece con il flottante "K". Se i valori risultanti delle due espressioni sono identici, possiamo concludere che la funzione trovata per i valori interi "K" è assolutamente applicabile a tutti i numeri interi e a quelli in virgola mobile nell'intervallo "0 ... +infinito". Eseguiamo il primo controllo per "N = 1000". Penso che questa divisione sia sufficiente per vedere l'identità di due numeri, se ce n'è una:

Come si può vedere, i due numeri sono praticamente identici. Logicamente, dovrebbero essere più identici per valori di "N" maggiori. Ciò può essere anche dimostrato assumendo quanto segue:

• Lim( N --> +infinity ) [  (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 )  ] = 1

Il numeratore di questo limite è la nostra espressione approssimativa per calcolare la durata media del nuovo corridoio, mentre il denominatore è un'espressione che presumibilmente descrive accuratamente lo stesso valore. Ho creato una semplice funzione che esegue gli stessi calcoli della schermata precedente. Ma questa volta viene applicato all'intero intervallo del numero "N" a partire da "1". Ora vediamo il risultato dell'esecuzione del programma:

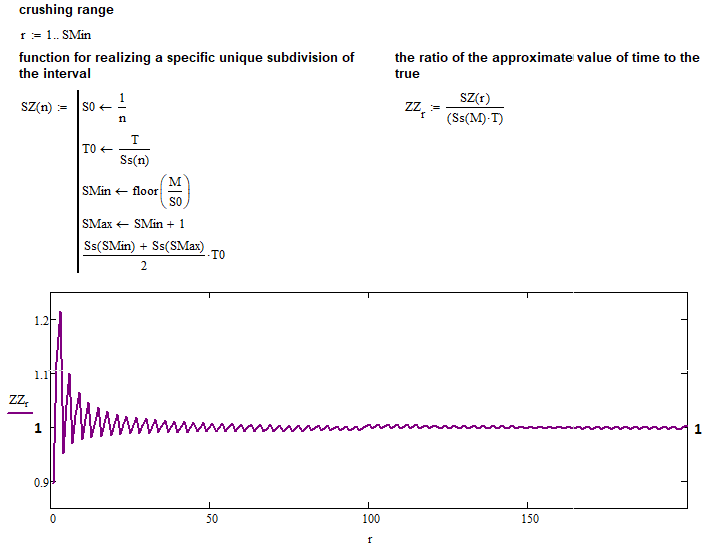
Tutte le ipotesi sono pienamente confermate: la funzione che abbiamo trovato per il numero intero "K" è assolutamente applicabile per qualsiasi "K" positivo. Ora abbiamo una singola funzione molto utile che può essere utilizzata come base per ulteriori azioni, ad esempio come base per ulteriori matematiche per descrivere l'intero frattale universale.

Frattale avanzato sviluppato dal frattale universale

Come ulteriore e utile esempio di applicazione di un frattale universale, possiamo prendere un frattale a un solo bordo, con, ad esempio, "n=1", "m ---> +infinity", "s = m+1", "p=0,5". Finora abbiamo considerato frattali con passi di uguale probabilità in entrambe le direzioni, il che è applicabile solo alla passeggiata aleatoria. Ma questo frattale offre tutte le possibilità. Per passare a un'analisi più approfondita di una struttura così complessa, è necessario innanzitutto considerare i fondamenti. Inoltre, in questa fase iniziale otteniamo formule utili e possiamo trarre conclusioni fondamentali su questi processi frattali. Ho testato il frattale con differenti valori di "s" e ho ottenuto i seguenti dati:

• s = 22 , FullSumm = 2,868 , UpperSummProbability = 0,831
• s = 32 , FullSumm = 3,618 , UpperSummProbability = 0,860
• s = 42 , FullSumm = 4,262 , UpperSummProbability = 0,877
• s = 45 , FullSumm = 4,499 , UpperSummProbability = 0,882

Un ulteriore aumento del numero di passi ammissibili porta alla singolarità del tempo di calcolo, in altre parole, il tempo di calcolo aumenta così tanto da richiedere ore o addirittura giorni. Ma se si osserva la velocità con cui aumenta la somma media delle probabilità, si può notare che non è possibile valutare la convergenza di queste serie utilizzando questo tipo di frattale. Ma sulla base della formula precedentemente derivata, possiamo valutare la convergenza utilizzando un tipo di frattale diverso ma molto utile. Questo frattale può anche aiutare a calcolare il tempo di una strategia molto popolare e redditizia chiamata "Carry trade". Prima mostrerò una figura e poi la spiegherò:

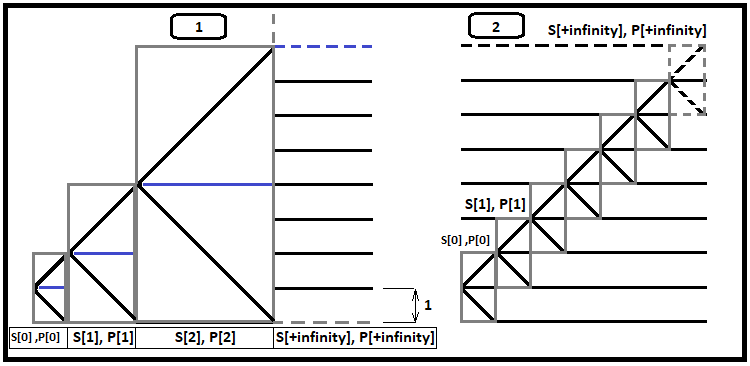
Immaginate che il processo di determinazione dei prezzi inizi a un passo dal confine, indipendentemente da dove si trovi il confine, in alto o in basso. La figura precedente mostra un esempio con il confine inferiore, in quanto più facile da percepire. Osservate da vicino il primo frattale. Ogni riquadro grigio contiene due scenari per ulteriori eventi:

1. Il prezzo raggiunge il bordo superiore del riquadro
2. Il prezzo raggiunge il bordo inferiore del riquadro

Quando il prezzo raggiunge il bordo superiore del corridoio, a questo punto inizia automaticamente un nuovo frattale più grande, e così via. Se consideriamo questo processo allo stesso modo del frattale universale, vedremo di nuovo le catene di probabilità. Ma ora la nostra formula ci dice il numero di passi da fare in un corridoio simmetrico, in base a quanti passi si inseriscono nel corridoio (ora vediamo che un passo è un corridoio più piccolo che si inserisce in quello originale).

Ora, non è necessario considerare l'intero frattale per calcolare il numero medio di passi. Applicare invece la formula derivata a ciascuno dei frattali. Il passo in questo caso non è lo stesso valore, ma viene effettuato quando si raggiunge il limite superiore o inferiore del frattale annidato successivo. Su questa base, possiamo creare catene di probabilità molto semplici. La probabilità di raggiungere il confine in corrispondenza del primo frattale P[0] è pari a 0,5. Ciò significa che esiste un secondo caso possibile in cui dobbiamo creare il prossimo frattale sperando che il prezzo raggiunga il confine. Tutti questi eventi sono annidati e tutte queste catene formano un gruppo completo.

La probabilità di raggiungere il limite in corrispondenza del secondo frattale P[1] è uguale alla probabilità precedente moltiplicata per 0,5. Questo processo può continuare all'infinito. Il numero medio di passi può essere determinato utilizzando la formula derivata e le probabilità della catena. A tal fine, definiamo innanzitutto una formula per la probabilità di ogni singola catena, tenendo conto che il numero medio di passi per superare il limite superiore e per superare il limite inferiore è uguale. Risulta che:

• PUp = PDown = P - il rapporto mostra che le probabilità di toccare i limiti superiore e inferiore di un frattale sono ugualmente probabili per tutti i limiti di tutti i frattali annidati
• P[j] = 0.5^(j+1), j = 0 ... + infinity - la probabilità che si verifichi la catena j
• S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ), i = 1... + infinity - una formula ricorrente per calcolare il numero totale mediamente probabile di passi per tutti i livelli frattali (mentre S[0] = 1*0.5 = 0.5)
• F(K) = K^2 - la nostra formula derivata per calcolare il numero medio di passi
• D(i) = 2^i - quanti passi inserire nel livello frattale successivo
• S[i-1]/P[i-1] - il numero medio di passi nel ramo rimanente non considerato, a condizione che si sia verificato il ramo corrente (perché oltre al corrente frattale annidato, è necessario tenere conto di tutti i passi avvenuti in precedenza)
  

Il secondo frattale è in realtà identico al primo, cioè le probabilità delle loro catene (l’array P[]) sono identiche. Perché ne abbiamo bisogno? Supponiamo di avere la strategia "Carry Trade". Abbiamo due conti, un conto con swap e un conto senza swap per bloccare le posizioni con uno swap positivo. Abbiamo anche bisogno di una formula per calcolare il tempo medio di tenuta della posizione profittevole. Questo tempo di tenuta medio deriva direttamente dalla formula del numero medio di passi. Non tratterò questo argomento in dettaglio in questo articolo. Voglio solo dimostrare l'importanza della matematica. Questo argomento sarà discusso in dettaglio più avanti. Definiamo ora una formula per i passi di probabilità medi per il secondo frattale:

• S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) - una formula ricorrente per calcolare il numero totale mediamente probabile di passi per tutti i livelli frattali (mentre S[0] = 1*0.5 = 0.5)

In questo caso, questa formula è solo un caso speciale di quella preziosa, perché nel secondo frattale K=1, sempre, per tutti i livelli frattali. Scopriamo quali sono i limiti delle somme di queste quantità per entrambi i frattali:

La prima serie diverge, il che significa che quando non esiste un limite superiore e il trading è infinito, il tempo medio è pari a infinito. Nel secondo caso otteniamo un limite chiaro pari a 2. Ciò significa che se apriamo una posizione con uno swap positivo, in media dovremo chiudere questa posizione dopo due passi (quindi il tempo medio di mantenimento della posizione sarà pari a 2*T, dove T è il tempo medio di mantenimento della posizione, a condizione che si chiuda la posizione quando raggiunge uno dei limiti). Nel secondo e più semplice caso, chiudiamo semplicemente entrambe le posizioni su entrambi i conti, anche se il conto swap mostra un numero positivo. Ovviamente la prima opzione è molto più interessante, ma la sua applicazione richiede un prelievo e un deposito rapidi e senza problemi su entrambi i conti. Se questa opzione non è possibile, dovremo utilizzare l'opzione classica, che genera meno profitti ma ha una maggiore stabilità.

Riassunto dei risultati

Nella seconda parte della serie di articoli, abbiamo ottenuto risultati molto interessanti, anche per quanto riguarda l'applicazione pratica nel trading. Ma cosa più importante, è ormai chiaro che la sfera delle possibili applicazioni dei frattali è enorme. Cosa abbiamo fatto nell'articolo:

• Definite chiare regole matematiche per la costruzione di un frattale universale
• Creazione di un codice funzionante in stile MQL5 basato sui principi matematici enunciati.
• I principi sono stati verificati con successo utilizzando due piattaforme, MetaTrader 5 e MathCad 15.
• Utilizzando gli algoritmi, si è ottenuta la prima formula per calcolare la durata di un corridoio arbitrario
• Testato e convalidato la formula utilizzando la programmazione per tutti i casi possibili
• Ottenuto un nuovo tipo di frattale più veloce, basato sulla formula ottenuta
• Il risultato ci ha consentito di accelerare i calcoli e di determinare ciò che non poteva essere determinato da un frattale universale.
• Toccato un caso particolare di utilizzo di un frattale avanzato per i problemi di swap trading.
• Ottenuti strumenti per l'ulteriore sviluppo della teoria

Inoltre, vorrei sottolineare che i miei strumenti si sono notevolmente ampliati. Ora possiamo analizzare i frattali con passi di diversa probabilità (situazioni di trend e situazioni legate all'analisi statistica del trading). Ancora una volta, notare che in questo articolo abbiamo considerato solo i casi in cui "p = 1 - p = q = 0,5". Ciò significa che tutti i calcoli sono applicabili solo alle situazioni che descrivono la passeggiata aleatoria. Quindi, ci sono molte più possibilità potenziali.

Di seguito è riportata la formula ottenuta dopo lo studio del frattale. Ancora una volta, lo spiegherò brevemente:

1. S = K^2 - il numero medio di passi del nuovo corridoio, basato sul fatto che un passo è uguale a un altro corridoio
2. T = S * T0 = T0 * K^2 - durata media di un corridoio sconosciuto
3. T0 - durata media di un corridoio conosciuto
4. P = K * P0 --> K = P/P0 - quante volte il corridoio conosciuto è più grande di quello sconosciuto
5. P - la larghezza del corridoio con una durata sconosciuta
6. P0 - la larghezza del corridoio conosciuto

Sostituendo 4 in 1, possiamo esprimere il numero medio di passi che si troveranno nel corridoio sconosciuto attraverso i valori noti, e sostituendo 1 in 2 otteniamo la durata media di questo corridoio, calcolata in base ai valori noti:

• T0, P0, P

Aggiungerò anche una risposta a una domanda che i lettori potrebbero avere all'inizio di questo articolo:

• Perché abbiamo bisogno di formule se possiamo raccogliere le statistiche di trading dal tester di strategie di MetaTrader 5?

Risposta:

• Bene, non è sempre possibile raccogliere statistiche, poiché non tutti i simboli finanziari hanno uno storico di trading sufficiente per tali valutazioni. Questo è impossibile per i corridoi di grandi dimensioni, poiché si potrebbe selezionare un corridoio che non ha mai attraversato i suoi confini. Utilizzando corridoi di larghezza inferiore e la formula, possiamo ottenere i dati che non possono essere ottenuti dalle statistiche. Inoltre, questo tipo di matematica offre una precisione e una flessibilità senza pari. Ci sono molti altri vantaggi.

Conclusioni

In questo articolo ho provato a descrivere la logica di calcolo, che può essere utilizzata per condurre ulteriori ricerche sui processi di determinazione dei prezzi. Finora non c'è molto per l'applicazione pratica. Ma sono sicuro che possiamo studiare tutte le varietà del frattale universale e ottenere possibili formule per descrivere i corridoi di prezzo asimmetrici e con un solo bordo. Nel prossimo articolo continuerò la ricerca sul frattale universale e cercherò di presentare tutti i risultati come semplici formule. Inoltre, includerò una nuova matematica molto interessante che consentirà di utilizzare le formule ottenute non solo per i processi di politica dei prezzi, ma anche per descrivere backtest e segnali di trading. Questo ci permetterà di analizzare con assoluta precisione qualsiasi strategia in termini di tempo e probabilità, che è in definitiva l'aspetto più importante del trading.

Riferimenti

• Combinatoria e teoria della probabilità per il trading (Parte I): Le basi