Previsão de séries temporais utilizando suavização exponencial

Introdução

Existe atualmente um grande número de diferentes métodos de previsão bem conhecidos que são baseados apenas na análise de valores passados de uma sequência de tempo, ou seja, métodos que empregam princípios utilizados normalmente na análise técnica. O principal instrumento desses métodos é o esquema de extrapolação, onde as propriedades de sequência identificadas em um determinado retardo de tempo vão além de seus limites.

Ao mesmo tempo, presume-se que as propriedades de sequência, no futuro, serão as mesmas no passado e no presente. Um esquema de extrapolação mais complexo, que envolva um estudo da dinâmica de mudanças nas características da sequência com relação à tal dinâmica dentro do intervalo de previsão é menos utilizado na previsão.

Os métodos de previsão mais conhecidos baseados na extrapolação são talvez aqueles utilizando o modelo autorregressivo, integrado de média móvel (ARIMA). A popularidade desses métodos é principalmente devido aos trabalhos de Box e Jenkins, que propuseram e desenvolveram um modelo ARIMA integrado. Há, naturalmente, outros modelos e métodos de previsão além dos modelos introduzidos por Box e Jenkins.

Este artigo abordará, de forma breve, modelos mais simples - modelos de suavização exponencial propostos por Holt e Brown bem antes dos trabalhos de Box e Jenkins aparecerem.

Apesar das ferramentas matemáticas mais simples e claras, a previsão com a utilização de modelos de suavização exponencial, muitas vezes leva a resultados comparáveis com os resultados obtidos utilizando o modelo ARIMA. Isso não está longe de ser surpreendente, visto que modelos de suavização exponencial são um caso especial do modelo ARIMA. Em outras palavras, cada modelo de suavização exponencial em estudo neste artigo tem um modelo ARIMA equivalente correspondente. Estes modelos equivalentes não serão considerados no artigo e são mencionados somente a título de informação.

Sabe-se que a previsão em cada caso particular requer uma abordagem individual e normalmente envolve uma série de procedimentos.

Por exemplo:

1. Análise de sequência de tempo para os valores faltantes e atípicos. Ajuste desses valores.
2. Identificação da tendência e do seu tipo. Determinação da periodicidade de sequência.
3. Verificação da estacionariedade da sequência.
4. Análise de processamento de sequência (logaritmos, diferenciação, etc.).
5. Seleção de modelo.
6. Determinação de parâmetro de modelo. Previsão baseada no modelo selecionado.
7. Avaliação precisa da previsão de modelo.
8. Análise de erros do modelo selecionado.
9. Determinação de adequação do modelo selecionado, caso necessário, substituição do modelo e retorno aos itens anteriores.

Essa não é nem de longe a lista completa de ações necessárias para previsão eficaz.

Deve-se enfatizar que a determinação de parâmetros do modelo e obtenção dos resultados previstos são apenas uma pequena parte do processo de previsão geral. Mas parece ser impossível abordar toda a gama de problemas, de uma forma ou de outra relacionados com a previsão em um artigo.

Este artigo, portanto, só lidará com modelos de suavização exponencial e usará cotações de moeda não pré-processadas​como sequências de teste. Questões associadas não podem certamente ser evitadas no artigo completo, mas serão ligeiramente mencionadas na medida em que forem necessárias para a avaliação dos modelos.

1. Estacionariedade

A noção de extrapolação adequada implica que o desenvolvimento futuro dos processos em estudo será a mesma que no passado e no presente. Em outras palavras, preocupa-se com o processo estacionário. Processos estacionários são muito atrativos do ponto de vista de previsão, mas, infelizmente, não existem em natureza, como um verdadeiro processo está sujeito a alterações, no curso do seu desenvolvimento.

Processos reais podem ter expectativa notoriamente diferente, variância e distribuição ao longo do tempo mas os processos cujas características mudam muito lentamente podem ser possivelmente atribuídos a processos estacionários. "Muito lentamente", neste caso, significa que as mudanças nas características do processo dentro do intervalo de observação finito parecem ser tão insignificantes que tais alterações podem ser negligenciadas.

é claro que quanto mais curto o intervalo de observação disponível (curta amostra), maior é a probabilidade de tomar a decisão errada em relação a estacionariedade do processo como um todo. Por outro lado, se estão mais interessadas no estado do processo em um momento posterior fazer uma previsão de curto prazo, a redução do tamanho da amostra pode, em alguns casos, conduzir ao aumento da precisão de tal previsão.

Se o processo está sujeito a mudanças, os parâmetros de sequência determinada dentro do intervalo de observação, será diferente fora de seus limites. Assim, quanto maior o intervalo de previsão, mais forte o efeito da variabilidade das características de sequência sobre o erro de previsão. Devido a este fato, temos de nos limitar a apenas à uma previsão de intervalo curto, uma redução significativa no intervalo de previsão permite esperar que as características de sequência alterando-se lentamente não resultarão em erros de previsão consideráveis.

Além disso, a variabilidade dos parâmetros das sequências leva ao fato de que o valor obtido na estimativa pelo intervalo de observação é a média, visto que os parâmetros não permanecera, constantes dentro do intervalo. Os valores dos parâmetros obtidos não serão, portanto, relacionados com o último instante deste intervalo, mas refletirão uma certa média disso. Infelizmente, não é possível eliminar completamente este fenômeno desagradável, mas ele pode ser diminuído, se o comprimento do intervalo de observação envolvido no modelo de estimação de parâmetros (intervalo de estudo) for reduzido na medida do possível.

Ao mesmo tempo, o intervalo de estudo não pode ser reduzido indefinidamente, porque caso extremamente reduzido, isso certamente diminuirá a precisão da estimativa de parâmetros de sequência. Deve-se procurar um compromisso entre o efeito de erros associados com a variabilidade das características de sequência e aumento de erros devido à redução extrema no intervalo do estudo.

Todos os itens acima se aplicam plenamente a modelos de suavização exponencial de uso de previsão, uma vez que são baseados no pressuposto de estacionariedade dos processos, como modelos ARIMA. No entanto, por uma questão de simplicidade, vamos doravante supor que convencionalmente a seguir os parâmetros de todas as sequências em questão variam dentro do intervalo de observação, mas de tal forma lentos que essas alterações possam ser negligenciadas.

Assim, o artigo abordará questões relacionadas com a previsão de curto intervalo de sequências com características alterando-se lentamente, com base em modelos de suavização exponencial. A "previsão de curto intervalo" deve, neste caso, significar previsão para um, dois ou mais intervalos de tempo à frente ao invés de uma previsão para um período de menos de um ano, como é geralmente entendida em economia.

2. Sequências de teste

Ao escrever este artigo, cotações anteriormente salvas de ERRUR, EURUSD, USDJPY e XAUUSD para M1, foram utilizados M5, M30 e H1. Cada um dos arquivos salvos contém 1.100 valores "abertos". O valor "mais velho" está localizado no começo do arquivo e o mais "recente" no final. O último valor salvo no arquivo corresponde ao momento em que o arquivo foi criado. Arquivos contendo sequências de teste foram criados usando o script HistoryToCSV.mq5. Os arquivos de dados e script que foram criados estão localizados no final do artigo em arquivos do tipo Files.zip.

Como já mencionado, as cotações salvas serão usadas nesse artigo, sem serem pré-processadas, apesar dos problemas óbvios que eu gostaria de chamar a sua atenção. Por exemplo, cotações EURRUR_H1 durante o dia contêm 12-13 barras, cotações XAUUSD às sextas-feiras contêm uma barra a menos do que em outros dias. Estes exemplos demonstram que as cotações são produzidas com intervalo de amostragem irregular, o que é totalmente inaceitável para os algoritmos projetados para trabalhar com sequências de tempo corretas que sugerem ter um intervalo de quantização uniforme.

Mesmo que os valores de cotações faltantes sejam reproduzidos usando extrapolação, a questão sobre a falta de cotações nos finais de semana permanece aberta. Podemos supor que os eventos que ocorrem no mundo nos finais de semana têm o mesmo impacto sobre a economia mundial como eventos durante a semana. Revoluções, ações naturais, escândalos conhecidos, mudanças de governo e outros eventos mais ou menos desse tipo de porte, podem ocorrer a qualquer momento. Se tal evento ocorreu no sábado, dificilmente teria uma influência menor nos mercados mundiais do que se tivesse ocorrido em um dia de semana.

São, talvez, esses eventos que levam a lacunas entre cotações tão frequentemente observadas em relação ao final da semana de trabalho. Aparentemente, o mundo continua passando por suas próprias regras, mesmo quando FOREX não funciona. Ainda não está claro se os valores nas cotações correspondentes aos finais de semana, que são destinadas a uma análise técnica devam ser reproduzidas e qual o benefício que isso poderia dar.

Obviamente, estas questões estão fora do âmbito deste artigo, mas à primeira vista, uma sequência sem quaisquer lacunas parece ser mais adequada para a análise, pelo menos em termos de detecção de componentes cíclicos (sazonal).

A importância da preparação preliminar dos dados para análise posterior não pode ser subestimada; no nosso caso, é uma questão importante independente como cotações, a forma como elas aparecem no Terminal, não são geralmente muito adequadas para uma análise técnica. Além das questões relacionadas com a lacuna acima, há uma série de outros problemas.

Ao formar as cotações, por exemplo, um ponto fixo de tempo é atribuído a valores "aberto" e "fechado" que não pertencem ao mesmo; estes valores correspondem ao tempo de formação de tick, ao invés de um momento fixo de um gráfico de intervalo de tempo selecionado, considerando que ticks sejam, por vezes, muito raros.

Outro exemplo pode ser visto em completo desprezo do teorema de Nyquist, pois ninguém pode garantir que a taxa de amostragem, mesmo dentro de um minuto de intervalo satisfaça o teorema acima (para não mencionar outros, intervalos maiores). Além disso, deve-se ter em mente a presença de um spread variável, que em alguns casos possa ser sobreposto sobre os valores de cotação.

Deixe-nos, porém, deixar essas questões fora do âmbito deste artigo e voltar ao assunto principal.

3. Suavização exponencial

Deixe-nos primeiramente dar uma olhada no modelo mais simples

,

onde:

• X(t) – processo (simulado) em estudo,
  
• L(t) – nível de processo variável,
  
• r(t)– média zero variável aleatória.

Como pode ser visto, este modelo inclui a soma de dois componentes; estamos particularmente interessados no nível de processo L(t) e tentaremos isolá-lo.

Bem se sabe que a média de uma sequência aleatória pode resultar na diminuição da variação, isto é, redução da amplitude do seu desvio da média. Podemos, portanto, supor que, se o processo descrito pelo nosso modelo simples é exposto à média (suavização), não conseguiremos nos desfazer de um componente aleatório r(t) completamente, mas podemos pelo menos enfraquecê-lo consideravelmente, portanto, selecionando o nível de objetivo L(t).

Para isso, vamos usar uma suavização exponencial simples (SES).

Nessa fórmula, bem conhecida, o grau de suavização é definido pelo coeficiente de alfa, que pode ser definido de 0 a 1. Se alfa é definido como zero, os novos valores de entrada da sequência de entrada X não terão nenhum efeito sobre o resultado de suavização. O resultado de suavização para qualquer ponto de tempo terá um valor constante.

Consequentemente, em casos extremos como esse, o componente aleatório incômodo será totalmente suprimido ainda que o nível do processo sob consideração será suavizado à uma linha horizontal reta. Se o coeficiente alfa for definido como um, a sequência de entrada não será nem um pouco afetada pela suavização. O nível em consideração L(t) não será distorcido, nesse caso e o componente aleatório também não será suprimido.

é intuitivamente claro que ao selecionar o valor alfa, tem-se a satisfazer simultaneamente as exigências conflitantes. Por um lado, o valor de alfa deve ser próximo de zero, a fim de suprimir eficazmente o componente aleatório de r(t). Por outro lado, é aconselhável definir o valor de alfa próximo da unidade para não distorcer o componente L(t) estamos tão interessados​dentro. Para obter o valor de alfa ideal, precisamos identificar um critério segundo o qual tal valor possa ser otimizado.

Ao determinar tal critério, lembre-se que este artigo lida com a previsão e não apenas suavização de sequências.

Nesse caso em relação ao modelo de suavização exponencial simples, é de costume considerar o valor obtido em um dado tempo como uma previsão para qualquer número de passos à frente.

Onde é a previsão de passo à frente-m no tempo t.

Assim, a previsão do valor de sequência no tempo t será uma previsão de um passo à frente feita no passo anterior

Nesse caso, pode-se utilizar um erro de previsão de um passo à frente como um critério para otimização do valor de coeficiente alfa

Assim, minimizando a soma dos quadrados destes erros ao longo de toda a amostra, pode-se determinar o valor ideal do coeficiente alfa para uma dada sequência. O melhor valor de alfa será, evidentemente, a de que a soma dos quadrados dos erros seja mínima.

A figura 1 mostra um gráfico da soma dos quadrados de erros de previsão de um passo à frente contra o valor do coeficiente alfa de um fragmento de sequência de teste USDJPY M1.

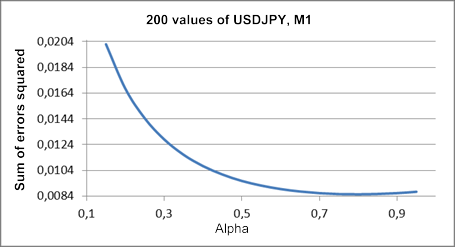
Figura 1. Suavização exponencial simples

O mínimo sobre o registro resultante é muito pouco perceptível e está localizado próximo ao valor de alfa de aproximadamente 0,8. Mas tal imagem não é sempre o caso no que diz respeito à suavização exponencial simples. Ao tentar obter o valor de alfa ideal para fragmentos de seqüência de teste utilizados no artigo, vamos com mais frequência do que não ter uma trama contínua queda da unidade.

Esses altos valores do coeficiente de suavização sugerem que este modelo simples não é muito adequado para a descrição de nossas sequências de teste (cotações). é tanto por causa que o nível de processo L(t) muda muito rápido ou porque é uma tendência presente no processo.

Vamos complicar nosso modelo um pouco, adicionando um outro componente

,

onde:

• X(t) – processo (simulado) em estudo;
  
• L(t) - nível de processo variável;
  
• T(t) - tendência linear;
  
• r(t)– variável aleatória de média zero.

Sabe-se que os coeficientes de regressão linear podem ser determinados através de uma dupla suavização de uma sequência:

Para obter coeficientes de a1 e a2 obtido desta maneira, a previsão de um passo à frente-m ao tempo t será igual também.

Deve ser notado que o mesmo coeficiente alfa é utilizado nas fórmulas acima para a primeira e para a suavização repetida. Este modelo é chamado o modelo aditivo de um parâmetro de crescimento linear.

Vamos demonstrar a diferença entre o modelo simples e o modelo de crescimento linear.

Suponha-se que por um longo período de tempo o processo em estudo representasse um componente constante, ou seja, que aparecesse no gráfico como uma linha horizontal reta, mas, em algum momento, uma tendência linear começasse a emergir. Uma previsão para este processo realizada utilizando os modelos acima mencionados é mostrado na Figura 2.

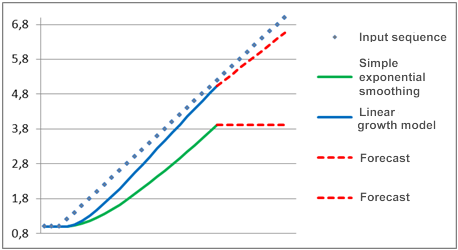
Figura 2. Comparação modelo

Como pode ser visto, o modelo de suavização exponencial simples está consideravelmente atrás da sequência de entrada linearmente variada e a previsão feita utilizando este modelo está movendo-se ainda mais longe. Podemos ver um padrão muito diferente quando o modelo de crescimento linear é usado. Quando a tendência surge, este modelo é como se sugerisse uma sequência linearmente variada e sua previsão é mais perto à direção de valores de entrada variados.

Se o coeficiente de suavização no exemplo dado fosse mais alto, o modelo de crescimento linear seria capaz de "alcançar" o sinal de entrada durante o tempo determinado e a sua previsão quase coincidiria com a sequência de entrada.

Apesar do fato de que o modelo de crescimento linear no estado estacionário dá bons resultados na presença de uma tendência linear, é fácil perceber que é necessário um certo tempo para a "alcançar", a tendência. Portanto, sempre haverá uma lacuna entre o modelo e a sequência de entrada, se a direção de uma tendência mudar frequentemente. Além disso, se a tendência aumenta de forma não linear, mas em vez disso segue a lei do quadrado, o modelo de crescimento linear não será capaz de "alcançá-la". Mas apesar destes inconvenientes, este modelo é mais benéfico do que o modelo de suavização exponencial simples na presença de uma tendência linear.

Como já foi mencionado, foi utilizado um modelo de um parâmetro de crescimento linear. A fim de encontrar o valor ideal do parâmetro alfa para um fragmento de sequência de teste USDJPY M1, vamos construir um registro da soma dos quadrados de erros de previsão de um passo à frente contra o valor do coeficiente alfa.

Este registro construído sobre a base do mesmo fragmento de sequência conforme o ilustrado na figura 1, está exibido na figura 3.

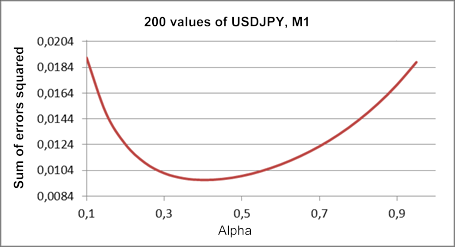
Figura 3. Modelo de crescimento linear

Quando comparado com o resultado na Figura 1, o valor ideal do coeficiente alfa, nesse caso, diminuiu para aproximadamente 0,4. A primeira e segunda suavização têm os mesmos coeficientes nesse modelo, embora teoricamente seus valores possam ser diferentes. O modelo de crescimento linear com dois coeficientes de suavização diferentes serão analisados mais adiante.

Ambos os modelos de suavização exponencial possuem seus analógicos no MetaTrader 5 onde existem na forma de indicadores. Estes são EMA e DEMA bem conhecidos que não são destinados para previsão mas para suavização de valores de sequência.

Deve notar-se que quando se utiliza indicador DEMA, um valor que corresponde ao coeficiente a1 é exibido em vez do valor de previsão de um passo. O coeficiente a2 (ver fórmulas acima para o modelo de crescimento linear) é, nesse caso, não calculado nem usado. Além disso, o coeficiente de suavização é calculado em termos de período equivalente n:

Por exemplo, alfa igual a 0,8 corresponderá a n sendo aproximadamente igual a 2 e se alfa for 0,4, n será igual a 4.

4. Valores iniciais

Como já mencionado, um valor de coeficiente de suavização deve, de uma forma ou de outra ser obtido mediante aplicação de suavização exponencial. Mas isso parece ser insuficiente. Uma vez que na suavização exponencial do valor atual é calculada com base na anterior, há uma situação em que tal valor ainda não exista no tempo zero. Em outras palavras, o valor inicial de S ou S1 e S2 no modelo de crescimento linear deve, de algum modo, ser calculado no tempo zero.

O problema da obtenção de valores iniciais não é sempre fácil de resolver. Se (como no caso da utilização de cotações no MetaTrader 5) tivermos um longo histórico disponível, a curva de suavização exponencial terá os valores iniciais determinados de forma imprecisa, terá tempo para estabilizar por um ponto atual, tendo corrigido nosso erro inicial. Isso necessitará cerca de 10 a 200 (e, às vezes, ainda mais) períodos dependendo do valor do coeficiente de suavização.

Nesse caso, seria o suficiente para estimar aproximadamente os valores iniciais e iniciar o processo de suavização exponencial 200-300 períodos antes do período de tempo alvo. Fica mais difícil, porém, quando a amostra disponível apenas contém por ex.100 valores.

Existem várias recomendações na bibliografia quanto à escolha de valores iniciais. Por exemplo, o valor inicial na suavização exponencial simples pode ser equacionado com o primeiro elemento de uma sequência ou calculado como a média de três a quatro elementos iniciais em sequência, com o objetivo de suavizar discrepâncias aleatórias. Os valores iniciais de S1 e S2, no modelo de crescimento linear pode ser determinado com base no pressuposto de que o nível inicial da curva de previsão deverá ser igual ao primeiro elemento em uma sequência e o declive da tendência linear deverá ser zero.

Pode-se encontrar ainda mais recomendações em fontes diferentes em relação à escolha dos valores iniciais, mas nenhum deles pode garantir a ausência de erros perceptíveis nos primeiros estágios do algoritmo de suavização. é particularmente notável com a utilização de coeficientes de suavização de baixo valor quando um grande número de períodos é necessário para se atingir um estado estacionário.

Portanto, para minimizar o impacto dos problemas associados com a escolha dos valores iniciais (especialmente para sequências curtas), utilizamos, muitas vezes, um método que envolve a procura por tais valores, que resultarão no erro de previsão mínimo. é uma questão de cálculo de um erro de previsão para os valores iniciais variados em pequenos incrementos ao longo de toda a sequência.

A variante mais adequada pode ser selecionada depois de calcular o erro dentro do intervalo de todas as combinações possíveis de valores iniciais. Este método é, entretanto, muito laborioso que requer uma grande quantidade de cálculos e quase nunca é usado na sua forma direta.

O problema descrito tem a ver com a otimização ou procura por um valor mínimo da função multivariável. Tais problemas podem ser resolvidos usando vários algoritmos desenvolvidos para reduzir consideravelmente o escopo de cálculos necessários. Vamos voltar às questões de otimização de parâmetros de suavização e de valores iniciais em previsão um pouco mais tarde.

5. Avaliação precisa da previsão

O procedimento de previsão e seleção de valores iniciais de modelo ou de parâmetros dão origem ao problema de estimar a precisão de previsão. A avaliação da precisão é também importante ao comparar dois modelos diferentes ou determinar a consistência da previsão obtida. Há um grande número de estimativas bem conhecidas para a avaliação da precisão de previsão, mas o cálculo de qualquer um deles requer o conhecimento de erro de previsão em cada passo.

Como já foi mencionado, um erro de previsão de um passo à frente no tempo t é igual em

onde:

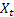• – valor de sequência de entrada no tempo t;
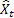• – previsão no tempo t realizada no passo anterior.

Provavelmente a estimativa de previsão mais comum é o erro quadrado médio (MSE):

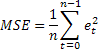
onde n é o número de elementos em uma sequência.

A extrema sensibilidade a erros individuais ocasionais de grande valor é muitas vezes apontada como uma desvantagem do MSE. Ela deriva do fato de que o valor de erro no cálculo MSE é quadrado. Como uma alternativa, é aconselhável usar nesse caso o erro absoluto (MAE).

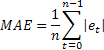
O erro quadrado aqui é substituído pelo valor absoluto do erro. Presume-se que as estimativas obtidas utilizando MAE sejam mais estáveis.

Ambas as estimativas são bastante apropriadas para, por exemplo, a avaliação da precisão de previsão da mesma sequência usando diferentes parâmetros de modelo ou modelos diferentes, mas eles parecem ser de pouca utilidade para a comparação dos resultados de previsão recebidos em diferentes sequências.

Além disso, os valores de tais estimativas não sugerem de modo explícito a qualidade do resultado de previsão. Por exemplo, não podemos dizer se o MAE obtido de 0,03 ou qualquer outro valor é bom ou ruim.

Para conseguirmos comparar a precisão de previsão de diferentes sequências, podemos usar estimativas relativas RelMSE e RelMAE:

As estimativas obtidas de precisão de previsão aqui são divididas pelas respectivas estimativas obtidas usando o método de teste de previsão. Como um método de teste, é apropriado utilizar o tão chamado método ingênuo sugerindo que o valor futuro do processo será igual ao valor atual.

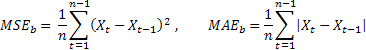
Se a média dos erros de previsão é igual ao valor dos erros obtidos usando o método ingênuo, o valor da estimativa relativa será igual a um. Se o valor da estimativa relativa é inferior a um, isso significa que, em média, o valor do erro de previsão é menor do que no método ingênuo. Em outras palavras, a precisão dos resultados de previsão classifica toda a precisão do método ingênuo. E vice-versa, se o valor de estimativa relativo for mais do que um, a precisão dos resultados de previsão é, na média, inferior a do método de previsão ingênuo.

Essas estimativas também são adequados para avaliação da precisão de previsão para dois ou mais passos à frente. Um erro de previsão de um passo em cálculos apenas precisa ser substituído com o valor dos erros de previsão para o número apropriado de passos à frente.

Como um exemplo, a tabela abaixo contém erros de previsão de um passo à frente estimados utilizando RelMAE em modelo de um parâmetro de crescimento linear. Os erros foram calculados utilizando os últimos 200 valores de cada sequência de teste.

alfa = 0,3 alfa = 0,4 alfa = 0,5 EURRUR M1 1,14 1,10 1,09 EURRUR M30 1,14 1,11 1,14 EURUSD M1 1,17 1,11 1,10 EURUSD M30 1,17 1,11 1,11 USDJPY M1 1,10 1,08 1,10 USDJPY M30 1,17 1,13 1,13 XAUUSD M1 1,20 1,11 1,10 XAUUSD M30 1,11 1,12 1,13

Tabela 1. Erros de previsão de um passo à frente estimados utilizando RelMAE

A estimativa RelMAE permite comparar a eficácia de um método selecionado ao prever diferentes sequências. Conforme os resultados sugeridos na Tabela 1, nossa previsão nunca foi mais precisa do que o método ingênuo - todos os valores RelMAE são mais do que um.

6. Modelos aditivos

Houve um modelo no início do artigo que englobava a soma de nível de processo, a tendência linear e uma variável aleatória. Aumentaremos a lista dos modelos analisados​ neste artigo adicionando um outro modelo que em adição aos componentes acima inclui um componente cíclico, sazonal.

Modelos de suavização exponencial compreendendo todos os componentes como uma soma são chamados os modelos aditivos. Além desses modelos existem modelos multiplicativos onde um, mais ou todos os componentes estão compreendidos como um produto. Vamos continuar a analisar o grupo de modelos aditivos.

O erro de previsão de um passo à frente foi mencionado repetidamente no início do artigo. Este erro deve ser calculado em quase qualquer aplicação relacionada à previsão com base em suavização exponencial. Sabendo o valor do erro de previsão, as fórmulas para os modelos de suavização exponencial introduzidas acima podem ser apresentadas de uma forma um pouco diferente (forma de correção de erros).

A forma da representação de modelo que vamos usar nesse caso contém um erro nas suas expressões que é parcialmente ou totalmente adicionado aos valores anteriormente obtidos. Tal representação é chamada de o modelo de erro aditivo. Modelos de suavização exponencial também podem ser expressos em uma forma de erro multiplicativa que não será, contudo, utilizada neste artigo.

Vamos dar uma olhada em modelos de suavização exponencial aditivos.

Suavização exponencial simples:

Modelo equivalente – ARIMA(0,1,1):

Modelo de crescimento linear aditivo:

Em contraste com o modelo de crescimento linear de um parâmetro anteriormente introduzido, dois parâmetros de suavização diferentes são usados​ aqui.

Modelo equivalente – ARIMA(0,2,2):

Modelo de crescimento linear com amortecimento:

O significado de tal amortecimento é que a tendência de inclinação recuará em cada passo de previsão subsequente dependendo do valor do coeficiente de amortecimento. O efeito é demonstrado na figura 4.

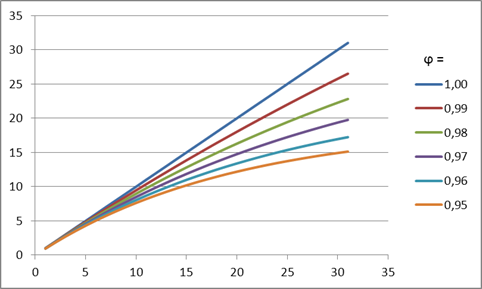
Figura 4. Efeito de coeficiente de amortecimento

Como pode ser visto na figura, ao fazer uma previsão, uma diminuição do valor do coeficiente de amortecimento fará com que a tendência perca sua força mais rapidamente, assim o crescimento linear ficará cada vez mais e mais amortecido.

Modelo equivalente – ARIMA(1,1,2):

Adicionando um componente sazonal como uma soma de cada um destes três modelos, obteremos mais três modelos.

Modelo simples com sazonalidade aditiva:

Modelo de crescimento linear com sazonalidade aditiva:

Modelo de crescimento linear com amortecimento e sazonalidade aditiva:

Há também modelos ARIMA equivalentes aos modelos com sazonalidade, mas eles vão ficar de fora aqui, pois dificilmente terão qualquer importância prática seja do que for.

Notas utilizadas nas fórmulas são fornecidas conforme a seguir:

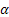• – parâmetro de suavização para o nível da sequência, [0:1];
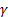• – parâmetro de suavização para a tendência, [0:1];
• – parâmetro de suavização para índices sazonais, [0:1];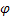
• – parâmetro de amortecimento, [0:1];
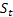• – nível de suavização de sequência calculada no tempo t após 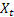ter sido observado;
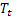• – tendência aditiva de suavização calculada no tempo t;
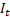• – índice sazonal de suavização calculado no tempo t;
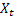• – valor de sequência no tempo t;
• m – número de passos à frente pelos quais a previsão é feita;
• p – número de períodos no ciclo sazonal;
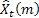• – previsão de passo à frente -m realizada no tempo t;
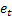• – erro de previsão de um passo à frente realizado no tempo t, .

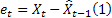É fácil ver que as fórmulas para o último modelo fornecido incluem todas as seis variantes sob consideração.

Se nas fórmulas para o modelo de crescimento linear com amortecimento e sazonalidade aditiva que usarmos

,

A sazonalidade não será levada em consideração na previsão. Mais adiante, onde , um modelo de crescimento linear será produzido e onde , obteremos um modelo de crescimento linear com amortecimento.

O modelo de suavização exponencial simples corresponderá a .

Ao empregar os modelos que envolvam sazonalidade, a presença de ciclicidade e período do ciclo deve primeiro ser determinada utilizando qualquer método disponível, a fim de utilizar mais esses dados para inicialização de valores de índices sazonais.

Não conseguimos detectar a ciclicidade estável considerável nos fragmentos de sequências de teste usados no nosso caso, onde a previsão é feita em intervalos de tempo curtos. Portanto, nesse artigo não daremos exemplos relevantes e não aumentaremos características associadas com sazonalidade.

A fim de determinar os intervalos de probabilidade de previsão no que diz respeito aos modelos considerados, usaremos derivações analíticas encontradas na bibliografia [3]. A média da soma dos quadrados dos erros de previsão de um passo à frente calculados sobre a totalidade da amostra de tamanho n será utilizada como a variação estimada de tais erros.

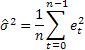
Em seguida, a seguinte expressão será verdadeira para a determinação da variação estimada em uma previsão para 2 e mais passos à frente para os modelos considerados:

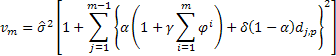
Onde iguala-se a um, se j módulo p for zero, caso contrário é zero.

Tendo calculado a variância estimada da previsão para cada etapa m, podemos encontrar os limites do intervalo de previsão de 95%:

Concordaremos em nomear tal intervalo de previsão como intervalo de confiança de previsão.

Vamos implementar as expressões fornecidas para os modelos de suavização exponencial em uma classe escrita no MQL5.

7. Implementação da classe AdditiveES

A implementação da classe envolveu o uso das expressões para o modelo de crescimento linear com amortecimento e sazonalidade aditiva.

Como mencionado anteriormente, outros modelos podem ser derivados dele por uma seleção apropriada de parâmetros.

//-----------------------------------------------------------------------------------
//                                                                     AdditiveES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

//-----------------------------------------------------------------------------------
// Forecasting. Exponential smoothing. Additive models.
// References:
// 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II.
//    June 3, 2005.
// 2. Rob J Hyndman. Forecasting based on state space models for exponential
//    smoothing. 29 August 2002.
// 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing
//    using two new classes of state space models. 30 January 2003.
//-----------------------------------------------------------------------------------
class AdditiveES:public CObject
  {
protected:
  double Alpha;    // Smoothed parameter for the level of the series
  double Gamma;    // Smoothed parameter for the trend
  double Phi;      // Autoregressive or damping parameter
  double Delta;    // Smoothed parameter for seasonal indices
  int    nSes;     // Number of periods in the seasonal cycle
  double S;        // Smoothed level of the series, computed after last Y is observed
  double T;        // Smoothed additive trend
  double Ises[];   // Smoothed seasonal indices
  int    p_Ises;   // Pointer for Ises[] shift register
  double F;        // Forecast for 1 period ahead from origin t

public:
         AdditiveES();
  double Init(double s,double t,double alpha=1,double gamma=0,
              double phi=1,double delta=0,int nses=1);
  double GetS()                 { return(S); }
  double GetT()                 { return(T); }
  double GetF()                 { return(F); }
  double GetIs(int m);
  void   IniIs(int m,double is);  // Initialization of smoothed seasonal indices
  double NewY(double y);          // Next calculating step
  double Fcast(int m);            // m-step ahead forecast
  double VarCoefficient(int m);   // Coefficient for calculating prediction intervals

  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void AdditiveES::AdditiveES()
  {
  Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0; S=0; T=0;
  }
//-----------------------------------------------------------------------------------
// Initialization
//-----------------------------------------------------------------------------------
double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0,
                       double phi=1,double delta=0,int nses=1)
  {
  S=s; T=t;
  Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1;
  Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1;
  Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1;
  Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1;
  nSes=nses; if(nSes<1)nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0;
  F=S+Phi*T;
  return(F);
  }
//-----------------------------------------------------------------------------------
// Calculations for the new Y
//-----------------------------------------------------------------------------------
double AdditiveES::NewY(double y)
  {
  double e;
  
  e=y-F;
  S=S+Phi*T+Alpha*e;
  T=Phi*T+Alpha*Gamma*e;
  Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e;
  p_Ises++; if(p_Ises>=nSes)p_Ises=0;
  F=S+Phi*T+GetIs(0);
  return(F);
  }
//-----------------------------------------------------------------------------------
// Return smoothed seasonal index
//-----------------------------------------------------------------------------------
double AdditiveES::GetIs(int m)
  {
  if(m<0)m=0;
  int i=(int)MathMod(m+p_Ises,nSes);
  return(Ises[i]);
  }
//-----------------------------------------------------------------------------------
// Initialization of smoothed seasonal indices
//-----------------------------------------------------------------------------------
void AdditiveES::IniIs(int m,double is)
  {
  if(m<0)m=0;
  if(m<nSes)
    {
    int i=(int)MathMod(m+p_Ises,nSes);
    Ises[i]=is;
    }
  }
//-----------------------------------------------------------------------------------
// m-step-ahead forecast
//-----------------------------------------------------------------------------------
double AdditiveES::Fcast(int m)
  {
  int i,h;
  double v,v1;

  if(m<1)h=1; else h=m;  
  v1=1; v=0;
  for(i=0;i<h;i++){v1=v1*Phi; v+=v1;}
  return(S+v*T+GetIs(h));
  }
//-----------------------------------------------------------------------------------
// Coefficient for calculating prediction intervals
//-----------------------------------------------------------------------------------
double AdditiveES::VarCoefficient(int m)
  {
  int i,h;
  double v,v1,a,sum,k;
  
  if(m<1)h=1; else h=m;
  if(h==1)return(1);
  v=0; v1=1; sum=0;
  for(i=1;i<h;i++)
    {
    v1=v1*Phi; v+=v1;
    if((int)MathMod(i,nSes)==0)k=1; else k=0;
    a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha);
    sum+=a*a;
    }
  return(1+sum);
  }
//-----------------------------------------------------------------------------------

Vamos revisar brevemente métodos de classe AdditiveES.

Método Init (Inicial)

Parâmetros de entrada:

• duplo s - estabelece o valor inicial do nível suavizado;
• duplo t - estabelece o valor inicial da tendência suavizada;
• duplo alfa=1 - estabelece o parâmetro de suavização para o nível da sequência;
• duplo gama=0 - estabelece o parâmetro de suavização para a tendência;
• duplo phi=1 - estabelece o parâmetro de amortecimento;
• duplo delta=0 - estabelece o parâmetro de suavização para índices sazonais;
• int nses=1 - estabelece o número de períodos no ciclo sazonal.

Valor retornado:

• Retorna uma previsão de um passo à frente calculada com base de valores iniciais estabelecidos.

O método Init deverá ser chamado em primeiro lugar. Isso é necessário para configurar os parâmetros de suavização e valores iniciais. Deve-se notar que o método Init não fornece a inicialização de índices sazonais de valores arbitrários, ao chamar esse método, os índices sazonais serão sempre definidos para zero.

Método Inils

Parâmetros de entrada:

• Int m - número de índice sazonal;
• duplo is - estabelece o valor do número m de índice sazonal.

Valor retornado:

• Nenhum.

O método IniIs(...) é chamado quando os valores iniciais de índices sazonais necessitam estar em outro valor se não zero. índices sazonais devem ser inicializados logo em seguida após a chamada do método Init(...).

Método NewY

Parâmetros de entrada:

• Duplo y - novo valor da sequência de entrada.

Valor retornado:

• Retorna uma previsão de um passo à frente calculada com base no novo valor da sequência.

Este método é projetado para calcular uma previsão de um passo à frente cada vez que um novo valor da sequência de entrada é inserido. Ele deve ser chamado após a classe de inicialização pelo Init e onde necessário, métodos Inils.

Método Fcast

Parâmetros de entrada:

• int m – horizonte de previsão de período 1,2,3,…;

Valor retornado:

• Retorna ao valor de previsão de passo à frente -m.

Este método calcula apenas o valor de previsão sem afetar o estado do processo de suavização. é geralmente chamado após a chamada do método NewY.

Método VarCoefficient

Parâmetros de entrada:

• int m – horizonte de previsão de período 1,2,3,…;

Valor retornado:

• Retorna o valor de coeficiente para calcular a variação de previsão.

Este valor do coeficiente mostra o aumento na variação de uma previsão de passo à frente -m comparada a variação da previsão de um passo à frente.

Métodos GetS, GetT, GetF, GetIs

Estes métodos fornecem acesso a variáveis protegidas da classe. Valores de retorno GetS, GetT e GetF do nível suavizado, tendência suavizada e uma previsão de um passo à frente, respectivamente. O método GetIs fornece acesso a índices sazonais e necessitam de indicação do número de índice m como um argumento de entrada.

O modelo mais complexo de todos os que revisamos é o modelo de crescimento linear com amortecimento e sazonalidade aditiva com base no qual a classe AdditiveES é criada. Isso levanta uma questão muito razoável - para que seriam necessários os modelos restantes, mais simples.

Apesar do fato de que os modelos mais complexos devam ter aparentemente uma clara vantagem sobre os mais simples, não é, na verdade, sempre o caso. Modelos mais simples que tenham menos parâmetros resultarão, na maioria dos casos, em menor variação de erros de previsão, por exemplo, sua operação será mais estável. Este fato é utilizado na criação de algoritmos de previsão com base em operação paralela simultânea de todos os modelos disponíveis, desde os mais simples até os mais complexos.

Uma vez que a sequência tenha sido totalmente processada, um modelo de previsão que demonstrou o menor erro, dado o número de seus parâmetros (por exemplo, sua complexidade), é selecionado. Há um número de critérios desenvolvidos para este propósito, por exemplo critério de informação de Akaike (AIC). Resultará na seleção de um modelo que se espera que produza a previsão mais estável.

Para demonstrar o uso da classe AdditiveES, um indicador simples foi criado com todos os parâmetros de suavização dos quais são configurados manualmente.

O código-fonte do indicador AdditiveES_Test.mq5 está apresentado abaixo.

//-----------------------------------------------------------------------------------
//                                                                AdditiveES_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"      // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "PInterval+"    // Prediction interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCadetBlue
#property indicator_style3  STYLE_SOLID
#property indicator_width3  1
#property indicator_label4  "PInterval-"    // Prediction interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCadetBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1

double HIST[];
double FORE[];
double PINT1[];
double PINT2[];

input double Alpha=0.2;     // Smoothed parameter for the level
input double Gamma=0.2;     // Smoothed parameter for the trend
input double Phi=0.8;       // Damping parameter
input double Delta=0;       // Smoothed parameter for seasonal indices
input int    nSes=1;        // Number of periods in the seasonal cycle
input int    nHist=250;     // History bars, nHist>=100
input int    nTest=150;     // Test interval, 50<=nTest<nHist
input int    nFore=12;      // Forecasting horizon, nFore>=2

#include "AdditiveES.mqh"
AdditiveES fc;

int    NHist;               // history bars
int    NFore;               // forecasting horizon
int    NTest;               // test interval
double ALPH;                // alpha
double GAMM;                // gamma
double PHI;                 // phi
double DELT;                // delta
int    nSES;                // Number of periods in the seasonal cycle
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NHist=nHist; if(NHist<100)NHist=100;
  NFore=nFore; if(NFore<2)NFore=2;
  NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50;
  ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1;
  GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1;
  PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1;
  DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1;
  nSES=nSes; if(nSES<1)nSES=1;

  MqlRates rates[];
  CopyRates(NULL,0,0,NHist,rates);           // Load missing data
  
  SetIndexBuffer(0,HIST,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,FORE,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFore);
  SetIndexBuffer(2,PINT1,INDICATOR_DATA);
  PlotIndexSetString(2,PLOT_LABEL,"Conf+");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFore);
  SetIndexBuffer(3,PINT2,INDICATOR_DATA);
  PlotIndexSetString(3,PLOT_LABEL,"Conf-");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFore);
  
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  int i,j,init,start;
  double v1,v2;
  
  if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1)
    {init=1; start=rates_total-NHist;}
  else
    {init=0; start=prev_calculated;}
  if(start==rates_total)return(rates_total);    // New tick but not new bar
//-----------------------
  if(init==1)                                   // Initialization
    {
    i=start;
    v2=(open[i+2]-open[i])/2;
    v1=(open[i]+open[i+1]+open[i+2])/3.0-v2;
    fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES);
    ArrayInitialize(HIST,EMPTY_VALUE);
    }
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore);

  for(i=start;i<rates_total;i++)                // History
    {
    HIST[i]=fc.NewY(open[i]);
    }
  v1=0;
  for(i=0;i<NTest;i++)                          // Variance
    {
    j=rates_total-NTest+i;
    v2=close[j]-HIST[j-1];
    v1+=v2*v2;
    }
  v1/=NTest;                                    // v1=var
  j=1;
  for(i=rates_total-NFore;i<rates_total;i++)
    {
    v2=1.96*MathSqrt(v1*fc.VarCoefficient(j));  // Prediction intervals
    FORE[i]=fc.Fcast(j++);                    // Forecasting
    PINT1[i]=FORE[i]+v2;
    PINT2[i]=FORE[i]-v2;
    }
  
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Uma chamada ou uma inicialização repetida do indicador define os valores iniciais de suavização exponencial

Não há configurações iniciais para os índices sazonais neste indicador, os valores iniciais são, portanto, sempre igual a zero. Mediante tal inicialização, a influência da sazonalidade sobre o resultado de previsão aumentará gradualmente a partir de zero até um certo valor fixo, com a introdução de novos valores de entrada.

O número de ciclos necessários para chegar a um estado de funcionamento em estado estacionário depende do valor do coeficiente de suavização para os índices sazonais: quanto menor for o valor do coeficiente de suavização, mais tempo ele precisará.

O resultado de operação do indicador AdditiveES_Test.mq5 com configurações padrão é mostrado na figura 5.

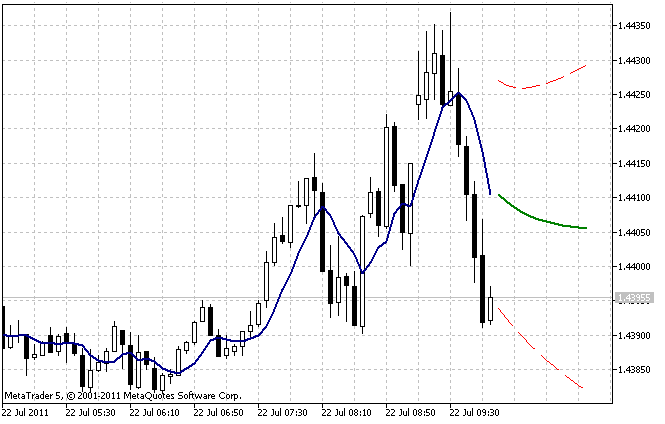
Figura 5. O indicador AdditiveES_Test.mq5

Além da previsão, o indicador mostra uma linha adicional correspondente à previsão de uma etapa para os valores passados da sequência e os limites do intervalo de confiança de previsão de 95%.

O intervalo de confiança baseia-se na estimativa de variância do erro de um passo à frente. Para reduzir o efeito de imprecisão dos valores iniciais selecionados, a variância estimada não é calculada sobre todo o comprimento nHist, mas apenas em relação às últimas barras cujo número é especificado no parâmetro de entrada nTest.

Arquivos.Files.zip no final do artigo incluem arquivos AdditiveES.mqh e AdditiveES_Test.mq5. Ao compilar o indicador, é necessário que o arquivo incluso AdditiveES.mqh esteja localizado no mesmo diretório que AdditiveES_Test.mq5.

Enquanto o problema da seleção de valores iniciais foi, de certa forma, resolvido ao criar o indicador AdditiveES_Test.mq5, o problema de selecionar os valores ideais dos parâmetros de suavização permaneceu aberto.

8. Seleção dos valores de parâmetro ideais

O modelo de suavização exponencial simples tem um único parâmetro de suavização e seu valor ideal pode ser encontrado utilizando o método de enumeração simples. Depois de calcular os valores de erro de previsão sobre toda a sequência, o valor do parâmetro é mudado em um pequeno incremento e um cálculo completo é feito novamente . Este procedimento é repetido até que todos os valores de parâmetros possíveis forem enumerados. Agora só precisamos selecionar o valor do parâmetro que resultou no menor valor de erro.

A fim de encontrar um valor ideal do coeficiente de alisamento na gama de 0,1 a 0,9 em incrementos de 0,05, o cálculo completo do valor do erro de previsão precisa ser feito dezessete vezes. Como pode ser visto, o número de cálculos necessários não é tão grande. Mas o modelo de crescimento linear com amortecimento envolve a otimização de três parâmetros de suavização e, nesse caso, levará 4.913 execuções de cálculo, a fim de enumerar todas as combinações possíveis na mesma faixa nos mesmos incrementos de 0,05.

O número de execuções completas necessárias para a enumeração de todos os possíveis valores de parâmetros aumenta rapidamente com o aumento do número de parâmetros, com a diminuição no incremento e com a expansão da gama de enumeração. Deve ser ainda necessário otimizar os valores iniciais dos modelos, além dos parâmetros de suavização, que será muito difícil de fazer, utilizando o método de contagem simples.

Problemas associados quanto a encontrar o mínimo de uma função de várias variáveis​são bem estudados e há uma porção de algoritmos deste tipo. A descrição e comparação de vários métodos para encontrar o mínimo de uma função podem ser encontradas na bibliografia [7]. Todos estes métodos são principalmente destinados a reduzir o número de chamadas da função objetiva, por exemplo, a redução dos esforços computacionais no processo de encontrar o mínimo.

Fontes diferentes geralmente contêm uma referência aos tão chamados métodos de otimização quasi-Newton. O mais provável é que isso tenha a ver com a sua elevada eficiência, mas a implementação de um método mais simples também deve ser suficiente para demonstrar uma abordagem para a otimização da previsão. Vamos optar por este método Método de Powell. O método de Powell não requer cálculo de derivativos da função objetiva e pertence a métodos de pesquisa.

Este método, tal como qualquer outro método, pode ser implementado por meio de programação de várias maneiras. A pesquisa deve ser concluída quando uma determinada precisão do valor da função objetiva ou o valor do argumento for atingido. Além disso, uma determinada aplicação pode incluir a possibilidade de utilização das limitações de taxa admissível de alterações de parâmetro de função.

No nosso caso, o algoritmo para encontrar um mínimo sem restrições utilizando o método de Powell é implementado em PowellsMethod.class. O algoritmo para de procurar uma vez que uma determinada precisão do valor da função objetiva for atingido. Na aplicação deste método, um algoritmo encontrado na bibliografia [8], foi usado como um protótipo.

Abaixo está todo o código fonte da classe PowellsMethod.

//-----------------------------------------------------------------------------------
//                                                                  PowellsMethod.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

#define GOLD   1.618034
#define CGOLD  0.3819660
#define GLIMIT 100.0
#define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d);
#define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a))
#define FMAX(a,b) (a>b?a:b)
//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
  double P[],Xi[];
  double Pcom[],Xicom[],Xt[];
  double Pt[],Ptt[],Xit[];
  int    N;
  double Fret;
  int    Iter;
  int    ItMaxPowell;
  double FtolPowell;
  int    ItMaxBrent;
  double FtolBrent;
  int    MaxIterFlag;
public:
  void   PowellsMethod(void);
  void   SetItMaxPowell(int n)           { ItMaxPowell=n; }
  void   SetFtolPowell(double er)        { FtolPowell=er; }
  void   SetItMaxBrent(int n)            { ItMaxBrent=n;  }
  void   SetFtolBrent(double er)         { FtolBrent=er;  }
  int    Optimize(double &p[],int n=0);
  double GetFret(void)                   { return(Fret);  }
  int    GetIter(void)                   { return(Iter);  }
private:
  void   powell(void);
  void   linmin(void);
  void   mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
  double brent(double ax,double bx,double cx,double &xmin);
  double f1dim(double x);
  virtual double func(const double &p[]) { return(0); }
  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void PowellsMethod::PowellsMethod(void)
  {
  ItMaxPowell= 200;
  FtolPowell = 1e-6;
  ItMaxBrent = 200;
  FtolBrent  = 1e-4;
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::powell(void)
  {
  int i,j,m,n,ibig;
  double del,fp,fptt,t;
  
  n=N; Fret=func(P);
  for(j=0;j<n;j++)Pt[j]=P[j];
  for(Iter=1;;Iter++)
    {
    fp=Fret; ibig=0; del=0.0;
    for(i=0;i<n;i++)
      {
      for(j=0;j<n;j++)Xit[j]=Xi[j+n*i];
      fptt=Fret;
      linmin();
      if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;}
      }
    if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return;
    if(Iter>=ItMaxPowell)
      {
      Print("powell exceeding maximum iterations!");
      MaxIterFlag=1; return;
      }
    for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];}
    fptt=func(Ptt);
    if(fptt<fp)
      {
      t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt);
      if(t<0.0)
        {
        linmin();
        for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];}
        }
      }
    }
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::linmin(void)
  {
  int j,n;
  double xx,xmin,fx,fb,fa,bx,ax;

  n=N;
  for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];}
  ax=0.0; xx=1.0;
  mnbrak(ax,xx,bx,fa,fx,fb);
  Fret=brent(ax,xx,bx,xmin);
  for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];}
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::mnbrak(double &ax,double &bx,double &cx,
                                 double &fa,double &fb,double &fc)
  {
  double ulim,u,r,q,fu,dum;

  fa=f1dim(ax); fb=f1dim(bx);
  if(fb>fa)
    {
    SHFT(dum,ax,bx,dum)
    SHFT(dum,fb,fa,dum)
    }
  cx=bx+GOLD*(bx-ax); fc=f1dim(cx);
  while(fb>fc)
    {
    r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa);
    u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r));
    ulim=bx+GLIMIT*(cx-bx);
    if((bx-u)*(u-cx)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;}
      else if(fu>fb){cx=u; fc=fu; return;}
      u=cx+GOLD*(cx-bx); fu=f1dim(u);
      }
    else if((cx-u)*(u-ulim)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc)
        {
        SHFT(bx,cx,u,cx+GOLD*(cx-bx))
        SHFT(fb,fc,fu,f1dim(u))
        }
      }
    else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);}
      else {u=cx+GOLD*(cx-bx); fu=f1dim(u);}
    SHFT(ax,bx,cx,u)
    SHFT(fa,fb,fc,fu)
    }
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::brent(double ax,double bx,double cx,double &xmin)
  {
  int    iter;
  double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm;

  a=(ax<cx?ax:cx); b=(ax>cx?ax:cx);
  d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x);
  for(iter=1;iter<=ItMaxBrent;iter++)
    {
    xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19);
    if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);}
    if(fabs(e)>tol1)
      {
      r=(x-w)*(fx-fv); q=(x-v)*(fx-fw);
      p=(x-v)*q-(x-w)*r; q=2.0*(q-r);
      if(q>0.0)p=-p; q=fabs(q);
      etemp=e; e=d;
      if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x))
        d=CGOLD*(e=(x>=xm?a-x:b-x));
      else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);}
      }
    else d=CGOLD*(e=(x>=xm?a-x:b-x));
    u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d));
    fu=f1dim(u);
    if(fu<=fx)
      {
      if(u>=x)a=x; else b=x;
      SHFT(v,w,x,u)
      SHFT(fv,fw,fx,fu)
      }
    else
      {
      if(u<x)a=u; else b=u;
      if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;}
      else if(fu<=fv||v==x||v==w){v=u; fv=fu;}
      }
    }
  Print("Too many iterations in brent");
  MaxIterFlag=1; xmin=x;
  return(fx);
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::f1dim(double x)
  {
  int j;
  double f;
  
  for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j];
  f=func(Xt);
  return(f);
  }
//-----------------------------------------------------------------------------------
int PowellsMethod::Optimize(double &p[],int n=0)
  {
  int i,j,k,ret;
  
  k=ArraySize(p);
  if(n==0)N=k;
  else N=n;
  if(N<1||N>k)return(0);
  ArrayResize(P,N); ArrayResize(Xi,N*N);
  ArrayResize(Pcom,N); ArrayResize(Xicom,N);
  ArrayResize(Xt,N); ArrayResize(Pt,N);
  ArrayResize(Ptt,N); ArrayResize(Xit,N);
  for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0);
  for(i=0;i<N;i++)P[i]=p[i];
  MaxIterFlag=0;
  powell();
  for(i=0;i<N;i++)p[i]=P[i];
  if(MaxIterFlag==1)ret=-1;
  else ret=Iter;
  return(ret);
  }
//-----------------------------------------------------------------------------------
    

O método de otimização é o método principal da classe.

Método de otimização

Parâmetros de entrada:

• duplo & p[] - cadeia que na entrada contém os valores iniciais dos parâmetros dos valores ideais dos quais devem ser encontrados, os valores ideais obtidos desses parâmetros estão na saída da cadeia.
• int n=0 - número de argumentos em cadeia p[]. Onde n=0, o número de parâmetros é considerado ser igual ao tamanho da cadeia p[].

Valor retornado:

• Retorna o número de iterações necessárias para operação do algoritmo, ou -1 se o número máximo admissível disso foi alcançado.

Ao pesquisar valores de parâmetro ideais, uma aproximação iterativa para o mínimo da função objetiva ocorre. O método de otimização devolve o número de iterações necessárias para alcançar o mínimo de função com uma determinada precisão. A função objetiva é chamada várias vezes em cada iteração, por exemplo, o número de chamadas da função objetiva pode ser significativamente (dez e até mesmo cem vezes) maior do que o número de iterações retornados pelo método de otimização.

Outros métodos da classe.

Método SetItMaxPowell

Parâmetros de entrada:

• Int n - número admissível de iterações no método de Powell. O valor padrão é 200.

Valor retornado:

• Nenhum.

Ele define o número máximo permitido de iterações, uma vez que este número é alcançado, a busca vai acabar, independentemente se o mínimo da função objetiva com uma dada precisão foi encontrado. E uma mensagem relevante será adicionada ao registro.

Método SetFtolPowell

Parâmetros de entrada:

• double er - precisão. Se este valor de desvio do valor mínimo da função objetiva for alcançado, o método de Powell para a busca. O valor padrão é 1e-6.

Valor retornado:

• Nenhum.

Método SetItMaxBrent

Parâmetros de entrada:

• Int n - número máximo admissível de iterações para um método auxiliar de Brent. O valor padrão é 200.

Valor retornado:

• Nenhum.

Ele define o número máximo permitido de iterações. Uma vez que seja atingido, o método auxiliar de Brent interromperá a busca e uma mensagem relevante será adicionada ao log.

Método SetFtolBrent

Parâmetros de entrada:

• double er – precisão. Este valor define a precisão na busca do mínimo para o método auxiliar de Brent. O valor padrão é 1e-4.

Valor retornado:

• Nenhum.

Método GetFret

Parâmetros de entrada:

• Nenhum.

Valor retornado:

• Retorna o valor mínimo da função objetiva obtido.

Método GetIter

Parâmetros de entrada:

• Nenhum.

Valor retornado:

• Retorna o número de iterações necessárias para operação do algoritmo.

Função virtual func(const double &p[])

Parâmetros de entrada:

• const double &p[] – endereçamento da cadeia que contém os parâmetros otimizados. O tamanho da cadeia corresponde ao número de parâmetros de função.

Valor retornado:

• Retorna o valor de função correspondente aos parâmetros passados a ela.

A função virtual func() deve, em cada caso particular, ser redefinida em uma classe derivada da classe PowellsMethod. A função func() é a função objetiva, os argumentos que correspondem ao valor mínimo retornado pela função será encontrado ao aplicar o algoritmo de busca.

Esta implementação do método de Powell emprega o método de interpolação parabólica de uma variável de Brent para determinar a direção de busca em relação a cada parâmetro. A precisão e o número máximo permitido de iterações para esses métodos podem ser definidas separadamente, chamando SetItMaxPowell, SetFtolPowell, SetItMaxBrent e SetFtolBrent.

Assim, as características padrão do algoritmo podem ser alteradas dessa maneira. Isto pode parecer útil quando a precisão padrão definida para uma determinada função objetiva passa a ser muito alta e o algoritmo necessita de muitas iterações no processo de busca. A alteração no valor da precisão necessária pode otimizar a busca no que se refere a diferentes categorias de funções objetivas.

Apesar da aparente complexidade do algoritmo, que emprega o método de Powell, é bem simples de usar.

Vamos rever um exemplo. Supondo que temos uma função

e precisamos encontrar os valores de parâmetros e em qual função terá o menor valor.

Vamos escrever um script demonstrando uma solução a este problema.

//-----------------------------------------------------------------------------------
//                                                                        PM_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
class PM_Test:public PowellsMethod
  {
public:
  void   PM_Test(void) {}
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
double PM_Test::func(const double &p[])
  {
  double f,r1,r2;
  
  r1=p[0]-0.5;
  r2=p[1]-6.0;
  f=r1*r1*4.0+r2*r2;
  return(f);
  }
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  int it;
  double p[2];

  p[0]=8; p[1]=9;                                 // Initial point
  PM_Test *pm = new PM_Test;
  it=pm.Optimize(p);
  Print("Iter= ",it,"        Fret= ",pm.GetFret());
  Print("p[0]= ",p[0],"    p[1]= ",p[1]);
  delete pm;
  }
//-----------------------------------------------------------------------------------

Ao escrever este script, primeiro criamos a função func() como um membro da classe PM_Test que calcula o valor da função de teste dado utilizando os valores passados​de parâmetros p[0] e p[1]. Em seguida, no corpo da função OnStart(), os valores iniciais são designados aos parâmetros necessários. A busca começará a partir destes valores.

Além disso, uma cópia da classe PM_Test é criada e a busca pelos valores necessários de p[0] e p[1] começa chamando o método de otimização; os métodos da classe pai PowellsMethod chamarão a função redefinida fun(). Após a conclusão da pesquisa, o número de iterações, o valor da função no ponto mínimo e os valores de parâmetro obtidos p[0]=0,5 e p[1]=6 serão adicionados ao registro.

PowellsMethod.mqh e um caso de teste PM_Test.mq5 estão localizados na extremidade do artigo no arquivo Files.zip. Para compilar PM_Test.mq5, ele deve estar localizado no mesmo diretório que PowellsMethod.mqh.

9. Otimização dos valores de parâmetro modelos

A seção anterior do artigo tratado com a implementação do método para encontrar o mínimo da função e deu um exemplo simples de seu uso. Vamos agora avançar para as questões relacionadas com a otimização dos parâmetros do modelo de suavização exponencial.

Para começar, vamos simplificar a classe AdditiveES apresentada anteriormente ao máximo, excluindo dela todos os elementos associados ao componente sazonal, pois os modelos que levam em consideração a sazonalidade não vão ser mais considerados neste artigo de qualquer forma. Isto permitirá fazer o código de fonte da classe muito mais fácil de compreender e de reduzir o número de cálculos. Além disso, também vamos excluir todos os cálculos relacionados com a previsão e cálculos dos intervalos de confiança de previsão de para uma demonstração fácil de uma abordagem à otimização dos parâmetros do modelo de crescimento linear com amortecimento em consideração.

//-----------------------------------------------------------------------------------
//                                                                     OptimizeES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class OptimizeES
//-----------------------------------------------------------------------------------
class OptimizeES:public PowellsMethod
  {
protected:
  double Dat[];            // Input data
  int    Dlen;             // Data lenght
  double Par[5];           // Parameters
  int    NCalc;            // Number of last elements for calculation
public:
  void   OptimizeES(void) {}
  int    Calc(string fname);
private:
  int    readCSV(string fnam,double &dat[]);
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// Calc
//-----------------------------------------------------------------------------------
int OptimizeES::Calc(string fname)
  {
  int i,it;
  double relmae,naiv,s,t,alp,gam,phi,e,ae,pt;
  
  if(readCSV(fname,Dat)<0){Print("Error."); return(-1);}
  Dlen=ArraySize(Dat);
  NCalc=200;                               // number of last elements for calculation
  if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);}
  Par[0]=Dat[Dlen-NCalc];                  // initial S
  Par[1]=0;                                // initial T
  Par[2]=0.5;                              // initial Alpha
  Par[3]=0.5;                              // initial Gamma
  Par[4]=0.5;                              // initial Phi
  it=Optimize(Par);                        // Powell's optimization
  s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4];
  relmae=0; naiv=0;
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t);
    relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]);
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  relmae/=naiv;
  PrintFormat("%s:    N=%i,  RelMAE=%.3f",fname,NCalc,relmae);
  PrintFormat("Iter= %i,  Fmin= %e",it,GetFret());
  PrintFormat("p[0]= %.5f,  p[1]= %.5f,  p[2]= %.2f,  p[3]= %.2f,  p[4]= %.2f",
                                             Par[0],Par[1],Par[2],Par[3],Par[4]);
  return(0);
  }
//-----------------------------------------------------------------------------------
// readCSV
//-----------------------------------------------------------------------------------
int OptimizeES::readCSV(string fnam,double &dat[])
  {
  int n,asize,fhand;
    
  fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
  if(fhand==INVALID_HANDLE)
    {
    Print("FileOpen Error!");
    return(-1);
    }
  asize=512;
  ArrayResize(dat,asize);
  n=0;
  while(FileIsEnding(fhand)!=true)
    {
    dat[n++]=FileReadNumber(fhand);
    if(n+128>asize)
      {
      asize+=128;
      ArrayResize(dat,asize);
      }
    }
  FileClose(fhand);
  ArrayResize(dat,n-1);
  return(0);

  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double OptimizeES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}                 // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}                 // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}                 // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}                 // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }                 // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}                 // Phi     < 0.05
  sse=0; 
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(NCalc*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

A classe OptimizeES deriva da classe PowellsMethod e inclui redefinição da função virtual func(). Como mencionado anteriormente, os parâmetros cujo valor calculado será minimizado no curso da otimização devem ser transmitidos na entrada desta função.

De acordo com o método de máxima verossimilhança, a função func() calcula o logaritmo da soma dos quadrados dos erros de previsão de um passo a frente. Os erros são calculados em um loop que diz respeito à valores recentes NCalcda da sequência.

Para preservar a estabilidade do modelo, devemos impor restrições à faixa de mudanças nos seus parâmetros. Esta gama de parâmetros alfa e gama será de 0,05-0,95 e para o parâmetro Phi - de 0,05 a 1,0. Mas, para a otimização no nosso caso, usamos um método para encontrar um mínimo ilimitado que não implique o uso de limitações nos argumentos da função objetiva.

Vamos tentar transformar o problema de encontrar o mínimo da função multivariável com limitações em um problema de encontrar um mínimo ilimitado, para sermos capaz de levar em consideração todas as limitações impostas nos parâmetros sem alterar o algoritmo de busca. Para isso, será utilizado o chamado método da função de penalidade. Este método pode ser facilmente demonstrado para um caso unidimensional.

Suponha que temos uma função de um único argumento (cujo domínio é de 2,0 a 3,0) e um algoritmo que no processo de busca pode determinar quaisquer valores a este parâmetro função. Neste caso, podemos fazer o seguinte: se o algoritmo de busca passou um argumento que excede o valor máximo permitido, por exemplo, 3,5, a função pode ser calculada para o argumento igual a 3,0 e o resultado obtido é ainda multiplicado por um coeficiente proporcional ao excesso do valor máximo, por exemplo, k=1+(3.5-3)*200.

Se as operações semelhantes são desempenhadas em relação a valores de argumento que acabaram sendo inferior ao valor mínimo permitido, a função objetiva resultante é garantida para aumentar fora da faixa permitida de mudanças em seu argumento. Tal aumento artificial do valor resultante da função objetiva permite manter o algoritmo de busca desconhecido do fato de que o argumento passado à função é, de alguma forma limitado e garante que o mínimo da função resultante será dentro dos limites fixos da argumento. Tal abordagem pode ser facilmente aplicada à uma função de várias variáveis.

O principal método da classe OptimizeES é o método Calc. A chamada deste método é responsável por ler dados de um arquivo, buscar os valores dos parâmetros ideais de um modelo e a estimativa da precisão de previsão usando RelMAE para os valores de parâmetro obtidos. O número de valores processados da sequência lida de um arquivo é, neste caso, definido na variável NCalc.

Abaixo está um exemplo de um script Optimization_Test.mq5 que utiliza a classe OptimizeES.

//-----------------------------------------------------------------------------------
//                                                              Optimization_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "OptimizeES.mqh"

OptimizeES es;
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  es.Calc("Dataset\\USDJPY_M1_1100.TXT");
  }
//-----------------------------------------------------------------------------------

Seguindo a execução deste script, o resultado obtido será como o resultado mostrado abaixo.

Figura 6. Resultado de script Optimization_Test.mq5

Apesar de que agora podemos encontrar os valores de parâmetro ideais e valores iniciais do modelo, há ainda um parâmetro que não pode ser otimizado utilizando ferramentas simples - o número de valores de sequência utilizados na otimização. Na otimização no que diz respeito a uma sequência de grande comprimento, obteremos os valores dos parâmetros ideais que, em média, assegurem erro mínimo ao longo de todo o comprimento da sequência.

No entanto, se a natureza da sequência variar dentro deste intervalo, os valores obtidos para alguns dos seus fragmentos já não será ideal. Por outro lado, se o comprimento da sequência for drasticamente diminuído, não há nenhuma garantia de que os parâmetros ideais obtidos para um intervalo tão curto serão ideais ao longo de um intervalo de tempo mais longo.

OptimizeES.mqh e Optimization_Test.mq5 estão localizados na extremidade do artigo em arquivos do tipo Files.zip. Ao compilar, é necessário que OptimizeES.mqh e PowellsMethod.mqh estejam localizados no mesmo diretório do Optimization_Test.mq5 compilado. No exemplo dado, o arquivo USDJPY_M1_1100.TXT é usado que contém a sequência de teste e que deve estar localizado no diretório\MQL5\Files\Dataset\.

A tabela 2 mostra as estimativas da precisão obtida utilizando RelMAE por meios deste script. A previsão foi feita com relação a oito sequências de testes mencionadas anteriormente no artigo, utilizando os últimos 100, 200 e 400 valores de cada uma dessas sequências.

N=100 N=200 N=400 EURRUR M1 0,980 1,000 0,968 EURRUR M30 0,959 0,992 0,981 EURUSD M1 0,995 0,981 0,981 EURUSD M30 1,023 0,985 0,999 USDJPY M1 1,004 0,976 0,989 USDJPY M30 0,993 0,987 0,988 XAUUSD M1 0,976 0,993 0,970 XAUUSD M30 0,973 0,985 0,999

Tabela 2. Estimativas de erros de previsão utilizando RelMAE

Como pode ser visto, as estimativas de erro de previsão são fechadas por unidades, mas na maioria dos casos, a previsão para as sequências dadas neste modelo é mais precisa que no método ingênuo.

10. O indicador IndicatorES.mq5

O indicador AdditiveES_Test.mq5 baseado na classe AdditiveES.mqh foi mencionado mais cedo sob revisão da classe. Todos os parâmetros de suavização neste indicador foram configurados manualmente.

Agora, depois de considerar o método que permite otimizar os parâmetros do modelo, podemos criar um indicador semelhante, onde os valores dos parâmetros ideais e valores iniciais serão determinados automaticamente e somente o comprimento da amostra processada precisará ser configurado manualmente. Dito isso, excluiremos todos os cálculos relacionados à sazonalidade.

O código-fonte da classe CIndiсatorES usado na criação do indicador está apresentado abaixo.

//-----------------------------------------------------------------------------------
//                                                                   CIndicatorES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class CIndicatorES
//-----------------------------------------------------------------------------------
class CIndicatorES:public PowellsMethod
  {
protected:
  double Dat[];                                              // Input data
  int    Dlen;                                               // Data lenght
  double Par[5];                                             // Parameters
public:
  void   CIndicatorES(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)            { if(n>=0||n<5)return(Par[n]); else return(0); }
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// CalcPar
//-----------------------------------------------------------------------------------
void CIndicatorES::CalcPar(double &dat[])
  {

  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayCopy(Dat,dat);
 
  Par[0]=Dat[0];                                             // initial S
  Par[1]=0;                                                  // initial T
  Par[2]=0.5;                                                // initial Alpha
  Par[3]=0.5;                                                // initial Gamma
  Par[4]=0.5;                                                // initial Phi
  Optimize(Par);                                             // Powell's optimization
  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}           // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}           // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}           // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}           // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }           // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}           // Phi     < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

Essa classe contém métodos CalcPar e GetPar, o primeiro é projetado para o cálculo dos valores de parâmetro ideais do modelo, o segundo é destinado para acessar tais valores. Além disso, a classe CIndicatorES compreende a redefinição da função virtual func().

O código-fonte do indicador IndicatorES.mq5:

//-----------------------------------------------------------------------------------
//                                                                    IndicatorES.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"                 // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"                   // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"                   // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CIndicatorES.mqh"
#define   NFORE 12

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[];
int       NDat;

CIndicatorES   Es;
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NDat=nHist; if(NDat<24)NDat=24;
  MqlRates rates[];
  CopyRates(NULL,0,0,NDat,rates);                   // Load missing data
  ArrayResize(Data,NDat);
    
  SetIndexBuffer(0,Hist,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,Fore,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
  SetIndexBuffer(2,Conf1,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
  SetIndexBuffer(3,Conf2,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
  int i,start;
  double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci;
  
  if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
  start=rates_total-NDat;
//-----------------------
  PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);
  
  for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
  Es.CalcPar(Data);                                    // Optimization of parameters
  s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4);
  f=(s+phi*t); var=0;
  for(i=0;i<NDat;i++)                                // History
    {
    e=Data[i]-f; var+=e*e;
    a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
    f=(s+phi*t); Hist[start+i]=f;
    }
  var/=(NDat-1); a1=1; a2=0; a3=1;
  for(i=rates_total-NFORE;i<rates_total;i++)
    {
    a1=a1*phi; a2+=a1;
    Fore[i]=s+a2*t;                                 // Forecast
    ci=1.96*MathSqrt(var*a3);                        // Confidence intervals
    a=alp*(1+a2*gam); a3+=a*a;
    Conf1[i]=Fore[i]+ci;
    Conf2[i]=Fore[i]-ci;
    }
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Com cada nova barra, o indicador encontra os valores ideais dos parâmetros do modelo, faz cálculos no modelo para um determinado número de barras NHist, constrói uma previsão e define os limites de confiança de previsão.

O único parâmetro do indicador é o comprimento da sequência processada que o valor mínimo é limitado a 24 barras. Todos os cálculos do indicador são feitos com base dos valores abertos[]. O horizonte de previsão é de 12 barras. O código do indicador IndicatorES.mq5 e arquivo CIndicatorES.mqh está localizado no final do artigo em arquivo do tipo Files.zip.

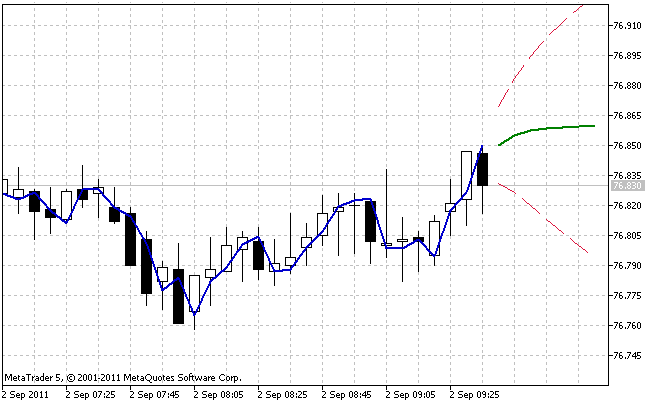
Figura 7. Resultado de operação do indicador IndicatorES.mq5

Um exemplo de resultado de operação do indicador IndicatorES.mq5 é mostrado na figura 7. No decorrer da operação do indicador, o Intervalo de confiança de previsão de 95% assumirá valores correspondentes aos valores de parâmetro ideais obtidos do modelo. Quanto maior os valores de parâmetro de suavização, mais rápido o aumento do Intervalo de confiança sobre o aumento do horizonte de previsão.

Com uma simples melhoria, o indicador IndicatorES.mq5 pode ser usado não somente para previsão de cotas de moeda corrente, mas também para previsão de valores de vários indicadores ou de dados pré-processados.

Conclusão

O objetivo principal do artigo foi familiarizar o leitor com modelos de suavização exponencial aditivos utilizados na previsão. Ao demonstrar sua utilidade prática, algumas questões que acompanham também foram tratadas. No entanto, os materiais fornecidos no artigo podem ser considerados apenas uma introdução à grande variedade de problemas e soluções associadas à previsão.

Gostaria de chamar a atenção para o fato de que as classes, funções, scripts e indicadores fornecidos foram criados no processo de escrever o artigo e foram projetados principalmente para servirem de exemplo para os materiais do artigo. Por isso, nenhum teste sério para a estabilidade e para erros foi realizado. Além disso, os indicadores apresentados no artigo devem ser considerado apenas uma demonstração da implementação dos métodos envolvidos.

A precisão das previsões do indicador IndicatorES.mq5 introduzida no artigo pode provavelmente ser um pouco melhorada usando as modificações do modelo aplicado, o que seria mais adequado em termos de peculiaridades das cotas em consideração. O indicador pode também ser amplificado por outros modelos. Mas estas questões ficam de fora do âmbito deste artigo.

Em conclusão, deve ser notado que os modelos de suavização exponencial podem em certos casos, produzirem previsões sobre a mesma precisão que as previsões obtidas através da aplicação de modelos mais complexos provando mais uma vez que mesmo o modelo mais complexo nem sempre é o melhor.

Referências

1. Everette S. Gardner Jr. Suavização Exponencial: O estado atual – Parte II. 3 de junho, 2005
2. Rob J Hyndman. Previsão com base nos modelos de espaço de estado para suavização exponencial. 29 de agosto de 2002
3. Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 de janeiro de 2003
4. Rob J Hyndman e Muhammad Akram. Alguns modelos de suavização exponencial não lineares são instáveis. 17 de janeiro de 2006
5. Rob J Hyndman e Anne B Koehler. Um outro olhar em medida de precisão de previsão. 2 de novembro de 2005.
6. Yu. P. Lukashin. Métodos favoráveis à adaptação para previsão de curto prazo de séries temporais: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
7. D. Himmelblau. Programação não linear aplicada. М.: Mir, 1975.
8. Numerical Recipes em C, A arte da ciência da computação. 2ª Edição. Cambridge University Press