
Estimativa da densidade de Kernel da função de densidade de probabilidade desconhecida
Introdução
A melhoria do desempenho de MQL5 e o constante crescimento da produtividade PC permite aos usuários da plataforma MetaTrader 5 aplicarem métodos matemáticos bastante sofisticados e avançados para a análise do mercado. Estes métodos podem pertencer a várias áreas da economia, econometria ou estatísticas, mas em qualquer caso, teremos que lidar com o conceito da função de densidade de probabilidade, enquanto usá-los.
Muitos métodos de análise comuns foram desenvolvidos com base na suposição de normalidade da distribuição dos dados ou erros de normalidade no modelo utilizado. Além disso, muitas vezes é necessário conhecer a distribuição dos vários componentes do modelo utilizado para avaliar os resultados da análise. Em ambos os casos temos uma tarefa de criar uma "ferramenta" (uma universal, no caso ideal), que permite estimar a função densidade de probabilidade desconhecida.
Neste artigo é feita uma tentativa de criar uma classe que realiza mais ou menos um algoritmo universal para estimar a função da densidade de probabilidade desconhecida. A ideia original era de que nenhum meio externo seria usado durante a estimativa, ou seja, tudo era para ser realizado apenas pelo meio de MQL5. Mas, finalmente, a ideia original foi alterada de certa forma. é claro que a tarefa de estimativa visual da função de densidade da probabilidade é constituída por duas partes independentes.
Em outras palavras, o cálculo da estimativa em si e sua visualização, por exemplo, são exibidos como um gráfico ou como um diagrama. Claro, os cálculos foram realizados por meio de MQL5, enquanto a visualização deve ser implementada através da criação de uma página HTML e sua exibição no navegador da web. Essa solução é usada para, eventualmente, obter gráficos em forma de vetor.
Mas como a exibição dos resultados e partes são realizados separadamente, um leitor pode, é claro, visualizar usando qualquer outro método disponível. Além disso, esperamos que várias bibliotecas, inclusive gráficos, apareçam no MetaTrader 5 (o trabalho está em curso, até onde sabemos). Não vai ser difícil alterar a parte de exibição na solução proposta, no caso, MetaTrader 5 fornece os meios avançados para a construção de gráficos e diagramas.
Deve-se preliminarmente observar que a criação de um algoritmo verdadeiramente universal para a estimativa das sequências da função de densidade de probabilidade provou ser uma meta inatingível. Ainda que a solução proposta não seja altamente especializada, ela não pode ser chamada de completamente universal também. O problema é que os critérios de otimização acabam sendo bastante diferentes durante a estimativa da densidade, por exemplo, para distribuição em forma de sino, como as normais e exponenciais.
Portanto, é sempre possível escolher a solução mais adequada para cada caso específico, se houver alguma informação preliminar sobre a distribuição estimada. Mas, mesmo assim, vamos supor que não sabemos nada sobre a natureza da densidade estimada. Essa abordagem certamente afetará a qualidade das estimativas, mas vamos esperar que a mesma compensará fornecendo a possibilidade de estimar densidades bastante diferentes.
Devido ao fato de que muitas vezes temos que lidar com sequências não-estacionárias, durante a análise de dados de mercado, estamos mais interessados na estimativa da densidade das sequências curtas e médias. Este é um momento importante que determina a escolha do método de estimativa utilizado.
Histogramas e P-spline podem ser usados com sucesso para sequências muito longas com mais de um milhão de valores. Mas alguns problemas aparecem quando tentamos construir efetivamente os histogramas para as sequências que contêm 10-20 valores. Portanto, vamos nos concentrar principalmente nas sequências com aproximadamente 10 a 10 000 valores mais adiante.
1. Métodos de estimativa da função de densidade de probabilidade
Muitos métodos, mais ou menos populares, de estimativa da função de densidade de probabilidade são conhecidos hoje em dia. Eles podem ser facilmente encontrados na internet, por exemplo, usando tais expressões chave como "estimativa de densidade de probabilidade", "densidade de probabilidade", "estimativa de densidade", etc. Mas, infelizmente, não conseguimos escolher o melhor entre eles. Todos eles possuem algumas certas vantagens, bem como desvantagens.
Os histogramas são, tradicionalmente, usados para estimar a densidade [1]. Utilizando os histogramas (inclusive os estáveis), permite-se fornecer qualidade elevada das estimativas de densidade de probabilidade, mas só no caso em que lidamos com sequências longas. Como foi mencionado anteriormente, não é possível dividir uma sequência curta em um grande número de grupos, enquanto um histograma que consiste de 2-3 barras não pode ilustrar a lei da distribuição da densidade de probabilidade de uma dada sequência. Por isso, tivemos que abandonar o uso de histogramas.
Outro método de estimativa razoavelmente bem conhecido é o da estimativa de densidade de kernel [2]. A ideia de usar a uniformização de kernel é mostrada muito bem em [3]. Por isso, optamos por esse método, apesar de todas as suas desvantagens. Alguns aspectos relacionados com a implementação deste método serão brevemente discutidos a seguir.
Também é necessário mencionar um método de estimativa de densidade muito interessante, que usa o algoritmo de "maximização de expectativa" [4]. Este algoritmo permite dividir uma sequência em componentes separados que têm, por exemplo, uma distribuição normal. é possível obter uma estimativa de densidade somando as curvas de distribuição obtidas depois que os parâmetros de componentes separados tenham sido determinados. Este método é mencionado em [5]. Este método não foi implementado e testado ao trabalhar sobre o artigo, bem como muitos outros. Um grande número de métodos de estimativa de densidade descritos em várias fontes impede de examinar todos eles na prática.
Vamos prosseguir com o método de estimativa de densidade kernel que foi escolhido para a implementação.
2. Estimativa da densidade kernel da função de densidade de probabilidade
A estimativa da densidade kernel da função de densidade de probabilidade é baseada no método de uniformização kernel. Os princípios do método podem ser encontrados, por exemplo, em [6], [7].
A ideia básica de uniformização kernel é bastante simples. Os usuários de MetaTrader 5 estão familiarizados com o indicador de média móvel (MA). Esse indicador pode ser facilmente retratado como uma janela deslizante ao longo de uma sequência com os seus valores ponderados sendo uniformizados por dentro. A janela pode ser retangular, exponencial ou ter alguma outra forma. Podemos facilmente ver a mesma janela deslizante durante a uniformização kernel (por exemplo, [3]). Mas, neste caso, ele é simétrico.
Exemplos de janelas que são mais frequentemente utilizadas na uniformização kernel podem ser encontradas em [8] No caso, uma regressão de ordem zero é usada na uniformização kernel, e os valores ponderados de sequências, que foram obtidas para a janela (kernel), são simplesmente uniformizadas como em MA. Podemos ver o mesmo tipo de aplicação da função de janela quando lidamos com questões de filtragem. Mas agora, o mesmo procedimento é apresentado um pouco diferente. As características de amplitude e fase das frequências são usadas, enquanto kernel (janela), é chamado de uma característica de impulso de filtro.
Estes exemplos mostram o fato de que muitas vezes uma coisa pode ser representada de diversas maneiras. Isso contribui ao instrumento matemático, é claro. Mas também pode levar a confusão ao discutir questões desse tipo.
Embora a estimativa de densidade kernel use os mesmos princípios, como a já mencionada uniformização kernel, seu algoritmo difere um pouco.
Vamos para a expressão que define a estimativa de densidade em um ponto.
![]()
onde
- x - sequência com comprimento n;
- K - kernel simétrico;
- h - intervalo, parâmetro de uniformização.
Apenas kernel Gaussiano será usado mais adiante para estimativas de densidade:
![]()
Como se segue a partir da expressão acima, a densidade no ponto X é calculada como a soma dos valores de kernel para as quantidades definidas pelas diferenças entre os valores do ponto X e a sequência. Além disso, os pontos X utilizados para o cálculo da densidade, podem não coincidir com os valores da própria sequência.
Aqui estão os passos básicos da implementação do algoritmo de estimativa de densidade kernel.
- Avaliar o valor médio e o desvio padrão da sequência de entrada.
- Normalizar a sequência de entrada. Deduzir a média obtida anteriormente a partir de cada um de seus valores e dividir pelo valor do desvio padrão. Após essa normalização, a sequência original terá média zero e um desvio padrão igual a um. Esta normalização não é necessária para calcular a densidade, mas permite unificar gráficos resultantes, como para qualquer sequência em escala X haverá valores expressos em unidades de desvio padrão.
- Encontrar valores altos e baixos na sequência normalizada.
- Criar duas matrizes, de tamanhos correspondentes ao número desejado de pontos apresentados no gráfico resultante. Por exemplo, se o gráfico é construído utilizando 200 pontos, o tamanho das matrizes devem incluir adequadamente os valores de 200 cada.
- Reservar uma das matrizes criadas para armazenar o resultado. A segunda é usada para formar os valores dos pontos, para os quais a estimativa da densidade foi realizada. Para fazer isso, precisamos formar 200 (neste caso) valores, igualmente espaçados entre os valores máximos e mínimos previamente preparados, e guardá-los na matriz que temos preparada.
- Usando a expressão mostrada antes, devemos realizar a estimativa de densidade em 200 pontos de testes (em nosso caso), salvando o resultado na matriz a qual preparamos no passo 4.
A implementação do software de algoritmo é mostrada abaixo.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
O método NTpoints() permite definir o número necessário de pontos de teste igualmente espaçados, para o qual a estimativa de densidade será realizada. Este método deve ser chamado antes de acionar o método Density(). A ligação com a matriz que contém os dados de entrada e o valor do intervalo (parâmetro de uniformização) é passada para o método Density() como seus parâmetros quando o método é chamado.
O método Density() retorna a zero no caso de uma conclusão bem sucedida, enquanto que os valores de pontos de teste e os resultados das estimativas encontram-se localizados nas matrizes T[] e Y[] dessa classe, respectivamente.
Os tamanhos das matrizes são definidos ao acessar NTpoints(), sendo igual a 200 valores por padrão.
O script do exemplo a seguir mostra o uso da classe CDens apresentada.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
As matrizes para armazenar a sequência da entrada de pontos e os resultados da estimativa são preparadas neste exemplo. Então, a matriz X[] é preenchida com valores aleatórios, por meio do exemplo. A cópia da classe CDens é criada após todos os dados terem sido preparados.
Então, o número necessário de pontos de teste é definido (npoint=300 no nosso caso), pelo método de invocação NTpoints(). No caso, não há necessidade de alterar o número padrão de pontos, o método de invocação NTpoints() pode ser excluído.
Os valores calculados são copiados para as matrizes pré-definidas após o método de invocação Density(). Em seguida, a cópia criada anteriormente da classe CDens é excluída. Este exemplo mostra somente a interação com a classe CDens. Sem mais ações com os resultados obtidos (as matrizes T[] e Y[]) são executadas.
Se estes resultados estão destinados a ser utilizados para a criação de um gráfico, eles podem facilmente ser feitos pela colocação dos valores a partir da matriz T[] na escala do gráfico X, enquanto que os valores apropriados da matriz Y[] devem ser colocados na escala Y.
3. Seleção do intervalo ideal
A Fig. 1 exibe os gráficos da estimativa de densidade para a sequência tendo a lei de distribuição normal e vários valores do intervalo h.
As estimativas são realizadas utilizando a classe CDens descrita acima. Os gráficos foram construídos sob a forma de páginas HTML. O método de construção de tais gráficos serão apresentados no final do artigo. A criação de gráficos e diagramas em formato HTML podem ser encontrados em [9].
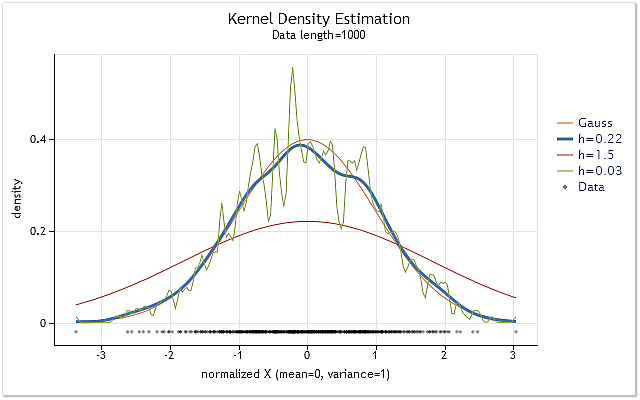
Fig. 1. Estimativa de densidade para diversos valores do intervalo h
A Fig. 1 também mostra a curva de densidade de distribuição normal verdadeira (distribuição de Gaussian), juntamente com três estimativas de densidade. Pode ser facilmente visto que o resultado mais adequado da estimativa foi obtido com h=0.22 nesse caso. Em dois outros casos, podemos observar "sobre uniformização" e "infra uniformização" definidas.
A Figura 1 mostra claramente a importância da correta seleção do intervalo h quando se usa a estimativa de densidade kernel. Em casos no qual o valor h foi escolhido de forma incorreta, uma estimativa será muito deslocada contra a verdadeira densidade ou bastante dispersa.
Muitos dos diversos trabalhos são dedicados a melhor seleção do intervalo h. A regra empírica de Silverman, simples e bem comprovada, é usada frequentemente para a seleção h (ver [10]).
![]()
Neste caso, A é o valor mais baixo a partir dos valores de desvio padrão da sequência e o intervalo interquartil dividido por 1.34.
Considerando que a sequência de entrada tem o desvio padrão igual a um na classe CDens acima mencionada, é bastante fácil implementar esta regra usando o seguinte fragmento de código:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Esta estimativa adapta as sequências com a função da densidade de probabilidade que está perto da normal pela sua forma.
Em muitos casos, a consideração do intervalo interquartil permite ajustar o valor h para o lado inferior, quando a forma da densidade avaliada desvia do normal. Isso faz com que este método de avaliação seja versátil o suficiente. Portanto, esta regra empírica é de uso válido como a estimativa do valor h básico inicial. Além disso, ela não necessita de quaisquer cálculos longos.
Além das estimativas do valor do intervalo h empírico e assimptótico, há também vários métodos baseados na análise da própria sequência de entrada. Neste caso, o melhor valor h é determinado considerando a estimativa preliminar da densidade desconhecida. A comparação da eficiência de alguns destes métodos pode ser encontrada em [11], [12].
De acordo com os resultados dos testes publicados em várias fontes, o método de encaixe Sheather-Jones (SJPI) é um dos métodos mais eficazes de estimativa de intervalo. Vamos optar por este método. A fim de não sobrecarregar o artigo de expressões matemáticas longas, apenas algumas das características do método serão discutidas mais adiante. Se necessário, a base matemática deste método pode ser encontrada em [13].
Nós usamos um kernel Gaussiano, que é um kernel com suporte ilimitado (ou seja, é especificado quando seus parâmetros mudam de menos a mais infinito). Como resultado da expressão acima, precisaremos de operações O(M*N) ao estimar a densidade em pontos M da sequência com comprimento N, usando o método de cálculo direto e kernel com suporte ilimitado. No caso, precisamos fazer estimativas em cada um dos pontos de sequência, este valor aumenta até as operações O(N*N) e o tempo gasto no cálculo aumentará proporcionalmente com o quadrado do comprimento da sequência.
Esta elevada demanda de recursos computacionais é um dos principais inconvenientes do método de uniformização kernel. Se passarmos para o método SJPI, veremos que ele não é melhor em termos de quantidade necessária de cálculo. Falando de forma curta, devemos primeiro calcular a soma de duas densidades derivadas ao longo de todo o comprimento da sequência de entrada duas vezes ao implementar o método SJPI.
Então, devemos calcular a estimativa repetidamente usando os resultados obtidos. O valor da estimativa deve ser igual a zero. O método de Newton-Raphson [14 ] pode ser usado para localizar o argumento, no qual esta função é igual a zero. No caso do cálculo direto, a aplicação do método SJPI para determinar o valor do intervalo ideal pode exigir cerca de dez vezes mais tempo que o cálculo das estimativas da densidade requer.
Existem vários métodos de acelerar os cálculos de uniformização kernel e a densidade estimativa da densidade kernel. No nosso caso, o kernel Gaussiano é utilizado, cujos valores podem ser assumidos como desprezivelmente pequenos para o argumento de valores superiores a 4 . Então, se o valor do argumento é maior do que 4 , não há qualquer necessidade de calcular os valores kernel. Portanto, podemos reduzir parcialmente o número necessário de cálculos. Dificilmente veremos qualquer diferença entre o gráfico com base em tal estimativa e a versão totalmente calculada.
Outra forma simples de acelerar os cálculos é reduzir o número de pontos, para os quais a estimativa é executada. Como foi mencionado acima, se M for menor que N, o número de operações necessárias será reduzido a partir de O(N*N) a O(M*N). Se tivermos uma sequência longa, por exemplo, N=100 000, podemos realizar estimativas apenas em M=200 pontos. Portanto, podemos reduzir consideravelmente o tempo de cálculos.
Além disso, métodos mais complexos podem ser usados para reduzir o número necessário de cálculos, por exemplo, as estimativas utilizando um algoritmo de transformação rápido de Fourier ou Wavelet. Os métodos baseados na redução da dimensão da sequência da entrada (por exemplo, "pré-processamento de dados" [15 ]), podem ser aplicados com sucesso para sequências muito longas.
A transformação Gaussiana rápida [16] também pode ser aplicada para acelerar os cálculos além dos métodos acima referidos, no caso em que o kernel Gaussiano é usado. Vamos usar o algoritmo baseado na transformação Gaussiana [17] para implementar o método SJPI da estimativa do valor de intervalo. A ligação acima mencionada lida com materiais que contêm tanto a descrição do método e os códigos de programa de implementação do algoritmo proposto.
4. Conexão Sheather-Jones (SJPI)
Tal como no caso das expressões matemáticas que determinam a essência do método SJPI, nós não copiaremos a base de cálculo da implementação do algoritmo, que pode ser encontrado em [17] neste artigo. Se necessário, você pode examinar as publicações em [17].
A classe CSJPlugin foi criada com base nos materiais localizados em [17]. Essa classe é destinada para o cálculo do valor do intervalo h ideal e inclui um único método público - o dobro CSJPlugin::SelectH(double &px[],double h,double stdev=1).
Os seguintes argumentos são passados a este método quando ele é chamado:
- duplo &px[] - link para a matriz contendo a sequência original;
- O h duplo é o valor do intervalo h inicial, relativo a qual a pesquisa é realizada, quando resolve as equações utilizando o algoritmo de Newton-Raphson. é desejável que este valor seja o mais próximo possível do pesquisado quanto possível. Isto pode reduzir significativamente o tempo gasto em resolver equações e diminuir a probabilidade dos casos quando Newton-Raphson pode perder sua fiabilidade. O valor encontrado usando a regra empírica de Silverman pode ser usado como o valor h inicial;
- duplo stdev=1 - valor do desvio padrão da sequência original. O valor padrão é um. Neste caso, não é necessário que alteremos o valor padrão, já que este método se destina a usar em conjunto a classe CDens, anteriormente mencionada, na qual a sequência original já foi normalizada e tem o desvio padrão igual a um.
O método SelectH() retorna o valor do intervalo h ideal obtido no caso de uma conclusão bem sucedida. O valor h inicial é retornado como um parâmetro em caso de falha. O código-fonte da classe CSJPlugin está localizado no arquivo CSJPlugin.mqh.
é necessário esclarecer algumas características desta implementação.
A sequência fonte é transformada para o intervalo [0,1] imediatamente, enquanto o valor inicial do intervalo h é normalizado proporcionalmente com a escala da transformação da sequência original. A normalização invertida é aplicada ao valor h ideal obtido durante os cálculos.
eps=1e-4 - precisão de cálculo das estimativas de densidade e seus derivados, e P_UL=500 - número máximo permitido do algoritmo de iterações internas são definidas no construtor da classe CSJPlugin. Para mais informações, consulte [17].
IMAX=20 - número máximo permitido de iterações para o método de Newton-Raphson, e PREC=1e-4 - a precisão da solução da equação utilizando este método é definida no método SelectH().
O uso tradicional do método de Newton-Raphson requer o cálculo da função do alvo e seu derivativo, no mesmo ponto de cada interação do valor. Neste caso, o cálculo do derivativo foi substituído pela sua estimativa calculada pela adição de um pequeno incremento no valor do seu argumento.
A figura 2 mostra o exemplo de utilização de dois métodos diferentes da estimativa do valor do intervalo h ideal.
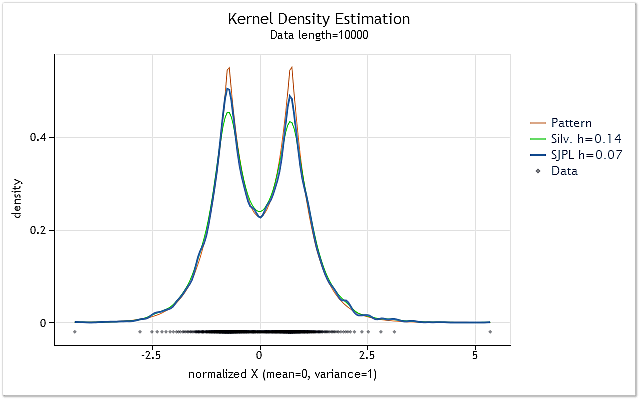
Fig. 2. Comparação das estimativas do valor do intervalo h ideal
A figura 2 mostra duas estimativas para a sequência aleatória, a densidade verdadeira da qual é mostrada como o gráfico vermelho (padrão).
As estimativas foram realizadas para a sequência possuindo 10 000 elementos no comprimento. O valor do intervalo h de 0.14 foi obtido para esta sequência ao usar a regra empírica de Silverman, enquanto foi de 0.07 ao usar o método SJPI.
Examinando os resultados da estimativa de densidade kernel para estes dois valores h mostrados na figura 2, podemos ver facilmente que a aplicação do método SJPI ajudou a obter uma estimativa h atrativa comparada a regra de Silverman. Como podemos ver, os cumes pontiagudos estão em uma forma muito melhor, enquanto quase não há dispersão aumentando em cavidades inclinadas no caso de h=0.07.
Como era esperado, a utilização do método SJPI permite em muitos casos obter estimativas de grande sucesso do intervalo h. Apesar do fato dos algoritmos bastante rápidos [17] terem sido usados para a criação da classe CSJPlugin, a estimativa do valor h usando este método ainda pode demorar muito tempo para sequências longas.
Outra desvantagem deste método é a sua tendência de superestimar o valor de h para sequências curtas que consistem em apenas 10-30 valores. As estimativas feitas usando o método SJPI podem exceder estimativas h feitas pela regra empírica de Silverman.
As seguintes regras serão utilizadas na implementação adicional de alguma forma para compensar estes inconvenientes:
- A estimativa de Silverman será a estimativa padrão para o intervalo h, enquanto será possível ativar o método SJPI por um comando separado;
- Quando se utiliza o método SJPI, o valor mais baixo dos obtidos pelos dois métodos mencionados serão sempre usados como o valor final h.
5. Efeito limite
Aspira ao uso como valor de intervalo ideal na estimativa da densidade, e como possível, tem levado a criação da classe CSJPlugin acima mencionada e bastante inconveniente. Mas há mais uma questão, além de especificar o tamanho do intervalo e a alta intensidade de recursos do método de uniformização kernel. Isto é o chamado efeito limite.
A questão é simples. Ele será exibido usando o kernel definido no intervalo [-1,1]. Tal kernel é chamado de um kernel com suporte limitado. Ele é igual a zero fora do intervalo especificado (não existe).
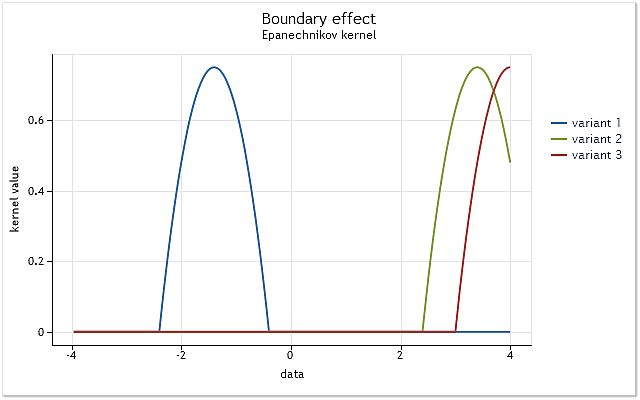
Fig. 3. A redução kernel no intervalo limite
Como mostrado na figura 3, no primeiro caso, o núcleo cobre completamente os dados originais localizados no intervalo [-1,1] relativo ao seu centro. Como o kernel está deslocando (por exemplo, para a direita), a situação surge quando os dados não são suficientes para utilizar plenamente a função kernel selecionada.
O kernel já cobre menos dados do que no primeiro caso. O pior caso é quando o centro kernel está localizado no limite da sequência de dados. A quantidade de dados abrangidos pelo kernel é reduzida para 50% nesse caso. Esta redução no número de dados utilizados para a estimativa da densidade leva a um desvio significativo das estimativas e aumenta a sua dispersão nos pontos próximos dos limites de intervalo.
A figura 3 mostra um exemplo de redução para um kernel com o apoio finito (kernel Epanechnikov) no intervalo limite. Deve notar-se que o kernel Gaussiano definido no intervalo limite (suporte ilimitado) tem sido utilizado durante a implementação do método de estimativa de densidade de kernel. Teoricamente, o corte desse kernel deve sempre ter lugar. Mas, considerando o fato de que o valor deste kernel é quase igual a zero para grandes argumentos, os efeitos limites são parecidos com ele na mesma maneira que ele faz com os kernels com suporte limite.
Esta característica não pode afetar os resultados da estimativa de densidade nos casos apresentados nas figuras 1 e 2, como em ambos os casos, a estimativa foi realizada para as distribuições, a função densidade de probabilidade que diminui nos limites quase até zero.
Vamos formar a sequência consistindo de números inteiros positivos X=1,2,3,4,5,6,... n para mostrar a influência do corte de kernel nas faixas limites. Esta sequência tem a mesma regra de distribuição de densidade de probabilidade. Isso significa que a estimativa da densidade dessa sequência deve ser uma linha reta horizontal, localizada em um nível diferente de zero.
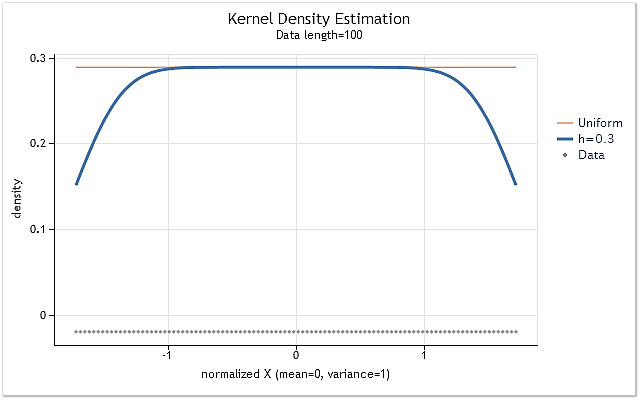
Fig. 4. Estimativa de densidade para a sequência tendo a mesma regra de distribuição
Como esperado, a figura 4 mostra claramente que há um deslocamento considerável da estimativa de densidade nas faixas limite. Há diversos métodos usados para reduzir o deslocamento para aumentar ou diminuir a extensão. Eles podem, em termos gerais, serem divididos nos seguintes grupos:
- Métodos de reflexão de dados;
- Métodos de transformação de dados;
- Métodos de pseudo-dados;
- Métodos kernel delimitadores.
A ideia do uso de dados devolvidos é aquela em que a sequência de entrada é intencionalmente aumentada pela adição de dados, que é uma espécie de um espelho de reflexão dessa sequência em relação aos limites do intervalo de sequência. Depois de um dado aumento, a estimativa de densidade é realizada para os mesmos pontos, como para a sequência original, mas os dados intencionalmente adicionados também são utilizados na estimativa.
Os métodos envolvendo transformação de dados são focados na transformação da sequência próxima ao seu limite de intervalo. Por exemplo, é possível usar um logaritmo ou qualquer outra transformação permitindo de alguma forma deformar a escala de dados ao se aproximar do limite do intervalo durante a estimativa de densidade.
Os então chamados pseudo-dados podem ser utilizados para a extensão intencional (alargamento) da sequência original. Este é o dado calculado na base dos valores da sequência original. Esses dados servem para considerar seu comportamento nos limites e complementá-lo da melhor maneira apropriada.
Há uma abundância de publicações dedicadas aos métodos de kernel limite. Nestes métodos, o kernel por alguns meios altera sua forma quando se aproxima do limite. Os formulários kernel mudam, para compensar a mudança de estimativas nos limites.
Alguns métodos dedicados a compensação das distorções que aparecem nos limites de intervalo, sua comparação e avaliação da eficiência podem ser encontrados em [18].
O método de reflexão de dados foi selecionado para uso posterior após alguns experimentos curtos. Essa escolha foi influenciada pelo fato de que esse método não implica situações em que a estimativa de densidade tem um valor negativo. Além disso, este método não requer cálculos matemáticos complexos. O número total de operações ainda aumenta devido à necessidade de fazer cada estimativa da sequência, o comprimento do qual é deliberadamente aumentado.
Há duas maneiras de implementar esse método. Em primeiro lugar, é possível complementar a sequência original por dados necessários e aumentar o seu tamanho por três vezes durante o processo. Em seguida, seremos capazes de fazer estimativas da mesma maneira tal como é mostrado na classe CDens anteriormente apresentada. Em segundo lugar, não é possível expandir a matriz de dados de entrada. Podemos apenas, mais uma vez, selecionar os dados a partir da mesma de uma determinada maneira. A segunda maneira foi selecionada para a implementação.
Na classe CDens mencionada acima, a estimativa de densidade foi implementada na função (duplo h) kdens vazia. Vamos mudar essa função adicionando correção de distorções limite.
A função aumentada pode parecer como se segue.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
A função é implementada assumindo o fato de que os dados de origem na matriz X[] já tenham sido classificados no momento em que a função foi chamada. Isto permite excluir facilmente dois elementos de sequência correspondentes aos valores dos intervalos extremos de outro processamento. Sempre que possível foi feita a tentativa de colocar operações matemáticas fora dos ciclos ao implementar esta função. Como resultado, a função reflete a ideia do algoritmo usado menos obviamente.
Já foi mencionado antes que é possível reduzir o número de cálculos, no caso, não calcularemos um valor kernel para valores grandes dos argumentos. Isso é exatamente o que foi implementado na função acima. Neste caso, é impossível detectar quaisquer alterações após a criação do gráfico da densidade avaliada.
Ao usar a versão modificada da função kdens(), a estimativa de densidade mostrada na figura 4 é transformada em uma linha reta e as cavidades limites desaparecem completamente. Mas tal correção ideal pode ser alcançada somente se a distribuição próxima aos limites tem gradiente zero, quer dizer, é representado por uma linha horizontal.
Se a densidade de distribuição estimada subir ou descer abruptamente perto do limite, o método de reflexão de dados selecionado não será capaz de ajustar completamente o efeito de limite. Isto é mostrado pelas seguintes figuras.
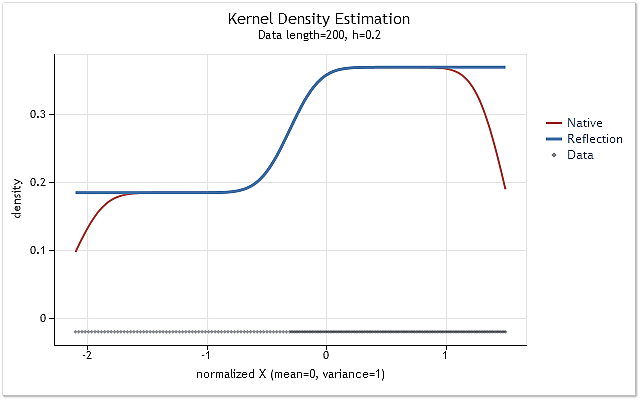
Fig. 5. A função da densidade de probabilidade mudando gradativamente
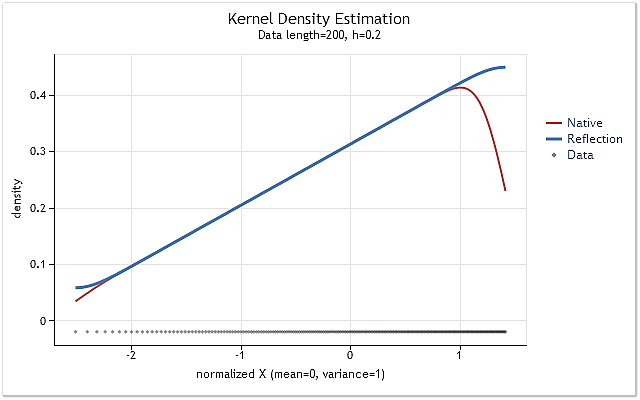
Fig. 6. A densidade de probabilidade aumentando linearmente
As figuras 5 e 6 exibem a estimativa de densidade obtida usando a versão original da função kdens() (vermelha) e a estimativa obtida considerando as alterações aplicadas que implementam o método de reflexão de dados (azul). O efeito limite foi totalmente corrigido na figura 5, enquanto que a mudança próxima aos limites não foi eliminada completamente na figura 6. Se a densidade estimada sobe ou desce abruptamente perto do limite, então isso parece ser um pouco mais suave perto desse limite.
O método de reflexão de dados selecionado para ajustar o efeito limite não é nem o melhor ou o pior dos métodos conhecidos. Embora este método não possa eliminar o efeito limite em todos os casos, é suficientemente estável e fácil de implementar. Este método permite obter um resultado lógico e previsível.
6. Implementação final. Classe CKDensity
Vamos adicionar a capacidade de selecionar automaticamente o valor de limite h e a correção do efeito limite para a classe CDens criada anteriormente.
Abaixo está o código-fonte de uma classe modificada.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
O método de densidade (double &x[],double hh=-1) é básico para essa classe. O primeiro argumento é a ligação com a matriz X[], na qual a sequência de entrada analisada deve ser contida. O comprimento da sequência de entrada não deve ser inferior a oito elementos. O segundo argumento (opcional) é utilizado para a definição forçada do valor de intervalo h.
Qualquer número positivo pode ser especificado. A configuração do valor h será sempre limitada por 0,005 abaixo. Se este parâmetro tem um valor negativo, o valor de intervalo será selecionado automaticamente. O método Density() retorna a zero no caso de uma conclusão feita com sucesso e ao negativo no caso de conclusão emergencial.
Depois de invocar o método Density() e se sua conclusão for bem sucedida, a matriz T[] conterá valores dos pontos de teste, para o qual foi realizada a estimativa de densidade, enquanto a matriz Y[] conterá os valores dessas estimativas. A matriz X[] conterá a sequência de entrada normalizada e classificada. O valor médio desta sequência é igual a zero, enquanto que o valor do desvio padrão é igual a um.
Os seguintes valores estão contidos nas variáveis que são membros da classe:
- N - comprimento da sequência de entrada;
- Np - número de pontos de teste, no qual foi realizada a estimativa de densidade;
- Média - sequência de entrada do valor médio;
- Var - variância da sequência de entrada;
- StDev - desvio padrão da sequência de entrada;
- H - valor do intervalo (parâmetro de uniformização);
- Pflag- bandeira da aplicação do método SJPI para determinar o valor ideal do intervalo h.
O método NTpoints(int n) é usado para definir o número de pontos de teste, na qual a estimativa de densidade será realizada. A definição do número de pontos de teste deve ser realizada antes de chamar o método básico Density(). Se o método NTpoints(int n) não é utilizado, o número de 200 pontos padrão será definido.
O método PluginMode(int m) permite ou proíbe o uso do método SJPI para avaliar o valor d intervalo ideal. Se o parâmetro igual a um é utilizado ao invocar este método, o método SJPI será aplicado para especificar o intervalo h. Se o valor deste parâmetro não é igual a um, o método SJPI não será utilizado. Se o método PluginMode(int m) não foi invocado, o método SJPI será desativado por padrão.
7. Criando gráficos
O método que pode ser encontrado em [9] foi utilizado ao escrever este artigo. Essa publicação trata com a aplicação da página HTML já feita, incluindo a biblioteca do JavaScript [19] de highcharts e a especificação completa de todas as suas invocações. Mais adiante, um programa MQL forma um arquivo de texto contendo os dados a serem exibidos e o mesmo se conecta à página HTML mencionada acima.
Nesse caso, é necessário editar uma página HTML alterando o código JavaScript implementado para fazer quaisquer correções na estrutura dos gráficos exibidos. Para evitar isso, uma interface simples foi desenvolvida permitindo invocar métodos JavaScript da biblioteca de highcharts diretamente do programa MQL.
Não houve nenhuma tarefa, ao criar a interface, para implementar o acesso a todas as possibilidades da biblioteca de highcharts. Portanto, apenas as possibilidades que permitem não mudar o arquivo de HTML criado anteriormente, ao escrever o artigo, foram implementadas.
O código-fonte da classe CLinDraw é exibido abaixo. Esta classe é usada para fornecer a conexão com os métodos da biblioteca de highcharts. Este código não deve ser considerado como uma implementação completa do software. Ele é apenas um exemplo que mostra como criar uma interface tendo a biblioteca JavaScript com gráficos.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Se queremos fazer esta classe funcionar corretamente, precisamos de uma página HTML já feita tendo implementado bibliotecas JavaScript. Um tamanho e uma localização do campo para a construção de gráfico(s) também devem ser especificados. Um exemplo da tal implementação de página pode ser encontrado nos arquivos anexados a este artigo.
Quando o método AddGraph() é invocado em um arquivo de texto, um código JavaScript apropriado é formado. O arquivo de texto é então incluído na página HTML criada anteriormente. O código mencionado refere-se à biblioteca de gráficos e proporciona a criação de um gráfico usando os dados submetidos ao método AddGraph() como um argumento. Um ou mais alguns gráficos podem ser adicionados no campo de saída ao invocar esse método novamente.
Três versões da função sobrecarregada de AddGraph() estão inclusas na classe CLinDraw. Uma das versões requer que apenas uma matriz com os dados apresentados seja transferida a mesma como um argumento. Ela foi projetada para construção de um gráfico de sequência onde o índice do elemento de sequência é exibido no eixo X.
A segunda versão recebe duas matrizes como um argumento. Essas matrizes contêm os valores apresentados no eixo X e Y, respectivamente. A terceira versão permite definir um valor constante para o eixo Y. Ela pode ser usada para a construção de uma linha horizontal. Os argumentos restantes destas funções são semelhantes:
- tipo de sequência - tipo de gráfico exibido. Pode ter valores de "linha", "ranhura" e "dispersão";
- nome de sequência - nome atribuído ao gráfico;
- int w=0 - largura da linha. Argumento opcional. Se o valor for 0, o valor da largura padrão de 2 é utilizado;
- sequência col="" - define a cor da linha e seu valor de opacidade. Argumento opcional.
O método LDraw() deve ser chamado por último. Este método, por padrão, completa a saída do código JavaScript e os dados no arquivo de texto criado no \MQL5\Files\. Em seguida, o arquivo é movido para o diretório que contém os arquivos da biblioteca de gráficos e o arquivo HTML.
O método LDraw() pode possuir um único argumento opcional. Se o valor do argumento não está definido ou é definido para um, um navegador web padrão será invocado e o gráfico será exibido depois de mover o arquivo de dados para um diretório apropriado. Se o argumento não tem qualquer outro valor, o arquivo de dados também será completamente formado, mas um navegador web não será invocado automaticamente.
Outros métodos da classe CLinDraw disponíveis permitem definir os cabeçalhos do gráfico e os rótulos do eixo. Não vamos considerar em detalhes neste artigo as questões de aplicação da biblioteca de highcharts e a classe CLinDraw. As informações completas sobre a biblioteca de gráficos highcharts podem ser encontradas em [19], enquanto que exemplos de sua aplicação para a criação de gráficos e diagramas podem ser encontrados em [9], [20].
O uso de bibliotecas externas deve ser permitido no terminal para a operação normal da classe CLinDraw.
8. Exemplo da estimativa de densidade e organização de arquivos
Nós eventualmente temos três classes - CKDensity, CSJPlugin e CLinDraw.
Abaixo se encontra o código-fonte do exemplo mostrando como as classes podem ser utilizadas.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
O dado, para o qual será realizado a avaliação da função de densidade de probabilidade, é preparado no início do script KDE_Example.mq5. Para conseguir isso, os valores "abertos" do símbolo e do período atual são copiados para a matriz X[]. Os retornos logarítmicos são então calculados em suas bases.
O próximo passo é a criação de uma cópia da classe CKDensity. A invocação do seu método PluginMode() permite utilizar o método SJPI para avaliação do intervalo h. A estimativa de densidade é, em seguida, realizada para a sequência criada na matriz X[]. O processo de avaliação é completo nesta etapa. Todas as outras etapas lidam com a visualização da estimativa de densidade obtida.
As estimativas obtidas devem ser comparadas com qualquer regra de distribuição bem conhecida. Para fazer isso, os valores correspondentes a regra de distribuição de Laplace são formados na matriz Z[]. O dado de entrada normalizado e classificado é então armazenado na matriz Sc[]. Se o comprimento da sequência de entrada excede 400 elementos, então nem todos os seus valores serão inclusos em Sc[]. Alguns deles serão ignorados. Portanto, o tamanho da matriz Sc[] nunca conterá mais de 400 elementos.
Uma vez que todos os dados necessários para a exibição foram preparados, uma cópia da classe CLinDraw é criada. Em seguida, os cabeçalhos são especificados e os gráficos necessários são adicionados usando o método AddGraph().
O primeiro deles é o gráfico da regra de distribuição Laplace que pretende ser um modelo. O mesmo é seguido pelo gráfico da estimativa de densidade obtido usando os dados de entrada. O gráfico inferior, mostrando o grupo de dados fonte, é adicionado por último. Depois de definir todos os elementos necessários para a exposição, o método LDraw() é invocado.
Como resultado, obtivemos o gráfico mostrado na figura 7.
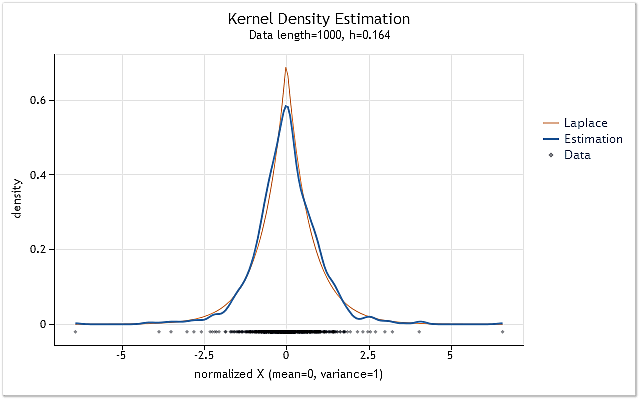
Fig. 7. Estimativa de densidade para retornos logarítmicos (USDJPY, Diário)
A estimativa mostrada na figura 7, foi realizada por 1000 valores de retorno logarítmicos para USDJPY, diariamente. Como podemos ver, a estimativa é muito semelhante à curva correspondente à distribuição de Laplace.
Todos os arquivos necessários para a estimativa de densidade e visualização estão localizados no arquivo KDEFiles.zip abaixo. O arquivo inclui os seguintes arquivos:
- DensityEstimation\ChartTools\CLinDraw.mqh – classe para interação com highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - biblioteca de highcharts JS v2.2.0 (16-02-2012);
- DensityEstimation\ChartTools\jquery.js – jQuery v1.7.1 library;
- DensityEstimation\ChartTools\LinDraw.htm – página HTML destinada à exibição;
- DensityEstimation\CKDensity.mqh – classe implementando a estimativa de densidade;
- DensityEstimation\CSJPlugin.mqh – classe de implementação do método SJPI de estimativa do valor do intervalo ideal;
- DensityEstimation\KDE_Example.mq5 – exemplo de estimativa de densidade para retornos logarítmicos.
Após descompactar o arquivo, o diretório DensityEstimation\ com todo o seu conteúdo deve ser colocado em diretórios dos scripts (ou indicadores) do terminal. é possível, depois, compilar imediatamente e iniciar o KDE_Example.mq5. O diretório da DensityEstimation pode ser renomeado, se necessário. Isso não afetará o funcionamento do programa.
Deve-se mencionar novamente que o uso de bibliotecas externas deve ser permitido no terminal para a operação normal da classe CLinDraw.
O diretório DensityEstimation\ inclui o subdiretório ChartTools\ que contém todos os componentes necessários para a visualização dos resultados obtidos. Os arquivos de visualização estão localizados em um subdiretório separado, de modo que o conteúdo do diretório DensityEstimation\ pode ser facilmente visto. O nome do subdiretório ChartTools\ é especificado diretamente no código-fonte. Por isso, ele não deve ser renomeado, caso contrário, será necessário fazer alterações no código-fonte.
Já foi mencionado que o arquivo de texto é criado durante a visualização. Este arquivo contém os dados necessários para a construção de gráficos. Este arquivo é criado originalmente em um diretório de arquivos especiais do terminal. Mas logo é movido para o diretório ChartTools mencionado. Assim, não haverá sinais da nossa atividade de exemplo teste deixado em Files\ ou em qualquer outro diretório terminal. Portanto, você pode simplesmente apagar o diretório DensityEstimation com todo o seu conteúdo para remover completamente os arquivos instalados deste artigo.
Conclusão
As expressões matemáticas que explicam a essência de alguns métodos específicos foram inclusas no artigo. Isso foi feito deliberadamente, numa tentativa de facilitar sua leitura. Se necessário, todos os cálculos matemáticos são encontrados em numerosas publicações. Os links para alguns deles são fornecidos abaixo.
Os códigos-fonte fornecidos no artigo não foram sujeitos a testes importantes. Por isso, eles devem ser considerados apenas como exemplos, e não como aplicações totalmente funcionais.
Referências
- Histogram.
- Kernel density estimation.
- Kernel smoother.
- Expectation–maximization algorithm.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. EM-Algorithm Having a Large Number of Components as a Means of Constructing Non-Parametric Density Estimations (in Russian).
- Hardle W. Applied Nonparametric Regression.
- Kernel (estatísticas).
- Charts and diagrams in HTML.
- Simon J. Sheather. (2004). Density Estimation.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). A Review and Comparison of Bandwidth Selection Methods for Kernel Regression.
- Clive R. Loader. (1999). Bandwidth Selection: Classical or Plug-In?.
- S. J. Sheather, M. C. Jones. (1991). A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.
- Newton's method.
- Data binning.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). Efficient Kernel Machines Using the Improved Fast Gauss Transform.
- Fast optimal bandwidth estimation for univariate KDE.
- R.J. Karunamuni and T. Alberts. (2005). A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation.
- Highcharts JS.
- Analysis of the Main Characteristics of Time Series.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/396
 US$ 200 por seu artigo sobre algotrading!
US$ 200 por seu artigo sobre algotrading!
 Fundamentos de estatística
Fundamentos de estatística
 Aplicação do método de coordenadas de Eigen para a análise estrutural de distribuições estatísticas não extensivas
Aplicação do método de coordenadas de Eigen para a análise estrutural de distribuições estatísticas não extensivas
 Quem é quem na MQL5.community?
Quem é quem na MQL5.community?
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso