Prévision de Séries Chronologiques à l'Aide du Lissage Exponentiel

Introduction

Il existe actuellement un grand nombre de méthodes de prévision bien connues axées uniquement sur l'analyse des valeurs passées d'un intervalle de temps, c'est-à-dire des méthodes qui emploient des principes normalement utilisés en analyse technique. L'instrument principal de ces méthodes est le schéma d'extrapolation où les propriétés d’intervalles identifiés à un certain décalage temporel dépassent ses limites.

En même temps, il est admis que les propriétés des intervalles à l'avenir seront les mêmes que dans le passé et le présent. Un schéma d'extrapolation plus complexe qui implique une étude de la dynamique des changements des caractéristiques de l’intervalle en tenant dûment compte de cette dynamique dans l'intervalle de prévision est moins fréquemment utilisé en prévision.

Les méthodes de prévision les plus connues axées sur l’extrapolation sont peut-être celles utilisantmodèle de moyenne mobile intégrée et auto-régressive (ARIMA). La popularité de ces méthodes est principalement due aux travaux de Box et Jenkins qui ont proposé et élaboré un modèle ARIMA intégré. Il existe bien sûr d'autres modèles et méthodes de prévision en dehors des modèles présentés par Box et Jenkins.

Cet article couvrira brièvement des modèles plus simples -modèles de lissage exponentiel proposés par Holt et Brown bien avant l'apparition des œuvres de Box et Jenkins.

Malgré les outils mathématiques plus simples et plus clairs, la prévision à l'aide de modèles de lissage exponentiel conduit souvent à des résultats comparables à ceux obtenus à l'aide du modèle ARIMA. Cela n'est guère surprenant car les modèles de lissage exponentiel sont un cas particulier du modèle ARIMA. En d'autres termes, chaque modèle de lissage exponentiel à l’examen dans cet article trouve un modèle ARIMA équivalent correspondant. Ces modèles équivalents ne seront pas examinés dans l'article et ne sont mentionnés qu'à titre indicatif.

On sait que la prévision dans chaque cas particulier nécessite une approche individuelle et implique normalement un certain nombre de procédures.

Par exemple :

1. Analyse de l’ intervalle de temps pour les valeurs manquantes et aberrantes. Ajustement de ces valeurs.
2. Identification de la tendance et de son type. Détermination de la périodicité de l’intervalle
3. Vérifier la stationnarité de l’intervalle
4. Analyse de prétraitement des intervalles (prise de logarithmes, différenciation, etc.).
5. Sélection du modèle.
6. Détermination des paramètres du modèle. Prévision basée sur le modèle sélectionné.
7. Évaluation de la précision des prévisions du modèle.
8. Analyse des erreurs du modèle sélectionné.
9. Détermination de l'adéquation du modèle sélectionné et, si nécessaire, remplacement du modèle et retour aux éléments précédents.

Ce n'est de loin pas la liste complète des actions requises pour une prévision efficace.

Il convient de souligner que la détermination des paramètres du modèle et l'obtention des résultats de prévision ne sont qu'une petite partie du processus général de prévision. Mais il semble impossible de couvrir l'ensemble des problèmes liés d'une manière ou d'une autre à la prévision dans un article.

Cet article ne traitera donc que des modèles de lissage exponentiel et utilisera des cotations de devise non-prétraitées comme séries de test. Les questions d'accompagnement ne peuvent certainement pas être complètement évitées dans l'article, mais elles ne seront abordées que dans la mesure où elles sont nécessaires à l'examen des modèles.

1. Stationnarité

La notion d'extrapolation proprement dite implique que le développement futur du processus à l'étude sera le même que dans le passé et le présent. En d'autres termes, il s'agit de la stationnarité du processus. Les processus stationnaires sont très attractifs du point de vue prévisionnel mais ils n'existent malheureusement pas dans la nature, car tout processus réel est susceptible de changer au cours de son développement.

Les processus réels peuvent remarquablement avoir une espérance de variance différente et une distribution tout au long le cours du temps mais les processus dont les caractéristiques varient très lentement peuvent vraisemblablement se voir attribués des processus stationnaires. "Très lentement" dans ce cas indique que les changements dans les caractéristiques du processus dans l'intervalle d'observation fini semblent être si insignifiants que de tels changements peuvent être négligés.

Il est clair que plus l'intervalle d'observation disponible est court (échantillon court), plus la probabilité de prendre la mauvaise décision concernant la stationnarité du processus dans son ensemble est élevée. D'autre part, si l'on s'intéresse davantage à l'état du processus à un moment ultérieur pour faire une prévision à court terme, la réduction de la taille de l'échantillon peut dans certains cas conduire à une augmentation de la précision de cette prévision.

Si le processus fait l’objet des changements, les paramètres de série déterminés dans l'intervalle d'observation seront différents en dehors de ses limites. Ainsi, plus l'intervalle de prévision est long, plus l'effet de la variabilité des caractéristiques de série sur l'erreur de prévision est fort. En raison ce fait, nous devons nous limiter à une prévision à court terme uniquement ; une réduction considérable de l'intervalle de prévision permet de s'attendre à ce que les caractéristiques de série changeant lentement n'entraîneront pas d'erreurs de prévision considérables.

Par ailleurs, la variabilité des paramètres d’intervalles conduit au fait que la valeur obtenue lors de l'estimation par l'intervalle d'observation est moyennée, car les paramètres ne sont pas restés constants dans l'intervalle. Les valeurs de paramètres obtenues ne seront donc pas liées au dernier instant de cet intervalle mais en refléteront une certaine moyenne. Malheureusement, il est impossible d'éliminer complètement ce phénomène désagréable mais il peut être diminué si la longueur de l'intervalle d'observation impliqué dans l'estimation des paramètres du modèle (intervalle d'étude) est réduite dans la mesure du possible.

Dans le même temps, l'intervalle d'étude ne peut pas être raccourci indéfiniment car s'il est extrêmement réduit, il diminuera certainement la précision de l'estimation des paramètres de série.. Il faut rechercher un compromis entre l'effet des erreurs liées à la variabilité des caractéristiques des séries et l'augmentation des erreurs due à la réduction extrême de l'intervalle d'étude.

Tout ce qui précède s'applique pleinement à la prévision utilisant des modèles de lissage exponentiel car ils sont basés sur l'hypothèse de stationnarité des processus, comme les modèles ARIMA. Néanmoins, par souci de simplicité, nous admettrons par la suite et de manière conventionnelle que les paramètres de tous les intervalles examinés varient dans l'intervalle d'observation mais d'une manière si lente que ces modifications puissent être négligées.

Ainsi, l'article abordera les problèmes liés à la prévision à court terme d’intervalles avec des caractéristiques à évolution lente sur la base de modèles de lissage exponentiel. La "prévision à court terme" devrait dans ce cas indiquer prévoir pour un, deux ou plusieurs intervalles de temps à l'avance au lieu de prévoir pour une période de moins d'un an comme on l'entend habituellement en économie.

2. intervalles de test

Après la rédaction de cet article, les cotations EURRUR, EURUSD, USDJPY et XAUUSD précédemment enregistrées pour M1, M5, M30 et H1 ont été utilisées. Chacun des fichiers enregistrés comporte 1100 valeurs "ouvertes". La valeur "la plus ancienne" se trouve au début du fichier et la plus "récente" à la fin. La dernière valeur enregistrée dans le fichier correspond à l'heure de création du fichier. Les fichiers comportant des séries de test ont été créés à l'aide du script HistoryToCSV.mq5. Les fichiers de données et le script à l'aide desquels ils ont été créés se trouvent à la fin de l'article dans l'archive Files.zip.

Tel que déjà mentionné, les cotations enregistrées sont utilisées dans cet article sans être prétraitées malgré les problèmes évidents vers lesquels je souhaiterais attirer votre attention. Par exemple, les cotations EURRUR_H1 pendant la journée comportent de 12 à 13 barres, les cotations XAUUSD le vendredi comportent une barre de moins que les autres jours. Ces exemples démontrent que les cotations sont produites avec un intervalle d'échantillonnage irrégulier ; ceci est totalement inacceptable pour des algorithmes conçus pour travailler avec des intervalles de temps correctes qui suggèrent d'avoir un intervalle de quantification uniforme.

Même si les valeurs manquantes des cotations sont reproduites par extrapolation, la question du manque de cotations le week-end reste ouverte. Nous pouvons admettre que les événements intervenant dans le monde le week-end ont le même impact sur l'économie mondiale que les événements en semaine. Des révolutions, des actes de la nature, des scandales très médiatisés, des changements de gouvernement et d'autres événements plus ou moins importants de ce genre peuvent intervenir à tout moment. Si un tel événement avait lieu un samedi, il n'aurait guère moins d'influence sur les marchés mondiaux que s'il s'était produit un jour de semaine.

Ce sont peut-être ces événements qui conduisent à des écarts de cotations si fréquemment observés en fin de semaine de travail. Apparemment, le monde continue à suivre ses propres règles même lorsque le FOREX ne fonctionne pas. On ne sait toujours pas si les valeurs des cotations correspondant aux week-ends destinées à une analyse technique doivent être reproduites et quel bénéfice cela pourrait apporter.

Évidemment, ces questions dépassent le cadre de cet article mais à première vue, une série sans lacunes semble être plus appropriée pour l'analyse, au moins en termes de détection des composants cycliques (saisonniers).

L'importance de la préparation préliminaire des données pour une analyse plus approfondie ne peut guère être surestimée ; dans notre cas, il s'agit d'une question indépendante majeure car les cotations, tels qu'elles apparaissent dans le Terminal, ne sont généralement pas vraiment adaptées à une analyse technique. Outre les problèmes liés aux lacunes ci-dessus, il existe de nombreux autres problèmes.

Lors de la formation des cotations, par exemple, un point de temps fixe se voit attribuer des valeurs "ouvert" et "clos" ne lui appartenant pas ; ces valeurs correspondent au temps de formation des ticks au lieu d'un moment fixe d'un graphique temporel sélectionné, alors qu'il est communément connu que les ticks sont parfois très rares.

Un autre exemple peut être vu au mépris total du théorème d'échantillonnage, car personne ne peut assurer que le taux d'échantillonnage, même dans un intervalle d'une minute, satisfait le théorème ci-dessus (sans parler d'autres intervalles plus grands). De plus, il faut garder à l'esprit la présence d'un spread variable qui dans certains cas peut se superposer aux valeurs de cotation.

Laissons cependant ces questions en dehors du cadre de cet article et revenons au sujet principal.

3. Lissage exponentiel

Voyons d'abord le modèle le plus simple

,

Où:

• X(t) – (simulé) processus à l’étude,
  
• L(t) – Niveau du processus du variable,
  
• r(t)–Variable de la moyenne zéro aléatoire.

Comme nous pouvons le voir, ce modèle comprend les sommes de deux composants; nous sommes particulièrement désireux du niveau du processusL(t)et nous tenterons de le distinguer.

Il est bien connu que le calcul de la moyenne d'une série aléatoire peut entraîner une diminution de la variance, c'est-à-dire une plage réduite de son écart par rapport à la moyenne. Nous pouvons,par conséquent, admettre que si le processus décrit par notre simple modèle est exposé au moyennage (lissage),nous pourrons ne pas être en mesure de se débarrasser complément d’un composant aléatoire r(t)mais nous pouvons au moins l’affaiblir et par conséquent, distinguer le niveau cibleL(t).

Pour cela, nous utiliserons un lissage exponentiel simple (SES).

Dans cette formule bien connue, le degré de lissage est défini par le coefficient alpha qui peut être défini de 0 à 1. Si alpha est défini à zéro, les nouvelles valeurs entrantes de l’ordre d'entrée X n'auront aucun effet sur le résultat du lissage. Le résultat du lissage pour n'importe quel moment sera une valeur constante.

Par conséquent, dans des cas extrêmes comme celui-ci, le composant aléatoire nuisible sera entièrement supprimé, mais le niveau de processus en question sera lissé en une ligne horizontale droite. Si le coefficient alpha est défini sur un, l’ordre d'entrée ne sera pas du tout affecté par le lissage. Le niveau en questionL(t)ne sera pas déformé dans ce cas et le composant aléatoire ne sera pas non plus supprimé.

Il est intuitivement évident que lors de la sélection de la valeur alpha, il faut simultanément répondre aux exigences contradictoires. D'une part, la valeur alpha doit être proche de zéro afin de supprimer efficacement le composant aléatoirer(t). D'autre part, il est conseillé de régler la valeur alpha proche de l'unité pour ne pas déformer le composant L(t) auquel nous nous intéressons tant. Afin d'obtenir la valeur optimale d’alpha, nous devons identifier un critère selon lequel une telle valeur peut être optimisée.

Lors de la détermination de ce critère, rappelez-vous que cet article traite de la prévision et pas seulement du lissage des séries.

Dans ce cas, concernant le modèle de lissage exponentiel simple, il est d'usage d’examiner la valeur obtenue à un instant donné comme une prévision pour un nombre quelconque de pas en avant.

Où est la prévision m d’une longueur d’avance de l’instant t.

Par conséquent, la prévision de la valeur de série à l'instant t sera une prévision d'une longueur d'avance faite à l'étape précédente

Dans ce cas,nous pouvons utiliser une erreur de prévision à une longueur d’avance comme critère d'optimisation de la valeur du coefficient alpha

Ainsi, en minimisant la somme des carrés de ces erreurs sur l'ensemble de l'échantillon, nous pouvons déterminer la valeur optimale du coefficient alpha pour une série donnée. La meilleure valeur alpha sera bien entendu celle pour laquelle la somme des carrés des erreurs serait minimale.

La figure 1 montre un graphique de la somme des carrés des erreurs de prévision d'une longueur d’avance par rapport à la valeur du coefficient alpha pour un fragment de la série de test USDJPY M1.

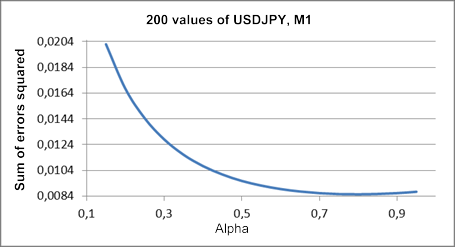
Figure 1. Lissage exponentiel simple

Le minimum sur le graphique résultant est à peine discernable et se situe près de la valeur alpha d'environ 0,8. Mais une telle image n'est pas toujours le cas par rapport au simple lissage exponentiel. En tentant d’obtenir la valeur optimale alpha du test des fragments de série utilisés dans l’article,nous serons plus souvent qu’autrement en passe d’obtenir un tracé penchant en permanence vers l’unité.

Des valeurs aussi élevées du coefficient de lissage suggèrent que ce modèle simple n'est pas tout à fait adéquat pour la description de nos séries de test (cotations). C'est soit que le niveau de processusL(t)change trop rapidement, soit qu'il y a une tendance bien présente dans le processus.

Compliquons un peu notre modèle en ajoutant un autre composant

,

Où :

• X(t) - (simulé)processus à l’étude;
  
• L(t) - niveau du processus de variable;
  
• T(t) - tendance linéaire;
  
• r(t) - variable de moyenne nulle aléatoire.

On sait que les coefficients de régression linéaire peuvent être déterminés par double lissage d'une série :

Pour les coefficients a1 et a2 obtenus de la sorte, la prévision m-de longueur d’avance à l'instant t sera égale à

Il convient de noter que le même coefficient alpha est utilisé dans les formules ci-dessus pour le premier lissage et le lissage répété. Ce modèle est appelé modèle additif à un paramètre de croissance linéaire.

Expliquons la différence entre le modèle simple et le modèle de croissance linéaire.

Admettons que pendant longtemps le processus à l'étude ait représenté un composant constant, c'est-à-dire qu'il apparaisse sur le graphique sous la forme d'une ligne droite horizontale mais qu'à un moment donné une tendance linéaire commence à émerger. Une prévision de ce processus réalisée à l'aide des modèles mentionnés ci-dessus est illustrée en figure 2.

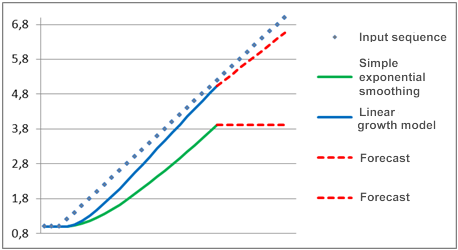
Figure 2. Comparaison de modèles

Comme nous pouvons le constater, le modèle de lissage exponentiel simple est sensiblement en retard sur la ordre d'entrée variant linéairement et la prévision faite à l'aide de ce modèle s'éloigne encore plus. Nous pouvons voir un modèle très différent lorsque le modèle de croissance linéaire est utilisé. Lorsque la tendance émerge, ce modèle est comme s'il essayait de trouver la série variant linéairement et sa prévision est plus proche de la direction des valeurs d'entrée variables.

Si le coefficient de lissage dans l'exemple donné était plus élevé, le modèle de croissance linéaire serait capable « d'atteindre » le signal d'entrée sur le temps donné et sa prévision coïnciderait presque avec l’ordre d'entrée.

Malgré le fait que le modèle de croissance linéaire en état stable donne de bons résultats en présence d'une tendance linéaire, il est facile de voir qu'il lui faut un certain temps pour « rattraper » la tendance. Par conséquent, il y aura toujours un écart entre le modèle et l’ordre d'entrée si la direction d'une tendance change fréquemment. En outre, si la tendance croît de manière non linéaire mais suit plutôt la loi des carrés, le modèle de croissance linéaire ne pourra pas "l'atteindre". Mais malgré ces inconvénients, ce modèle est plus avantageux que le simple modèle de lissage exponentiel en présence d'une tendance linéaire.

Tel que déjà mentionné, nous avons utilisé un modèle de croissance linéaire à un paramètre. Afin de découvrir la valeur optimale du paramètre alpha pour un fragment de la série de test USDJPY M1, créons un graphique de la somme des carrés des erreurs de prévision d'une longueur d’avance par rapport à la valeur du coefficient alpha.

Ce tracé créé sur la base du même fragment de série que celui de la figure 1, est affiché à la figure 3.

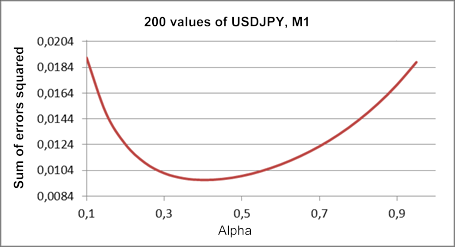
Figure 3. Modèle de croissance linéaire

Par rapport au résultat de la figure 1, la valeur optimale du coefficient alpha a dans ce cas diminué d’environ 0,4. Le premier et le second lissage ont les mêmes coefficients dans ce modèle, bien que théoriquement leurs valeurs puissent être différentes. Le modèle de croissance linéaire avec deux coefficients de lissage différents sera examiné plus loin.

Les deux modèles exponentiels de lissages que nous avons examinés disposent de leurs analogues enMetaTrader 5 où ils existent sous forme d’indicateurs. Ceux sont des indicateurs de tendance bien-connus EMA et DEMA qui ne sont pas conçus pour la prévision mais pour le lissage de valeurs de séquence.

Il convient de noter que lors de l'utilisation de l'indicateur DEMA, une valeur correspondant au coefficient a1 est affichée à la place de la valeur de prévision en une étape. Le coefficient a2 (voir les formules ci-dessus pour le modèle de croissance linéaire) n'est dans ce cas ni calculé ni utilisé. De plus, le coefficient de lissage est calculé en fonction de la période équivalente n

Par exemple, alpha égal à 0,8 correspondra à n à peu près égal à 2 et si alpha est égal à 0,4, n est égal à 4.

4. Valeurs initiales

Tel que déjà mentionné, une valeur de coefficient de lissage doit d'une manière ou d'une autre être obtenue lors de l'application d'un lissage exponentiel. Mais cela semble insuffisant. Étant donné que dans le lissage exponentiel, la valeur actuelle est calculée sur la base de la précédente, il existe une situation où une telle valeur n'existe pas encore à l'instant zéro. En d'autres termes, la valeur initiale de S or S1 et S2 dans le modèle de croissance linéaire doit en quelque sorte être calculée au temps zéro.

Le problème de l'obtention des valeurs initiales n'est pas toujours facile à résoudre. Si (comme dans le cas de l'utilisation des cotations dans MetaTrader 5) nous avons un très long historique disponible, la courbe de lissage exponentiel aura, si les valeurs initiales avaient été déterminées de manière inexacte, le temps de se stabiliser à un point courant, après avoir corrigé notre erreur initiale. Cela nécessitera environ 10 à 200 (et parfois même plus) périodes selon la valeur du coefficient de lissage.

Dans ce cas, il suffirait d'estimer approximativement les valeurs initiales et de lancer le processus de lissage exponentiel 200 à 300 périodes avant la période cible. Cela devient plus difficile, cependant, lorsque l'échantillon disponible ne comporte, par exemple, que 100 valeurs.

Il existe diverses recommandations dans la bibliographie/documentation concernant le choix des valeurs initiales. Par exemple, la valeur initiale du lissage exponentiel simple peut être assimilée au premier élément d'une série ou calculée comme la moyenne de trois à quatre éléments initiaux d'une série en vue de lisser les valeurs aberrantes aléatoires. Les valeurs initiales S1et S2dans le modèle de croissance linéaire peuvent être déterminées sur la base de l'hypothèse que le niveau initial de la courbe de prévision doit être égal au premier élément d'une série et que la pente de la tendance linéaire doit être nulle.

Nous pouvons découvrir encore plus de recommandations dans différentes sources concernant le choix des valeurs initiales, mais aucune d'entre elles ne peut garantir l'absence d'erreurs notables aux premiers stades de l'algorithme de lissage. Il est particulièrement perceptible avec l'utilisation de coefficients de lissage de faible valeur lorsqu'un grand nombre de périodes est nécessaire pour atteindre un état stable.

Par conséquent, afin de minimiser l'impact des problèmes liés au choix des valeurs initiales (en particulier pour les séries courtes), nous utilisons parfois une méthode qui implique une recherche de telles valeurs qui conduiront à l'erreur de prévision minimale. C’est une question de calculer une erreur de prévision pour les valeurs initiales variant par petits incréments sur toute la série.

La variante la plus appropriée peut être sélectionnée après avoir calculé l'erreur dans la plage de toutes les combinaisons possibles de valeurs initiales. Cette méthode est cependant très laborieuse nécessitant beaucoup de calculs et n'est quasiment jamais utilisée sous sa forme directe.

Le problème décrit concerne l'optimisation ou la recherche d'une valeur minimale de fonction multivariable. De tels problèmes peuvent être résolus à l'aide de divers algorithmes développés pour réduire considérablement la portée des calculs requis. Nous reviendrons un peu plus loin sur les problèmes d'optimisation des paramètres de lissage et des valeurs initiales en prévision.

5. Évaluation de la Précision des Prévisions

La procédure de prévision et la sélection des valeurs ou paramètres initiaux du modèle posent le problème de l'estimation de la précision de la prévision. L'évaluation de l'exactitude est également importante lors de la comparaison de deux modèles différents ou de la détermination de la cohérence de la prévision obtenue. Il existe un grand nombre d'estimations bien connues pour l'évaluation de l'exactitude des prévisions, mais le calcul de chacune d'entre elles nécessite la connaissance de l'erreur de prévision à chaque étape.

Tel que déjà mentionné, une erreur de prévision d'un pas à l'instant t est égale à

Où :

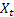• – valeur d’ordre d'entrée à l'instant t;
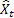• – prévision à l'instant t faite à l'étape précédente.

L'estimation de la précision des prévisions la plus courante est probablement l'erreur quadratique moyenne (MSE) :

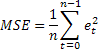
où n est le nombre d'éléments dans une série.

Une sensibilité extrême aux erreurs uniques occasionnelles de grande valeur est parfois signalée comme un inconvénient de la MSE. Cela provient du fait que la valeur d'erreur lors du calcul de la MSE est au carré. Comme alternative, il est conseillé d'utiliser dans ce cas l'erreur absolue moyenne (MAE).

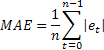
L'erreur au carré est remplacée ici par la valeur absolue de l'erreur. Il est admis que les estimations obtenues à l'aide de la MAE sont plus stables.

Les deux estimations sont tout à fait appropriées pour, par exemple, l'évaluation de l'exactitude des prévisions de la même série en utilisant différents paramètres de modèle ou différents modèles, mais elles semblent être de peu d'utilité pour la comparaison des résultats de prévision reçus dans différentes séries.

Par ailleurs, les valeurs de ces estimations ne suggèrent pas expressément la qualité du résultat prévu. Par exemple, nous ne pouvons pas dire si la MAE obtenue de 0,03 ou toute autre valeur est bonne ou mauvaise.

Pour être en mesure de comparer l’exactitude de la prévision de différentes séries , nous pouvons utiliser des estimations relatives RelMSE et RelMAE:

Les estimations obtenues de l'exactitude des prévisions sont ici divisées par les estimations respectives obtenues en utilisant la méthode de test de prévision. Comme méthode de test, il convient d'utiliser la méthode dite naïve suggérant que la valeur future du processus sera égale à la valeur actuelle.

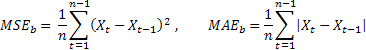
Si la moyenne des erreurs de prévision est égale à la valeur des erreurs obtenues en utilisant la méthode naïve, la valeur d'estimation relative sera égale à un. Si la valeur d'estimation relative est inférieure à un, cela signifie qu'en moyenne, la valeur d'erreur de prévision est inférieure à celle de la méthode naïve. En d'autres termes, l'exactitude des résultats des prévisions l'emporte sur l'exactitude de la méthode naïve. Et vice versa, si la valeur d'estimation relative est supérieure à un, la précision des résultats de la prévision est, en moyenne, plus faible que dans la méthode naïve de prévision.

Ces estimations conviennent également à l'évaluation de l'exactitude des prévisions pour deux étapes ou plus à venir. Une erreur de prévision en une étape dans les calculs doit simplement être remplacée par la valeur des erreurs de prévision pour le nombre approprié d'étapes à venir.

À titre d'exemple, le tableau ci-dessous comporte des erreurs de prévision d'une longueur d'avance estimées à l'aide de RelMAE dans un modèle de croissance linéaire à un paramètre. Les erreurs ont été calculées en utilisant les 200 dernières valeurs de chaque série de test.

alpha = 0,3 alpha = 0,4 alpha = 0,5 EURRUR M1 1.14 1.10 1.09 EURRUR M30 1.14 1.11 1.14 EURUSD M1 1.17 1.11 1.10 EURUSD M30 1.17 1.11 1.11 USDJPY M1 1.10 1.08 1.10 USDJPY M30 1.17 1.13 1.13 XAUUSD M1 1.20 1.11 1.10 XAUUSD M30 1.11 1.12 1.13

Tableau 1. Erreurs de prévision d’une longueur d’avance estimées à l'aide de RelMAE

L'estimation RelMAE permet de comparer l'efficacité d'une méthode sélectionnée lors de la prévision de différentes séries. Comme le suggèrent les résultats du tableau 1, notre prévision n'a jamais été plus précise que la méthode naïve - toutes les valeurs RelMAE sont plus d'une.

6. Modèles additifs

Il y avait un modèle plus tôt dans l'article qui comprenait la somme du niveau de processus, de la tendance linéaire et d'une variable aléatoire. Nous allons étendre la liste des modèles examinés dans cet article en ajoutant un autre modèle qui, en plus des composants ci-dessus, comprend un composant cyclique et saisonnier

Les modèles de lissage exponentiel comprenant tous les composants sous forme de somme sont appelés modèles additifs. En dehors de ces modèles, il existe des modèles multiplicatifs dans lesquels un, plusieurs ou tous les composants sont compris en tant que produit. Passons en revue le groupe des modèles additifs.

L'erreur de prévision avec une longueur d'avance a été mentionnée à plusieurs reprises plus tôt dans l'article. Cette erreur doit être calculée dans presque toutes les applications liées à la prévision basée sur le lissage exponentiel. Connaissant la valeur de l'erreur de prévision, les formules des modèles de lissage exponentiel introduites ci-dessus peuvent être présentées sous une forme quelque peu différente (forme de correction d'erreur).

La forme de la représentation du modèle que nous allons utiliser dans notre cas comporte une erreur dans ses expressions qui s'ajoute partiellement ou totalement aux valeurs précédemment obtenues. Une telle représentation est appelée le modèle d'erreur additif. Les modèles de lissage exponentiel peuvent également être exprimés sous une forme d'erreur multiplicative qui ne sera cependant pas utilisée dans cet article.

Examinons les modèles de lissage exponentiel additif.

Lissage exponentiel simple :

Modèle équivalent – ARIMA(0,1,1) :

Modèle de croissance linéaire additif :

Contrairement au modèle de croissance linéaire à un paramètre introduit précédemment, deux paramètres de lissage différents sont utilisés ici.

Modèle équivalent – ARIMA(0,2,2) :

Modèle de croissance linéaire avec amortissement :

La signification d'un tel amortissement est que la pente de tendance diminuera à chaque étape de prévision ultérieure en fonction de la valeur du coefficient d'amortissement. Cet effet est démontré dans la figure 4.

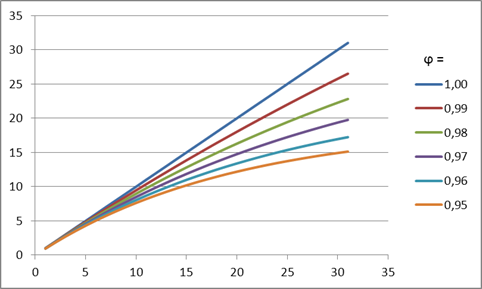
Figure 4. Effet du coefficient d'amortissement

Comme nous pouvons le voir sur la figure, lors d'une prévision, une valeur décroissante du coefficient d'amortissement entraînera une perte de force plus rapide de la tendance, ainsi la croissance linéaire sera de plus en plus amortie.

Modèle équivalent - ARIMA(1,1,2) :

En ajoutant un composant saisonnier en somme à chacun de ces trois modèles, nous obtiendrons trois autres modèles.

Modèle simple avec saisonnalité additive :

Modèle de croissance linéaire avec saisonnalité additive :

Modèle de croissance linéaire avec amortissement et saisonnalité additive :

Il existe également des modèles ARIMA équivalents aux modèles avec saisonnalité, mais ils seront laissés de côté car ils n'auront pratiquement aucune importance pratique.

Les notations utilisées dans les formules fournies sont les suivantes :

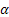• – paramètre de lissage pour le niveau de la série, [0:1];
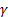• – paramètre de lissage pour la tendance, [0:1];
• – paramètre de lissage pour les indices saisonniers, [0:1];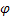
• – paramètre d'amortissement, [0:1];
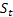• – Niveau lissé de la série calculée à l’instant T plus tard 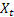a été observé;
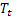• – tendance additive lissée calculée à l'instant t ;
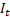• – indice saisonnier lissé calculé à l'instant t ;
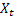• – valeur de la série à l'instant t;
• m – nombre de pas en avant pour lesquels la prévision est faite;
• p-nombre de périodes dans le cycle saisonnier
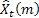• – prévision m-de longueur d’avance faite à l'instant t;
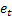• – Prévision d’erreur de longueur d’avance au moment t.

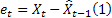Il est facile de voir que les formules pour le dernier modèle fourni comprennent les six variantes à l'étude.

Si dans les formules du modèle de croissance linéaire avec amortissement et saisonnalité additive, nous prenons

,

la saisonnalité ne sera pas prise en compte dans les prévisions. Plus loin où, le modèle de croissance linéaire sera créé et où, nous aurons un modèle de croissance linéaire avec amortissement.

Le modèle de lissage exponentiel simple correspondra à .

Lors de l'utilisation des modèles qui impliquent la saisonnalité, la présence de cyclicité et la période du cycle doivent d'abord être déterminées à l'aide de toute méthode disponible afin d'utiliser davantage ces données pour l'initialisation des valeurs des indices saisonniers.

Nous n’avons pas pu détecter la cyclicité stable et considérable dans les fragments de séries de test utilisés dans notre cas où la prévision est menée sur de brefs intervalles de temps. Par conséquent, dans cet article, nous ne donnerons pas d'exemples pertinents et ne développerons pas les caractéristiques associées à la saisonnalité.

Afin de déterminer les intervalles de prédiction de probabilité au regard des modèles étudiés, nous utiliserons des dérivations analytiques trouvées dans la bibliographie [3]. La moyenne de la somme des carrés des erreurs de prévision d'une langueur d’avance calculée sur l'ensemble de l'échantillon de taille n sera utilisée comme variance estimée de ces erreurs.

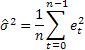
Ensuite, l'expression suivante sera vraie pour la détermination de la variance estimée dans une prévision pour 2 étapes et plus d'avance pour les modèles étudiés :

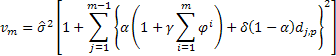
où égale à l’un si le modulo p est zéro est zéro.

Après avoir calculé la variance estimée de la prévision pour chaque pas m, nous pouvons découvrir les limites de l'intervalle de prévision à 95 % :

Nous conviendrons à nommer cet intervalle de prévision l'intervalle de confiance de la prévision.

Implémentons les expressions fournies pour les modèles de lissage exponentiel dans une classe écrite en MQL5.

7. Implémentation de la classe AdditiveES

L’implémentation de la classe impliquait l'utilisation des expressions pour le modèle de croissance linéaire avec amortissement et saisonnalité additive.

Comme mentionné précédemment, d'autres modèles peuvent en être dérivés par une sélection appropriée de paramètres.

//-----------------------------------------------------------------------------------
//                                                                     AdditiveES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

//-----------------------------------------------------------------------------------
// Forecasting. Exponential smoothing. Additive models.
// References:
// 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II.
//    June 3, 2005.
// 2. Rob J Hyndman. Forecasting based on state space models for exponential
//    smoothing. 29 August 2002.
// 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing
//    using two new classes of state space models. 30 January 2003.
//-----------------------------------------------------------------------------------
class AdditiveES:public CObject
  {
protected:
  double Alpha;    // Smoothed parameter for the level of the series
  double Gamma;    // Smoothed parameter for the trend
  double Phi;      // Autoregressive or damping parameter
  double Delta;    // Smoothed parameter for seasonal indices
  int    nSes;     // Number of periods in the seasonal cycle
  double S;        // Smoothed level of the series, computed after last Y is observed
  double T;        // Smoothed additive trend
  double Ises[];   // Smoothed seasonal indices
  int    p_Ises;   // Pointer for Ises[] shift register
  double F;        // Forecast for 1 period ahead from origin t

public:
         AdditiveES();
  double Init(double s,double t,double alpha=1,double gamma=0,
              double phi=1,double delta=0,int nses=1);
  double GetS()                 { return(S); }
  double GetT()                 { return(T); }
  double GetF()                 { return(F); }
  double GetIs(int m);
  void   IniIs(int m,double is);  // Initialization of smoothed seasonal indices
  double NewY(double y);          // Next calculating step
  double Fcast(int m);            // m-step ahead forecast
  double VarCoefficient(int m);   // Coefficient for calculating prediction intervals

  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void AdditiveES::AdditiveES()
  {
  Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0; S=0; T=0;
  }
//-----------------------------------------------------------------------------------
// Initialization
//-----------------------------------------------------------------------------------
double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0,
                       double phi=1,double delta=0,int nses=1)
  {
  S=s; T=t;
  Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1;
  Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1;
  Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1;
  Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1;
  nSes=nses; if(nSes<1)nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0;
  F=S+Phi*T;
  return(F);
  }
//-----------------------------------------------------------------------------------
// Calculations for the new Y
//-----------------------------------------------------------------------------------
double AdditiveES::NewY(double y)
  {
  double e;
  
  e=y-F;
  S=S+Phi*T+Alpha*e;
  T=Phi*T+Alpha*Gamma*e;
  Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e;
  p_Ises++; if(p_Ises>=nSes)p_Ises=0;
  F=S+Phi*T+GetIs(0);
  return(F);
  }
//-----------------------------------------------------------------------------------
// Return smoothed seasonal index
//-----------------------------------------------------------------------------------
double AdditiveES::GetIs(int m)
  {
  if(m<0)m=0;
  int i=(int)MathMod(m+p_Ises,nSes);
  return(Ises[i]);
  }
//-----------------------------------------------------------------------------------
// Initialization of smoothed seasonal indices
//-----------------------------------------------------------------------------------
void AdditiveES::IniIs(int m,double is)
  {
  if(m<0)m=0;
  if(m<nSes)
    {
    int i=(int)MathMod(m+p_Ises,nSes);
    Ises[i]=is;
    }
  }
//-----------------------------------------------------------------------------------
// m-step-ahead forecast
//-----------------------------------------------------------------------------------
double AdditiveES::Fcast(int m)
  {
  int i,h;
  double v,v1;

  if(m<1)h=1; else h=m;  
  v1=1; v=0;
  for(i=0;i<h;i++){v1=v1*Phi; v+=v1;}
  return(S+v*T+GetIs(h));
  }
//-----------------------------------------------------------------------------------
// Coefficient for calculating prediction intervals
//-----------------------------------------------------------------------------------
double AdditiveES::VarCoefficient(int m)
  {
  int i,h;
  double v,v1,a,sum,k;
  
  if(m<1)h=1; else h=m;
  if(h==1)return(1);
  v=0; v1=1; sum=0;
  for(i=1;i<h;i++)
    {
    v1=v1*Phi; v+=v1;
    if((int)MathMod(i,nSes)==0)k=1; else k=0;
    a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha);
    sum+=a*a;
    }
  return(1+sum);
  }
//-----------------------------------------------------------------------------------

Passons brièvement en revue les méthodes de la classe AdditiveES.

Méthode Init

Paramètres d’entrée

• double s - définit la valeur initiale du niveau lissé；
• double t - définit la valeur initiale de la tendance lissée；
• double alpha=1 - définit le paramètre de lissage pour le niveau de la série；
• double gamma=0 - définit le paramètre de lissage pour la tendance；
• double phi=1 - définit le paramètre d'amortissement；
• double delta=0 - définit le paramètre de lissage pour les indices saisonniers；
• int nses=1 - définit le nombre de périodes dans le cycle saisonnier.

Valeur renvoyée :

• Il renvoie une prévision d’une longueur d’avance calculée sur la base des valeurs initiales définies.

La méthode Init doit être appelée en premier lieu. Ceci est nécessaire pour définir les paramètres de lissage et les valeurs initiales. Il est à noter que la méthode Init ne permet pas d'initialiser les indices saisonniers à des valeurs arbitraires ; lors de l'appel de cette méthode, les indices saisonniers seront toujours mis à zéro.

Méthode IniIs

Paramètres d’entrée

• Int m - indice saisonnier ;
• double is - définit la valeur du numéro d'index saisonnier m.

Valeur renvoyée :

• Aucun

La méthode IniIs(...) est appelée lorsque les valeurs initiales des indices saisonniers doivent être autres que zéro. Les indices saisonniers doivent être initialisés juste après l'appel de la méthode Init(...).

Méthode NewY

Paramètres d’entrée

• double y – nouvelle valeur de l’ordre d'entrée

Valeur renvoyée :

• Il renvoie une prévision d’une longueur d’avance calculée sur la base de la nouvelle valeur de la série.

Cette méthode est conçue pour calculer une prévision d’une longueur d'avance à chaque fois qu'une nouvelle valeur de l’ordre d'entrée est saisie. Il ne doit être appelé qu'après l'initialisation de la classe par les méthodes Init et Inils, cas échéant.

Méthode Fcast

Paramètres d’entrée

• int m – horizon de prévision de la période 1,2,3,… ;

Valeur renvoyée :

• Il renvoie la valeur de prévision m-d’une longueur d’avance

Cette méthode calcule uniquement la valeur prévisionnelle sans affecter l'état du processus de lissage. Elle est généralement appelée après avoir appelé la méthode NewY.

Méthode VarCoefficient

Paramètres d’entrée

• int m – horizon de prévision de la période 1,2,3,… ;

Valeur renvoyée :

• Il renvoie la valeur du coefficient pour le calcul de la variance de la prévision.

Cette valeur de coefficient indique l'augmentation de la variance d'une prévision à une longueur d’avance par rapport à la variance de la prévision à une longueur d’avance.

Méthodes GetS, GetT, GetF, GetIs

Ces méthodes donnent accès aux variables protégées de la classe. GetS, GetT et GetF renvoient les valeurs respectivement du niveau lissé, de la tendance lissée et d'une prévision à une longueur d’avance. La méthode GetIs donne accès aux indices saisonniers et exige l'indication du numéro d'index m comme argument d'entrée.

Le modèle le plus complexe de tous que nous avons passé en revue est le modèle de croissance linéaire avec amortissement et saisonnalité additiveà base de laquelle la classe AdditiveES class est créée. Cela soulève une question très raisonnable - quelle serait la nécessité des modèles plus simples restants.

Malgré le fait que les modèles plus complexes devraient apparemment avoir un net avantage sur les plus simples, ce n'est en fait pas toujours le cas. Des modèles plus simples qui ont moins de paramètres entraîneront dans la grande majorité des cas une moindre variance des erreurs de prévision, c'est-à-dire que leur fonctionnement sera plus stable. Ce fait est utilisé pour créer des algorithmes de prévision basés sur le fonctionnement parallèle simultané de tous les modèles disponibles, des plus simples aux plus complexes.

Une fois la série entièrement traitée, un modèle de prévision présentant l'erreur la plus faible compte tenu du nombre de ses paramètres (c'est-à-dire de sa complexité) est sélectionné. Il existe un certain nombre de critères créés à cette fin, par exemple.Akaike’s Information Criterion (AIC) Il en découlera la sélection d'un modèle qui devrait produire les prévisions les plus stables.

Pour démontrer l'utilisation de la classe AdditiveES, un indicateur simple a été créé dont tous les paramètres de lissage sont définis manuellement.

Le code source de l'indicateur AdditiveES_Test.mq5 est présenté ci-dessous.

//-----------------------------------------------------------------------------------
//                                                                AdditiveES_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"      // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "PInterval+"    // Prediction interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCadetBlue
#property indicator_style3  STYLE_SOLID
#property indicator_width3  1
#property indicator_label4  "PInterval-"    // Prediction interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCadetBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1

double HIST[];
double FORE[];
double PINT1[];
double PINT2[];

input double Alpha=0.2;     // Smoothed parameter for the level
input double Gamma=0.2;     // Smoothed parameter for the trend
input double Phi=0.8;       // Damping parameter
input double Delta=0;       // Smoothed parameter for seasonal indices
input int    nSes=1;        // Number of periods in the seasonal cycle
input int    nHist=250;     // History bars, nHist>=100
input int    nTest=150;     // Test interval, 50<=nTest<nHist
input int    nFore=12;      // Forecasting horizon, nFore>=2

#include "AdditiveES.mqh"
AdditiveES fc;

int    NHist;               // history bars
int    NFore;               // forecasting horizon
int    NTest;               // test interval
double ALPH;                // alpha
double GAMM;                // gamma
double PHI;                 // phi
double DELT;                // delta
int    nSES;                // Number of periods in the seasonal cycle
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NHist=nHist; if(NHist<100)NHist=100;
  NFore=nFore; if(NFore<2)NFore=2;
  NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50;
  ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1;
  GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1;
  PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1;
  DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1;
  nSES=nSes; if(nSES<1)nSES=1;

  MqlRates rates[];
  CopyRates(NULL,0,0,NHist,rates);           // Load missing data
  
  SetIndexBuffer(0,HIST,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,FORE,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFore);
  SetIndexBuffer(2,PINT1,INDICATOR_DATA);
  PlotIndexSetString(2,PLOT_LABEL,"Conf+");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFore);
  SetIndexBuffer(3,PINT2,INDICATOR_DATA);
  PlotIndexSetString(3,PLOT_LABEL,"Conf-");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFore);
  
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  int i,j,init,start;
  double v1,v2;
  
  if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1)
    {init=1; start=rates_total-NHist;}
  else
    {init=0; start=prev_calculated;}
  if(start==rates_total)return(rates_total);    // New tick but not new bar
//-----------------------
  if(init==1)                                   // Initialization
    {
    i=start;
    v2=(open[i+2]-open[i])/2;
    v1=(open[i]+open[i+1]+open[i+2])/3.0-v2;
    fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES);
    ArrayInitialize(HIST,EMPTY_VALUE);
    }
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore);

  for(i=start;i<rates_total;i++)                // History
    {
    HIST[i]=fc.NewY(open[i]);
    }
  v1=0;
  for(i=0;i<NTest;i++)                          // Variance
    {
    j=rates_total-NTest+i;
    v2=close[j]-HIST[j-1];
    v1+=v2*v2;
    }
  v1/=NTest;                                    // v1=var
  j=1;
  for(i=rates_total-NFore;i<rates_total;i++)
    {
    v2=1.96*MathSqrt(v1*fc.VarCoefficient(j));  // Prediction intervals
    FORE[i]=fc.Fcast(j++);                    // Forecasting
    PINT1[i]=FORE[i]+v2;
    PINT2[i]=FORE[i]-v2;
    }
  
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Un appel ou une initialisation à répétition de l’indicateur définit les valeurs initiales du lissage exponentiel.

Il n'y a pas de réglages initiaux des indices saisonniers dans cet indicateur, leurs valeurs initiales sont donc toujours égales à zéro. Après une cette initialisation, l'influence de la saisonnalité sur le résultat de la prévision augmentera progressivement de zéro à une certaine valeur stable, avec l'introduction de nouvelles valeurs entrantes.

Le nombre de cycles nécessaires pour atteindre un régime de fonctionnement en état stable dépend de la valeur du coefficient de lissage pour les indices saisonniers : plus la valeur du coefficient de lissage est faible, plus il faudra de temps.

Le résultat de l'opération de l'indicateur AdditiveES_Test.mq5 avec les paramètres par défaut est illustré à la figure 5.

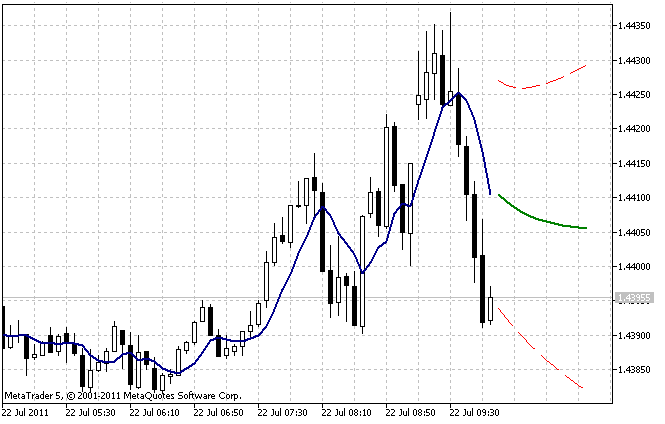
Figure 5. L'indicateur AdditiveES_Test.mq5

Outre la prévision, l'indicateur affiche une ligne supplémentaire correspondant à la prévision en une étape pour les valeurs passées de la série et les limites de l'intervalle de confiance de prévision à 95%.

L'intervalle de confiance est basé sur la variance estimée de l'erreur de longueur d’avance. Pour réduire l'effet d'imprécision des valeurs initiales sélectionnées, la variance estimée n'est pas calculée sur toute la longueur nHist mais uniquement par rapport aux dernières barres dont le nombre est précisé dans le paramètre d'entrée nTest.

L'archive Files.zip à la fin de l'article comprend les fichiers AdditiveES.mqh et AdditiveES_Test.mq5. Lors de la compilation de l'indicateur, il est nécessaire que le fichier include AdditiveES.mqh se trouve dans le même répertoire que AdditiveES_Test.mq5.

Alors que le problème de la sélection des valeurs initiales a été en partie résolu lors de la création de l'indicateur AdditiveES_Test.mq5, le problème de la sélection des valeurs optimales des paramètres de lissage est resté ouvert.

8. Sélection des Valeurs Optimales des Paramètres

Le modèle de lissage exponentiel simple a un seul paramètre de lissage et sa valeur optimale peut être trouvée en utilisant la méthode d'énumération simple. Après avoir calculé les valeurs d'erreur de prévision sur l'ensemble de la série, la valeur du paramètre est modifiée par un petit incrément et un calcul complet est à nouveau effectué. Cette procédure est répétée jusqu'à ce que toutes les valeurs de paramètres possibles aient été énumérées. Il ne nous reste plus qu'à sélectionner la valeur du paramètre qui a entraîné la plus petite valeur d'erreur.

Afin de trouver une valeur optimale du coefficient de lissage dans la plage de 0,1 à 0,9 par incréments de 0,05, le calcul complet de la valeur d'erreur de prévision devra être effectué dix-sept fois. Comme nous pouvons le voir, le nombre de calculs requis n'est pas si grand. Mais le modèle de croissance linéaire avec amortissement implique l'optimisation de trois paramètres de lissage et dans ce cas, il faudra 4913 calculs pour énumérer toutes leurs combinaisons dans la même plage aux mêmes incréments de 0,05.

Le nombre d'exécutions complètes requises pour l'énumération de toutes les valeurs de paramètres possibles augmente rapidement avec la hausse du nombre de paramètres, la diminution de l'incrément et l'extension de la plage d'énumération. S'il s'avérait en outre nécessaire d'optimiser les valeurs initiales des modèles en plus des paramètres de lissage, il serait assez difficile de le faire en utilisant la méthode d’énumération simple.

Les problèmes liés à la recherche du minimum d'une fonction de plusieurs variables sont bien étudiés et il existe pas mal d'algorithmes de ce genre. La description et la comparaison de différentes méthodes pour trouver le minimum d'une fonction peuvent être trouvées dans la bibliographie/documentation [7]. Toutes ces méthodes visent principalement à réduire le nombre d'appels de la fonction objective, c'est-à-dire à réduire les efforts de calcul dans le processus de recherche du minimum.

Différentes sources comportent souvent une référence aux méthodes d'optimisation dites quasi-Newton méthodes d’optimisation. Cela est probablement dû à leur grande efficacité, mais l’implémentation d'une méthode plus simple devrait également suffire à démontrer une approche d'optimisation de la prévision. Optons pour méthode Powell's. La méthode de Powell ne nécessite pas de calcul de dérivées de la fonction objective et appartient aux méthodes de recherche.

Cette méthode, comme toute autre méthode, peut être implémentée par programmation de diverses manières. La recherche doit être achevée lorsqu'une certaine précision de la valeur de la fonction objective ou de la valeur de l'argument est atteinte. En outre, une certaine implémentation peut inclure la possibilité d'utiliser des limitations sur la plage admissible de changements de paramètres de fonction.

Dans notre cas, l'algorithme pour trouver un minimum sans contrainte en utilisant la méthode de Powell est implémenté dans PowellsMethod.class. L'algorithme interrompt la recherche une fois qu'une certaine précision de la valeur de la fonction objective est atteinte. Dans l’implémentation de cette méthode, un algorithme trouvé dans la bibliographie/documentation [8] a été utilisé comme prototype.

Vous trouverez ci-dessous le code source de la classe PowellsMethod.

//-----------------------------------------------------------------------------------
//                                                                  PowellsMethod.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

#define GOLD   1.618034
#define CGOLD  0.3819660
#define GLIMIT 100.0
#define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d);
#define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a))
#define FMAX(a,b) (a>b?a:b)
//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
  double P[],Xi[];
  double Pcom[],Xicom[],Xt[];
  double Pt[],Ptt[],Xit[];
  int    N;
  double Fret;
  int    Iter;
  int    ItMaxPowell;
  double FtolPowell;
  int    ItMaxBrent;
  double FtolBrent;
  int    MaxIterFlag;
public:
  void   PowellsMethod(void);
  void   SetItMaxPowell(int n)           { ItMaxPowell=n; }
  void   SetFtolPowell(double er)        { FtolPowell=er; }
  void   SetItMaxBrent(int n)            { ItMaxBrent=n;  }
  void   SetFtolBrent(double er)         { FtolBrent=er;  }
  int    Optimize(double &p[],int n=0);
  double GetFret(void)                   { return(Fret);  }
  int    GetIter(void)                   { return(Iter);  }
private:
  void   powell(void);
  void   linmin(void);
  void   mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
  double brent(double ax,double bx,double cx,double &xmin);
  double f1dim(double x);
  virtual double func(const double &p[]) { return(0); }
  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void PowellsMethod::PowellsMethod(void)
  {
  ItMaxPowell= 200;
  FtolPowell = 1e-6;
  ItMaxBrent = 200;
  FtolBrent  = 1e-4;
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::powell(void)
  {
  int i,j,m,n,ibig;
  double del,fp,fptt,t;
  
  n=N; Fret=func(P);
  for(j=0;j<n;j++)Pt[j]=P[j];
  for(Iter=1;;Iter++)
    {
    fp=Fret; ibig=0; del=0.0;
    for(i=0;i<n;i++)
      {
      for(j=0;j<n;j++)Xit[j]=Xi[j+n*i];
      fptt=Fret;
      linmin();
      if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;}
      }
    if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return;
    if(Iter>=ItMaxPowell)
      {
      Print("powell exceeding maximum iterations!");
      MaxIterFlag=1; return;
      }
    for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];}
    fptt=func(Ptt);
    if(fptt<fp)
      {
      t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt);
      if(t<0.0)
        {
        linmin();
        for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];}
        }
      }
    }
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::linmin(void)
  {
  int j,n;
  double xx,xmin,fx,fb,fa,bx,ax;

  n=N;
  for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];}
  ax=0.0; xx=1.0;
  mnbrak(ax,xx,bx,fa,fx,fb);
  Fret=brent(ax,xx,bx,xmin);
  for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];}
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::mnbrak(double &ax,double &bx,double &cx,
                                 double &fa,double &fb,double &fc)
  {
  double ulim,u,r,q,fu,dum;

  fa=f1dim(ax); fb=f1dim(bx);
  if(fb>fa)
    {
    SHFT(dum,ax,bx,dum)
    SHFT(dum,fb,fa,dum)
    }
  cx=bx+GOLD*(bx-ax); fc=f1dim(cx);
  while(fb>fc)
    {
    r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa);
    u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r));
    ulim=bx+GLIMIT*(cx-bx);
    if((bx-u)*(u-cx)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;}
      else if(fu>fb){cx=u; fc=fu; return;}
      u=cx+GOLD*(cx-bx); fu=f1dim(u);
      }
    else if((cx-u)*(u-ulim)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc)
        {
        SHFT(bx,cx,u,cx+GOLD*(cx-bx))
        SHFT(fb,fc,fu,f1dim(u))
        }
      }
    else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);}
      else {u=cx+GOLD*(cx-bx); fu=f1dim(u);}
    SHFT(ax,bx,cx,u)
    SHFT(fa,fb,fc,fu)
    }
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::brent(double ax,double bx,double cx,double &xmin)
  {
  int    iter;
  double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm;

  a=(ax<cx?ax:cx); b=(ax>cx?ax:cx);
  d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x);
  for(iter=1;iter<=ItMaxBrent;iter++)
    {
    xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19);
    if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);}
    if(fabs(e)>tol1)
      {
      r=(x-w)*(fx-fv); q=(x-v)*(fx-fw);
      p=(x-v)*q-(x-w)*r; q=2.0*(q-r);
      if(q>0.0)p=-p; q=fabs(q);
      etemp=e; e=d;
      if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x))
        d=CGOLD*(e=(x>=xm?a-x:b-x));
      else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);}
      }
    else d=CGOLD*(e=(x>=xm?a-x:b-x));
    u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d));
    fu=f1dim(u);
    if(fu<=fx)
      {
      if(u>=x)a=x; else b=x;
      SHFT(v,w,x,u)
      SHFT(fv,fw,fx,fu)
      }
    else
      {
      if(u<x)a=u; else b=u;
      if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;}
      else if(fu<=fv||v==x||v==w){v=u; fv=fu;}
      }
    }
  Print("Too many iterations in brent");
  MaxIterFlag=1; xmin=x;
  return(fx);
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::f1dim(double x)
  {
  int j;
  double f;
  
  for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j];
  f=func(Xt);
  return(f);
  }
//-----------------------------------------------------------------------------------
int PowellsMethod::Optimize(double &p[],int n=0)
  {
  int i,j,k,ret;
  
  k=ArraySize(p);
  if(n==0)N=k;
  else N=n;
  if(N<1||N>k)return(0);
  ArrayResize(P,N); ArrayResize(Xi,N*N);
  ArrayResize(Pcom,N); ArrayResize(Xicom,N);
  ArrayResize(Xt,N); ArrayResize(Pt,N);
  ArrayResize(Ptt,N); ArrayResize(Xit,N);
  for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0);
  for(i=0;i<N;i++)P[i]=p[i];
  MaxIterFlag=0;
  powell();
  for(i=0;i<N;i++)p[i]=P[i];
  if(MaxIterFlag==1)ret=-1;
  else ret=Iter;
  return(ret);
  }
//-----------------------------------------------------------------------------------

La méthode Optimize est la méthode principale de la classe.

Méthode Optimize

Paramètres d’entrée:

• double &p[] - tableau qui comporte en entrée les valeurs initiales des paramètres dont les valeurs optimales doivent être trouvées ; les valeurs optimales obtenues de ces paramètres sont en sortie du tableau.
• int n=0 - nombre d'arguments dans le tableau p[]. Où n=0, le nombre de paramètres est considéré égal à la taille du tableau p[].

Valeur renvoyée :

• Ca renvoie le nombre des itérations nécessaire dans le fonctionnement de l’algorithme, ou -1 si le nombre maximal admissible de celui-ci a été atteint.

Lors de la recherche de valeurs de paramètres optimales, une approximation itérative du minimum de la fonction objective se produit. La méthode Optimize renvoie le nombre d'itérations nécessaires pour atteindre le minimum de la fonction avec une certaine précision La fonction objective est appelée à plusieurs reprises à chaque itération, c'est-à-dire que le nombre d'appels de la fonction objective peut être considérablement(dix voire cent fois) supérieur au nombre d'itérations renvoyé par la méthode Optimize.

Autres méthodes de la classe.

Méthode SetItMaxPowell

Paramètres d’entrée

• Int n - nombre maximal autorisé d'itérations dans la méthode de Powell. La valeur par défaut est 200

Valeur renvoyée :

• Aucun

Il définit le nombre maximal d'itérations admissible ; une fois ce nombre atteint, la recherche sera terminée indépendamment du fait que le minimum de la fonction objective avec une précision donnée ait été trouvé. Et un message pertinent sera ajouté au journal.

Méthode SetFtolPowell

Paramètres d’entrée

• double er - précision. Si cette valeur d'écart par rapport à la valeur minimale de la fonction objective est atteinte, la méthode de Powell interrompt la recherche. La valeur par défaut est 1e-6

Valeur renvoyée :

• Aucun

Méthode SetItMaxBrent

Paramètres d’entrée

• Int n - nombre maximal autorisé d'itérations pour une méthode de Brent auxiliaire. La valeur par défaut est 200

Valeur renvoyée :

• Aucun

Il définit le nombre maximal d'itérations autorisé. Une fois atteint, la méthode de l'auxiliaire Brent interrompra la recherche et un message pertinent sera ajouté au journal.

Méthode SetFtolBrent

Paramètres d’entrée

• double er – précision. Cette valeur définit la précision dans la recherche du minimum pour la méthode de Brent auxiliaire. La valeur par défaut est 1e-4

Valeur renvoyée :

• Aucun

Méthode GetFret

Paramètres d’entrée

• Aucun

Valeur renvoyée :

• Il renvoie la valeur minimale de la fonction objective obtenue.

Méthode GetIter

Paramètres d’entrée

• Aucun

Valeur renvoyée :

• Il renvoie le nombre d'itérations nécessaires au fonctionnement de l'algorithme.

Fonction virtuelle func(const double &p[])

Paramètres d’entrée

• const double &p[] – adresse du tableau comportant les paramètres optimisés. La taille du tableau correspond au nombre de paramètres de fonction.

Valeur renvoyée :

• Il renvoie la valeur de la fonction correspondant aux paramètres qui lui sont transmis.

La fonction virtuelle func() doit dans chaque cas particulier être redéfinie dans une classe dérivée de la classe PowellsMethod. La fonction func() est la fonction objective dont on retrouvera les arguments correspondant à la valeur minimale renvoyée par la fonction lors de l'application de l'algorithme de recherche.

Cette implémentation de la méthode de Powell utilise la méthode d'interpolation parabolique à variable unique de Brent pour déterminer la direction de la recherche en ce qui concerne chaque paramètre. La précision et le nombre maximal autorisé d'itérations pour ces méthodes peuvent être définis séparément en appelant SetItMaxPowell, SetFtolPowell, SetItMaxBrent et SetFtolBrent.

Ainsi, les caractéristiques par défaut de l'algorithme peuvent être modifiées de cette manière. Cela peut sembler utile lorsque la précision par défaut définie pour une certaine fonction objective s'avère trop élevée et que l'algorithme nécessite trop d'itérations dans le processus de recherche. Le changement de la valeur de la précision requise permet d'optimiser la recherche au regard de différentes catégories de fonctions objectives.

Malgré l'apparente complexité de l'algorithme qui utilise la méthode de Powell, son utilisation est assez simple.

Passons en revue un exemple. Admettons que nous avons une fonction

et nous devons trouver les valeurs de paramètres et dont la fonction aura la valeur la plus petite.

Écrivons un script démontrant une solution à ce problème.

//-----------------------------------------------------------------------------------
//                                                                        PM_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
class PM_Test:public PowellsMethod
  {
public:
  void   PM_Test(void) {}
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
double PM_Test::func(const double &p[])
  {
  double f,r1,r2;
  
  r1=p[0]-0.5;
  r2=p[1]-6.0;
  f=r1*r1*4.0+r2*r2;
  return(f);
  }
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  int it;
  double p[2];

  p[0]=8; p[1]=9;                                 // Initial point
  PM_Test *pm = new PM_Test;
  it=pm.Optimize(p);
  Print("Iter= ",it,"        Fret= ",pm.GetFret());
  Print("p[0]= ",p[0],"    p[1]= ",p[1]);
  delete pm;
  }
//-----------------------------------------------------------------------------------

Lors de l'écriture de ce script, nous créons d'abord la fonction func() en tant que membre de la classe PM_Test qui calcule la valeur de la fonction de test donnée en utilisant les valeurs passées des paramètres p[0] et p[1]. Ensuite, dans le corps de la fonction OnStart(), les valeurs initiales sont affectées aux paramètres requis. La recherche commencera à partir de ces valeurs.

De plus, une copie de la classe PM_Test est créée et la recherche des valeurs requises de p[0] et p[1] commence par l'appel de la méthode Optimize ; les méthodes de la classe parente PowellsMethod appelleront la fonction func() redéfinie. Au terme de la recherche, le nombre d'itérations, la valeur de la fonction au point minimum et les valeurs de paramètre obtenues p[0]=0,5 et p[1]=6 seront ajoutés au journal.

PowellsMethod.mqh et un cas de test PM_Test.mq5 se trouvent à la fin de l'article dans l'archive Files.zip. Afin de compiler PM_Test.mq5, il doit se trouver dans le même répertoire que PowellsMethod.mqh.

9. Optimisation des Valeurs des Paramètres du Modèle

La section précédente de l'article traitait de l’implémentation de la méthode de recherche de la fonction minimum et donnait un exemple simple de son utilisation. Nous allons maintenant passer aux problèmes liés à l'optimisation des paramètres du modèle de lissage exponentiel.

Pour commencer, simplifions au maximum la classe AdditiveES introduite précédemment en écartant de celle-ci tous les éléments associés au composant saisonnier, car les modèles qui prennent en compte la saisonnalité ne seront de toute façon pas examinés davantage dans cet article. Cela permettra de rendre le code source de la classe beaucoup plus facile à comprendre et de réduire le nombre de calculs. De plus, nous écarterons également tous les calculs liés à la prévision et aux calculs des intervalles de confiance de prévision pour une démonstration facile d'une approche d'optimisation des paramètres du modèle de croissance linéaire avec amortissement à l’étude.

//-----------------------------------------------------------------------------------
//                                                                     OptimizeES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class OptimizeES
//-----------------------------------------------------------------------------------
class OptimizeES:public PowellsMethod
  {
protected:
  double Dat[];            // Input data
  int    Dlen;             // Data lenght
  double Par[5];           // Parameters
  int    NCalc;            // Number of last elements for calculation
public:
  void   OptimizeES(void) {}
  int    Calc(string fname);
private:
  int    readCSV(string fnam,double &dat[]);
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// Calc
//-----------------------------------------------------------------------------------
int OptimizeES::Calc(string fname)
  {
  int i,it;
  double relmae,naiv,s,t,alp,gam,phi,e,ae,pt;
  
  if(readCSV(fname,Dat)<0){Print("Error."); return(-1);}
  Dlen=ArraySize(Dat);
  NCalc=200;                               // number of last elements for calculation
  if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);}
  Par[0]=Dat[Dlen-NCalc];                  // initial S
  Par[1]=0;                                // initial T
  Par[2]=0.5;                              // initial Alpha
  Par[3]=0.5;                              // initial Gamma
  Par[4]=0.5;                              // initial Phi
  it=Optimize(Par);                        // Powell's optimization
  s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4];
  relmae=0; naiv=0;
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t);
    relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]);
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  relmae/=naiv;
  PrintFormat("%s:    N=%i,  RelMAE=%.3f",fname,NCalc,relmae);
  PrintFormat("Iter= %i,  Fmin= %e",it,GetFret());
  PrintFormat("p[0]= %.5f,  p[1]= %.5f,  p[2]= %.2f,  p[3]= %.2f,  p[4]= %.2f",
                                             Par[0],Par[1],Par[2],Par[3],Par[4]);
  return(0);
  }
//-----------------------------------------------------------------------------------
// readCSV
//-----------------------------------------------------------------------------------
int OptimizeES::readCSV(string fnam,double &dat[])
  {
  int n,asize,fhand;
    
  fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
  if(fhand==INVALID_HANDLE)
    {
    Print("FileOpen Error!");
    return(-1);
    }
  asize=512;
  ArrayResize(dat,asize);
  n=0;
  while(FileIsEnding(fhand)!=true)
    {
    dat[n++]=FileReadNumber(fhand);
    if(n+128>asize)
      {
      asize+=128;
      ArrayResize(dat,asize);
      }
    }
  FileClose(fhand);
  ArrayResize(dat,n-1);
  return(0);

  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double OptimizeES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}                 // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}                 // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}                 // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}                 // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }                 // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}                 // Phi     < 0.05
  sse=0; 
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(NCalc*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

La classe OptimizeES dérive de la classe PowellsMethod et inclut la redéfinition de la fonction virtuelle func(). Tel que précédemment mentionné, les paramètres dont la valeur calculée sera minimisée au cours de l'optimisation seront transmis en entrée de cette fonction.

Conformément à la méthode du maximum de vraisemblance, la fonction func() calcule le logarithme de la somme des carrés des erreurs de prévision à une longueur d’avance. Les erreurs sont calculées en boucle par rapport aux valeurs récentes NCalc de la série.

Pour préserver la stabilité du modèle, nous devrions imposer des limitations sur la gamme de changements de ses paramètres. Cette plage pour les paramètres Alpha et Gamma sera de 0,05 à 0,95, et pour le paramètre Phi - de 0,05 à 1,0. Mais pour l'optimisation dans notre cas, nous utilisons une méthode pour trouver un minimum sans contrainte qui n'implique pas l'utilisation de limitations sur les arguments de la fonction objective.

Nous essaierons de transformer le problème de trouver le minimum de la fonction multivariable avec des limitations en un problème de trouver un minimum sans contrainte, pour pouvoir prendre en considération toutes les limitations imposées aux paramètres sans changer l'algorithme de recherche. A cet effet, la méthode dite de la fonction de pénalité sera utilisée. Cette méthode peut être facilement démontrée pour un cas unidimensionnel.

Admettons que nous ayons une fonction d'un seul argument (dont le domaine est de 2.0 à 3.0) et un algorithme qui, dans le processus de recherche, peut attribuer n'importe quelle valeur à ce paramètre de fonction. Dans ce cas, nous pouvons procéder comme suit : si l'algorithme de recherche a transmis un argument qui dépasse la valeur maximale admissible, par exemple 3,5, la fonction peut être calculée pour l'argument égal à 3,0 et le résultat obtenu est encore multiplié par un coefficient proportionnel au-delà de la valeur maximale, par exemple k=1+(3,5-3)*200.

Si des opérations similaires sont effectuées à l’égard des valeurs d'argument qui s'avèrent être inférieures à la valeur minimale admissible, la fonction objective subséquente est assurée d'augmenter en dehors de la plage admissible de changements dans son argument. Une telle augmentation artificielle de la valeur subséquente de la fonction objective permet de garder l'algorithme de recherche inconscient du fait que l'argument transmis à la fonction était de quelque manière que ce soit limité et la garantie que le minimum de la fonction subséquente sera dans les limites définies de l’argument. Une telle approche s'applique facilement à une fonction de plusieurs variables.

La méthode principale de la classe OptimizeES est la méthode Calc. Un appel de cette méthode est chargé de lire les données d'un fichier, de rechercher des valeurs optimales des paramètres d'un modèle et d’estimer la précision des prévisions à l'aide de RelMAE pour les valeurs des paramètres obtenues. Le nombre de valeurs traitées de la série lue dans un fichier est dans ce cas défini dans la variable NCalc.

Vous trouverez ci-dessous l'exemple du script Optimization_Test.mq5 qui utilise la classe OptimizeES.

//-----------------------------------------------------------------------------------
//                                                              Optimization_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "OptimizeES.mqh"

OptimizeES es;
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  es.Calc("Dataset\\USDJPY_M1_1100.TXT");
  }
//-----------------------------------------------------------------------------------

Suite à l'exécution de ce script, le résultat obtenu sera comme indiqué ci-dessous.

 

Figure 6. Résultat du script Optimization_Test.mq5

Bien que nous puissions maintenant trouver les valeurs optimales des paramètres et les valeurs initiales du modèle, il existe encore un paramètre qui ne peut pas être optimisé à l'aide d'outils simples - le nombre de valeurs de série utilisées dans l'optimisation. En optimisation par rapport à une série de grande longueur, nous obtiendrons les valeurs optimales des paramètres qui, en moyenne, assurent une erreur minimale sur toute la longueur de la série.

Cependant si la nature de la intervalles variait dans cet intervalle, les valeurs obtenues pour certains de ses fragments ne seront plus optimales. D'autre part, si la longueur de la série est considérablement diminuée, il n'y a aucune garantie que les paramètres optimaux obtenus pour un intervalle aussi court soient optimaux sur un délai plus long.

OptimizeES.mqh et Optimization_Test.mq5 se trouvent à la fin de l'article dans l'archive Files.zip. Lors de la compilation, il est nécessaire que OptimizeES.mqh et PowellsMethod.mqh se trouvent dans le même répertoire que le Optimization_Test.mq5 compilé. Dans l'exemple donné, le fichier USDJPY_M1_1100.TXT est utilisé comprenant la série de test et qui doit être situé dans le répertoire \MQL5\Files\Dataset\.

Le tableau 2 montre les estimations de l'exactitude des prévisions obtenues à l'aide de RelMAE au moyen de ce script. La prévision a été menée sur huit séries de test précédemment mentionnées dans l'article en utilisant les 100, 200 et 400 dernières valeurs de chacune de ces séries.

N=100 N=200 N=400 EURRUR M1 0.980 1.000 0.968 EURRUR M30 0.959 0.992 0.981 EURUSD M1 0.995 0.981 0.981 EURUSD M30 1.023 0.985 0.999 USDJPY M1 1.004 0.976 0.989 USDJPY M30 0.993 0.987 0.988 XAUUSD M1 0.976 0.993 0.970 XAUUSD M30 0.973 0.985 0.999

Tableau 2. Erreurs de prévision estimées à l'aide de RelMAE

Comme nous pouvons le voir, les estimations d'erreur de prévision sont proches de l'unité mais dans la majorité des cas, la prévision pour les séries données dans ce modèle est plus précise que dans la méthode naïve.

10. L'indicateur IndicatorES.mq5

L'indicateur AdditiveES_Test.mq5 basé sur la classe AdditiveES.mqh a été mentionné précédemment lors de l'examen de la classe. Tous les paramètres de lissage de cet indicateur ont été manuellement définis.

Maintenant, après avoir examiné la méthode permettant d'optimiser les paramètres du modèle, nous pouvons créer un indicateur similaire où les valeurs optimales des paramètres et les valeurs initiales seront automatiquement déterminées et seule la longueur de l'échantillon traité devra être manuellement définie. Cela dit, nous écarterons tous les calculs liés à la saisonnalité.

Le code source de la classe CIndiсatorES utilisée pour créer l'indicateur est présenté ci-dessous.

//-----------------------------------------------------------------------------------
//                                                                   CIndicatorES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class CIndicatorES
//-----------------------------------------------------------------------------------
class CIndicatorES:public PowellsMethod
  {
protected:
  double Dat[];                                              // Input data
  int    Dlen;                                               // Data lenght
  double Par[5];                                             // Parameters
public:
  void   CIndicatorES(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)            { if(n>=0||n<5)return(Par[n]); else return(0); }
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// CalcPar
//-----------------------------------------------------------------------------------
void CIndicatorES::CalcPar(double &dat[])
  {

  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayCopy(Dat,dat);
 
  Par[0]=Dat[0];                                             // initial S
  Par[1]=0;                                                  // initial T
  Par[2]=0.5;                                                // initial Alpha
  Par[3]=0.5;                                                // initial Gamma
  Par[4]=0.5;                                                // initial Phi
  Optimize(Par);                                             // Powell's optimization
  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}           // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}           // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}           // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}           // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }           // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}           // Phi     < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

Cette classe comporte les méthodes CalcPar et GetPar ; le premier est conçu pour le calcul des valeurs optimales des paramètres du modèle, le second est destiné à accéder à ces valeurs. Par ailleurs, la classe CIndicatorES comprend la redéfinition de la fonction virtuelle func().

Le code source de l'indicateur IndicatorES.mq5 :

//-----------------------------------------------------------------------------------
//                                                                    IndicatorES.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"                 // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"                   // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"                   // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CIndicatorES.mqh"
#define   NFORE 12

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[];
int       NDat;

CIndicatorES   Es;
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NDat=nHist; if(NDat<24)NDat=24;
  MqlRates rates[];
  CopyRates(NULL,0,0,NDat,rates);                   // Load missing data
  ArrayResize(Data,NDat);
    
  SetIndexBuffer(0,Hist,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,Fore,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
  SetIndexBuffer(2,Conf1,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
  SetIndexBuffer(3,Conf2,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
  int i,start;
  double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci;
  
  if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
  start=rates_total-NDat;
//-----------------------
  PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);
  
  for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
  Es.CalcPar(Data);                                    // Optimization of parameters
  s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4);
  f=(s+phi*t); var=0;
  for(i=0;i<NDat;i++)                                // History
    {
    e=Data[i]-f; var+=e*e;
    a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
    f=(s+phi*t); Hist[start+i]=f;
    }
  var/=(NDat-1); a1=1; a2=0; a3=1;
  for(i=rates_total-NFORE;i<rates_total;i++)
    {
    a1=a1*phi; a2+=a1;
    Fore[i]=s+a2*t;                                 // Forecast
    ci=1.96*MathSqrt(var*a3);                        // Confidence intervals
    a=alp*(1+a2*gam); a3+=a*a;
    Conf1[i]=Fore[i]+ci;
    Conf2[i]=Fore[i]-ci;
    }
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

A chaque nouvelle barre, l'indicateur trouve les valeurs optimales des paramètres du modèle, effectue des calculs dans le modèle pour un nombre donné de barres NHist, créé une prévision et définit les limites de confiance des prévisions.

Le seul paramètre de l'indicateur est la longueur de la série traitée dont la valeur minimale est limitée à 24 barres. Tous les calculs de l'indicateur sont effectués sur la base des valeurs open[]. L'horizon de prévision est de 12 barres. Le code de l'indicateur IndicatorES.mq5 et le fichier CIndicatorES.mqh se trouvent à la fin de l'article dans l'archive Files.zip.

 

Figure 7. Résultat de l'opération de l'indicateur IndicatorES.mq5

Un exemple du résultat de l'opération de l'indicateur IndicatorES.mq5 est illustré en Figure 7. Au cours du fonctionnement de l'indicateur, l'intervalle de confiance de prévision à 95 % prendra des valeurs correspondant aux valeurs optimales des paramètres du modèle obtenues. Plus les valeurs des paramètres de lissage sont élevées, plus l'augmentation de l'intervalle de confiance est rapide au fur et à mesure que l'horizon de prévision augmente.

Avec une simple amélioration, l’Indicateur IndicatorES.mq5 peut être utilisé non seulement pour la prévision des cotations de devise mais aussi pour les valeurs de prévision de plusieurs indicateurs ou données prétraitées.

Conclusion

L'objectif principal de l'article était de familiariser le lecteur avec les modèles de lissage exponentiel additif utilisés en prévision. Tout en démontrant leur utilisation pratique, certaines questions connexes ont également été traitées. Cependant, la documentation fournie dans l'article peut être considérée comme une simple introduction à la vaste gamme de problèmes et de solutions associés à la prévision.

Je voudrais attirer votre attention au fait que les classes, fonctions, scripts et indicateurs fournis ont été créés lors de la rédaction de l'article et sont principalement conçus pour servir d'exemples aux documents de l'article. Par conséquent, aucun test sérieux de stabilité et d'erreurs n'a été effectué. Par ailleurs, les indicateurs énoncés dans l'article ne doivent être considérés que comme une démonstration de l’implémentation des méthodes impliquées.

La précision des prévisions de l'indicateur IndicatorES.mq5 introduit dans l'article peut très probablement être quelque peu améliorée en utilisant les modifications du modèle appliqué qui seraient plus adéquates en termes de spécificités des cotations à l’étude. L'indicateur peut également être amplifié par d'autres modèles. Mais ces questions dépassent le cadre de cet article.

En conclusion, il faut noter que les modèles de lissage exponentiel peuvent dans certains cas produire des prévisions de même précision que les prévisions obtenues en appliquant des modèles plus complexes prouvant ainsi une fois de plus que même le modèle le plus complexe n'est pas toujours le meilleur.

Les références

1. Everette S. Gardner Jr. Exponential Smoothing: État des lieux – Part II. 3 juin 2005
2. Rob J Hyndman. Prévisions axées sur des modèles d'espace d'état pour le lissage exponentiel. 29 août 2002.
3. Rob J Hyndman et al. Intervalles de prédiction pour le lissage exponentiel à l'aide de deux nouvelles classes de modèles d'espace d'état. 30 janvier 2003.
4. Rob J Hyndman and Muhammad Akram. Certains modèles de lissage exponentiel non linéaire sont instables. 17 Janvier 2006.
5. Rob J Hyndman and Anne B Koehler Un autre regard sur les mesures de la précision des prévisions. 2 Novembre 2005
6. Yu. P. Lukashin. Méthodes adaptatives pour la prévision à court terme des séries chronologiques : Cahier de texte. - M: Finansy i Statistika, 2003.-416 p.
7. D. Himmelblau. Programmation Non Linéaire Appliquée. M.: Mir, 1975.
8. Numerical Recipes in C. The Art of Scientific Computing. Deuxième édition. Edition universitaire de Cambridge.