利用指数平滑法进行时间序列预测
9 539
0
简介
目前较为知名的预测方法林林总总，这些方法仅基于时间序列过去值的分析，也就是说，其采用的原则通常用于技术分析。这些方法主要使用外推方案，其中在某特定时间延迟处识别的序列属性超出了其限制。
同时，它还假定未来的序列属性与过去和当前相同。一种更为复杂的外推方案在预测中不太常用，该方案涉及到对于序列特性中变化动态的研究，并适当注意到预测区间内的此类动态。
基于外推的最具知名度的预测方法，可能就是采用 自回归求和移动平均线模型 (ARIMA) 的方法。而上述方法之所以流行，主要是因为 Box 和 Jenkins 的作品中提出并开发了求和 ARIMA 集成模型。当然，除了 Box 与 Jenkins 引入的模型之外，还有其他模型和预测方法。
本文将简单介绍一下更简单的模型 - 由 Holt 和 Brown 早在 Box 与 Jenkins 作品问世之前就提出的 指数平滑模型。
尽管还有更加简单明晰的数学工具，但利用指数平滑模型预测产生的结果通常与使用 ARIMA 模型的结果差不多。这毫不奇怪，因为指数平滑模型就是 ARIMA 模型的一个特例。换句话说，本文研究的每种指数平滑模型都有一个对等的 ARIMA 模型。但本文不会研究这些等效模型，大家了解下就好。
我们都清楚，在每种特定情况下进行预测都需要一套独有的方法，而且通常都涉及到大量的流程。
例如：
- 缺失值与离群值时间序列分析。上述值的调整。
- 趋势及其类型的识别。序列周期性的确定。
- 序列稳定性的检查。
- 序列预处理分析（取对数、差分等）。
- 模型选择。
- 模型参数确定。基于选定模型的预测。
- 模型预测精确度评估。
- 选定模型误差分析。
- 确定选定模型是否合适，如有必要，更换模型并返回前项。
很明显，这还远非有效预测所需操作的完整列表。
要强调的是，模型参数确定和预测结果的获取，只是总体预测过程中的一小部分。但要在一篇文章里通过一种方式涵盖与预测相关的全部问题，似乎是不可能的。
因此，本文仅论述指数平滑模型，且使用未预处理过的货币报价作为测试序列。当然，随之而来的问题，本文中并不会一一作答，而只会涉及那些对于模型的研究有必要的问题。
1. 稳定性
外推法概念本身就恰当地暗示了所研究过程的未来发展与过去和现在别无二致。换句话说，它涉及到的是过程的稳定性。从预测的角度来看，平稳的过程极具吸引力，但遗憾的是它并不存在，因为任何实际过程在其发展的过程中都会面临变化。
在实际过程中，随着时间的推移，无论是预期、方差还是分布都会出现显著差异，但特性变化非常慢的过程可能归结于平稳的过程。这里所说的“非常慢”，是指过程特性在有限观测区间内的变化似乎无关紧要、可以忽略。
很明显，可用的观测区间越短（短样本），就越有可能对过程整体的稳定性做出错误决定。另一方面，如果我们更想了解过程以后的状态，同时计划做一个短期预测，则在某些情况下减少样本量可能会提高预测精确度。
如果过程有所变化，在观测区间内确定的序列参数就会有所不同，并超过其限制范围。因此，预测区间越长，序列特性变异对于预测误差的影响就越强。有鉴于此，我们必须将自己局限于单纯的短期预测；预测区间内如有大幅缩减，则能预计缓慢变化的序列特性，而不会导致相当大的预测误差。
此外，序列参数的变异还会导致按观测区间进行估测时获取的值采用平均值，因为此区间内的参数未能保持恒定。因此，获得的参数值不再与此区间的最后时刻相关，但却会由此反映出某个特定的平均值。遗憾的是，要完全消除这种恼人的现象是不可能的。但是，只要模型参数估计（研究区间）中涉及到的观测区间长度缩减到可能的程度，就能减少这种现象的发生。
同时，研究区间并不能无限制地缩短，因为极度缩减一定会降低序列参数估计的精确度。要在序列特性变异相关误差的影响与由于研究区间内极端缩减导致的误差增加之间寻求一种折中。
上述所有内容均完全适用于利用指数平滑模型所做的预测，因为它们像 ARIMA 模型一样，都是基于过程稳定性的假设。但是，为简单起见，下文中我们还是按照惯例，假设研究中的所有序列参数在观测区间内都会发生缓慢且可忽略的变化。
因此，本文要处理的是基于指数平滑模型、与带有缓慢变化特性的序列短期预测相关的问题。这里所说的“短期预测”是指提前一个、两个或更多时间区间进行的预测，而不是经济学中通常所理解的短于一年周期的预测。
2. 测试序列
到撰写本文时，此前保存的针对 M1、M5、M30 和 H1 的 EURRUR、EURUSD、USDJPY 和 XAUUSD 报价均已用到。每一份保存文件中都包含了 1100 个 "open" 值。最早的值位于文件开头，而最新值则位于文件末尾。文件中保存的最后一个值，对应的是文件创建的时间。包含测试序列的文件均利用 HistoryToCSV.mq5 脚本创建。而其借以创建的数据文件和脚本则位于本文末尾处的 Files.zip 存档中。
前面提到过，本文使用的已保存报价均未经过预处理，尽管这样存在明显问题，我仍想提醒您注意一下。比如说：一天当中的 EURRUR_H1 报价包含 12 到 13 个柱，而周五的 XAUUSD 报价包含的柱则比一周中的其他天少一个。上述示例表明，报价是利用不规则采样区间生成的；对于专为使用正确时间序列（意味着有个统一的量化区间）而设计的算法而言，这完全不能接受。
即便是利用外推法重现缺失的报价值，关于周末报价缺失的问题仍有讨论余地。我们通过推测得知，周末在全球范围发生的事件与工作日发生的事件对于世界经济的影响别无两样。革命、自然灾害、引人注目的丑闻、政府更迭等等，为数众多的此类大小事件随时都可能发生。如果这种事件发生在周六，其对世界市场的影响，几乎不亚于某个工作日发生的事件的影响。
很可能正是这些事件导致了一周工作结束后报价缺口的频现。很显然，就算外汇市场不运营，这个世界还是会按其自有的规则持续运转。对于是否应重现周末对应报价中的值（旨在对其进行技术分析），以及这样做有何益处，目前尚不明确。
这些问题明显超出了本文范畴，但初步来看，似乎没有任何制品的序列更适于分析，至少在判断周期（季节性）分量方面是这样。
用于未来分析的数据的初步准备，其重要性如何高估都不过分；就本例而言，它与报价一样都是一个重大的独立问题。而其于终端中的显示方式，一般来说不太适于技术分析。除了上述缺口相关问题之外，还存在许多其他问题。
比如说，生成报价时，某个固定时间点会被赋予不属于其的 "open" 和 "close" 值；这些值对应订单号的生成时间，而不是选定时间框架图表的某个固定时刻，然而众所周知，订单号有时非常罕见。
完全无视采样定理再举一例，因为就算是在一个分钟区间内，也没人可以担保采样率满足上述定理（更不必说其他更大的区间了）。而且，大家要记住，变量点差在某些情况下可能与报价值重叠出现。
好了，我们还是不管本文范畴之外的这些问题了，还是回到我们的主题上吧。
3. 指数平滑
我们先来看看最简单的模型
,
其中：
- X(t) – （模拟的）研究过程；
- L(t) – 变量过程级别；
- r(t)– 零均值随机变量。
可以看出，此模型由两个分量的和构成；我们特别感兴趣的是过程级别 L(t)，所以试着把它挑出来。
众所周知，随机序列求平均数可能会导致方差减少，即缩小其与平均值的偏差范围。因此我们可以假设，如果简单模型所描述的过程接受平均化（平滑），我们可能不具备完全摆脱随机分量 r(t) 的能力，但至少可以实现相当程度的弱化，并由此挑出目标级别 L(t)。
为此，我们会采用一种简单的指数平滑法 (SES)。
在这个著名的公式中，平滑程度通过 alpha 系数（从 0 到 1）的设置进行定义。如将 alpha 设置为零，则输入序列 X 的新进值不会对平滑结果造成任何影响。任何时间点的平滑结果都会是一个恒定值。
因此，在这种极端情况中，不受欢迎的随机分量会被完全抑制，而所研究的过程等级也会被平滑为一条水平直线。如将 alpha 系数设置为一，则输入序列根本不会受到平滑的影响。在这种情况下，研究中的级别 L(t) 不会失真，随机分量也不会受到抑制。
显而易见，如果选择 alpha 值，则同时还要满足相互冲突方面的要求。一方面，alpha 值要接近零，才能有效抑制随机分量 r(t)。而另一方面，alpha 值的设置最好还要接近一，才能让我们感兴趣的 L(t) 分量不失真。要获得最优 alpha 值，我们需要找到一个标准，并依据它对该值进行优化。
确定该标准时请记住，本文要论述的是预测，而不仅仅是序列的平滑。
就该简单指数平滑模型而言，在这种情况下，通常都是将在某指定时间获取的值 
视为在采取任意步骤之前的预测。
其中 
是时间 t 处提前 m 步的预测。
因此，对于时间 t 处序列值的预测，就会成为在上一步完成时进行的提前一步预测
在这种情况下，可以将某个提前一步预测的误差用作 alpha 系数值优化的标准
因此，通过在整个样本范围内实现这些误差平方和的最小化，我们就可以确定某指定序列 alpha 系数的最优值。当然，alpha 最优值也就是误差平方和最小的那一个。
图 1 显示了提前一步预测误差平方和与测试序列 USDJPY M1 某片断 alpha 系数值的对比图。
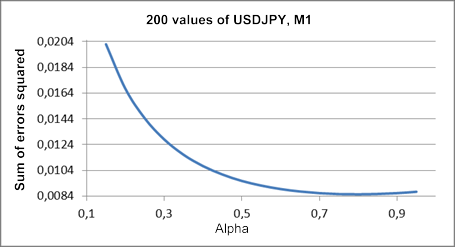
图 1. 简单指数平滑法
效果图上的最小值几乎无法辨别，近似大概 0.8 的 alpha 值。但简单指数平滑法并不总是该图所示的这种情况。当我们尝试获取本文中使用的测试序列片断 alpha 最优值时，通常都会见到一张 alpha 值持续下跌到一的图。
平滑系数值如此之高，表明该简单模型并不足以完全描述我们的测试序列（报价）。其中原因是过程级别 L(t) 变化过快，或是过程中出现了一个趋势。
我们再加入一个分量，让这个模型复杂一点
,
其中：
- X(t) – （模拟的）研究过程；
- L(t) - 变量过程级别；
- T(t) - 线性趋势；
- r(t)- 零均值随机变量。
大家都知道，线性回归系数可通过序列的双平滑来确定：
至于以这种方式获取的系数 a1 和 a2，时间 t 处的提前 m 步预测将等于
要注意的是，上述公式也采用了相同的 alpha 系数执行第一次平滑和重复平滑。此模型被称为线性增长附加的单一参数模型。
我们来说明下该简单模型与线性增长模型之间的区别。
假定所研究过程在很长一段时间内都显示为一个恒定分量，即在图表上显示为一条水平直线，但在某处开始呈现出线性趋势。对于利用上述模型生成的该过程的预测，请参见图 2。
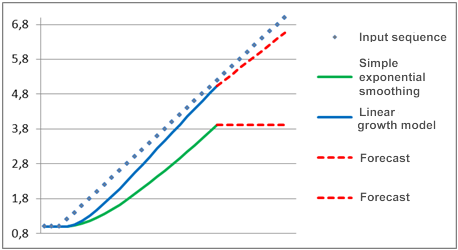
图 2. 模型对比
可以看出，简单指数平滑模型明显落后于线性变化输入序列，而且，利用该模型所做的预测还在进一步拉大差距。如果使用线性增长模型，我们就会看到一个非常不同的图案。趋势出现后，该模型就像是要努力赶上线性变化序列似的，且其预测结果与变化输入值的方向也更为贴近。
如果指定示例中的平滑系数较高，则线性增长模型就能够在指定时间内“触碰到”该输入信号，且其预测结果也将与输入序列几乎一致。
尽管处于稳定状态下的线性增长模型在面对线性趋势时显示了良好效果，但也容易看出，它是花了一段时间才“赶上”这个趋势的。因此，如果趋势频繁变化，该模型与输入序列之间就会存在一段差距。此外，如果趋势未呈线性增长、而是呈平方律增长，则线性增长模型就无法“赶上”该趋势了。尽管有这些缺点，但在面对线性趋势的时候，该模型还是要优于简单指数平滑模型。
前面提到过，我们使用了一种线性增长的单一参数模型。为了找到测试序列 USDJPY M1 某片断 alpha 参数的最优值，让我们来绘制一个提前一步预测误差的平方和与 alpha 系数值的对比图。
此图以图 1 中相同的序列片断为基础，如图 3 所示。
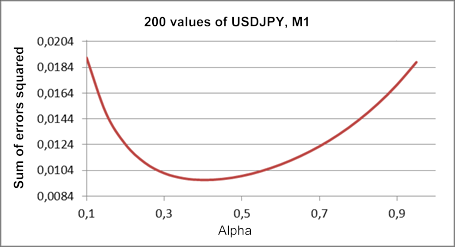
图 3. 线性增长模型
对比图 1 中的结果，可发现本例中 alpha 系数的最优值已减至 0.4 左右。该模型中第一次与第二次平滑的系数相同，尽管理论上来讲，两者的值可以不同。至于包含两个不同平滑系数的线性增长模型，我们稍后再深入探讨。
我们谈到的两种指数平滑模型在 MetaTrader 5 中都有着以指数形式存在的类似物。这就是众所周知的 EMA 和 DEMA - 原本设计用于序列值的平滑而非预测之用。
要注意的是，使用 DEMA 指标时，所显示的是 a1 系数对应的一个值，而非提前一步预测值。在这种情况下，不会计算或使用 a2 系数（参见上述线性增长模型公式）。此外，平滑系统则会以对应周期 n 的形式来计算
例如，等于 0.8 的 alpha 将对应约等于 2 的 n；如果 alpha 为 0.4，则 n 等于 4。
4. 初始值
前面提到过，平滑系数值要在应用指数平滑法后以某种方式获取。但这样看似还不够。由于指数平滑法中的当前值是根据前一个值计算的，所以会存在该值在时间零点尚不存在的情况。换句话说，对于线性增长模型中 S 或 S1 与 S2 的初始值，要通过某种方式在时间零点处计算得出。
要解决获取初始值的问题并不总是轻而易举。如果（就像在 MetaTrader 5 中使用报价的情况下）我们有一段很长时间的可用历史数据，且初始值未准确确定，则指数平滑曲线就有时间在到达某个当前点之前保持稳定，同时也已纠正了我们的初始误差。大约需要 10 到 200 个（有时更多）周期，具体取决于平滑系数值。
在这种情况下，粗略估算一下初始值，再在目标时间周期之前启动指数平滑过程的 200-300 个周期就足够了。不过，比如说可用样本包含 100 个值，其难度就好增大。
有关初始值选择的文献中，有着各种各样的建议。比如说，简单指数平滑法中的初始值可以等同于序列中的第一个元素，或是被计算为序列中以平滑随机离群值为目的的三四个初始元素的平均值。线性增长模型中的初始值 S1 与 S2 可基于以下假设，即预测曲线的初始级别应相当于序列中第一个元素、且线性趋势的斜率应为零。
虽然还可以在与初始值选择相关的不同来源中发现更多建议，但没有人可以确保在平滑算法的早期阶段中没有显著误差。在为了达到稳定状态而需要大量周期、并使用低值平滑系数时，这一点尤其明显。
因此，为了将初始值选择相关问题的影响降至最低（尤其是针对短序列），我们有时会采用一种方法，其中涉及到搜索导致预测误差最少的此类值。这就是一个针对初始值（整个序列内以小幅增量变化）计算预测误差的问题。
在所有初始值可能组合的范围内计算误差之后，即可选择最适合的变量。但这种方法非常费力，需要进行大量计算，所以几乎从未被直接使用。
所述问题与某个多变量函数最小值的优化或搜索有关。此类问题可利用各种专为大幅缩小所需计算范围而开发的算法来解决。我们会在稍后的预测中重新探讨平滑参数和初始值的优化问题。
5. 预测精确度评估
预测流程与模型初始值或参数的选择，引发了预测精确度评估这一问题。在比较两种不同模型或确定所获预测的一致性时，精确度评估也很重要。虽然针对预测精确度评估的知名估算法非常多，但其中任何一种算法都要求在每一步了解预测误差的情况。
前面已经提到，时间 t 处的提前一步预测误差等于
其中：
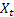– 时间 t 处的输入序列值；
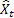– 在前一步所做的时间 t 处的预测。
最常见的预测精确度评估法很可能就是利用均方误差 (MSE) 来评估：
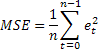
其中 n 为序列中的元素数。
有时也有人指出，对于较大值偶尔出现的单个误差的极端敏感也是 MSE 的一项劣势。其原因是在计算 MSE 时对其误差值求平方。作为替代方案，在这种情况下使用平均绝对误差 (MAE) 也不错。
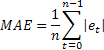
这里的均方误差由误差的绝对值所取代。人们认为利用 MAE 得到的估算更为稳定。
比如，两种估算方法都非常适合采用不同模型参数或模型进行的相同序列预测精确度的评估，但它们对于从不同序列中接收到的预测结果的对比似乎没什么用处。
此外，这些估算值并不能明确表明预测结果的质量。比如说，我们不能说所获得的 0,03 或任何其他值的 MAE 是好是坏。
要想对比不同序列的预测精确度，我们可以使用相对评估法 RelMSE 和 RelMAE：
这里将获取的预测精确度估算值除以通过预测测试方法计算出的各个估算值。作为一种测试方法，它适合使用所谓的朴素法，即暗示过程的未来值将与当前值相等。
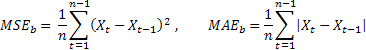
如果预测误差的平均值与利用朴素法获得的误差值相等，则相对估算值将等于一。如果相对估算值小于一，则意味着平均来讲，该预测误差值小于朴素法中的相应值。换句话说，预测结果的精确度要高于使用朴素法时的精确度。反之，如果相对估算值大于一，则预测结果的精确度一般要低于预测时使用的朴素法。
这些评估还适用于提前两步或更多步的预测精确度估测。计算中的提前一步预测误差需要替换成相应提前步骤的数量的预测误差值。
比如说，下表中就包含利用线性增长单一参数模型中 RelMAE 估算出的提前一步预测误差，而这些错误都是利用每个测试序列的最后 200 个值计算出来的。
|
表 1. 利用 RelMAE 估算的提前一步预测误差
RelMAE 评估允许在预测不同序列时对比某一选定方法的效率。表 1 中的结果表明，我们预测的精确度从未超过朴素法 - 所有的 RelMAE 值都大于一。
6. 加法模型
前文中我们介绍过一个由过程级别、线性趋势和一个随机变量的总和所构成的模型。我们会在上述分量（包括一个周期、季节分量）之外添加另一模型，从而扩展本文要讲述的模型列表。
指数平滑模型由所有分量构成，其总和被称为加法模型。除上述模型外，还存在由一个、多个或所有分量作为乘数的乘法模型。我们继续来研究加法模型这一组别。
前文中，我们反复提到了提前一步预测误差。在基于指数平滑法的相关预测应用中，几乎每种应用都必须计算出该误差。知道预测误差值后，上面介绍的指数平滑模型则可表现为稍有不同的方式（纠错方式）。
本例中要采用的模型表示方式的表达式（已部分或全部添加到之前获取值）中包含一个误差。这种表示方式被称为加法误差模型。指数平滑模型也可以一种乘法误差方式表示，但本文中不会使用。
我们来看看加法指数平滑模型。
简单指数平滑法：
等效模型 – ARIMA(0,1,1)：
线性增长加法模型：
与前文介绍的单一参数线性增长模型形成对照的是，这里采用了两种不同的平滑参数。
等效模型 – ARIMA(0,2,2)： 
呈线性衰减的增长模型：
这里所说的衰减，指的是趋势斜率会根据衰减系数的值，在每个后续预测步骤处有所减弱。其效应见图 4 所示。
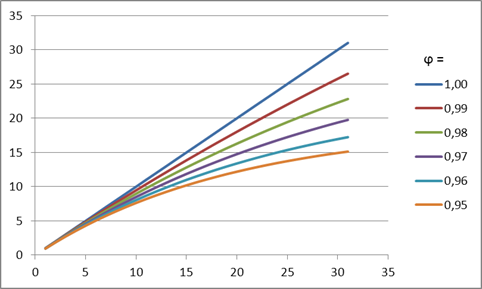
图 4. 衰减系数效应
从图中可以看出，进行预测时，衰减系数值的递减会造成趋势快速失去效力，线性增长也因此越来越衰减。
等效模型 – ARIMA(1,1,2)： 
将季节分量作为总和添加到上述所有三个模型中后，就会再得到三个模型。
简单的加法季节模型：
呈线性增长的加法季节模型：
呈线性衰减的增长模型和呈线性增长的加法季节模型：
虽然也有等同于季节模型的 ARIMA 模型，但在此处不予讨论，因为此类模型几乎没有任何实用价值。
公式中使用的标记如下：
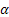– 序列级别的平滑参数，[0:1]；
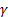– 趋势的平滑参数，[0:1]；
– 季节指数的平滑参数，[0:1]；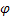
– 衰减参数，[0:1]；
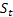– 观测到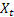 
后，于时间 t 处计算得出的平滑序列级别；
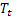– 于时间 t 处计算得出的平滑加法趋势；
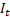– 于时间 t 处计算得出的平滑季节指数；
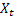– 时间 t 处的序列值；- m – 所做预测的提前步数；
- p – 季节循环中的周期数；
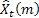– 于时间 t 处所做的提前 m 步预测；
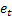– 于时间 t 处所做的提前一步预测误差，
。
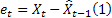显而易见，最后一个模型的公式中包含了研究中的所有六个变量。
如果是在呈线性衰减的增长模型和呈线性增长的加法季节模型的公式中，我们取以下值：
,
预测期间将忽略季节性。而且，如果 
，则会生成一个线性增长模型；而如果 
，我们就会得到一个呈线性衰减的增长模型。
简单指数平滑模型的对应情况是：
。
如果采用季节模型，则要首先利用任何一种可行方法来确定是否存在循环以及循环周期是多少，从而进一步使用该数据实现季节指数值的初始化。
在本例（通过短时间区间进行预测）中使用的测试序列片断中，我们未能发现相当稳定的循环。因此，本文中不会给出相关示例，也不会详细阐述与季节性关联的特性。
为了确定与研究中模型相关的概率预测区间，我们会用到文献 [3] 中的派生分析法。通过大小为 n 的整个样本计算得出的提前一步预测误差的平方和的平均值，将被用作此类误差的估计方差。
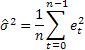
之后，下述表达式即适用于针对研究中模型、提前 2 步及更多步预测中估计方差的确定：
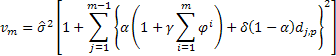
其中，如果 j 模数 p 为零，则 
等于一，否则 
为零。
计算出每步 m 的估计方差后，我们就能找到 95% 预测区间的限制值：
我们会同意将该预测区间指定为预测置信区间。
我们来实施在 MQL5 中编写的某个类中为指数平滑模型提供的表达式。
7. AdditiveES 类的实现
该类的实现涉及到使用呈线性衰减的增长模型和呈线性增长的加法季节模型的表达式。
前面提到过，其他模型均可通过选择相应的参数派生而来。
//----------------------------------------------------------------------------------- // AdditiveES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Forecasting. Exponential smoothing. Additive models. // References: // 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II. // June 3, 2005. // 2. Rob J Hyndman. Forecasting based on state space models for exponential // smoothing. 29 August 2002. // 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing // using two new classes of state space models. 30 January 2003. //----------------------------------------------------------------------------------- class AdditiveES:public CObject { protected: double Alpha; // Smoothed parameter for the level of the series double Gamma; // Smoothed parameter for the trend double Phi; // Autoregressive or damping parameter double Delta; // Smoothed parameter for seasonal indices int nSes; // Number of periods in the seasonal cycle double S; // Smoothed level of the series, computed after last Y is observed double T; // Smoothed additive trend double Ises[]; // Smoothed seasonal indices int p_Ises; // Pointer for Ises[] shift register double F; // Forecast for 1 period ahead from origin t public: AdditiveES(); double Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1); double GetS() { return(S); } double GetT() { return(T); } double GetF() { return(F); } double GetIs(int m); void IniIs(int m,double is); // Initialization of smoothed seasonal indices double NewY(double y); // Next calculating step double Fcast(int m); // m-step ahead forecast double VarCoefficient(int m); // Coefficient for calculating prediction intervals }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void AdditiveES::AdditiveES() { Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; S=0; T=0; } //----------------------------------------------------------------------------------- // Initialization //----------------------------------------------------------------------------------- double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1) { S=s; T=t; Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1; Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1; Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1; Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1; nSes=nses; if(nSes<1)nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; F=S+Phi*T; return(F); } //----------------------------------------------------------------------------------- // Calculations for the new Y //----------------------------------------------------------------------------------- double AdditiveES::NewY(double y) { double e; e=y-F; S=S+Phi*T+Alpha*e; T=Phi*T+Alpha*Gamma*e; Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e; p_Ises++; if(p_Ises>=nSes)p_Ises=0; F=S+Phi*T+GetIs(0); return(F); } //----------------------------------------------------------------------------------- // Return smoothed seasonal index //----------------------------------------------------------------------------------- double AdditiveES::GetIs(int m) { if(m<0)m=0; int i=(int)MathMod(m+p_Ises,nSes); return(Ises[i]); } //----------------------------------------------------------------------------------- // Initialization of smoothed seasonal indices //----------------------------------------------------------------------------------- void AdditiveES::IniIs(int m,double is) { if(m<0)m=0; if(m<nSes) { int i=(int)MathMod(m+p_Ises,nSes); Ises[i]=is; } } //----------------------------------------------------------------------------------- // m-step-ahead forecast //----------------------------------------------------------------------------------- double AdditiveES::Fcast(int m) { int i,h; double v,v1; if(m<1)h=1; else h=m; v1=1; v=0; for(i=0;i<h;i++){v1=v1*Phi; v+=v1;} return(S+v*T+GetIs(h)); } //----------------------------------------------------------------------------------- // Coefficient for calculating prediction intervals //----------------------------------------------------------------------------------- double AdditiveES::VarCoefficient(int m) { int i,h; double v,v1,a,sum,k; if(m<1)h=1; else h=m; if(h==1)return(1); v=0; v1=1; sum=0; for(i=1;i<h;i++) { v1=v1*Phi; v+=v1; if((int)MathMod(i,nSes)==0)k=1; else k=0; a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha); sum+=a*a; } return(1+sum); } //-----------------------------------------------------------------------------------
我们简要地说下 AdditiveES 类的方法。
Init 方法
输入参数：
- double s - 设置平滑级别的初始值；
- double t - 设置平滑趋势的初始值；
- double alpha=1 - 设置序列级别的平滑参数；
- double gamma=0 - 设置趋势的平滑参数；
- double phi=1 - 设置衰减参数；
- double delta=0 - 设置季节指数的平滑参数；
- int nses=1 - 设置季节循环中的周期数。
返回值：
- 它会返回一个根据设定初始值计算得出的提前一步预测值。
首先要调用 Init 方法。此为设置平滑参数和初始值所必需的方法。要注意的是，Init 方法并不能实现任意值季节指数的初始化；如调用此方法，季节指数应始终设置为零。
IniIs 方法
输入参数：
- Int m - 季节指数；
- double is - 设置季节指数 m 的值。
返回值：
- 无
如果季节指数需要非零，则调用 IniIs(...) 方法。调用 Init(...) 方法后应实现季节指数的初始化。
NewY 方法
输入参数：
- double y – 输入序列的新值
返回值：
- 它会返回一个根据序列新值计算得出的提前一步预测值
此方法适用于在每次录入输入序列新值时计算出一个提前一步预测值。只有在通过 Init 完成类的初始化（必要时采用 IniIs 方法）后才可调用此方法。
Fcast 方法
输入参数：
- int m – 预测 1,2,3,… 周期的范围；
返回值：
- 它会返回提前 m 步的预测值。
该方法会在不影响平滑过程状态的情况下只计算出预测值。通常在调用 NewY 方法后再调用该方法。
VarCoefficient 方法
输入参数：
- int m – 预测 1,2,3,… 周期的范围；
返回值：
- 它会返回计算预测方差的系数值。
该系数值会显示提前 m 步预测的方差相较于提前一步预测方差的增加情况。
GetS、GetT、GetF 和 GetIs 方法
这些方法可实现对某个类中受保护变量的访问。GetS、GetT 和 GetF 分别会返回平滑级别、平滑趋势和提前一步预测值。GetIs 方法可实现对于季节指数的访问，且要求将指数 m 表示为一个输入自变量。
在我们讲过的所有模型中，最复杂的莫过于呈线性衰减的增长模型和呈线性增长的加法季节模型，而 AdditiveES 类就是以其为基础创建的。这样就会提出一个非常合理的问题 - 还需要其他较简单的模型做些什么？
尽管更为复杂的模型似乎应具备明显超越简单模型的优势，但实际上并非总是如此。参数较少的简单模型在绝大多数情况下都会导致预测误差的方差减小，也就是说它们的运行更加平稳。在基于所有可用模型（从最简单到最复杂）的同时并行操作生成预测算法的过程中，也用到了这一事实。
一旦序列处理完毕，就会选定一个指出最低误差、并给出其参数数量（用于说明其复杂性）的预测模型。已为此开发出大量标准，比如 阿凯克信息论准则 (AIC)。它会导致选择一种有望生成最稳定预测的模型。
为说明 AdditiveES 类的使用，我们创建了一个简单指标，其中所有平滑参数均为手动设置。
以下列出了 AdditiveES_Test.mq5 指标的源代码。
//----------------------------------------------------------------------------------- // AdditiveES_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "PInterval+" // Prediction interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCadetBlue #property indicator_style3 STYLE_SOLID #property indicator_width3 1 #property indicator_label4 "PInterval-" // Prediction interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCadetBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 1 double HIST[]; double FORE[]; double PINT1[]; double PINT2[]; input double Alpha=0.2; // Smoothed parameter for the level input double Gamma=0.2; // Smoothed parameter for the trend input double Phi=0.8; // Damping parameter input double Delta=0; // Smoothed parameter for seasonal indices input int nSes=1; // Number of periods in the seasonal cycle input int nHist=250; // History bars, nHist>=100 input int nTest=150; // Test interval, 50<=nTest<nHist input int nFore=12; // Forecasting horizon, nFore>=2 #include "AdditiveES.mqh" AdditiveES fc; int NHist; // history bars int NFore; // forecasting horizon int NTest; // test interval double ALPH; // alpha double GAMM; // gamma double PHI; // phi double DELT; // delta int nSES; // Number of periods in the seasonal cycle //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NHist=nHist; if(NHist<100)NHist=100; NFore=nFore; if(NFore<2)NFore=2; NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50; ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1; GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1; PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1; DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1; nSES=nSes; if(nSES<1)nSES=1; MqlRates rates[]; CopyRates(NULL,0,0,NHist,rates); // Load missing data SetIndexBuffer(0,HIST,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,FORE,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFore); SetIndexBuffer(2,PINT1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"Conf+"); PlotIndexSetInteger(2,PLOT_SHIFT,NFore); SetIndexBuffer(3,PINT2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"Conf-"); PlotIndexSetInteger(3,PLOT_SHIFT,NFore); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,init,start; double v1,v2; if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1) {init=1; start=rates_total-NHist;} else {init=0; start=prev_calculated;} if(start==rates_total)return(rates_total); // New tick but not new bar //----------------------- if(init==1) // Initialization { i=start; v2=(open[i+2]-open[i])/2; v1=(open[i]+open[i+1]+open[i+2])/3.0-v2; fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES); ArrayInitialize(HIST,EMPTY_VALUE); } PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore); for(i=start;i<rates_total;i++) // History { HIST[i]=fc.NewY(open[i]); } v1=0; for(i=0;i<NTest;i++) // Variance { j=rates_total-NTest+i; v2=close[j]-HIST[j-1]; v1+=v2*v2; } v1/=NTest; // v1=var j=1; for(i=rates_total-NFore;i<rates_total;i++) { v2=1.96*MathSqrt(v1*fc.VarCoefficient(j)); // Prediction intervals FORE[i]=fc.Fcast(j++); // Forecasting PINT1[i]=FORE[i]+v2; PINT2[i]=FORE[i]-v2; } return(rates_total); } //-----------------------------------------------------------------------------------
调用指标或重复对其初始化会设置指数平滑法中的初始值
该指标中没有季节指数初始设置，因此其初始值始终为零。经过此类初始化后，随着新值的输入，季节性对于预测结果的影响会从零逐渐增加到某个特定的稳定值。
达到某平稳运行状态所需的周期数取决于季节指数的平滑系数值。平滑系数值越小，所需的时间就越长。
采用默认设置的 AdditiveES_Test.mq5 指标的运行结果如图 5 所示。
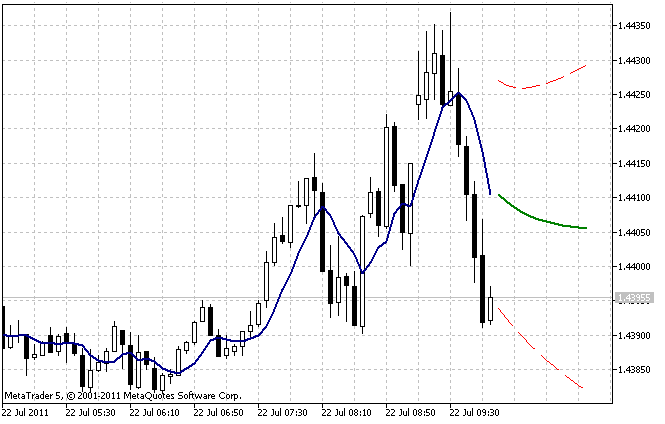
图 5. AdditiveES_Test.mq5 指标
除预测值外，该指标还会显示另一条线，其对应所在序列过去值的提前一步预测值以及 95% 预测置信区间的限制值。
置信区间基于提前一步误差的估计方差。为降低选定初始值不精确造成的影响，不会计算整个长度 nHist 的估计方差，而只会针对最近几根柱计算得出，此处在输入参数 nTest 中指定了柱的数量。
本文末尾处的 Files.zip 存档包含了 AdditiveES.mqh 和 AdditiveES_Test.mq5 文件。编辑该指标时，AdditiveES.mqh 文件必须与 AdditiveES_Test.mq5 处于同一目录下。
虽然选择初始值的问题在创建 AdditiveES_Test.mq5 指标时已在某种程度上得到了解决，但选择平滑参数最优值的问题却仍无定论。
8. 选择最优参数值
该简单指数平滑模型具有一个单独的平滑参数，其最优值可通过使用简单枚举法找到。在整个序列完成预测误差值的计算后，该参数值会基于较小的增量进行变化，并再次执行完整计算。此过程会一直重复，直到枚举出所有可能的参数值为止。现在我们只需选择生成最小误差值的参数值即可。
要在 0.1 到 0.9 的范围内基于 0.05 的增量找到平滑系数的最优值，就需要对预测误差值执行 17 次完整计算。看得出来，所需的计算次数并不算太多。但是，呈线性衰减的增长模型中包含三种平滑参数的优化，而且在这种情况下，它会执行 4913 次计算来完成同样范围内按 0.05 增量其所有组合的枚举。
所有可能参数值枚举所需的完整运行数量都会随着参数数量的增长、增量的减小和枚举范围的扩大而快速增加。如果更进一步，即在平滑参数之外还要优化模型的初始值，那么利用简单枚举法就很难完成了。
针对查找各变量中某函数最小值相关问题的研究已经非常充分，所以此类算法也非常多。而用于查找函数最小值的各种方法的描述和对比，也见诸于相关文献 [7] 中。所有这些方法都主要用于减少目标函数的调用次数，即减少查找最小值过程中的计算工作量。
不同来源通常都引用所谓的 拟牛顿法。这样做可能是为了提高效率，但使用一种更简单的方法也足以证明其有利于预测优化。我们选择 鲍威尔法吧。鲍威尔法是一种搜索方法，无需计算目标函数的导数。
与其他所有方法相类似，该方法也可采用多种编程方法予以实现。获取目标函数值或自变量值的特定精确度后，该搜索即告完成。此外，在特定实施过程中可能会用到函数参数变化允许范围的相关限制。
本例中，在 PowellsMethod.class 中实施了利用鲍威尔法查找无约束最小值这一算法。只要获得某个目标函数值的指定精确度，此算法即停止搜索。该方法的实施过程以文献 [8] 中的算法为原型。
以下是 PowellsMethod 类的源代码。
//----------------------------------------------------------------------------------- // PowellsMethod.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #define GOLD 1.618034 #define CGOLD 0.3819660 #define GLIMIT 100.0 #define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d); #define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a)) #define FMAX(a,b) (a>b?a:b) //----------------------------------------------------------------------------------- // Minimization of Functions. // Unconstrained Powell’s Method. // References: // 1. Numerical Recipes in C. The Art of Scientific Computing. //----------------------------------------------------------------------------------- class PowellsMethod:public CObject { protected: double P[],Xi[]; double Pcom[],Xicom[],Xt[]; double Pt[],Ptt[],Xit[]; int N; double Fret; int Iter; int ItMaxPowell; double FtolPowell; int ItMaxBrent; double FtolBrent; int MaxIterFlag; public: void PowellsMethod(void); void SetItMaxPowell(int n) { ItMaxPowell=n; } void SetFtolPowell(double er) { FtolPowell=er; } void SetItMaxBrent(int n) { ItMaxBrent=n; } void SetFtolBrent(double er) { FtolBrent=er; } int Optimize(double &p[],int n=0); double GetFret(void) { return(Fret); } int GetIter(void) { return(Iter); } private: void powell(void); void linmin(void); void mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc); double brent(double ax,double bx,double cx,double &xmin); double f1dim(double x); virtual double func(const double &p[]) { return(0); } }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void PowellsMethod::PowellsMethod(void) { ItMaxPowell= 200; FtolPowell = 1e-6; ItMaxBrent = 200; FtolBrent = 1e-4; } //----------------------------------------------------------------------------------- void PowellsMethod::powell(void) { int i,j,m,n,ibig; double del,fp,fptt,t; n=N; Fret=func(P); for(j=0;j<n;j++)Pt[j]=P[j]; for(Iter=1;;Iter++) { fp=Fret; ibig=0; del=0.0; for(i=0;i<n;i++) { for(j=0;j<n;j++)Xit[j]=Xi[j+n*i]; fptt=Fret; linmin(); if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;} } if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return; if(Iter>=ItMaxPowell) { Print("powell exceeding maximum iterations!"); MaxIterFlag=1; return; } for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];} fptt=func(Ptt); if(fptt<fp) { t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt); if(t<0.0) { linmin(); for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];} } } } } //----------------------------------------------------------------------------------- void PowellsMethod::linmin(void) { int j,n; double xx,xmin,fx,fb,fa,bx,ax; n=N; for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];} ax=0.0; xx=1.0; mnbrak(ax,xx,bx,fa,fx,fb); Fret=brent(ax,xx,bx,xmin); for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];} } //----------------------------------------------------------------------------------- void PowellsMethod::mnbrak(double &ax,double &bx,double &cx, double &fa,double &fb,double &fc) { double ulim,u,r,q,fu,dum; fa=f1dim(ax); fb=f1dim(bx); if(fb>fa) { SHFT(dum,ax,bx,dum) SHFT(dum,fb,fa,dum) } cx=bx+GOLD*(bx-ax); fc=f1dim(cx); while(fb>fc) { r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa); u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r)); ulim=bx+GLIMIT*(cx-bx); if((bx-u)*(u-cx)>0.0) { fu=f1dim(u); if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;} else if(fu>fb){cx=u; fc=fu; return;} u=cx+GOLD*(cx-bx); fu=f1dim(u); } else if((cx-u)*(u-ulim)>0.0) { fu=f1dim(u); if(fu<fc) { SHFT(bx,cx,u,cx+GOLD*(cx-bx)) SHFT(fb,fc,fu,f1dim(u)) } } else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);} else {u=cx+GOLD*(cx-bx); fu=f1dim(u);} SHFT(ax,bx,cx,u) SHFT(fa,fb,fc,fu) } } //----------------------------------------------------------------------------------- double PowellsMethod::brent(double ax,double bx,double cx,double &xmin) { int iter; double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm; a=(ax<cx?ax:cx); b=(ax>cx?ax:cx); d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x); for(iter=1;iter<=ItMaxBrent;iter++) { xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19); if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);} if(fabs(e)>tol1) { r=(x-w)*(fx-fv); q=(x-v)*(fx-fw); p=(x-v)*q-(x-w)*r; q=2.0*(q-r); if(q>0.0)p=-p; q=fabs(q); etemp=e; e=d; if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)) d=CGOLD*(e=(x>=xm?a-x:b-x)); else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);} } else d=CGOLD*(e=(x>=xm?a-x:b-x)); u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d)); fu=f1dim(u); if(fu<=fx) { if(u>=x)a=x; else b=x; SHFT(v,w,x,u) SHFT(fv,fw,fx,fu) } else { if(u<x)a=u; else b=u; if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;} else if(fu<=fv||v==x||v==w){v=u; fv=fu;} } } Print("Too many iterations in brent"); MaxIterFlag=1; xmin=x; return(fx); } //----------------------------------------------------------------------------------- double PowellsMethod::f1dim(double x) { int j; double f; for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j]; f=func(Xt); return(f); } //----------------------------------------------------------------------------------- int PowellsMethod::Optimize(double &p[],int n=0) { int i,j,k,ret; k=ArraySize(p); if(n==0)N=k; else N=n; if(N<1||N>k)return(0); ArrayResize(P,N); ArrayResize(Xi,N*N); ArrayResize(Pcom,N); ArrayResize(Xicom,N); ArrayResize(Xt,N); ArrayResize(Pt,N); ArrayResize(Ptt,N); ArrayResize(Xit,N); for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0); for(i=0;i<N;i++)P[i]=p[i]; MaxIterFlag=0; powell(); for(i=0;i<N;i++)p[i]=P[i]; if(MaxIterFlag==1)ret=-1; else ret=Iter; return(ret); } //-----------------------------------------------------------------------------------
Optimize 方法是该类的主要方法。
Optimize 方法
输入参数：
- double &p[] - 输入处的数组，包含参数的初始值，而要找到的最优值就在其中；取得的这些参数的最优值位于该数组的输出处。
- int n=0 - 数组 p[] 中自变量的数量。如果 n=0，则参数数量被视为与数组 p[] 的大小相等。
返回值：
- 返回值会返回该算法运行所需的迭代数；如果因此达到了最大允许次数，返回值则为 -1。
在搜索最优参数值时，会利用迭代逼近法求得目标函数的最小值。Optimize 方法会返回按某指定精确度达到函数最小值所需的迭代数。每次迭代过程中都会多次调用目标函数，也就是说，目标函数的调用次数可能会大幅（10 倍甚至 100 倍）超过使用 Optimize 方法时返回的迭代数。
该类中的其他方法。
SetItMaxPowell 方法
输入参数：
- Int n - 鲍威尔法中迭代的最大允许次数。默认值为 200。
返回值：
- 无。
通过该方法可设置迭代的最大允许次数；一旦达到该数量，不管是否找到带有指定精确度的目标函数最小值，搜索都会停止，且日志中会添加一条相关消息。
SetFtolPowell 方法
输入参数：
- double er - 精确度。如果与目标函数最小值的偏差达到了该值，鲍威尔法就会停止搜索。默认值为 1e-6。
返回值：
- 无。
SetItMaxBrent 方法
输入参数：
- Int n - 辅助使用的布伦特法中迭代的最大允许次数。默认值为 200。
返回值：
- 无。
该方法会设置迭代的最大允许次数。达到该次数后，辅助使用的布伦特法就会停止搜索，且日志中会添加一条相关消息。
SetFtolBrent 方法
输入参数：
- double er - 精确度。该值会在辅助使用布伦特法时定义搜索最小值过程中的精确度。默认值为 1e-4。
返回值：
- 无。
GetFret 方法
输入参数：
- 无。
返回值：
- 该方法会返回所获目标函数的最小值。
GetIter 方法
输入参数：
- 无。
返回值：
- 该方法会返回算法运行所需的迭代数。
虚函数 func(const double &p[])
输入参数：
- const double &p[] – 用于处理包含最优参数的数组。数组的大小与函数参数的数量相对应。
返回值：
- 该方法会返回与传递给它的参数相对应的函数值。
在每种特定情况下，都会在 PowellsMethod 类派生出的一个类中对虚函数 func() 进行重新定义。func() 函数是一种目标函数，其自变量对应于函数返回的最小值，在使用搜索算法时可以找到该目标函数。
这里使用的鲍威尔法会采用布伦特的单变元抛物线插值法来确定与每个参数相关的搜索方向。这些方法的精确度和最大允许迭代数可分别通过调用 SetItMaxPowell、SetFtolPowell、SetItMaxBrent 和 SetFtolBrent 进行设置。
因此也可以通过这种方式更改该算法的默认特性。如果某特定目标函数设置的默认精确度过高，且算法所要求的搜索过程中的迭代次数过多，则这种方式可能也有用。通过更改所需精确度的值可以优化与各类目标函数相关的搜索。
尽管采用鲍威尔法的算法看似复杂，使用却非常简单。
我们来举个例子。假设我们有一个函数，
并需要找出函数取最小值时参数 
和 
的值。
我们通过编写一个脚本，就此问题给出一个解决方案。
//----------------------------------------------------------------------------------- // PM_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- class PM_Test:public PowellsMethod { public: void PM_Test(void) {} private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- double PM_Test::func(const double &p[]) { double f,r1,r2; r1=p[0]-0.5; r2=p[1]-6.0; f=r1*r1*4.0+r2*r2; return(f); } //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { int it; double p[2]; p[0]=8; p[1]=9; // Initial point PM_Test *pm = new PM_Test; it=pm.Optimize(p); Print("Iter= ",it," Fret= ",pm.GetFret()); Print("p[0]= ",p[0]," p[1]= ",p[1]); delete pm; } //-----------------------------------------------------------------------------------
编写脚本时，我们首先将 func() 函数创建为 PM_Test 类的一个成员，而 PM_Test 类会利用参数 p[0] 与 p[1] 的传递值计算出指定测试函数的值。接下来在 OnStart() 函数的主体中，将初始值分配给所需参数。搜索即从这些值开始。
然后会创建一个 PM_Test 类的副本，再调用 Optimize 方法开始搜索所需的 p[0] 与 p[1] 值；父类 PowellsMethod 的方法则会调用重新定义的 func() 函数。搜索完成后，迭代数、最小点的函数值以及得到的参数值 p[0]=0.5 与 p[1]=6 都会被添加到日志中。
PowellsMethod.mqh 和测试案例 PM_Test.mq5 位于本文末尾处的 Files.zip 存档中。要想编译 PM_Test.mq5，应该将其放置在与 PowellsMethod.mqh 相同的目录下。
9. 模型参数值的优化
本文前面章节谈到了查找函数最小值方法的实现，并提供了一个简单的使用示例。现在，我们继续讨论指数平滑模型参数优化的相关问题。
首先，我们最大限度地简化了之前介绍过的 AdditiveES 类（将所有与季节分量相关的元素排除于外），因为本文不会再进一步探讨将季节性纳入考虑范畴的模型了。这样做能够让此类源代码更容易理解并减少计算量。此外，我们还会排除与置信区间预测和运算相关的所有计算，以方便说明研究中的带衰减线性增长模型的参数优化方法。
//----------------------------------------------------------------------------------- // OptimizeES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class OptimizeES //----------------------------------------------------------------------------------- class OptimizeES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters int NCalc; // Number of last elements for calculation public: void OptimizeES(void) {} int Calc(string fname); private: int readCSV(string fnam,double &dat[]); virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // Calc //----------------------------------------------------------------------------------- int OptimizeES::Calc(string fname) { int i,it; double relmae,naiv,s,t,alp,gam,phi,e,ae,pt; if(readCSV(fname,Dat)<0){Print("Error."); return(-1);} Dlen=ArraySize(Dat); NCalc=200; // number of last elements for calculation if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);} Par[0]=Dat[Dlen-NCalc]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi it=Optimize(Par); // Powell's optimization s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4]; relmae=0; naiv=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]); ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } relmae/=naiv; PrintFormat("%s: N=%i, RelMAE=%.3f",fname,NCalc,relmae); PrintFormat("Iter= %i, Fmin= %e",it,GetFret()); PrintFormat("p[0]= %.5f, p[1]= %.5f, p[2]= %.2f, p[3]= %.2f, p[4]= %.2f", Par[0],Par[1],Par[2],Par[3],Par[4]); return(0); } //----------------------------------------------------------------------------------- // readCSV //----------------------------------------------------------------------------------- int OptimizeES::readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double OptimizeES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(NCalc*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
OptimizeES 类由 PowellsMethod 类派生，包括对虚函数 func() 的重新定义。如前文所述，应在输入该函数时就传递那些计算值会在优化过程中被最小化的参数。
根据最大似然法，func() 函数会计算提前一步预测误差平方和的对数。此类误差是在序列 NCalc 最近值的循环中进行计算。
为保持模型的稳定性，我们要对其参数内的变化范围进行限制。针对 Alpha 和 Gamma 参数的范围从 0.05 到 0.95，而针对 Phi 参数的范围则是从 0.05 到 1.0。但是，为了实现本例中的优化，我们采用了一种查找无约束最小值（其并不意味着对目标函数的自变量进行限制）的方法。
我们会尝试将查找多变量函数（带限制）最小值的问题转变为查找无约束最小值的问题，从而在不更改搜索算法的情况下，将所有施加给参数的限制都纳入考虑范畴。为此，就会用到所谓的惩罚函数法。在一维情况下，此方法很容易就能实现。
假设我们有一个单一自变量（域范围从 2.0 到 3.0）函数，且搜索过程中的算法可以向该函数参数分配任何值。在这种情况下，我们可以执行以下操作：如果该搜索算法已传递一个超过最大允许值的自变量，比如 3.5，则该函数可计算出自变量等于 3.0，再将所得结果乘以一个与超出最大值成正比的系数，比如 k=1+(3.5-3)*200。
如果对低于最小允许值的自变量值执行类似操作，则生成的目标函数的自变量变化一定会超出允许范围。目标函数结果值中的这种人为增加情况，会让搜索算法一直不清楚传递到函数的自变量已通过某种方式进行限制，并保证作为结果的函数的最小值会在自变量所设限制的范围内。该方法可轻松应用于多个变量的函数。
OptimizeES 类中的主要方法是 Calc 方法。由于调用了该方法，所以就能够从文件读取数据、搜索某模型的最优参数值，以及利用 RelMAE 来评估所获参数值的预测精确度。在本例中，从文件读取的序列处理值数量在 NCalc 变量中进行了设定。
下面是采用 OptimizeES 类的 Optimization_Test.mq5 脚本的示例。
//----------------------------------------------------------------------------------- // Optimization_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "OptimizeES.mqh" OptimizeES es; //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { es.Calc("Dataset\\USDJPY_M1_1100.TXT"); } //-----------------------------------------------------------------------------------
执行此脚本后会得到如下所示的值。
图 6. Optimization_Test.mq5 脚本结果
尽管我们现在可以找到模型的最优参数值和初始值，但还是有一个参数是简单工具优化不了的，那就是优化过程中使用的序列值数量。在与超长序列相关的优化中，我们会获取一般说来可确保整个序列长度误差最小的最优参数值。
但是，如果序列的性质在此区间内发生变化，则其部分片断的获取值就不再是最优值。另一方面，如果序列长度显著减少，则无法保证在这种在短区间所获的最优参数在较长时间的延迟后仍保持为最优。
OptimizeES.mqh 和 Optimization_Test.mq5 均位于本文末尾处的 Files.zip 存档中。编译时，OptimizeES.mqh 和 PowellsMethod.mqh 必须位于与 Optimization_Test.mq5 相同的目录下。指定示例中用到了包含测试序列的 USDJPY_M1_1100.TXT 文件，该文件位于 \MQL5\Files\Dataset\ 目录下。
表 2 显示了通过该脚本并使用 RelMAE 获取的预测精确度估算值。前文提到了八个测试序列的预测，都已使用每个序列的最后 100、200 和 400 个值予以完成。
|
表 2. 利用 RelMAE 估算的预测误差
可以看出，预测误差估算值接近于一，但在绝大多数情况下，针对此模型中指定序列的预测都比朴素法中的预测更为精确。
10. IndicatorES.mq5 指标
前文在研究 AdditiveES.mqh 类时曾提到过基于此类的 AdditiveES_Test.mq5 指标。该指标中的所有平滑参数均为手动设置。
现在，在考虑完允许优化模型参数的方法之后，我们可以创建一个类似的指标，其中的最优参数值与初始值会自动确定，且只有处理过的样本长度才需要手动设置。也就是说，我们会排除掉与季节性相关的所有计算。
下面列出的是创建指标过程中使用的 CIndiсatorES 类的源代码。
//----------------------------------------------------------------------------------- // CIndicatorES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class CIndicatorES //----------------------------------------------------------------------------------- class CIndicatorES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters public: void CIndicatorES(void) { } void CalcPar(double &dat[]); double GetPar(int n) { if(n>=0||n<5)return(Par[n]); else return(0); } private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // CalcPar //----------------------------------------------------------------------------------- void CIndicatorES::CalcPar(double &dat[]) { Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayCopy(Dat,dat); Par[0]=Dat[0]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi Optimize(Par); // Powell's optimization } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
该类包含 CalcPar 和 GetPar 方法；第一种方法被设计用于模型优化参数值的计算，而第二种则用于访问这些值。此外，CIndicatorES 类由重新定义的虚函数 func() 构成。
IndicatorES.mq5 指标的源代码：
//----------------------------------------------------------------------------------- // IndicatorES.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CIndicatorES.mqh" #define NFORE 12 double Hist[],Fore[],Conf1[],Conf2[]; double Data[]; int NDat; CIndicatorES Es; //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,start; double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4); f=(s+phi*t); var=0; for(i=0;i<NDat;i++) // History { e=Data[i]-f; var+=e*e; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; } var/=(NDat-1); a1=1; a2=0; a3=1; for(i=rates_total-NFORE;i<rates_total;i++) { a1=a1*phi; a2+=a1; Fore[i]=s+a2*t; // Forecast ci=1.96*MathSqrt(var*a3); // Confidence intervals a=alp*(1+a2*gam); a3+=a*a; Conf1[i]=Fore[i]+ci; Conf2[i]=Fore[i]-ci; } return(rates_total); } //-----------------------------------------------------------------------------------
每出现一个新柱，该指标都会找到模型参数的最优值，在模型中就指定数量的 NHist 柱进行计算，生成预测并定义预测置信界限。
该指标的唯一参数是处理序列的长度，而其最小值被限定为 24 柱。该指标中的所有计算均基于 open[] 值完成。预测范围为 12 柱。IndicatorES.mq5 指标的代码与 CIndicatorES.mqh 文件均位于本文末尾处的 Files.zip 存档中。
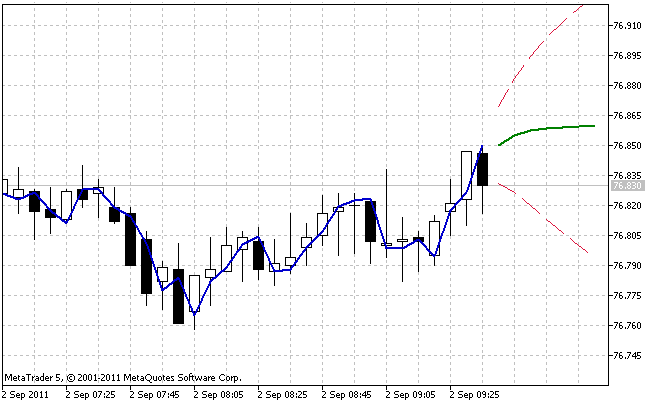
图 7. IndicatorES.mq5 指标的运行结果
图 7 显示了 IndicatorES.mq5 指标运行结果的一个示例。在该指标运行过程中，95% 预测置信区间会取与所获模型最优参数值相对应的值。平滑参数值越大，预测范围递增时置信区间中的增长就越快。
通过简单改进后，IndicatorES.mq5 指标就可以既用于预测当前报价，也用于预测各种指标或预处理数据的值。
总结
本文的主要目的是让读者熟悉预测中用到的各种加法指数平滑模型。在展示其实际使用的同时，还处理了一些随之而来的问题。但是，本文所提供的材料只能被视为与预测相关的大量问题与解决方案的简要介绍而已。
大家要注意：这里提供的类、函数、脚本和指标，都是在撰写本文时创建的，主要就是充当本文的材料示例，因此并未对其稳定性和误差进行严格测试。此外，本文中讲到的指标也仅应视为所涉及方法的示范而已。
本文介绍的 IndicatorES.mq5 指标的预测精确度，极有可能通过更改应用模型而在某种程度上得以改进，从而让拟议中的报价在独特性方面更为完善。该指标也可通过其他模型进行扩充。但这已超出本文的论述范围。
综上所述，需要指出的是：在特定情况下，指数平滑模型所生成的预测精确度等同于通过应用更复杂模型才能生成的预测精确度，由此再一次证明，即便是最复杂的模型也未必就是最好。
参考文献
- Everette S. Gardner Jr. Exponential Smoothing:The State of the Art – Part II.June 3, 2005.
- Rob J Hyndman.Forecasting Based on State Space Models for Exponential Smoothing.29 August 2002.
- Rob J Hyndman et al.Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models.30 January 2003.
- Rob J Hyndman and Muhammad Akram.Some Nonlinear Exponential Smoothing Models Are Unstable.17 January 2006.
- Rob J Hyndman and Anne B Koehler.Another Look at Measures of Forecast Accuracy.2 November 2005.
- Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series:Textbook.- М.:Finansy i Statistika, 2003.-416 pp.
- D. Himmelblau. Applied Nonlinear Programming.М.:Mir, 1975.
- Numerical Recipes in C. The Art of Scientific Computing.Second Edition.Cambridge University Press.
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/318
分析指标统计参数
MQL5 傻瓜式向导
William Blau 的 MQL5 指标与交易系统。第一部分：指标
源代码的跟踪、调试和结构分析
