Técnicas do MQL5 Wizard que você deve conhecer (Parte 18): Pesquisa de Arquitetura Neural com Vetores Próprios
Prefácio
Damos continuidade à série sobre a implementação do MQL5 Wizard analisando a Pesquisa de Arquitetura Neural, enfocando especificamente o papel que os Vetores Próprios podem desempenhar ao tornar esse processo de agilização do treinamento da rede mais eficiente. Redes neurais são, sem dúvida, uma forma de ajuste de uma curva a um conjunto de dados, pois ajudam a criar uma expressão formulaica que, quando aplicada aos dados de entrada (x), fornece um valor alvo (y), assim como uma equação quadrática faz com uma curva. No entanto, os pontos de dados x e y podem ser, e frequentemente são, multidimensionais, o que explica a popularidade crescente das redes neurais. Ainda assim, o princípio de criar uma expressão formulaica permanece, motivo pelo qual as redes neurais são apenas um meio de se chegar a isso, e não o único.Introdução
Se optarmos por usar redes neurais para definir a relação entre um conjunto de dados de treinamento e seu alvo, como é o caso deste artigo, então teremos que lidar com a questão de quais configurações essa rede usará? Existem vários tipos de redes, o que implica que os designs e configurações aplicáveis também são muitos. Para este artigo, consideramos um caso muito básico, frequentemente chamado de perceptron multicamadas. Com esse tipo, as configurações nas quais nos aprofundaremos serão apenas o número de camadas ocultas e o tamanho de cada camada oculta.
A Pesquisa de Arquitetura Neural (NAS) pode, em geral, ajudar a identificar essas duas configurações e muito mais. Por exemplo, mesmo com MLPs simples, a questão de qual tipo de ativação usar, os pesos iniciais, bem como os vieses iniciais, são todos fatores sensíveis ao desempenho e à precisão da rede. Esses fatores, no entanto, serão resumidos aqui, pois o espaço de busca é muito extenso, e os recursos computacionais necessários para a propagação direta e reversa em um conjunto de dados de tamanho moderado seriam proibitivos.
A abordagem de NAS adotada aqui, no entanto, é um pouco inovadora, pois envolve o uso de vetores e valores próprios em um espaço de busca matricial para identificar as configurações ideais. Convencionalmente, o NAS é realizado por meio de aprendizado por reforço, ou algoritmos evolutivos, ou otimização bayesiana, ou busca aleatória.
Cada uma dessas abordagens convencionais envolve treinar e validar uma rede com as configurações selecionadas (também conhecidas como arquitetura), comparando o desempenho de cada uma com o alvo, para fins de comparação. O que as diferencia é o quão exaustivas elas são, ou sua abordagem para serem eficientes sem serem exaustivas no espaço de busca. O aprendizado por reforço depende de um algoritmo que pré-avalia uma rede dentro do espaço de busca com base em suas configurações, e esse algoritmo vai se aprimorando com cada seleção. Os algoritmos evolutivos combinam ou cruzam redes dentro do espaço de busca para chegar a novas redes que talvez não estivessem inicialmente no espaço de busca, avaliando novamente seu desempenho em comparação com o alvo. A otimização bayesiana, como a busca aleatória, baseia-se no espaço de busca sendo organizado em um formato de matriz ou onde as diferentes configurações da rede podem ser percebidas como coordenadas dentro do espaço de busca. Por exemplo, se um espaço de busca for bidimensional, com apenas duas variáveis (o tamanho padrão de uma camada oculta e o número de camadas ocultas), essas opções seriam distribuídas ao longo dessa matriz em uma ordem ascendente (ou descendente) na diagonal, como na imagem abaixo.
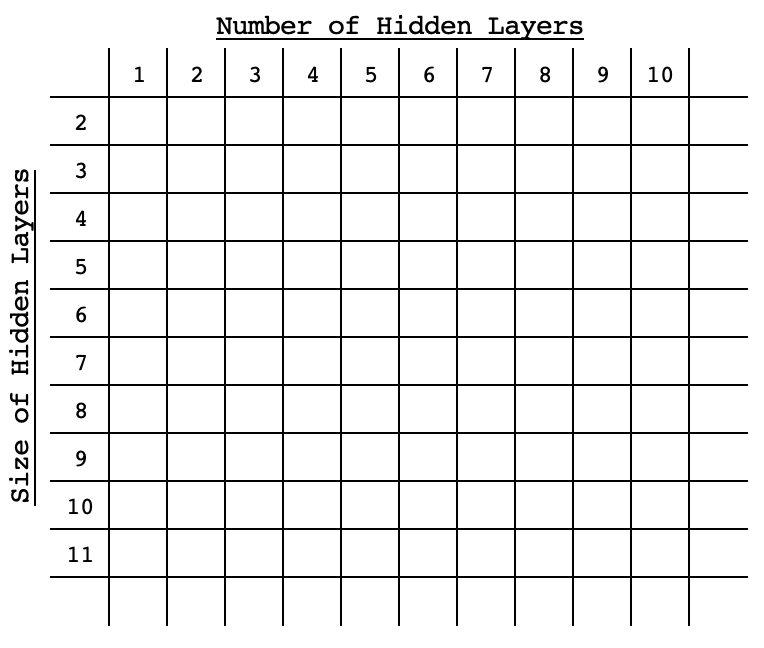
Com esse arranjo, o desempenho de qualquer rede seria vinculado às suas ‘coordenadas’ dentro do espaço, e métodos estatísticos seriam usados a cada nova seleção para refinar a escolha da rede que apresentaria o melhor desempenho. Este artigo sobre vetores próprios e PCA, escrito há alguns dias, usou um espaço de busca matricial para selecionar um dia útil ideal e um preço aplicado para negociar o EURUSD ao usar o gráfico de 4 horas. Isso foi feito a partir de uma matriz cruzada de mudanças de preço para cada um dos 5 dias úteis e em cada um dos preços aplicados considerados.
Vamos considerar uma abordagem de busca semelhante para este artigo. Como o treinamento exaustivo de todas as redes é um problema que estamos tentando ‘resolver’, nossos benchmarks serão simplesmente pontuações de passagem direta dos valores alvo em redes que são inicializadas com pesos e vieses padrão. Faremos apenas execuções diretas em uma amostra de dados, e a pontuação média de cada configuração servirá como benchmark dentro da matriz.O Papel dos Vetores Próprios no NAS
A matriz de autovalores que usaremos para o NAS será bidimensional, para simplificar, como mencionado acima. Se considerarmos um MLP simples em que todas as camadas ocultas têm o mesmo tamanho, as únicas duas questões que queremos responder são quantas camadas ocultas o MLP deve ter e qual o tamanho de cada camada oculta.
As respostas possíveis para essas perguntas podem ser facilmente apresentadas em uma matriz, com o desempenho padrão de cada rede registrado em cada combinação de tamanho e número de camadas. As redes variarão em configurações conforme refletido na tabela da matriz, no entanto, suas camadas de entrada e saída serão padrão. Para este artigo, teremos uma camada de entrada de tamanho 4 e uma camada de saída de tamanho 1. Estamos analisando um cenário comum onde prevemos o próximo preço de fechamento com base nos 4 últimos valores de preço de fechamento.O símbolo de teste será EURJPY ao longo do ano de 2022 no período de tempo de 4 horas. Isso significa que nossos dados serão os preços de fechamento a cada 4 horas durante o ano de 2022. No ‘treinamento’ deste modelo, tudo o que faremos é registrar a média de desvios dos valores alvo ao longo do ano para todas as configurações de rede. Nossas configurações variam de uma única camada oculta até 10 camadas ocultas ao longo das linhas da matriz, enquanto as colunas apresentarão os tamanhos das camadas ocultas, que variam de 2 a 11. Essas configurações de teste são arbitrárias e, como o código-fonte completo está anexado no final deste artigo, o leitor pode personalizá-las conforme sua preferência.
Para reiterar, o ‘treinamento’ do modelo envolverá uma única passagem direta em cada uma das redes disponíveis, todas com pesos e vieses padrão ao longo do ano de 2022, com cada previsão de barra comparada ao preço de fechamento real. Não haverá retropropagação ou treinamento típico de rede durante este ‘treinamento’.
Utilizamos uma classe de rede que analisamos neste artigo para implementar o MLP. Ela simplesmente requer um array de inteiros cujo tamanho define o número total de camadas, onde o valor inteiro em cada índice define o tamanho da camada.
Embora este artigo e série estejam destacando o MQL5 Wizard, o ‘treinamento’ mencionado acima será feito por script, como foi o caso no último artigo sobre vetores próprios, e usaremos os resultados/recomendações para codificar uma instância da classe de sinal para testar com um expert advisor montado pelo wizard. Nosso teste do expert advisor montado terá o treinamento usual da rede em cada barra ou com cada novo ponto de dados. O resultado do testador de estratégias da rede recomendada será comparado ao pior resultado, como controle, para que possamos avaliar a tese de que os vetores próprios e valores podem ser úteis no NAS.
Se recapitulamos o que abordamos no último artigo sobre vetores próprios e valores, a redução de dimensionalidade usada nos forneceu um único vetor a partir de uma matriz em análise. Então, em nosso caso, o desempenho registrado de cada rede que temos em uma matriz será reduzido a um vetor. No último artigo, queríamos obter o dia útil e o preço aplicado que capturaram a maior parte da variância do par EURJPY ao longo de um ano no gráfico de 4 horas. Isso implicava que focávamos nos valores máximos dos vetores próprios dentro da matriz projetada, já que eles se correlacionavam positivamente com nosso alvo.
Neste caso, porém, nossa matriz registrou desvios dos valores alvo, o que implica que o que temos em nossa matriz é o fator de erro de cada rede. Como, para fins de teste, queremos usar a rede com o menor erro, nossas seleções para o número de camadas e o tamanho de cada camada serão os mínimos em cada um dos vetores próprios, conforme recuperados da matriz projetada. Esse pré-processamento, como mencionado, é todo tratado por script, e pode ser dividido em 5 seções, a saber, a) inicialização das redes:
//initialise networks ArrayResize(__M.row, __SIZE); for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { ArrayResize(__M.row[r].col, __SIZE); ArrayResize(__M.row[r].col[c].settings, 2 + __LEAST_LAYERS + r); ArrayFill(__M.row[r].col[c].settings, 0, __LEAST_LAYERS + r + 2, __LEAST_SIZE + c); __M.row[r].col[c].settings[0] = __INPUTS; __M.row[r].col[c].settings[__LEAST_LAYERS + r + 1] = __OUTPUTS; __M.row[r].col[c].n = new Cnetwork(__M.row[r].col[c].settings, __initial_weight, __initial_bias); } }
b) benchmarking das redes:
//benchmark networks int _buffer_size = (52*PeriodSeconds(PERIOD_W1))/PeriodSeconds(Period()); PrintFormat(__FUNCSIG__ + " buffered: %i", _buffer_size); if(_buffer_size >= __INPUTS) { for(int i = _buffer_size - 1; i >= 0; i--) { for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { vector _in,_out; vector _in_new,_out_new,_in_old,_out_old; _in_new.CopyRates(Symbol(), Period(), 8, i + 1, __INPUTS); _in_old.CopyRates(Symbol(), Period(), 8, i + 1 + 1, __INPUTS); _out_new.CopyRates(Symbol(), Period(), 8, i, __OUTPUTS); _out_old.CopyRates(Symbol(), Period(), 8, i + 1, __OUTPUTS); _in = Norm(_in_new, _in_old); _out = Norm(_out_new, _out_old); __M.row[r].col[c].n.Set(_in); __M.row[r].col[c].n.Forward(); __M.row[r].col[c].benchmark += fabs(__M.row[r].col[c].n.output[0]-_out[0]); } } } }
c) copiar benchmarks para matriz de análise:
//copy benchmarks to analysis matrix matrix _m; _m.Init(__SIZE, __SIZE); _m.Fill(0.0); for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { _m[r][c] = __M.row[r].col[c].benchmark; } }
d) normalizar a matriz e gerar os vetores e valores próprios:
//generating eigens PrintFormat(" for: %s, with: %s", Symbol(), EnumToString(Period())); matrix _z = ZNorm(_m); matrix _cov_col = _z.Cov(false); matrix _e_vectors; vector _e_values; _cov_col.Eig(_e_vectors, _e_values);
e) e finalmente interpretar os vetores próprios para recuperar números de camadas de rede ideais e piores e tamanhos de camadas da matriz de projeção:
//interpreting the eigens from projection matrix _t = _e_vectors.Transpose(); matrix _p = _m * _t; vector _max_row = _p.Max(0); vector _max_col = _p.Max(1); string _layers[__SIZE]; for(int i=0;i<__SIZE;i++) { _layers[i] = IntegerToString(i + __LEAST_LAYERS)+" layer"; } double _nr_layers[]; _max_row.Swap(_nr_layers); //since network performance inversely relates to network deviation from target PrintFormat(" est. número ideal of layers is: %s", _layers[ArrayMinimum(_nr_layers)]); PrintFormat(" est. pior número of layers is: %s", _layers[ArrayMaximum(_nr_layers)]); string _sizes[__SIZE]; for(int i=0;i<__SIZE;i++) { _sizes[i] = "size "+IntegerToString(i + __LEAST_SIZE); } double _size_nr[]; _max_col.Swap(_size_nr); PrintFormat(" est. O tamanho ideal das camadas é: %s", _sizes[ArrayMinimum(_size_nr)]; PrintFormat(" est. O pior tamanho das camadas é: %s", _sizes[ArrayMaximum(_size_nr)];A execução do script acima em um espaço de busca de 100 execuções leva apenas alguns segundos, o que é um bom sinal. No entanto, pode-se argumentar que o espaço não é abrangente o suficiente, e isso é uma observação válida. Por esse motivo, o script anexado tem os atributos de tamanho do espaço como uma variável global que o usuário pode modificar para criar algo mais rigoroso. Além disso, precisávamos de uma estrutura para lidar com as instâncias da rede e seus benchmarks. Isso é definido no cabeçalho da seguinte forma:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ struct Scol { int settings[]; Cnetwork *n; double benchmark; Scol() { ArrayFree(settings); benchmark = 0.0; } ~Scol(){ delete n; }; }; struct Srow { Scol col[]; Srow(){}; ~Srow(){}; }; struct Smatrix { Srow row[]; Smatrix(){}; ~Smatrix(){}; }; Smatrix __M; //matrix of networks
Testando o Expert Advisor
Se executarmos o script acima, que ajuda a filtrar as configurações ideais da rede, obtemos os seguintes registros quando anexados ao EURJPY no período de 4 horas:
2024.05.03 18:22:39.336 nas_1_changes (EURJPY.ln,H4) void OnStart() buffered: 2184 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) for: EURJPY.ln, with: PERIOD_H4 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. número ideal of layers is: 6 layer 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. pior número of layers is: 9 layer 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal size of layers is: size 2 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst size of layers is: size 4As configurações recomendadas da rede são para uma rede de 6 camadas, onde o tamanho de cada uma é 2! Como nota lateral, os dados-alvo (valores y) usados para avaliar a matriz foram normalizados para estarem no intervalo de 0,0 a 1,0, onde uma leitura de 0,5 implica que a mudança de preço resultante foi zero, enquanto qualquer valor abaixo de 0,5 indicaria uma queda no preço e um valor acima de 0,5 apontaria para uma alta no preço. O código da função que realiza essa normalização está listado abaixo:
//+------------------------------------------------------------------+ //| Normalization (0.0 - 1.0, with 0.5 for 0 | //+------------------------------------------------------------------+ vector Norm(vector &A, vector &B) { vector _n; _n.Init(A.Size()); if(A.Size() > 0 && B.Size() > 0 && A.Size() == B.Size() && A.Min() > 0.0 && B.Min() > 0.0) { int _size = int(A.Size()); _n.Fill(0.5); for(int i = 0; i < _size; i++) { if(A[i] > B[i]) { _n[i] += (0.5*((A[i] - B[i])/A[i])); } else if(A[i] < B[i]) { _n[i] -= (0.5*((B[i] - A[i])/B[i])); } } } return(_n); }Essa normalização foi necessária porque, dado o pequeno conjunto de dados que estamos considerando, treinar uma rede para desenvolver pesos e vieses capazes de lidar com valores negativos e positivos como saídas exigiria conjuntos de dados extensivamente grandes, configurações de rede mais complexas e, certamente, mais recursos computacionais. Nenhum desses cenários é explorado neste artigo, mas podem ser aventurados se forem considerados viáveis. Assim, com nossa normalização, somos capazes de obter resultados sensíveis da nossa rede com treinamento e conjuntos de dados modestos.
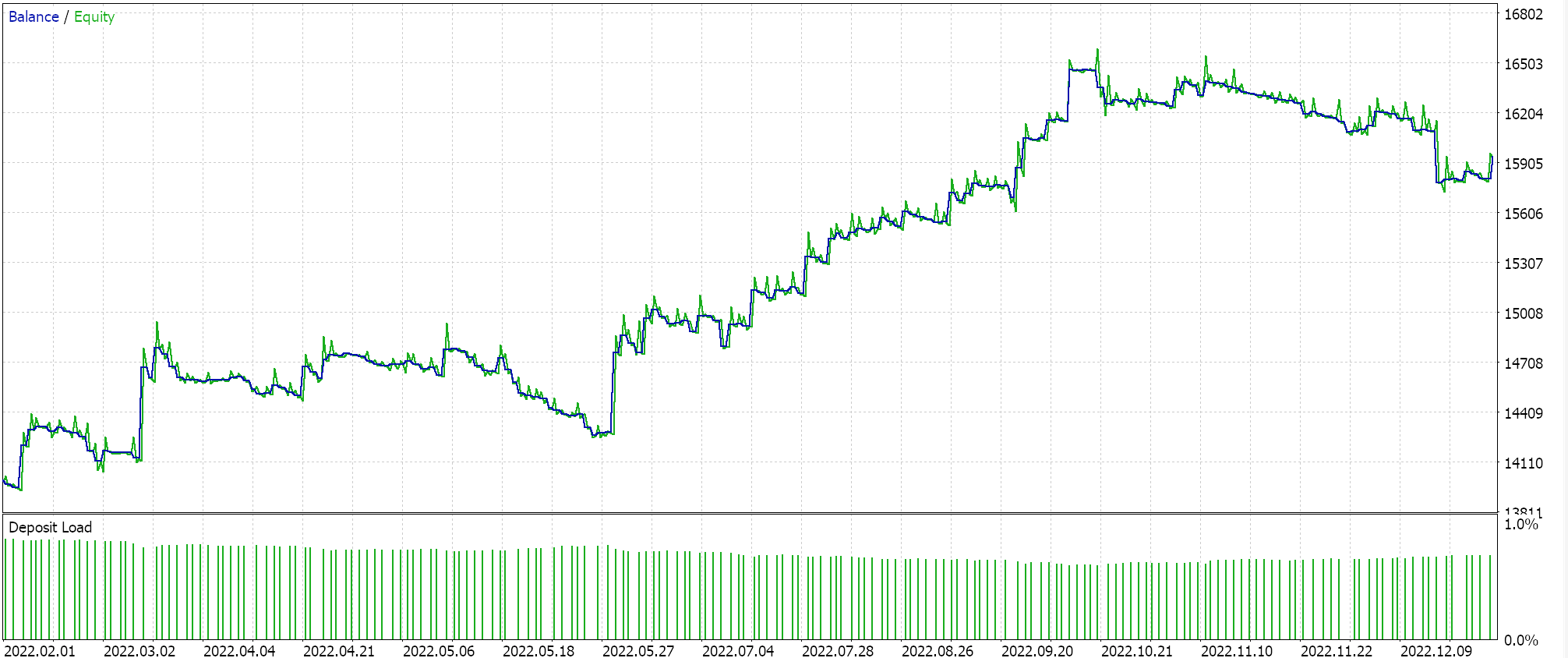
Se executarmos testes com a configuração recomendada de 6 camadas com tamanho 2, obteremos o relatório e a curva de equidade apresentados abaixo:
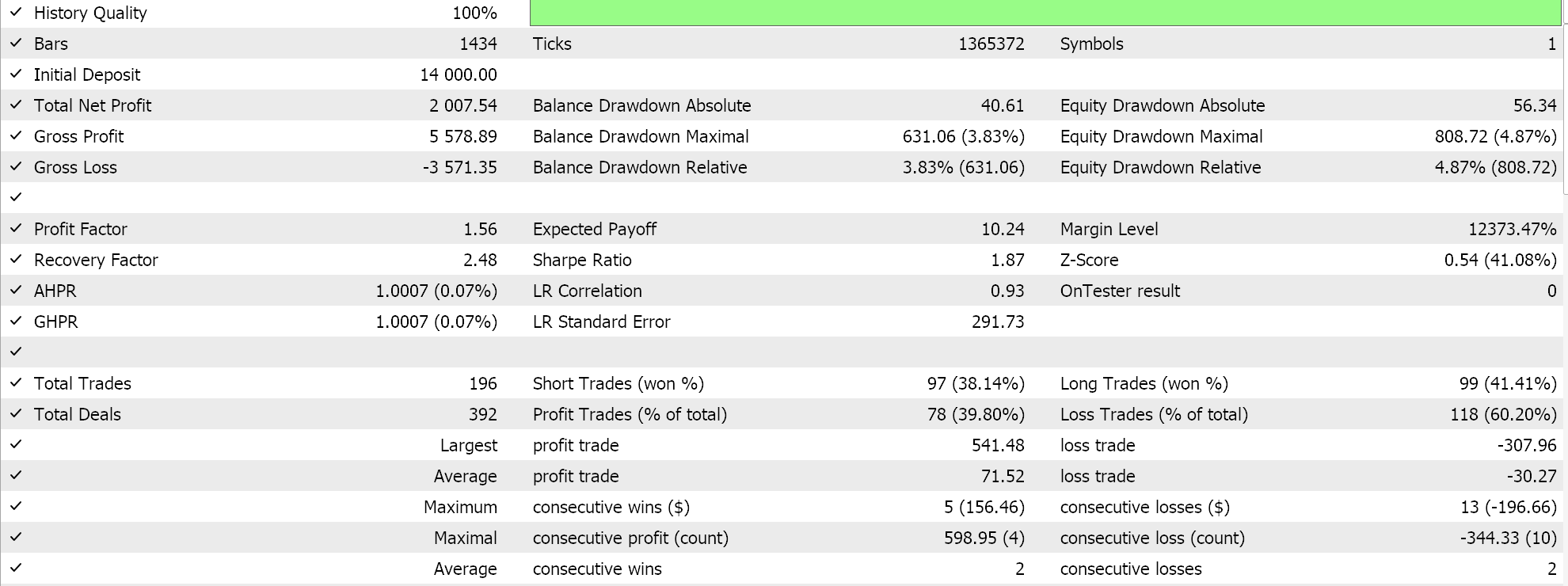
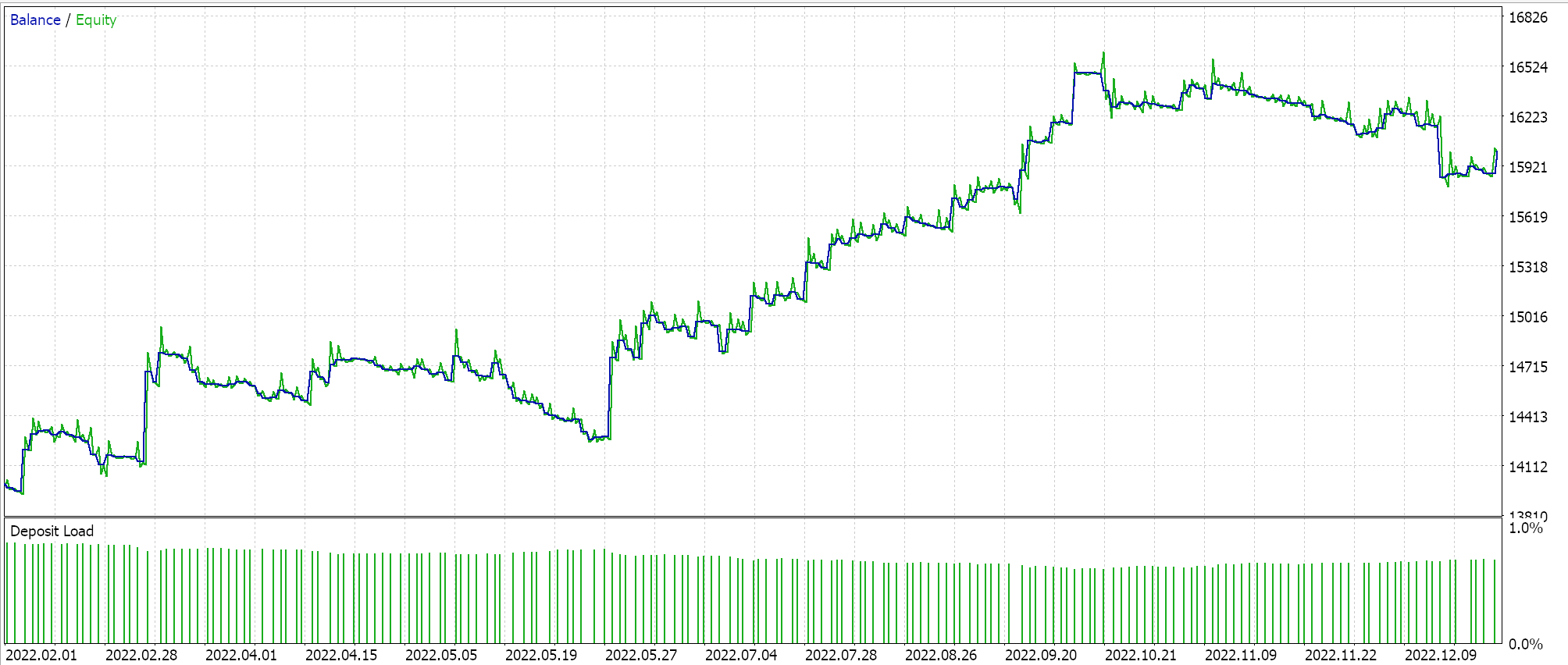
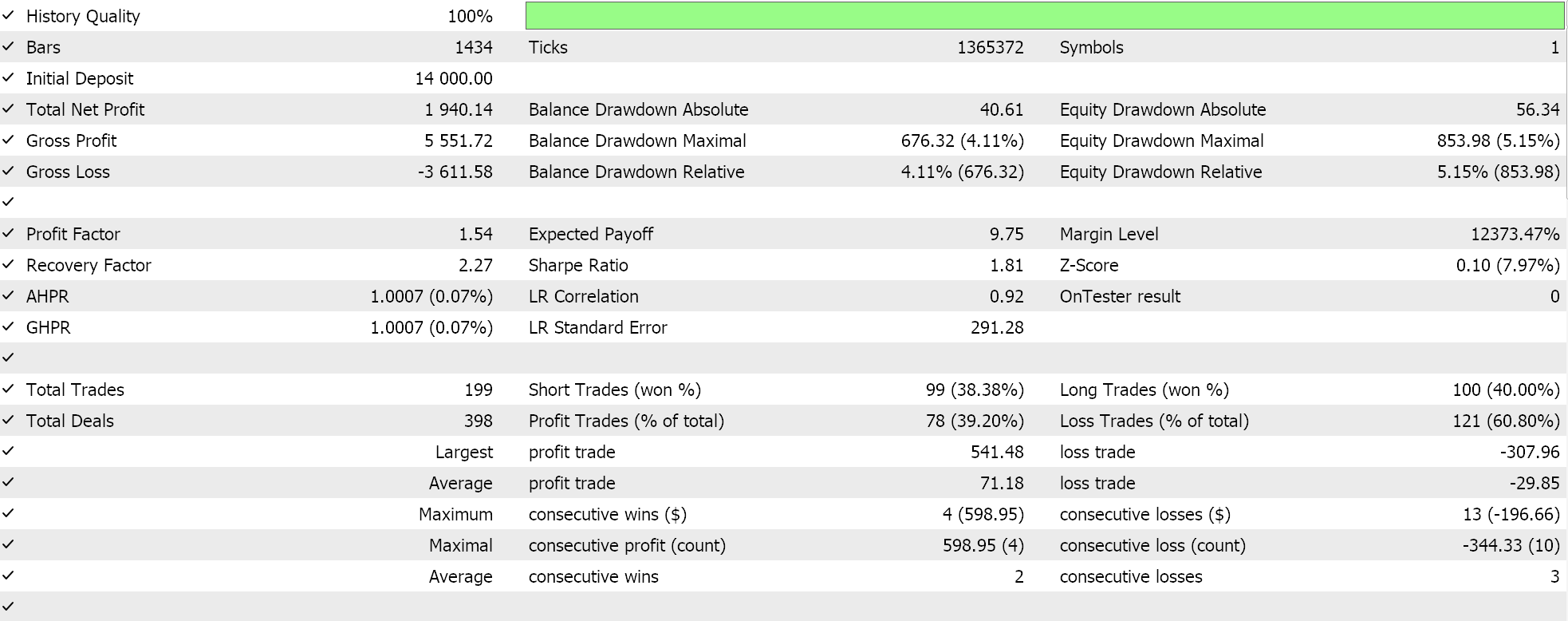
Redes neurais podem sofrer de <a2>redundância em sua capacidade, onde diferentes configurações (ou arquiteturas) aprendem os mesmos relacionamentos subjacentes nos dados, mesmo tendo estruturas diferentes. Lembre-se de que, em ambas as execuções, as redes estavam treinando, então tanto os pesos quanto os vieses estavam sendo aprimorados. Assim, enquanto os vetores próprios com maior variância capturam um conjunto mais amplo de características e aqueles com menor variância se concentram nos detalhes, qualquer uma das configurações de rede pode aprender os conceitos básicos para um bom desempenho.
Embora o número de camadas ocultas e seu tamanho sejam fatores cruciais para determinar o desempenho da rede nessa situação, pode haver outros fatores dominantes em jogo, como nossa escolha da função de ativação (usamos soft plus) ou a taxa de aprendizado utilizada. Cada um ou todos esses fatores podem ter tido uma influência desproporcional no desempenho das redes.
Outra possível explicação pode estar relacionada às limitações do espaço de busca. Consideramos 10 tamanhos de camada diferentes e 10 opções de camada oculta, todas se moldando a uma forma retangular. Isso pode ter restringido inerentemente as possíveis combinações de rede ao mapear esse conjunto de dados específico, de modo que uma dessas poucas opções poderia facilmente chegar à solução desejada.
Conclusão
Vimos como o NAS pode ser realizado de forma não ortodoxa com vetores e valores próprios quando enfrentamos um escopo modesto de configurações de rede neural para escolher. Esse processo pode ser escalado e, talvez, até expandido para incluir ou considerar outros fatores que não faziam parte da matriz de análise, adicionando formas de camada oculta (analisamos apenas retângulos) ou até tipos de ativação. Este último é o mais fácil de adicionar a uma matriz como a analisada neste artigo, já que existem apenas 2 a 3 tipos principais de ativação, e isso poderia simplesmente significar triplicar o número de colunas enquanto também expandimos o número de linhas para garantir que uma matriz quadrada seja mantida, um pré-requisito para a análise de vetores próprios. A adição de formas de camada oculta também poderia ser feita de maneira semelhante se as várias formas a serem consideradas fossem enumeradas em tipos claros. Notas:
Os arquivos anexados podem ser utilizados seguindo os guias de montagem do Expert Advisor Wizard que estão disponíveis aqui e aqui.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/14845
 MetaTrader 4 no macOS
MetaTrader 4 no macOS
 Arbitragem Estatística com previsões
Arbitragem Estatística com previsões
 Regressões Espúrias em Python
Regressões Espúrias em Python
 Desenvolvendo um sistema de Replay (Parte 67): Refinando o Indicador de controle
Desenvolvendo um sistema de Replay (Parte 67): Refinando o Indicador de controle
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso