Técnicas do MQL5 Wizard que você deve conhecer (Parte 19): Inferência Bayesiana

Introdução

Continuamos nossa exploração do MQL5 Wizard revisando a inferência bayesiana, um método estatístico que processa e atualiza probabilidades com cada nova informação recebida. Ele claramente tem um amplo espectro de possíveis aplicações, mas, para nosso propósito como traders, focaremos em seu papel na previsão de séries temporais. As séries temporais disponíveis para análise pelos traders são, principalmente, os preços dos títulos negociados, mas, como veremos neste artigo, essas séries podem ser "expandidas" para também considerar alternativas, como o histórico de negociações de títulos.

Em teoria, a Inferência Bayesiana deve melhorar a adaptabilidade ao mercado de qualquer sistema de negociação, uma vez que a reavaliação de qualquer hipótese é inerente. Isso deve levar a menos ajuste de curva quando testado em dados históricos e, posteriormente, dado a testes avançados ou simulações em contas reais. Mas isso é a teoria e, na prática, a implementação pode arruinar uma ideia sólida, e é por isso que tentaremos considerar mais de uma possível implementação da Inferência Bayesiana para este artigo.

Nosso artigo, portanto, está estruturado em um formato simples que cobre a definição de inferência bayesiana, exemplos de aplicação que incluem ilustrações em uma classe de sinal personalizada, classe de gerenciamento de dinheiro e classe de trailing stop; relatórios de teste de estratégias e, finalmente, uma conclusão.

Definição

A Inferência Bayesiana (IB) é sustentada pela fórmula P(H|E) = [P(E|H) * P(H)] / P(E), onde:

• H representa a hipótese, e
• E, a evidência, de modo que;
• P(H) é a probabilidade anterior da hipótese, enquanto,
• P(E) é a probabilidade da evidência, também conhecida como verossimilhança marginal.
• P(H|E) e P(E|H) são as respectivas probabilidades condicionais acima, e também são referidas como probabilidade posterior e verossimilhança, respectivamente.

A fórmula acima, embora simples e direta, apresenta um problema do tipo "ovo e galinha", ou seja, como encontramos: P(E|H). Isso ocorre porque implica, pela fórmula listada acima, que sua solução é:

P(E|H) = [P(H|E) * P(E)] / P(H).

No entanto, isso também pode ser reescrito como P(E|H) = [P(E∩H)] / P(H). O que nos permitiria fazer algumas soluções manuais nesta situação, como veremos abaixo.

Classes de Sinais

A classe de sinal geralmente estabelece a posição que um Expert Advisor deve tomar, seja longa ou curta. Ela faz isso somando os pesos dos indicadores, e o valor da soma sempre varia de 0 a 100. Ao usar a IB, enfrentamos uma ampla variedade de escolhas de séries temporais. No entanto, este artigo, para a classe de sinal, ilustrará apenas com a série temporal de mudança no preço de fechamento.

Para usar essa série temporal, ou qualquer outro tipo, precisamos primeiro encontrar uma maneira "sistemática" de classificar os valores da série temporal ou agrupar esses valores. Esse passo óbvio é importante porque não só normaliza nossos dados de séries temporais, mas também permite identificá-los adequadamente ao processar sua probabilidade.

O agrupamento é não supervisionado, e usamos uma abordagem rudimentar, atribuindo um grupo a cada ponto de dados, dependendo do tipo de mudança de preço. Todos os valores positivos recebem um grupo, valores zero têm seu próprio grupo, e os valores negativos também têm o seu próprio. Já consideramos abordagens alternativas de agrupamento no passado nesta série de artigos, e o leitor é convidado a experimentar essas abordagens. No entanto, para este artigo, como o agrupamento não é o assunto principal, consideramos algo muito elementar.

Mesmo com essa abordagem básica de agrupamento, fica claro que podemos melhor "identificar" os pontos de dados e, portanto, avaliar suas probabilidades. Sem isso, como os dados são números de ponto flutuante, cada um seria único, o que, na essência, significaria um tipo de grupo único, o que claramente frustraria nosso propósito de obter e calcular os valores de probabilidade. Nossa abordagem simples é implementada no código-fonte abaixo:

//+------------------------------------------------------------------+
//| Function to assign cluster for each data point                   |
//+------------------------------------------------------------------+
void CSignalBAYES::SetCluster(matrix &Series)
{  for(int i = 0; i < int(Series.Rows()); i++)
   {  if(Series[i][0] < 0.0)
      {  Series[i][1] = 0.0;
      }
      else if(Series[i][0] == 0.0)
      {  Series[i][1] = 1.0;
      }
      else if(Series[i][0] > 0.0)
      {  Series[i][1] = 2.0;
      }
   }
}

Uma vez que tenhamos os pontos de dados "identificados", prosseguimos para calcular a probabilidade posterior conforme definido na equação da fórmula acima. Ao fazer isso, no entanto, precisaríamos de um tipo de cluster específico que sirva como nossa hipótese. Este cluster será único para posições longas e curtas, portanto, temos parâmetros de entrada personalizados para cada um que servem como índices que identificam o tipo de cluster a ser usado em cada caso. Esses são rotulados como ‘m_cluster_long’ e ‘m_cluster_short’, respectivamente.

Então, para obter a probabilidade posterior, este índice de cluster, juntamente com a série temporal "identificada" ou agrupada, seriam necessários como entradas. Nossa função que calcula a probabilidade posterior está obtendo a probabilidade de ocorrência do cluster do tipo de posição, dado o tipo de cluster atual. Como estamos fornecendo uma série de pontos de dados recentes, cada um com seu índice de cluster em um formato de matriz, essencialmente temos o ponto de dados de índice zero como o cluster atual.

Para resolver a possível situação do tipo "ovo e galinha" mencionada anteriormente, trabalhamos como P(E|H).

A partir dos princípios básicos. Como H é representado pelo respectivo índice de posição, conforme explicado acima, a evidência E é o cluster atual ou o tipo de cluster no índice zero dentro da série de entrada. Assim, nossa probabilidade posterior é descobrir a probabilidade de que o tipo de cluster da posição ocorra a seguir, dado que a evidência mais recente (cluster no índice 0) ocorreu.

Portanto, para encontrar P(E|H), revisitamos a série de entrada e fazemos uma enumeração de quando o índice de posição H ocorreu, seguido pelo índice zero E (a evidência). Isso também é uma probabilidade, então primeiro enumeramos o espaço, ou seja, encontramos as ocorrências de H e, dentro desse espaço, quantificamos quantas vezes o índice de evidência ocorreu em sucessão.

Isso claramente implica que nossa série de entrada tem um comprimento suficiente, sujeito ao número de tipos de clusters considerados. Em nosso exemplo muito simples, temos 3 tipos de clusters (na verdade 2, considerando que a mudança de preço zero raramente ocorre) e isso poderia funcionar com uma série de entrada de menos de 50. No entanto, se optar por uma abordagem de agrupamento mais ousada, com 5/6 ou mais tipos de clusters, o tamanho padrão da série de entrada precisará ser substancial o suficiente para capturar a ocorrência de todos esses tipos de clusters para que nossa função posterior funcione. A listagem da função posterior está abaixo:

//+------------------------------------------------------------------+
//| Function to calculate the posterior probability for each cluster |
//+------------------------------------------------------------------+
double CSignalBAYES::GetPosterior(int Type, matrix &Series)
{  double _eh_sum = 0.0, _eh = 0.0, _e = 0.0, _h = 0.0;
   for(int i = 0; i < int(Series.Rows()); i++)
   {  if(Type == Series[i][1])
      {  _h += 1.0;
         if(i != 0)
         {  _eh_sum += 1.0;
            if(Series[i][1] == Series[i - 1][1])
            {  _eh += 1.0;
            }
         }
      }
      if(i != 0 && Series[0][1] == Series[i][1])
      {  _e += 1.0;
      }
   }
   _h /= double(Series.Rows() - 1);
   _e /= double(Series.Rows() - 1);
   if(_eh_sum > 0.0)
   {  _eh /= _eh_sum;
   }
   double _posterior = 0.0;
   if(_e > 0.0)
   {  _posterior += ((_eh * _h) / _e);
   }
   return(_posterior);
}

Uma vez que obtemos nossa probabilidade posterior, ela representaria a probabilidade de o tipo de cluster ideal da posição (seja ‘m_cluster_long’ ou ‘m_cluster_short’) ocorrer, dado o tipo de cluster atual (ou seja, a evidência ou o tipo de cluster para o ponto de dados no índice zero). Este seria um valor na faixa de 0,0 a 1,0. Para que a hipótese respectiva, seja para posições longas ou curtas, seja provável, o valor retornado idealmente precisaria ser superior a 0,5. No entanto, situações especiais podem ser exploradas pelo leitor, onde valores ligeiramente menores podem produzir resultados interessantes.

O valor decimal, no entanto, precisaria ser normalizado para a faixa padrão de 0 a 100, que é a saída das funções de condição longa e curta. Para conseguir isso, simplesmente multiplicamos por 100,0. A listagem típica de uma condição longa ou curta está listada abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalBAYES::LongCondition(void)
{  int result = 0;
   vector _s_new, _s_old, _s;
   _s_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_series_size);
   _s_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_series_size);
   _s = _s_new - _s_old;
   matrix _series;
   _series.Init(_s.Size(), 2);
   for(int i = 0; i < int(_s.Size()); i++)
   {  _series[i][0] = _s[i];
   }
   SetCluster(_series);
   double _cond = GetPosterior(m_long_cluster, _series);
   _cond *= 100.0;
   //printf(__FUNCSIG__ + " cond: %.2f", _cond);
   //return(result);
   if(_cond > 50.0)
   {  result = int(2.0 * (_cond - 50.0));
   }
   return(result);
}

Com esta classe de sinal, ela pode ser facilmente montada em qualquer Expert Advisor via o MQL5 Wizard, utilizando os guias que estão aqui e aqui para leitores que possam ser novos no MQL5 Wizard.

Classe de Gerenciamento de Dinheiro

Uma classe personalizada de gerenciamento de dinheiro (MM) também pode ser implementada utilizando a Inferência Bayesiana. Mais uma vez, para começar, precisaríamos selecionar uma série temporal apropriada para basear nossa análise. No entanto, como mencionado na introdução, nossa escolha para isso com o MM será o desempenho histórico de negociações. Assim, como nosso Expert Advisor montado pelo wizard estará negociando apenas um símbolo, todo o histórico de negociações disponível para seleção, quando consultado, será aplicável ao Expert Advisor.

Ao utilizar a série temporal de histórico de negociações como base para a análise, estaremos adotando uma abordagem de uma das classes de gerenciamento de dinheiro integradas que é "otimizada em tamanho", onde o tamanho do volume de negociação é reduzido em proporção ao número recente de perdas consecutivas. Em nosso caso, no entanto, reduziremos o tamanho do lote se a probabilidade de nosso índice de cluster preferido (a hipótese) cair abaixo de outro parâmetro otimizável que estamos chamando de ‘m_condition’.

Então, o que estamos tentando estabelecer, em essência, é o índice de cluster ideal no qual podemos usar o dimensionamento regular de lotes em proporção à margem livre. Este índice de cluster é um identificador do tipo de curva de capital (como apenas um símbolo é negociado) no qual estamos livres para ajustar o tamanho do lote em proporção à margem livre. A referência ao "tipo de curva de capital" é um pouco ampla, já que nosso agrupamento segue o formato simples adotado na classe de sinal. Portanto, o que está sendo especificamente identificado aqui é o tipo de resultado da negociação, ou seja, se foi um ganho ou perda (resultados de lucro zero recebem um índice, mas é improvável que apareçam de forma significativa na análise).

Isso significa, por exemplo, que se o resultado favorável da negociação para o ajuste do tamanho do lote com a margem livre for um resultado de negociação lucrativo, estaríamos examinando a sequência de resultados de negociações anteriores e tentando estabelecer a probabilidade de ter outro resultado lucrativo à luz da evidência (o resultado da negociação no índice zero da série de entrada).

Isso meio que exige outro parâmetro otimizável na forma de um limite de probabilidade que avalia a probabilidade de repetir as condições favoráveis ​​alvo, de modo que, se o resultado posterior ficar aquém desse limite, o dimensionamento da posição é reduzido em proporção ao número de perdas contadas, como é o caso na classe de gerenciamento de dinheiro original "tamanho otimizado". A listagem para a função de otimização está abaixo:

//+------------------------------------------------------------------+
//| Optimizing lot size for open.                                    |
//+------------------------------------------------------------------+
double CMoneyBAYES::Optimize(int Type, double lots)
{  double lot = lots;
//--- calculate number of losses orders without a break
   if(m_decrease_factor > 0)
   {  //--- select history for access
      HistorySelect(0, TimeCurrent());
      //---
      int       orders = HistoryDealsTotal(); // total history deals
      int       losses=0;                    // number of consequent losing orders
      //--
      int      size=0;
      matrix series;
      series.Init(fmin(m_series_size,orders), 2);
      series.Fill(0.0);
      //--
      CDealInfo deal;
      //---
      for(int i = orders - 1; i >= 0; i--)
      {  deal.Ticket(HistoryDealGetTicket(i));
         if(deal.Ticket() == 0)
         {  Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history");
            break;
         }
         //--- check symbol
         if(deal.Symbol() != m_symbol.Name())
            continue;
         //--- check profit
         double profit = deal.Profit();
         //--
         series[size][0] = profit;
         size++;
         //--
         if(size >= m_series_size)
            break;
         if(profit<0.0)
            losses++;
      }
      //--
      series.Resize(size,2);
      SetCluster(series);
      double _cond = GetPosterior(Type, series);
      //--
      //---
      if(_cond < m_condition)
         lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2);
   }
//--- normalize and check limits


...

//---

...

//---

...

//---
   return(lot);
}

Todos os outros parâmetros de fator de diminuição e porcentagem de margem investida permanecem os mesmos que na classe original de MM "otimizada em tamanho".

Para comparação com a Inferência Bayesiana, podemos considerar o Critério de Kelly, que considera os resultados vencedores e a razão risco-retorno, mas com uma visão de longo prazo e não necessariamente atualizando os critérios de alocação por meio do desempenho recente ou intermediário. Sua fórmula é dada como K = W – ((1 - W) / R).

onde:

• K é a porcentagem de alocação.
• W é a porcentagem de vitórias, e
• R é o fator de lucro.
  

Essa abordagem foi adotada por alguns gurus de investimento devido à sua visão de longo prazo na alocação de capital, no entanto, pode-se argumentar que é o posicionamento que deveria ter uma abordagem de longo prazo, não a alocação. Perspectivas de longo prazo são frequentemente adotadas em questões operacionais, mas onde o risco está envolvido, o curto prazo tende a ser mais crítico, o que é por isso que a execução é um assunto separado.

Portanto, as vantagens da Inferência Bayesiana sobre o Critério de Kelly (KC) podem ser resumidas com o argumento de que o KC assume uma vantagem constante nos mercados, o que pode ser verdade em casos onde se tem um horizonte muito longo. A ignorância dos custos de transação e deslizamento é outro argumento semelhante contra o KC, e embora ambos possam ser ignorados no longo prazo, é justo dizer que a maneira como a maioria dos mercados está estruturada permite que alguém negocie em nome de, ou com o capital de outra pessoa. Isso implica inerentemente que um grau considerável de sensibilidade precisa ser aplicado a essas excursões de curto prazo, pois elas podem determinar se o trader ou investidor ainda será confiável com o capital em jogo.

Classe de Trailing Stop

Finalmente, analisamos uma implementação personalizada de trailing stop que também utiliza a Inferência Bayesiana. Nossa série temporal para isso terá que focar no intervalo da barra de preço, pois isso é sempre um bom indicador de volatilidade, uma métrica chave que influencia em quanto um nível de stop loss deve ser ajustado para posições abertas. Temos usado mudanças nos valores de séries temporais; para o sinal, usamos mudanças no preço de fechamento, enquanto para o gerenciamento de dinheiro usamos o resultado da negociação (lucros, em vez de níveis de patrimônio da conta), que são, de fato, mudanças nos níveis de patrimônio da conta. Mudanças, quando aplicadas ao nosso método rudimentar de agrupamento, nos dão um conjunto básico, mas funcional, de índices que são úteis para agrupar esses pontos de dados de ponto flutuante.

Uma abordagem semelhante para uma classe de trailing stop focaria nas mudanças no intervalo de preço entre o valor máximo e mínimo. Nossa hipótese com essa abordagem seria que estamos procurando um índice de cluster ('m_long_cluster' ou 'm_short_cluster', ambos poderiam ser iguais nesta situação de trailing) de forma que, quando for mais provável que ele siga na série temporal, devemos mover nosso stop loss por um valor proporcional ao intervalo atual da barra de preço.

Usamos parâmetros de entrada separados para posições longas e curtas, mas, em princípio, poderíamos ter usado apenas um para servir tanto para o ajuste de stop loss em posições longas quanto curtas. Nossa listagem que implementa isso está abaixo para posições longas:

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingBAYES::CheckTrailingStopLong(CPositionInfo *position,double &sl,double &tp)
  {
//--- check

...

//---
 
...

//---
   sl=EMPTY_VALUE;
   tp=EMPTY_VALUE;
   //
   
   vector _h_new, _h_old, _l_new, _l_old, _s;
   _h_new.CopyRates(m_symbol.Name(), m_period, COPY_RATES_HIGH, 0, m_series_size);
   _h_old.CopyRates(m_symbol.Name(), m_period, COPY_RATES_HIGH, 1, m_series_size);
   _l_new.CopyRates(m_symbol.Name(), m_period, COPY_RATES_LOW, 0, m_series_size);
   _l_old.CopyRates(m_symbol.Name(), m_period, COPY_RATES_LOW, 1, m_series_size);
   _s = (_h_new - _l_new) - (_h_old - _l_old);
   matrix _series;
   _series.Init(_s.Size(), 2);
   for(int i = 0; i < int(_s.Size()); i++)
   {  _series[i][0] = _s[i];
   }
   SetCluster(_series);
   double _cond = GetPosterior(m_long_cluster, _series);
   //
   delta=0.5*(_h_new[0] - _l_new[0]);
   if(_cond>0.5&&price-base>delta)
     {
      sl=price-delta;
     }
//---
   return(sl!=EMPTY_VALUE);
  }

Uma comparação desta com classes alternativas de trailing stop, como as incorporadas na biblioteca MQL5, é fornecida na seção de testes e relatórios abaixo.

Testes e Relatórios

Realizamos testes no EUR JPY no intervalo de 4 horas para o ano de 2022. Como desenvolvemos 3 classes personalizadas separadas que podem ser usadas em experts criados pelo wizard, montaremos sequencialmente 3 Expert Advisors separados, sendo que o primeiro terá apenas a classe de sinal enquanto o gerenciamento de dinheiro utilizará lotes fixos e nenhum trailing stop será usado; o segundo terá a mesma classe de sinal, mas com a adição da classe de gerenciamento de dinheiro que codificamos acima e sem trailing stop; enquanto o último Expert Advisor terá todas as 3 classes que codificamos acima. Diretrizes sobre como montar essas classes via o wizard estão disponíveis aqui.

Se executarmos testes nos três Expert Advisors, obteremos os seguintes relatórios e curvas de patrimônio:

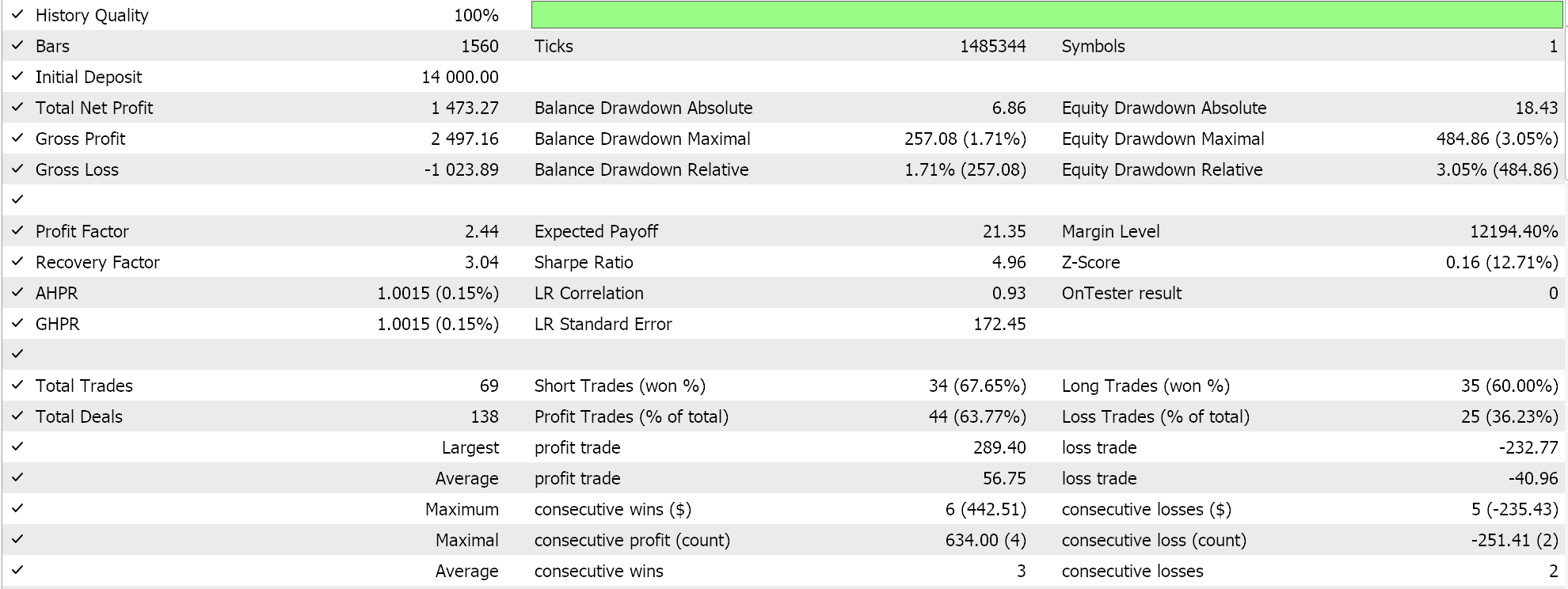
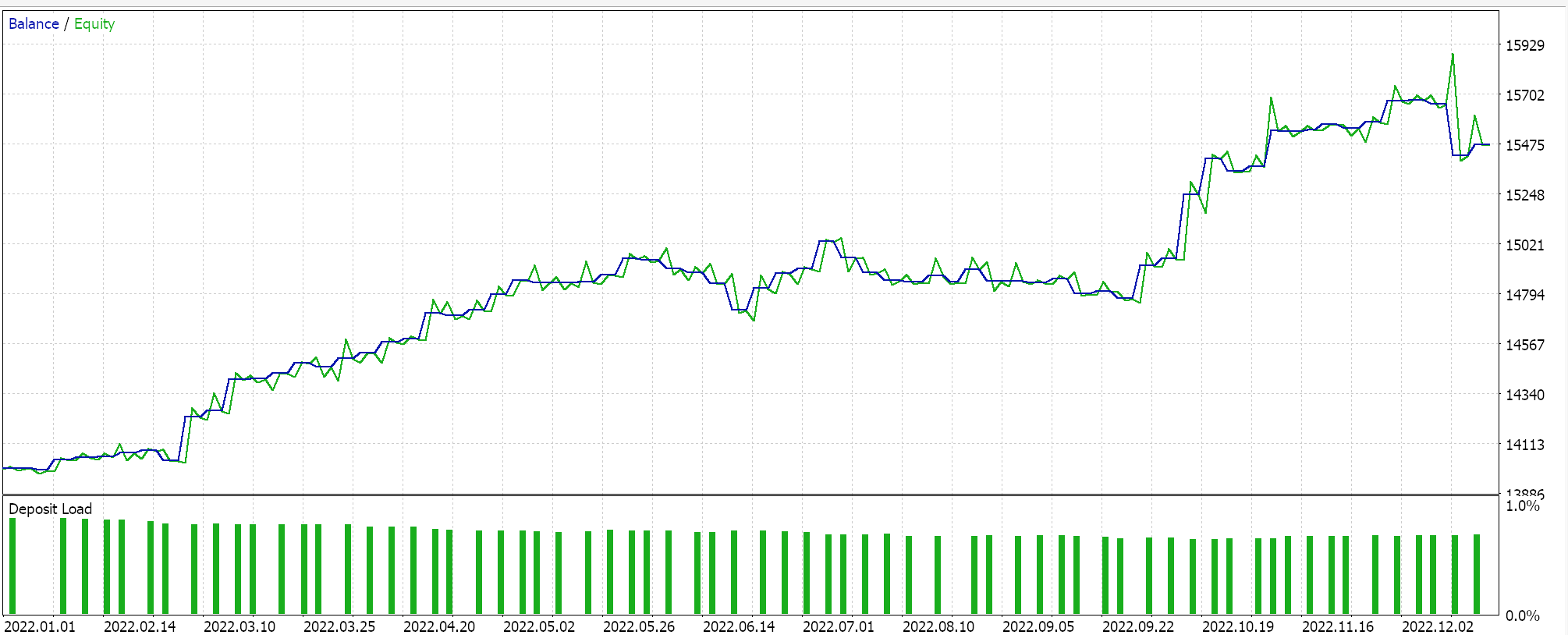
Relatório e curva de patrimônio do Expert Advisor com apenas a classe de sinal BI.

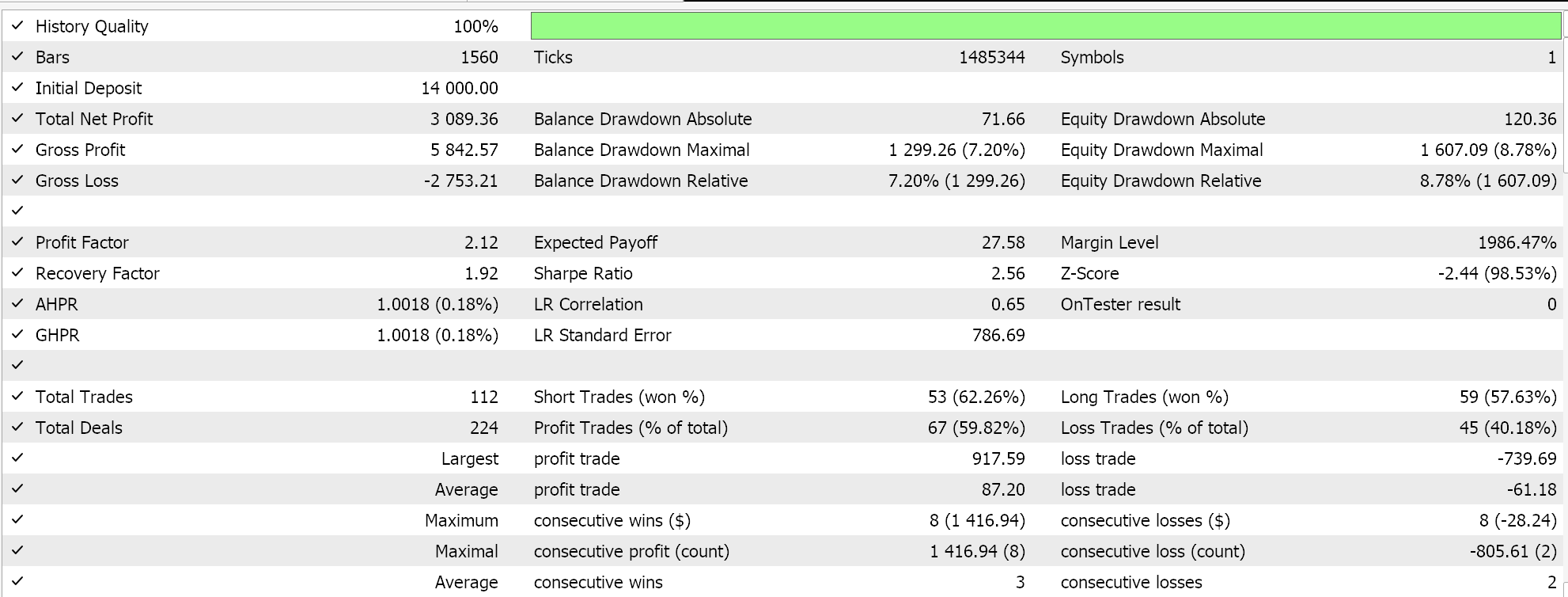
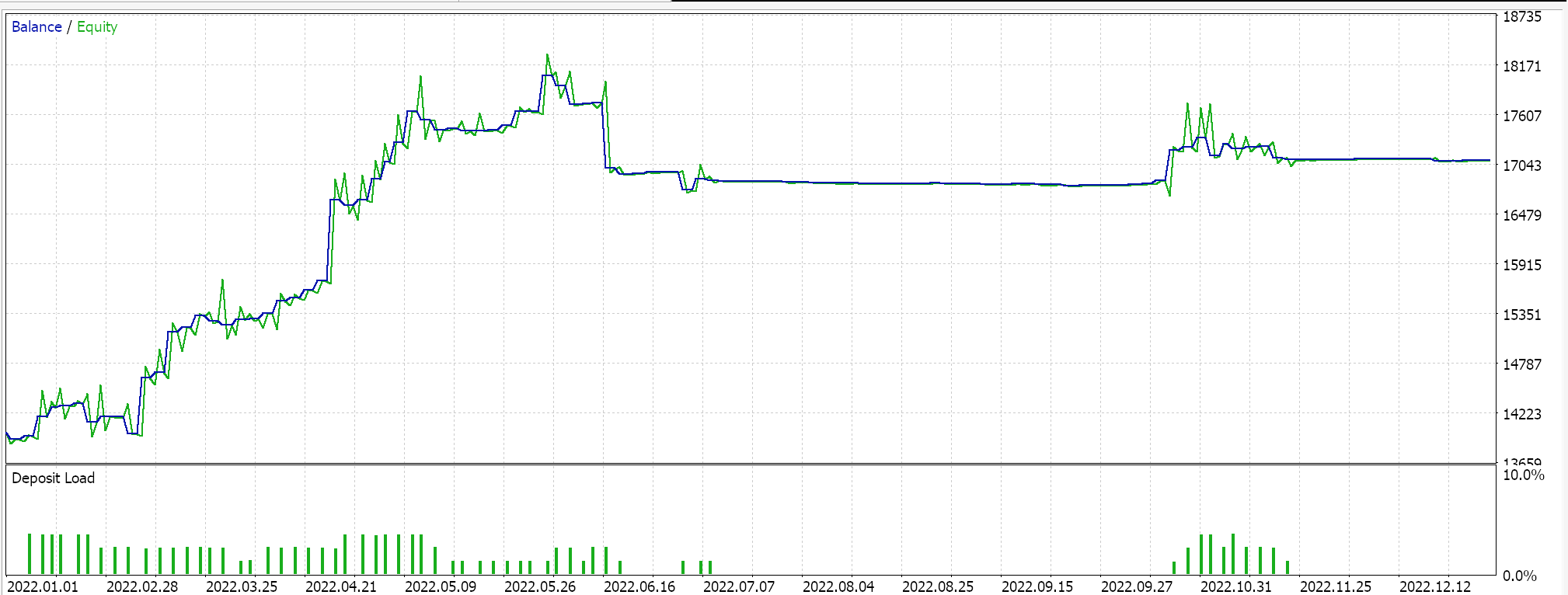
Relatório e curva de patrimônio do Expert Advisor com classe de sinal BI e classe de gerenciamento de dinheiro.

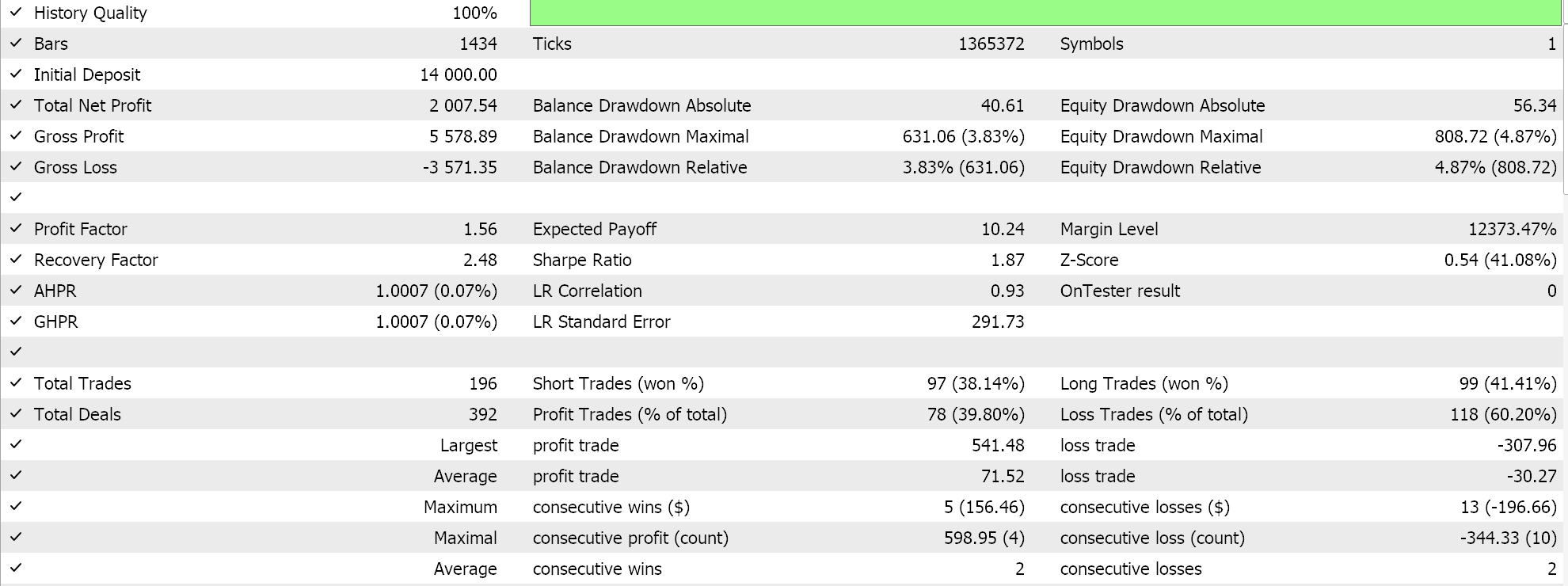
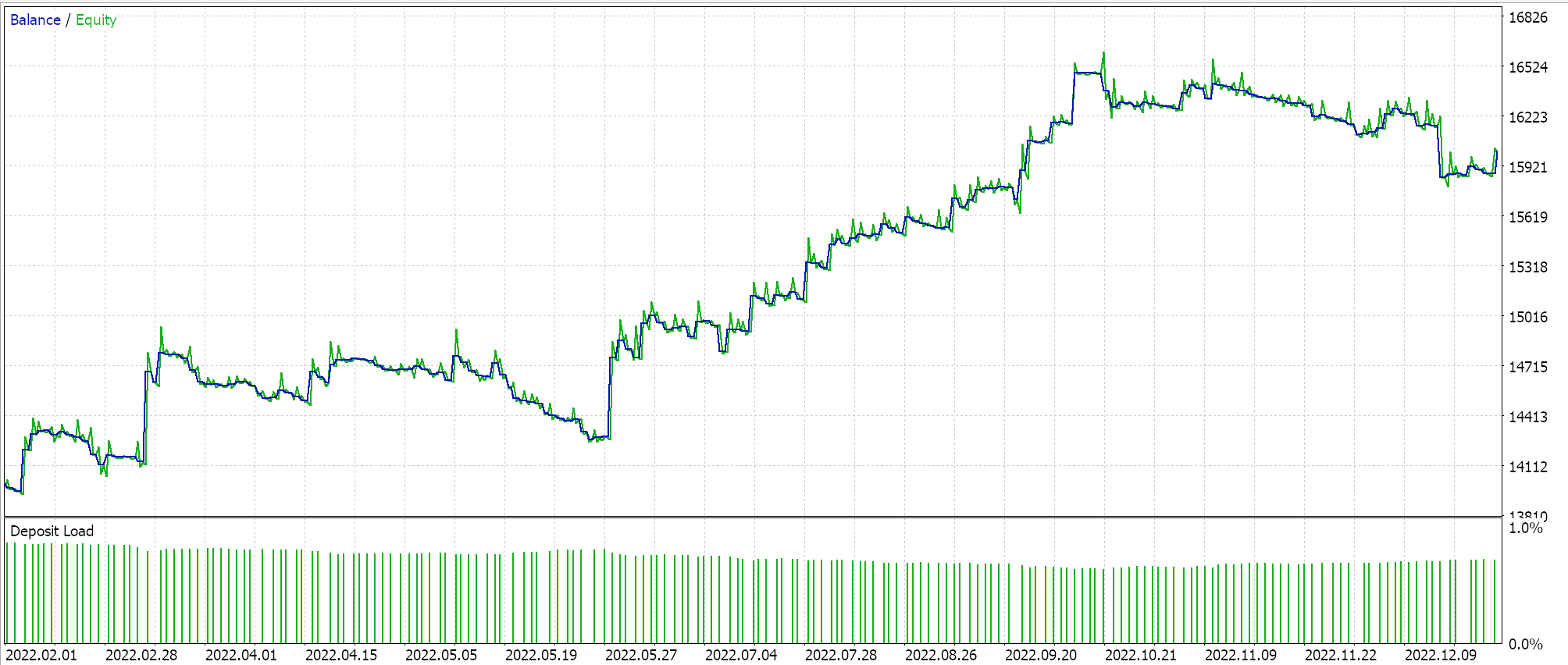
Relatório e curva de patrimônio do Expert Advisor com classe de sinal BI, classe de gerenciamento de dinheiro e trailing stop.

Parece que, à medida que mais adaptação da Inferência Bayesiana, desde a classe de sinal até o gerenciamento de dinheiro e a trailing stop, é feita, o desempenho geral tende a se correlacionar positivamente. Este teste foi feito com ticks reais, mas, como sempre, testes independentes por períodos mais longos são ideais, e é algo que o leitor deve ter em mente. Como controle, podemos otimizar 3 Expert Advisors separados que usam as classes da biblioteca. Em todas essas execuções de teste, não usamos metas de preço de saída e confiamos apenas no sinal de abertura e fechamento para controlar as saídas. Escolhemos a classe de sinal do awesome oscillator, a classe de gerenciamento de dinheiro otimizada em tamanho e a classe de trailing stop de média móvel para usar nos Expert Advisors de "controle". Testes semelhantes aos acima produzem os seguintes resultados:

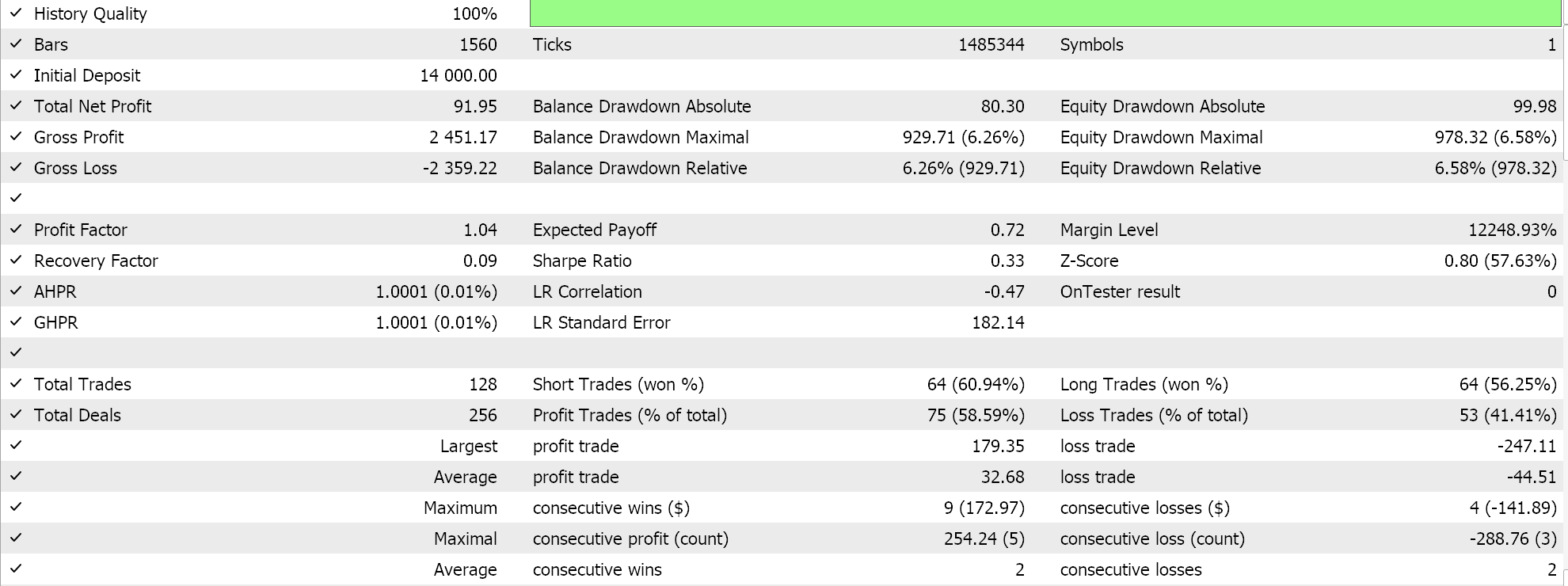
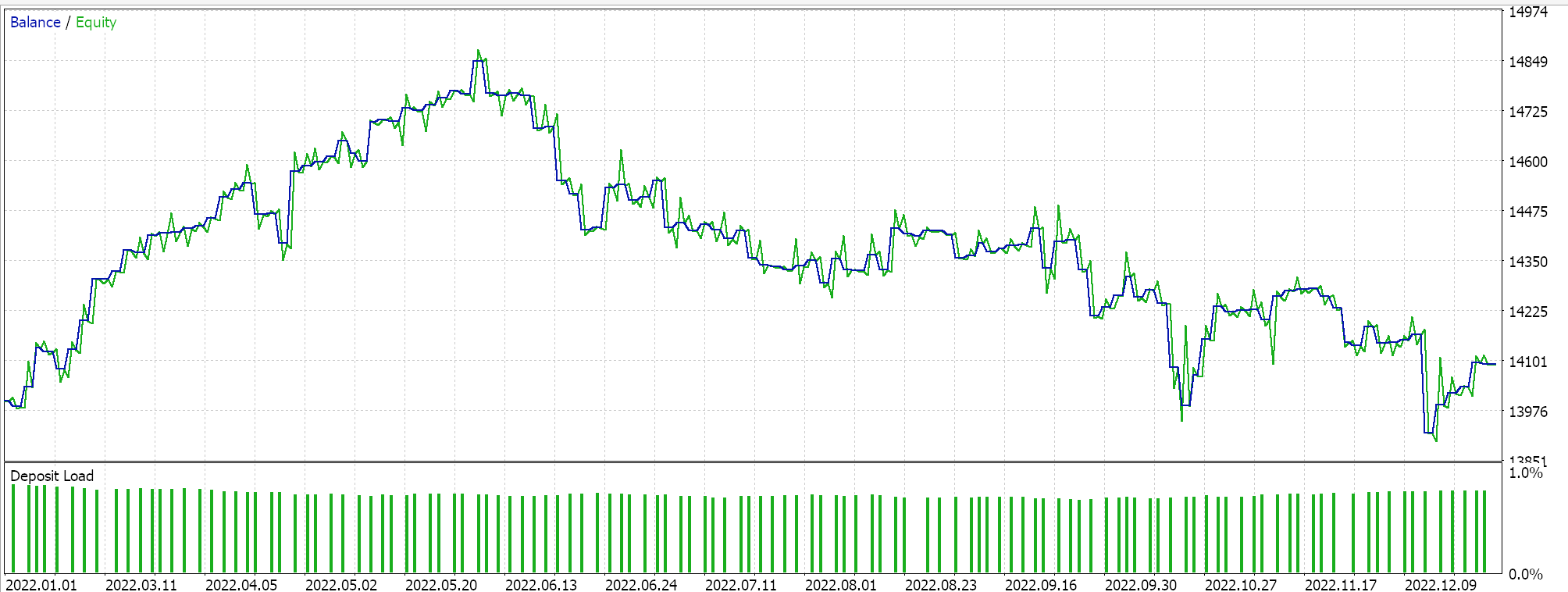
Relatório e curva de patrimônio do Expert Advisor com apenas a classe do awesome oscillator.

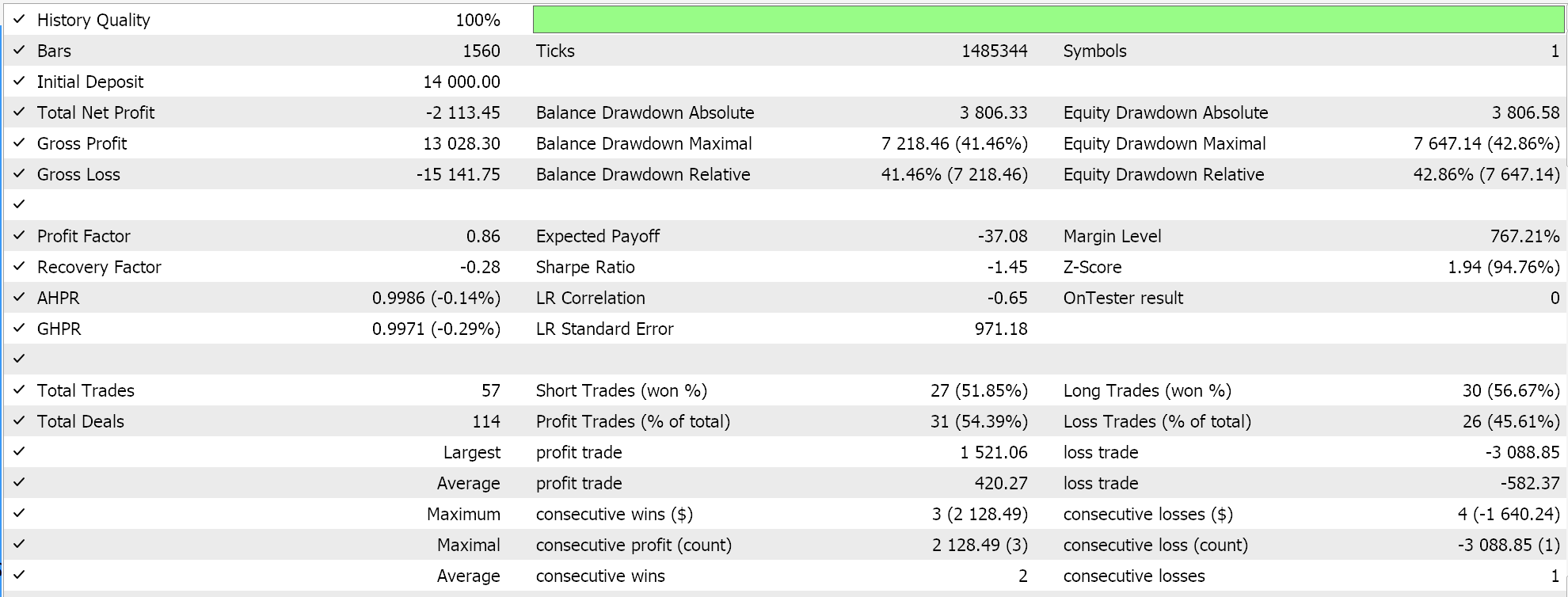
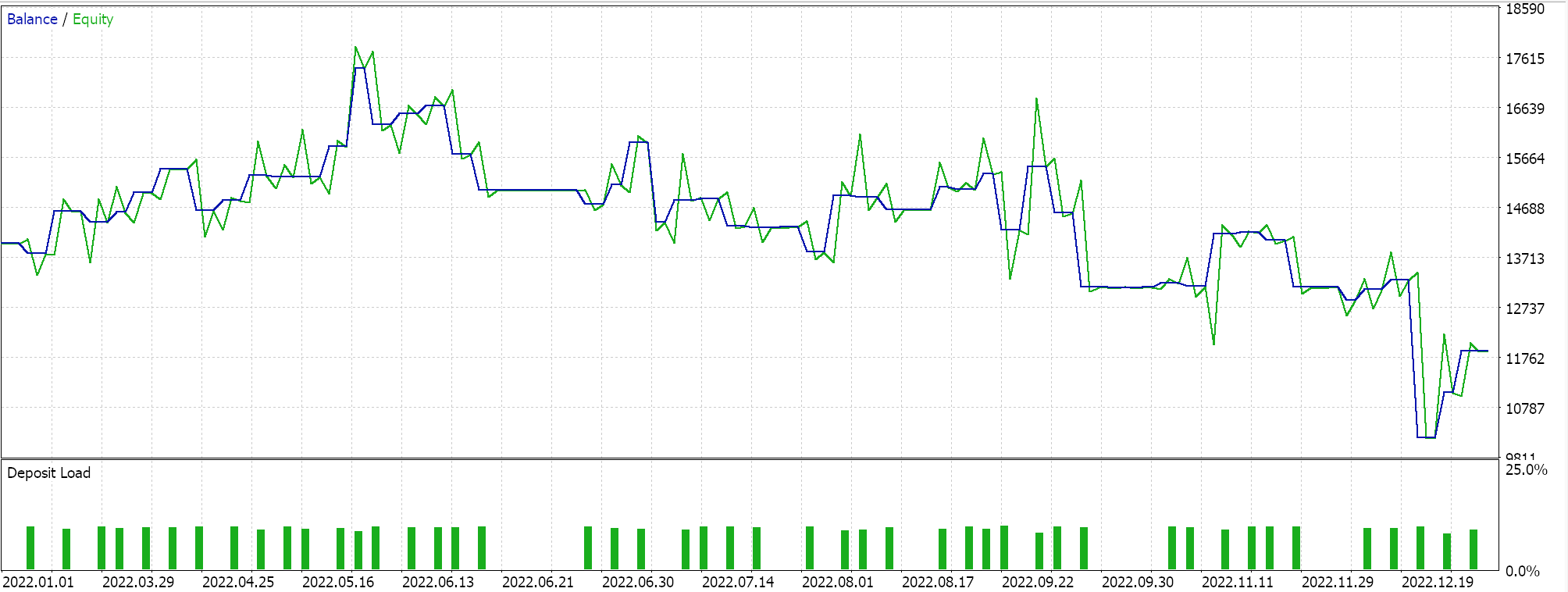
Relatório e curva de patrimônio do Expert Advisor de controle com 2 das classes selecionadas.

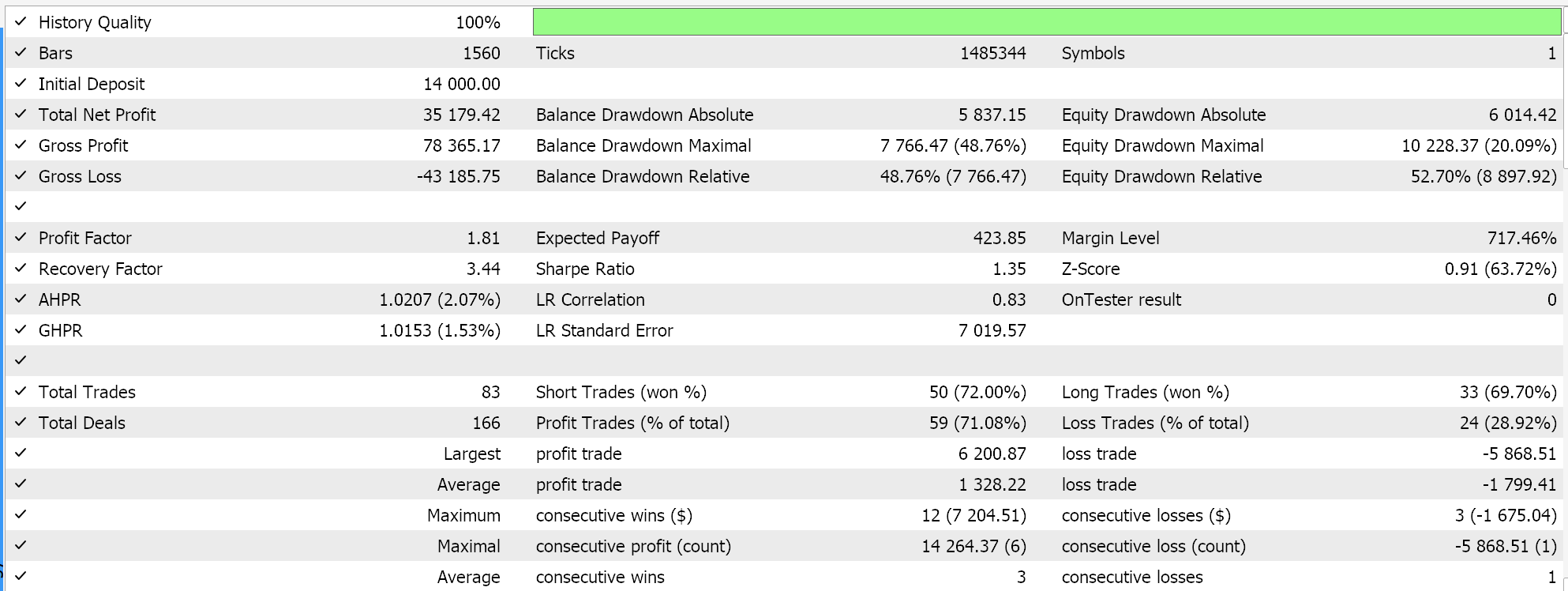
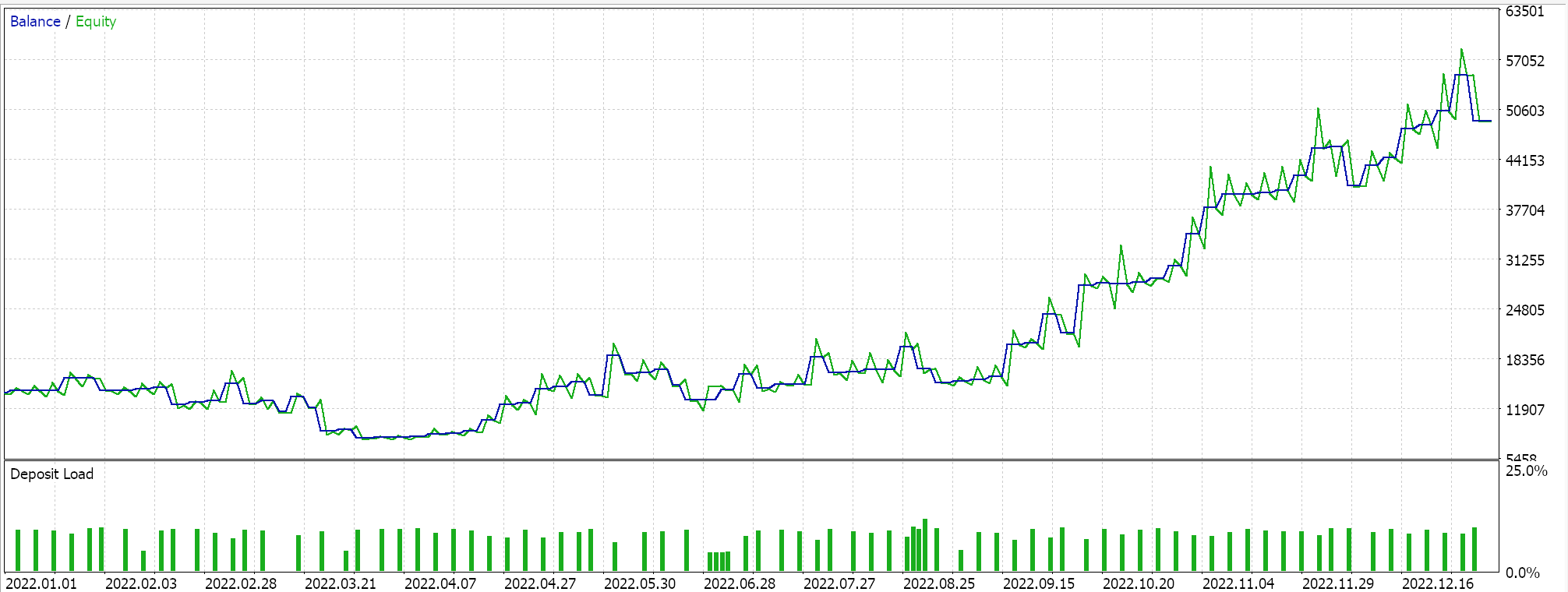
Relatório e curva de patrimônio do Expert Advisor de controle com todas as 3 classes selecionadas.

O desempenho do nosso controle fica atrás do expert BI, com exceção do terceiro teste. Nossa escolha de classe de sinal, gerenciamento de dinheiro e trailing alternativas também influenciou bastante esse "resultado", no entanto, o objetivo geral era estabelecer se há uma variação significativa no desempenho entre nosso Expert Advisor com Inferência Bayesiana e o que está disponível na biblioteca MQL5, e para isso, a resposta é clara.

Conclusão

Para concluir, testamos o papel da Inferência Bayesiana na construção de um Expert Advisor simples, incorporando suas ideias básicas nas três classes principais dos Expert Advisors montados pelo wizard do MQL5. Nossa abordagem aqui foi estritamente introdutória e não cobriu aspectos significativos, especialmente no que diz respeito ao uso de algoritmos de cluster mais elaborados ou até mesmo conjuntos de dados multidimensionais. Essas são todas áreas que podem ser exploradas e que podem fornecer uma vantagem, se testadas adequadamente em períodos históricos decentes, com dados de ticks de boa qualidade. Muito mais pode ser testado sob a Inferência Bayesiana, e o leitor é bem-vindo a explorar isso, já que os experts montados pelo wizard continuam sendo uma ferramenta confiável para testar e prototipar ideias.