ニューラルネットワークが簡単に（第21部）：変分オートエンコーダ(Variational autoencoder、VAE)

MetaTrader 5 — トレーディングシステム | 1 11月 2022, 09:47

416

Dmitriy Gizlyk

内容

はじめに

教師なし学習法の研究を続けます。前回の記事で、オートエンコーダについて学びました。オートエンコーダのトピックは幅広く、1つの記事には収まりません。このトピックを続けて、オートエンコーダのバリエーションの1つである変分オートエンコーダを紹介したいと思います。

1.変分オートエンコーダのアーキテクチャ

変分オートエンコーダのアーキテクチャーについての学習に移る前に、前回の記事で見つけた要点に戻りましょう。

オートエンコーダは、バックプロパゲーション法によって訓練されるニューラルネットワークである
オートエンコーダは、エンコーダブロックとデコーダブロックで構成される
エンコーダのソースデータ層とデコーダの結果層には同じ数の要素が含まれる
エンコーダとデコーダは初期状態に関する圧縮された情報を含む潜在状態の「ボトルネック」によって結合される

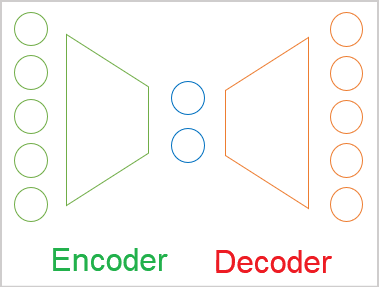
訓練の過程で、デコーダによる潜在状態のデコードの結果と元のデータとの間の最大の類似性を目標にします。この場合、元のデータに関する最大限の情報が潜在状態で暗号化されていると断言できます。そして、このデータはある程度の確率で元のデータを復元するのに十分です。ただし、オートエンコーダには、データ圧縮の問題に対しての他に幅広い用途があります。

次に、オートエンコーダを使用して画像を生成するときに特定された問題に対処します。初期データを特定のクラウドで表すことにします。訓練中に、モデルはランダムに選択された2つのオブジェクトAとBを完全に復元することを学習しました。簡単に言えば、エンコーダとデコーダは、潜在状態のオブジェクトAに1を指定し、オブジェクトBに5を指定することに合意しました。これはデータ圧縮の問題を解決するときには問題にありません。それどころか、オブジェクトは十分に分離可能であり、モデルはそれらを復元できます。

データクラウド

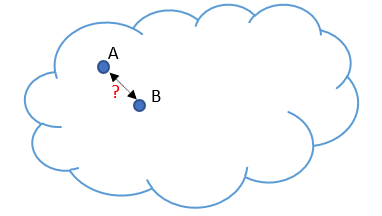
ただし、研究者がオートエンコーダを使用して画像を生成しようとしたとき、2つのオブジェクト間の潜在状態値のギャップが問題であることが判明しました。実験では、オブジェクトに近いゾーンで潜在状態の値がオブジェクトAからオブジェクトBに変化すると、デコーダは指定されたオブジェクトを多少の歪みで復元することが示されました。しかし、インターバルの途中で、デコーダが元のデータの特徴ではない何かを生成しました。

言い換えれば、元のデータがエンコードおよび圧縮されるオートエンコーダの潜在状態は、不連続である場合もあれば、何らかの補間が可能である場合もあります。これは、オートエンコーダをデータ生成に適用した場合の基本的な問題です。

もちろん、ここではデータを生成するつもりはありませんが、世界は絶えず変化していることを忘れないでください。市場の状況を調査する過程で、将来、数学的精度をもって訓練セットからパターンを取得できる確率は非常に小さくなります。しかし、私たちが望むのは、市場の状況を正しく処理し、適切な結果を生み出すモデルを持つことです。したがって、生成モデルだけでなく、適用分野でもこの問題の解決策を見つける必要があります。

この問題に対する簡単な解決策はありません。訓練標本の増加と、さまざまな潜在状態の正則化手法の使用により、問題のスケーリングがおこなわれます。例は、正則化を適用することで、オブジェクトの潜在状態のベクトル間の距離を縮めることです。例として、数字1と2があるとします。ただし、1.5としてエンコードされるオブジェクトが表示される場合があり、これによってデコーダが混乱します。オーバーラップに近づくと、オブジェクトを分離するのが難しくなる可能性があります。

各状態が離散的なままであるため、訓練標本を増やすと同様の効果があります。さらに、訓練標本の増加は、訓練に費やされる時間とリソースの増加につながります。同時に、ソースデータの個々のパターンを選択しようとするオートエンコーダは、最も近い隣接状態までの距離を最大化しようとします。

私たちのモデルとは異なり、離散状態のそれぞれが特定のクラスのオブジェクトの代表であることがわかっています。私たちのソースデータクラウドでは、そのようなオブジェクトは互いに近くにあり、特定の分散法則に従って分散されています。モデルに事前知識を追加しましょう。

データクラウド

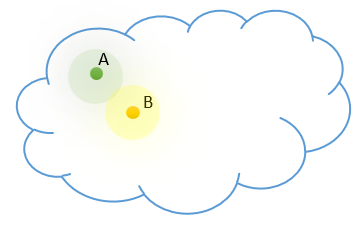
でも、モデルが単一の値ではなく、値の範囲全体を返すようにするにはどうすればよいでしょうか。この値の範囲では、離散値の数とその広がりが異なる場合があります。これは、クラスタリングの問題を思い起こさせるかもしれませんが、クラス数はわかっていません。この数は、使用されるソースデータ標本によって異なる場合があるので、より一般的なデータ表現モデルが必要です。

すでに述べたように、ソースデータクラウド内の各クラスのオブジェクトの配置は、ある程度の分布の影響を受けます。おそらく最も一般的に使用されるのは正規分布なので、エンコーダ出力での潜在状態の各特徴が正規分布に対応すると仮定しましょう。正規分布は、数学的な期待値と標準偏差の2つのパラメータによって決定されます。特徴ごとに1つの離散値ではなく、分析されたソースデータパターンが属する分布の数学的期待値（平均値）と標準偏差の2つを返すようにエンコーダに頼んてみます。

しかし、エンコーダ出力で値をどのように呼び出しても、デコーダはそれらを数値として認識します。これが変分オートエンコーダのアーキテクチャです。このアーキテクチャでは、エンコーダとデコーダの間で値を直接送信することはありません。逆に、エンコーダから分布パラメータを取得し、指定された分布からランダムな値をサンプリングして、デコーダに入力します。したがって、エンコーダによって同じソースデータパターンを処理した結果、デコーダ入力は値の異なるベクトルを持つ場合がありますが、常に同じ正規分布に従います。

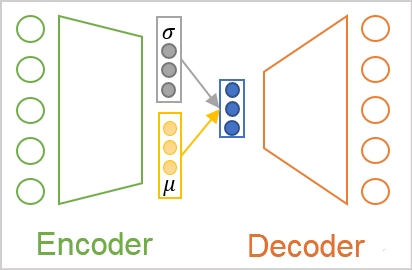
ご覧のとおり、このような操作の結果として、デコーダ入力は常にエンコーダ出力の2分の1の値になります。

しかし、ここでモデルの訓練の問題に直面します。モデルはバックプロパゲーション法を使用して訓練されます。この方法の主な要件の1つは、誤差勾配のパスに沿ったすべての関数の微分可能性です。残念ながら、これは乱数発生器には当てはまりません。

しかし、この問題も解決されました。正規分布の特性とそれを表すパラメータを詳しく見てみましょう。正規分布は、数学的期待値を中心とする数学的確率分布です。値の68%は、分布の中心から標準偏差以下の距離にあります。したがって、数学的期待値の変化によって分布の中心がシフトします。標準偏差を変更すると、中心付近の値の分布がスケーリングされます。

したがって、指定されたパラメータを使用して正規分布から単一の値を取得するには、数学的な期待値「0」と標準偏差「1」の標準正規分布の値を生成できます。次に、結果の値に指定された標準偏差が乗算され、指定された数学的期待値に加算されます。このアプローチは、reparameterization trick（再パラメータ化トリック）と呼ばれます。

その結果、フォワードパスで標準正規分布から乱数値を生成して保存します。次に、指定されたパラメータを使用して修正されたベクトルをデコーダに入力します。バックプロパゲーションパスでは、簡単に区別できる加算演算と乗算演算によってエラー勾配をエンコーダに簡単に渡します。微分不可能な乱数発生器は、このモデルでは使用されていません。

パズルを解いて、すべての落とし穴を回避できたように思えますが、実際の実験では、モデルが新しいルールに従ってプレイすることを望んでいないことが示されています。新しい入力でより複雑なルールを学習する代わりに、オートエンコーダは学習プロセス中に標準偏差の特徴を0に単純化しました。0を乗算すると、確率変数の効果がなくなり、デコーダは数学的な期待値の離散値を入力として受け取ります。標準偏差の特徴を0にすることで、モデルは上記のすべての努力を無効にし、エンコーダとデコーダの間での離散値の交換に戻ります。

モデルをルールに従って機能させるには、追加のルールと制限を導入する必要があります。まず、数学的期待値と標準偏差の特徴が標準正規分布のパラメータに可能な限り対応する必要があることをモデルに示します。これは、偏差ペナルティを追加することで実装できます。このような偏差の尺度として、カルバック・ライブラー情報量が選択されました。ここでは、数学的計算の詳細には触れません。正規分布パラメータから逸脱した経験値の誤差の結果は次のとおりです。この関数を使用して、潜在状態の値を正則化します。実際には、その値を潜在状態の誤差に加算します。

標準分布のカルバック・ライブラー情報量

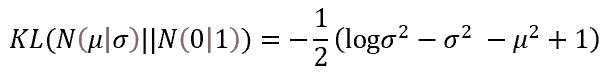
したがって、特徴パラメータが参照値（この場合は標準分布）から逸脱したときにモデルにペナルティを課すたびに、各特徴の分布パラメータを標準分布のパラメータ（0の数学的期待値と1の標準偏差）に近づけるようにモデルを強制します。

ここで、エンコーダ出力でこのように特徴を「プル」することは、個々のオブジェクトの特徴を抽出するという主な問題に反することに言及しなければなりません。正則化の追加により、すべての特徴が同じ力で参照値に引き寄せられます。つまり、パラメータを同じにしようとします。同時に、デコーダの誤差勾配は、異なるオブジェクトの特徴を可能な限り分離しようとします。実行された2つのタスクの間には明らかに利益相反があるため、モデルは問題を解決する際にバランスを見つける必要があります。ただし、バランスが常に期待に応えられるとは限りません。この平衡点を制御するために、追加のハイパーパラメータをモデルに導入します。全体的な結果に対するカルバック・ライブラー情報量の影響を制御します。

2.実装

変分オートエンコーダアルゴリズムの理論的側面を検討した後は、実用的な部分に進むことができます。変分オートエンコーダのエンコーダとデコーダを実装するために、以前に作成したライブラリから完全に接続されたニューラル層を再び使用します。本格的な変分オートエンコーダを実装するには、潜在状態を操作するためのブロックが必要です。このブロックでは、変分オートエンコーダの上記のすべての革新を実装します。

ライブラリでニューラルネットワークを編成する一般的なアプローチを維持するために、潜在状態処理アルゴリズム全体を別のニューラルレイヤーCVAEでラップします。クラスの実装に進む前に、デバイスのOpenCL側に機能を実装するカーネルを作成しましょう。

フィードフォワードカーネルから始めましょう。潜在状態の特徴の正規分布を表すレイヤーパラメータを入力します。1つ注意点があります。数学的な期待値は、任意の値を取ることができますが、標準偏差は負でない値しか取りません。異なるニューラル層を使用してパラメータを生成した場合、異なるニューロン活性化関数を使用できますが、私たちのライブラリアーキテクチャでは線形モデルしか作成できません。同時に、1つのニューラル層内で使用できる活性化関数は1つだけです。

繰り返しますが、値がどのように呼び出されるかはモデルには関係ありません。モデルは数式を実行するだけです。これは、モデルの正しい構築を可能にするため、私たちにとってのみ重要です。上記のカルバック・ライブラー情報量の式に注目してください。分散とその対数が使用されています。分布の分散は標準偏差の2乗に等しく、負にはありません。その対数の値は、正負の両方になることができます。引数の2乗の自然対数のグラフを見てください。X座標と関数グラフの交点は、ちょうど1です。この値は、標準偏差の目標です。さらに、-1から1までの関数値の間隔では、関数の引数は0.6から1.6までの値をとり、標準偏差に対する期待を満たしています。

自然対数x^2

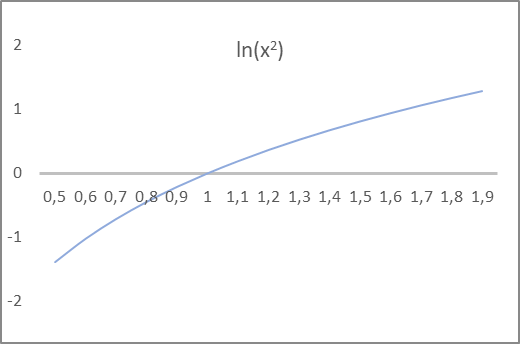
したがって、数学的期待値と分布分散の自然対数を出力するようにモデルエンコーダに指示します。ニューラル層の活性化関数として双曲線正接を使用できます。これは、その値の範囲が、分布の数学的期待値とその分散の対数の両方に対する期待値を満たすためです。

これで、概念的なアプローチは明確です。次に、関数のプログラミングに移りましょう。フィードフォワードカーネルのVAE_FeedForwardから始めます。カーネルは、3つのデータバッファへのポインタをパラメータで受け取ります。そのうちの2つは元のデータを含み、1つは結果バッファです。OpenCL側には、疑似乱数発生器はありません。そのため、メインプログラム側で標準配布の要素をサンプリングします。次に、それらをrandomバッファによってフィードフォワードカーネルに渡します。

2番目のソースデータバッファには、エンコーダの結果が含まれます。おそらくすでにお察しのとおり、数学的期待値のベクトルと分散の対数のベクトルは、同じinputsバッファに含まれます。

次に、カーネル本体に再パラメータ化トリックを実装するだけです。エンコーダが標準偏差の代わりに分散の対数を提供することを忘れないでください。したがって、トリックを実行する前に、標準偏差値を取得する必要があります。

自然対数の逆数は指数関数です。この関数を使用して分散を見つけることができます。分散の平方根を抽出すると、標準偏差が得られます。オプションとして、累乗の性質を使用して、分散の対数の半分の指数を求めれば、これも標準偏差です。

累乗の性質

フィードフォワードカーネルの本体では、まず現在のスレッドの識別子と実行中のスレッドの総数を特定します。これらは、必要なセルへのソースバッファと結果バッファ内のポインタとして機能します。次に、分散の対数から得られた標準偏差を使用して、再パラメータ化トリックを実行します。結果バッファの対応する要素に結果を書き込み、カーネルを終了します。

__kernel void VAE_FeedForward(__global float* inputs,
                              __global float* random,
                              __global float* outputs
                             )
  {
   uint i = (uint)get_global_id(0);
   uint total = (uint)get_global_size(0);
   outputs[i] = inputs[i] + exp(0.5f * inputs[i + total]) * random[i];
  }

このように、フィードフォワードカーネルアルゴリズムは非常に単純です。次に、OpenCLコンテキスト側でのバックプロパゲーションパスの整理に進みます。変分オートエンコーダの潜在状態層には、訓練可能なパラメータは含まれません。したがって、バックプロパゲーションプロセス全体は、デコーダからエンコーダへの誤差勾配の送信を整理することになります。これは、VAE_CalcHiddenGradientカーネルに実装されます。

このカーネルを実装するときは、フィードフォワードパス中にエンコーダの結果ベクトルから2つの要素を取得し、再パラメータ化トリックの後に1つの機能をデコーダへの入力として渡したことに注意してください。したがって、デコーダから1つの誤差勾配を取得し、それを対応する2つのエンコーダ要素に分配する必要があります。

数学的な期待値については、すべてが単純です（加算すると、誤差勾配は両方の項に完全に転送されます）。ただし、分散対数については、複雑な関数の導関数を扱います。

分散の対数の導関数

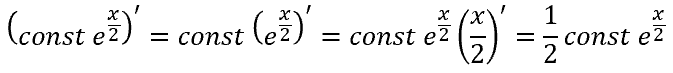
ただし、逆の見方もあります。モデルをルールに従って機能させるために、カルバック・ライブラー情報量を導入しました。次に、標準分布基準値からの分布パラメータの偏差の誤差勾配を、デコーダから受け取った誤差勾配に追加します。

カーネルVAE_CalcHiddenGradientの実装を見てみましょう。このカーネルは、パラメータで4つのデータバッファと1つの定数へのポインタを受け取ります。受け取ったバッファのうち3つは元の情報を保持し、1つは勾配の結果を記録してエンコーダレベルに転送するために使用されます。

inputs：エンコーダフィードフォワードの結果バッファ（数学的期待値と特徴分散の対数が含まれる）
random：フィードフォワードパスで使用される標準偏差要素の値
gradient：デコーダから受け取ったエラー勾配
inp_grad：エンコーダに渡されたエラー勾配を書き込むための結果バッファ
kld_mult：合計結果に対するカルバック・ライブラー情報量の影響係数の離散値

カーネル本体では、まず現在のスレッドのシリアル番号と実行中のカーネルスレッドの総数を特定します。これらの値は、入力バッファと結果バッファの必要な要素へのポインタとして使用されます。

次に、カルバック・ライブラー情報量の値を決定します。経験的分布と参照分布の間の距離を最小限に抑えるように努力していることに注意してください。つまり、距離を0に減らします。つまり、誤差は符号が反対の偏差値に等しくなります。不要な操作をなくすには、偏差を求める式の前にあるマイナス記号を削除します。結果に対する発散の影響係数によって値を調整します。

次に、誤差勾配をエンコーダレベルに渡します。ここでは、上記の関数の導関数に従って、各分布パラメータの2つの勾配の合計を渡します。

__kernel void VAE_CalcHiddenGradient(__global float* inputs,
                                     __global float* inp_grad,
                                     __global float* random,
                                     __global float* gradient,
                                     const float kld_mult
                                    )
  {
   uint i = (uint)get_global_id(0);
   uint total = (uint)get_global_size(0);
   float kld = kld_mult * 0.5f * (inputs[i + total] - exp(inputs[i + total]) - pow(inputs[i], 2.0f) + 1);
   inp_grad[i] = gradient[i] + kld * inputs[i];
   inp_grad[i + total] = 0.5f * (gradient[i] * random[i] * exp(0.5f * inputs[i + total]) -
                                 kld * (1 - exp(inputs[i + total]))) ;
  }

OpenCLプログラムで操作を完了し、メインプログラム側の機能の実装に進みます。まず、ニューラル層の基本クラスCNeuronBaseOCLから派生した新しいニューラル層クラスCVAEを作成します。

このクラスでは、1つの変数m_fKLD_Multを追加して全体的な結果に対するカルバック・ライブラーの影響係数を格納し、それを指定するSetKLDMultメソッドを追加します。また、標準偏差のランダムな値を書き込むために、追加のバッファm_cRandomを作成します。値は、統計および数学演算用の標準ライブラリ「Math\Stat\Normal.mqh」を使用してサンプリングされます。

さらに、機能を実装するために、フィードフォワードメソッドとバックプロパゲーションメソッドをオーバーライドします。ファイルを操作するためのメソッドもオーバーライドします。

class CVAE : public CNeuronBaseOCL
  {
protected:
   float             m_fKLD_Mult;
   CBufferDouble*    m_cRandom;

   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL); 
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } 

public:
                     CVAE();
                    ~CVAE();
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual void      SetKLDMult(float value) { m_fKLD_Mult = value;}
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);      
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronVAEOCL; }
  };

クラスのコンストラクタとデストラクタは非常に単純です。最初の例では、新しい変数の初期値を設定し、データバッファインスタンスを初期化して一連の確率変数を処理します。

CVAE::CVAE()   : m_fKLD_Mult(0.01f)
  {
   m_cRandom = new CBufferDouble();
  }

クラスデストラクタでは、コンストラクタで作成されたバッファのオブジェクトを削除します。

CVAE::~CVAE()
  {
   if(!!m_cRandom)
      delete m_cRandom;
  }

クラスインスタンスの初期化メソッドは複雑ではありません。実際、ほとんどすべてのオブジェクト初期化の機能は、親クラスのメソッドによって実装されます。ここでは、継承されたオブジェクトを初期化するために必要なすべてのコントロールと機能を実装します。変分エンコーダクラスメソッドでは親クラスメソッドを呼び出すだけです。正常に実行された後、ランダムシーケンスを使用するためにバッファを初期化します。OpenCLコンテキストメモリにバッファを作成します。

bool CVAE::Init(uint numOutputs,

                uint myIndex,
                COpenCLMy *open_cl,

                uint numNeurons,
                ENUM_OPTIMIZATION optimization_type,

                uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;
//---
   if(!m_cRandom)
     {
      m_cRandom = new CBufferDouble();
      if(!m_cRandom)
         return false;
     }
   if(!m_cRandom.BufferInit(numNeurons, 0.0))
      return false;
   if(!m_cRandom.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

フィードフォワードパスCVAE::feedForwardを使用して、クラスの主な機能の実装を開始しましょう。他のニューラル層メソッドと同様、このメソッドはパラメータで前のニューラル層のオブジェクトへのポインタを受け取ります。この後に制御ブロックが続きます。主に、使用されているオブジェクトへのポインタの有効性を確認します。その後、受信した初期データのサイズを確認します。前の層の結果バッファ内の要素の数は、2の倍数である必要があり、作成されるニューラル層の結果バッファの2倍である必要があります。変分オートエンコーダのアーキテクチャでは、このような厳密な対応が必要とされます。エンコーダは、特徴ごとに2つの値を返し、各特徴の分布の数学的期待値と標準偏差を記述します。

bool CVAE::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !m_cRandom)
      return false;
   if(NeuronOCL.Neurons() % 2 != 0 ||
      NeuronOCL.Neurons() / 2 != Neurons())
      return false;

確認が成功したら、標準偏差のランダム値のサンプリングを実装し、それらの値を適切なバッファに転送します。

   double random[];
   if(!MathRandomNormal(0, 1, m_cRandom.Total(), random))
      return false;
   if(!m_cRandom.AssignArray(random))
      return false;
   if(!m_cRandom.BufferWrite())
      return false;

さらに処理するために、生成された値をOpenCLコンテキストメモリに渡します。

次に、対応するカーネルの呼び出しを実装します。まず、カーネルが使用するデータバッファへのポインタを渡します。生成されたケースバッファのみをコンテキストメモリに渡したことに注意してください。他のすべての使用済みデータバッファは、既にコンテキストメモリにあると想定しています。以前にコンテキストメモリにバッファを作成したことがない場合、またはメインプログラム側でバッファデータに変更を加えた場合は、バッファポインタをカーネルパラメータに渡す前に、データをOpenCLコンテキストメモリに渡す必要があります。OpenCLプログラムは、コンピュータのグローバルメモリにアクセスせずに、そのコンテキストメモリでのみ動作することを決して忘れないでください。プロセッサで統合グラフィックスカードまたはOpenCLライブラリを使用しているとしてもです。

   if(!OpenCL.SetArgumentBuffer(def_k_VAEFeedForward, def_k_vaeff_inputs, NeuronOCL.getOutput().GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_VAEFeedForward, def_k_vaeff_random, m_cRandom.GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_VAEFeedForward, def_k_vaeff_outputd, Output.GetIndex()))
      return false;

メソッドの最後で、タスクの次元と各次元のオフセットを指定し、メソッドを呼び出して実行のためにカーネルをキューに入れます。

   uint off_set[] = {0};
   uint NDrange[] = {Neurons()};
   if(!OpenCL.Execute(def_k_VAEFeedForward, 1, off_set, NDrange))
      return false;
//---
   return true;
  }

各手順で結果を確認することを忘れないでください。

操作が正常に完了したら、メソッドをtrueで終了します。

フィードフォワードパスの後には、バックプロパゲーションが続きます。以前、いくつかのメソッドを使用してバックワードパスを実装しました。まず、calcOutputGradients、calcHiddenGradients、calcInputGradientsを使用して、ニューラル出力層から入力データ層まで、モデル全体で誤差勾配の計算と受け渡しを順番に実装しました。次に、updateInputWeightsを使用して、訓練済みパラメータを逆勾配に変更します。

変分オートエンコーダの潜在層を操作するためのニューラル層には、訓練可能なパラメータが含まれていません。したがって、パラメータ最適化の最後のメソッドを、メソッドが呼び出されるたびに常にtrueを返すスタブでオーバーライドします。

実際、クラスでのバックパスプロセスの通常の実装では、calcInputGradientsメソッドのみを再定義する必要があります。機能的には、フォワードパスメソッドとバックワードパスメソッドのデータフロー方向は逆ですが、メソッドの内容は非常に似ています。これは、アルゴリズムの機能がOpenCLコンテキストサイトに実装されているためです。メインプログラム側でおこなうのは、カーネルを呼び出すための準備作業のみです。それらは単一のテンプレートに従って呼び出されます。

フィードフォワード方式と同様、まず、使用されているオブジェクトへのポインタの有効性を確認します。データをOpenCLコンテキストに再度渡すことはありません。ただし、必要な情報がすべてコンテキストメモリにあると確信できない場合は、ここでOpenCLコンテキストメモリに再度渡すことをお勧めします。その後、パラメータをカーネルに渡すことができます。

パラメータの転送が成功した後には、カーネルの実行を開始する操作のブロックがあります。まず、問題のサイズと各次元に沿ったオフセットを設定します。次に、カーネルを実行キューに入れるメソッドを呼び出します。

bool CVAE::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
//---
   if(!OpenCL.SetArgumentBuffer(def_k_VAECalcHiddenGradient, def_k_vaehg_input,
                                                        NeuronOCL.getOutput().GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_VAECalcHiddenGradient, def_k_vaehg_inp_grad,
                                                        NeuronOCL.getGradient().GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_VAECalcHiddenGradient, def_k_vaehg_random, Weights.GetIndex()))
      return false;
   if(!OpenCL.SetArgumentBuffer(def_k_VAECalcHiddenGradient, def_k_vaehg_gradient, Gradient.GetIndex()))
      return false;
   if(!OpenCL.SetArgument(def_k_VAECalcHiddenGradient, def_k_vaehg_kld_mult, m_fKLD_Mult))
      return false;
   int off_set[] = {0};
   int NDrange[] = {Neurons()};
   if(!OpenCL.Execute(def_k_VAECalcHiddenGradient, 1, off_set, NDrange))
      return false;
//---
   return true;
  }

すべての操作の結果を確認し、メソッドを終了します。

クラスの主な機能の実装はこれで終わりですが、もう1つの重要な機能があります。ファイルの操作です。したがって、これらのメソッドでクラスの機能を捕捉します。クラスメソッドの記述に進む前に、モデルのパフォーマンスを正常に復元するために保存する必要がある情報について考えてみましょう。このクラスでは、1つの変数と1つのデータバッファのみを作成しています。バッファにはフォワードパスごとに乱数が入力されるため、このデータを保存する必要はありません。変数の値はハイパーパラメータであり、保存する必要があります。

したがって、オブジェクトのsaveメソッドには2つの操作のみが含まれます。

必要なすべての制御を実行し、継承されたオブジェクトを保存する同様の親クラスメソッドを呼び出す
全体的な結果に対するカルバック・ライブラー情報量の影響のハイパーパラメータを保存する

bool CVAE::Save(const int file_handle)
  {
//---
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, m_fKLD_Mult) < sizeof(m_fKLD_Mult))
      return false;
//---
   return true;
  }

操作実行結果の確認も忘れてはいけません。操作が正常に完了したら、メソッドをtrueで終了します。

モデルのパフォーマンスを復元するために、ファイルから保存されたデータは、データの書き込み順序に厳密に従って読み込まれます。まず、同様の親クラスメソッドを呼び出します。必要なすべての制御を含み、継承されたオブジェクトが読み込まれます。

bool CVAE::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;
   m_fKLD_Mult=FileReadFloat(file_handle);

親クラスメソッドの実行が成功したら、ファイルからハイパーパラメータ値を読み取り、対応する変数に書き込みます。ただし、データを保存するメソッドとは異なり、データを読み込むメソッドはここで終わりではありません。確かに、このクラスに読み込むファイルにはこれ以上の情報はありませんが、正しく操作できるようにするには、正しいサイズの確率変数で動作するようにバッファを初期化する必要があります。現在のニューラル層の結果の読み込まれたバッファと同じサイズのバッファを作成します（親クラスのメソッドによって読み込まれた）。また、関連するバッファをOpenCLコンテキストメモリに作成します。

   if(!m_cRandom)
     {
      m_cRandom = new CBufferDouble();
      if(!m_cRandom)
         return false;
     }
   if(!m_cRandom.BufferInit(Neurons(), 0.0))
      return false;
   if(!m_cRandom.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

操作が正常に完了したら、メソッドをtrueで終了します。

これで、変分オートエンコーダの潜在状態処理クラスが完成しました。すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。

新しいクラスの準備は整いましたが、ニューラルネットワークの操作を編成するディスパッチクラスは、まだそれについて何も知りません。NeuroNet.mqhにアクセスして、CNetクラスを見つけてください。

まず、クラスコンストラクタに移動し、新しいニューラル層を作成する手順を記述します。また、使用するOpenCLカーネルの数を増やし、2つの新しいカーネルを宣言します。

CNet::CNet(CArrayObj *Description)  :  recentAverageError(0),
                                       backPropCount(0)
  {
  .................
  .................
//---
   for(int i = 0; i < total; i++)
     {
  .................
  .................
      if(CheckPointer(opencl) != POINTER_INVALID)
        {
         CNeuronBaseOCL *neuron_ocl = NULL;
         CNeuronConvOCL *neuron_conv_ocl = NULL;
         CNeuronProofOCL *neuron_proof_ocl = NULL;
         CNeuronAttentionOCL *neuron_attention_ocl = NULL;
         CNeuronMLMHAttentionOCL *neuron_mlattention_ocl = NULL;
         CNeuronDropoutOCL *dropout = NULL;
         CNeuronBatchNormOCL *batch = NULL;
         CVAE *vae = NULL;
         switch(desc.type)
           {
  .................
  .................
            //---
            case defNeuronVAEOCL:
               vae = new CVAE();
               if(!vae)
                 {
                  delete temp;
                  return;
                 }
               if(!vae.Init(outputs, 0, opencl, desc.count, desc.optimization, desc.batch))
                 {
                  delete vae;
                  delete temp;
                  return;
                 }
               if(!temp.Add(vae))
                 {
                  delete vae;
                  delete temp;
                  return;
                 }
               vae = NULL;
               break;
            default:
               return;
               break;
           }
        }
      else
         for(int n = 0; n < neurons; n++)
           {
  .................
  .................
           }
      if(!layers.Add(temp))
        {
         delete temp;
         delete layers;
         return;
        }
     }
//---
   if(CheckPointer(opencl) == POINTER_INVALID)
      return;
//--- create kernels
   opencl.SetKernelsCount(32);
  .................
  .................
   opencl.KernelCreate(def_k_VAEFeedForward, "VAE_FeedForward");
   opencl.KernelCreate(def_k_VAECalcHiddenGradient, "VAE_CalcHiddenGradient");
//---
   return;
  }

モデルを読み込むCNet::Loadメソッドに同様の変更を実装します。この記事ではコードを繰り返しません。コード全体は添付ファイルに記載されています。

次に、CLayer::CreateElementメソッドとCLayer::Loadメソッドで新しいクラスへのポインタを追加します。

最後に、基本ニューラル層のディスパッチャーメソッドCNeuronBaseOCLFeedForward、calcHiddenGradients、UpdateInputWeightsに新しいクラスポインタを追加します。

必要な追加をすべておこなった後は、モデルの実装とテストを開始できます。すべてのクラスとそのメソッドの完全なコードは、添付ファイルにあります。

3.テスト

変分オートエンコーダの動作をテストするために、以前の記事のモデルを使用します。新しいファイル「vae.mq5」に保存しました。そのモデルでは、エンコーダは5番目のニューラル層で2つの値を返しました。変分オートエンコーダの操作を適切に整理するために、エンコーダ出力のレイヤーサイズを4ニューロンに増やしました。また、変分オートエンコーダの潜在状態を6番目のニューロンとして処理する新しいニューラル層を挿入しました。モデルは、パラメータを変更せずに、EURUSDデータとH1時間枠で訓練されました。デル訓練の期間として過去15年間が使用されました。多層オートエンコーダと変分オートエンコーダの学習ダイナミクスの比較グラフを下の図に示します。

学習結果の比較

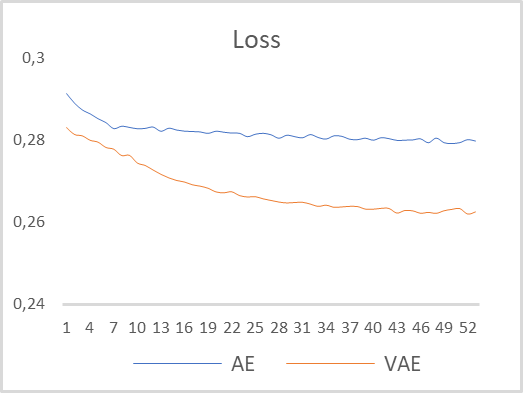
ご覧のとおり、モデル訓練の結果によると、変分オートエンコーダのデータ復元誤差は訓練期間全体を通じて大幅に減少しました。さらに、変分オートエンコーダは、より高い誤差削減ダイナミクスを示しました。

テスト結果に基づいて、EURUSD価格ダイナミクスの例を使用して時系列特徴を抽出する問題を解決するために、変分オートエンコーダは個々のパターン記述特徴を抽出する大きな可能性を秘めていると結論付けることができます。

結論

この記事では、変分オートエンコーダアルゴリズムについて説明しました。変分オートエンコーダアルゴリズムを実装するクラスを作成して、実際の履歴データで変分オートエンコーダモデルのテスト訓練を実施しました。テスト結果では、市場状況を説明する個々の特徴を抽出することを目的としたモデルの予備訓練として使用した場合の変分オートエンコーダモデルの一貫性が示されました。このような訓練の結果は、教師あり学習方法を使用してさらに訓練できる取引パターンを作成するために使用できます。

参考文献リスト

記事で使用されているプログラム

#	名前	タイプ	詳細
1	vae.mq5	EA	変分オートエンコーダ学習ExpertAdvisor
2	vae2.mq5	EA	可視化用のデータを準備するためのEA
3	VAE.mqh	クラスライブラリ	変分オートエンコーダ潜在層クラスライブラリ
4	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
5	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ