Data Science et Apprentissage Automatique (partie 6) : Descente de Gradient
L'optimisation prématurée est la racine de tous les maux en programmation
-Donald Knuth
Introduction
Selon Wikipedia, la descente de gradient (aussi souvent appelée descente la plus abrupte) est un algorithme d'optimisation itératif du premier ordre permettant de trouver le minimum local d'une fonction différentiable. L'idée est d'effectuer des pas répétés dans la direction opposée au gradient (ou gradient approximatif) de la fonction, au point actuel, car c'est la direction de la descente la plus raide. Inversement, le fait d'avancer dans la direction du gradient conduira au maximum local de cette fonction ; la procédure est alors appelée ascension du gradient. Fondamentalement, la descente de gradient est un algorithme d'optimisation utilisé pour trouver le minimum d'une fonction :
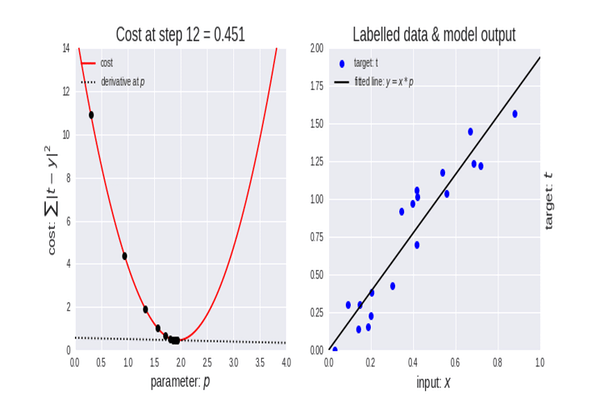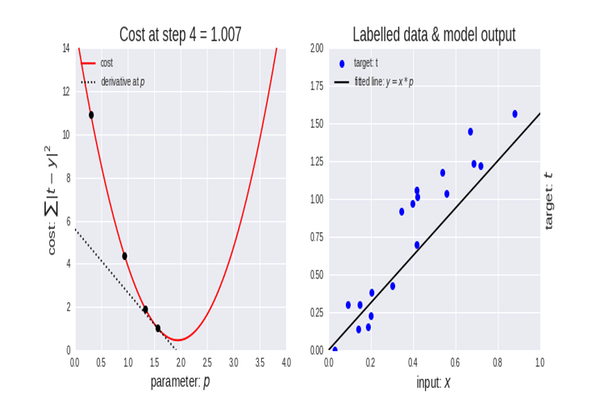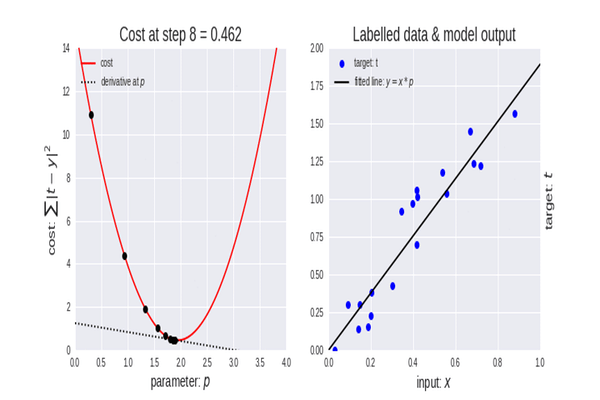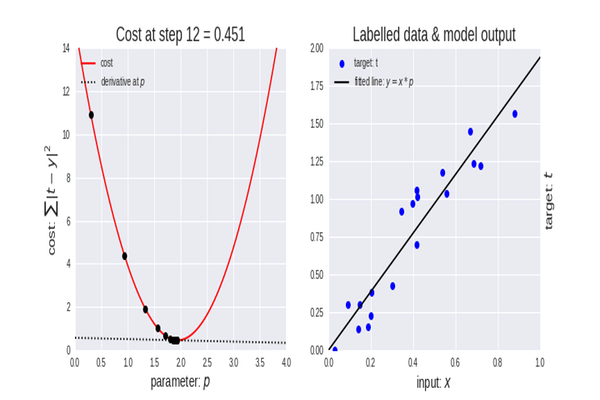
La descente de gradient est un algorithme très important dans l'apprentissage automatique car il nous aide à trouver les paramètres du meilleur modèle pour notre ensemble de données. Mais permettez-moi d'abord d'expliquer le terme de Fonction de Coût.
Fonction de Coût
Certains appellent cela la fonction de perte (loss). C'est une métrique permettant de calculer dans quelle mesure notre modèle est bon ou mauvais pour prédire la relation entre les valeurs de x et y.
Il existe de nombreuses mesures pouvant être utilisées pour déterminer la façon dont le modèle fait ses prédictions. Mais contrairement à toutes ces mesures, la fonction de coût détermine la perte moyenne sur l'ensemble des données. Plus la fonction de coût est grande, plus notre modèle est mauvais pour trouver les relations dans notre ensemble de données.
La descente par gradient vise à minimiser la fonction de coût, car le modèle ayant la fonction de coût la plus faible est le meilleur modèle. Pour vous permettre de comprendre ce que je viens d'expliquer, voyons l'exemple suivant.
Supposons que notre fonction de coût soit l'équation suivante :
![]()
Si nous traçons le graphique de cette fonction avec python, voici à quoi il ressemblera :
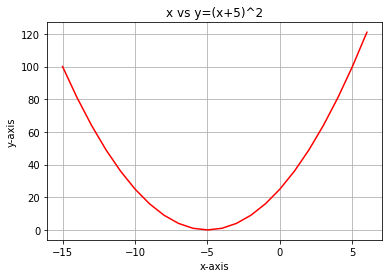
La toute première étape que nous devons effectuer est de différencier la fonction de coût, en utilisant la Règle de la Chaîne :
L'équation y = (x+5)^2 est une fonction composite (il y a une fonction à l'intérieur d'une autre) : la fonction extérieure est (x+5)^2 et la fonction intérieure est (x+5). Pour différencier cela, appliquons la Règle de la Chaîne. Voyez cette image :

Si vous avez du mal à comprendre, vous trouverez à la fin de l’article un lien vers une vidéo où je fais les calculs à la main. Cette fonction que nous venons d'obtenir est le Gradient. Le processus de recherche du gradient d'une équation est l'étape la plus importante de toutes et j'aurais aimé que mes professeurs de mathématiques me disent à l'époque que le but de la différenciation de la fonction est d'obtenir le gradient d'une fonction.
Il s'agit de la première étape, la plus importante. Voici maintenant la deuxième étape.
Étape 2 :
Nous nous déplaçons dans la direction négative du gradient. Ici, la question se pose de savoir de combien nous devons nous déplacer. C'est là que le Taux d'Apprentissage entre en jeu.
Taux d'Apprentissage
Par définition, il s'agit de la taille du pas à chaque itération, tout en se déplaçant vers le minimum d'une fonction de perte. Prenons l'exemple d'une personne qui descend la montagne, ses pas représentent le taux d'apprentissage : plus les pas sont petits, plus il lui faudra de temps pour atteindre le bas de la montagne, et vice versa.
Maintenez le taux d'apprentissage de l'algorithme à des valeurs plus petites (mais pas trop petites) comme 0,0001. Ce faisant, vous augmentez le temps d'exécution du programme, car l'algorithme prendra plus de temps pour atteindre les valeurs minimales. En revanche, si vous utilisez de grands nombres pour le taux d'apprentissage, l'algorithme sautera les valeurs minimales, ce qui, au final, pourrait vous faire manquer la valeur minimale visée.
Le taux d'apprentissage par défaut est de 0,01.
Effectuons une itération pour voir comment l'algorithme fonctionne.
Première itération : Nous choisissons un point aléatoire comme point de départ de notre algorithme. J'ai choisi 0 comme première valeur de x. Voici la formule pour mettre à jour les valeurs de x :

A chaque itération, nous descendons vers la valeur minimale de la fonction, d'où le nom de « descente de gradient ». Cela a plus de sens je pense

Voyons maintenant comment cela fonctionne en détail. Calculons les valeurs manuellement sur 2 itérations pour bien comprendre ce qui se passe :
1ère itération
formule : x1 = x0 - taux d'apprentissage * ( 2*(x+5) )
x1 = 0 - 0,01 * 0,01 * 2*(0+5)
x1 = -0,01 * 10
x1 = -0,1 (enfin)
Nous mettons enfin à jour les valeurs en assignant la nouvelle valeur à l'ancienne. Et nous répétons la procédure autant d'itérations que nécessaire, jusqu'à ce que nous atteignions le minimum d'une fonction :
x0 = x1
2ème itération
x1 = -0,1 - 0,01 * 2*(-0,1+5)
x1 = -0,198
Alors : x0 = x1
Si nous répétons cette procédure plusieurs fois, le résultat des 10 premières itérations est le suivant :
RS 0 17:15:16.793 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction CUSTOM QQ 0 17:15:16.793 gradient-descent test (EURUSD,M1) 1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000 ES 0 17:15:16.793 gradient-descent test (EURUSD,M1) 2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000 PR 0 17:15:16.793 gradient-descent test (EURUSD,M1) 3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000 LE 0 17:15:16.793 gradient-descent test (EURUSD,M1) 4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000 JD 0 17:15:16.793 gradient-descent test (EURUSD,M1) 5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086 JF 0 17:15:16.793 gradient-descent test (EURUSD,M1) 8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325 NI 0 17:15:16.793 gradient-descent test (EURUSD,M1) 9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258 CK 0 17:15:16.793 gradient-descent test (EURUSD,M1) 10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213
Voyons également les 10 autres valeurs de l'algorithme lorsqu'il est très proche du minimum de la fonction :
GK 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060 IH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059 NH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058 QI 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057 II 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055 RN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054 KN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049 HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local miminum found =-4.999999997546217
Après 1 062 itérations, l'algorithme a pu atteindre le minimum local de cette fonction.
Une chose à retenir de cet algorithme
En examinant les valeurs de la fonction de coût, vous remarquerez d'énormes changements dans les valeurs au début, mais de très petits changements notables dans les dernières valeurs.
La descente du gradient fait des pas plus grands lorsqu'elle n'est pas proche du minimum d'une fonction, et des pas plus petits lorsqu'elle est proche du minimum de la fonction. C’est la même chose que vous feriez lorsque vous êtes au pied de la montagne. Donc maintenant vous savez que la descente du gradient est plutôt intelligente !
Au final, le minimum local est :
HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local miminum found =-4.999999997546217
Ce qui est la valeur exacte car le minimum de cette fonction est -5,0 !
La Vraie Question
Comment le Gradient sait-il quand il doit s'arrêter ? Nous pouvons laisser l'algorithme continuer à itérer jusqu'à l'infini, ou du moins jusqu'à la fin de la capacité de calcul de l'ordinateur.
Lorsque la fonction de coût est nulle, nous savons que la descente du gradient a fait son travail parfaitement.
Codons maintenant toute cette opération en MQL5 :
while (true) { iterations++; x1 = x0 - m_learning_rate * CustomCostFunction(x0); printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0); break; } x0 = x1; }
Le bloc de code ci-dessus est celui qui nous a permis d'obtenir les résultats souhaités. Mais il n’y a pas que lui dans la classe CGradientDescent. La fonction CustomCostFunction est l'endroit où notre équation différentiée est conservée et calculée. La voici :
double CGradientDescent::CustomCostFunction(double x) { return(2 * ( x + 5 )); }
Quel est le But ?
On pourrait se demander à quoi servent tous ces calculs quand on peut simplement utiliser le modèle linéaire par défaut créé par les bibliothèques dont nous avons parlé dans cette série d'articles. Mais le modèle créé à l'aide des valeurs par défaut n'est pas nécessairement le meilleur modèle. Vous devez donc laisser l'ordinateur apprendre les meilleurs paramètres pour le modèle avec peu d'erreurs (meilleur modèle).
Nous sommes à quelques articles près de la construction de réseaux neuronaux artificiels. Pour que chacun puisse comprendre comment les réseaux neuronaux apprennent (s'enseignent à eux-mêmes les modèles) dans le processus de rétro-propagation et autres techniques, la descente de gradient est l'algorithme le plus populaire qui a rendu tout cela possible. Soyez sûr d’avoir une bonne connaissance de tout cela car les choses vont se compliquer.
Descente de Gradient pour un Modèle de Régression
En utilisant l'ensemble de données sur les salaires, nous allons construire le meilleur modèle grâce à la descente de gradient.
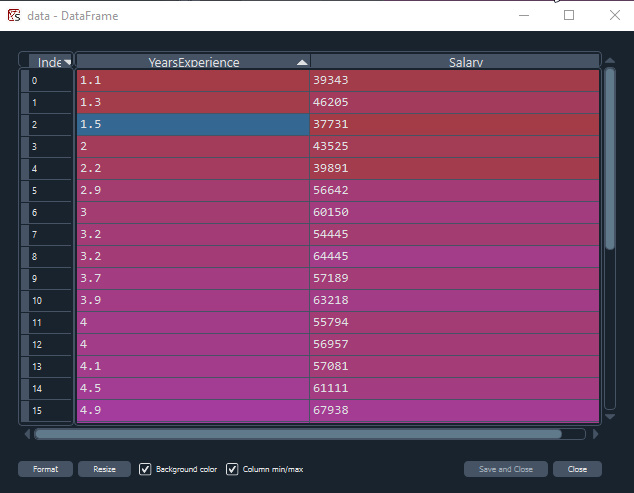
Visualisons les données en Python :
import pandas as pd import numpy as np import matplotlib.pyplot as plt data = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv") print(data.head(10)) x = data["YearsExperience"] y = data["Salary"] plt.figure(figsize=(16,9)) plt.title("Experience vs Salary") plt.scatter(x,y,c="green") plt.xlabel(xlabel="Years of Experience") plt.ylabel(ylabel="Salary") plt.show()
Voici notre graphique :
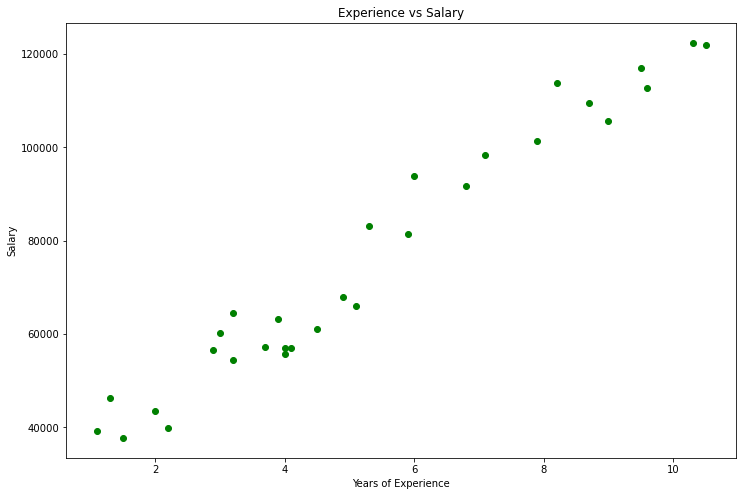
En regardant notre jeu de données, nous pouvons remarquer qu’il est destiné à un problème de régression. Mais nous pouvons avoir un million de modèles pour nous aider à faire la prédiction ou tout ce qui est nécessaire pour nous aider à le réaliser.
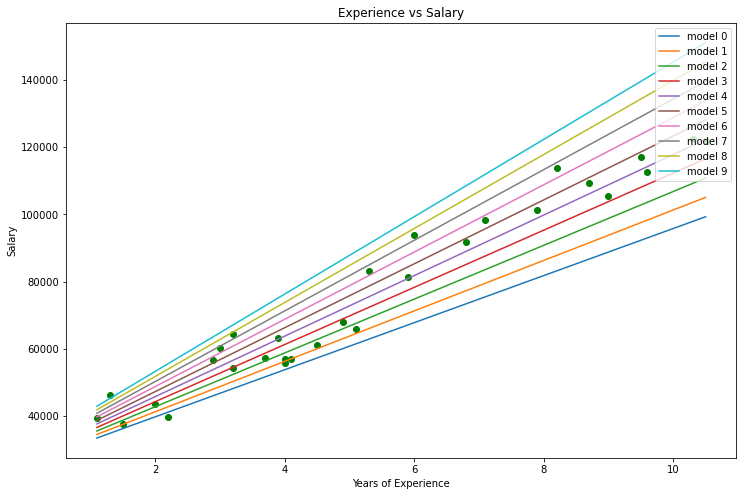
Quel est le meilleur modèle à utiliser pour faire des prédictions sur l'expérience d'une personne et sur son salaire futur ? C'est ce que nous allons découvrir. Mais d'abord, nous devons dériver la fonction de coût pour notre modèle de régression.
Théorie
Laissez-moi vous rappeler la régression linéaire.
Nous savons que tout modèle linéaire est associé à des erreurs. Nous savons également que nous pouvons créer un million de lignes dans ce graphique et que la ligne la mieux ajustée sera toujours celle qui présente le moins d'erreurs.
La fonction de coût représente l'erreur entre nos valeurs réelles et les valeurs prédites. La formule de la fonction de coût peut être écrite comme étant :
Erreur = Y actuel - Y prédit
La magnitude des erreurs est élevée au carré. Notre formule devient maintenant :
![]()
Mais nous recherchons les erreurs dans l'ensemble de notre jeu de données. Nous devons donc faire la somme :
![]()
Nous divisons enfin la somme des erreurs par m, qui est le nombre d'éléments dans l'ensemble de données :
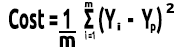
Voici la vidéo de l'ensemble des étapes mathématiques effectuées à la main :
Maintenant que nous avons la fonction de coût, codons la descente du gradient et trouvons les meilleurs paramètres pour les deux. Le coefficient de X (Pente) est noté B0 et l'ordonnée à l'origine de Y est notée B1.
double cost_B0=0, cost_B1=0; if (costFunction == MSE) { int iterations=0; for (int i=0; i<m_iterations; i++, iterations++) { cost_B0 = Mse(b0,b1,Intercept); cost_B1 = Mse(b0,b1,Slope); b0 = b0 - m_learning_rate * cost_B0; b1 = b1 - m_learning_rate * cost_B1; printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1); DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1); if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0) break; } printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f || B1(Coefficient) = %.5f",iterations,b0,b1); }
Remarquez ces éléments du code de la descente en gradient :
- Le processus est toujours le même que celui que nous avons effectué auparavant, mais cette fois-ci, nous trouvons et mettons à jour les deux valeurs à la fois, B0 et B1.
- Il y a un nombre limité d'itération, Quelqu'un a dit un jour que la meilleure façon de faire une boucle infinie est d'utiliser une boucle while. Nous n'utilisons pas la boucle while cette fois-ci mais nous voulons plutôt limiter le nombre d’exécutions de l'algorithme pour trouver les coefficients du meilleur modèle.
- DBL_MAX_MIN est une fonction de débogage chargée de vérifier et de nous avertir si nous avons atteint les limites mathématiques de l'ordinateur.
Voici le résultat des opérations de l'algorithme : Taux d'apprentissage = 0,01 Itérations = 10 000
PD 0 17:29:17.999 gradient-descent test (EURUSD,M1) [20] 91738.0000 98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000 JS 0 17:29:17.999 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE RF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000 OP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667 LP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770 QN 0 17:29:17.999 gradient-descent test (EURUSD,M1) 3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357 LO 0 17:29:17.999 gradient-descent test (EURUSD,M1) 4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058 GH 0 17:29:17.999 gradient-descent test (EURUSD,M1) 5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134 CJ 0 17:29:17.999 gradient-descent test (EURUSD,M1) 6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060 DD 0 17:29:17.999 gradient-descent test (EURUSD,M1) 7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310 HF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> EI 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 NG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GD 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PR 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IS 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RQ 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 KN 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 DL 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RM 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IK 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PH 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GF 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 MG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000 LE 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 Iterations Local Minima are OJ 0 17:29:48.247 gradient-descent test (EURUSD,M1) B0(Intercept) = 25792.20020 || B1(Coefficient) = 9449.96232
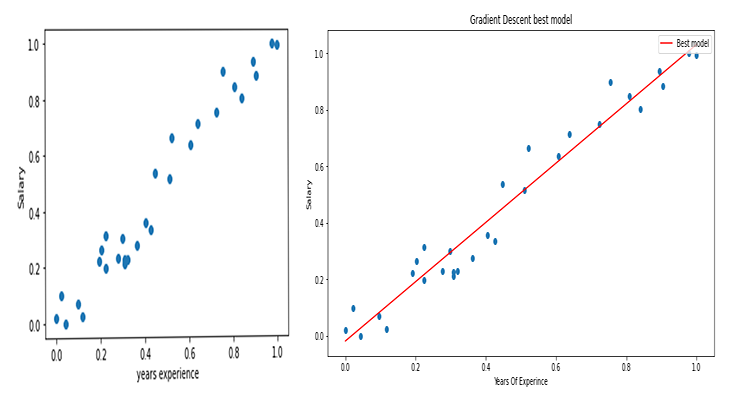
Traçons le graphique avec matplotlib
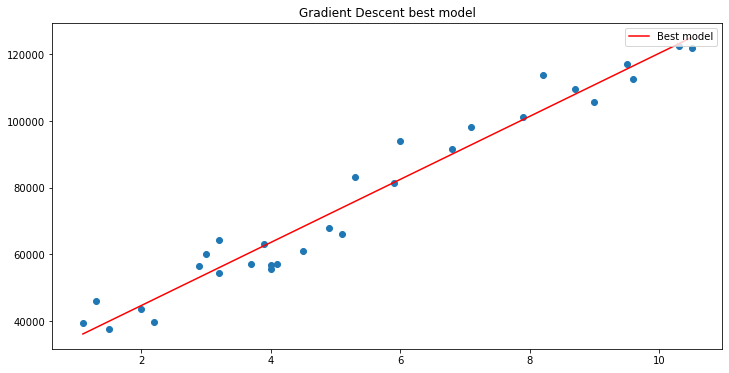
B A M ! La descente de gradient a réussi à obtenir le meilleur modèle parmi les 10 000 modèles que nous avons essayés. C'est bien mais il y a une étape cruciale que nous manquons et qui peut faire que notre modèle se comporte bizarrement et nous fasse obtenir les résultats que nous ne voulons pas.
Normalisation des Données des Variables d’Entrée de la Régression Linéaire
Nous savons que pour différents ensembles de données, les meilleurs modèles peuvent être trouvés après plusieurs itérations. Certains peuvent prendre 100 itérations pour atteindre les meilleurs modèles et d'autres peuvent prendre 10 000 ou jusqu'à un million d'itérations pour que la fonction de coût devienne nulle, sans mentionner que si nous obtenons de mauvaises valeurs pour le taux d'apprentissage, nous pouvons finir par manquer les minima locaux. Et si nous manquons cette cible, nous finirons par atteindre les limites mathématiques de l'ordinateur. Voyons cela en pratique.
Taux d'apprentissage = 0,1 Iterations 1 000
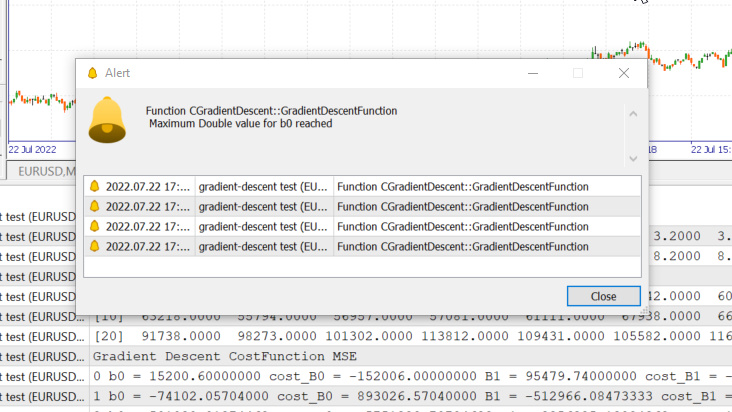
Nous venons d'atteindre la valeur de type « double » maximale autorisée par le système. Voici les logs :
GM 0 17:28:14.819 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE OP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000 GR 0 17:28:14.819 gradient-descent test (EURUSD,M1) 1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333 NM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952 LH 0 17:28:14.819 gradient-descent test (EURUSD,M1) 3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822 KD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084 OQ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984 FM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615 JJ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730 MP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422 MM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625 HD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500 DP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000
Cela signifie que si nous nous trompons dans le taux d'apprentissage, nous avons peu de chances de trouver le meilleur modèle. Et il y a de fortes chances que nous finissions par atteindre la limite mathématique de l’ordinateur, comme vous venez de le voir.
Mais si j'essaie 0,01 pour le taux d'apprentissage dans cet ensemble de données, nous n'aurons pas de problèmes, bien que le processus de formation devienne beaucoup plus lent. Mais si j'utilise ce taux d'apprentissage pour ce jeu de données, je finirai par me heurter à des limites mathématiques. Donc maintenant vous savez que chaque ensemble de données a son propre taux d'apprentissage. Mais nous n'aurons peut-être pas la chance d'optimiser le taux d'apprentissage parce que parfois nous avons des ensembles de données complexes avec de multiples variables et c'est aussi une façon inefficace de faire tout ce processus.
La solution à tous ces problèmes est de normaliser l'ensemble des données afin qu'elles soient sur la même échelle, ce qui améliore la lisibilité lorsque nous traçons les valeurs sur le même axe et améliore également le temps d'apprentissage (car les valeurs normalisées sont généralement comprises entre 0 et 1). De plus, nous n'avons plus à nous soucier du taux d'apprentissage car une fois que nous avons un seul paramètre de taux d'apprentissage, nous pouvons l'utiliser pour n'importe quel ensemble de données auquel nous sommes confrontés. Par exemple le taux d'apprentissage de 0,01. Vous pouvez en apprendre plus sur la normalisation ici.
Dernier point, mais non le moindre
Nous savons également que les valeurs de nos données salariales sont comprises entre 39 343 et 121 782, et que les années d'expérience sont comprises entre 1,1 et 10,5. Si nous conservons les données de cette manière, les valeurs salariales sont énormes et peuvent faire croire au modèle qu'elles sont plus importantes que toutes les autres valeurs, elles auront donc un impact énorme par rapport aux années d'expérience, nous avons besoin que toutes les variables indépendantes aient les mêmes impacts que les autres variables.
(Normalisation) Scalaire Min-Max
Dans cette approche, nous normalisons les données pour qu'elles soient comprises entre 0 et 1. La formule est la suivante :
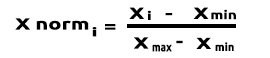
En convertissant cette formule en code MQL5, on obtient :
void CGradientDescent::MinMaxScaler(double &Array[]) { double mean = Mean(Array); double max,min; double Norm[]; ArrayResize(Norm,ArraySize(Array)); max = Array[ArrayMaximum(Array)]; min = Array[ArrayMinimum(Array)]; for (int i=0; i<ArraySize(Array); i++) Norm[i] = (Array[i] - min) / (max - min); printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm)); ArrayFree(Array); ArrayCopy(Array,Norm); }
La fonction std() ne sert qu'à nous donner l'écart-type une fois que les données ont été normalisées. Voici le code :
double CGradientDescent::std(double &data[]) { double mean = Mean(data); double sum = 0; for (int i=0; i<ArraySize(data); i++) sum += MathPow(data[i] - mean,2); return(MathSqrt(sum/ArraySize(data))); }
Appelons maintenant tout cela et affichons la sortie pour voir ce qui se passe :
void OnStart() { //--- string filename = "Salary_Data.csv"; double XMatrix[]; double YMatrix[]; grad = new CGradientDescent(1, 0.01,1000); grad.ReadCsvCol(filename,1,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.MinMaxScaler(XMatrix); grad.MinMaxScaler(YMatrix); ArrayPrint("Normalized X",XMatrix); ArrayPrint("Normalized Y",YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,MSE); delete (grad); }
Sortie :
OK 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.44823 Std = 0.29683 MG 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.45207 Std = 0.31838 MP 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized X JG 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617 ER 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000 NQ 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized Y IF 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762 IS 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939
Les graphiques ressemblent maintenant à ceux-ci :
Descente de Gradient pour la Régression Logistique
Nous avons vu le côté linéaire de la descente de gradient. Voyons maintenant le côté logistique.
Nous faisons ici les mêmes étapes que ce que nous venons de faire sur la partie régression linéaire, car les processus impliqués sont exactement les mêmes. Seul le processus de différenciation de la régression logistique devient plus complexe que celui d'un modèle linéaire. Voyons d'abord la fonction de coût.
Comme nous l'avons vu dans le deuxième article de la série sur la régression logistique, la fonction de coût d'un modèle de régression logistique est l'entropie croisée binaire (Log Loss), présentée ci-dessous :

Faisons maintenant la partie la plus difficile : différencier cette fonction pour obtenir son gradient.
Après avoir trouvé les dérivées :
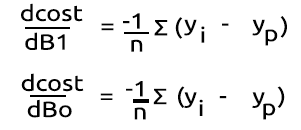
Transformons les formules en code MQL5 dans la fonction BCE (qui signifie Binary Cross Entropy).
double CGradientDescent::Bce(double Bo,double B1,Beta wrt) { double sum_sqr=0; double m = ArraySize(Y); double x[]; MatrixColumn(m_XMatrix,x,2); if (wrt == Slope) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp) * x[i]; } if (wrt == Intercept) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp); } return((-1/m)*sum_sqr); }
Puisque nous traitons du modèle de classification, notre jeu de données de choix est le jeu de données du Titanic que nous avons utilisé dans la régression logistique. Notre variable indépendante est Pclass (classe Passenger) et notre variable dépendante est Survived.
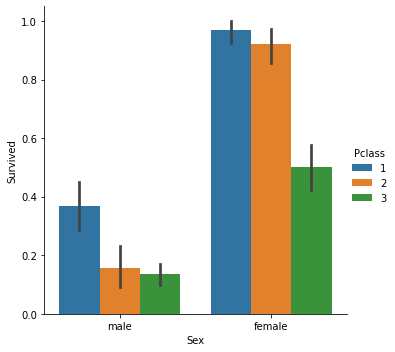
Nuage de points classé
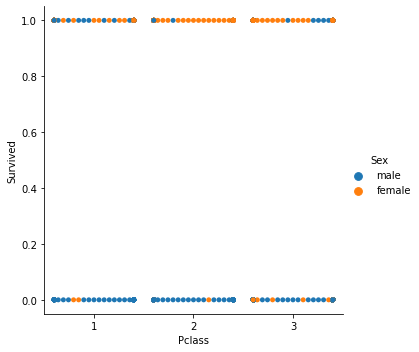
Nous allons maintenant appeler la classe Descente de Gradient, mais cette fois avec la BCE (Entropie Croisée Binaire) comme fonction de coût.
filename = "titanic.csv"; ZeroMemory(XMatrix); ZeroMemory(YMatrix); grad.ReadCsvCol(filename,3,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,BCE); delete (grad);
Voyons le résultat :
CP 0 07:19:08.906 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction BCE KD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391 FD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541 KE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898 QE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566 EE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123 CF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108 MF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329 JG 0 07:19:08.907 gradient-descent test (EURUSD,M1) 7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146 HE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129 ME 0 07:19:08.907 gradient-descent test (EURUSD,M1) 9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065 JQ 0 07:19:08.907 gradient-descent test (EURUSD,M1) 10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600 <<<<<< Last 10 iterations >>>>>> FN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 NM 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 KL 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 RK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MJ 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 HI 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 CH 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MH 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 QG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000 NG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 Iterations Local Minima are MJ 0 07:19:09.727 gradient-descent test (EURUSD,M1) B0(Intercept) = 1.44679 || B1(Coefficient) = -0.85011
Nous ne normalisons pas et nous ne mettons pas à l'échelle les données classées pour la régression logistique comme nous l'avons fait pour la régression linéaire.
Vous avez ici la descente de gradient pour les deux et les plus importants modèles d’apprentissage automatique. J'espère que cela était facile à comprendre et utile. Le code python utilisé dans cet article et le jeu de données sont liés à ce dépôt GitHub.
Conclusion
Nous avons vu la descente de gradient pour une variable indépendante et pour une variable dépendante. Pour des variables indépendantes multiples, vous devez utiliser la forme vectorielle/matricielle des équations. Je pense que cette fois-ci, il sera facile pour quiconque d'essayer et de trouver par lui-même maintenant que nous avons la bibliothèque pour les matrices récemment publiée par MQL5. Pour toute aide sur les matrices, n'hésitez pas à me contacter, je serai plus qu'heureux de vous aider.
Meilleures salutations
En savoir plus sur les calculs :
- https://www.youtube.com/watch?v=5yfh5cf4-0w
- https://www.youtube.com/watch?v=yg_497u6JnA
- https://www.youtube.com/watch?v=HaHsqDjWMLU
Traduit de l’anglais par MetaQuotes Ltd.
Article original : https://www.mql5.com/en/articles/11200
 Développer un Expert Advisor de trading à partir de zéro (Partie 16) : Accès aux données sur le web (2)
Développer un Expert Advisor de trading à partir de zéro (Partie 16) : Accès aux données sur le web (2)
 Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 5) : Arbres de Décision
Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 5) : Arbres de Décision
 Développer un Expert Advisor de trading à partir de zéro (Partie 17) : Accès aux données sur le web (3)
Développer un Expert Advisor de trading à partir de zéro (Partie 17) : Accès aux données sur le web (3)
 Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 4) : Prévoir le Krach Boursier Actuel
Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 4) : Prévoir le Krach Boursier Actuel
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation