
Manuale statistico del trader ipotesi
Introduzione
Qualsiasi trader disposto a creare il proprio sistema di trading diventerà prima o poi un analista. Questi trader sono costantemente alla ricerca delle tendenze del mercato e testano sempre idee di trading. La verifica di un'idea può essere basata su diversi approcci: da una consueta ricerca dei migliori valori dei parametri nella modalità di ottimizzazione dello Strategy Tester alla ricerca di mercato scientifica (a volte pseudo scientifica).
In questo articolo suggerisco di considerare l'ipotesi statistica, uno strumento di analisi statistica per la ricerca e la verifica dell'inferenza. Testiamo varie ipotesi con il pacchetto Statistica e la libreria di analisi numerica pilotata ALGLIB MQL5 utilizzando esempi.
1. Il concetto di ipotesi
Esistono diverse definizioni del concetto di "ipotesi statistica". Alcune di esse implicano una supposizione sulle proprietà statistiche dell'oggetto o del fenomeno in esame.
Un'ipotesi statistica è un'assunzione sulle leggi probabilistiche a cui aderisce un fenomeno in questione.
Altre definizioni indicano che le proprietà statistiche devono essere collegate alla distribuzione di alcune variabili casuali o parametri di questa distribuzione.
L'ipotesi statistica è una supposizione riguardante i parametri della distribuzione statistica o il principio della distribuzione delle variabili casuali.
Nella letteratura sulla statistica matematica, la nozione di "ipotesi" è interpretata nel secondo modo. Allora possiamo distinguere:
- Ipotesi parametrica (ipotesi sui valori dei parametri di distribuzione o sul valore comparativo dei parametri di due distribuzioni);
- Ipotesi non parametrica (ipotesi sul tipo di una distribuzione casuale di valori).
Nella prossima sezione discuteremo di un metodo di verifica delle ipotesi.
2. Ipotesi di verifica. Teoria
L'ipotesi da verificare è detta ipotesi nulla (Н0). Un'ipotesi concorrente (Н1) è la sua alternativa. È il rovescio della medaglia dello 0, cioè rifiuta logicamente l'ipotesi nulla.
Immagina che ci sia una popolazione di dati sugli Stop Loss di qualche sistema di trading. Ci accingiamo a formulare due ipotesi che costituiscono una base per i test.
Н0 – valore medio di Stop Loss pari a 30 punti;
Н1 – valore medio di Stop Loss non pari a 30 punti.
Varianti di accettazione e rifiuto di ipotesi:
- Н0 è vero ed è accettato;
- Н0 è sbagliato e viene rifiutato a favore di Н1;
- Н0 è vero ma viene rifiutato a favore di Н1;
- Н0 è sbagliato ma è accettato.
Le ultime due varianti sono collegate ad errori.
Ora è necessario specificare il valore del livello di significatività. È la probabilità che l'ipotesi alternativa venga accettata mentre l'ipotesi vera è quella nulla (terza variante). È preferibile minimizzare questa probabilità.
Nel nostro caso tale errore si verificherà se assumiamo che lo Stop Loss alla media non sia uguale a 30 punti anche se in realtà lo è.
Solitamente il livello di significatività (α) è pari a 0,05. Ciò significa che il valore statistico del test dell'ipotesi nulla può popolare la regione critica in non più di 5 casi su 100.
Nel nostro caso il valore statistico del test sarà valutato su un classico grafico (Fig.1).
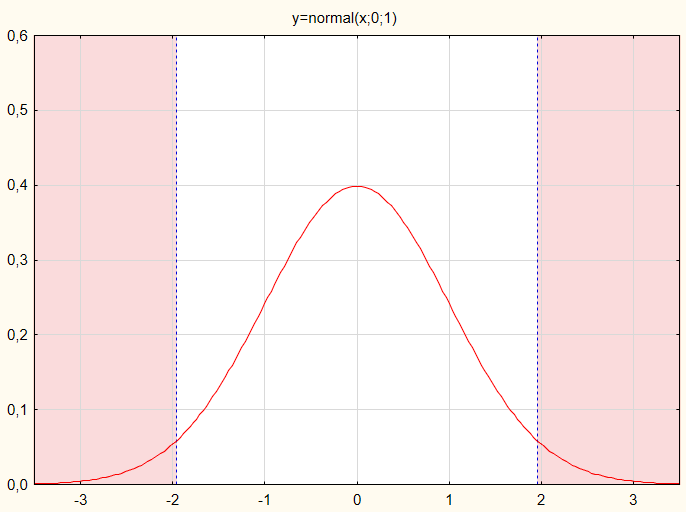
Fig.1. Verifica la distribuzione del valore statistico per legge di probabilità normale
Affinché l'ipotesi nulla sia accettata, i valori statistici del test non dovrebbero raggiungere le zone rosse. Ai fini dell'esempio, supponiamo che i valori statistici del test siano distribuiti normalmente.
Ogni test ha una propria formula con cui calcolare il valore statistico del test.
La variante 4 implica che c'è un errore del secondo tipo (β). Nel nostro caso tale errore si verificherà se si presume che lo Stop Loss alla media sia pari a 30 punti e non sia uguale a quel numero di punti.
3. Esempi di test di ipotesi statistiche
I dati di origine utilizzati per gli esempi sono archiviati nel file Data.xls.
3.1. Test del campione dipendente
Immagina la seguente situazione. Supponiamo che ci sia un sistema di trading che genera una popolazione di affari. Prendiamo un esempio di affari redditizi con un volume di 100 unità. I dati di origine sono nel foglio "Profitti".
Le statistiche descrittive del campione Profitti dopo l'eliminazione dei casi periferici sono presentate nella Tabella 1:
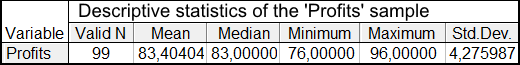
Tabella 1. Statistiche del campione Profitti
L'istogramma del campione appare come segue (Fig.2).
Fig.2. L'istogramma di esempio dei profitti
Il valore della media è 83,4 punti e la mediana è 83 punti.
Cosa succede se il punto di ingresso al mercato viene modificato di alcuni punti? Ad esempio, un ordine limite che migliora il prezzo di entrata può essere piazzato dopo la comparsa di un segnale di trading.
Come influenzerà i risultati? A questa domanda si può rispondere con ipotesi statistiche.
Nel pacchetto Statistica controlliamo formalmente se i campioni non sono stati prelevati da una popolazione:
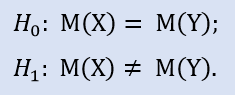
Se modifichiamo il prezzo di entrata di 15 punti, riceveremo il campione NewProfits. Idealmente, l'immagine del risultato dovrebbe essere la seguente (Fig.3).
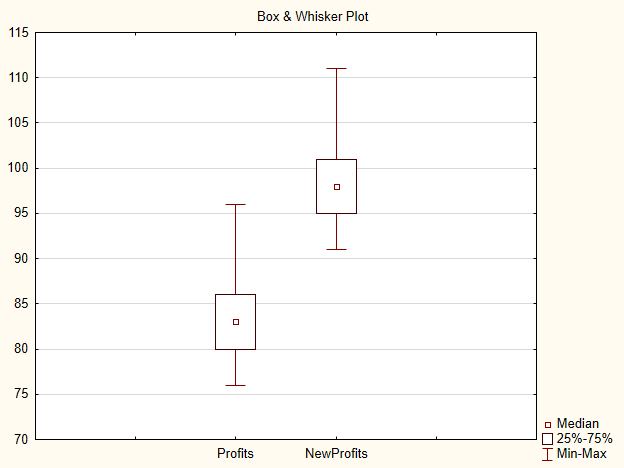
Fig.3. Grafico per campioni Profits e NewProfits
La probabilità che l'ipotesi alternativa venga accettata è alta poiché le mediane dei campioni differiscono.
Questa immagine, tuttavia, sarà difficile da ottenere in quanto potrebbero non esserci prezzi migliori sul mercato. Nel mio caso, il secondo campione comprendeva 84 offerte dopo la modifica del prezzo di entrata. Gli altri 15 accordi semplicemente non sono stati eseguiti. Questo campione corretto si chiamerà NewProfitsReal.
Sulla trama del tipo "scatola e baffi" non c'è molta differenza tra due campioni.
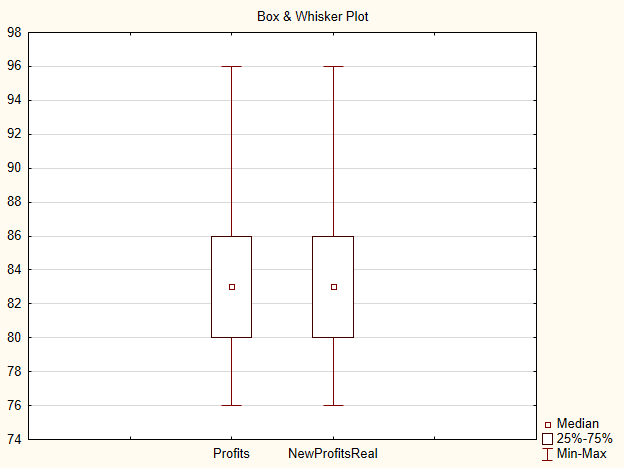
Fig.4. Trama per i Profitti e Nuovi Profitti Campioni reali
Conduciamo un test non parametrico Wilcoxon firmato-rank test per il campione connesso.
I risultati sono nella tabella 2:

Tabella 2. Risultati del test Wilcoxon per i campioni Profits e NewProfitsReal
Il livello di significatività è molto alto, il che favorisce l'ipotesi nulla.
In questo modo possiamo dire che la modifica del punto di ingresso non ha influenzato la resa del sistema. È in termini relativi. In termini assoluti, il sistema si è rivelato meno redditizio a causa dei punti di ingresso mancati.
Il test Wilcoxon può essere condotto in modo programmatico in MQL5. Sebbene confronti la mediana della distribuzione con il valore specificato di m, questa differenza non è significativa.
Stiamo andando a controllare:
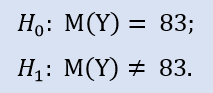
La libreria ALGLIB contiene la seguente procedura: CAlglib::WilcoxonSignedRankTest(). Fornisce un risultato per tre tipi di test: bilaterale, sinistro e destro.
Lo script test_profits.mq5 fornisce un esempio di questo calcolo. Il giornale "Esperti" ha i seguenti risultati per il campione NewProfitsReal:
OO 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the two-sided test: 0.7472 HD 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the left-sided test: 0.6285 CM 0 12:04:08.814 test_profits (EURUSD.e,H1) p-value for the right-sided test: 0.3736
Il test del lato sinistro ha la forma di:
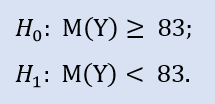
Qui controlliamo l'alternativa in quanto la mediana del campione NewProfitsReal può essere maggiore o uguale a 83. La probabilità di errore nel rifiutare H0 è 0,63. Quindi H0 è accettato.
Il test sul lato destro è simile a:
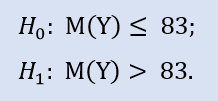
In questo test verifichiamo l'alternativa che la mediana del campione NewProfitsReal possa essere minore o uguale a 83. La probabilità di errore al rifiuto di H0 è pari a 0,37. Quindi H0 è accettato.
3.2. Test di campioni indipendenti
Supponiamo di dover verificare quanto velocemente i diversi broker elaborano gli ordini di trading e se c'è una differenza tra i broker in relazione al tempo di esecuzione degli ordini di trading.
Quindi, ci sono due campioni di dati di origine per l'analisi. Ogni campione conteneva inizialmente 50 osservazioni. Dopo aver eliminato i casi periferici, sono rimaste 48 osservazioni nel primo campione (broker А) e 49 osservazioni nel secondo (broker B). I dati possono essere trovati nel foglio "ExecutionTime".
Stiamo andando a controllare:
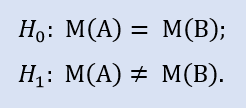
Rappresentiamo indici campione su un'immagine (Fig.5). Secondo il grafico, i valori delle mediane differiscono anche se non in modo significativo.
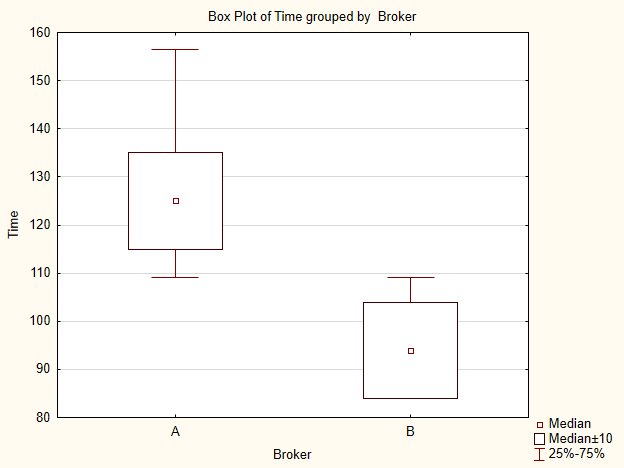
Fig.5. Grafico per i campioni di dati dei broker A e B
Poiché non sappiamo a quale distribuzione appartenga ogni campione, faremo riferimento a test non parametrici per il confronto.
Ad esempio, eseguiamo Mann — Whitney U-test (tabella 3). Si ritiene che sia il più informativo.

Tabella 3. Mann — Risultati Whitney U-test per campioni di dati dei broker A e B
Conclusione: i risultati dei test differiscono e quindi l'ipotesi nulla sull'uguaglianza dei campioni viene respinta a favore di Н1.
Mann — Whitney U-test può essere condotto in modo programmatico in MQL5. Nella libreria ALGLIB è presente il CAlglib:: Procedura MannWhitneyUTest(). Fornisce un risultato per tre tipi di test: bilaterale, sinistro e destro.
Lo script test_time_execution.mq5 fornisce un esempio di calcolo. Il diario "Esperto" ha il seguente risultato che può essere utilizzato per confrontare i campioni:
MR 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the two sided test: 0.0001 QF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the left-sided test: 1.0000 PF 0 12:55:08.577 test_time_execution (EURUSD.e,H1) p-value for the right-sided test: 0.0001
Il test del lato sinistro ha la forma di:
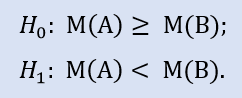
L'ipotesi nulla è che la mediana del campione di dati del broker A possa essere maggiore o uguale alla mediana del campione di dati del broker B. L'alternativa è il suo rifiuto. La probabilità di errore nel rifiutare H0 è 1.0. Quindi H0 è accettato.
Il test sul lato destro è simile a:
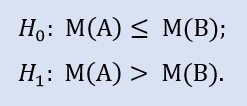
L'ipotesi nulla è che la mediana del campione di dati del broker A possa essere minore o uguale alla mediana del campione di dati del broker B. L'alternativa è il suo rifiuto.
La probabilità di errore nel rifiutare H0 è 0,0. Pertanto H0 viene rifiutato a favore di Н1.
3.3. Test di correlazione
Immagina un portafoglio di strategie. L'obiettivo è ridurre il numero di strategie in portafoglio.
Il criterio di scelta sarà il seguente: se due strategie sono uguali nel confronto delle serie Stop Loss, una delle strategie verrà rimossa dal portafoglio. Prendiamo due campioni con i dati di Stop Loss di due sistemi diversi. Assunzione: i sistemi reagiscono allo stesso modo all'ingresso nel mercato e reagiscono in modo diverso all'uscita dal mercato.
Useremo il test di correlazione tra rango e ordine di Spearman. Ci sono tre esempi nel foglio "Correlazione" del file di dati.
Controlla se il coefficiente di correlazione è uguale a zero:
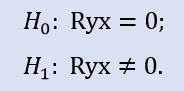
Il confronto della coppia dei campioni Stops1-Stops2 darà il seguente risultato (Tabella 4).

Tabella 4. Test di correlazione tra rango e ordine di Spearman per i campioni Stops1 e Stops2
In questo caso l'ipotesi nulla di assenza di connessione tra elementi di campioni non può essere respinta a favore dell'alternativa. Pertanto è accettato.
Il grafico in Fig.6 mostra che i dati non formano alcuna configurazione evidente. I dati sono sparsi sul piano del grafico.
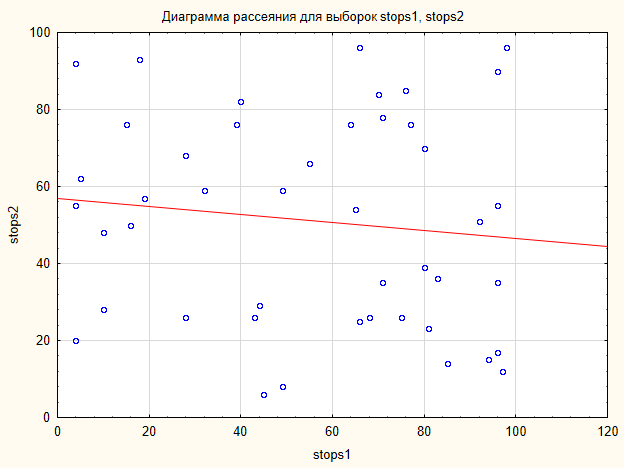
Fig.6. Grafico a dispersione per i campioni Stops1 e Stops2
I risultati di un controllo della relazione tra i campioni Stops1-Stops3 sono mostrati nella Tabella 5:
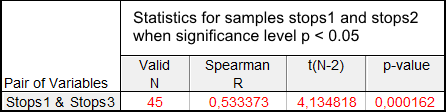
Tabella 5. Risultati del test di correlazione dell'ordine di rango di Spearman per i campioni Stops1 e Stops3
In questo caso l'ipotesi nulla può essere respinta in quanto la probabilità di errore è molto bassa.
Quindi, l'alternativa su una relazione esistente è accettata. La relazione sembra (Fig.7).
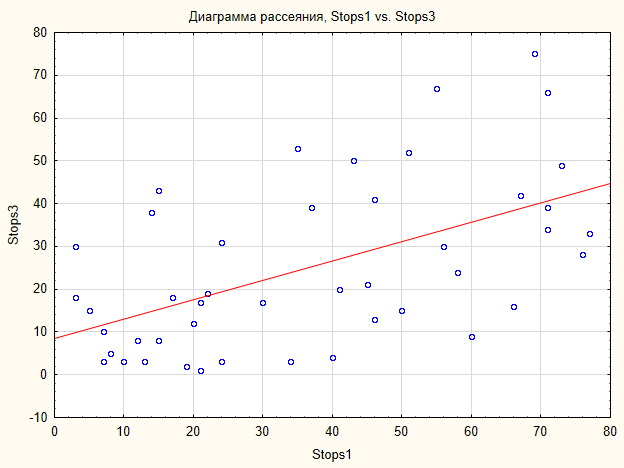
Fig.7. Grafico a dispersione per i campioni Stops1 e Stops3
Conferma il risultato con il codice in MQL5. Il test_correlation.mq5 contiene un esempio di calcolo.
La libreria ALGLIB contiene la procedura CAlglib::SpearmanRankCorrelationSignificance(), che implementa il test per il significato del coefficiente di correlazione Rank-Order di Spearman.
La rivista contiene le seguenti registrazioni:
OO 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops2===--- GO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.9840 KK 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.4920 JJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.5080 DM 0 12:57:43.545 test_correlation (EURUSD.e,H1) HJ 0 12:57:43.545 test_correlation (EURUSD.e,H1) ---===Samples Stops1 and Stops3===--- NS 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the two-sided test: 0.0002 RO 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the left-sided test: 0.9999 FG 0 12:57:43.545 test_correlation (EURUSD.e,H1) p-value for the right-sided test: 0.0001
Il test del lato sinistro ha la forma di:
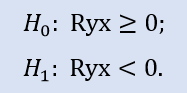
In questo test viene verificata l'ipotesi nulla che ci sia una correlazione non negativa tra le variabili (cioè la correlazione è zero o negativa).
Il test sul lato sinistro mostra che per la coppia di campioni Stops1-Stops2, l'ipotesi zero è accettata. Il test del lato sinistro mostra che per la coppia di campioni Stops1-Stops3 viene accettata anche l'ipotesi nulla. Una domanda logica da porsi sarà "Perché non c'è alcun collegamento tra i campioni Stops1-Stops2 e ce n'è uno tra Stops1-Stops3?" Il motivo è che l'istruzione in check è "maggiore o uguale a zero". Nel primo caso, "uguale a zero" è importante per H0, e nel secondo caso è "maggiore di zero".
Il test sul lato destro è simile a:
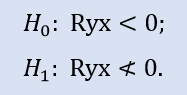
Qui viene verificata l'ipotesi nulla di che cosa sia una correlazione negativa.
Per la coppia di campioni Stops1-Stops2, il test sul lato destro mostra che l'ipotesi nulla è accettata. Per la coppia di campioni Stops1-Stops3 il test del lato destro mostra che l'ipotesi nulla è respinta.
Un ultimo commento. Il test ha rivelato che esiste una connessione probabilistica positiva tra i campioni di Stops1-Stops3. La forza di questa connessione è nella media. Pertanto spetta al trader decidere se rifiutare la strategia 1 o 3.
Conclusione
In questo articolo ho cercato di mostrare su esempi che le variabili quantitative possono essere valutate utilizzando la statistica matematica. Spero che gli sviluppatori alle prime armi trovino questo articolo utile per i loro futuri sistemi di trading. Spero anche che la serie di articoli sull'uso dei metodi della statistica matematica continui.
I file della libreria ALGLIB devono essere scaricati separatamente.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/1240
 Programmazione delle modalità di EA utilizzando l'approccio orientato agli oggetti
Programmazione delle modalità di EA utilizzando l'approccio orientato agli oggetti
 Fondamenti di programmazione MQL5: Variabili Globali del Terminale
Fondamenti di programmazione MQL5: Variabili Globali del Terminale
 Principi dei prezzi di scambio attraverso l'esempio del mercato dei derivati della Borsa di Mosca
Principi dei prezzi di scambio attraverso l'esempio del mercato dei derivati della Borsa di Mosca
 Grafico liquido
Grafico liquido
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso