Combinatoire et théorie des probabilités pour le trading (Partie I) : L'essentiel

Sommaire

• Introduction
• Comment la théorie des probabilités peut-elle être utile dans l'analyse des marchés ?
• Spécificités de la théorie des probabilités appliquée au trading manuel et au trading automatisé
• Arbres de probabilité et hypothèses
• À propos des fractales
• Schéma de Bernoulli
• Création de la première fractale
• Résumé
• Conclusion

Introduction

Je pense que le langage de la théorie des probabilités peut fournir un niveau de compréhension complètement différent des processus qui se déroulent sur le marché. Après avoir compris les spécificités de la théorie des probabilités, vous commencerez à penser d'une manière complètement nouvelle. Des idées vagues ou des conseils non prouvés ne donneront plus envie de se dépêcher de trader sur un compte réel. Mais d'un autre côté, je comprends que cette nouvelle approche puisse ne pas convenir à tout le monde. Dans cette série, je veux vous montrer une approche réelle et correcte du trading. Toutes les décisions doivent être fondées uniquement sur des chiffres et éviter les hypothèses telles que "peut-être", "et si", "il semble" et autres.

Comment la théorie des probabilités peut-elle être utile dans l'analyse des marchés ?

J'ai été impliqué dans les sciences techniques pendant une assez longue période de ma vie, mais la théorie des probabilités a été la plus difficile pour moi. C'est parce que je ne comprenais pas l'étendue de ses possibilités. L'avantage indiscutable réside dans ses capacités illimitées, qui ne dépendent que de votre ingéniosité et de votre diligence, et bien sûr de votre intelligence. Après des années d'études techniques, je me suis rendu compte que l'intelligence n'est pas une question de rapidité et d'attention dans l'exécution des mêmes types d'opérations, mais qu'il s'agit de la flexibilité de votre esprit. Si nous considérons, par exemple, les mathématiques différentielles, la théorie des champs vectoriels et scalaires, ou même l'algèbre scolaire, elles impliquent toutes un certain ensemble de règles ou de recommandations, grâce auxquelles vous pouvez résoudre presque n'importe quel problème. Chaque tâche non standard est un choc pour notre cerveau. Dans la théorie des probabilités, il existe un nombre infini de moments de ce type. C'est là que de nombreux problèmes ne peuvent être résolus que par des approches complètement différentes. En d'autres termes, l'intelligence ne peut être développée que par l'assiduité et la volonté de résoudre un problème donné, et la théorie des probabilités peut vous y aider.

Le cadre de la théorie des probabilités décrit des concepts de trading fondamentaux tels que l'espérance mathématique, les probabilités possibles de divers événements, les valeurs moyennes, les percentiles, etc. Selon la théorie des probabilités, il n'existe pas de système de trading parfait, et chaque système comporte ses propres risques. Ce que nous pouvons faire, c'est choisir uniquement le système de trading dont les risques ne sont pas trop gênants. Le plus important est d'interpréter correctement ces risques. En d'autres termes, nous passons d'un langage imprécis de sensations ou d'approximations visuelles à des critères quantitatifs clairs. Bien entendu, les estimations visuelles sont également importantes, mais elles sont plus efficaces lorsqu'elles sont combinées à des variables quantitatives. Il est impossible de décrire tous les détails et toutes les nuances dans un seul article. Mais je vais essayer d'inclure ici quelques informations intéressantes. J'espère que vous y trouverez quelque chose d'utile.

Spécificités de la théorie des probabilités appliquée au trading manuel et au trading automatisé

Avant d'utiliser la théorie des probabilités pour l'analyse des marchés, nous devons d'abord nous familiariser avec les événements et leurs probabilités. Un événement est un ensemble de résultats répondant à certains critères, ou regroupés selon certains critères dans un certain ensemble. Un résultat est un certain élément unitaire qui est égal à tous les autres éléments du groupe donné. Le groupe fait référence à tous les résultats possibles d'un processus. Il n'est pas important de savoir de quel type de processus il s'agit, quelles sont ses caractéristiques physiques ou combien de temps il dure. L'important est qu'à l'issue de ce processus, nous obtenions quelque chose qui n'existait pas avant la fin du processus. Les résultats qui se rapportent à notre événement sont essentiellement notre événement - par commodité, nous les combinons en un seul objet. L'idée ci-dessus peut être visualisée comme suit :

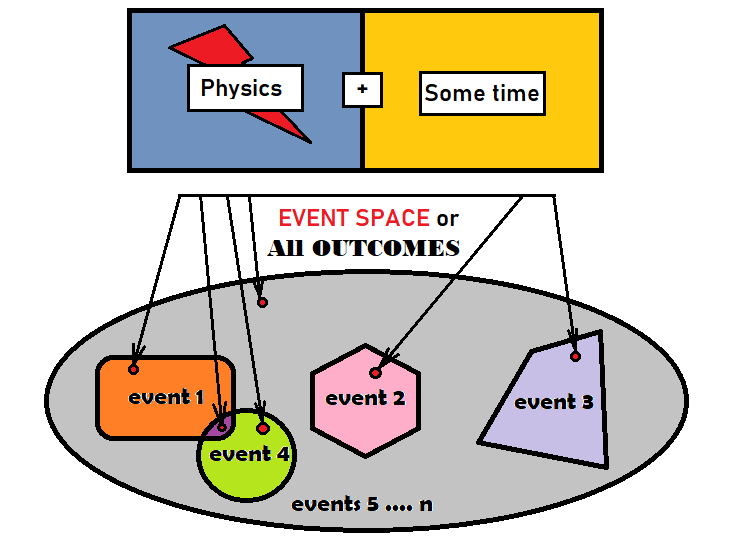
L'ellipse grise dans la figure ci-dessus représente tous les résultats. En mathématiques, on parle d'espace événementiel. Cela ne signifie pas que l'espace événementiel a une forme géométrique. Mais elle est tout à fait appropriée pour décrire ces concepts. Il y a 4 événements à l'intérieur de l'ellipse. Comme le montre la figure, un petit point rouge apparaît à l'intérieur de chaque événement. Le nombre de ces points peut être limité ou illimité - cela dépend du processus considéré. Deux des événements de la figure se croisent. Ces événements sont appelés "chevauchement". Il y a donc des résultats qui appartiennent aux 2 événements. Tous les autres événements ne se chevauchent pas car ils sont situés dans des parties différentes de l'ellipse et ne se croisent pas géométriquement. Le reste de la zone grise peut être considéré comme le dernier événement, ou peut être décomposé en parties plus petites jusqu'à ce qu'il n'y ait plus de zones grises.

Chaque événement a au moins un nombre correspondant qui est généralement appelé probabilité. La probabilité correspond à la fréquence à laquelle cet événement apparaîtrait lors des répétitions du même processus si nous pouvions réaliser la même expérience indéfiniment. Il existe 2 types d'espaces événementiels :

1. Avec un nombre fini de résultats possibles
2. Avec un nombre infini de résultats possibles

Si le nombre de résultats est fini, la probabilité peut être calculée comme suit :

• P = S/N, où S est le nombre de résultats qui répondent au critère d'événement, et N le nombre total de tous les résultats dans l'espace d'événement.

Dans certains cas, lorsque le nombre de résultats dans un espace donné est infini, cette probabilité peut également être déterminée, par exemple à l'aide d'intégrales. Dans le cas de l'image ci-dessus, les valeurs "S" et "N" peuvent être remplacées par les aires de leurs formes géométriques.

Il n'est pas toujours possible de définir clairement ce qu'est l'espace des événements, ni de définir le nombre de résultats et la physique décrite par les événements. Ces représentations graphiques devraient aider notre cerveau à faire l'analogie entre les données, de sorte qu'au lieu de travailler sans géométrie, en essayant de comprendre ce qui se passe, le cerveau pourrait s'habituer à l'idée que nous ne travaillons qu'avec des probabilités et des nombres supplémentaires qui correspondent à ces probabilités. Les événements peuvent également être appelés "états". Si nous utilisons la logique des états, la probabilité est exactement la fréquence de survenue d'un état spécifique à la suite de la répétition des mêmes expériences. 

Par analogie avec les aires des figures, la somme des aires de toutes les figures incluses dans l'ellipse est exactement égale à l'aire de cette ellipse. En ce qui concerne les mathématiques, le domaine est le nombre de résultats qui s'y rapportent. D'où :

• N = S[1] + S[2] + ... + S[n]
  
• S est le nombre de résultats d'un événement particulier
• N est l'ensemble des résultats de l'espace événementiel

En divisant les deux côtés de l'égalité par la valeur N, nous obtenons une relation intéressante et très importante qui sous-tend toute la théorie des probabilités :

• 1 = S[1]/N + S[2]/N + ... +S[n]/N

Veuillez noter que ce ratio ne fonctionne que pour des événements qui ne se chevauchent pas. En effet, si les événements sont joints, les aires des formes se chevauchent et la somme de leurs aires sera supérieure à l'aire de l'ellipse d'origine. C’est similaire à un puzzle, dans lequel la surface de toutes les pièces du puzzle est exactement égale à l'image résultante. Dans ce cas, une pièce de puzzle représente l'un des événements. Toutes ces fractions représentent les probabilités d'événements spécifiques :

• 1 = P[1] + P[2] + ... +P[n]

Ce ratio sert de base à l'expression "ensemble d'événements collectivement exhaustifs". Un ensemble d'événements collectivement exhaustif est l'unité de tous les événements qui ne se chevauchent pas et qui forment un certain espace d'événements. Pour un puzzle, un ensemble collectivement exhaustif est constitué de toutes les pièces du puzzle. La probabilité totale de tous ces événements doit être égale à un, ce qui signifie que l'un de ces événements doit nécessairement se produire à la suite de l'expérience. Nous ne savons pas quel événement se produira, mais nous le découvrirons grâce au résultat de l'expérience.

Conformément à ce qui précède, tout ensemble de résultats provenant de l'espace événementiel sélectionné peut servir d'événement. Cela signifie qu'un ensemble collectivement exhaustif peut être collecté de toutes les manières et combinaisons possibles. Lorsque nous avons affaire à un nombre fini de résultats, il peut y avoir un nombre limité de ces combinaisons ; pour un nombre infini de résultats, le nombre de combinaisons serait toujours infini. Si l'on sait que le nombre de résultats est égal à l'infini, les mathématiciens considèrent le concept de valeur aléatoire. Dans certains cas, il est plus pratique d'utiliser des valeurs aléatoires si la tâche le permet. Une valeur aléatoire est une méthode quelque peu différente pour décrire l'espace événementiel. Dans ce cas, le résultat est l'ensemble clair d'un ou de plusieurs nombres. On peut dire qu'il s'agit d'un vecteur. Ce modèle de considération implique le concept de densité de probabilité. 

Ces concepts seront utilisés plus loin, lors de l'exploration de ce sujet, alors considérons-les dès maintenant. La densité de probabilité est une fonction qui décrit l'ensemble de l'espace événementiel. La dimension de cette fonction est exactement égale à la quantité de nombres requis pour décrire chaque résultat dans cet espace d'événements. Par exemple, si nous considérons le problème du tir sur une cible dans un stand de tir, la dimension de cette fonction sera égale à 2, car la cible est plate (bidimensionnelle). Dans ce cas, un résultat particulier sera caractérisé par des coordonnées X et Y. Ces nombres sont nos variables aléatoires, et nous pouvons donc écrire ce qui suit :

• R = R(X,Y)
• R est la densité de probabilité qu'une balle frappe un point dont les coordonnées sont (X,Y)

Les propriétés de cette fonction sont telles que l'intégrale de moins à plus l'infini pour toutes les variables de cette fonction sera égale à 1, ce qui prouve l'équation ci-dessus. Les probabilités ne sont déterminées que par les intégrales de la zone dans laquelle la fonction est présentée. Différents événements peuvent être composés de régions intégrées par morceaux. Il est donc possible de décrire autant d'événements que nécessaire, car leur nombre est infini. Cette définition est suffisante dans le cadre de cet article.

J'aimerais ajouter quelques détails supplémentaires sur les événements qui se chevauchent. Ces événements sont également très importants pour la compréhension générale de l'image dans son ensemble. Il est clair que les événements qui ne se chevauchent pas devraient être plus faciles à traiter que ceux qui se chevauchent. La théorie des probabilités doit parfois traiter de la combinaison ou de la division d'événements. Mais nous ne nous intéressons ici qu'aux probabilités qui apparaissent à la suite de ces transformations. Pour cela, nous utiliserons les concepts de somme et de produit d’événements, ainsi que de l'opération d'inversion. Ces opérations n'ont pas la même signification qu'en mathématiques. Elles ne fonctionnent de plus qu'avec des probabilités. Les probabilités d'événements conjoints ne peuvent pas être ajoutées, car cela violerait l'intégrité de l'ensemble. En général, ces 3 opérations appliquées aux événements sources peuvent décrire tous les événements possibles pouvant être composés de morceaux d'événements sources. En prenant l'exemple de 2 événements qui se chevauchent, je peux montrer ce que cela peut donner dans le plan :

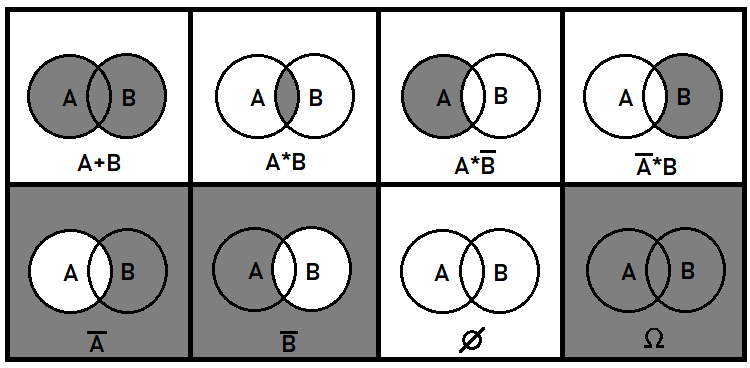
D'autres opérations algébriques peuvent être composées à partir de celles présentées ci-dessus. Par exemple, la division booléenne est équivalente aux 3ème et 4ème situations de la figure ci-dessus, puisque la division est équivalente à la multiplication par l'inverse de l'événement sélectionné. Au sens strict, les 2 premiers événements suffisent à décrire tous les événements possibles pouvant être composés de parties d'événements sources. Les cas où plus de deux événements se chevauchent sont beaucoup plus difficiles. Dans cet article, nous ne traiterons que des événements qui ne se chevauchent pas.

Les mathématiques du marché sont principalement basées sur un concept de marche aléatoire. Nous examinerons ce concept. Il sera ensuite possible de généraliser ces événements par la présence de modèles. Supposons que nous ouvrions une position avec le stop loss et le take profit à égale distance des prix d'ouverture. Nous ne considérons pas les spreads, les commissions et les swaps. Ainsi, si nous ouvrons une position gratuite et que nous effectuons des transactions aléatoires dans différentes directions et à différents points du graphique, le rapport bénéfice/perte sera égal à 1. En d'autres termes, le nombre de positions rentables sera égal au nombre de positions perdantes dans le cadre d'un trading sans fin. D'après ce qui précède, le bénéfice serait nul quelle que soit la durée de l'opération. Si vous appliquez toutes les commissions, les spreads et les swaps, le résultat final sera négatif.

La marche aléatoire peut sembler dénuée de sens, car les mathématiques de ce processus conduisent toujours à des pertes. Mais la marche aléatoire peut aider à calculer les probabilités de différents événements. Il peut s'agir d'une fermeture par des stops asymétriques ou du prix moyen que le graphique passera dans une certaine fourchette de prix. Nous pouvons également calculer la durée de vie des positions et d'autres variables utiles qui peuvent vous aider à calculer les risques ou à tenter de maximiser les profits ou de minimiser les pertes.

Arbres de probabilité et hypothèses

Un exemple très utile pour développer vos lobes frontaux est celui des arbres d'événements, ou arbres de probabilités. Ce thème trouve son origine dans le schéma de Bernoulli, qui est à la base de tous les arbres de probabilité. Ce système examine les chaînes d'événements qui ne se chevauchent pas et qui se succèdent. Mais avant cela, considérons la formule de la probabilité totale. En étudiant cette construction importante, nous pouvons passer au schéma de Bernoulli, puis aux arbres de probabilité. La formule est la suivante :

• P(A) = Somme(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] - probabilité de l'événement A
• P(H[i]) — probabilité de l'hypothèse H[i]
  
• P(A|H[i]) — probabilité que l'événement A se produise dans le cadre de l'hypothèse H[i]

J'aimerais dire que lorsque l'on travaille avec des probabilités, il est préférable de les écrire dans le style de l'hypothèse. Par exemple, l'entrée P(H[k]|H[i]) signifierait :

1. La probabilité de l'événement H[k] calculée par rapport à l'espace H[i]

De cette façon, il est clair quel événement est considéré comme un espace et quel événement est imbriqué. En effet, chaque événement est un espace événementiel plus petit, à l'intérieur duquel peuvent se dérouler d'autres événements, qui peuvent également servir d'espaces événementiels, et ainsi de suite. Selon cette logique, l'entrée P(H[i]) peut être écrite comme suit :

• P(H[i]|O) — parce que cette probabilité est estimée par rapport à O.
  

Divisons maintenant la formule de la probabilité totale en plusieurs parties afin de comprendre ce qui la sous-tend. La formule peut sembler difficile à première vue, alors clarifions-la. Tout d'abord, je vais réécrire la formule sous une forme légèrement différente :

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O = S[0]/O + ... + S[i]/O + ... + S[n]/O = (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — la surface du segment spécifique d'intersection de l'hypothèse H[i]
• N[i] — la surface de l'ensemble de l'hypothèse H[i] (y compris S[i])
• O — tous les résultats, ou la zone de l'ellipse entière

Après de petites transformations, qui ont consisté à multiplier le numérateur et le dénominateur par la valeur N[i], nous pouvons voir les probabilités qui sont présentes dans la formule originale :

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Elle peut être représentée graphiquement comme suit :

 

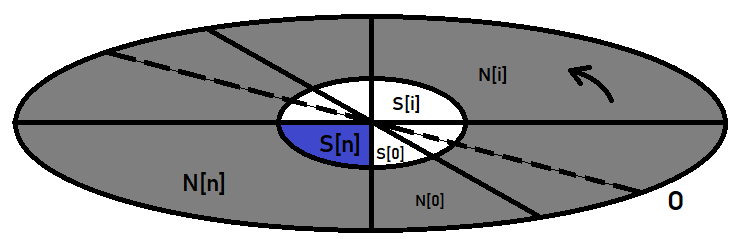
L'ellipse extérieure est l'espace de l'événement. L'ellipse centrale représente l’événement dont nous recherchons la probabilité. Supposons qu'il s'agisse d'une horloge : dessinez le diamètre de l'ellipse, faites-la tourner dans le sens inverse des aiguilles d'une montre et coupez l'ellipse en segments qui sont des hypothèses. Une hypothèse n'est qu'un nom spécial pour des événements. Mais il s'agit en fait des mêmes événements, qui ne diffèrent pas de celui pour lequel nous calculons la probabilité.

Cette formule présente un cas particulier qui nous aidera à construire le schéma de Bernoulli. Imaginons que l'ellipse centrale soit entièrement comprise dans l'une de ces hypothèses. Il s'avère ensuite que tous les termes de cette somme, qui sont liés au reste des hypothèses, sont automatiquement mis à 0, car la probabilité d'occurrence de l'événement A dans ces hypothèses est impossible ou égale à 0, ce qui a pour effet de mettre ces termes à 0. Il s'avère donc que :

• P(A) = P(H) * P(A|H)
• H — la probabilité de l'hypothèse à l'intérieur de laquelle l'événement sélectionné est entièrement situé.

Mais que se passe-t-il si nous supposons que l'événement A est également appelé une hypothèse ? Pourquoi pas ? Une hypothèse est un événement, donc tout événement est une hypothèse. Supposons maintenant qu'il existe un autre événement B, situé à l'intérieur de A. Alors A est une hypothèse par rapport à B, et la formule précédente est applicable à ces deux événements :

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Remplacez P(A) par le ratio précédent — vous pouvez voir un certain modèle dans la construction d'une formule générale pour n'importe quel nombre d'hypothèses ou d'événements imbriqués. Quel est l'objectif ? Il s'agit du prototype direct de la formule de Bernoulli que nous examinerons un peu plus loin. Mais il y a un autre élément intéressant à prendre en compte.

À propos des fractales

Selon la formule ci-dessus, si P(A) + P(B) = 1, il s'agit d'un ensemble d'événements collectivement exhaustif. Cela signifie qu'un groupe complet peut être composé de 2 chaînes arbitraires d'hypothèses imbriquées l'une dans l'autre. Mais ces hypothèses peuvent se chevaucher. Si nous exigeons que toutes les hypothèses imbriquées possibles ne se recoupent pas avec les hypothèses d'autres chaînes, alors automatiquement toutes les chaînes ne se recouperont pas avec toutes les chaînes de cet espace événementiel. La représentation graphique de ce modèle est très intéressante :

Ce modèle est appelé fractale, car ce type de structure n’a pas de fin et peut être construite indéfiniment. Dans la figure ci-dessus, la structure n'a que 3 niveaux de profondeur. Les rectangles bleus représentent la fin d'une chaîne de probabilités distincte. Si nous additionnons les probabilités de toutes ces chaînes, elles formeront un ensemble d'événements collectivement exhaustif.

De telles fractales peuvent être décrites par des combinaisons. Les combinaisons sont basées sur le concept de factorielle. Il existe un autre concept, la permutation, qui se situe entre la factorielle et la combinaison. La formule de permutation est dérivée de la formule factorielle. Et le concept de combinaison est dérivé de la formule de permutation. Voici les formules correspondantes :

• n! - factorielle du nombre n
• P(n, k) = n! / ( n - k )! — permutations de N éléments par K éléments
• С(n, k) = n! / ( k! * ( n - k )! ) — combinaisons de N éléments par K éléments

Une factorielle est le produit de tous les nombres naturels commençant par 1 et se terminant par n, avec "0! = 1". C'est-à-dire que la factorielle de 0 est égale à 1. Dans ce cas, il s'agit simplement d'une exception à la règle. Mais je n'ai pas vu un seul cas où cette exception interférerait avec les calculs ou compliquerait les algorithmes.

Les permutations sont un peu plus compliquées. Imaginez que vous ayez un jeu de cartes, et que ce jeu contienne un certain nombre de cartes. Réalisez une expérience simple : mélangez le jeu et retirez quelques cartes du jeu de manière totalement arbitraire, puis placez-les sur la table dans l'ordre dans lequel elles ont été retirées du jeu. Les permutations représentent donc le nombre de résultats possibles de cette expérience, l'ordre des cartes est également considéré comme un identifiant unique d'un résultat particulier. Cette permutation est applicable à tous les éléments souhaités.

La première carte peut être prise du jeu de n façons différentes, la seconde peut être prise de "n-1" façons, puisque la première carte n'est plus dans le jeu. Et ainsi de suite, jusqu'à la carte "n-k-1". Pour obtenir le nombre de toutes les permutations possibles, il faut multiplier tous les nombres de "n-k-1" à "n". Cette procédure ressemble à une factorielle. Si nous prenons "n!" et la divisons par "n-k" facteurs, nous obtiendrons le produit original qui est exactement égal à "(n-k)! C'est ainsi que l'on obtient la formule de la permutation.

La formule de combinaison est un peu plus compliquée. Mais elle est aussi très facile à déduire. Nous disposons de toutes les permutations possibles, mais l'ordre des éléments n'a pas d'importance — seules les cartes de ce jeu comptent. Il s'agit maintenant de trouver le nombre de ces cas, chaque cas ayant un jeu de cartes différent. En fait, chaque permutation contient déjà l'un de ces ensembles uniques, mais nous n'avons pas besoin de tous les avoir. Changeons de logique et essayons de rassembler toutes les permutations de toutes les combinaisons possibles : il s'avère que si nous prenons une combinaison, quelle que soit la façon dont nous réarrangeons les éléments qui la composent, elles seront uniques. Si nous prenons toutes les combinaisons uniques et que nous produisons toutes les permutations possibles à l'intérieur de celles-ci, nous obtenons également ce qui suit :

• P(n, k) = C(n, k) * P(k, k)

Le nombre de toutes les permutations uniques possibles à l'intérieur d'une combinaison est égal à "P(k, k)", car nous devons collecter à partir de "k" variantes toutes les permutations possibles pour ces "k" variantes. En divisant les 2 parties de l'équation par "P(k, k)", nous obtenons la formule de la combinaison :

• C(n, k) = P(n, k)/P(k, k) = n! / ( k! * ( n - k )! )
  

Les permutations et les combinaisons sont largement utilisées pour résoudre divers problèmes liés à la théorie des probabilités. En ce qui concerne les applications pratiques, ce sont les combinaisons qui nous sont le plus utiles. Les combinaisons sont utilisées dans la construction de fonctions fractales à des fins diverses. Il serait peut-être plus correct de les appeler récurrentes, mais pour une raison quelconque, j'appelle ces fonctions fractales (probablement parce qu'elles sont vraiment fractales, et qu'il ne s'agit donc pas seulement d'une récursion, mais d'un arbre entier d'appels).

Schéma de Bernoulli

Avant d'étudier ces fonctions fractales, examinons la célèbre formule de Bernoulli. Supposons que nous ayons une chaîne d'expériences identiques que nous devons répéter plusieurs fois. L'expérience doit aboutir à l'apparition ou à la non-apparition d'un événement avec une certaine probabilité. Supposons également que nous voulions trouver la probabilité que, dans une chaîne de "n" expériences, notre événement apparaisse exactement "k" fois. La formule de Bernoulli permet de répondre à cette question :

• P = C(n, k) * Pow(p, k) * Pow(q, n-k) — Formule de Bernoulli
  
• p — la probabilité d'occurrence de l'événement à la suite d'une seule expérience
• q = 1 - p — la probabilité que l'événement ne se produise pas à la suite de l'expérience

Vous souvenez-vous de la formule dérivée précédemment pour les chaînes probabilistes ? Étendons-la à une grande longueur de chaîne arbitraire :

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n — le nombre de segments dans la chaîne
• O — l'ensemble des résultats ; il peut être noté H[0].

Cette formule calcule la probabilité que la chaîne d'hypothèses exactement requise se produise. La formule peut être représentée visuellement comme suit :

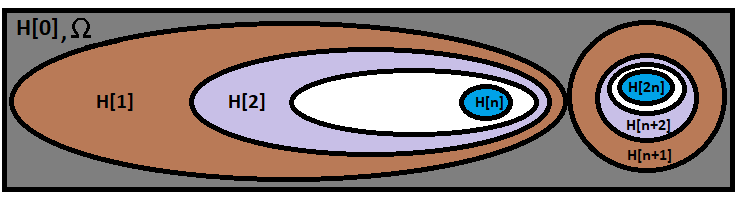
Notre formule se trouve dans la première ellipse, la plus grande, une autre chaîne à droite ne se superpose pas à la nôtre et symbolise une autre branche issue d'une combinaison différente. Il y a exactement autant de branches que de variantes pour le calcul des combinaisons dans notre formule. Il ne faut donc pas confondre les combinaisons avec les variantes de calcul des combinaisons. Le nombre de variantes pour le calcul des combinaisons est égal à :

• n+1 (car les combinaisons de résultats "0" sont également comptabilisées)
• n est le nombre de tests indépendants dans la chaîne d'expériences

Imaginons maintenant que les probabilités de toutes ces hypothèses soient égales à "p" ou "q". La formule est ensuite simplifiée :

• P(n) = Pow(p, k) * Pow(q, n-k)
• k — combien de facteurs égaux à "p" y a-t-il dans le produit ?
• n-k — combien de facteurs égaux à "q" y a-t-il dans le produit ?

Elle ressemble déjà à la formule de Bernoulli, mais il lui manque la combinaison. Si l'on réfléchit bien, il apparaît clairement que les variantes de chaînes ayant une probabilité similaire et la quantité de "k" et "n-k" sont exactement égales à "C(n,k)". Étant donné que toutes les chaînes de probabilités ne se chevauchent pas, la probabilité d'obtenir l'une de ces chaînes est la somme des probabilités de toutes ces chaînes. Comme toutes ces probabilités sont identiques, nous pouvons multiplier la probabilité d'une chaîne par leur nombre pour obtenir la formule de Bernoulli :

• P = C(n, k) * Pow(p, k) * Pow(q, n-k)

Cette formule peut être étendue, par exemple, lorsque nous devons trouver la probabilité non pas d'une combinaison strictement fixe, mais d'un événement se produisant k fois et plus, k fois et moins, et toutes les combinaisons similaires. Dans ce cas, il s'agit de la somme des probabilités de toutes les combinaisons requises. Par exemple, la probabilité que l'événement se produise plus de k fois est calculée comme suit :

• P = Somme(k+1 ... i ... n)[C(n, i) * Pow(p, i) * Pow(q, n-i)]

Il est important de comprendre que :

• P = Somme(0 ... i ... n)[C(n, i) * Pow(p, i) * Pow(q, n-i) ] = 1

En d'autres termes, toutes les chaînes possibles forment un ensemble d'événements collectivement exhaustif. Une autre équation importante est la suivante :

• Somme(0 ... i ... n)[C(n, i)] = Pow(2, n)
  

C'est logique, étant donné que chaque segment de la chaîne de probabilité n'a que 2 états : "l'événement s'est produit" et "l'événement ne s'est pas produit". L'état dans lequel l'événement ne s'est pas produit est également un événement, ce qui implique qu'un autre événement s'est produit.

Les combinaisons ont une autre propriété intéressante :

• C(n, k) = C(n, n-k)
  

Elle est calculée comme suit : calculer "C(n, n-k)" et comparer avec "C(n, k)". Après quelques transformations mineures, on constate que les 2 expressions sont identiques. J'ai créé un petit programme basé sur MathCad 15 afin de vérifier toutes les affirmations ci-dessus : 

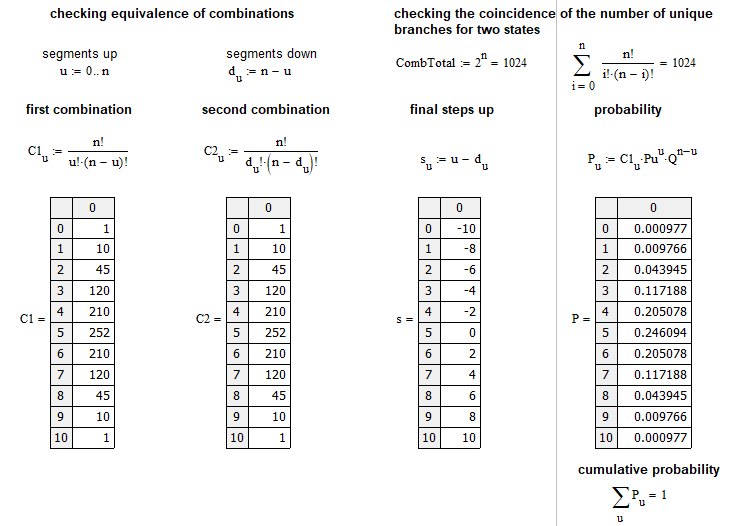
Cet exemple est proche du marché. Il calcule la probabilité que, sur n étapes, le marché progresse de u étapes. Un pas est le mouvement du prix à un certain nombre de points vers le haut ou vers le bas, par rapport au pas précédent. Le tableau graphique des probabilités pour chaque "u" peut être représenté comme suit :

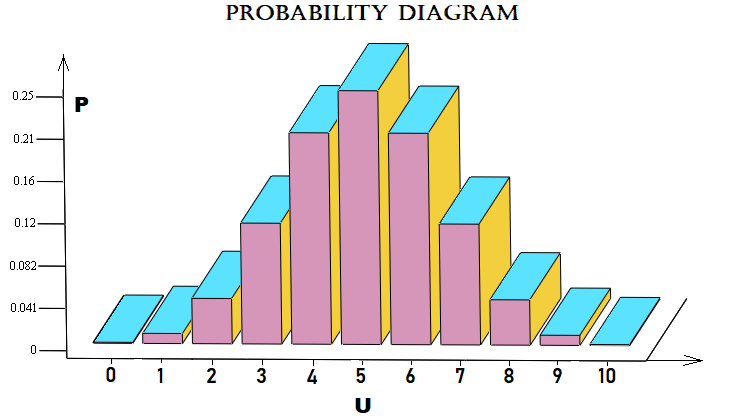
Par souci de simplicité, j'ai utilisé un schéma de Bernoulli à 10 étapes. Le fichier est attaché ci-dessous, afin que vous puissiez le tester. Il n'est pas nécessaire d'appliquer ce schéma aux prix. Il peut également s'appliquer aux ordres ou à toute autre chose.

Création de la première fractale

Une attention particulière doit être accordée aux problèmes liés aux niveaux des stop loss et des take profit. Nous devrions calculer d'une manière ou d'une autre la probabilité qu'une transaction soit clôturée par un stop loss ou par un take profit lorsque nous connaissons les valeurs du stop loss et du take profit en points (distance par rapport au prix actuel). Cette valeur peut être calculée à tout moment, même s'il ne s'agit plus du prix d’ouverture, car tous ces aspects dépendent directement des mécanismes de calcul du prix. Dans cet exemple, je veux vous donner la preuve de la formule à l'aide de fractales. Dans le cas d'une marche aléatoire, cette probabilité peut être calculée comme suit :

• P(TP) = SL / ( TP + SL ) — la probabilité d'atteindre le take profit
• P(SL) = TP / ( TP + SL ) — la probabilité d'atteindre le stop loss
• SL — la distance entre le point et le stop loss
  
• TP — la distance entre le point et le take profit

Ces deux probabilités forment un ensemble d'événements collectivement exhaustif :

• P(TP) + P(SL) = 1
  

Selon cette formule, pour un trading aléatoire, l'espérance mathématique de ces stratégies sera nulle, si l'on exclut le spread, la commission et le swap :

• M = P(TP) * TP - P(SL) * SL = 0

C'est le cas le plus simple lorsque nous fixons un niveau d'arrêt fixe. Mais il est possible de la généraliser à n'importe quelle stratégie. Prouvons maintenant la formule en utilisant le même MathCad 15. Je travaille avec ce programme depuis longtemps. Il peut effectuer des calculs de presque tous les niveaux de complexité, même en utilisant la programmation. Dans cet exemple, en plus de prouver les formules ci-dessus, nous verrons le premier exemple de construction d'une formule fractale. Commençons par esquisser le processus de mouvement des prix. Nous ne pouvons pas utiliser de fonctions continues ici, mais seulement des fonctions discrètes. Pour ce faire, prenons notre ordre conditionnel et calculons les distances des niveaux de stop vers le haut et vers le bas, après quoi nous divisons ces segments en parties avec des étapes égales, de sorte que chaque étape comprenne un nombre entier d'étapes. Imaginons que le prix évolue de la manière suivante. Les marches étant égales, la probabilité d'une marche dans l'une des deux directions est de 0,5. Nous avons besoin d'une représentation graphique pour mettre en œuvre la fractale appropriée :

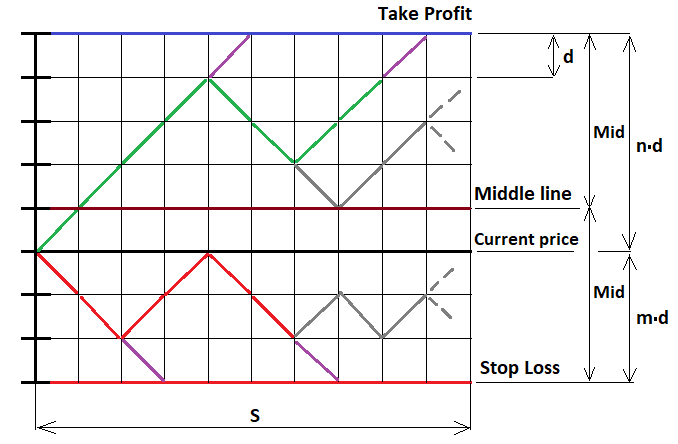
Pour résoudre ce problème, examinons trois cas possibles de continuation fractale :

1. Nous sommes au-dessus de la ligne médiane ( U > Ligne médiane )
2. Nous sommes en dessous de la ligne médiane ( U < Ligne médiane )
3. Nous sommes au niveau de la ligne médiane ( U = MiddleLine )

"U" est le nombre total de pas "u-d" vers le haut par rapport au prix d’ouverture. Si le point à partir duquel nous allons continuer à construire la fractale est en dessous du prix, alors U prend des valeurs négatives conformément à la fonction. Si nous nous trouvons sur la ligne médiane, le nombre de pas que nous pouvons faire sans craindre de franchir la ligne est inférieur d'une unité à Mid. Mais avant de procéder à la construction, nous devons limiter la construction fractale au nombre de pas que le prix ou les ordres peuvent faire. Si le nombre d'étapes dépasse le nombre requis, nous devons interrompre la poursuite de la construction. Sinon, nous obtiendrons une récursion infinie, dont il sera impossible de sortir. Son temps de calcul sera égal à l'infini.

Dans la figure, j'ai dessiné plusieurs étapes en violet : à ces points, nous rassemblons les probabilités et les additionnons en une variable commune. Ensuite, nous devons faire tourner notre chaîne vers le haut ou vers le bas, en fonction du niveau qu'elle a touché, afin qu'elle puisse continuer à se déplacer pour construire de nouveaux niveaux fractals imbriqués. En d'autres termes, nous pouvons librement construire des niveaux fractals complets basés sur le schéma de Bernoulli.

Lorsqu'il est possible de créer un arbre basé sur le schéma de Bernoulli, nous devons d'abord déterminer le nombre de pas que nous pouvons faire, en tenant compte des cas extrêmes, lorsque tous les pas sont uniquement vers le haut ou vers le bas. Dans les trois cas, la valeur est égale à :

• (n - 1) - U — lorsque notre chaîne est déjà au-dessus de la ligne médiane (puisqu'une augmentation de U entraîne une diminution de la distance jusqu'à la limite supérieure)
• (m - 1) + U — lorsque notre chaîne est déjà en dessous de la ligne médiane (puisqu'une diminution de U entraîne une diminution de la distance jusqu'à la limite inférieure)
• (floor(Mid)-1) — lorsque notre chaîne se trouve exactement sur la ligne médiane
• n — le nombre de segments vers le haut
• m — le nombre de segments vers le bas
• floor — la fonction ne tient pas compte de la partie fractionnaire (cela peut ne pas être nécessaire)

Nous devons d'abord calculer 2 valeurs auxiliaires :

• Mid = (m+n)/2 — la moitié de la largeur de la plage (en pas)
• Middle = (m+n)/2 - m — la valeur "U" pour la ligne du milieu (en pas)

Ces valeurs seront utilisées ultérieurement pour décrire la logique de ramification fractale. Pour l'instant, nous ne créerons la fractale que pour les cas où "n>=m". Cependant, ces données ne sont pas suffisantes pour construire une fractale. Pour pouvoir construire des niveaux fractals plus profonds, il est nécessaire de redéfinir "U" pour chaque nouvelle combinaison du schéma de Bernoulli et de la transmettre à un nouveau niveau fractal. Il est également nécessaire d'incrémenter correctement le nombre d'étapes réalisées et de les faire suivre correctement. De même, nous devons collecter la probabilité de l'ensemble de la chaîne en utilisant les multiplicateurs du niveau fractal suivant et transmettre la probabilité de la chaîne intermédiaire au niveau suivant, jusqu'à ce que ce processus s'achève par le franchissement réussi du niveau souhaité. L'image ci-dessous explique ces trois variantes :

  

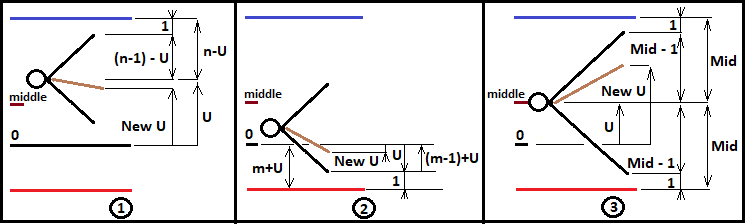
D'après ce diagramme, nous pouvons maintenant écrire à quoi les valeurs "NewU" et les autres valeurs auxiliaires seront égales pour chaque cas présenté. Prenons l'exemple de la construction d'une fractale pour calculer la probabilité de franchir la limite supérieure :

Pour le cas 1 :

Examinons l'image ci-dessus et décrivons mathématiquement ce qui s'y passe. Cette figure montre un résumé de mon programme dans MathCad 15. Le code complet du programme est joint ci-dessous. Je donne ici les détails les plus importants qui sont à la base de la fractale. Le premier rectangle est dans une boucle, et il itère sur "i" pour décrire toutes les combinaisons possibles. Cette logique peut être répétée dans l'IDE MetaEditor. Commençons par la première illustration du schéma. Pour définir "NewU", il faut d'abord définir quelques formules fondamentales :

• ( n - 1 ) - U = f — c'est le nombre de pas de l'arbre des combinaisons futures (la distance est déterminée par la distance à la bordure la plus proche de la plage fractale)
• u + d = f — la même valeur, mais exprimée en termes de nombre de segments ascendants et descendants
• s = u - d — le nombre d'étapes finales, exprimé en termes de segments descendants et ascendants
• u = i — c'est parce que mon programme utilise "i" comme incrément (il faut s'en souvenir)

Pour calculer toutes les valeurs requises, nous devons exprimer "s" par "U" et "i". Pour ce faire, nous devons exclure la variable "d". Exprimez-la d'abord, puis substituez-la dans l'expression de "s" :

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

Ensuite, en utilisant le "s" trouvé, trouvez "NewU" et toutes les valeurs à transmettre au niveau fractal suivant :

• NewU = s + U = -( n - 1 ) + 2*i + 2*U — notre nouveau "U" à transmettre au niveau fractal suivant
• NewP = P * C(f, i) * Pow(p, i) * Pow(1-p, f-i) = P * C( ( n - 1 ) - U, i) * Pow(p, i) * Pow(1-p, ( n - 1 ) - U -i) — notre nouvelle probabilité pour la chaîne "P" d’être passée au niveau fractal suivant (obtenue en multipliant par la probabilité du nouveau segment de la chaîne)
• NewS = S + f = S + ( n - 1 ) - U — nouveau "S" à transmettre au niveau fractal suivant

Maintenant, regardez le rectangle du bas. Nous traitons ici les cas où la chaîne de pas a atteint la limite supérieure du canal. Deux cas doivent être traités ici :

1. Collecte de la probabilité de la chaîne qui croise la bordure (soulignée en rouge)
2. Actions similaires, incrémentant de nouvelles valeurs que nous transmettrons au niveau fractal suivant

Ce cas est très simple car il n'y a que 2 variantes possibles :

1. Toucher la bordure
2. Revenir depuis la bordure

Ces actions ne nécessitent pas un schéma de Bernoulli, car chaque cas n'implique qu'une seule étape. La probabilité du renversement est en outre multipliée par "(1-p)", car la probabilité d'intersection est "p", et ces deux événements devraient former un ensemble collectivement exhaustif, comme le montrent les calculs précédents. Les pas sont incrémentés de 1, et "U" est diminué de "1", car il s'agit d'une réflexion qui va vers le bas. Nous disposons à présent de tous les éléments nécessaires pour constituer correctement ce dossier. Ces règles seront identiques pour la construction des fractales principales, dont nous avons besoin pour des cas complètement différents.

Pour le cas 2 :

Le calcul est presque similaire dans ce cas. La seule différence est que "f" prend une valeur différente :

• ( m - 1 ) + U = f

Exprimez à nouveau "s" par "U" et "i", en utilisant les mêmes formules que dans le cas précédent :

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

Trouvez également toutes les autres valeurs dont nous avons besoin pour passer au niveau fractal suivant :

• NewU = s + U = -( m - 1 ) + 2*i — nouveau "U" à transmettre au niveau fractal suivant
• NewP = P * C(f, i) * Pow(p, i) * Pow(1-p, f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p, i) * Pow(1-p,( m - 1 ) + U -i)  — notre nouvelle probabilité pour la chaîne "P" d'être transmise au niveau fractal suivant.
• NewS = S + f = S + ( m - 1 ) + U — notre nouveau "S" à transmettre au niveau fractal suivant

Le rectangle inférieur est presque identique au cas précédent, sauf que nous augmentons "U" de 1, parce que la réflexion augmente et donc "U" est augmenté. Les probabilités ne sont pas collectées dans ce cas, car nous ne nous intéressons pas à l'intersection avec la limite inférieure de cette fractale. Voici maintenant le dernier cas, lorsque la chaîne s'est produite à la ligne médiane du canal.

Pour le cas 3 :

Définir "f" :

• floor(Mid) - 1 = f

Trouver "s" :

1. d = f - i = floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Trouvez enfin les valeurs à transmettre au niveau fractal suivant :

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i) — notre nouvelle probabilité de chaîne "P" à transmettre au niveau fractal suivant
• NewS = S + f = S + (floor(Mid) - 1) — notre nouveau "S" à transmettre au niveau fractal suivant

Ce cas se distingue par le fait que le bloc ne collecte pas de probabilités, car celles-ci ne peuvent être collectées qu'aux valeurs limites de "U", où les chaînes de probabilités sont également renvoyées dans la chaîne afin qu'elles puissent se propager davantage. La création d'une fractale pour calculer la probabilité de franchir la bordure supérieure sera identique, mais les probabilités seront comptées dans le second cas, et non dans le premier.

Une caractéristique intéressante de la construction de ces fractales est la présence obligatoire de la formule de Bernoulli dans ces fonctions. Les combinaisons sont surlignées en rose et les produits des probabilités sont indiqués en jaune. Ces deux multiplicateurs forment ensemble la formule de Bernoulli.

Vérifions maintenant 2 choses en même temps : l'exactitude de la construction de la fractale entière et l'hypothèse selon laquelle le gain attendu ne dépend que de la capacité de prédiction. Les étapes peuvent être présentées sous forme de points ou de transactions. Dans ce dernier cas, les points doivent être multipliés par le coefficient de proportionnalité approprié, qui dépend des lots et de la taille du tick. Nous utiliserons ici des points - cette représentation est universelle :

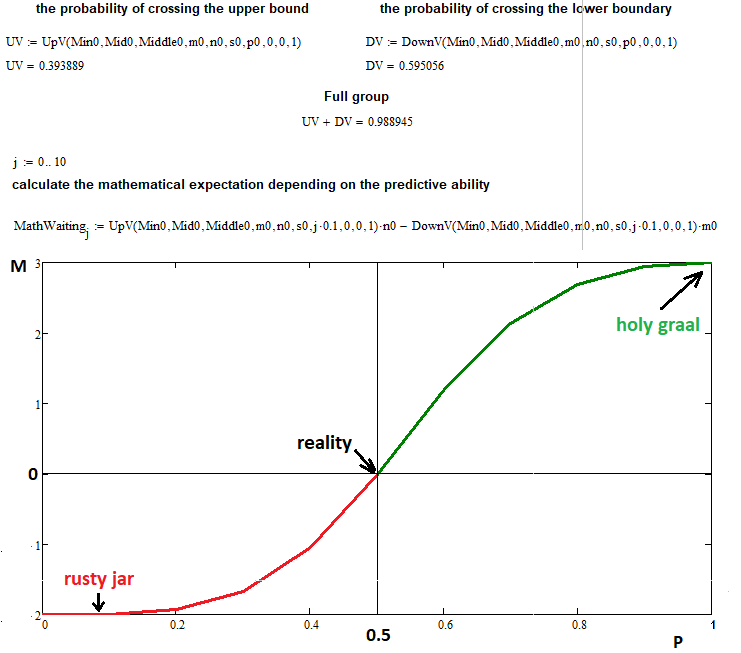
Dans cet exemple, j'ai utilisé les données d'entrée suivantes pour tracer l'espérance mathématique en fonction de la probabilité d'un passage à l'échelon supérieur :

• n = 3 — nombre de segments haussiers
• m = 2 — nombre de segments baissiers
• s = 22 — nombre d'étapes autorisées pour une réaction en chaîne de la fonction fractale (si vous augmentez cette valeur, cela créera une charge supplémentaire sur l'ordinateur, donc ce nombre d'étapes est tout à fait suffisant)
• 0 ... 0.1 ... 0.2 ...... 1,0 — division de l'intervalle des probabilités d'échelon supérieur en 10 parties avec un pas de 0,1

Comme vous pouvez le constater, pour la probabilité de 0,5, l'espérance mathématique de nos transactions est égale à zéro, comme le prévoyait la formule. Aux points extrêmes 0 et 1, la valeur de la fonction tend vers "n" et "-m", ce qui confirme nos hypothèses. La fractale a rempli sa mission avec succès, bien qu'elle ait révélé un inconvénient : une forte augmentation du temps de calcul et de la complexité. Mais il est tout à fait acceptable d'attendre quelques heures, voire une journée, pour des tâches similaires.

Cette fractale ne fonctionne que dans les cas où n >= m, c'est-à-dire lorsque la distance jusqu'au bord supérieur est supérieure à la distance jusqu'au bord inférieur, mais il n'est pas nécessaire de l'indiquer dans la fractale. Cette construction peut être inversée : si n < m, nous pouvons calculer la fractale en lui passant m au lieu de n et n au lieu de m. Il suffit ensuite d'intervertir les probabilités pour obtenir le résultat souhaité. Ces fractales peuvent être utilisées non seulement pour prouver des formules, mais aussi pour un processus inverse. Certaines formules ne peuvent être obtenues qu'en utilisant des fractales.

Résumé

Je pense que les conclusions suivantes, très importantes, ont été tirées dans cet article :

• La théorie des probabilités combinée à la programmation peut fournir une base théorique pour décrire de nombreux processus de marché.
• Les fractales combinées aux principales dispositions de la théorie des probabilités peuvent répondre aux questions les plus difficiles.
• Nous avons vu un exemple de création d'une fractale assez complexe.
• L'ensemble de la théorie a été testé en pratique en utilisant la programmation dans l'environnement MathCad 15.
• L'article a prouvé que le schéma de Bernoulli permet de créer n'importe quelle fractale avec 2 états d'étape.

Conclusion

J'espère que le lecteur y verra quelque chose de nouveau, qui pourra être mis en pratique dans le cadre de ses activités de trading. En rédigeant cet article, j'ai essayé de transmettre toute la puissance des mathématiques discrètes et de la théorie des probabilités, afin de vous préparer à une autre tâche difficile : décrire les processus de marché à l'aide de chaînes de probabilité fractales. J'ai essayé de combiner toutes les dispositions principales de la théorie des probabilités en un seul document, qui peut aider à résoudre des tâches complexes pour le trading pratique. J'ai également essayé de supprimer tous les détails non pertinents. Le prochain article fournira de nouveaux exemples d'application pratique des fractales et des réponses à d'autres questions importantes.