선형 회귀 예시를 통한 인디케이터 가속 그 3가지 방법

계산 속도

인디케이터의 신속한 계산은 몹시 중요한 작업입니다. 계산은 각기 다른 메소드들에 의해 가속될 수 있습니다. 이 문제를 다루는 문서가 여럿 있습니다.

이제 계산을 가속화하고 코드 자체를 단순화하기 위해 3가지 방법을 더 검토하겠습니다. 설명된 메소드는 모두 알고리즘적 관점에서 보아졌습니다. 즉, 과거 처리량을 줄이던지 프로세서 유닛의 추가 코어를 활성화시키는 등 은 하지 않습니다.. 직접 알고리즘을 최적화할 것입니다.

기본 인디케이터

세 가지 방법을 모두 표시하기 위해 사용되는 인디케이터는 선형 회귀 인디케이터입니다. 각 바에 회귀 함수를 생성하고(마지막 바의 정의된 수에 따라), 이 바에 어떤 값이 있어야 하는지 보여줍니다. 이 실선을 결과로 얻습니다:

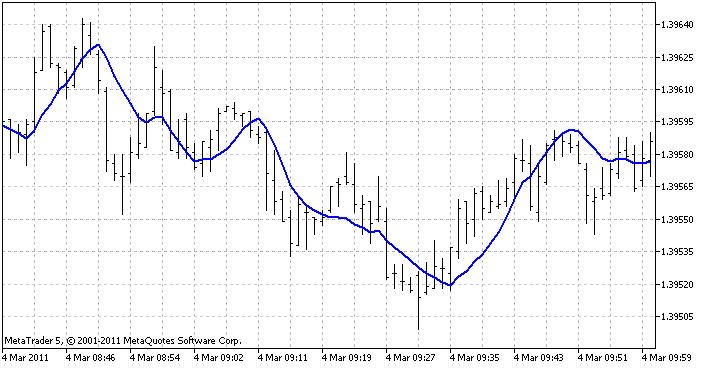
터미널에서 인디케이터는 이렇게 보입니다

 

선형 회귀는 다음과 같이 보입니다:

우리의 경우 x는 바의 숫자고 y는 매매가입니다.

언급된 방정식의 비율은 다음과 같이 계산됩니다:

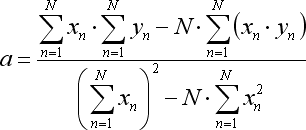
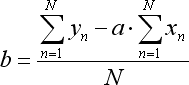
N은 회귀 선을 형성하기 위해 사용되는 바의 개수입니다.

MQL5에서는 이러한 방정식이 다음과 같이 표시됩니다(모든 히스토리 바 사이클 내부):

            // Finding intermediate values-sums
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Regression ratios
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

인디케이터의 전체 코드가 문서에 첨부되어 있습니다. 그 첨부파일에는 이 문서에서 다뤄진 모든 메소드도 담겨있습니다. 따라서, "표준" 계산 메소드를 인디케이터 설정에서 선택해야합니다::

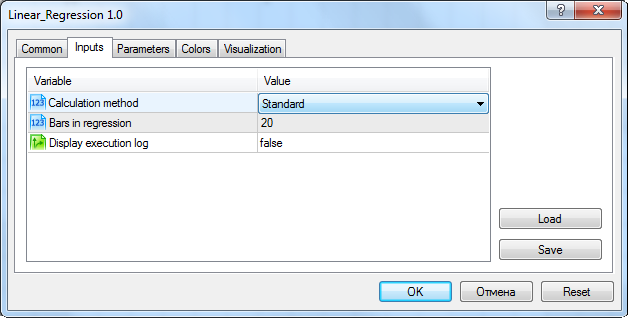
차트 위에 세팅되었을 때의 인디케이터 입력 패러미터 세팅 창 

첫번째 최적화 방법 이동 총량

바 시퀀스 값의 총 수치가 각 값에서 계산되는 인디케이터는 매우 많습니다. 이 시퀀스는 바에 따라 계속 변합니다. 가장 잘 알려진 것은 이동 평균(Moving Average, MA) 입니다. N개의 마지막 바의 합계를 계산한 다음 이 값을 바의 수로 나눕니다.

저는 꽤 많은 사람들이 그와 같이 움직이는 총계 계산을 가속화할 수 있는 우아한 방법이 있다는 것을 알고 있다고 생각합니다. 제가 이 방법이 MetaTrader 4 그리고 5의 MA-인디케이터에 쓰이고 있다는 것을 알아차렸을 때엔, 이미 이 방법을 꽤나 오래 사용하고 있던 중이었습니다. (MetaTrader 인디케이터들이 개발자들에 의해 제대로 최적화된 것을 제가 알게된 것이 이게 처음은 아닙니다. 오래 전, 저는 빠른 ZigZag 인디케이터를 찾고 있었고 기본 인디케이터가 외부 인디케이터 대부분보다 효율적이라는 것을 알게 됐습니다. 그나저나, 혹시 찾으시는 분이 있을지도 모르니 언급한 포럼 토픽에서 ZIgZag 최적화 메소드 역시 찾아볼 수 있습니다).

다시 이동 총량으로 돌아가겠습니다. 두 개의 인접한 바에 대해 계산된 합계를 비교해보겠습니다. 아래 그림은 이러한 합계에 상당한 공통 부분이 있음을 보여줍니다(녹색으로 표시됨). 0번 바에 대해 계산된 합계는 1번 바의 합계와 다릅니다. 오래된 바 1개(왼쪽의 빨간색 막대)는 포함되지 않지만 새 바 1개(오른쪽의 파란색 막대)는 포함됩니다.

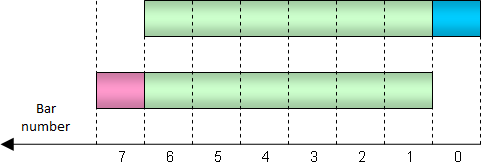
1 바 이동 중에 총량에서 제외된, 그리고 포함된 값들

 

따라서 0번 바의 합계를 계산하면서 필요한 바를 모두 다시 합할 필요가 없습니다. 1번 바에서 합계를 구해서 한 값을 빼고 새 값을 추가할 수 있습니다. 딱 두개의 수학 계산이 필요합니다. 그러한 방법을 사용하여 지표 계산을 상당히 가속화할 수 있습니다.

이동 평균에서는 인디케이터가 모든 평균 값을 버퍼에만 유지하므로 이러한 방법이 일상적으로 사용됩니다. 그리고 이는 합계를 N으로 나눈 것, 즉 합계에 포함된 바의 수일 뿐입니다. 버퍼의 값에 N을 곱하면 원하는 바에 대한 합계를 쉽게 얻을 수 있으며 위에서 설명한 방법을 적용할 수 있습니다.

이제 이 방법을 좀 더 복잡한 인디케이터인 선형 회귀 분석에서 적용하는 방법을 보여 드리겠습니다. 회귀 함수 비율 계산 공식에는 x, y, x*x, x*y의 합계가 포함되어 있다는 것을 이미 보셨습니다. 총량 계산에는 버퍼가 필요합니다. 이를 위해서는 인디케이터 내의 각 총량에 대한 버퍼를 할당해야 합니다.

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

버퍼는 차트 상에서는 보이지 않을 수도 있습니다. MetaTrader 5에는 특별한 버퍼 타입 - 중급계산용이 있습니다. 우리는 이것을 OnInit에서 버퍼 수 들에 할당하기 위해 사용할 것입니다.:

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

이제 다음에 대한 표준 선형 회귀 계산 코드가 변경됩니다:

            // (The very first bar was calculated using the standard method)        
        
            // Previous bar
            int prevbar = bar-1;
            
            //--- Calculating new values of intermediate totals 
            //    from the previous bar values
            
            Sx  = ExtBufSx [prevbar]; 
            
            // An old price comes out, a new one comes in
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // All the old prices come out once, a new one comes in with an appropriate weight
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Regression ratios (calculated the same way as in the standard method)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

인디케이터의 전체 코드가 문서에 첨부되어 있습니다. "이동 총량" 계산 메소드는 인디케이터 설정에서 세팅되어야합니다.

두번째 방법. 단순화

이것은 수학 애호가 분들이 즐길 방법입니다. 복잡한 방정식에서는 일부 파트가 알고보니 다른 알려진 방정식에서도 발견되는 경우가 있습니다. 따라서 그런 파트를 남은 파트로 교체할 수 있는 가능성을 제공합니다(보통 변수는 하나). 다른말로는, 복잡한 방정식을 단순화할 수 있다는 것입니다. 그리고 이 단순화된 방정식의 일부 요소는 이미 인디케이터로 인식되고 있는 것으로 보일 수 있습니다. 그런 경우에는 해당 방정식을 포함하는 인디케이터의 코드는 순차적으로 상당히 단순화할 수 있습니다.

그 결과, 효율적인 메모리 관리가 가능하며 간단한 코드가 생성되었습니다. 또한 경우에 따라서는 코드에 구현된 인디케이터가 매우 신속하게 최적화되어 있는 경우에도 더욱 빨라질 수 있습니다.

선형 회귀 방정식도 단순화할 수 있고 그 계산은 여러 MetaTrader 5 표준 인디케이터의 초기화로 대체될 수 있는 것으로 보인다. 그 안의 많은 요소가 다양한 계산 모드에서 이동 평균 인디케이터로 계산됩니다:

• 합계 y는 단순 이동 평균(Simple Moving Average)로:

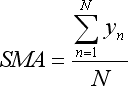
• 합계 x*y는 선형 가중 이동 평균(Linear Weighted Moving Average)으로:

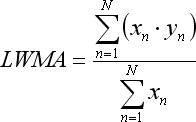
선형 가중 이동 평균 공식의 경우 우리가 바를 1에서 N까지 순차적으로 따질때에만 참이라는 점을 염두에 두시기 바랍니다:

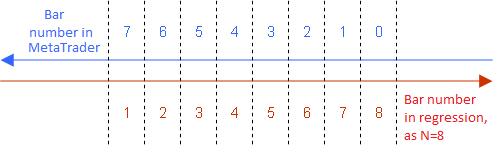
선형 가중 이동 평균 인디케이터를 사용하기위해 회귀용 바를 간편하게 열거하는 방법 

 

따라서 다른 모든 방정식에도 동일한 열거법을 사용해야 합니다.

계속해서 메소드를 사용해봅시다:

• x 총량은 다음 방정식으로 대체할 수 있는 시리즈 총합 (1 + 2 + ... + N)에 지나지 않습니다.:

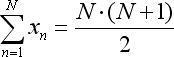
• x*x 총량은 다른 수식으로 간소화할 수 있습니다:

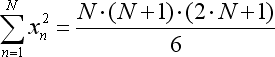
• 인디케이터 차트를 작성하기 위해 우리는 x == N인 마지막 바에 대해서만 회귀 함수를 계산해야 합니다. 즉, 회귀 함수 방정식을 특정 사례로 대체할 수 있다는 것입니다.

따라서 마지막 5개 식이 비율 비율 계산 공식 내의 모든 변수인 a 및 b 뿐만 아니라 회귀 함수 자체에 대해서도 대안을 제공해줍니다. 대체를 완료하게되면 회귀 값을 계산하기 위한 신규 계산 식을 얻게 됩니다. 이는 이동 평균 인디케이터와 N 값만 포함할 것입니다. 요소를 모두 줄인 후에는 다음과 같은 우아한 방정식을 얻을 수 있습니다:

이 방정식은 선형 회귀 기본 지표에서 실행된 모든 계산을 대체합니다. 그 방정식을 가진 인디케이터 코드가 메모리 면에서 훨씬 효율적일 것이라는 것은 누구나 알 수 있습니다. "속도 비교" 챕터에서 우리는 코드가 실제로 더 빠르게 실행되는지 확인할 것입니다.

인디케이터의 해당 파트:

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

선형 가중 이동 평균 및 표준 이동 평균 인디케이터는 미리 OnInit에서 생성됩니다:

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

전체 코드는 이 문서에 첨부되어 있습니다.. 인디케이터 설정에서 "간소화" 계산 메소드가 설정되어 있어야 합니다.

이 메소드에서 우리는 터미널에 내장된 인디케이터를 사용했다는 점을 주목해주시기 바랍니다. 예를 들어, 적절한 평활법을 사용한 iMA 함수는 iCustom 대신 쓰였습니다. 이건 꽤나 중요한데, 이는 이론적으로 내장형 인디케이터는 매우 빠르게 작동해야 하기 때문입니다. 일부 표준 인디케이터는 터미널 내장입니다 (iMA처럼 "i"로 시작하는 함수에 의해 만들어짐). 간소화 방법을 사용할 때는 해당 지표로 방정식을 간소화하는 것이 훨씬 좋습니다.

세번째 방법. 근사법

이 방법의 기본 아이디어는 전문가가 사용하는 "무거운" 인디케이터를 필요한 값을 대략적으로 계산하는 훨씬 더 빠른 인디케이터로 대체할 수 있다는 것입니다. 이 방법을 사용하면 당신의 매매 전략을 더 빠르게 테스트해볼 수 있습니다. 애초에 디버깅 단계에서는 예측 정확도는 그렇게 중요하지않으니까요.

또한 이 방법 패러미터를 대충 최적화하는 작업 전략과 함께 사용할 수 있습니다. 패러미터의 효과값들을 빠르게 찾을 수 있게 해줍니다. 그런 다음 세밀한 조정을 위해 "무거운" 인디케이터로 처리할 수 있습니다.

그나저나, 전략이 제대로 작동하기 위해서는 대략적인 계산으로도 충분할 것으로 보입니다. 그 경우엔 "경령화된" 인디케이터를 실거래에서도 사용할 수 있습니다.

회귀와 유사한 효과를 갖는 선형 회귀 분석에 대해 빠른 방정식을 개발할 수 있습니다. 예를 들어, 회귀 분석 바를 두 그룹으로 나누고, 각 그룹의 평균 값을 계산하고, 이 두 평균 지점을 통과하는 선을 그리고, 마지막 바에서 선의 값을 정의할 수 있습니다.

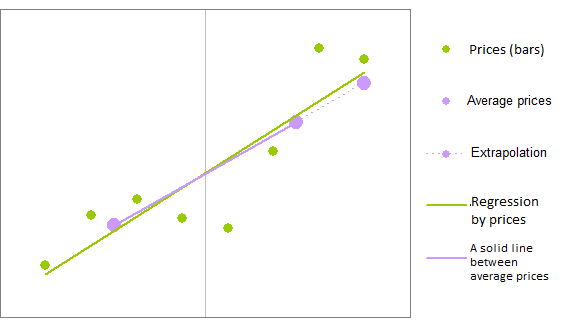
포인트들은 좌, 우, 두 그룹으로 나뉘어서 계산되었습니다.

 

그런 계산이 회귀 처리보다 더 적은 산수 작업을 요구합니다. 그것이 바로 계산을 가속화하는 방법입니다.

           // The interval midpoint
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Average price of the first half
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Average price of the second half
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Price excess by one bar
           double k = (s1-s2)/(LRPeriod/2);
           
           // Extrapolated price at the last bar
           lrvalue = s1 + k * (HalfPeriod-1)/2;

인디케이터의 전체 코드가 문서에 첨부되어 있습니다. "근사" 계산 메소드는 인디케이터 설정에서 설정되어야합니다.

이제 어떻게 해야 오리지널에 가깝게 근사할 수 있을지 분석해봅시다. 이를 달성하기 위해서 한 차트 위에 표준 및 근사 계산 방법을 다루도록 인디케이터를 세팅해야합니다. 또한 꽤 약하게 회귀와 유사한 다른 인디케이터들을 추가해야 합니다. 그러나, 과거의 바들을 이용하여 추세 또한 계산해야합니다. 이동 평균이면 충분합니다(표준 이동 평균이 아니라 선형 가중 이동 평균을 사용했습니다. 회귀 관리도와 훨씬 유사합니다). 그 옆에서 우리는 괜찮은 근사를 얻었는지 아닌지 평가할 수 있습니다. 제가 보기엔 꽤 괜찮네요:

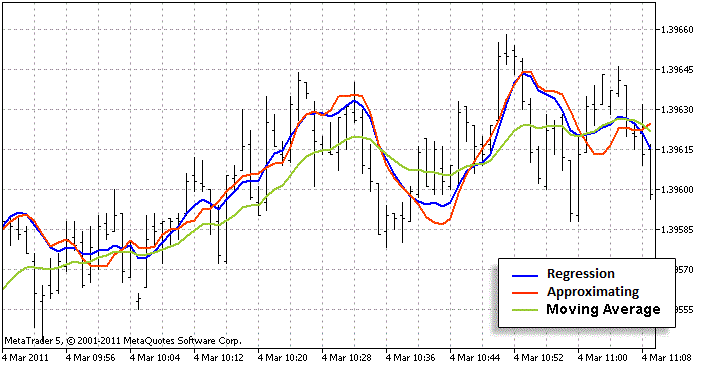
 빨간 선이 녹색 선 보다 파란 선에 가깝네요. 이는 근사 알고리즘이 좋다는 의미입니다.

속도 비교

인디케이터 패러미터에서 로그 디스플레이를 가동시킬 수 있습니다.

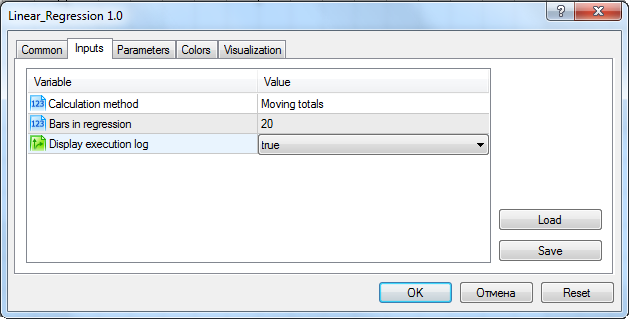
인디케이터를 가동 시간 평가용으로 세팅하기

 

이 경우에 해당 인디케이터는 experts messages log에서 속도 평가에 필요한 모든 필수 데이터를 표시할 것입니다: OnInit() 이벤트 처리 시작 시간 및 OnCalculate()가 끝난 시간. 왜 이 두 값에 의해서 속도가 평가받아야되는지 설명하겠습니다. OnInit() 에이전트는 방법을 가리지 않고 거의 즉각적으로 실행되며 OnCalculate()은 방법을 가리지 않고 OnInit()의 바로 뒤에 실행되기 때문입니다. 유일한 예외는 표준 이동 평균 및 선형 가중 이동 평균 인디케이터 같은 간소화 메소드가 OnInit()에서 생성되는 경우 뿐입니다. 언급한 메소드의 경우에는(그리고 이 경우에만!) OnInit()가 끝나고 OnCalculate()이 실행되는데까지 딜레이가 생깁니다:

터미널의 experts journal 내 인디케이터에 의해 표시된 실행 로그 

 

이는 이 지연이 당시 일부 계산을 실행하고 있던 새로 생성된 표준 이동 평균 및 선형 가중 이동 평균에 의해 발생한다는 것을 의미합니다. 따라서 이 계산의 지속시간도 고려해야 하며, 따라서 회귀 인디케이터 초기화부터 계산 종료까지 항상 "방해받지않고" 평가할 것입니다.

다른 방법의 속도 차이를 더 정확하게 주목하기 위해, 모든 평가는 최대 접근 가능한 이력 깊이의 거대한 데이터 어레이 – M1 시간대를 사용하여 수행됩니다. 400만 바가 넘습니다. 각 메소드는 두번씩 평가될 것입니다: 회귀에서 20 그리고 2000 바.

결과는 다음과 같습니다:

 

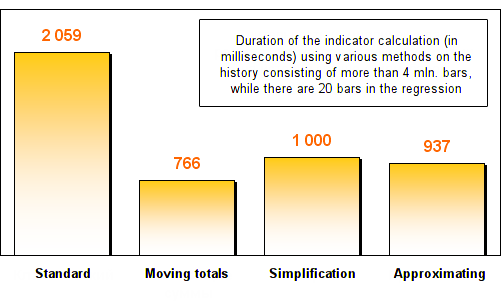
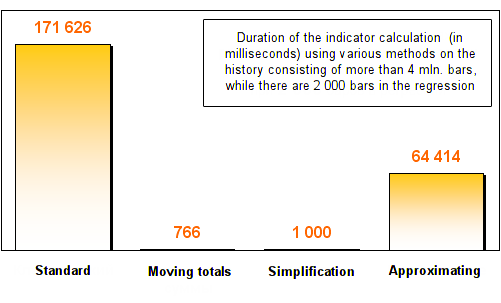
보시다시피 세 가지 최적화 방법 모두 표준 회귀 계산 방법에 비해 최소 2 배 이상 빨라졌습니다. 회귀 분석에서 바의 수가 증가하자 이동 총합 및 간소화 방법이 환상적인 속도를 보여주네요. 표준 버전보다 수백배는 빠르게 됐습니다!

이 두 가지 방법에 의한 계산에 필요한 시간은 실질적으로 변경되지 않았음을 유념해야 합니다. 그 점은 쉽게 설명할 수 있습니다. 회귀 분석을 위해 얼마나 많은 바가 사용되었든 간에 이동 총합 메소드에서는 단 2개의 작업만 실행됩니다. 즉, 오래된 바가 나가고 새 바가 들어옵니다. 회귀 길이에 의존하는 사이클이 하나도 없습니다. 따라서 회귀 분석에 20,000 또는 200,000 바가 포함되어 있더라도 방법 실행 시간은 20 바에 비해 크게 증가하지 않습니다.

단순화 메소드는 수식 내 각기 다른 모드에서 Moving Average를 사용합니다. 앞서 말씀드린 바와 같이, 이 인디케이터는 이동 토탈 방식으로 쉽게 최적화할 수 있으며 터미널 개발자들이 이 인디케이터를 사용하고 있습니다. 회귀 길이가 증가해도 간소화 방법 실행 시간이 변경되지 않는 것은 당연합니다.

실험을 통해 이동 총합 메소드가 가장 빠른 방법이란 것을 알 수 있었습니다.

 

마치며

몇몇 트레이더는 테스터 내 매매 시스템의 패러미터 최적화가 끝날 때까지 그냥 기다립니다. 하지만 이미 그 시간에 매매를 시도하여 돈을 버는 몇몇 트레이더들도 있습니다. 설명된 방법에 의해 얻은 계산 속도는 왜 이 트레이더 그룹들 사이에 그러한 차이가 있는지 명백하게 설명해줍니다. 그리고 왜 거래 알고리즘의 품질에 주목하는 것이 그렇게 중요한가.

터미널 용 프로그램을 직접 쓰던지, 서드 파티 프로그래머들에게 의뢰하던지 (예를들어, "Jobs" 섹션을 통해) 상관 없습니다. 어떠한 경우에건 만약 당신이 노력과 약간의 돈을 쓸 준비가 되어있다면 작동하는 인디케이터와 전략을 얻는 것에 그치지 않고, 빠르게 작동하는 것을 얻게됩니다.

알고리즘 가속 방법을 사용하면 표준 알고리즘에 비해 속도가 수십 배에서 수백 배까지 향상됩니다. 예를 들어 테스터에서 거래 전략의 패러미터를 100배 더 빠르게 최적화할 수 있습니다. 그리고 더 침착하게, 빈번하게 만드십시오. 말할 것도 없이, 이를 통해 매매에서 올릴 이득이 늘어납니다.