直線回帰例によるインディケータスピードアップの3手法

計算スピード

インディケータを速く計算することはきわめて重要なタスクです。計算速度を上げるのに利用できる方法は複数あります。また本件に関する読み物も数多く存在します。

ここでは、計算スピードアップのため3種類の方法を考察し、またその中でコード自体も簡略化していきます。ここで述べる方法はすべてアルゴリズムに関わるものです。すなわち、履歴を浅くすることはせず、また 有効なプロセッサユニットの増設コアも減らしません。計算アルゴリズムを直接最適化していくのです。

基本のインディケータ

3方法をすべて表示するためのインディケータは直線回帰 インディケータです。それは各バー（定義された最終バー数に応じて）で回帰関数を作成し、そのバーの値を表示します。結果として実線を取得します。

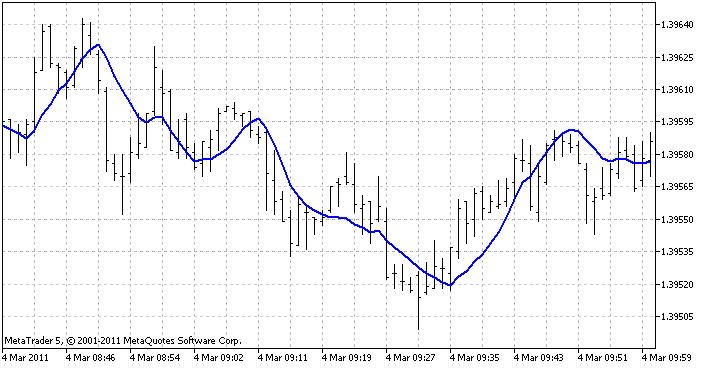
端末でインディケータはこのように見えます。

 

直線回帰方程式は以下です。

ここで、x はバー数、y は価格です。

この方程式の比率は以下のように計算されます。

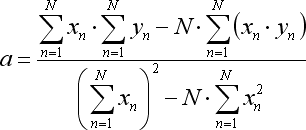
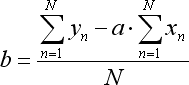
ここで N は 回帰ラインから取られるバー数です。

MQL5 （全履歴バーサイクル内）ではそういった方程式は以下のように表示されます。

            // Finding intermediate values-sums
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Regression ratios
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

インディケータのコード全体は本稿に添付があります。またそれには本稿にあるメソッドがすべて含まれています。「標準的」計算メソッドはインディケータ設定内で選択する必要があります。

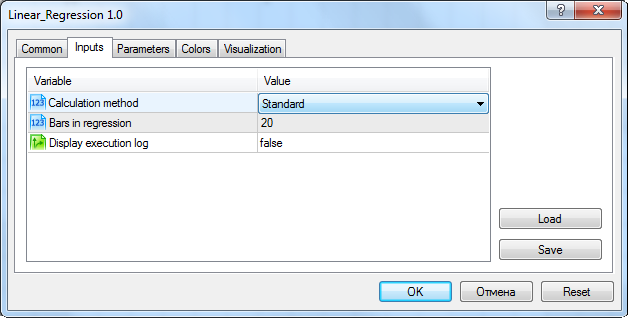
チャートに設定される場合のインディケータ入力パラメータ設定 

最初の最適化手法移動和

バーシーケンス値の合計数量をひとつずつ計算するインディケータの量は莫大なものです。またこのシーケンスはそれぞれのバーで常に移動します。もっともよく知られる例は 移動平均 (MA)です。移動平均を計算するには、 N最終バーの合計を計算し、この値をその数で割ります。

移動和の計算スピードを大幅に上げる洗練された方法をご存じの方はそういらっしゃらないのではないかと思います。MetaTrader 4およびMetaTrader 5のMAインディケータでも使われているのを知る前から、私は個人のインディケータでかなり長い間この方法を使ってきています。（MetaTrader インディケータが開発者によって適切に最適化されているのを発見したのはそれが初めてではありません。ずいぶん以前になりますが内部インディケータよりも効果的なことを証明しようと高速ZigZag インディケータと通常インディケータを探していました。フォーラムの話題にはZigZag 最適化手法もあります。もし必要な方がいらっしゃったら、ご参考までに。）

では移動和の話に戻ります。隣り合う2本のバーの合計を比較します。下記のグラフはこれら合計には重なる部分（グリーンで表示されています）かなりあることを示しています。バー0に対して計算されたトータルはバー1に対して計算されたトータルとは異なります。これはトータルには1個古いデータ（左側の赤い部分）は含まれず、1個新規バー（右側のブルーの部分）は含まれまれるためです。

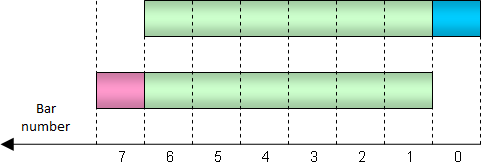
1バー移動中、トータルに除外される値と含まれる値

 

よってバー0のトータルを計算する間、必要なバーをすべて再び合計する必要はありません。バー1の合計を取り、1バー分の値を引き、新規バー分の値を足せばよいのです。二段階の計算だけですみます。そのような方法でインディケータの計算スピードをかなり上げることができます。

移動平均では、そのような方法は日常的に使用されています。インディケータはすべての平均値をその唯一のバッファに保持するからです。そしてトータルが N、すなわちトータルに含まれるバー数で割られるだけです。バッファから Nでかけ算しなおすと、簡単にあらゆるバーのトータルを得ることができ、そして前述の方法を使うのです。

この方法をより複雑なインディケータ、直線回帰に適用する方法を述べます。回帰関数比率の計算式には x、y、x*x、x*y が含まれることはすでに確認しました。そのトータル計算はバッファに格納する必要があります。インディケータ内の各トータルに対するバッファはこのために割り当てられます。

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

バッファはチャート上に必ずしも表示される必要はありません。MetaTrader 5 には特別な 中間計算用のバッファタイプがあります。OnInitにバッファ数を割り当てるためにそれを使います。

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

標準直線回帰計算コードは次のように変更します。

            // (The very first bar was calculated using the standard method)        
        
            // Previous bar
            int prevbar = bar-1;
            
            //--- Calculating new values of intermediate totals 
            //    from the previous bar values
            
            Sx  = ExtBufSx [prevbar]; 
            
            // An old price comes out, a new one comes in
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // All the old prices come out once, a new one comes in with an appropriate weight
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Regression ratios (calculated the same way as in the standard method)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

インディケータのコード全体は本稿に添付があります。「移動和」計算方法はインディケータ設定に設定する必要があります。

第二の最適化手法簡略化

これは数学ファンにはうれしい方法です。複雑な方程式における断片はしばしば他の既知の方程式の右辺であるらしいことがわかります。ということは、その断片は別の式の左辺（通常は変数1個）と置き換え可能であるということです。要するに、複雑な式を簡略化できるということです。この簡略化された式のエレメントのいくつかはすでにインディケータだと理解されているようです。その場合、その式を持つインディケータコードはそれでかなり簡略化されるのです。

そして少なくとも省スペースのシンプルなコードを得ることができます。またコードに実装されているインディケータがスピード的に最適化されれば、計算スピードが速くなる場合もあります。

直線回帰式も簡略化され、その計算は複数のMetaTrader 5 標準インディケータの初期化に使用可能なようです。そのエレメントの多くは異なる計算モードにより「移動平均」インディケータで計算されます。

• 合計y は「単純移動平均」に存在します。

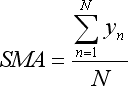
• 合計x*y 合計y は「線形加重移動平均」に存在します。Linear Weighted Moving Average:

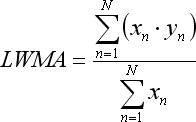
LWMA の式は過去から未来への昇順で 1 ～ N の回帰にあるバーを列挙する場合のみtrueであることに注意が必要です。

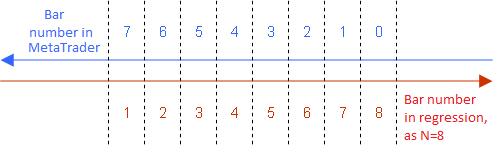
LWMA インディケータ使用のための回帰にたいするバーの従来の列挙方法 

 

よってその他すべての式で同様の列挙を使用する必要があります。

この方法を進めていきます。

• トータルxは、 以下の式に置き換わる数列トータル (1 + 2 + ... + N) です。

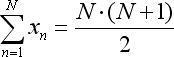
• トータル x*x はもうひとつ別の式に応じて簡略化されます。

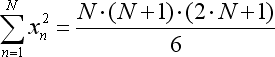
• インディケータチャートを作成するには x が Nに等しい最後のバーに対してのみ回帰関数の平均を計算する必要があります。すなわち、回帰関数式はその特殊なケースと置き換え可能です。

よってこれまでの5個の式により、比率計算式の変数をすべて回帰方程式内で aおよびb と置き換えることができます。置き換えがすべて完了したら、回帰値を計算するための全く新しい式ができます。それは移動平均インディケータ値と数量N だけで構成されます。エレメントの約分をすべて終えたら洗練された式を取得します。

この式は直線回帰の基本インディケータで実行されるすべての計算を置き換えます。この式を持つインディケータコードがより省スペースなのは明らかです。のちに『スピード比較』項では、このコードが速く動作することも確認します。

インディケータの特記部分を示します。

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

インディケータLWMA および SMA はあらかじめOnInitに作成されています。

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

インディケータのコード全体は本稿に添付があります。「簡略化」計算方法はインディケータ設定に設定する必要があります。

この方法では、端末内蔵インディケータを使用することに留意が必要です iCustomではなく、適切な平滑化メソッドを選択する関数iMAを使用しているのです。 セオリーでは内蔵インディケータはひじょうに速く動作するため、この点は重要です。端末には他にも標準インディケータ が内蔵されています。（iMAのように接頭辞"i"を伴う関数によって作成されます。）簡略化手法を使用するにあたり、そのインディケータに対する式を簡略化するとよりよいでしょう。

第三の最適化手法近似法

この方法の発想は、エキスパートで使用されている「重い」インディケータを要求される近似的に計算する、よりスピードの速いインディケータに置き換える、というものです。この方法を使うと、ご自身の戦略をより速く検証することができます。最終的に、デバッグ段階は予測精度はそれほど重要ではありません。

このメソッドはパラメータをおおざっぱに最適化するワーキング戦略とも併用できます。それによりパラメータの有効値領域をすばやく見つけることができます。その後、得た結果を「重い」インディケータにより処理することで微調整が可能です。

その上、近似値計算は戦略を適切に動作させるには十分であるように思われます。ここで「軽い」インディケータはまた実トレーディングにも使用可能です。

回帰に対すると同様の効果がある直線回帰に対する速い式を作成することも可能です。たとえば、回帰バーを2つにグループ分けし、それぞれの平均値を計算し、2個の平均点を通る線を引き、最後のバーで線の値を決めることができるのです。

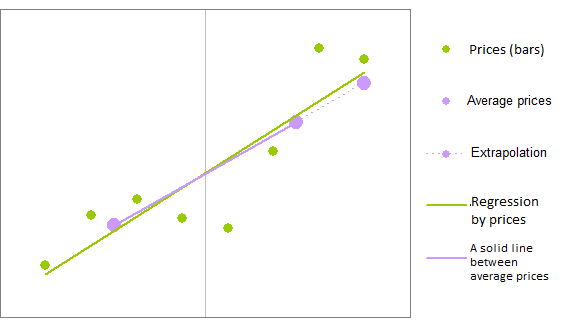
ポイントは左右2グループに分けられ、計算が行われました。

 

そのような計算には回帰式とは異なり、算術演算はそれほど含まれません。それで計算スピードが上がるのです。

           // The interval midpoint
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Average price of the first half
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Average price of the second half
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Price excess by one bar
           double k = (s1-s2)/(LRPeriod/2);
           
           // Extrapolated price at the last bar
           lrvalue = s1 + k * (HalfPeriod-1)/2;

インディケータのコード全体は本稿に添付があります。「近似」計算方法はインディケータ設定に設定する必要があります。

この近似がオリジナルにどれくらい近いか分析していきます。そのために、チャート上で標準計算と近似計算を備えるインディケータを設定する必要があります。また、回帰に似せて故意に弱めた別のインディケータも追加します。 そうしないと、過去バーを用いていくらかトレンド計算を行ってしまいます。移動平均はそれを問題なく行います。（私はSMA ではなくLWMAを採用しました。その方が回帰グラフにずっと近いからです。）それと比較するとよい近似値を得たかどうか判定することができます。私は良い近似を得たと思います。

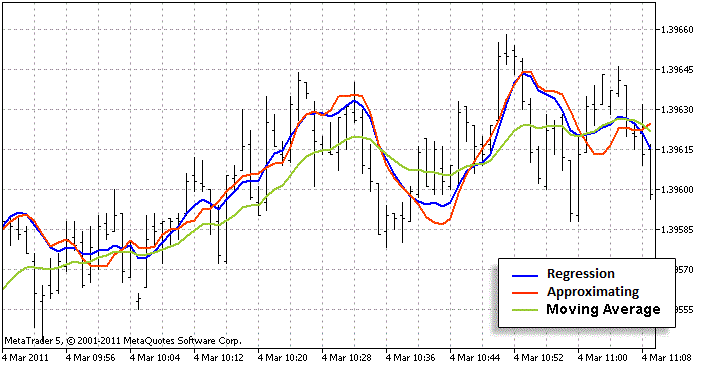
 赤い線はグリーンよりもブルーの線に接近しています。これは近似手法アルゴリズムが優れていることを意味します。

スピード比較

インディケータパラメータ内でログ表示をオンにすることができます。

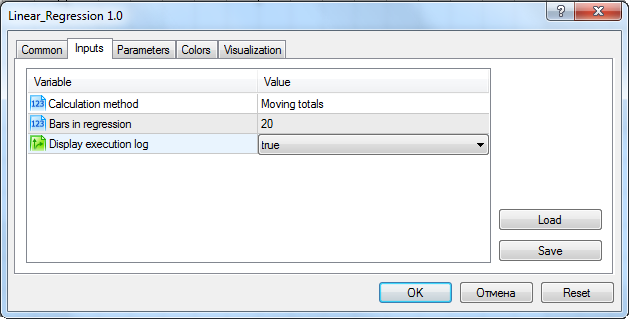
実行スピード判定用インディケータ設定

 

今回の場合、インディケータは エクスパートメッセージログスピード判定にとって必要なデータをすべて表示します。OnInit() イベント処理開始時刻およびOnCalculate()の終了。なぜこの2つの値によってスピードを判定する必要があるのか説明します。OnInit() エージェントはあらゆるメソッドでほとんど間を置かずに実行され、 OnCalculate() はほとんどすべての手法でOnInit() の直後にスタートします。唯一の例外は、インディケータSMA および LWMA が OnInit()で計算される簡略化手法です。遅延は簡略化方法（ここでだけです！）において、OnInit() の終わりと OnCalculate() の始まりの間に起こります。

端末のエキスパートジャーナル内インディケータによって表示される実行ログ 

 

この遅延は、そのときなんらかの計算を実行する新規に作成されるSMA および LWMA によって発生するものであるということです。この計算の継続時間も考慮されるべきです。よって回帰インディケータの初期化から計算の終了まで、全時間を「途切れなく」判定します。

異なる手法間の計算スピードの違いをより正確に知るには、大きなデータ配列を使用してすべての判定を行ないます。 対象はM1 時間枠で、できる限りの深さの履歴です。それは4百万バー以上にのぼります。各手法は二度ずつ判定されます。回帰に伴うのは20バーと2000バーです。

以下が結果です。

 

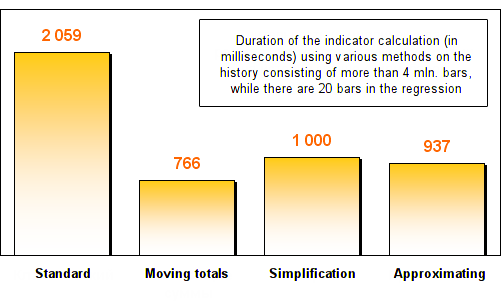
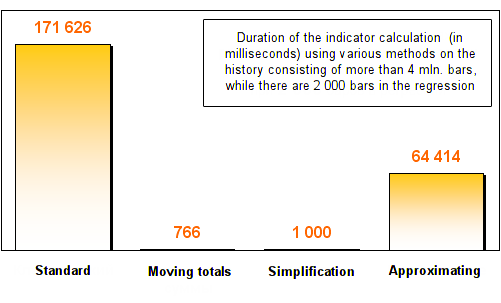
ご覧のとおり、3つの最適化手法すべてが標準回帰計算手法に比べ、最低2倍速くなっています。回帰内バー数を増やしたあと、移動和および簡略化手法はすばらしいスピードを表示しました。標準手法より何百倍も速く計算したのです！

この2つの方法による計算に必要な時間は実際には変わらない点をお知らせします。この事実は簡単に説明することができます。回帰作成にどれほど多くのバーが使われようと、移動和手法ではただ2つの処理が実行されるだけです。古いバーが出ていき、新しいバーが入ってくるのです。回帰長に依存するサイクルはひとつもありません。よって、回帰が2万バーを含もうが、20万バーを含もうが実行時間は20バーに比べたいして増えないのです。

簡略化手法はその式の中で移動平均を異なるモードで使用します。すでにお話したとおり、このインディケータは移動和手法によって簡単に最適化でき、それは端末開発者によって利用されています。簡略化手法実行時間は回帰長が減少する場合も変化しないのは驚くに値しません。

移動和手法は今回の実験では最も速度が速いと証明しました。

 

おわりに

トレーダーの中にはテスターでトレーディングシステムのパラメータ最適化 手順が終わるのを待ってじっと座っているだけの人もいるでしょう。また中には、その時間すでにトレーディングを行いお金を稼いでいる人もいるでしょう。ここに述べた手法で得る計算スピードはあきらかにトレーダーのそういうグループ間に差が出る理由を説明しています。また、トレーディングアルゴリズムの質に注意をはらうことの重要性についても説明しています。

ご自身でターミナルへのプログラムを書くか、他のプログラマーに注文するかは関係ありません（たとえば、 『ジョブ』項の助けを借りて）。いずれにせよ、いくばくかの努力をするかいくばくかのお金を費やせば、動作するインディケータとストラテジーを得るだけでなく、動作速度の速いものを手にすることができるのです。

何らかのアルゴリズムのスピードアップ手法を使用するなら、スピードに関して標準アルゴリズムに比べ、何十倍から何百倍のメリットを得ます。それは、たとえば百倍速いテスターでトレーディング戦略パラメータを最適化することができることを意味しています。それをより注意して頻繁に行うのです。いうまでもありませんが、トレーディングによる収入は増えます。