
Le Rôle des Distributions Statistiques dans le Travail des Traders
Les régularités nous facilitent la vie mais il est tout aussi important de profiter de l'aléatoire.
(George Alexandrov)
Introduction
Cet article est une suite logique de mon article Distributions de Probabilité Statistique en MQL5 qui présente les classes pour travailler avec certaines distributions statistiques théoriques. J'ai estimé nécessaire de jeter d'abord les bases sous la forme de classes de distribution afin qu'il soit plus pratique pour un utilisateur de les utiliser plus tard dans la pratique.
Maintenant que nous disposons d'une base théorique, je suggère que nous procédions directement à des ensembles de données réelles et que nous essayions de faire un usage informatif de cette base. En même temps, nous éclairerons certaines questions relatives aux statistiques mathématiques.
1. Génération de Nombres Aléatoires avec une Distribution Donnée
Mais avant d’examiner des ensembles de données réels, il semble très important de pouvoir obtenir un ensemble de valeurs qui seraient intimement liées à une distribution théorique souhaitée.
En d'autres termes, un utilisateur ne doit définir que les paramètres de la distribution et de la taille d'échantillon souhaitées. Un programme (dans notre cas, une hiérarchie de classes) devrait générer et faire sortir un tel échantillon de valeurs pour un travail ultérieur.
Un autre détail important est que les échantillons générés par une loi spécifiée sont utilisés pour vérifier divers tests statistiques. Le domaine des statistiques mathématiques - génération de variables aléatoires avec différentes lois de distribution - est assez intéressant et stimulant.
Pour mes besoins, j'ai utilisé un générateur de haute qualité décrit dans le livreNumerical Recipes: L'art de l'informatique scientifique [2]. Sa période est à peu prés égale à 3.138*1057 Le code C a été assez facilement transmis dans MQL5.
Et j'ai donc créé la classeRandom , comme suit :
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
Nous pouvons maintenant créer des classes pour les valeurs échantillonnées à partir d'une distribution.
A titre d'exemple, examinons une variable aléatoire de la distribution normale. La classeCNormaldev est la suivante :
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Comme on peut le voir, la classe a une donnée membre N de type CNormaldist Le code C d'origine n'avait pas une telle connexion avec la distribution. J'ai estimé nécessaire qu'une variable aléatoire générée par la classe (ici, par la classe CNormaldev) ait un lien logique et programmatique avec sa distribution.
Dans la version originale, le typeNormaldev était défini comme suit :
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
Les nombres aléatoires sont générés ici à partir de la distribution normale à l'aide de la méthode du rapportrapport d’uniformes de méthode
Toutes les autres classes qui aident au calcul des variables aléatoires de diverses distributions se trouvent dans le fichier includeRandom_class.mqh.
Nous allons maintenant terminer par la génération et voir, dans la partie pratique de l'article, comment créer un tableau de valeurs et tester un échantillon.
2. Estimation des Paramètres de Distribution, Hypothèses Statistiques
Il est clair que nous allons nous intéresser aux variables discrètes. En pratique cependant, si le nombre de variables discrètes est considérable, il est plus commode de considérer l'ensemble de ces variables discrètes comme un groupe de variables continues. Il s'agit d'une approchestandard en statistique mathématique. Par conséquent, pour leur analyse, nous pouvons utiliser des distributions définies par des formules analytiques liées à des variables continues.
Passons donc à l'analyse de la distribution empirique.
Il est admis qu'un échantillon d'une population générale dont les membres répondent au critère de représentativité est à l'étude. De plus, les exigences relatives aux estimations spécifiées à la section 8.3 [9] sont remplies. Les paramètres de distribution numérique peuvent être trouvés au moyen de méthodes d'estimation ponctuelle et d'intervalle.
2.1 Exemple de Traitement à l'aide de la Classe CExpStatistics
Il faut d'abord supprimer lesoutliers de l'échantillon ; il s'agit d'observations qui s'écartent sensiblement des observations de la majeure partie de l'échantillon (tant à la hausse qu'à la baisse). Il n'existe pas de méthode universelle pour supprimer les valeurs aberrantes.
Je suggère d'utiliser celui décrit par SV Bulashev dans la section 6.3 [5] Dans le forumMQL4 , une bibliothèque de fonctions statistiques a été créée sur la base de laquelle le problème donné peut être facilement résolu. Cela dit, nous allons sûrement appliquer OOP et la mettre à jour un peu.
J'ai appelé la classe créée d'estimations de caractéristiques statistiques CExpStatistics (Class of Expected Statistics).
C'est grosso modo, comme suit :
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
L’implémentation de chaque méthode peut être étudiée en détail dans le fichier includeExpStatistics_class.mqh , je vais donc le laisser de côté ici.
L’important est que cette classe renvoie le tableau sans valeurs aberrantes(Parr[]) , le cas échéant. En outre, cela aide à obtenir des statistiques descriptives de l'échantillonnage et de leurs estimations.
2.2 Création d'un Histogramme d' Échantillon Traité
Maintenant que le tableau est exempt de valeurs aberrantes, unhistogram (distribution de fréquence) peut être tracé en fonction de ses données. Cela nous aidera à visuellement estimer la loi de distribution des variables aléatoires. Il existe une procédure étape par étape pour créer un histogramme.
Il faut d'abord calculer le nombre de classes requises. Dans ce contexte, le terme « classe » indique regroupement, intervalle. Le nombre de classes est calculé par la formule de Sturges :
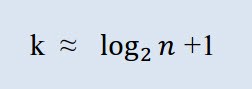
Où k est le nombre de classes, nest le nombre d'observations.
En MQL5, la formule peut être représentée comme suit :
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
Lorsque le nombre requis de classes (intervalles) a été reçu à l'aide de la formule de Sturges, il est temps de décomposer les données du tableau en classes. Ces données sont appelées observations (sing. observation). Nous le ferons en utilisant la fonctionAllocate , comme suit :
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
Comme on peut le constater, la fonction prend dans le tableau des observations initiales (données), sa longueur (n), nombre de classes (k) et alloue des observations à certaine à f[i] classe de f tableau b[i] est la f[i] classe du milieu. Les données de l'histogramme sont maintenant prêtes.
Nous afficherons l'histogramme à l'aide des outils décrits dans les HTML. Pour cela j'ai écrit la fonction histogramSave qui affichera l'histogramme de la série à l'étude en HTML. La fonction prend 2 paramètres : un tableau de classes et (f) un tableau de milieux de classes(b).
À titre d'exemple, j'ai créé un histogramme pour les différences absolues entre les maximums et les minimums de 500 barres de la paire EURUSD sur une plage de quatre heures en points à l'aide du script volatilityTest.mq5
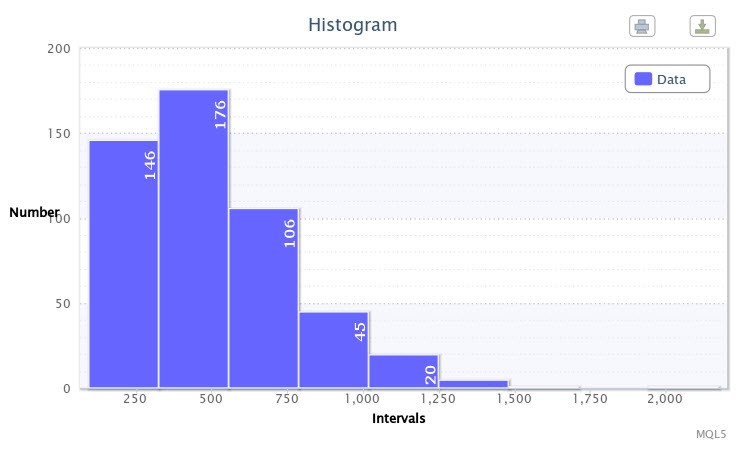
Figure 1. Histogramme des données (volatilité absolue de l' EURUSD H4)
Comme le montre l'histogramme (Fig. 1), la première classe dispose de 146 observations, la deuxième classe en dispose de 176 observations, etc. La fonction de l'histogramme est de donner une idée visuelle de la distribution empirique de l'échantillon à l'étude.
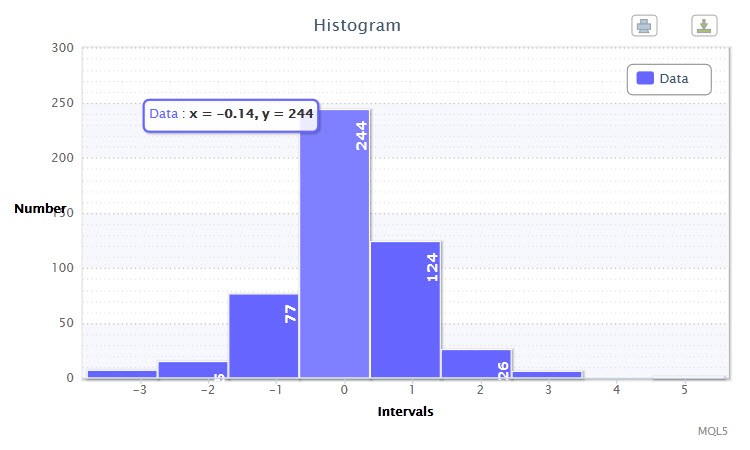
Figure 2. Histogramme des données (rendements standardisés de l' EURUSD H4)
L'autre histogramme (Fig.2) affiche les rendements logarithmiquesstandardisés de 500 barres de la paire EURUSD sur la période H4. Comme vous pouvez le constater, les quatrième et cinquième classes sont les plus impressionnantes puisqu'elles disposent respectivement de244 et 124 observations. Cet histogramme a été crée à l'aide du script returnsTest.mq5
Ainsi, l'histogramme permet de choisir la loi de distribution dont les paramètres seront ultérieurement estimés. Lorsque la distribution à privilégier n'est pas visuellement évidente, vous pouvez estimer les paramètres de plusieurs distributions théoriques.
Les deux distributions que nous avons considérées ne ressemblent pas en apparence aux distributions normales, en particulier la première. Cependant ne nous fions pas à la représentation visuelle et passons aux chiffres.
2.3 Hypothèse de Normalité
Il est coutumier de résoudre , en premier lieu,et tester la supposition (hypothèse) de la normalité de la distribution en question. Une telle hypothèse est appelée L’hypothèse principale L'une des méthodes les plus populaires pour tester la normalité d'un échantillon est le testJarque-Bera test.
Son algorithme, bien que pas le plus complexe, est assez volumineux en raison de l'approximation. Il existe quelques versions de l'algorithme en C++ et dans d'autres langues. L'une des versions les plus réussies et les plus éprouvées est une version située dans une bibliothèque d'analyse numérique multiplateforme ALGLIB Son auteur [SA Bochkanov] a fait un travail énorme, notamment dans la compilation du tableau quantiletest Je viens de le mettre à jour légèrement pour les besoins deMQL5
La fonction principale dejarqueberatest est la suivante :
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
Il traite l’échantillon initial des données (x) et renvoie р-value,c’est à dire la valeur qui caractérise la probabilité de rejet de l’hypothèse nulle si l’hypothèse nulle est en réalité vraie.
Il y a 2 fonctions auxiliaires dans le corps de fonction. La première fonction - jarquebera_jarqueberastatistic - calcule la statistique de Jarque-BeraJarque-Bera statistic, et la seconde- jarquebera_jarqueberaapprox - calcule la valeur-p Il est à noter que ce dernier, à son tour, met en œuvre des fonctions auxiliaires liées à l'approximation, qui sont près de 30 dans l'algorithme.
Essayons donc de tester la normalité de nos échantillons. Nous utiliserons le scriptreturnsTest.mq5 qui traitera l'échantillon de rendements standardisés de l' EURUSD H4.
Comme prévu, le test a montré que la probabilité de rejeter une véritable hypothèse nulle est de 0,0000. Autrement dit, la distribution de cet échantillon n'appartient pas à la famille des distributions normales. Afin de traiter l'échantillon de volatilité absolue de la paireEURUSD, exécutez le scriptvolatilityTest.mq5 . Le résultat sera le même - la distribution n'est pas normale.
3. Raccord de Distribution
Il existe quelques méthodes en statistique mathématique qui permettent de comparer la distribution empirique avec la distribution normale. Le plus gros problème est que les paramètres de distribution normale ne nous sont inconnuset il existe une hypothèse selon laquelle les données à l'étude ne reflètent pas la normalité d'une distribution.
Par conséquent, nous devons utiliser des tests non paramétriques et remplir les paramètres inconnus avec les estimations obtenues à partir de la distribution empirique.
3.1 Estimation Et Test
L'un des tests les plus populaires et, ce qui est le plus important, adéquat dans cette situation estχ2 test. Il est basé sur la mesurela qualité d’ajustement de Pearson.
Nous allons effectuer le test en utilisant la fonction chsone
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Comme on peut le voir dans la liste, une instance de la classeCGamma est utilisée représentant la fonction incomplète de gamma comprise dans le fichierDistribution_class.mqh ainsi que toutes les distributions mentionnées. Il convient également de noter que le tableau des fréquences attendues(ebins) sera obtenu en utilisant les fonctions estimateDistribution et expFrequency
Nous devons ,à présent, sélectionner les paramètres numériques qui sont compris dans la formule analytique de la distribution théorique. Le nombre de paramètres dépend de la distribution particulière. Par exemple, il y a deux paramètres dans la distribution normale, et un paramètre dans la distribution exponentielle, etc.
Lors de la détermination des paramètres de distribution, nous utilisons généralement des méthodes d'estimation ponctuelle telles que la méthode des moments, la méthode des quantiles et la méthode du maximum de probabilité.. La première est plus simple car elle implique que les estimations d'échantillonnage (espérance, variance, asymétrie, etc.) doivent coïncider avec les estimations générales.
Essayons de sélectionner une distribution théorique pour notre échantillon à l'aide d'un exemple. Nous allons prendre une série de rendements standardisés de l'EURUSD H4pour lesquels nous avons déjà tracé un histogramme.
La première impression est que la distribution normale n'est pas appropriée pour la série car l'excès de coefficient d'aplatissement est observé. A titre de comparaison, essayons d'appliquer une autre distribution.
Ainsi, lors du démarrage du script returnsTest.mq5 déjà connu, nous allons essayer de sélectionner une distribution telle queHypersec. De plus, le script estimera et affichera les paramètres de distribution sélectionnés à l'aide de la fonctionestimateDistribution et exécutera immédiatement le testχ2 . Les paramètres de distribution sélectionnés se sont avérés être les suivants :
Distribution Sécante Hyperbolique : X~HS(-0.00, 1.00);
et les résultats des tests étaient les suivants :
"Statistique du Khi-deux : 1,89 ; probabilité de rejeter une hypothèse vraie nulle : 0.8648"
Il convient de noter que la distribution sélectionnée est bien ajustée car la valeur de la statistique χ2 est assez petite.
Par ailleurs, utiliser la fonction histogramSaveE un double histogramme pour les rapprorts de fréquence observés et prévus (le rapport de fréquence est exprimé en fraction our pourcent)des retours standardisés seront dessinés (Fig. 3). Vous pouvez voir que les barres se dupliquent presque les unes les autres. C'est la preuve d'un montage réussi.
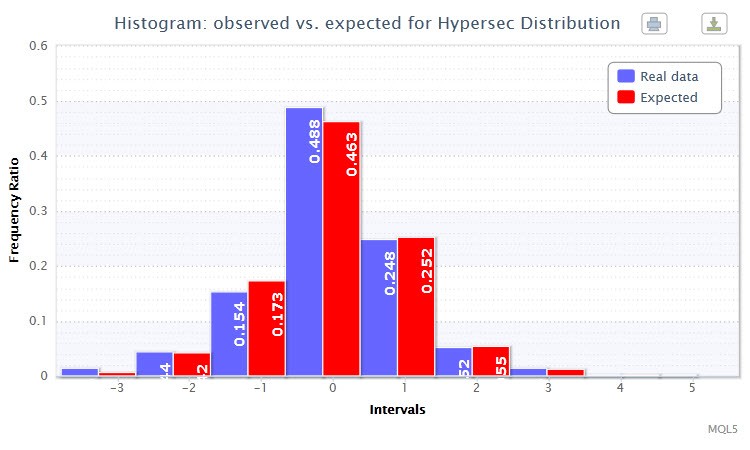
Figure 3. Histogramme des rapports de fréquence observés et estimés (rendements standardisés de l'EURUSD H4)
Exécutons une procédure similaire pour les données de volatilité en utilisant levolatilityTest.mq5 déjà connu.
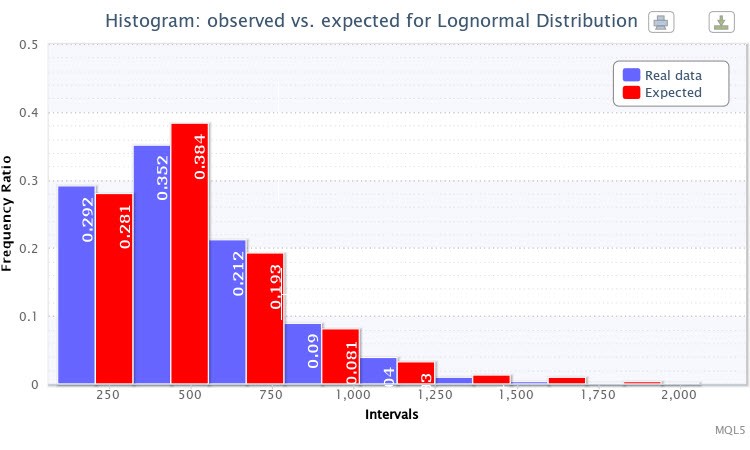
Figure 4. Histogramme des rapports de fréquence observés et estimés (volatilité absolue de l' EURUSD H4)
J'ai sélectionné la distribution lognormal Lognormalpour les tests. En conséquence, l'estimation suivante des paramètres a été reçue :
Distribution lognormale X~Logn(6.09, 0.53);
et les résultats des tests étaient les suivants :
"Statistique du Khi-deux : 6.17 ; probabilité de rejeter une hypothèse vraie nulle : 0.4040"
La distribution théorique de cette distribution empirique a également été sélectionnée avec succès. Ainsi, on peut considérer que l'hypothèse nulle ne peut pas être rejetée (à la norme niveau de confiance p=0.05). Nous pouvons constater sur la figure 4 que les barres des rapports de fréquence estimés et observés sont également très similaires.
Permettez-moi maintenant de vous rappeler que nous avons une autre possibilité de générer un échantillon de variables aléatoires à partir d'une distribution avec des paramètres définis. Afin d'utiliser une hiérarchie de classes liées à une telle opération, j'ai écrit le scriptrandomTest.mq5 .
Au début de celui-ci, nous devons entrer les paramètres comme indiqué sur la Fig. 5.
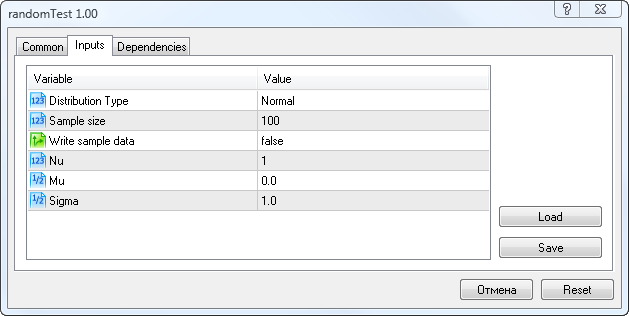
Figure 5. Paramètres d'entrée du script randomTest.mq5
Ici vous pouvez sélectionner le type de distribution (Distribution Type),le nombre de variables aléatoires dans un échantillon (Taille de l’échantillon), l’option de sauvegarde de l’échantillon (écrire un échantillon de données), le Nu paramètre( pour la distribution de l’étudiant-t), le Mu et les paramètres Sigma.
Si vous définissez pourWrite sample data la valeur true, le script sauvegardera l'échantillon de variables aléatoires avec les paramètres personnalisés dans le fichier Randoms.csv Sinon, il lira les exemples de données de ce fichier, puis effectuera des tests statistiques.
Pour certaines distributions avec des paramètres Mu etSigmamanquants, j'ai fourni un tableau de corrélation des paramètres avec les champs de la fenêtre de démarrage du script.
| Distribution | Premier paramètre de distribution | Deuxième paramètre de distribution |
|---|---|---|
| La logistique | alph Mu | pari Sigma |
| Exponentiel | lambda Mu | -- |
| Gamma | alph Mu | pari Sigma |
| Bêta | alph Mu | pari Sigma |
| Laplace | alph Mu | pari Sigma |
| Binôme | n Mu | pe Sigma |
| Poisson | lambda Mu | -- |
Par exemple si la distribution Poisson est sélectionnée, le paramètre lambda sera inséré à travers le champ Mu etc.
Le script n'estime pas les paramètres de la distribution t de Student car dans la majorité absolue des cas, il n'est utilisé que dans quelques procédures statistiques : estimation ponctuelle, création d'intervalles de confiance et test d'hypothèses concernant la moyenne inconnue d'un échantillon statistique de la distribution normale.
À titre d'exemple, j'ai exécuté le script pour la distribution normale avec les paramètres X~Nor(3.50, 2.77) where Write sample data=true Le script a d'abord généré un échantillon. Lors de la deuxième exécution àWrite sample data=false, un histogramme a été tracé comme le montre la Fig.6.
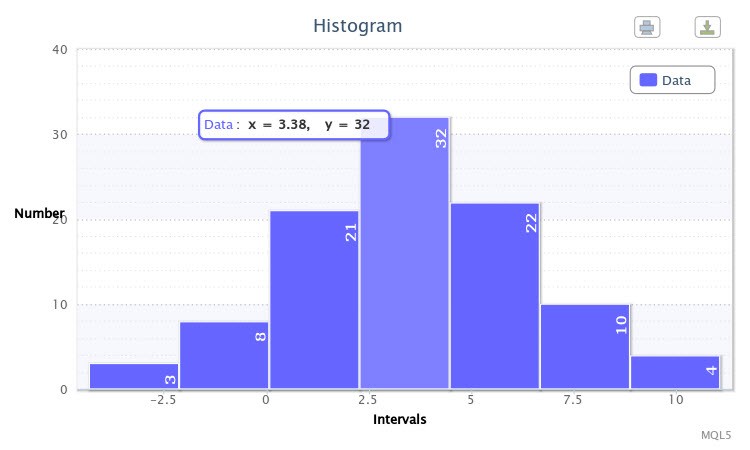
Figure 6. L'échantillon de variables aléatoires X~Nor(3.50,2.77)
Les autres informations affichées dans la fenêtre Terminal sont les suivantes :
Le test de Jarque-Bera : « Le test de Jarque-Bera : la probabilité de rejeter une hypothèse nulle vraie est de 0,9381 » ;
Estimation des paramètres : Distribution normale X~Nor (3,58, 2,94);
Résultats du test du Khi-deux : "Statistique du Khi-deux : 0,38 ; probabilité de rejeter une hypothèse vraie nulle : 0.9843".
Et enfin, un autre double histogramme des rapports de fréquence observés et estimés pour l'échantillon a été affiché (Fig. 7).
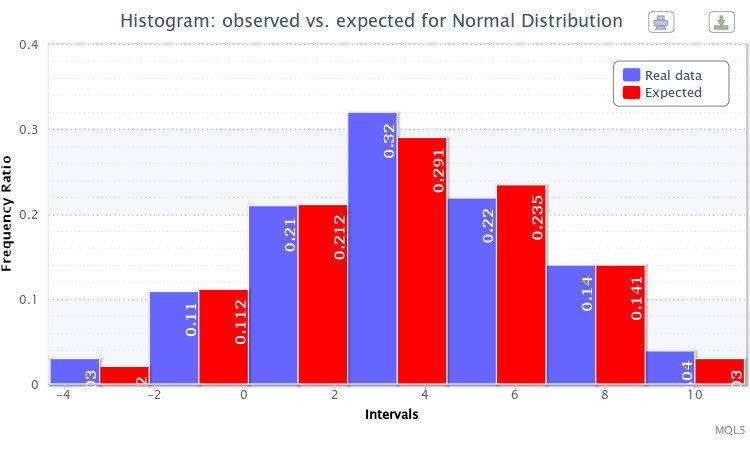
Figure 7. Histogramme des rapports de fréquence observés et estimés pour X~Nor(3.50,2.77)
En général, la génération de la distribution spécifiée a réussi.
J'ai également écrit le script fitAll.mq5 qui fonctionne de manière similaire au scriptrandomTest.mq5 . La seule différence est que le premier dispose de lafitDistributions fonction J'ai défini la tâche suivante dans le but d’ : ajuster toutes les distributions disponibles à un échantillon de variables aléatoires et effectuer un test statistique.
Il n'est pas toujours possible d'ajuster une distribution à un échantillon en raison de l'inadéquation des paramètres qui conduit à l'apparition de lignes dans le Terminal avisant que l'estimation n'est pas possible, par exemple "La distribution bêta ne peut pas être estimée !".
De plus, j'ai décidé que ce script devrait visualiser les résultats statistiques sous la forme d'un petit rapport HTML dont un exemple peut être trouvé dans l'article"Graphiques et Diagrammes dans HTML"(Fig. 8).
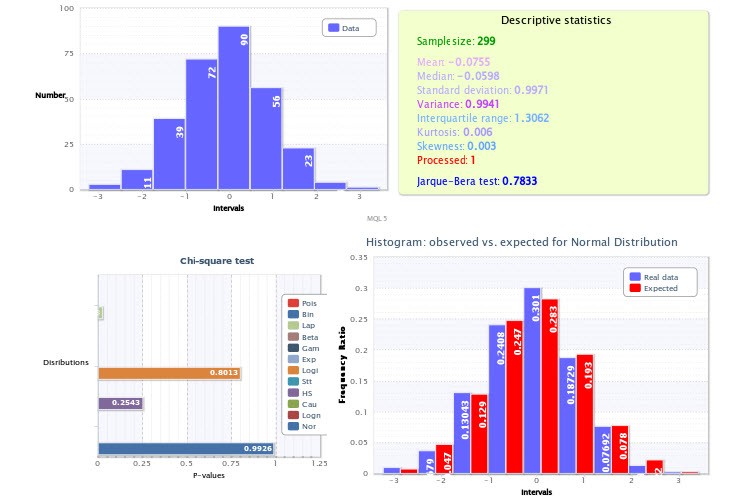
Figure 8. Rapport statistique sur l'estimation de l'échantillon
Un histogramme standard de l'échantillon est affiché dans le quart supérieur gauche ; le quart supérieur droit représente les statistiques descriptives et valeur Jarque-Bera résultat du test où la variable traitée égale à 1 signifie que les valeurs aberrantes ont été supprimées tandis qu'une valeur de 0 indique que il n'y avait pas de valeurs aberrantes.
Les valeurs p du test χ2 testpour chaque distribution sélectionnée sont affichées dans le quart inférieur gauche. Ici, la distribution normale s'est avérée la meilleure en termes d'ajustement (p=0,9926). Par conséquent, un histogramme des rapports de fréquence observés et estimés a été tracé dans le quart inférieur droit.
Il n'y a pas encore autant de distributions dans ma galerie. Mais ce script vous fera gagner beaucoup de temps s'il y a un grand nombre de distributions.
Maintenant que nous connaissons exactement les paramètres de distribution des échantillons étudiés, nous pouvons procéder à un raisonnement probabiliste.
3.2 Probabilités de valeurs de variables aléatoires
Dans l’article de sur les distributions théoriques , j’ai donné le scriptcontinuousDistribution.mq5 comme exemple. En l'utilisant, nous tenterons d'afficher n'importe quelle loi de distribution avec des paramètres connus qui peuvent nous intéresser.
Ainsi, concernant les données de volatilité, nous allons entrer les paramètres de distribution lognormale obtenus précédemment (Mu=6.09, Sigma=0.53), sélectionner le type de distributionLognormalet le mode cdf(Fig.9).
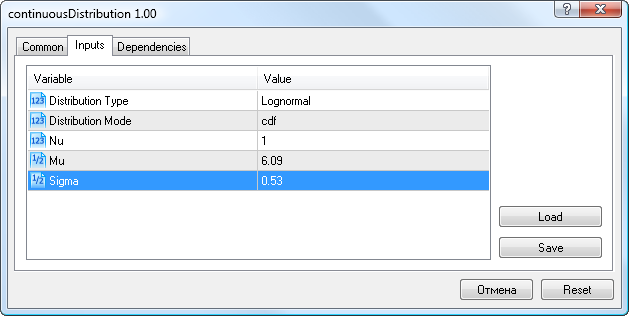
Figure 9. Paramètres de distribution lognormale X~Logn (6,09, 0,53)
Le script affichera ensuite la fonction de distribution pour notre échantillon. Il apparaîtra comme le montre la figure 10.
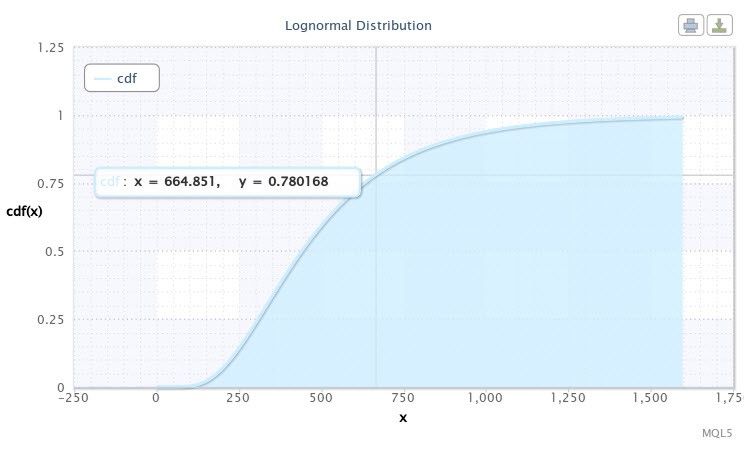
Figure 10. Fonction de distribution pour X~Logn (6,09, 0,53)
Nous constatons sur le graphique que le curseur est pointé sur un point dont les coordonnées sont à peu près [665;0.78]. Cela indique qu’il y a une probabilité de 78% que la volatilitéEURUSD H4 ne dépassera pas les 665 points Ces informations peuvent s'avérer très utiles pour le développeur d'un Expert Advisor. Nous pouvons sûrement prendre d'autres valeurs sur la courbe en déplaçant le curseur.
Admettons que nous nous intéressons à la probabilité de l'événement lorsque la valeur de volatilité se situera dans l'intervalle entre 500 and 750 points. A cet effet, l'opération suivante doit être effectuée :
.cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
Ainsi, dans un quart des événements la volatilité de la paire fluctue dans l'intervalle entre 500 and 750 points.
Exécutons à nouveau le script avec les mêmes paramètres de distribution en ne sélectionnant quesfcomme loi de mode de distribution. La fonction de fiabilité (survie) sera représentée comme suit (Fig.11).
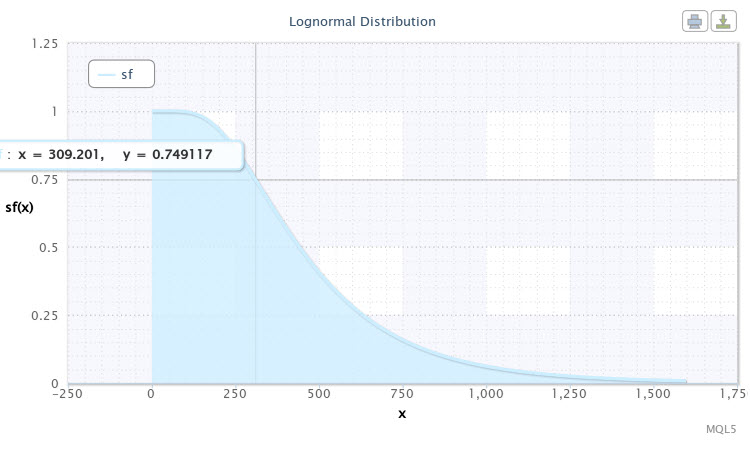
Figure 11. La fonction de survie pour X~Logn (6,09, 0,53)
Le point marqué dans le graphique de la courbe peut être interprété comme suit : on peut s'attendre avec près de 75% de probabilité à ce que la volatilité de la paire soit de 310 points. Plus nous descendons la courbe, moins la probabilité d'augmentation de la volatilité est grande. Ainsi, une volatilité supérieure à 1000 points peut déjà être considérée comme un événement rare car la probabilité de survenance de celle-ci est inférieure à 5%
Des courbes de distribution similaires peuvent être créées pour l'échantillon de rendements standardisés ainsi que pour d'autres échantillons. Je suppose que la méthodologie est généralement claire.
Conclusion
Il convient de noter que les dérivations analytiques proposées ne sont pas entièrement réussies car les séries ont tendance à varier. Bien que, par exemple, il ne s'agisse pas de séries de rendements logarithmiques. Cependant, je ne me suis pas fixé pour tâche d'évaluer les méthodes dans cet article. Je suggère au lecteur intéressé de commenter cette question.
Il est important de noter la nécessité d’examiner le marché, les instruments de marché et les experts en trade du point de vue des probabilités. C'est l'approche que j'ai essayée de démontrer. J'espère que ce sujet suscitera l'intérêt du lecteur et mènera à une discussion constructive.
Emplacement des fichiers :
| # | __FILE__ | Chemin : | Description |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Galerie des cours de distribution |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Cours pour l'affichage graphique des distributions |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Cours pour la génération d'un échantillon de nombres aléatoires |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | Classe et fonctions des estimations de caractéristiques statistiques |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | Script pour l'estimation de l'échantillon de volatilité EURUSD H4 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | Script pour l'estimation de l'échantillon de rendements EURUSD H4 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Script pour l'estimation de l'échantillon de variables aléatoires |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Script pour l'ajustement et l'estimation de toutes les distributions |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | Échantillon de fichier de données de volatilité EURUSD H4 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | L'EURUSD H4 renvoie un échantillon de fichier de données |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | Exemple de fichier de données de variables aléatoires |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | Histogramme de l'échantillon en HTML |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | Double histogramme de l'échantillon en HTML |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Rapport statistique HTML de l'estimation de l'échantillon |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Données pour l’affichage d’ un histogramme d'échantillons |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Données pour l’affichage d’ un double histogramme d'échantillons |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | Données pour l'affichage du rapport HTML |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | Bibliothèque JavaScript de graphiques interactifs |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | bibliothèque JavaScript |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Indicateur de retours logarithmiques |
Documentation de référence:
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/257
 Filtrage des Signaux en Fonction des Données Statistiques de la Corrélation des Prix.
Filtrage des Signaux en Fonction des Données Statistiques de la Corrélation des Prix.
 Utilisation de Pseudo-Modèles comme Alternative aux Modèles C++
Utilisation de Pseudo-Modèles comme Alternative aux Modèles C++
 3 Méthodes d'Accélération des Indicateurs par l'Exemple de la Régression Linéaire
3 Méthodes d'Accélération des Indicateurs par l'Exemple de la Régression Linéaire
 Utilisation des Indicateurs MetaTrader 5 avec le Cadre d'Apprentissage Automatique ENCOG pour la Prédiction de Séries Chronologiques
Utilisation des Indicateurs MetaTrader 5 avec le Cadre d'Apprentissage Automatique ENCOG pour la Prédiction de Séries Chronologiques
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation