Matemáticas puras, física, lógica (braingames.ru): juegos cerebrales no relacionados con el comercio - página 125
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Parece que se ajusta a todas las opciones en 2 pesajes
este dibujo es algo ajeno...
Qué raro, me pareció más claro, creo que la imagen es más ilustrativa que las palabras. Bien, algunos comentarios:
Para la primera pesada ponemos dos bolas en cada vaso de la balanza, de forma que en cada vaso tengamos 1 bola del color elegido y una bola de algún otro color diferente a los colores de las bolas de la cesta opuesta. (En la imagen es una bola roja con una verde y una roja con una azul). Los resultados de 1 pesaje pueden ser diferentes: opción 1.1) la balanza está equilibrada y opción 2) la balanza está desequilibrada, uno de los vasos supera al 2.1). Es decir, tenemos dos ramas de la solución.
En la primera variante, dividimos las bolas en dos grupos homogéneos (grupo ' y grupo '), y luego 1.2) simplemente pesamos ambos grupos (3 bolas por vaso de la balanza) y determinamos cuál es el más pesado. Eso es todo, las bolas pesadas se encuentran.
La segunda opción puede darse en dos casos (generalizados). Cuando las dos bolas de color de la primera pesada en cada vaso son pesadas o ligeras. Por (2.2) después de marcar las bolas en grupos (grupo ' y grupo ') determinamos con una sola pesada con una bola pesada, cual de los grupos pertenece al grupo pesado y cual al ligero.
Esta es una imagen de Internet....
Bien, algunos comentarios:
Ahora el patrón está claro.
La segunda opción puede darse en dos casos (generalizados). Cuando las dos bolas de color de la primera pesada en cada vaso son pesadas o ligeras.
Qué raro, me pareció más claro, creo que la imagen es más ilustrativa que las palabras. Bien, algunos comentarios:
Para la primera pesada ponemos dos bolas en cada vaso de la balanza, de forma que en cada vaso tengamos 1 bola del color elegido y una bola de algún otro color diferente a los colores de las bolas de la cesta opuesta. (En la imagen es una bola roja con una verde y una roja con una azul). Los resultados de 1 pesaje pueden ser diferentes: opción 1.1) la balanza está equilibrada y opción 2) la balanza está desequilibrada, uno de los vasos supera al 2.1). Es decir, tenemos dos ramas de la solución.
En la primera variante, dividimos las bolas en dos grupos homogéneos (grupo ' y grupo '), y luego 1.2) simplemente pesamos ambos grupos (3 bolas por vaso de la balanza) y determinamos cuál es el más pesado. Eso es todo, las bolas pesadas se encuentran.
La segunda opción puede darse en dos casos (generalizados). Cuando las dos bolas de color de la primera pesada en cada vaso son pesadas o ligeras. Por (2.2) determinamos con una sola pesada (grupo ' y grupo '), cuál es la pesada y cuál la ligera.
Guarda tus dudas para ti. CensuradoSin ánimo de ofender...
Opción 1.1 que sugerí en privado. el comienzo es erróneo.
Gracias por las felicitaciones, chicos, pero la verdad es lo primero.
En resumen: ¿dos o tres?
Si son dos, dame un diagrama, ya que yo mismo sé que son tres.
Bien gracias, entonces la segunda rama de la solución diverge en tres opciones (se añade la opción c)
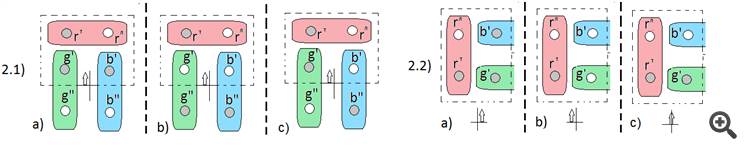
Y el segundo pesaje se organizará a partir de las mismas bolas que el primero, pero con una disposición diferente. Como resultado, después de la segunda pesada tendremos una de las tres respuestas, mediante la cual podemos reconstruir la posición de las bolas en la primera pesada, y conociendo la bola pesada de la primera pesada (la verde pesada) podemos determinar el peso de las demás.Andrei, ¿cuál es tu solución para las tres bolas (basta con la disposición inicial de cada pesaje)?
Existe la opinión de que hay varias soluciones.
Andrei, ¿cuál es tu solución para tres bolas (basta con una disposición inicial para cada pesaje)?
No tengo ninguna opción :) la solución anterior parece ser correcta.
______________
Y feliz cumpleaños :) Más problemas de rompecabezas interesantes para ti y para resolverlos todos.
No tengo ninguna opción :) la solución anterior parece ser la correcta.
______________
Y feliz cumpleaños :) Te deseo muchos problemas de rompecabezas interesantes y que los resuelvas todos.
Gracias, Andrew.
Me temo que tendré que publicar los que no he resuelto más a menudo. Pero resuélvelas urgentemente (¡no me gusta leer las soluciones de los demás si no las he resuelto yo mismo!)
P.D. ¿Has resuelto el problema del 53?