Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal

Contenido

• Introducción
• 1. El problema
• 2. Experimento 1
• 3. Experimento 2
• 4. Experimento 3
• Conclusión
• Enlaces
• Programas utilizados en el artículo

Introducción

Ya nos hemos familiarizado con los principios de funcionamiento y los métodos de implementación de un perceptrón totalmente conectado y las redes convolucionales y recurrentes. Para entrenar todas las redes, hemos utilizado el descenso de gradiente. Este método consiste en determinar el error de predicción de la red en cada salto y ajustar los coeficientes de peso para disminuir el error. En este caso, además, no eliminamos por completo el error en cada salto, sino que solo ajustamos ligeramente los pesos para reducirlo. Por consiguiente, intentamos encontrar los pesos capaces de repetir el conjunto de entrenamiento lo más cerca posible a lo largo de toda su longitud. Y es precisamente la tasa de aprendizaje la responsable de la velocidad de minimización del error en cada salto.

1. El problema

¿En qué reside el problema de la elección de la tasa de aprendizaje? Vamos a definir las preguntas básicas relacionadas con la elección de la tasa de aprendizaje.

1. ¿Por qué no podemos usar la tasa "1" (o un valor cercano) e inmediatamente compensar el error?
En ese caso, tendríamos una red neuronal sobreentrenada para esta última situación. Como resultado, tomaremos otras decisiones basadas solo en los datos más recientes, ignorando la historia.

2. ¿Cuál sería el riesgo derivado de una tasa ciertamente pequeña, que permitiría promediar los valores de toda la muestra?
El primer problema con este enfoque reside en el tiempo de entrenamiento de la red neuronal. Si la tasa de aprendizaje es muy pequeña, necesitaremos realizar una gran cantidad de saltos de este tipo. Esto requiere de tiempo y recursos.

El segundo problema con este enfoque es que el camino hacia nuestro objetivo no siempre resulta fácil. Podemos encontrar valles y colinas. Si nos desplazamos en saltos muy pequeños, podemos quedarnos estancados en alguno de estos valores, determinándolo erróneamente como mínimo global. En ese caso, nunca alcanzaremos nuestro objetivo. Esto se puede resolver de manera parcial usando un impulso en la fórmula de actualización de los pesos, pero el problema persiste.

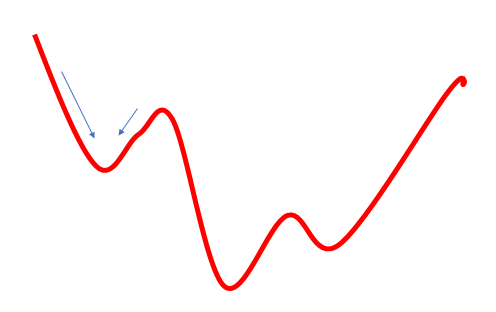
3. ¿Cuál es el riesgo de usar una tasa demasiado elevada que permitirá promediar los valores a una determinada distancia y superar los mínimos locales?
Este intento de resolver el problema del mínimo local incrementando la tasa de aprendizaje oculta otro problema: la utilización de una tasa de aprendizaje sobreestimada muchas veces no permite minimizar el error, porque con la próxima actualización de los pesos, su cambio resultará superior al requerido, y como resultado, "sobrevolaremos" el mínimo global. En el posterior regreso, nos encontramos con una situación similar. Como resultado, oscilaremos en una cierta proximidad con el mínimo global.

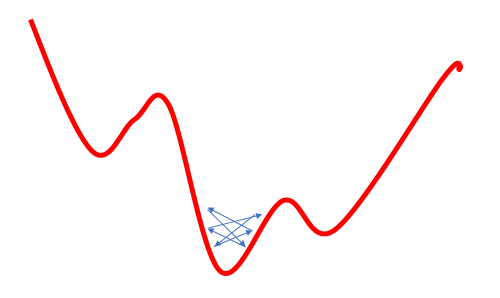
Estos problemas son ampliamente conocidos y los encontramos con frecuencia en la literatura, pero no hemos encontrado en ninguna parte una indicación clara sobre la elección de la tasa (ritmo) de aprendizaje. Todo se reduce a la selección empírica de la tasa para cada tarea. Asimismo, en algunos trabajos se nos propone reducir gradualmente durante el aprendizaje la tasa para minimizar el riesgo 3, descrito anteriormente.

En este artículo, proponemos realizar experimentos sobre el entrenamiento de una red neuronal con diferentes tasas de ritmo de aprendizaje y comprobar su impacto en el entrenamiento de una red neuronal.    

2. Experimento 1

Para que el experimento resulte más cómodo, vamos a mover la variable eta de la clase CNeuronBaseOCL a las variables globales.

double   eta=0.01;
#include "NeuroNet.mqh"

y

class CNeuronBaseOCL    :  public CObject
  {
protected:
   ........
   ........
//---
   //const double      eta;

Ahora, vamos a crear tres copias del asesor experto con diferentes parámetros de tasa de aprendizaje (0.1; 0.01; 0.001). Además, crearemos un cuarto asesor en el que la tasa de aprendizaje inicial se establecerá en 0.01 y se reducirá 10 veces cada 10 épocas. Para conseguirlo, añadiremos el siguiente código al ciclo de entrenamiento en la función Train.

         if(discount>0)
            discount--;
         else
           {
            eta*=0.1;
            discount=10;
           }

Los cuatro asesores se ha iniciado simultáneamente en una misma plataforma. En este experimento, hemos utilizado los parámetros de prueba del asesor anterior: símbolo EURUSD, gráfico de tiempo H1, red alimentada con los datos de 20 velas consecutivas, entrenamiento realizado usando la historia de los últimos dos años. La muestra de entrenamiento ha sido de aproximadamente 12,4 mil barras.

Todos los asesores se han iniciado con pesos aleatorios que van de -1 a 1, excluyendo los valores iguales a cero.

Por desgracia, el asesor con una tasa de aprendizaje de 0.1 tuvo un error cercano a 1, por lo que no se muestra en los gráficos. Las dinámicas de aprendizaje de los otros asesores se muestran en los siguientes gráficos.

Después de 5 épocas, el error de todos los asesores ha alcanzado el nivel 0,42, oscilando después en esa zona durante el resto del tiempo. El error del asesor con la tasa de aprendizaje de 0,001 ha sido ligeramente menor. Las diferencias han aparecido en el tercer decimal (0,420 frente a 0,422 de los otros dos asesores).

La trayectoria de error del asesor con una tasa de aprendizaje variable repite la línea de error del asesor con una tasa de aprendizaje de 0.01. Esto resulta bastante esperado en las primeras diez temporadas, pero no existe desviación cuando la tasa disminuye.

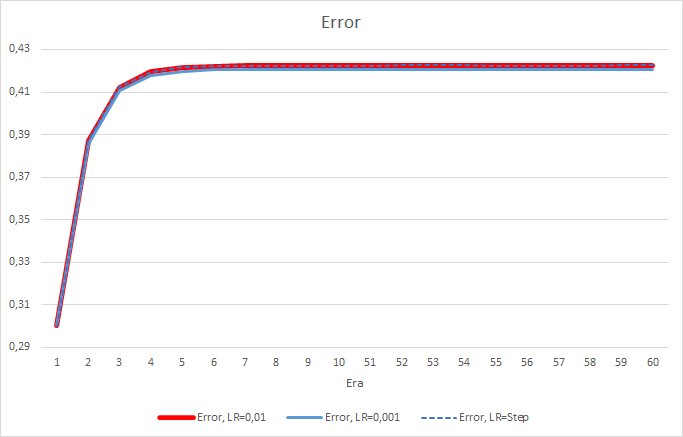
Vamos a echar un vistazo con mayor detalle a la diferencia entre los errores de los asesores en el experimento. Prácticamente durante todo el experimento, la diferencia entre los errores de los asesores con tasas de aprendizaje constantes de 0.01 y 0.001 osciló alrededor de la marca de 0.0018. En este caso, además, una disminución en la tasa de aprendizaje en el asesor cada 10 épocas casi no tiene efecto, mientras que la desviación del asesor con una tasa de 0.01 (igual a la tasa de aprendizaje inicial) oscila alrededor de "0".

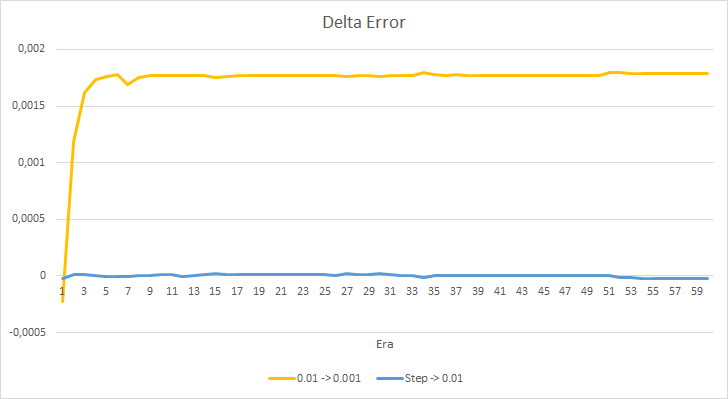
Los indicadores de error obtenidos muestran que, en nuestro caso, una ritmo de aprendizaje de 0.1 no es aplicable, pero utilizar una tasa de aprendizaje de 0.01 e inferior da resultados similares con un error de alrededor del 42%.

La imagen con el error estadístico de la red neuronal está clara, pero ¿cómo influirá esto en el funcinamiento de nuestro asesor? Veamos el número de fractales omitidos. Por desgracia, durante el experimento, los indicadores de todos los asesores para este indicador son decepcionantes: todos se encuentran cerca del 100% de omisión de fractales. Además, si un asesor con una tasa de aprendizaje de 0.01 determina aproximadamente el 2.5% de los fractales, entonces, con una tasa de aprendizaje de 0.001, se omitirán el 100% de los fractales. Debemos señalar que después de la época 52, el asesor con una tasa de aprendizaje de 0.01 ha mostrado tender hacia una disminución en el número de fractales omitidos. El asesor con una tasa de aprendizaje variable, a su vez, no muestra tal tendencia. 

   

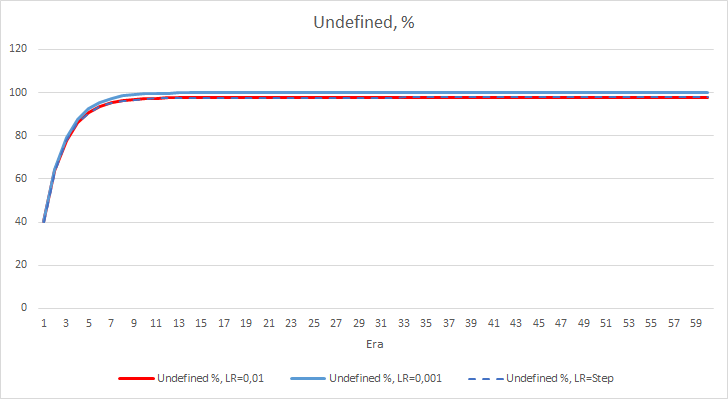
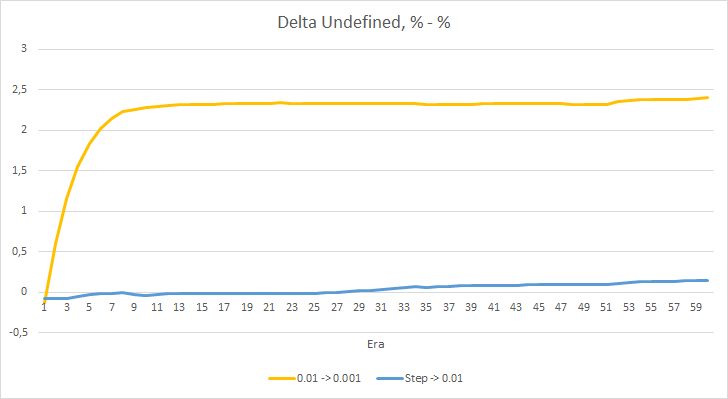
El gráfico de deltas de los fractales omitidos también muestra un aumento gradual en la diferencia a favor del asesor con una tasa de aprendizaje de 0.01.

Ya hemos analizado dos métricas de rendimiento de la red neuronal y, hasta ahora, el asesor con una tasa de aprendizaje más baja tiene un error menor, pero omite fractales. Ahora, vamos a analizar el tercer valor, el "acierto" de los fractales predichos.

Los siguientes gráficos muestran un aumento en el porcentaje de "aciertos" en el entrenamiento del asesor con una tasa de aprendizaje de 0.01 y con una tasa dinámicamente decreciente. En este caso, además, al disminuir el ritmo de aprendizaje, se reduce la velocidad de crecimiento de este indicador. El asesor con una tasa de aprendizaje de 0,001 ha tenido un porcentaje de "aciertos" que se mantiene alrededor de 0, lo cual resulta bastante natural porque falla el 100% de los fractales. 

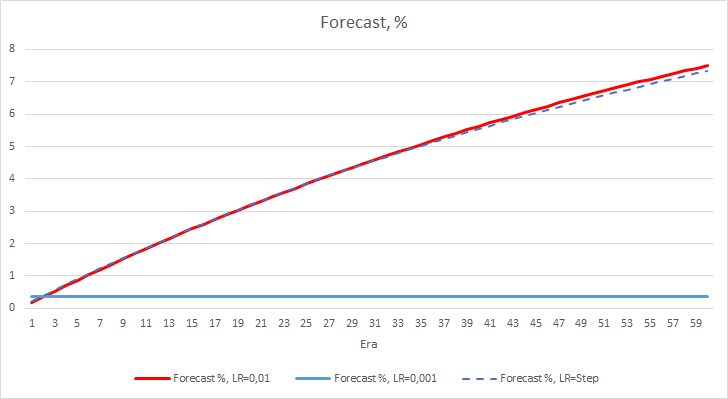
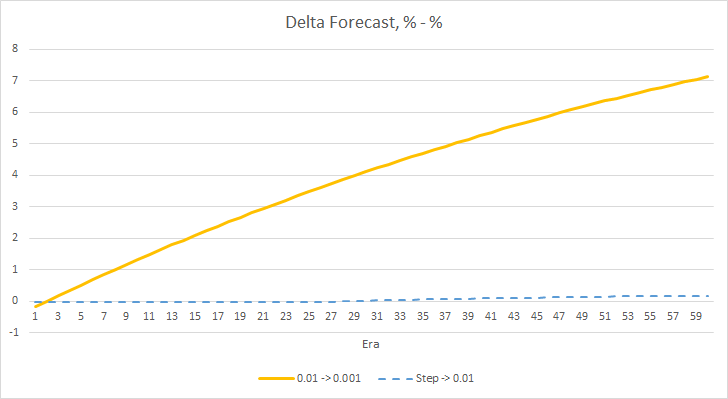
El experimento realizado indica que, en nuestra tarea, resulta óptimo usar una tasa de aprendizaje cercana al 0,01 para entrenar una red neuronal. Al mismo tiempo, una disminución gradual en la tasa de aprendizaje no ha dado un resultado positivo. Probablemente, el efecto de la reducción de la tasa sea diferente si, en lugar de modificarlo tras 10 épocas, lo hacemos con menos frecuencia. Quizá tras 100 o 1000 épocas. Pero también debemos verificar esto de forma experimental.

3. Experimento 2

En el primer experimento, las matrices de los pesos de la red neuronal se han inicializado aleatoriamente. Y, por consiguiente, todos los asesores tienen diferentes estados iniciales. Para eliminar la influencia de la aleatoriedad sobre los resultados del experimento, cargamos la matriz de pesos obtenida en el experimento anterior con el asesor que tiene una tasa de aprendizaje igual a 0.01 en los tres asesores y continuamos el entrenamiento durante otras 30 épocas.

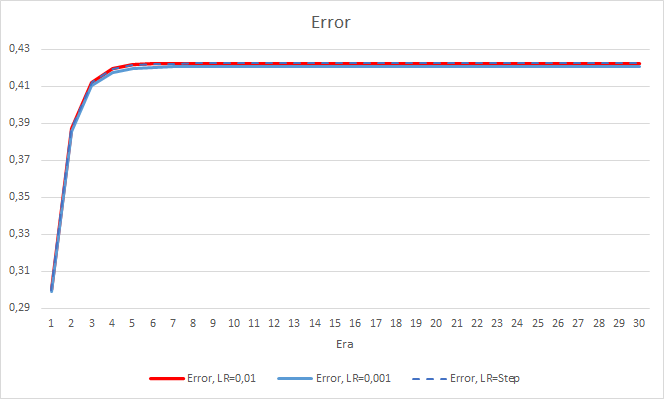
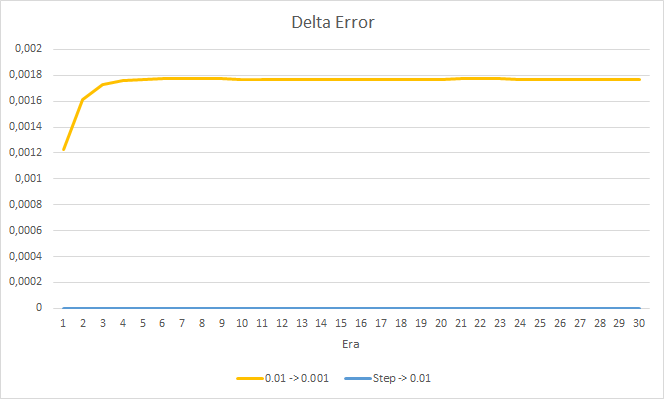
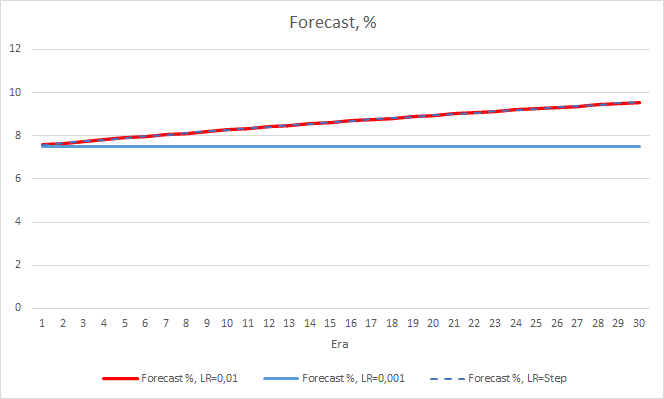
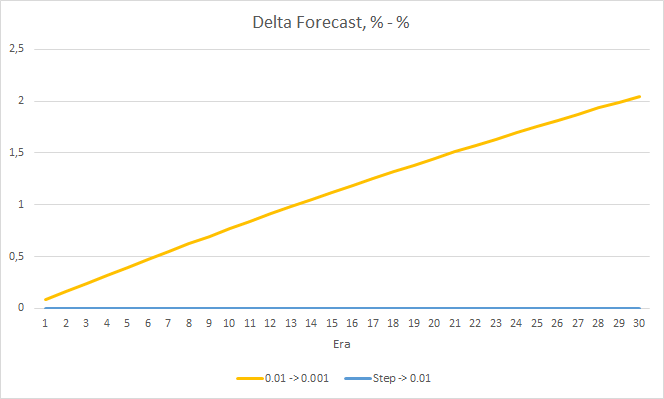
La nueva formación confirma los resultados obtenidos anteriormente. Vemos un error promedio de alrededor de 0.42 en los tres asesores. El asesor con la tasa de aprendizaje más baja (0,001) ha vuelto a tener un error ligeramente menor (con la misma diferencia de 0,0018). El efecto de una disminución gradual en la tasa de aprendizaje es casi igual a "0".

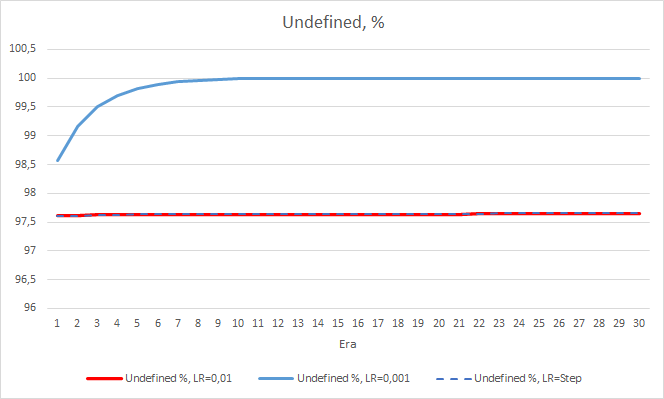
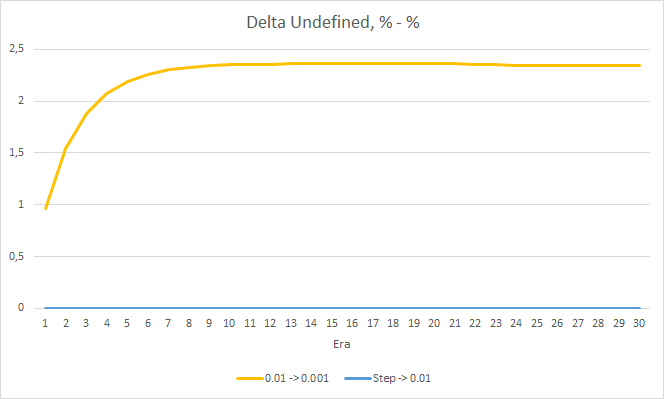
El porcentaje de fractales omitidos también confirma los resultados obtenidos anteriormente. El asesor experto con la tasa de aprendizaje más baja durante 10 épocas se ha acercado al 100% de los fractales omitidos, es decir, el asesor no puede indicar fractales. Los otros dos asesores se mantienen a un nivel del 97,6%. El efecto de una disminución gradual en la tasa de aprendizaje se acerca a "0".  

El porcentaje de "aciertos" del asesor con una tasa de aprendizaje de 0.01 continúa aumentando paulatinamente, mientras que la disminución gradual en la tasa de aprendizaje no afecta el indicador. 

 

4. Experimento 3

El tercer experimento supone una ligera desviación respecto al tema principal del artículo. Su idea surgió durante los dos primeros experimentos. Entonces, decidimos compartirlo con el lector. Al observar el entrenamiento de la red neuronal, vimos que la probabilidad de omitir un fractal oscila alrededor del 60-70%, y rara vez cae por debajo del 50%. La probabilidad de aparición de un fractal, ya sea de compra o venta, se encuentra alrededor del 20-30%. Esto resulta bastante natural, ya que hay muchos menos fractales en el gráfico que velas dentro de las tendencias. Por consiguiente, nuestra red neuronal se sobreentrena y obtenemos los resultados anteriores. Casi el 100% de los fractales se omiten y solo en raras ocasiones se pueden detectar.  

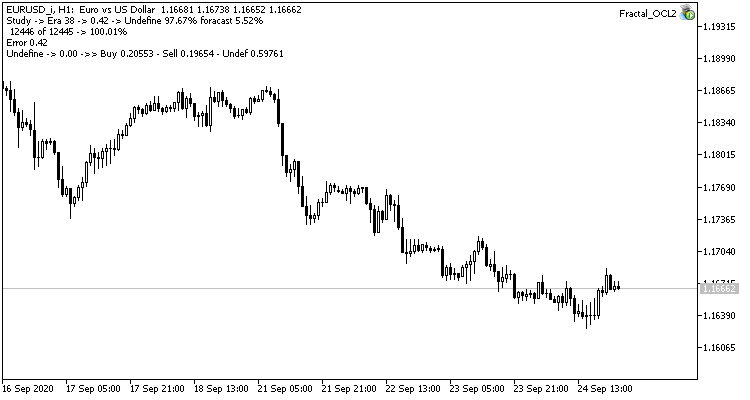
Para solucionar este problema, hemos decidido compensar ligeramente el desequilibrio de la muestra y, ante la inexistencia de un fractal en el valor de referencia, hemos indicado 0.5 en lugar de 1 al entrenar la red.

            TempData.Add((double)buy);
            TempData.Add((double)sell);
            TempData.Add((double)((!buy && !sell) ? 0.5 : 0));

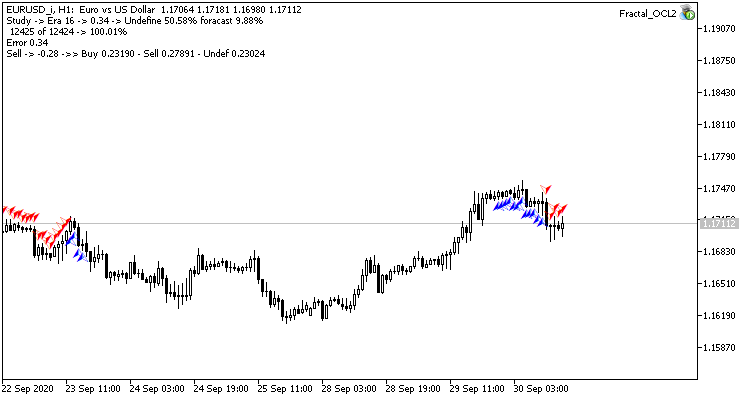
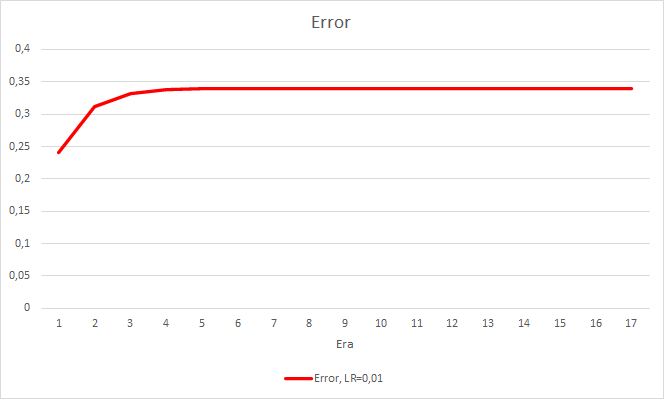
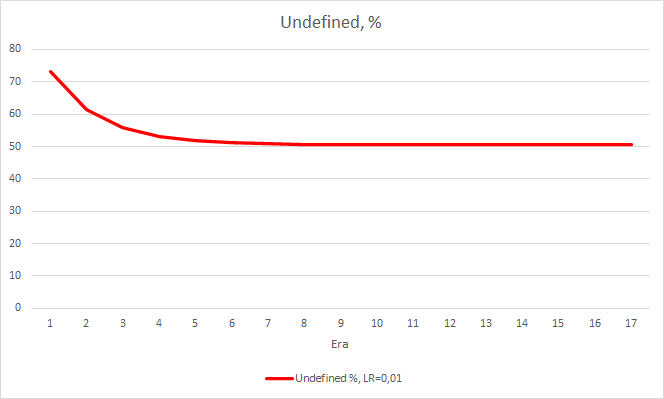
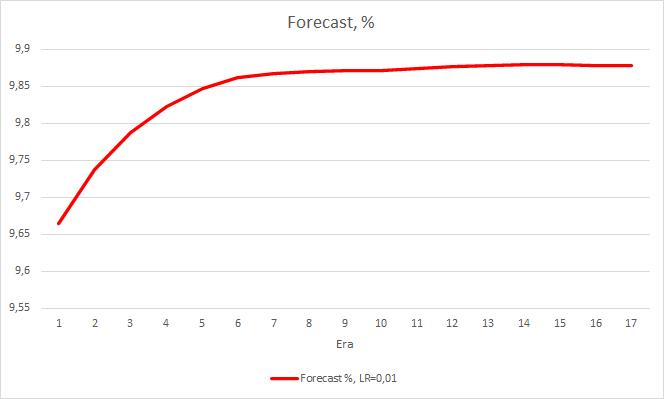
Este paso ha dado sus frutos. Tras iniciar el asesor experto con una tasa de aprendizaje de 0.01 y una matriz de pesos tras los experimentos previos y después de 5 épocas de entrenamiento, vemos una estabilización del error en torno al 0.34. En este caso, además, la proporción de fractales omitidos disminuyó al 51%, y los "aciertos" aumentaron en un 9,88%. En el gráfico, podemos ver que el asesor emite señales en grupos, definiendo así algunas zonas. Está claro que la idea requiere de elaboración y pruebas adicionales, pero los resultados obtenidos indican la consistencia de este enfoque. 

Conclusión

En el presente artículo, hemos mostrado 3 experimentos. Los primeros 2 experimentos han ilustrado la importancia de seleccionar correctamente la tasa de aprendizaje de la red neuronal. El resultado general del entrenamiento de la red neuronal depende de su correcta selección. Sin embargo, por el momento no existe una regla clara para elegir el ritmo de aprendizaje. Por consiguiente, en la práctica, deberemos seleccionarlo de forma experimental.

El tercer experimento ha mostrado que, a la hora de resolver el problema, un enfoque no estándar puede mejorar el resultado general, pero la aplicación de cada solución tiene que estar respaldada de forma experimental.

Enlaces

1. Redes neuronales: así de sencillo
2. Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
3. Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
4. Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
5. Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL

Programas utilizados en el artículo

#	Nombre	Tipo	Descripción
1	Fractal_OCL1.mq5	Asesor	Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la tecnología OpenCL. Ritmo de aprendizaje 0.1
2	Fractal_OCL2.mq5	Asesor	Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la tecnología OpenCL. Ritmo de aprendizaje 0.01
3	Fractal_OCL3.mq5	Asesor	Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la tecnología OpenCL. Ritmo de aprendizaje 0.001
4	Fractal_OCL_step.mq5	Asesor	Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la tecnología OpenCL. Ritmo de aprendizaje con una reducción de 10 veces desde 0.01 cada 10 épocas
5	NeuroNet.mqh	Biblioteca de clase	Biblioteca de clases para crear la red neuronal
6	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL