
Neuroredes profundas (Parte VII). Conjunto de neuroredes: stacking
Contenido
- Introducción
- 1. Preparando los datos de entrada para el combinador entrenable
- 2. Modelos de comparación básicos
- 3. Las bibliotecas keras/tensorflow. Descripción general e instalación
- 4. Combinador de salidas del conjunto bagging — red neuronal
- 5. Análisis del resultado de los experimentos
- Conclusión
- Anexos
Introducción
Los modelos del nivel básico del conjunto (clasificadores individuales) se entrenan con el conjunto (set) completo. A continuación, el metamodelo se entrena con las salidas del conjunto obtenidas al predecir el conjunto de prueba. Las salidas de los clasificadores del conjunto, en este caso, se convierten en datos de entrada para el nuevo clasificador entrenable, que propiamente supone un combinador. Este enfoque se llama «generalización compleja» o "generalización sin aprendizaje", o simplemente stacking.
Uno de los problemas de esta combinación es la construcción de un conjunto de entrenamiento para el meta-clasificador.
Vamos a experimentar con la construcción y la simulación de conjuntos stacking. En ellos usaremos un conjunto de clasificadores de redes neuronales ELM con los hiperparámetros óptimos obtenidos anteriormente. En el primer experimento usamos las salidas del conjunto podado, y en el segundo, todas las salidas del conjunto. Los combinadores en ambas variantes se convertirán en redes neuronales plenamente conectadas, pero con diferente estructura. En experimentos posteriores comprobaremos cómo influyen la modalidad múltiple y la tarea múltiple en la calidad de la clasificación de la red neuronal.
Para valorar la calidad de predicción en estas variantes, usaremos modelos básicos de comparación.
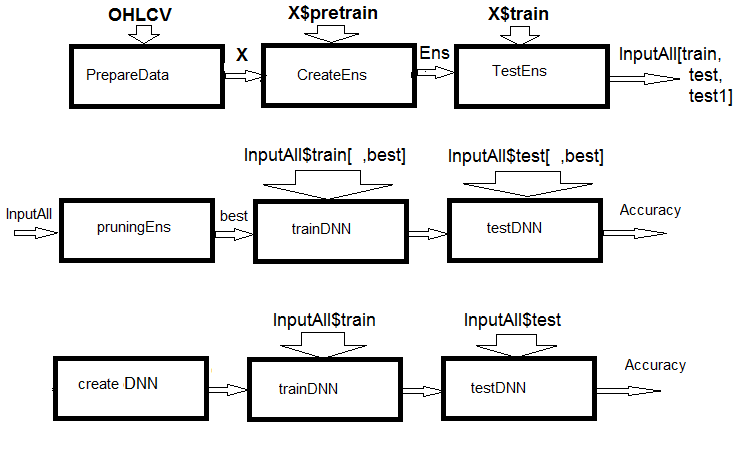
Fig.1. Estructura del esquema de cálculos
Como podemos ver por la figura, el experimento consta de tres partes.
- Preparamos los datos de entrada para el conjunto, entrenamos el conjunto ELM y obtenemos las predicciones con los conjuntos train/test/test1. Estos conjuntos precisamente serán las entradas InputAll para los combinadores entrenables.
- Podamos el conjunto: elegimos las mejores predicciones ELM según la importancia de la información. Pondremos a prueba los modelos básicos de comparación para comprender la métrica de las referencias. Entrenaremos y pondremos a prueba una DNN con estos datos, calcularemos las métricas de los modelos y las compararemos con las métricas del modelo básico.
- Crearemos redes neuronales de modalidad múltiple y tarea múltiple, las entrenaremos y las pondremos a prueba con los conjuntos InputAll. Calcularemos las métricas de los modelos obtenidos y los compararemos con las métricas del modelo básico.
1. Preparando los datos de entrada para el combinador entrenable
Para realizar los experimentos, usaremos la versión R 3.4.4. En ella hay varios paquetes que no hemos utilizado hasta el momento.
Iniciamos RStudio. Cargamos desde GitHub/Part_I el archivo Cotir.RData con las cotizaciones del terminal y los archivos Importar.R, Libary.R, FunPrepareData_VII.R, FUN_Stacking.R con las funciones de prepación de datos de GitHub/Part_VII. Preste atención: ¡la secuencia de carga de los archivos es importante! Hemos mejorado un poco las funciones para acelerar los cálculos y aumentar la legibilidad de los scripts. También hemos añadido una serie de predictores necesarios para los experimentos.
Usaremos las mismas cotizaciones y las dividiremos en las mismas muestras, como en los anteriores artículos de esta serie. Luego escribiremos un script para preparar los datos fuente. No vamos a detenernos en los detalles del cálculo, estos han sido descritos anteriormente. Hemos realizado cambios usando el paquete dplyr y la importación de paquetes y funciones al entorno de trabajo. El paquete dplyr es muy útil, simplifica la manipulación de datos, durante la depuración a veces da alguna sorpresa que provoca una larga búsqueda de errores.
Vamos a aclarar este punto. Al cargar la biblioteca dplyr recibimos en la consola las siguientes advertencias:
> library(dplyr) Attaching package: ‘dplyr’ The following objects are masked from ‘package:stats’: filter, lag The following objects are masked from ‘package:base’: intersect, setdiff, setequal, union
Tenemos un conflicto con los nombres de las funciones. Para aclarar el problema, hemos tenido que indicar explícitamente de qué paquete usamos una función concreta. Por ejemplo, dplyr::filter(), dplyr::lag. El segundo problema es que con frecuencia necesitamos solo una o dos funciones del paquete, pero tenemos que cargarlo al completo. Y es que algunos paquetes (por ejemplo, caret) son muy pesados y arrastran paquetes dependientes que no necesitamos. En este sentido, el estilo de importación de las funciones y paquetes de Python es más lógico. Por ejmplo:
from theano import function, config, shared, tensor import numpy as np import time
En la primera línea se importa una serie de funciones del paquete theano, en la segunda línea, el paquete numpy, con el pseudónimo np, y en la tercera, el paquete time. Para conseguir esta posibilidad en R, existe el paquete importar, que tiene solo dos funciones: import() y import_fun(). La primera da la posibilidad de importar paquetes, la segunda, funciones. Bien es cierto que hemos tenido que renombrar la primera como import_pack(), para que no se cruce con la función reticulate::import().
Además, hemos añadido nuevas variables que necesitaremos para realizar los experimentos. Formaremos dos conjuntos de datos: data1 y data2. Vamos a ordenar los predictores en ellos según la importancia de la información.
Abajo se muestra el script de preparación de los datos fuente para los experimentos. Se encuentra en el archivo Prepare.R.
#--0--Library------------- # source(file = "importar.R") # source(file = "Library.R") # source(file = "FunPrepareData_VII.R") # source(file = "FUN_Stacking.R") #--1-prepare---- evalq({ # combinamos las cotizaciones de OHLCV, Med, Typ, W en un frame de datos # calculamos los predictores y la variable objetivo dt <- PrepareData(Data, Open, High, Low, Close, Volume) # dividimos el conjunto inicial en pretrain/train/val/test DT <- SplitData(dt$feature, 4000, 1000, 500, 250, start = 1) # definimos los parámetros de los valores atípicos pre.outl <- PreOutlier(DT$pretrain) # importamos las muestras en todos los valores atípicos DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) # establecemos el método de normalización de los predictores meth <- "spatialSign" #"expoTrans" "range" "spatialSign", # definimos los parámetros de normalización preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) # normalizamos los predictores en todos los conjuntos DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
En el bloque 0 (Library) cargamos las bibliotecas y funciones necesarias. Hay que cargar los cuatros archivos con los scripts en la secuencia indicada. En el bloque 1 (prepare) creamos los predictores y los normalizamos quitando los valores atípicos. Podemos cambiar el método de normalización.
Ahora vamos a formar dos conjuntos de datos: data1 y data2. En el primer conjunto se usarán como predictores filtros digitales y sus diferencias de primer orden; como variable objetivo, usaremos el signo de cambio de la diferencia de primer orden de ZigZag. En el segundo conjunto, actuarán como predictores las diferencias de primer orden de las cotizaciones High/Low/Close y las diferencias de las cotizaciones CO/HO/LO/HL; como variable objetivo, actuará la diferencia de primer orden de ZigZag. El script mostrado más abajo se encuentra en el archivo Prepare.R.
#--2-Data X------------- evalq({ foreach(i = 1:length(DTcap)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 list(pretrain = X1[[1]] , train = X1[[2]] , test = X1[[3]] , test1 = X1[[4]] ) -> X1 }, env) #----------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 list(pretrain = X2[[1]] , train = X2[[2]] , test = X2[[3]] , test1 = X2[[4]] ) -> X2 }, env)
Ordenamos los predictores en ambos conjuntos en orden descendente según la importancia de su información. Veamos cómo se clasifican. El script mostrado a continuación se encuentra en el archivo Prepare.R.
#---3--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX1 }, env) colnames(env$X1$pretrain$x)[env$orderX1] [1] "v.fatl" "v.rbci" "v.ftlm" "fars" "v.satl" "stlm" [7] "rbci" "ftlm" "v.stlm" "v.rftl" "pcci" "v.rstl" [13] "v.pcci evalq({ orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX2 }, env) colnames(env$X2$pretrain$x)[env$orderX2] [1] "dC" "CO" "HO" "LO" "dH" "dL" "HL"
El orden de los predictores de las cotizaciones es interesante.
Para preparar los datos de entrada para los combinadores, necesitamos:
- crear un conjunto ELM y entrenarlo con el conjunto de entrenamiento X1$pretrain;
- hacer una predicción del conjunto X1$train con la ayuda del conjunto de entrenamiento. Será el conjunto de entrenamiento InputTrain;
- hacer una predicción del conjunto X1$test con la ayuda del conjunto de entrenamiento. Será el conjunto de prueba InputTest;
- hacer una predicción del conjunto X1$test1 con la ayuda del conjunto de entrenamiento. Será el conjunto de prueba InputTest1.
Definimos las variables y constantes, escribimos las funciones createEns() y GetInputData(), ella retornará el valor de todas las salidas del conjunto. Los valores de los parámetros de la función createEns() ya los hemos obtenido tras la optimización del conjunto. Usted puede tener otros valores. El script mostrado abajo se encuentra en el archivo FUN_Stacking().
#----Library------------- import_fun(rminer, holdout, holdout) #source(file = "FunPrepareData_VII.R") #----Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 #---createENS---------------------- createEns <- function(numFeature = 8L, r = 7L, nh = 5L, fact = 7L, order, X){ # definimos los índices de los mejores predictores bestF <<- order %>% head(numFeature) # elegimos los mejores predictores para el conjunto de entrenamiento Xtrain <- X$pretrain$x[ , bestF] #setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---creste Ensemble--- Ens <<- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #---GetInputData -FUN----------- GetInputData <- function(Ens, X){ #---predict-InputTrain-- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> predEns #[ ,n] #---predict--InputTest---- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X$test1$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputTrain = predEns, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
Creamos un conjunto y calculamos las entradas para los combinadores entrenables:
#---4--createEns---------------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) createEns(order = orderX1, X = X1) -> Ens GetInputData(Ens, X1) -> res }, env)
Estructura del resultado:
> env$res %>% str() List of 3 $ InputTrain: num [1:1001, 1:500] 0.811 0.882 0.924 0.817 0.782 ... $ InputTest : num [1:501, 1:500] 0.5 0.383 0.366 0.488 0.359 ... $ InputTest1: num [1:251, 1:500] 0.32 0.246 0.471 0.563 0.451 ...
2. Modelos de comparación básicos
Vamos a crear dos combinadores entrenables. Uno sustituirá la promediación de las salidas de las mejores redes neuronales del conjunto, y el segundo elemento sistituirá la poda y la promediación. Por eso necesitaremos índices de calidad de la clasificación para ambas variantes.
Conjunto de redes neuronales
Para la primera variante del modelo básico de comparación será un conjunto ELM con parámetros óptimos.
Puesto que en la segunda variante hay 500 datos de entrada, usaremos el paquete varbvs. En este existen algoritmos más rápidos para elegir los modelos bayesianos de selección de variables y cálculo de los coeficientes de Bayes, donde el resultado se modela usando una regresión lineal o logística. Los algoritmos se basan en las aproximaciones variacionales descritas en el artículo "Inferencia variable escalable para la selección de variables bayesianas en regresión y su precisión en estudios de asociación genética". Este software se aplica a grandes conjuntos de datos con más de un millón de variables y mil muestras.
Para la primera opción vamos a escribir las funciones adicionales getBest(), testAver(), testVot() y calcular las métricas. Las funciones se encuentran en el archivo FUN_Stacking.R.
evalq({
getBest <- function(Ens, x, y, nb){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
predict(Ens[[i]], newdata = x)} -> y.pr
foreach(i = 1:n, .combine = "c") %do% {
median(y.pr[ ,i])} ->> th
foreach(i = 1:n, .combine = "c") %do% {
ifelse(y.pr[ ,i] > th[i], 1, 0) -> Ypred
Evaluate(actual = y, predicted = Ypred)$Metrics$F1 %>%
mean()
} -> Score
Score %>% order(decreasing = TRUE) %>% head(2*nb + 1) -> best
y.pr[ ,best] %>%
apply(1, sum) %>%
divide_by(length(best)) %>%
median() -> med
return(list(Score = Score, bestNN = best, med = med))
}
testAver <- function(Ens, x, y, best, med){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(1, sum) %>% divide_by(length(best)) -> ensPred
ifelse(ensPred > med, 1, 0) -> clAver
Evaluate(actual = y, predicted = clAver)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ensPred, clAver = clAver))
}
testVot <- function(Ens, x, y, best){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(2, function(x) ifelse(x > th[i], 1, -1)) %>%
apply(1, function(x) sum(x)) -> vot
ifelse(vot > 0, 1, 0) -> ClVot
Evaluate(actual = y, predicted = ClVot)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ClVot))
}
}, env)
Ya hemos analizado estas funciones, por eso no vamos a detenernos en su descripción. Pero las salidas sí que merecen nuestra atención.
- La función getBest() retorna las métricas (Score), los índices de los mejores clasificadores individuales del conjunto (bestNN) y la mediana de la salida promediada del conjunto (med), que se usará al poner a prueba el modelo. En el entorno se resetea el vector de la mediana th[500] de todas las salidas del conjunto.
- La función testAver() retorna las métricas (Score), la predicción promediada continua del conjunto (Ypred) y la predicción nominal del conjunto (clAver).
- La función testVot() retorna las métricas (Score) y la predicción nominal del conjunto (Ypred).
Vamos a poner a prueba el conjunto con dos conjuntos (set) de prueba usando la promediación y el voto por mayoría, y después analizaremos las métricas.
#--2---test---- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) Ens <- createEns(order = orderX1, X = X1) #---3------ resBest <- getBest(Ens, x = X1$train$x[ , bestF], y = Ytest, nb = 3) #---4--averaging--- ScoreAver <- testAver(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN, med = resBest$med) ScoreAver1 <- testAver(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN, med = resBest$med) #---5--voting---- ScoreVot <- testVot(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN) ScoreVot1 <- testVot(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN) }, env) > env$ScoreAver$Score Accuracy Precision Recall F1 0 0.75 0.708 0.778 0.741 1 0.75 0.794 0.727 0.759 > env$ScoreAver1$Score Accuracy Precision Recall F1 0 0.753 0.750 0.826 0.786 1 0.753 0.758 0.664 0.708 > env$ScoreVot$Score Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 > env$ScoreVot1$Score Accuracy Precision Recall F1 0 0.741 0.739 0.819 0.777 1 0.741 0.745 0.646 0.692
Hay buenos índices en ambos conjuntos de prueba. Más abajo, al analizar los resultados, descomponemos el error de clasificación en bias/variance/noise y valoramos la contribución de cada componente al error general.
Para la segunda opción (500 entradas), mostramos a continuación el script de entrenamiento del modelo. Se encuentra en el archivo varb.R.
library(varbvs) evalq({ vr <- varbvs(X = res$InputTrain, Z = NULL, y = Ytest, family = "binomial", optimize.eta = TRUE, logodds = seq(-6,-2, 0.25), nr = 250, initialize.params = TRUE, maxiter = 1e5, verbose = FALSE) summary(vr, cred.int = 0.95, nv = 7, nr = 1e5) %>% print() }, env) Summary of fitted Bayesian variable selection model: family: binomial num. hyperparameter settings: 17 samples: 1001 iid variable selection prior: yes variables: 500 fit prior var. of coefs (sa): yes covariates: 1 fit approx. factors (eta): yes maximum log-likelihood lower bound: -579.4602 Hyperparameters: estimate Pr>0.95 candidate values sa 8.09 [7.63,8.54] NA--NA logodds -2.26 [-2.75,-2.00] (-6.00)--(-2.00) Selected variables by probability cutoff: >0.10 >0.25 >0.50 >0.75 >0.90 >0.95 3 3 3 3 3 3 Top 7 variables by inclusion probability: index variable prob PVE coef* Pr(coef.>0.95) X18 18 X18 1.00000 NA 4.529 [+3.861,+5.195] X5 5 X5 1.00000 NA 1.955 [+1.543,+2.370] X255 255 X255 1.00000 NA 2.097 [+1.537,+2.660] X109 109 X109 0.00948 NA -1.033 [-2.008,-0.057] X404 404 X404 0.00467 NA -0.665 [-1.350,+0.024] X275 275 X275 0.00312 NA -0.726 [-1.735,+0.286] X343 343 X343 0.00299 NA -0.604 [-1.353,+0.149] *See help(varbvs) about interpreting coefficients in logistic regression.
Usando el modelo obtenido, calculamos la predicción con dos conjuntos de prueba y calculamos las métricas.
env$vr$pip %>% order() %>% tail(7) -> bestNN_vr evalq({ predict(vr, res$InputTest) -> pr.vr1 Evaluate(actual = Ytest1, predicted = pr.vr1)$Metrics[ ,2:5] %>% round(3) -> metr.test confus(table(Ytest1, pr.vr1)) -> cm1 predict(vr, res$InputTest1) -> pr.vr2 Evaluate(actual = Ytest2, predicted = pr.vr2)$Metrics[ ,2:5] %>% round(3) -> metr.test1 confus(table(Ytest2, pr.vr2)) -> cm2 }, env) > env$metr.test Accuracy Precision Recall F1 0 0.78 0.750 0.783 0.766 1 0.78 0.808 0.779 0.793 > env$metr.test1 Accuracy Precision Recall F1 0 0.729 0.765 0.732 0.748 1 0.729 0.689 0.726 0.707
Hemos obtenido un resultado fabuloso, mejor que las métricas del conjunto general.
Ya están listos todos los datos necesarios para continuar el experimento.
Puesto que en el futuro vamos a usar las bibliotecas keras / tensorflow, las veremos brevemente más abajo.
3. Bibliotecas keras/nensorflow. Descripción general e instalación
La esfera de estudio de las redes neuronales, debido a su febril desarrollo, se ha ido llenando de bibliotecas de código abierto. Entre ellas, TensorFlow(Google), CNTK(Microsoft), Apache MXNet y muchas otras. Gracias a que todos estos y otros desarrolladores de software entran en el Consorcio R, todas estas bibliotecas disponen de API y R.
Todas las bibliotecas enumeradas anteriormente son de nivel bajo. Son complicadas de estudiar y usar para los principiantes. Teniendo esto en cuenta, el equipo de Rstudio ha desarrollado el paquete keras para R.
Keras es una API de alto nivel de redes neuronales. El paquete ha sido desarrollado centrándose en la posibilididad de crear rápidamente prototipos y comprobar la funcionalidad del modelo de forma experimental. Aquí tenemos las peculiaridades de Keras:
- Permite trabajar igualmente en CPU o en un procesador gráfico.
- Es una API amistosa que permite hacer fácilmente prototipos de modelos de aprendizaje profundo.
- Incorpora soporte para redes convolucionales (para visión de computadoras), redes recurrentes (para procesar secuencias) y cualquier combinación de las mismas.
- Da soporte a arquitecturas de red aleatorias: modelos con varias entradas o varias salidas, uso conjunto de capas, uso conjunto de modelos, etc. Esto significa que Keras es adecuado para la construcción, en esencia, de cualquier modelo de aprendizaje profundo, desde una red de memoria hasta la máquina neuronal de Turing.
- Es capaz de trabajar por encima de varios back-end, incluyendo TensorFlow, CNTK o Theano.
Keras es una API pensada para la gente, y no para máquinas. El paquete reduce la carga cognitiva: ofrece APIs sencillas y consistentes, minimiza el número de acciones por parte del usuario y ofrece una retroalimentación efectiva sobre los errores del usuario. Todo ello hace Keras sencillo de estudiar y simple de usar. Pero esto no se relaciona con una reducción de la flexibilidad: puesto que Keras se integra con lenguajes de bajo nivel de aprendizaje profundo (en particular, TensorFlow), permite implementar todo lo que podríamos crear en un lenguaje básico.
Podemos desarrollar el modelo Keras usando varios módulos de aprendizaje profundo. Cualquier modelo de Keras que use solo capas incorporadas, puede trasladarse sin cambios por todos estos back-end: usted puede entrenar el modelo con un back-end y cargarlo en otro (por ejemplo, para el despliegue). Los bak-ends disponibles incluyen:
- TensorFlow backend (from Google)
- CNTK backend (from Microsoft)
- Theano backend
Podemos entrenar el modelo Keras en varias plataformas de hardware, no solo CPU:
- NVIDIA GPUs
- Google TPUs, via the TensorFlow backend and Google Cloud
- OpenCL-enabled GPUs, such as those from AMD, via the PlaidML Keras backend
Instalación de keras y tensorflow backend
Keras y TensorFlow se pueden configurar para que funcionen en CPU o procesadores gráficos. La versión de CPU es mucho más sencilla en cuanto a la instalación y el ajuste, por eso es la mejor elección para comenzar a trabajar con el paquete. Aquí tenemos el manual de las versiones CPU y GPU del sitio web de TensorFlow:
- TensorFlow solo de CPU. Le recomendamos que instale primero esta versión, especialmente si su sistema no tiene un procesador gráfico NVIDIA®.
- TensorFlow con soporte de GPU. Normalmente los programas TensorFlow funcionan en GPU más rápido que en el procesador. Por eso, si su sistema tiene un procesador gráfico NVIDIA® que cumpla todas las condiciones preliminares, y usted necesita iniciar aplicaciones de alto rendimiento, deberá al final instalar esta versión.
El único método de instalación soportado por Windows es "conda". Esto significa que antes de instalar Keras, usted deberá instalar Anaconda 3.x(Phyton 3.5.x/3.6.x) para Windows. Nosotros hemos instalado Anaconda3(Python3.6).
Primero instalamos el paquete keras de CRAN:
install.packages("keras")
La interfaz Keras R usa por defecto TensorFlow. Para instalar tanto la biblioteca básica Keras, como el back-end TensorFlow, use la función install_keras ():
# default installation library(keras) install_keras()
Así, se instalarán las versiones de CPU de Keras y TensorFlow. Si usted necesita una instalación individual, por ejemplo, con un procesador gráfico NVIDIA, analice la documentación. Para instalar TensorFlow de una versión determinada, o que use GPU, hay que ejecutar:
# install with GPU version of TensorFlow # (NOTE: only do this if you have an NVIDIA GPU + CUDA!) install_keras(tensorflow = "gpu") # install a specific version of TensorFlow install_keras(tensorflow = "1.5") install_keras(tensorflow = "1.5-gpu")
Para más información, mire aquí.
Para realizar experimentos con TensorFlow, se ha pensado el paquete de soporte tfruns. Se trata de un conjunto de herramienas para gestionar el aprendizaje y los experimentos de TensorFlow de R.
- Monitoree los hiperparámetros, las métricas, los datos de entrada y el código fuente de cada ciclo de entrenamiento.
- Compare los hiperparámetros y las métricas entre pasadas, para así encontrar el modelo más efectivo.
- Cree automáticamente informes para visualizar pasadas de entrenamiento individuales o para comparar pasadas.
- No es necesario introducir ningún cambio en el código fuente (los datos del inicio se registran automáticamente para todos los modelos Keras y tfestimators).
TensorBoard ofrece la mejor calidad de visualización del proceso y los mejores resultados de entrenamiento de DNN.
Los expertos en aprendizaje profundo tienen la posibilidad de trabajar directamente con la biblioteca de bajo nivel TensorFlow con la ayuda del paquete tensorflow.
Todos estos paquetes se basan en uno principal: reticulate, que supone una interfaz R para módulos, funciones y clases Python. Al llamar en Python, los tipos de datos R se transforman automáticamente en sus equivalentes de Python. Los valores retornados de Python se transforman de nuevo en los tipos R.
Todos estos paquetes están perfectamente documentados e ilustrados con multitud de ejemplos, y se desarrollan constantemente. Gracias a ello, podemos usar en los expertos e indicadores del terminal los modelos más avanzados de aprendizaje profundo (DNN, RNN, CNN, LSTM, VAE и др), aprendizaje con refuerzo (RL) y muchos otros desarrollos de Python. La única limitación viene marcada por los valores y la experiencia del tráder.
Destacaremos otros dos paquetes interesantes: kerasR y kerasformula. Del primero hay pruebas que confirman la velocidad de su funcionamiento, mayor que la del "tensorflow-1.5"original. El segundo supone una variante simplificada del modelo usando una fórmula.
El objeto de este artículo es solo mostrar ejemplos para comenzar de forma sencilla en un nuevo campo. Entre nuestras tareas no se incluye abarcar la diversidad de oportunidades y obtener índices altos de calidad del modelo.
Antes de comenzar con los experimentos, hay que comprobar si tenemos instalado Python y si R interactúa con él.
> library(reticulate)
> py_config()
python: K:\Anaconda3\envs\r-tensorflow\python.exe
libpython: K:/Anaconda3/envs/r-tensorflow/python36.dll
pythonhome: K:\ANACON~1\envs\R-TENS~1
version: 3.6.5 | packaged by conda-forge | (default, Apr 6 2018, 16:13:55)
[MSC v.1900 64 bit (AMD64)]
Architecture: 64bit
numpy: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\numpy
numpy_version: 1.14.2
tensorflow: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow
python versions found:
K:\Anaconda3\envs\r-tensorflow\python.exe
K:\ANACON~1\python.exe
K:\Anaconda3\python.exe
Veamos qué versión de tensorflow se usa:
> library(tensorflow) > tf_config() TensorFlow v1.5.1 (K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow) Python v3.6 (K:\Anaconda3\envs\r-tensorflow\python.exe)
Todo está listo para continuar los experimentos.
4. Combinador de salidas del conjunto bagging — red neuronal
Vamos a realizar dos experimentos. En primer lugar, en vez de promediar las mejores salidas del conjunto, aplicaremos la función softmax. En segundo lugar, sustituiremos la poda y la promediación por una red neuronal, suministrando a su entrada las 500 salidas del conjunto. El esquema estructural de los experimentos se muestra en la figura de abajo.
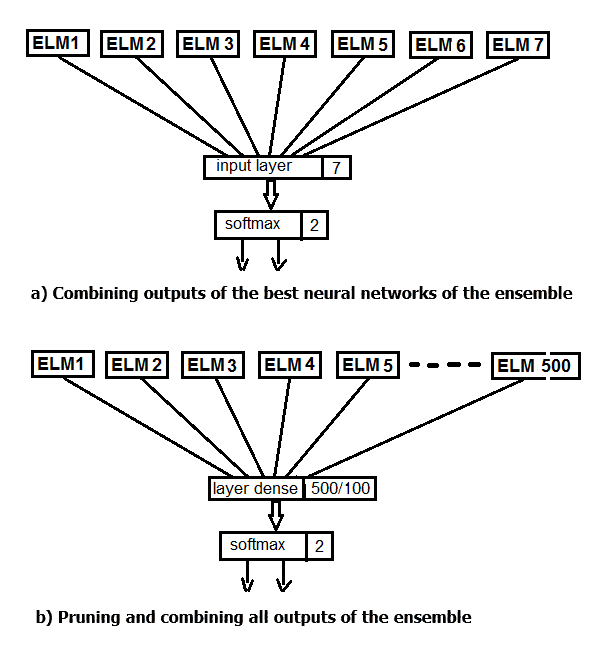
Fig.2. Sustitución de la promediación de las salidas del conjunto por una red neuronal
La estructura básica de los datos de Keras es un modelo, un método para organizar las capas. El tipo más sencillo es un modelo secuencial (Sequential model) que representa un grupo lineal de capas.
Primero creamos un sencillo modelo secuencial, y luego comenzamos a añadir capas con la ayuda del operador pipe (%>%). Para el primer experimento, crearemos una red neuronal que conste solo de una capa de entrada y otra de salida. A la entrada suministraremos las salidas del conjunto general después de la poda, obtenidas en el conjunto de prueba. Para la validación usaremos el 20% del conjunto de entrenamiento. La creación, entrenamiento y simulación de redes neuronales en este paquete son muy simples.
Establecemos los parámetros constantes del modelo, definimos el conjunto de entrenamiento y los conjuntos de prueba para la DNN.
#===========Keras=========================================== library(keras) num_classes <- 2L batch_size <- 32L epochs <- 300L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical()
Creamos el modelo. El código del script se muestra más abajo. Definimos y compilamos el modelo con la estructura NN(7, 2) — 7 neuronas en la entrada y 2 en la salida. Optimizador — función "rmsprop ", función de pérdida — 'binary'_crossentropy', métricas de los resultados de simulación — "accuracy".
##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_dense(units = num_classes, input_shape = dim(x_train)[2]) %>% layer_activation(activation = 'softmax') %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(), metrics = 'accuracy' )
Entrenamos y simulamos el modelo (el script se muestra más abajo). Guardamos la historia del entrenamiento. Indicamos de forma adicional:
- no hay que mostrar en el terminal el resultado de cada iteración;
- no hay que mostrar en Viever/Rstudio los gráficos en tiempo real;
- hay que mezclar los datos de entrada después de cada época de entrenamiento.
Para la validación usamos un 20% del conjunto de entrenamiento.
## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = FALSE, shuffle = TRUE, validation_split = 0.2) -> history # Output metrics score <- model %>% evaluate(x_test, y_test, verbose = 0) cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.518 cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.754 #--------------- score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.55 cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.737
Los datos cuantitativos no son malos, son prácticamente iguales a los resultados de la promediación de nuestro conjunto. Echemos un vistazo a la historia del entrenamiento y la simulación de este modelo:
#--plot------------------------
plot(history)
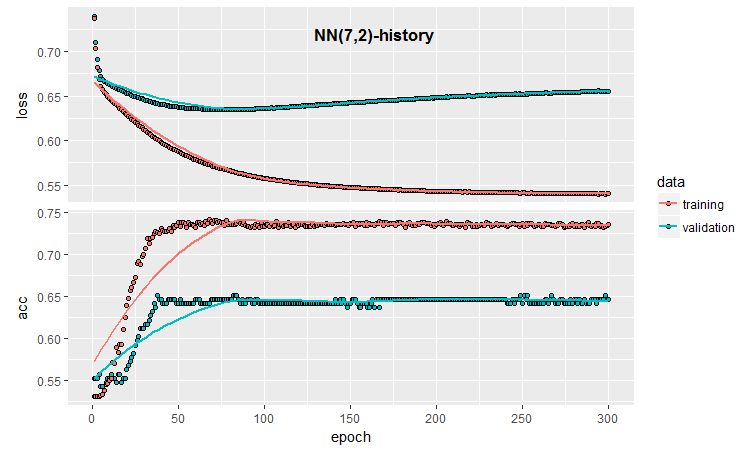
Fig.3. Historia del entrenamiento del modelo (7, 2)
Podemos ver por el gráfico que aproximadamente tras 30 épocas, el modelo ha sido claramente sobreentrenado, y después de 50, Accuracy alcanza una meseta.
Recordemos una vez más que el proceso de inicialización de la red neuronal no es casual. Es decir, con cada nueva creación, entrenamiento y simulación del modelo, obtendremos diferentes resultados.
Incluso con esta mínima configuración de la red neuronal tenemos muchas posibilidades de influir en la calidad de la clasificación y el sobreentrenamiento. Vamos a enumerar brevemente algunas de ellas: la detención temprana del entrenamiento ( earlystopping ); el método de inicialización de las neuronas; la regularización de la función de activación, etc. De estas, solo comprobaremos la detención temprana del entrenamiento, la adición de ruido a los datos de entrada y la regularización de la función de activación; además, mostraremos una imagen gráfica más detallada de los resultados del entrenamiento. Para ello, usaremos la posibilidad que ofrece keras de realizar la llamada inversa durante el entrenamiento (callback).
callback_early_stopping(monitor = "val_loss", min_delta = 0, patience = 0, verbose = 0, mode = c("auto", "min", "max")) callback_tensorboard(log_dir = NULL, histogram_freq = 0, batch_size = 32, write_graph = TRUE, write_grads = FALSE, write_images = FALSE, embeddings_freq = 0, embeddings_layer_names = NULL, embeddings_metadata = NULL)
Definimos la función de llamada inversa.
early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_1") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE)
En la primera hemos indicado que se debe monitorear el valor "accuracy". Si su valor llega a ser menor que min_delta durante un número patiente de épocas, tendremos que detener el entrenamiento. En la segunda, hemos indicado la ruta al directorio donde debemos guardar los resultados del entrenamiento para su posterior reproducción, así como la ubicación exacta del guardado. Vamos a escribir el script completo usando estas funciones y a echarle un vistazo.
##=====Variant earlystopping================================= #--prepare data-------------------------- library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() ##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, callbacks = list(early_stopping, tensboard)) -> history
Métricas de los dos conjuntos de prueba, e historia de entrenamiento con salida temprana.
# Output metrics > score <- model %>% evaluate(x_test, y_test, verbose = 0) > cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.539 > cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.756 > #--------------- > score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) > cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.571 > cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.713
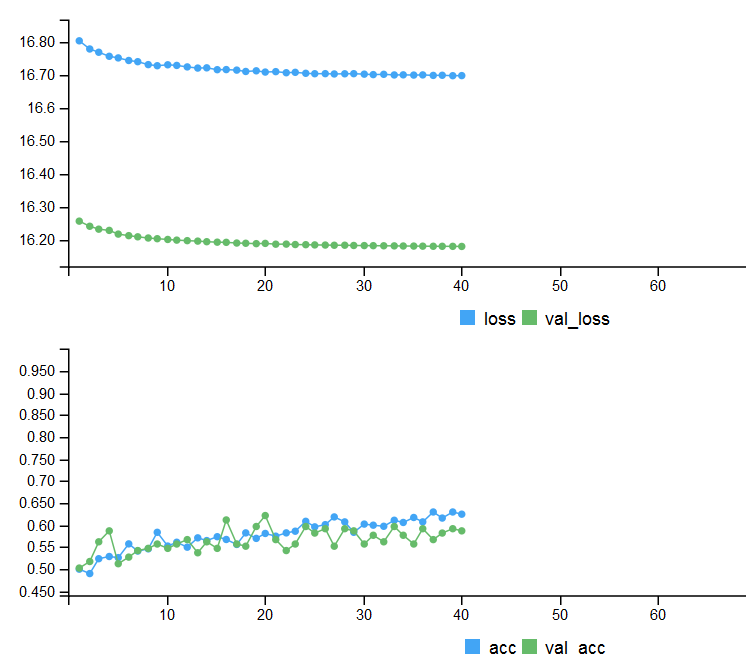
Fig. 4. Historia de entrenamiento del modelo con detención temprana
Para mostrar información gráfica detallada sobre el proceso de entrenamiento de la red neuronal, usamos las capacidades de tensorboard:
> tensorboard(log_dir = log_dir) TensorBoard 1.7.0 at http://127.0.0.1:7451 (Press CTRL+C to quit) Started TensorBoard at http://127.0.0.1:7451
En el navegador se abrirá una página donde podremos analizar todos los detalles internos de la red neuronal. Aquí tenemos ejemplos de las capturas de pantalla:
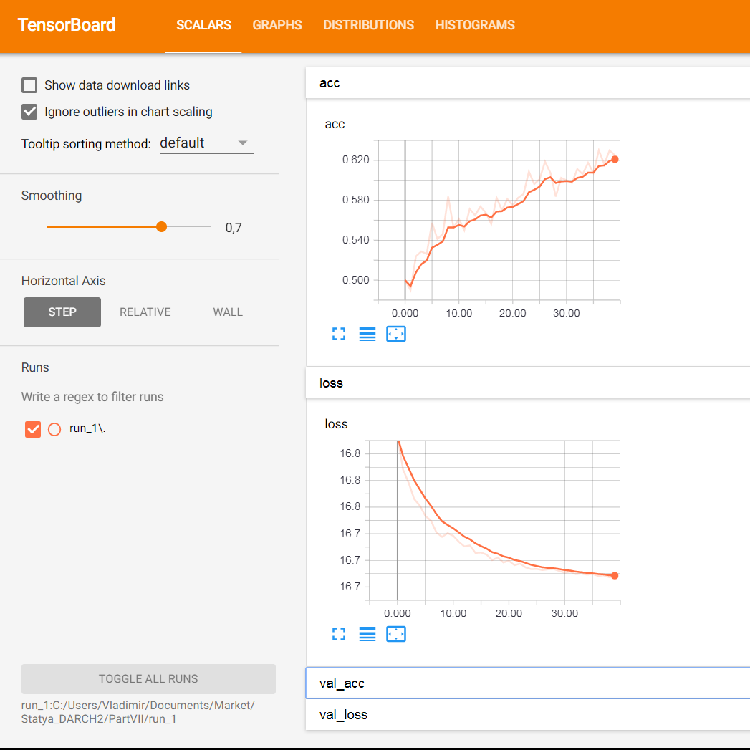
Fig. 5. Gráficos de pérdida y precisión al entrenar el conjunto de entrenamiento, datos de validación de val_acc y val_loss
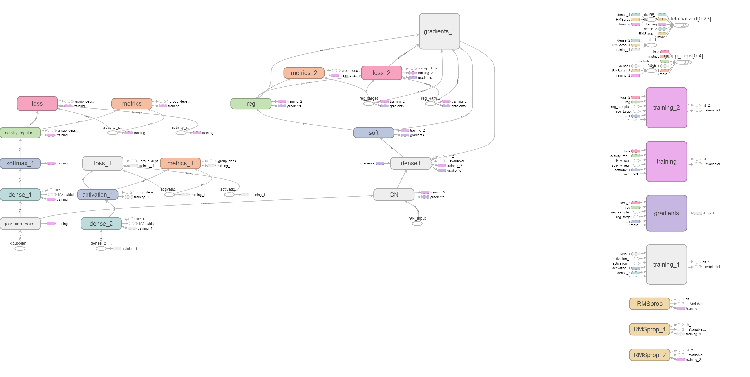
Fig. 6. Grafo de cálculo de la red neuronal
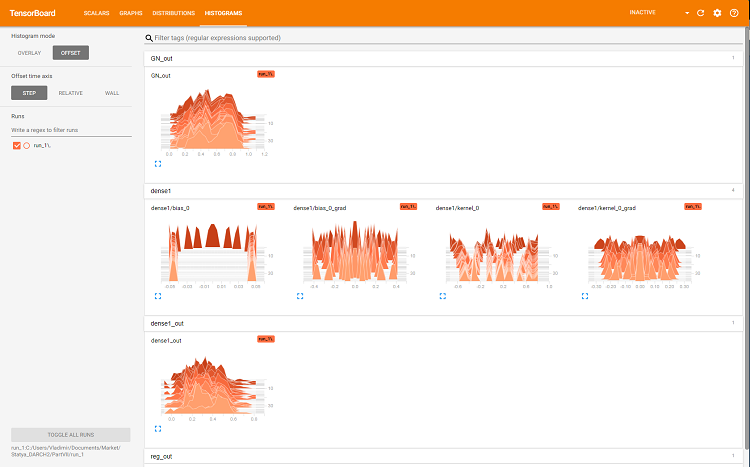
Fig. 7. Histograma de la capa "dense"
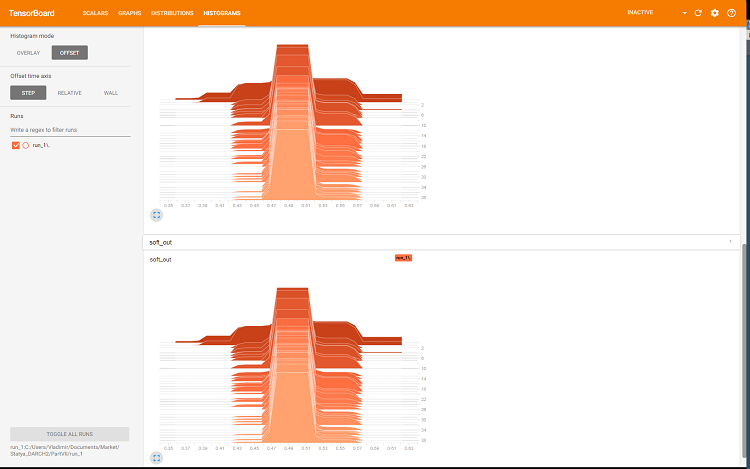
Fig. 8. Histograma de las salidas de sotmax y regularization
Estos gráficos son una potente herramienta para depurar los parámetros de la red neuronal, pero su análisis queda fuera de la temática de este artículo.
Con cada nuevo inicio de tensorboard debemos cambiar la ruta de guardado a log_dir o eliminar la usada anteriormente.
Veamos cómo cambia la calidad de la clasificación con los mismos parámetros, pero usando el conjunto de prueba para la validación. El script se muestra más abajo y se encuentra en el archivo:
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_2") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE) ##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_data = list(x_test, y_test), callbacks = list(early_stopping, tensboard)) -> history
Echemos un vistazo a las métricas en el segundo conjunto de prueba:
#--model--test1------------------------------------------------- predict(model, x_test1) -> Ypr.test1 Ypr.test1 %>% max.col()-1 -> y_pr_test1 #Ypr.test1 %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test1 evalq(res_mod_test1 <- Eval(Ytest2, y_pr_test1), env) > env$res_mod_test1 $metrics Accuracy Precision Recall F1 0 0.713 0.704 0.826 0.760 1 0.713 0.730 0.575 0.644 $confMatr Confusion Matrix and Statistics predicted actual 0 1 0 114 24 1 48 65 Accuracy : 0.7131 95% CI : (0.6529, 0.7683) No Information Rate : 0.6454 P-Value [Acc > NIR] : 0.013728 Kappa : 0.4092 Mcnemar's Test P-Value : 0.006717 Sensitivity : 0.7037 Specificity : 0.7303 Pos Pred Value : 0.8261 Neg Pred Value : 0.5752 Prevalence : 0.6454 Detection Rate : 0.4542 Detection Prevalence : 0.5498 Balanced Accuracy : 0.7170 'Positive' Class : 0
Prácticamente no se diferencian de la primera opción. Podemos comparar visualmente las dos variantes con la ayuda de tensorboard.
#-----plot------------------ tensorboard(log_dir = c(paste0(getwd(),"/run_1"), paste0(getwd(),"/run_2")))
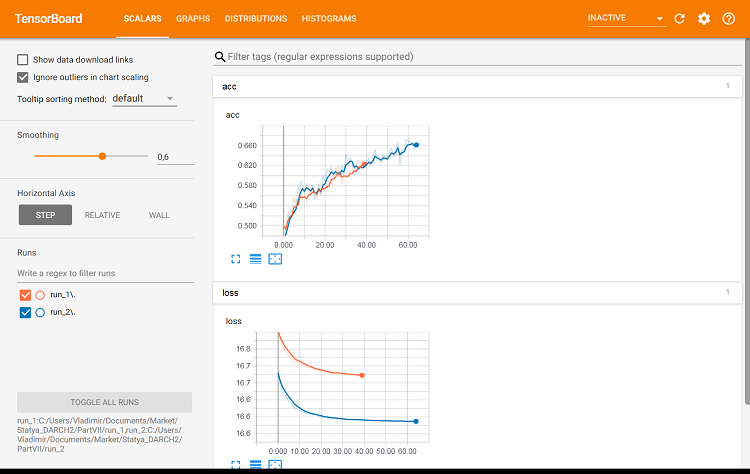
Fig. 9. Métricas en el conjunto de entrenamiento
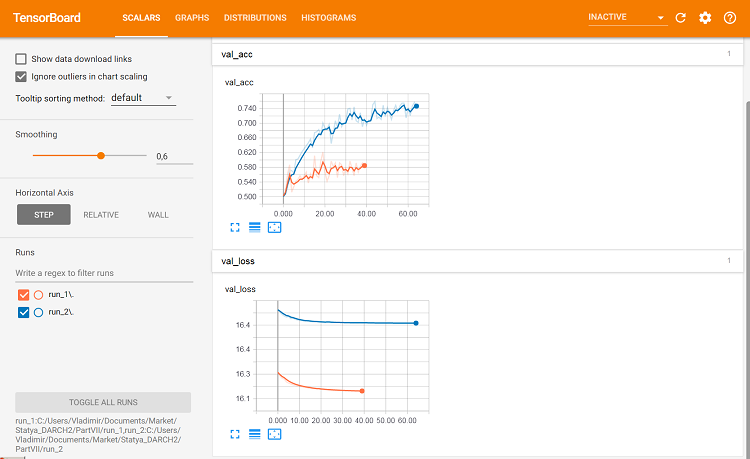
Fig. 10. Métricas en el conjunto de validación
Aquí ya se ven ciertas diferencias.
Vamos a realiza un último experimento. A la entrada de una red neuronal multicapa suministramos las 500 salidas del conjunto. De esta forma, la red neuronal ejecutará la poda y combinación al mismo tiempo. El script se muestra más abajo y también se encuentra en el archivo modelDNN_500.R.
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.0001 epochs <- 100L #--------- x_train <- env$res$InputTrain y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1 y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto")
Hemos cargado las bibliotecas y constantes, hemos definido los conjuntos para el entrenamiento y la simulación, y también la función de detención temprana.
##----modelDNN--keras------------------------- # define model modDNN <- keras_model_sequential() # add layers and compile modDNN %>% layer_gaussian_noise(stddev = 0.001, input_shape = dim(x_train)[2], name = "GN") %>% layer_batch_normalization() %>% layer_dense(units = 100, activation = "elu", name = "dense1") %>% layer_dropout(rate = 0.5, name = "dp1") %>% layer_batch_normalization() %>% layer_dense(units = 50, activation = "elu", name = "dense2") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.5, name = "dp2") %>% layer_dense(units = 10, activation = "elu", name = "dense3") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.2, name = "dp3") %>% layer_dense(units = num_classes, activation = "softmax", name = "soft") %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.0001), metrics = 'accuracy' )
De esta forma, hemos determinado la red neuronal, indicando la secuencia y los parámetros de las capas. Asimismo, hemos indicado al compilador qué función de pérdida, qué optimizador y qué métrica usar al entrenar el modelo. Ahora entrenamos el modelo:
## Training & Evaluation --------------------------- # Fit model to data modDNN %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, #validation_data = list(x_test, y_test), callbacks = list(early_stopping)) -> history
Durante el entrenamiento, mostraremos las métricas y mezclaremos los datos de entrada; para la validación, usaremos el 20% del conjunto de entrenamiento y utilizaremos una detención temprana. Simulamos el modelo con el conjunto de prueba:
#--model--test------------------------- predict(modDNN, x_test) -> Ypr.test Ypr.test %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test evalq(res_mod_test <- Eval(Ytest1, y_pr_test), env)
Vemos el resultado en cifras, a la par de la promediación del conjunto general:
> env$res_mod_test $metrics Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 $confMatr Confusion Matrix and Statistics predicted actual 0 1 0 184 46 1 78 193 Accuracy : 0.7525 95% CI : (0.7123, 0.7897) No Information Rate : 0.523 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5068 Mcnemar's Test P-Value : 0.005371 Sensitivity : 0.7023 Specificity : 0.8075 Pos Pred Value : 0.8000 Neg Pred Value : 0.7122 Prevalence : 0.5230 Detection Rate : 0.3673 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7549 'Positive' Class : 0
Construimos la historia del entrenamiento:
plot(history)
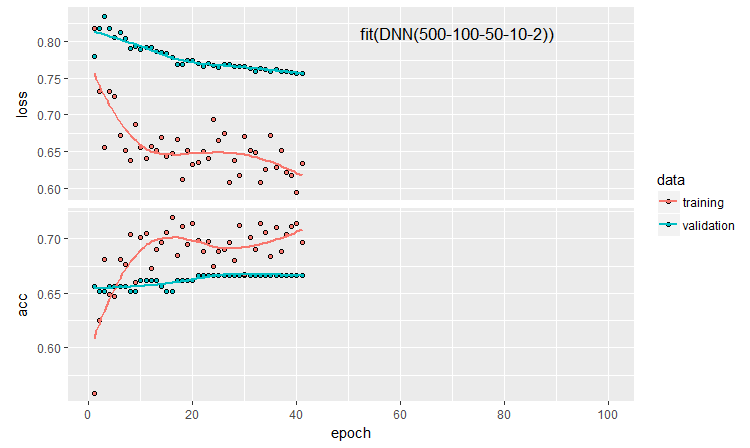
Fig. 11. Historia del entrenamiento de la red neuronal DNN500
Para mejorar la calidad de la clasificación, podemos modificar multitud de hiperparámetros: el método de inicialización de las neuronas, la regularización de la activación de las neuronas y sus pesos, etc. Los resultados obtenidos con parámetros casi intuitivos muestran una calidad prometedora, pero sus limitaciones dejan un mal sabor de boca. Sin optimización, no hemos logrado que Accuracy supere 0.82. La conclusión es que necesitamos optimizar los hiperparámetros de la red neuronal. En las anteriores partes, hemos experimentado con la optimización bayesiana. Creemos que también es aplicable aquí, pero se trata de un tema aparte, y bastante complejo.
La definición secuencial del modelo da la posibilidad de construir y ajustar modelos de distinta complejidad y profundidad. Pero con la ayuda de la API funcional keras, podemos crear estructuras más complejas de redes neuronales: por ejemplo, con multitud de entradas y salidas. Hablaremos sobre ello en el próximo artículo.
5. Análisis del resultado de los experimentos
Bien, ya tenemos los resultados del entrenamiento y la simulación de cinco modelos:
- conjunto con promediación (EnsAver);
- conjunto con voto por mayoría (EnsVot);
- modelo de regresión logística varb;
- red neuronal DNN(7,2);
- red neuronal DNN500.
Reunimos en un recuadro los índices de calidad de todos estos modelos, descomponemos el error de clasificación por componentes y valoramos su contribución al error general. Usamos la función randomUniformForest::biasVarCov() (Bias-Variance-Covariance Decomposition). Podrá leer más información sobre esta función en la descripción del paquete. A continuación, mostramos el código de descomposición del error de clasificación de los conjuntos EnsAver y EnsVot. Para el resto de modelos, los scripts son análogos.
#---bias--test------------------------------- import_fun(randomUniformForest, biasVarCov, BiasVar) evalq({ target = Ytest1 biasAver <- BiasVar(predictions = ScoreAver$clAver, target = target, regression = FALSE, idx = 1:length(target)) biasVot <- BiasVar(predictions = ScoreVot$ClVot, target = target, regression = FALSE, idx = 1:length(target)) }, env) ----------------------------- Noise: 0.2488224 Squared bias: 0.002107561 Variance of estimator: 0.250475 Covariance of estimator and target: 0.1257046 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2499958 --------------------- Noise: 0.2488224 Squared bias: 0.004079665 Variance of estimator: 0.2499721 Covariance of estimator and target: 0.1274411 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2479918
Mostramos de forma compacta:
> env$biasAver $predError [1] 0.2499958 $squaredBias [1] 0.002107561 $predictionsVar [1] 0.250475 $predictionsTargetCov [1] 0.1257046
| 95%CI Acc | Precision | Recall | F1 | PredErr | sqBias | predVar | predTargCov | |
|---|---|---|---|---|---|---|---|---|
| EnsAver | 0.7102, 0.7880 (0.7500) | 0.708 0.794 |
0.778 0.727 |
0.741 0.759 |
0.2499 | 0.0021 | 0.2505 | 0.1257 |
| EnsVot | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.248 | 0.0041 | 0.25 | 0.1274 |
| varb | 0.7416, 0.8159 (0.7804) | 0.790 0.808 |
0.783 0.779 |
0.766 0.793 |
0.2199 | 0.000398 | 0.25 | 0.13964 |
| DNN(7, 2) | 0.7165, 0.7935 (0.7565) | 0.765 0.751 |
0.678 0.823 |
0.719 0.785 |
0.2460 | 0.000195 | 0.2498 | 0.1264 |
| DNN500 | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.2779 | 0.01294 | 0.2452 | 0.1145 |
Qué vemos en el recuadro unificado:
- El mejor dato de Accuracy entre los modelos básicos pertenece a varb, que combina las 500 salidas del conjunto. Entre los combinadores entrenables, el mejor valor de este índice lo muestra el modelo — DNN(7,2), que combina las 7 salidas del conjunto.
- El menor error de prueba para la muestra de prueba (PredErr), pertenece a varb y DNN(7,2).
- El cuadrado del sesgo (sqBias ) es en esos mismos modelos claremente mejor que en el resto.
- La varianza del error (PredVar) es prácticamente igual en todos los modelos. Esto parece extraño: el conjunto debería dar una reducción de la varianza, y nosotros hemos obtenido un sesgo bajo.
- La mejor covariación entre la valoración y la respuesta (predictionTargetCov ), la tiene varb. Como magnitud independiente no indica nada, solo se usa para comparar modelos.
- El modelo DNN500 tiene los peores índices. Conclusión: la complicación de los modelos para las tareas sencillas no mejora los resultados.
Conclusión
El conjunto de clasificadores ELM de redes neuronales con promediación o el voto por mayoría muestra una buena calidad de clasificación a grandes velocidades de cálculo. Es posible mejorar la calidad optimizando el umbral de conversión de las salidas de continua a nominal y calibrando las salidas antes de la promediación. No se ha detectado una disminución considerable en la varianza del error.
La sustitución de la promediación de las salidas del conjunto por la función softmax de una red neuronal simple dismunye considerablemente el sesgo sin que se dé una disminución notable de la varianza. El uso de modelos más complejos de red neuronal para sustitur la poda y promediación no ha demostrado buenos resultados.
El modelo de regresión lógica obtenido con ayuda de los procesos bayesianos de selección de predictores (paquete varbvs) muestra muy buenos resultados. Podemos usar las mejores salidas definidas por este paquete para la red neuronal.
El 24% del ruido, que parece inamovible comenzando desde el pre-procesado, de nuevo sugiere que en alguna etapa hay que etiquetar nuevamente los ejemplos de ruido en una clase aparte.
Hay que usar las características de keras y trabajar con las secuencias (series temporales), que precisamente son nuestros datos. Esto puede mejorar los índices de calidad de la clasificación.
Anexos
En GitHub/PartVII se encuentran los siguientes archivos:
- Importar.R — funciones de importación de paquetes.
- Library.R — bibliotecas necesarias.
- FunPrepareData_VII.R — funciones de preparación de los datos fuente.
- FunStacking.R — funciones de creación y simulación del conjunto.
- Prepare.R — funciones y scripts de preparación de los datos fuente para los combinadores entrenables.
- Varb.R — scripts del modelo básico varb.
- model_DNN7_2.R — scripts de la red neuronal DNN(7-2).
- model_DNN_500.R — scrips de la red neuronal DNN500.
- SessionInfo_VII.txt — lista de paquetes usados en los scripts del artículo.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/4228
 Cómo crear una Tarea Técnica al encargar un robot
Cómo crear una Tarea Técnica al encargar un robot
 Monitoreo de la cuenta comercial: una herramienta imprescindible para el tráder
Monitoreo de la cuenta comercial: una herramienta imprescindible para el tráder
 Constructor gráfico de estrategias. Creando robots comerciales sin programación
Constructor gráfico de estrategias. Creando robots comerciales sin programación
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso