
Neuroredes profundas (Parte VI). Conjunto de clasificadores de redes neuronales: bagging
Contenido
- Introducción
- Conjuntos de clasificadores de redes neuronales
- bagging
- Formación de los conjuntos iniciales de datos
- Ordenación de los predictores según la importancia de la información
- Creación, entrenamiento y prueba del conjunto de clasificadores
- Combinación de las salidas individuales de los clasificadores (averaging/voting)
- Poda del conjunto y sus métodos
- Optimización de los hiperparámetros de los miembros del conjunto. Peculiaridades y métodos
- Entrenamiento y prueba de un conjunto con hiperparámetros óptimos
- Conclusión
- Anexos
Introducción
En el artículo anterior de esta serie, optimizamos los hiperparámetros del modelo DNN, lo entrenamos en diversas variantes y lo probamos. La calidad del modelo obtenido resultó bastante alta.
También analizamos qué opciones tenemos para mejorar la calidad de la clasificación. Uno de ellas es usar un conjunto de redes neuronales. En este artículo, vamos a analizar precisamente esta variante de refuerzo.
1 Conjuntos de clasificadores de redes neuronales
Las investigaciones muestran que los conjuntos de clasificadores son normalmente más precisos que los clasificadores individuales. Uno de estos conjuntos se muestra en la fig.1a. En este se implementan varios clasificadores, cada uno de los cuales toma una decisión sobre el objeto presentado en la entrada. A continuación, estas soluciones individuales se agregan a un combinador. En la salida, el conjunto genera una etiqueta de clase para el objeto.
Podemos comprender de forma intuitiva que es imposible dar una definición estricta de un conjunto de clasificadores. Esta ausencia general de determinación se ilustra en la fig.1 b-d. En esencia, cualquier conjunto es en sí mismo un clasificador (fig. 1b). Los clasificadores básicos que lo componen extraerán de la secuencia de datos funciones complejas de regularidades (a menudo implícitas), y el combinador se convertirá en un simple clasificador que agrega estas funciones.
Por otra parte, nada nos impide llamar conjunto al clasificador de red neuronal estándar normal (figura 1c). Las neuronas en su penúltima capa se pueden considerar como clasificadores separados. Sus decisiones deben ser "descifradas" en el combinador, cuya función desempeña la capa superior.
Y, finalmente, podemos considerar las funciones como clasificadores primitivos, y el clasificador como su combinador complejo (figura 1d)
Vamos a combinar clasificadores entrenados simples para obtener una solución de clasificación precisa. Pero, ¿nos estamos moviendo en la dirección correcta?
En el artículo crítico «Combinando varios clasificadores: lecciones y próximos pasos", publicado en 2002, Ting Ho escribe:
"En lugar de buscar el mejor conjunto de funciones y un clasificador, ahora estamos buscando el mejor conjunto de clasificadores y luego el mejor método para combinarlos. Podemos suponer que encontraremos muy pronto el mejor conjunto de métodos combinacionales, y luego la mejor manera de usarlos todos. Si no analizamos los problemas fundamentales que surgen en relación con este desafío, nos encontraremos inevitablemente ante una repetición interminable, arrastrando esquemas y teorías cada vez más complejas de combinar y perdiendo gradualmente de vista el problema original de "
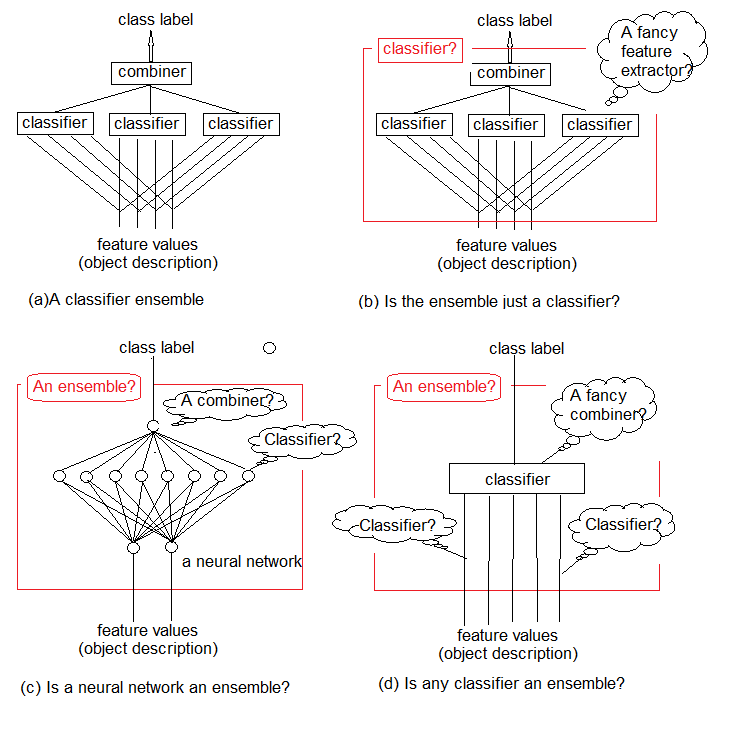
Fig. 1. ¿Qué es un conjunto de clasificadores?
La lección consiste en que debemos encontrar la mejor manera de utilizar las herramientas y los métodos existentes antes de crear nuevos proyectos complejos.
Ya sabemos que los clasificadores de redes neuronales son "aproximadores universales". Esto significa que cualquier límite de clasificación, sin importar su complejidad, puede ser aproximado por una red neuronal finita con cualquier precisión necesaria. Sin embargo, este conocimiento no nos ofrece una forma de crear o entrenar dicha red. La idea de combinar clasificadores constituye un intento de resolver el problema creando una red de bloques de construcción gestionables.
Los métodos de composición de un conjunto suponen meta-algoritmos que combinan varios métodos de aprendizaje automático en un modelo de pronóstico para:
- reducir la varianza (variance) — bagging;
- reducir el sesgo (bias) — boosting;
- mejorar los pronósticos — stacking.
Estos métodos se pueden dividir en dos grupos:
- los métodos paralelos de construcción de conjuntos, en los que modelos básicos se generan paralelamente (por ejemplo, un bosque aleatorio). El sentido reside en utilizar la independenca entre modelos básicos, y reducir el error con el método de promediación. Por lo tanto, el requisito básico para los modelos será una baja correlación mutua y una variedad amplia.
- los métodos de conjunto secuencial en los que los modelos base se generan secuencialmente (por ejemplo, AdaBoost, XGBoost). La idea principal aquí es usar la dependencia entre los modelos base. Podemos mejorar su calidad general asignando pesos más altos a los ejemplos que previamente se clasificaron incorrectamente.
La mayoría de los métodos de conjunto para crear modelos de base homogéneos utilizan un único algoritmo básico de aprendizaje. Esto lleva a que los conjuntos sean homogéneos. También hay métodos que usan modelos heterogéneos (modelos de diferentes tipos). Como resultado, se forman conjuntos heterogéneos. Para garantizar que los conjuntos sean más precisos que cualquiera de sus miembros individuales, los modelos básicos deben ser cuanto más diversos, mejor. En otras palabras, cuanto más información provenga de los clasificadores básicos, mayor será la precisión del conjunto.
En la fig. 2 se muestran los 4 niveles de creación de un conjunto de clasificadores. En cada uno de ellos hay preguntas, cuyas respuestas analizaremos ahora.

Fig.2. Los cuatro niveles de creación de un conjunto de clasificadores
Vamos a hablar de esto con más detalle.
1 Combinador
Algunos métodos de conjunto no definen un combinador. Pero para los métodos que hacen esto, hay tres tipos de combinadores.
- No-entrenable (Nontrainable). Un ejemplo de un método así es el "voto por mayoría" simple (majority voting).
- Entrenable (Trainable). Este grupo incluye el "voto por mayoría ponderada" (weighted majority voting) y Naive Bayes, así como el enfoque “classifier selection”, el que un único clasificador del conjunto toma una decisión sobre este objeto.
- Meta-clasificador (Meta classifier). Las salidas de los clasificadores base se consideran entradas para el nuevo clasificador de aprendizaje, que se convierte en un combinador. Este enfoque se llama "generalización compleja", "generalización a través del entrenamiento" o simplemente apilamiento (stacking). Crear un conjunto de entrenamiento para un meta-clasificador es uno de los principales problemas de este unificador.
2. Construyendo un conjunto
¿Debemos entrenar los clasificadores base paralelamente (independientemente) o de manera secuencial? Un ejemplo de entrenamiento secuencial es AdaBoost, donde el conjunto de entrenamiento de cada clasificador agregado depende del conjunto creado antes.
3. Variedad
¿Cómo generar diferencias en el conjunto? Se ofrecen las siguientes opciones.
- Manipular los parámetros de aprendizaje. Use diferentes enfoques y parámetros al entrenar los clasificadores básicos individuales. Por ejemplo, puede iniciar los pesos de las neuronas de las capas ocultas de la red neuronal de cada clasificador base mediante diferentes variables aleatorias. O bien puede configurar los hiperparámetros aleatoriamente.
- Manipular las muestras: consiste en tomar una muestra de arranque (bootstrap) del conjunto de entrenamiento para cada miembro del conjunto.
- Manipular los predictores: consiste en preparar para cada clasificador básico su propio conjunto de predictores, determinados aleatoriamente. Esta es la llamada división vertical del conjunto de entrenamiento.
4. Tamaño del conjunto
¿Cómo definir el número de clasificadores en un conjunto? ¿Se crea el conjunto mediante el entrenamiento simultáneo del número necesario de clasificadores, o iterativamente, usando la adición/eliminación de clasificadores? Posibles opciones:
- La cantidad se reserva por adelantado
- La cantidad se establece en el transcurso del entrenamiento
- Tiene lugar una sobreproducción de clasificadores y su elección posterior
5. Universalidad (relativa al clasificador básico)
Algunos enfoques de conjunto se pueden utilizar con cualquier modelo clasificador, mientras que otros se vinculan a un determinado tipo de clasificador. Un ejemplo de un conjunto "clasificador-específico", es el bosque aleatorio (Random Forest). Su clasificador básico es el árbol de decisión. Entonces, hay dos variantes de enfoque:
- Solo se puede utilizar un modelo determinado de clasificador base;
- Se puede usar cualquier modelo de clasificador básico.
A la hora de entrenar y optimizar los parámetros del conjunto de clasificadores, debemos distinguir entre la optimización de la solución y la optimización de la cobertura.
- La optimización de la toma de decisiones se refiere a la elección de un combinador para un conjunto fijo de clasificadores básicos (nivel A en la fig. 2).
- La optimización de la cobertura alternativa se refiere a la creación de una variedad de clasificadores básicos con un combinador fijo (niveles B, C y D en la fig. 2).
Esta descomposición del diseño del conjunto reduce la complejidad del problema, por lo que parece razonable.
En los libros "Combining Pattern Classifiers. Methods and Algorithms, Second Edition. Ludmila Kuncheva" y "Ensemble Methods. Foundations and Algorithms", se analizan con todo detalle y gran profundidad los métodos de conjunto. Le recomendamos que le eche un vistazo.
2. Bagging
El nombre del método proviene de la expresión Bootstrap AGGregatING. Los conjuntos de bagging se crean así:
- del conjunto de entrenamiento se extrae la muestra de arranque;
- cada clasificador se entrena con su propia muestra;
- las salidas individuales de los clasificadores separados se combinan en una etiqueta de clase. Si las salidas individuales tienen forma de etiqueta de clase, entonces se usa el voto por mayoría simple. Si el resultado de los clasificadores es una variable continua, se aplica o bien el promedio o bien la transferencia de esta variable a una etiqueta de clase y luego se vota por mayoría simple.
Vamos a volver a la figura 2, en la que analizaremos todos los niveles de creación de un conjunto de clasificadores aplicado al método de bagging.
A: el nivel de agregación
En este nivel, tiene lugar la combinación de los datos obtenidos de los clasificadores, y la agregación de la salida única.
¿Cómo podemos combinar las salidas individuales? Vamos a usarun enfoque que utiliza un combinador no entrenable (promediación, voto por mayoría simple).
B: el nivel de los clasificadores
En el nivel B, se incluye todo el trabajo con clasificadores. Aquí surgen varias preguntas.
- ¿Usamos clasificadores diferentes o idénticos? Con el enfoque de bagging se usan los mismos identificadores.
- ¿Qué clasificador se toma como calsificador básico? Nosotros usaremos ELM (Extreme Learning Machines).
Vamos a detenernos en este punto con más detalle. La elección del clasificador y su justificación es un momento clave del trabajo. Vamos a enumerar los requisitos esenciales de los clasificadores básicos para conseguir un conjunto de calidad.
Primero, el clasificador debe ser simple: no se recomienda aplicar redes neuronales profundas.
Segundo, los clasificadores deben ser diferentes: con diferente inicialización, parámetros de aprendizaje, conjuntos de entrenamiento, etcétera.
Tercero, la velocidad del clasificador es importante: los modelos no deben entrenarse durante horas.
Cuarto, los modelos de clasificación deben ser débiles y dar un resultado de predicción ligeramente mejor del 50%.
Y, quinto y último, la inestabilidad del clasificador es importante, los resultados de la predicción deben tener un rango amplio.
Tenemos un candidato que cumple con todos estos requisitos. Se trata de un tipo especial de red neuronal ELM (máquinas de aprendizaje extremo), propuesto como algoritmos alternativos de aprendizaje en lugar de MLP. Desde un punto de vista formal, constituye una red neuronal plenamente conectada con una capa oculta. Pero la ausencia de procesos iterativos de definición de pesos (aprendizaje) la hace extremadamente rápida. Elige al azar los pesos de las neuronas de la capa oculta una vez durante la inicialización y luego determina de manera analítica su peso de salida, de acuerdo con la función de activación seleccionada. Podrá encontrar una descripción detallada del algoritmo ELM y una descripción general de sus múltiples variedades en el archivo adjunto.
- ¿Cuántos clasificadores necesitamos? Tomaremos 500 con la consecuente poda del conjunto.
- ¿Usamos un entrenamiento de clasificadores en paralelo o secuencial? Usaremos el aprendizaje paralelo, que se ejecuta simultáneamente para todos los clasificadores.
- ¿Qué parámetros de los clasificadores básicos podemos manipular? El número de neuronas ocultas, la función de activación y el tamaño de la muestra del conjunto de entrenamiento. Todos estos parámetros se someten a optimización.
C: el nivel de las funciones de las leyes encontradas
- ¿Usamos todos los predictores o solo subconjuntos individuales para cada clasificador? Todos los clasificadores usan un subconjunto de predictores. Pero el número de predictores puede optimizarse.
- ¿Cómo elegimos/extraemos semejante subconjunto? En nuestro caso, se usan algoritmos especiales.
D: el nivel de los datos de entrada y su manipulación
En este nivel, tiene lugar el suministro de datos de origen a la entrada de la red neuronal para el entrenamiento.
¿Cómo manipular los datos de entrada para garantizar una alta diversidad y alta precisión individual? Usaremos muestras de arranque para cada clasificador de forma individual. El tamaño de la muestra de arranque para todos los miembros del conjunto es el mismo, pero se optimizará.
Para realizar experimientos con los conjuntos ELM, disponemos de dos paquetes en R (elmNN, ELMR) y un paquete en Python (hpelm). Por el momento, vamos a ver las posibilidades del paquete elmNN, en el que se implementa el clásico ELM. El paquete elmNN se ha diseñado para crear, entrenar y poner a prueba con la ayuda del método ELM batch. De esta forma, las muestras de entreamiento y prueba están listas antes del entrenamiento, y los modelos se envían una vez. El paquete es muy sencillo.
El experimento constará de las siguientes etapas.
- Formación de los conjuntos iniciales de datos
- Ordenación de los predictores según la importancia de la información
- Entrenamiento y prueba del conjunto de clasificadores
- Combinación de las salidas individuales de los clasificadores (averaging/voting)
- Poda del conjunto y sus métodos
- Búsqueda de métricas de calidad de la clasificación del conjunto
- Definición de los parámetros óptimos de los miembros del conjunto. Métodos
- Entrenamiento y prueba del conjunto con parámetros óptimos
Formación de los conjuntos iniciales de datos
Para realizar los experimentos, usaremos la última versión de MRO 3.4.3. En ella se implementan varios paquetes nuevos para nosotros.
Iniciamos RStudio, cargamos desde GitHub/Part_I el archivo Cotir.RData con las cotizaciones recibidas del terminal, y el archivo FunPrepareData.R con las funciones de preparación de datos desde GitHub/Part_IV.
Ya hemos determinado anteriormente que un conjunto de datos con las muestras imputadas y los datos normalizados permite obtener mejores resultados cuando se entrena con preentrenamiento. Precisamente vamos a utilizar ese formato. Usted también podrá comprobar las otras opciones de preprocesamiento que hemos analizado con anterioridad.
Al dividir los apartados en pretrain/train/val/test, usamos la primera posibilidad de mejora de la calidad de la clasificación, ya que estamos aumentando el número de ejemplos para el entrenamiento. En el apartado pretrain, aumentamos el número de ejemplos hasta 4000.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Modificando el parámetro start en la función SplitData(), podemos obtener conjuntos desplazados a la derecha en la magnitud start. Esto nos permitirá comprobar la calidad en diferentes partes del rango de precios, y determinar cómo cambia en la historia.
Vamos a crear los conjuntos de datos (pretrain/train/test/test1) para el entrenamiento y la prueba reunidos en la lista X. Transformamos la variable objetivo de factor a nominal (0.1).
#---Data X-------------
evalq({
list(
pretrain = list(
x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1)
),
train = list(
x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1)
),
test = list(
x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1)
),
test1 = list(
x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1)
)
) -> X
}, env)
Ordenación de los predictores según la importancia de la información
Ahora pondremos a prueba la función clusterSim::HINoV.Mod() (vea la descripción detallada en el paquete). Clasifica las variables basándose en la agrupación con diferentes distancias y métodos. Vamos a usar los parámetros por defecto. También podrá experimentar con otros parámetros. La constante numFeature <- 10 da la posibilidad de cambiar el número de mejores predictores bestF suministrados por el modelo.
Realizaremos los cálculos con el conjunto X$pretrain
require(clusterSim)
evalq({
numFeature <- 10
HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> r
r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
[,1] [,2]
[1,] 5 0.9242887
[2,] 11 0.8775318
[3,] 9 0.8265240
[4,] 3 0.6093157
[5,] 6 0.6004115
[6,] 10 0.5730556
[7,] 1 0.5722479
[8,] 7 0.4730875
[9,] 4 0.3780357
[10,] 8 0.3181561
[11,] 2 0.2960231
[12,] 12 0.1009184
Puede ver en qué orden se clasifican los predictores en la lista de códigos anterior. A continuación, se muestran los 10 mejores, que usaremos en lo sucesivo.
> colnames(env$X$pretrain$x)[env$bestF] [1] "v.fatl" "v.rbci" "v.ftlm" "rbci" "v.satl" "v.stlm" "ftlm" [8] "v.rftl" "pcci" "v.rstl"
Los conjuntos para la realización de experimentos ya están listos.
La función Evaluate(), que calcula la métrica según los resultados de prueba, la tomaremos del artículo anterior de esta serie. El valor mean(F1) lo usaremos como criterio de optimización (maximización). Cargamos esta función en el entorno env.
Creación, entrenamiento y prueba del conjunto
Entrenamos el conjunto de redes neuronales (n <- 500 uds), combinándolas en Ens. Cada red neuronal será entrenada en su propia muestra. Formaremos la muestra extrayendo aleatoriamente del conjunto de entrenamiento 7/10 ejemplos, con un reemplazo. Para el modelo, necesitamos establecer dos parámetros: nh - el número de neuronas en la capa oculta, y act - la función de activación. El paquete ofrece las siguientes opciones para las funciones de activación:
- - sig: sigmoid
- - sin: sine
- - radbas: radial basis
- - hardlim: hard-limit
- - hardlims: symmetric hard-limit
- - satlins: satlins
- - tansig: tan-sigmoid
- - tribas: triangular basis
- - poslin: positive linear
- - purelin: linear
Considerando que tenemos 10 variabes de entrada, adoptaremos de forma preliminar nh = 5. Como función de activación, adoptaremos actfun = "sin". El conjunto se entrena rápidamente. Hemos elegido los parámetros de forma intuitiva, en función de nuestra experiencia al trabajar con redes neuronales. Usted puede probar otras opciones.
#---3-----Train---------------------------- evalq({ n <- 500 r <- 7 nh <- 5 Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } }, env)
Vamos a hablar brevemente sobre los cálculos en el script. Definimos las constantes n (número de redes neuronales en el conjunto) y r (tamaño de la muestra de arranque suministrada para el entrenamiento de la red neuronal. Esta muestra será diferente para cada red neuronal en el conjunto). nh — número de neuronas en la red oculta. A continuación, definimos el conjunto de datos de entrada Xtrain, usando el conjunto principal X$pretrain y dejamos en él solo los predictores bestF determinados.
Así, hemos obtenido el conjunto Ens[[500]] de 500 clasificadores individuales de redes neuronales. Lo ponemos a prueba con el conjunto de prueba Xtest, obtenido a partir del conjunto principal X$train con los mejores predictores bestF . Obtenemos como resultado y.pr[1001, 500], un frame de datos de 500 variables predictivas continuas.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env)
Combinación de las salidas individuales de los clasificadores. Métodos (averaging/voting)
Los clasificadores básicos de un conjunto pueden tener los siguientes tipos de resultados:
- Etiquetas de clases (Class labels)
- Ranking de las etiquetas de clases (Ranked class labels), al clasificarse con un número de clases >2
- Predicción/nivel numérico continuo de soporte.
Nuestros clasificadores básicos tienen una variable numérica continua (grado de soporte) en la salida. Los niveles de soporte para esta entrada X se pueden interpretar de diferentes maneras. Puede tratarse de la fiabilidad de las etiquetas propuestas y la evaluación de probabilidades posibles para las clases. Para nuestro caso, la salida será la veracidad de las etiquetas de clasificación propuestas.
La primera opción de combianción es la promediación: obtenemos el valor promedio de las salidas individuales. A continuación, lo trasladamos a las etiquetas de clase, además, en este caso, adoptaremos el umbral de paso como igual a 0.5.
La segunda opción de combinación es sencilla: el voto por mayoría. Para ello, primero tenemos que pasar cada salida desde una variable continua a las etiquetas de clase [-1, 1] (el umbral de paso es igual 0,5). Después sumamos todas las salidas, y si el resultado es superior a 0, entonces se asigna la clase 1, de lo contrario, 0.
Usando las etiquetas de clase obtenidas, definimos las métricas (Accuracy, Precision, Recall y F1).
Poda del conjunto (Ensemble pruning). Métodos
Inicialmente hemos introducido un número excesivo de clasificadores básicos para posteriormente elegir los mejores de ellos. Para conseguirlo, se aplican los siguientes métodos:
- ordered-base pruning — selección de un conjunto ordenado según un determinado índice de calidad:
- reduce-error pruning — ordenamos los clasificadores según el error de clasificación y seleccionamos varios de los mejores (con el menor error);
- kappa pruning — ordenamos los miembros del conjunto según el índice Kappa, seleccionamos el número necesario con los menores índices.
- clustering-base pruning — agrupamos con cualquier método los resultados de la predicción del conjunto, después de lo cual, seleccionamos varios representantes de cada clúster. Métodos de clusterización:
- partitiong (por ejemplo SOM, k-mean);
- hierarchical;
- dencity-based (por ejemplo dbscan);
- GMM-based.
- optimization-base pruning — para elegir los mejores, usamos algoritmos evolutivos o genéticos.
La poda del conjunto: es la porpia selección de predictores. Por lo tanto, se aplican a esta los mismos métodos que a la hora de seleccionar los predictores (este hecho se analizó en los artículos anteriores de la serie).
En los cálculos posteriores, elegiremos un conjunto ordenado según la clasificación de los errores (reduce-error prunning).
En total, en los experimentos utilizaremos los siguientes métodos:
- método de combinación — promediación y voto por mayoría simple;
- métricas — Accuracy, Precision, Recall y F1;
- poda — selección del conjunto ordenado según el error de clasificación basado en mean(F1).
El umbral de paso de las salidas individuales desde una variable continua a las etiquetas de clase es 0.5. Avisamos de inmediato: esta opción no es la mejor, pero es la más fácil. Más tarde se podrá mejorar.
а) Definimos los mejores clasificadores individuales del conjunto
Definimos mean(F1) de las 500 redes neuronales, seleccionamos varios bestNN con los mejores índices. El número de los mejores de voto por mayoría debe ser impar, entonces lo definiremos así: (numEns*2 + 1).
#---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
Vamos a hablar brevemente sobre los cálculos en el script. En el ciclo foreach() pasamos la predicción continua y.pr[ ,i] de cada red neuronal a una nominal [0,1], definimos mean(F1) de esta predicción y mostramos el valor con el vector Score[500]. Luego ordenamos los datos de este vector Score en orden descendente y definimos los índices bestNN de las redes neuronales con los mejores (mayores) índices. Mostramos el valor de las métricas de los mejores miembros del conjunto Score[bestNN] redondeándolos hasta 3 dígitos. Como podemos ver, los resultados individuales no son muy altos.
Nota: ¡Cada inicio del entrenamiento y la prueba producirá un resultado diferente, ya que las muestras y la inicialización inicial de las redes neuronales serán diferentes!
Bien, ya hemos definido los mejores clasificadores individuales en el conjunto. Vamos a probarlos en los conjuntos X$test y X$test1, usando los siguientes métodos de combinación: el promedio y el voto por mayoría simple.
б) Promediación
#---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.75 0.723 0.739 0.731 1 0.75 0.774 0.760 0.767
Vamos a hablar brevemente sobre los cálculos en el script. Definimos el tamaño dle conjunto n, la variable de entrada Xtest y la variable objetivo Ytest, usando el conjunto principal X$test. A continuación, en el ciclo foreach (solo cuando el índice es igual a los índices bestNN), calculamos los predictores de estos mejores NN, los sumamos, y los dividimos por el número de mejores NN. Pasamos la salida de variable continua a nominal (0,1) y calculamos las métricas. Como puede ver, los índices de calidad de la clasificación son mucho más altos que los de los clasificadores individuales.
Realizamos el mismo test en el conjunto X$test1, ubicado tras X$test. Valoramos la calidad.
#--6.1 ---test averaging(test1)--------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
La calidad de la clasificación se ha mantenido prácticamente sin cambios y sigue siendo bastante alta. Este resultado muestra que el conjunto de calsificadores de redes neuronales mantiene una alta calidad de clasificación después del entrenamiento y la poda para un periodo significativamente más largo (en nuestro ejemplo, 750 barras) que la DNN obtenida por nosotros en el artículo anterior.
c) Voro por mayoría simple
Definimos las métricas de predicción obtenidas de los mejores clasificadores del conjunto, pero combinadas con voto por mayoría simple. Primero, pasamos las predicciones continuas de los mejores clasificadores a etiquetas de clase (-1 / + 1), luego sumamos todas las etiquetas de predicción. Si la suma es mayor a 0, entonces damos en 1a salida la clase 1, de lo contrario, la clase 0. Primero, ponemos a prueba todo con el conjunto X$test:
#--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
El resultado es prácticamente igual al resultado obtenido al promediar. Vamos a probar con el conjunto X$test1:
#--7.1 --test--voting(test1)-------------------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.761 0.787 0.775 0.781 1 0.761 0.730 0.743 0.737
Es algo inesperado, pero el resultado ha sido mejor que todos los anteriores, y esto teniendo en cuenta que el conjunto X$test1 se encuentra tras X$test.
Por lo tanto, la calidad de clasificación del mismo conjunto con los mismos datos, pero con un método diferente de unificación, puede variar mucho.
A pesar del hecho de que los hiperparámetros de los clasificadores individuales del conjunto hayan sido elegidos de forma intuitiva y obviamente no sean óptimos, hemos obtenido una calidad de clasificación alta y estable utilizando promedios y con una mayoría simple.
Vamos a resumir todo lo anterior. Esquemáticamente, todo el proceso de creación y prueba del conjunto de redes neuronales se puede dividir condicionalmente en 4 etapas:
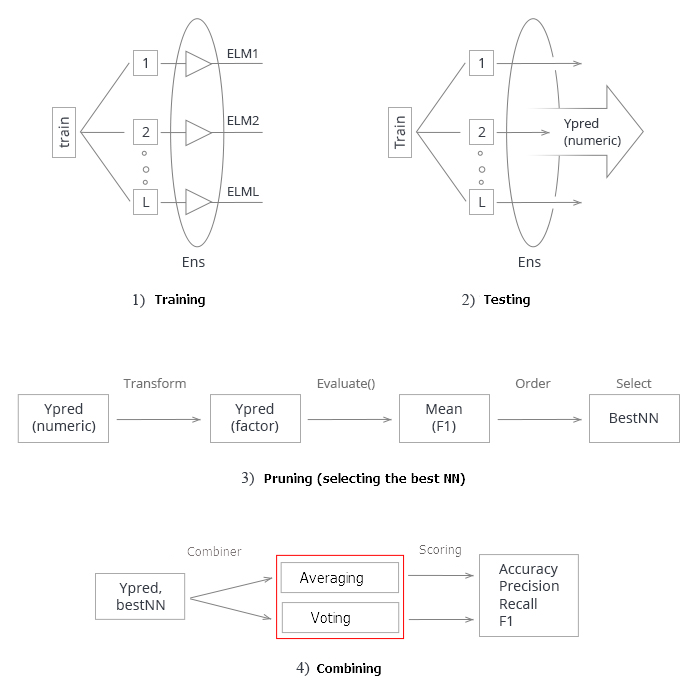
Fig.3 Esquema estructural del entrenamiento y la prueba de un conjunto de redes neuronales con un combinador de averaging/voting
1 Entrenamiento del conjunto. Entrenamos L redes neuronales con muestras aleatorias (arranque) del conjunto de entrenamiento. Obtenemos un conjunto de redes neuronales entrenadas.
2. Vamos a probar el conjunto de redes neuronales con el conjunto de prueba. Obtenemos predicciones continuas de clasificadores individuales.
3. Podamos el conjunto, eligiendo las n mejores según un cierto criterio de calidad de clasificación. En nuestro caso, se trata de mean(F1).
4. Utilizando las predicciones continuas de los mejores clasificadores individuales, los combinamos, usando el promedio o el voto por mayoría simple. Después de ello, definimos las métricas.
Las dos últimas etapas (poda y combinación) tienen muchas opciones de implementación. En este caso, además, la poda exitosa del conjunto (definición correcta de los mejores) puede aumentar seriamente el rendimiento. Nos referimos a la definición del umbral óptimo para el paso de una predicción continua a una nominal. Por lo tanto, encontrar los parámetros óptimos en estas etapas es una tarea laboriosa. Es mejor ejecutar estos pasos automáticamente y con el mejor resultado. ¿Tenemos la oportunidad de hacerlo así y mejorar los índices de calidad del conjunto? Disponemos de al menos dos formas de hacerlo, vamos a comprobarlas.
- Optimizamos los hiperparámetros de los clasificadores individuales del conjunto (optimizador bayesiano).
- Como combinador de las salidas individuales del conjunto, usamos una DNN. Vamos a realizar la generalización a través del entrenamiento.
Definimos los parámetros óptimos de los clasificadores individuales del conjunto. Métodos
Los clasificadores individuales en nuestro conjunto son las redes neuronales ELM. La principal característica de las ELM es que sus propiedades y su calidad dependen principalmente de la inicialización aleatoria de los pesos de las neuronas de capa la oculta. En igualdad de condiciones (número de neuronas y función de activación), cada inicio del entrenamiento generará una nueva red neuronal.
Para crear los conjuntos, esta característica de las ELM es simplemente perfecta. En el conjunto, no solo iniciamos los pesos de cada clasificador mediante variables aleatorias, sino que también proporcionamos a cada clasificador una muestra de entrenamiento separada y creada de forma aleatoria.
Pero para elegir los mejores hiperparámetros de una red neuronal, necesitamos que su calidad solo dependa del cambio de este hiperparámetro y de nada más. De lo contrario, se pierde el significado de la búsqueda.
Así, surge una contradicción: por un lado, necesitamos un conjunto con tantos miembros distintos como sea posible, y por otro lado, un conjunto con miembros diversos pero permanentes.
Necesitamos una variedad permanente reproducible.
¿Es esto posible? Vamos a mostrarlo usando el ejemplo de la formación del conjunto. Necesitaremos el paquete "doRNG" (Reproducible random number generation RNG). Para reproducir los resultados, es mejor realizar los cálculos en un flujo.
Vamos a comenzar un nuevo experimento desde un entorno global puro. Cargamos de nuevo las cotizaciones, las bibliotecas necesarias, definimos y ordenamos una vez más los datos fuente y seleccionamos otra vez numFeature de los mejores predictores. Iniciamos todo en un solo script.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) library(doRNG) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) #--1-Data X------------- list( pretrain = list( x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) ), train = list( x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) ), test = list( x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) ), test1 = list( x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) ) ) -> X #---2--bestF----------------------------------- #require(clusterSim) numFeature <- 10 HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX orderX %>% head(numFeature) -> bestF }, env)
Ya tenemos listos todos los datos fuente necesarios. Entrenamos el conjunto de redes neuronales:
#---3-----Train---------------------------- evalq({ Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y setMKLthreads(1) n <- 500 r <- 7 nh <- 5 k <- 1 rng <- RNGseq(n, 12345) Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) k <- k + 1 idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } setMKLthreads(2) }, env)
¿Qué sucede al ejecutarlo? Definimos los datos de entrada y salida para el entrenamiento (Xtrain, Ytrain), instalamos la biblioteca MKL en el modo de un solo flujo. Inicializamos ciertas constantes y creamos la secuencia de números aleatorios rng, con los cuales se iniciará el generador de números aleatorios en cada nueva iteración foreach().
Después de ejecutar las iteraciones, no se olvide de pasar MKL al modo multiflujo. En el modo de un solo flujo, los resultados del cálculo son ligeramente peores.
Por lo tanto, obtendremos un conjunto con diferentes clasificadores individuales, pero con cada reinicio del entrenamiento, estos clasificadores de conjunto permanecerán sin cambios. Esto es fácil de comprobar, repitiendo las 4 etapas (train/predict/best/test) varias veces. Calculamos por orden: train/predict/best/test_averaging/test_voting.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env) #---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) # [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713 #---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.75 0.711 0.770 0.739 # 1 0.75 0.790 0.734 0.761 #--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.749 0.711 0.761 0.735 # 1 0.749 0.784 0.738 0.760
Y no importa cuántas veces repitamos estos cálculos (por supuesto, con los mismos parámetros), el resultado no cambiará. Precisamente esto es lo que necesitamos para optimizar los hiperparámetros de las redes neuronales incluidas en el conjunto.
En primer lugar, vamos a definir la lista de hiperparámetros optimizados, encontrando los límites de sus cambios y escribiendo una función de adecuación que debe retornar el criterio de optimización (maximización) y la predicción del conjunto. Son cuatro los parámetros que influyen en la calidad de los clasificadores individuales:
- el número de predictores en los datos de entrada;
- el tamaño de la muestra suministrado para el entrenamiento;
- el número de neuronas de la capa oculta;
- la función de activación.
Vamos a escribir los hiperparámetros y los límites de sus cambios:
evalq({
#type of activation function.
Fact <- c("sig", #: sigmoid
"sin", #: sine
"radbas", #: radial basis
"hardlim", #: hard-limit
"hardlims", #: symmetric hard-limit
"satlins", #: satlins
"tansig", #: tan-sigmoid
"tribas", #: triangular basis
"poslin", #: positive linear
"purelin") #: linear
bonds <- list(
numFeature = c(3L, 12L),
r = c(1L, 10L),
nh <- c(1L, 50L),
fact = c(1L, 10L)
)
}, env)
Echemos un vistazo más de cerca al código de arriba. En él, Fact es el vector de posibles funciones de activación. La lista bonds define los parámetros que deben ser optimizados y sus límite de cambio.
- numFeature es el número de predictores en la entrada, su mínimo es 3, su máximo es 12;
- r es la parte del conjunto entrenado utilizada en el arranque. Antes de realizar el cálculo, lo dividimos por 10.
- nh es el número de neuronas de la capa oculta, su mínimo es 1, su máximo es 50.
- fact es el índice de la función de activación en el vector Fact.
Vamos a definir la función de adecuación.
#---Fitnes -FUN----------- evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Vamos a aclarar un poco este script. Definimos las variables objetivo (Ytrain, Ytest, Ytest1) de la función de adecuación, puesto que a la hora de iterar los parámetros son inmutables. Iniciamos las constantes:
n es el número de redes neuronales en el conjunto;
numEns es el número de los mejores clasificadores individuales (numEns*2 + 1), cuyas predicciones vamos a combinar.
Propiamente, la función fitnes() tiene 4 parámetros formales que queremos optimizar. A continuación, entrenamos el conjunto con la función por orden, calculamos predict y definimos bestNN de los mejores. Al final, combinamos las predicciones de estos mejores mediante promediación y calculamos las métricas. La función retorna una lista que contiene los criterios de optimización Score = mean(F1) y la predicción. Optimizamos el conjunto en el que se usa la integración por promediación. La función de adecuación para optimizar los hiperparámetros del conjunto con combinación con voto por mayoría simple es similar, excepto en la parte final. Puede realizar la optimización usted mismo.
Vamos a comprobar la función de adecuación y su tiempo de ejecución:
#---------- evalq( system.time( res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2) ) , env) user system elapsed 8.65 0.19 7.86
Para obtener un resultado, se han invertido en todos los cálculos 9 segundos.
> env$res$Score [1] 0.761
Ahora podemos iniciar la optimización de los hiperparámetros con 10 puntos de inicialización aleatorios y 20 iteraciones. Vamos a ver el mejor resultado.
#------ evalq( OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 10, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 23 numFeature = 8.0000 r = 3.0000 nh = 3.0000 fact = 7.0000 Value = 0.7770
Ordenamos la historia de optimización según el valor Value y elegimos los mejores 10 índices:
evalq({
OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init
best.init
}, env)
numFeature r nh fact Value
1 8 3 3 7 0.777
2 8 1 5 7 0.767
3 8 3 2 7 0.760
4 10 7 9 8 0.759
5 8 5 4 7 0.758
6 8 2 7 8 0.756
7 8 6 9 7 0.755
8 8 3 4 8 0.754
9 9 2 13 9 0.752
10 11 2 24 4 0.751
Desciframos los hiperparámetros obtenidos del mejor resultado. Número de predictores 8, tamaño de la muestra 0.3, número de neuronas en la capa oculta 3, función de activación "radbas". Una vez más, podemos comprobar que la optimización bayesiana ofrece un abanico con varios modelos difíciles de obtener de manera intuitiva. Tendremos que repetir la optimización varias veces y seleccionar el mejor resultado.
Bien, ahora tenemos los hiperparámetros de entrenamiento óptimos. Vamos a poner a prueba el conjunto con ellos.
Entrenamiento y prueba del conjunto con parámetros óptimos
Probamos el conjunto entrenado con los parámetros óptimos (que obtuvimos arriba), usando el conjunto de prueba. Definimos los mejores miembros del conjunto, combinamos sus resultados promediando y observamos las métricas finales. Más abajo se muestra el script.
Al entrenar el conjunto de redes neuronales, lo creamos de la misma forma que en la optimización.
#--1-Train--optEns-predict--best--test-average------------------------ evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 #--BestParams-------------------------- best.par <- OPT_Res$Best_Par %>% unname numFeature <- best.par[1] # 8L r <- best.par[2] # 3L nh <- best.par[3] # 3L fact <- best.par[4] # 7L bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(OptEns[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(OptEns[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) -> OptScore caret::confusionMatrix(Ytest1, ensPred) -> cm }, env)
Vamos a ver los resultados de los 7 mejores conjuntos de redes neuronales:
> env$Score[env$bestNN] [1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981 0.7099502
Resultado después de promediar las mejores redes neuronales:
> env$OptScore Accuracy Precision Recall F1 0 0.778 0.751 0.774 0.762 1 0.778 0.803 0.782 0.793 > env$cm Confusion Matrix and Statistics Reference Prediction 0 1 0 178 52 1 59 212 Accuracy : 0.7784 95% CI : (0.7395, 0.8141) No Information Rate : 0.5269 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5549 Mcnemar's Test P-Value : 0.569 Sensitivity : 0.7511 Specificity : 0.8030 Pos Pred Value : 0.7739 Neg Pred Value : 0.7823 Prevalence : 0.4731 Detection Rate : 0.3553 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7770 'Positive' Class : 0
Este resultado es notoriamente mejor al de cualquier red neuronal individual en el conjunto. Comparamos con los resultados de la DNN con los parámetros óptimos obtenidos por nosotros en el anterior artículo de esta serie.
Conclusión
- Los conjuntos de clasificadores de redes neuronales compuestos de redes neuronales simples y rápidas ELM, muestran una calidad de clasificación comparable con modelos más complejos (DNN).
- La optimización de los hiperparámetros de los clasificadores del conjunto aumenta la calidad de la clasificación hasta Acc = 0.77(95% CI = 0.73 - 0.81).
- La calidad de la clasificación del conjunto con promediación y con el voto por mayoría simple es aproximadamente igual.
- La preservación de la calidad de la clasificación del conjunto después del entrenamiento se mantiene a una profundidad de más de la mitad del tamaño del conjunto de entrenamiento. En nuestro conjunto se guarda hasta 750 barras, lo cual es muy superior al propio índice obtenido en la DNN (250 barras).
- La calidad de la clasificación del conjunto puede mejorarse significativamente optimizando el umbral de paso de la variable predictiva continua a variable nominal (calibración, CutOff óptimo, búsqueda genética).
- La calidad de clasificación del conjunto se puede aumentar aplicando como combinador el modelo entrenado (stacking). Puede tratarse de una red neuronal o de un conjunto de redes neuronales. En la próxima parte del artíclo, comprobaremos estas dos opciones de stacking. Para construir las redes neuronales, pondremos a prueba las nuevas posibilidades ofrecidas por el grupo de bibliotecas TensorFlow.
Anexos
En GitHub/PartVI se encuentran:
- FUN_Ensemble.R — funciones necesarias para realizar todos los cálculos descritos en este artículo.
- RUN_Ensemble.R — scripts para crear, entrenar y probar el conjunto
- Optim_Ensemble.R — scripts para optimizar los hiperparámetros de las redes neuronales del conjunto
- SessionInfo_RunEns. txt — paquetes usados al crear y probar el conjunto
- SessionInfo_OptEns. txt — paquetes usados al optimizar los hiperparámetros del conjunto NN
- ELM.zip — archivo de artículos sobre las redes ELM.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/4227
 Mejorando el trabajo con Paneles: cómo añadir transparencia, cambiar el color del fondo y heredar a partir de CAppDialog/CWndClient
Mejorando el trabajo con Paneles: cómo añadir transparencia, cambiar el color del fondo y heredar a partir de CAppDialog/CWndClient
 Simulación de patrones de parejas de divisas: Uso y perspectivas para el trading real. Parte IV
Simulación de patrones de parejas de divisas: Uso y perspectivas para el trading real. Parte IV
 Cómo transferir los cálculos de cualquier indicador al código de un asesor experto
Cómo transferir los cálculos de cualquier indicador al código de un asesor experto
 Cómo crear un panel gráfico de cualquier nivel de complejidad
Cómo crear un panel gráfico de cualquier nivel de complejidad
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso