
Redes Neurais Profundas (Parte VI). Ensemble de classificadores de redes neurais: bagging
Conteúdo
- Introdução
- Ensembles de classificadores de redes neurais
- Bagging
- Geração dos conjuntos de dados iniciais
- Ordenação dos preditores por importância da informação
- Criação, treinamento e teste do ensemble de classificadores
- Combinação das saídas individuais dos classificadores (média/votação)
- Poda do ensemble e seus métodos
- Otimização de hiperparâmetros dos membros do ensemble. Recursos e métodos
- Treinamento e teste do ensemble com hiperparâmetros ótimos
- Conclusão
- Anexos
Introdução
No artigo anterior desta série nós discutimos os hiperparâmetros do modelo DNN, treinamos ele com vários exemplos e o testamos. A qualidade do modelo resultante foi bastante alta.
Nós também discutimos as possibilidades de como melhorar a qualidade da classificação. Uma delas é usar um ensemble de redes neurais. Esta variante de amplificação será discutida neste artigo.
1. Ensembles de classificadores de redes neurais
Estudos mostram que os ensembles de classificadores são geralmente mais precisos que os classificadores individuais. Um desses ensembles é mostrado na Figura 1a. Ele usa vários classificadores, com cada um deles tomando uma decisão sobre o objeto alimentado como entrada. Então, essas decisões individuais são agregadas em um combinador. O ensemble produz um rótulo de classe para o objeto.
É intuitivo que o ensemble de classificadores não possa ser estritamente definido. Esta incerteza geral é ilustrada na Figura 1b-d. Em essência, qualquer ensemble é o próprio classificador (Figura 1b). Os classificadores base que o compõem extraem funções complexas de regularidades (muitas vezes implícitas), e o combinador se tornará um classificador simples agregando essas funções.
Por outro lado, nada nos impede de chamar um classificador de rede neural padrão convencional de um ensemble (Figura 1c). Os neurônios em sua penúltima camada podem ser considerados como classificadores separados. Suas decisões devem ser "decifradas" no combinador, cujo papel é desempenhado pela camada superior.
E finalmente, as funções podem ser consideradas como classificadores primitivos, e o classificador como seu combinador complexo (Figura 1d).
Nós combinamos os classificadores simples treináveis para obter uma decisão precisa sobre a classificação. Mas este é o caminho certo a seguir?
Em seu artigo de revisão crítica "Multiple Classifier Combination: Lessons and Next steps", publicado em 2002, Tin Kam Ho escreveu:
"Em vez de procurar o melhor conjunto de recursos e o melhor classificador, agora procuramos o melhor conjunto de classificadores e, em seguida, o melhor método de combinação. Pode-se imaginar que, muito em breve, estaremos procurando o melhor conjunto de métodos de combinação e, em seguida, a melhor maneira de usar todos eles. Se não aproveitarmos a oportunidade para rever os problemas fundamentais decorrentes deste desafio, nós estaremos fadados a ser levados a tal recorrência infinita, arrastando esquemas e teorias de combinação cada vez mais complicadas, e gradualmente perdendo de vista o problema original. "
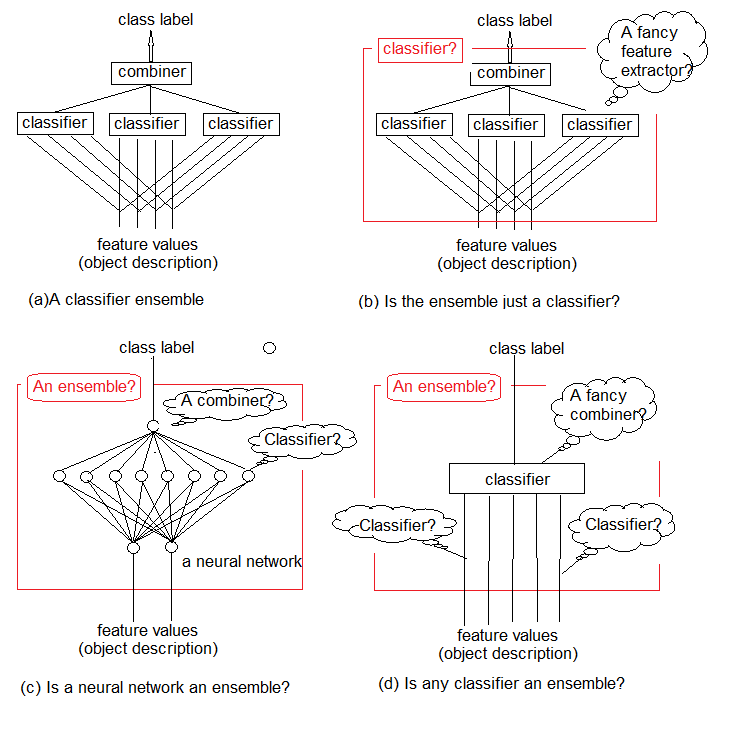
Fig.1. O que é um ensemble de classificadores?
A lição é que temos que encontrar a maneira ideal de usar ferramentas e métodos existentes antes de criar novos projetos complexos.
Sabe-se que os classificadores de redes neurais são "aproximadores universais". Isso significa que qualquer limite de classificação, não importando sua complexidade, pode ser aproximado por uma rede neural finita com qualquer precisão necessária. No entanto, esse conhecimento não nos dá uma maneira de criar ou treinar essa rede. A ideia de combinar classificadores é uma tentativa de resolver o problema compondo uma rede de blocos de construção gerenciados.
Os métodos para compor um ensemble são os meta algoritmos que combinam vários métodos de aprendizado de máquina em um modelo preditivo, a fim de:
- reduzir a variância — bagging;
- reduzir o viés — boosting;
- melhorar as previsões — stacking.
Esses métodos podem ser divididos em dois grupos:
- os métodos paralelos de construção de um ensemble, onde os modelos base são gerados em paralelo (por exemplo, uma floresta aleatória). A ideia é usar a independência entre os modelos base e para reduzir o erro pela média. Por isso, o principal requisito para os modelos é a baixa correlação mútua e a alta diversidade.
- os métodos de ensemble sequencial, em que os modelos base são gerados sequencialmente (por exemplo, AdaBoost, XGBoost). A ideia principal aqui é usar a dependência entre os modelos base. Aqui, a qualidade geral pode ser aumentada atribuindo-se pesos maiores a exemplos anteriormente classificados incorretamente.
A maioria dos métodos de ensemble usam um algoritmo de aprendizado base único ao criar os modelos homogêneos base. Isso leva a ensembles homogêneos. Existem também os métodos usando os modelos heterogêneos (modelos de tipos diferentes). Como resultado, são formados ensembles heterogêneos. Para que os ensembles sejam mais precisos do que qualquer um de seus membros individuais, os modelos básicos devem ser o mais diversos possíveis. Em outras palavras, quanto mais informações oriundas dos classificadores base, maior a precisão do ensemble.
A Figura 2 mostra 4 níveis de criação de um ensemble de classificadores. As perguntas surgem em cada um deles, eles serão discutidos abaixo.

Fig.2. Quatro níveis de criação de um ensemble de classificadores
Vamos discutir isso em mais detalhes.
1. Combinador
Alguns métodos do ensemble não definem um combinador. Mas para os métodos que existem, existem três tipos de combinadores.
- Não treinável. Um exemplo de tal método é um simples "voto por maioria".
- Treinável. Este grupo inclui a "votação ponderada por maioria" e "Naive Bayes", bem como a abordagem de "seleção do classificador", em que a decisão sobre um determinado objeto é feita por um classificador do ensemble.
- Meta classificador. As saídas dos classificadores base são consideradas como entradas para o novo classificador a ser treinado, o que se torna um combinador. Essa abordagem é chamada de "generalização complexa", "generalização por treinamento" ou simplesmente "stacking". Construir um conjunto de treinamento para um meta classificador é um dos principais problemas deste combinador.
2. Construção de um ensemble
Os classificadores base devem ser treinados em paralelo (independentemente) ou sequencialmente? Um exemplo de treinamento sequencial é o AdaBoost, onde o conjunto de treinamento de cada classificador adicionado depende do ensemble criado antes dele.
3. Diversidade
Como gerar diferenças no ensemble? São sugeridas as seguintes opções.
- Manipular os parâmetros de treinamento. Usar diferentes abordagens e parâmetros ao treinar os classificadores base individuais. Por exemplo, é possível inicializar os pesos dos neurônios nas camadas ocultas da rede neural de cada classificador base com diferentes variáveis aleatórias. Também é possível definir os hiperparâmetros aleatoriamente.
- Manipular as amostras — obter um exemplo de bootstrap personalizado do conjunto de treinamento de cada membro do ensemble.
- Manipular os preditores — preparar um conjunto personalizado de preditores determinados aleatoriamente para cada classificador base. Essa é a chamada divisão vertical do conjunto de treinamento.
4 Tamanho do ensemble
Como determinar o número de classificadores em um ensemble? O ensemble é construído pelo treinamento simultâneo do número necessário de classificadores ou iterativamente pela adição/remoção de classificadores? Opções possíveis:
- O número é reservado com antecedência
- O número é definido no curso do treinamento
- Os classificadores são superproduzidos e depois selecionados
5. Versatilidade (em relação ao classificador base)
Algumas abordagens podem ser usadas com qualquer modelo de classificador, enquanto outras estão ligadas a um certo tipo de classificador. Um exemplo de um ensemble "específico de classificador" é uma Floresta Aleatória. Seu classificador base é uma árvore de decisão. Então, existem duas variantes de abordagens:
- poder usar somente um modelo específico do classificador base;
- poder usar qualquer modelo de classificador base.
Ao treinar e otimizar os parâmetros do ensemble de classificadores, deve-se distinguir a otimização da solução e otimização da cobertura.
- A otimização da tomada de decisão refere-se à seleção de um combinador para um conjunto fixo de classificadores base (nível A na Figura 2).
- Otimização de cobertura alternativa refere-se à criação de diversos classificadores base com um combinador fixo (níveis B, C e D na Figura 2).
Esta decomposição do design do ensemble reduz a complexidade do problema, por isso ela parece razoável.
Uma análise muito detalhada e profunda dos métodos de ensemble são considerados nos livros Combining Pattern Classifiers. Methods and Algorithms, Second Edition. Ludmila Kuncheva e Ensemble Methods. Foundations and Algorithms. Eles são recomendados para leitura.
2. Bagging
O nome do método é derivado da frase Bootstrap AGGregatING. Bagging de ensembles são criados da seguinte forma:
- uma amostra de bootstrap é extraída do conjunto de treinamento;
- cada classificador é treinado em sua própria amostra;
- as saídas individuais dos classificadores separados são combinadas em um rótulo de classe. Se os resultados individuais tiverem a forma de um rótulo de classe, a votação por maioria simples será usada. Se a saída dos classificadores for uma variável contínua, a média será aplicada ou a variável será convertida em um rótulo de classe, seguido por uma votação por maioria simples.
Vamos retornar à Figura 2 e analisar todos os níveis de criação de um ensemble de classificadores aplicados ao método de bagging.
A: nível de agregação
Nesse nível, os dados obtidos dos classificadores são combinados e uma única saída é agregada.
Como nós combinamos as saídas individuais? Usando um combinador não treinável (média, voto simples pela maioria).
B: nível dos classificadores
No nível B, ocorre todo o trabalho com os classificadores. Várias questões surgem aqui.
- Nós usamos diferentes ou os mesmos classificadores? Os mesmos classificadores são usados na abordagem de bagging.
- Qual classificador é considerado o classificador base? Nós usamos o ELM (Extreme Learning Machines).
Permitam-nos analisar isso com mais detalhes. A seleção do classificador e seu raciocínio é uma parte importante do trabalho. Vamos listar os principais requisitos para os classificadores base criarem um ensemble de alta qualidade.
Em primeiro lugar, o classificador deve ser simples: as redes neurais profundas não são recomendadas.
Em segundo lugar, os classificadores devem ser diferentes: com inicialização diferente, parâmetros de aprendizagem, conjuntos de treinamento, etc.
Em terceiro lugar, a velocidade do classificador é importante: os modelos não devem levar horas para serem treinados.
Em quarto lugar, os modelos de classificação devem ser fracos e dar um resultado de previsão ligeiramente melhor que 50%.
E, finalmente, a instabilidade do classificador é importante, de modo que os resultados da previsão tenham um amplo intervalo.
Existe uma opção que atende a todos esses requisitos. É um tipo especial de rede neural — ELM (Extreme Learning Machines), que foram propostas como algoritmos alternativos de aprendizado ao invés da MLP. Formalmente, ele é uma rede neural totalmente conectada com uma camada oculta. Mas sem a determinação iterativa dos pesos (treinamento), ela se torna excepcionalmente rápida. Ela seleciona aleatoriamente os pesos dos neurônios na camada oculta uma vez durante a inicialização e, em seguida, ela determina analiticamente o seu peso de saída de acordo com a função de ativação selecionada. Uma descrição detalhada do algoritmo ELM e uma visão geral de suas diversas variedades podem ser encontradas no arquivo em anexo.
- Quantos classificadores são necessários? Vamos pegar 500 e depois podar o ensemble.
- O treinamento paralelo ou sequencial dos classificadores é usado? Nós usamos o treinamento paralelo, que ocorre para todos os classificadores simultaneamente.
- Quais parâmetros dos classificadores base podem ser manipulados? O número de camadas ocultas, a função de ativação, o tamanho da amostra do conjunto de treinamento. Todos esses parâmetros estão sujeitos a otimização.
C: nível de funções para as regularidades identificadas
- Todos os preditores são usados ou apenas os subconjuntos individuais para cada classificador? Todos os classificadores usam um subconjunto de preditores. Mas o número de preditores pode ser otimizado.
- Como escolher um subconjunto desse tipo? Nesse caso, são usados os algoritmos especiais.
D: nível de dados de entrada e suas manipulações
Nesse nível, os dados de origem são enviados para a entrada da rede neural para treinamento.
Como manipular os dados de entrada para fornecer uma alta diversidade e alta precisão individual? Amostras de bootstrap serão usadas para cada classificador individualmente. O tamanho do exemplo de bootstrap é o mesmo para todos os membros do grupo, mas ele será otimizado.
Para realizar experimentos com ensembles de ELM, existem dois pacotes em R (elmNN, ELMR) e um pacote em Python (hpelm). Por enquanto, vamos testar os recursos do pacote elmNN, que implementa o ELM clássico. O pacote elmNN é projetado para criar, treinar e testar usando o método em lote ELM. Assim, as amostras de treinamento e teste estão prontas antes do treinamento e são alimentadas ao modelo uma vez. O pacote é muito simples.
O experimento consistirá das seguintes etapas.
- Geração dos conjuntos de dados iniciais
- Ordenação dos preditores por importância da informação
- Treinamento e teste do ensemble de classificadores
- Combinação das saídas individuais dos classificadores (média/votação)
- Poda do ensemble e seus métodos
- Busca por métricas da qualidade do ensemble de classificação
- Determinar os parâmetros ótimos dos membros do ensemble. Métodos
- Treine e teste o ensemble com os parâmetros ótimos
Geração dos conjuntos de dados iniciais
A última versão do MRO 3.4.3 será usada para os experimentos. Ela implementa vários novos pacotes adequados ao nosso trabalho.
Execute o RStudio, vá para GitHub/Part_ para baixar o arquivo Cotir.RData com aspas, obtido a partir do terminal, e busque o arquivo FunPrepareData.R com as funções de preparação de dados do GitHub/Part_IV.
Anteriormente, foi determinado que um conjunto de dados com outliers imputados e dados normalizados possibilita obter melhores resultados no treinamento com pré-treinamento. Nós vamos usá-lo. Você também pode testar as outras opções de pré-processamento consideradas anteriormente.
Ao dividir em subconjuntos pretrain/train/val/test, nós usamos a primeira oportunidade para melhorar a qualidade da classificação — aumentar o número de amostras para treinamento. O número de amostras no subconjunto 'pretrain' será aumentado para 4000.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Ao mudar o parâmetro start na função SplitData(), é possível obter conjuntos deslocados à direita pela quantidade de 'start'. Isso permite verificar a qualidade em diferentes partes da faixa de preço no futuro e determinar como ela se altera no histórico.
Cria conjuntos de dados (pretrain/train/test/test1) para treinamento e teste, reunidos na lista X. Converte a variável objetivo do fator para o tipo numérico (0.1).
#---Data X-------------
evalq({
list(
pretrain = list(
x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1)
),
train = list(
x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1)
),
test = list(
x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1)
),
test1 = list(
x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1)
)
) -> X
}, env)
Ordenação dos preditores por importância da informação
Teste da função clusterSim::HINoV.Mod() (veja o pacote para mais detalhes). Ele classifica as variáveis com base no clustering com diferentes distâncias e métodos. Nós vamos usar os parâmetros padrão. Você está livre para experimentar usando outros parâmetros. A constante numFeature <- 10 permite alterar o número dos melhores preditores bestF alimentado ao modelo.
Os cálculos são realizados no conjunto X$pretrain
require(clusterSim)
evalq({
numFeature <- 10
HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> r
r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
[,1] [,2]
[1,] 5 0.9242887
[2,] 11 0.8775318
[3,] 9 0.8265240
[4,] 3 0.6093157
[5,] 6 0.6004115
[6,] 10 0.5730556
[7,] 1 0.5722479
[8,] 7 0.4730875
[9,] 4 0.3780357
[10,] 8 0.3181561
[11,] 2 0.2960231
[12,] 12 0.1009184
A ordem de classificação dos preditores é mostrada no código listado acima. Os 10 principais estão listados abaixo, eles serão usados no futuro.
> colnames(env$X$pretrain$x)[env$bestF] [1] "v.fatl" "v.rbci" "v.ftlm" "rbci" "v.satl" "v.stlm" "ftlm" [8] "v.rftl" "pcci" "v.rstl"
Os conjuntos para os experimentos estão prontos.
A função Evaluate() para calcular as métricas dos resultados do teste será obtida do artigo anterior desta série. O valor da média (F1) será usado como critério de otimização (maximização). Carregue esta função no ambiente 'env'.
Criação, treinamento e teste do ensemble
Treinamos o ensemble de redes neurais (n <- 500 unidades), combinando-os em Ens. Cada rede neural é treinada em sua própria amostra. A amostra será gerada extraindo 7/10 exemplos do conjunto de treinamento aleatoriamente com a substituição. É necessário definir dois parâmetros para o modelo: 'nh' — o número de neurônios na camada oculta e 'act' — a função de ativação. O pacote oferece as seguintes opções para as funções de ativação:
- - sig: sigmoid
- - sin: sine
- - radbas: radial basis
- - hardlim: hard-limit
- - hardlims: symmetric hard-limit
- - satlins: satlins
- - tansig: tan-sigmoid
- - tribas: triangular basis
- - poslin: positive linear
- - purelin: linear
Considerando que existem 10 variáveis de entrada, nós tomamos primeiro nh = 5. A função de ativação é tomada como actfun = "sin". O ensemble aprende rápido. Eu escolhi os parâmetros intuitivamente, com base na minha experiência com redes neurais. Você pode tentar outras opções.
#---3-----Train---------------------------- evalq({ n <- 500 r <- 7 nh <- 5 Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } }, env)
Vamos considerar brevemente os cálculos no script. Definimos as constantes n (o número de redes neurais no ensemble) e r (o tamanho da amostra de bootstrap usada para treinar a rede neural. Esta amostra será diferente para cada rede neural no ensemble). nh é o número de neurônios na camada oculta. Em seguida, definimos o conjunto de dados de entrada Xtrain usando o conjunto principal X$pretrain e deixando apenas certos preditores bestF.
Isso produz um ensemble Ens[500], consistindo de 500 classificadores de redes neurais individuais. Testamos no conjunto de teste Xtest obtido a partir do conjunto principal X$train com os melhores preditores bestF. O resultado gerado é y.pr[1001, 500] - um quadro de dados de 500 variáveis preditivas contínuas.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env)
Combinação das saídas individuais dos classificadores. Métodos (média/votação)
Os classificadores base de um ensemble podem ter os seguintes tipos de saída:
- Rótulos de classe
- Ranking dos rótulos de classes, ao classificar-se com o número de classes >2
- Previsão numérica contínua/grau de suporte.
Os classificadores base possuem uma variável numérica contínua (o grau de suporte) na saída. Os graus de suporte para essa entrada X podem ser interpretados de maneiras diferentes. Pode ser a confiabilidade dos rótulos propostos ou a avaliação de possíveis probabilidades para as classes. Para nosso caso, a confiabilidade dos rótulos de classificação propostos servirá como saída.
A primeira variante da combinação é a média: obtém o valor médio das saídas individuais. Em seguida, ela é convertida em rótulos de classe, enquanto que o limite de conversão é tomado como 0.5.
A segunda variante da combinação é uma simples votação por maioria. Para fazer isso, cada saída é primeiro convertida de uma variável contínua em rótulos de classe [-1, 1] (o limite de conversão é 0.5). Em seguida, todas as saídas são somadas e, se o resultado for maior que 0, a classe 1 será atribuída, caso contrário, a classe 0.
Usando os rótulos de classe obtidos, determinamos as métricas (Accuracy, Precision, Recall e F1)
Poda do ensemble. Métodos
Inicialmente, o número de classificadores base era supérfluo para selecionar o melhor deles mais tarde. Os seguintes métodos são aplicados para fazer isso:
- ordering-based pruning — seleção de um ensemble ordenado por um determinado índice de qualidade:
- reduce-error pruning — classifica os classificadores pelo erro de classificação e escolhe os melhores (com o menor erro);
- kappa pruning — ordena os membros do ensemble de acordo com a estatística Kappa, seleciona o número desejado com a menor pontuação.
- clustering-based pruning — Os resultados de previsão do ensemble são agrupados por qualquer método, após o qual vários representantes de cada cluster são selecionados. Métodos de clusterização:
- particionamento (por exemplo, SOM, k-mean);
- hierárquico;
- baseado em densidade (por exemplo, dbscan);
- Baseado em GMM.
- optimization-based pruning — são usados os algoritmos evolutivos ou genéticos para selecionar os melhores.
A poda do ensemble é a mesma seleção de preditores. Portanto, os mesmos métodos podem ser aplicados a ele como ao selecionar os preditores (isso foi abordado nos artigos anteriores da série).
A seleção de um ensemble ordenado por erro de classificação (reduce-error pruning) será usada para os cálculos adicionais.
No total, os seguintes métodos serão usados nos experimentos:
- método de combinação — média e votação por maioria simples;
- métricas — Accuracy, Precision, Recall e F1;
- poda — seleção do ensemble ordenado por erro de classificação baseado na mean(F1).
O limite para converter as saídas individuais das variáveis contínuas em rótulos de classe é 0.5. Esteja avisado: esta não é a melhor opção, mas é a mais simples. Ela pode ser melhorada mais tarde.
a) Determinar os melhores classificadores individuais do ensemble
Definimos a mean(F1) de todas as 500 redes neurais, escolhemos vários 'bestNN' com as melhores pontuações. O número das melhores redes neurais para votação majoritária deve ser ímpar, então ele será definido como: (numEns*2 + 1).
#---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
Vamos considerar brevemente os cálculos no script. No loop foreach(), convertemos a previsão contínua y.pr[ ,i] de cada rede neural em valor numérico [0,1], determinamos a mean(F1) desta predição e produzimos o valor como o vetor Score[500]. Em seguida, ordenamos os dados do vetor Score em ordem decrescente, determinamos os índices das redes neurais bestNN com as melhores pontuações (mais altas). Mostramos os valores das métricas desses melhores membros de Score[bestNN], arredondado para 3 casas decimais. Como você pode ver, os resultados individuais não são muito altos.
Nota: cada treinamento e teste executado produzirá um resultado diferente, já que as amostras e a inicialização inicial das redes neurais serão diferentes!
Assim, os melhores classificadores individuais do ensemble foram identificados. Vamos testá-los nas amostras X$test e X$test1, usando os seguintes métodos de combinação: média e votação por maioria simples.
b) Média
#---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.75 0.723 0.739 0.731 1 0.75 0.774 0.760 0.767
Algumas palavras sobre os cálculos no script. Determinamos o tamanho do ensemble n, entradas Xtest e objetivo Ytest, usando o conjunto principal X$test. Então, no loop foreach (somente quando o índice é igual ao dos índices 'bestNN'), calculamos as previsões dessas melhores redes neurais, somamos elas, dividimos pelo número das melhores redes neurais. Convertemos a saída de uma variável contínua em uma variável numérica (0,1) e calculamos as métricas. Como você pode ver, os escores de qualidade de classificação são muito mais altos que os dos classificadores individuais.
Realizamos o mesmo teste no conjunto X$test1, localizado ao lado do X$test. Estimamos a qualidade.
#--6.1 ---test averaging(test1)--------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
A qualidade da classificação permaneceu praticamente inalterada e permanece bastante alta. Este resultado mostra que o ensemble de classificadores de redes neurais mantém uma alta qualidade de classificação após o treinamento e a poda por um período muito mais longo (em nosso exemplo, 750 barras) do que o DNN obtido no artigo anterior.
c) Voto por maioria simples
Vamos determinar as métricas da previsão obtida dos melhores classificadores do ensemble, mas combinadas por votação simples. Primeiro, convertemos as previsões contínuas dos melhores classificadores em rótulos de classe (-1/+1) e, em seguida, somamos todos os rótulos de previsão. Se a soma for maior que 0, então a classe 1 será a saída, caso contrário — classe 0. Primeiro, testamos tudo no conjunto de X$test:
#--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
O resultado é praticamente o mesmo que o resultado da média. Teste no conjunto X$test1:
#--7.1 --test--voting(test1)-------------------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.761 0.787 0.775 0.781 1 0.761 0.730 0.743 0.737
Inesperadamente, o resultado acabou sendo melhor do que todos os anteriores, e isso ocorre apesar do fato de o conjunto X$test1 estar localizado após o X$test.
Isso significa que a qualidade de classificação do mesmo ensemble nos mesmos dados, mas com o método de combinação diferente, pode variar muito.
Apesar do fato de que os hiperparâmetros dos classificadores individuais no ensemble foram escolhidos intuitivamente e obviamente não são ótimos, obteve-se uma qualidade de classificação alta e estável, ambos usando a média e uma votação por maioria simples.
Resumindo tudo acima. Esquematicamente, todo o processo de criação e teste de um ensemble de redes neurais pode ser dividido em 4 etapas:
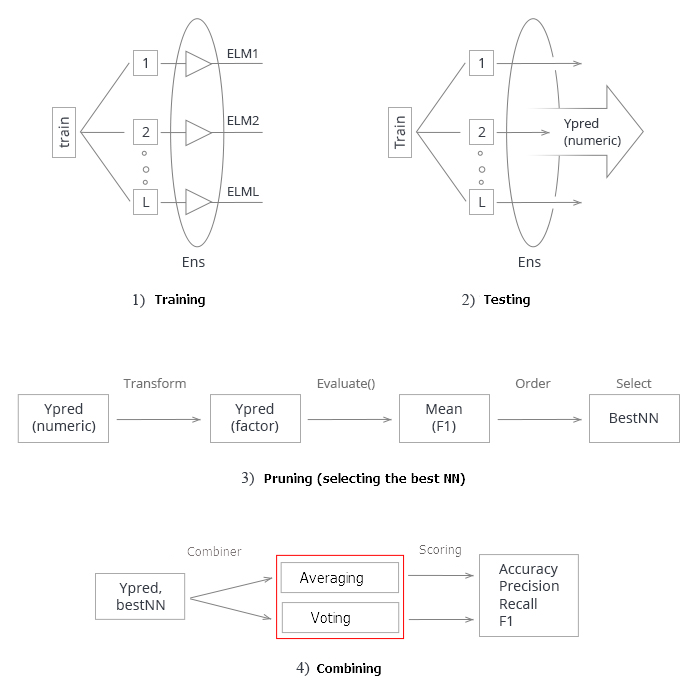
Fig.3. Estrutura de treinamento e teste do ensemble de redes neurais com o combinador de média/votação
1. Treinamento do ensemble. Treinar L redes neurais em amostras aleatórias (bootstrap) do conjunto de treinamento. Obter o ensemble de redes neurais treinadas.
2. Testar o ensemble de redes neurais no conjunto de testes. Obter as previsões contínuas dos classificadores individuais.
3. Poda do ensemble, escolhendo o melhor n por um certo critério de qualidade de classificação. Nesse caso, é a mean(F1).
4 Usando as previsões contínuas dos melhores classificadores individuais, combinamos eles com a ajuda da média ou votação por maioria simples. Depois disso, determinamos as métricas.
As duas últimas etapas (remoção e combinação) têm várias opções de implementação. Ao mesmo tempo, a poda bem sucedida do ensemble (identificação correta dos melhores) pode aumentar significativamente o desempenho. Nesse caso, ele está encontrando o limite de conversão ideal de uma previsão contínua em um valor numérico. Portanto, encontrar os parâmetros ótimos nesses estágios é uma tarefa trabalhosa. Esses estágios são melhor realizados automaticamente e com o melhor resultado. Será que temos a capacidade de fazer isso e melhorar as pontuações de qualidade do ensemble? Existem pelo menos duas maneiras de fazer isso, vamos verificá-las.
- Otimizar os hiperparâmetros dos classificadores individuais do ensemble (otimizador Bayesiano).
- A DNN será usada como um combinador de saídas individuais do ensemble. A generalização será realizada através da aprendizagem.
Determinamos os parâmetros ideais dos classificadores individuais do ensemble. Métodos
Os classificadores individuais em nosso ensemble são as redes neurais ELM. A principal característica do ELM é que suas propriedades e qualidade dependem principalmente da inicialização aleatória dos pesos dos neurônios da camada oculta. Outras coisas sendo iguais (o número de neurônios e funções de ativação), cada execução do treinamento produzirá uma nova rede neural.
Esse recurso do ELM é perfeito para criar ensembles. No ensemble, não inicializamos apenas os pesos de cada classificador com valores aleatórios, mas também fornecemos a cada classificador uma amostra de treinamento separada gerada aleatoriamente.
Mas, para selecionar os melhores hiperparâmetros de uma rede neural, sua qualidade depende apenas das mudanças de um determinado hiperparâmetro e de nada mais. Caso contrário, o significado da pesquisa será perdido.
Surge uma contradição: por um lado, nós precisamos de um ensemble com membros tão diversos quanto possível e, por outro lado, um ensemble com membros diversos, mas permanentes.
Uma variedade permanente reprodutível é necessária.
Isso é possível? Vamos usar um exemplo de ensemble treinamento para mostrar isso. O pacote "doRNG" (Reproducible random number generation RNG) será usado. Para a reprodutibilidade dos resultados, é melhor realizar os cálculos em uma thread.
Começamos um novo experimento com um ambiente global limpo. Carregamos as cotações e as bibliotecas necessárias novamente, definimos e classificamos os dados iniciais mais uma vez e selecionamos novamente os melhores preditores do numFeature. Executamos tudo em um script.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) library(doRNG) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) #--1-Data X------------- list( pretrain = list( x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) ), train = list( x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) ), test = list( x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) ), test1 = list( x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) ) ) -> X #---2--bestF----------------------------------- #require(clusterSim) numFeature <- 10 HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX orderX %>% head(numFeature) -> bestF }, env)
Todos os dados iniciais necessários estão prontos. Treinamos o ensemble de redes neurais:
#---3-----Train---------------------------- evalq({ Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y setMKLthreads(1) n <- 500 r <- 7 nh <- 5 k <- 1 rng <- RNGseq(n, 12345) Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) k <- k + 1 idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } setMKLthreads(2) }, env)
O que acontece durante a execução? Definimos os dados de entrada e saída para o treinamento (Xtrain, Ytrain), definimos a biblioteca MKL para o modo single-threaded. Inicializamos certas constantes criando uma sequência de números aleatórios rng, que irá inicializar o gerador de números aleatórios a cada nova iteração de foreach().
Depois de concluir as iterações, não se esqueça de configurar o MKL novamente para o modo multithread. No modo single-threaded, os resultados do cálculo são um pouco piores.
Assim, nós obtemos um ensemble com diferentes classificadores individuais, mas a cada repetição do treinamento, esses classificadores do ensemble permanecerão inalterados. Isto pode ser facilmente verificado repetindo os cálculos de 4 estágios (train/predict/best/test) várias vezes. Ordem de cálculo: train/predict/best/test_averaging/test_voting.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env) #---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) # [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713 #---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.75 0.711 0.770 0.739 # 1 0.75 0.790 0.734 0.761 #--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.749 0.711 0.761 0.735 # 1 0.749 0.784 0.738 0.760
Não importa quantas vezes esses cálculos sejam repetidos (naturalmente, com os mesmos parâmetros), o resultado permanecerá inalterado. Isso é exatamente o que nós precisamos para otimizar os hiperparâmetros das redes neurais que compõem o ensemble.
Primeiro, definimos a lista de hiperparâmetros a serem otimizados, encontramos seus intervalos de valores e escrevemos uma função de avaliação para retornar o critério de otimização (maximização) e a previsão do ensemble. A qualidade dos classificadores individuais é afetada por quatro parâmetros:
- o número de preditores nos dados de entrada;
- o tamanho da amostra utilizada para treinamento;
- o número de neurônios na camada oculta;
- a função de ativação.
Vamos listar os hiperparâmetros e seus intervalos de valores:
evalq({
#type of activation function.
Fact <- c("sig", #: sigmoid
"sin", #: sine
"radbas", #: radial basis
"hardlim", #: hard-limit
"hardlims", #: symmetric hard-limit
"satlins", #: satlins
"tansig", #: tan-sigmoid
"tribas", #: triangular basis
"poslin", #: positive linear
"purelin") #: linear
bonds <- list(
numFeature = c(3L, 12L),
r = c(1L, 10L),
nh <- c(1L, 50L),
fact = c(1L, 10L)
)
}, env)
Vamos examinar o código acima com mais detalhes. Lá, Fact é um vetor de possíveis funções de ativação. A lista bonds define os parâmetros a serem otimizados e seus intervalos de valores.
- numFeature — o número de preditores alimentados como entrada; mínimo 3, máximo 12;
- r — proporção do conjunto de treinamento usado em bootstrap. Antes de calcular, divida-o por 10.
- nh — o número de neurônios na camada oculta; mínimo 1, máximo 50.
- fact — índice da função de ativação no vetor Fact.
Determinação da função de fitness.
#---Fitnes -FUN----------- evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Aqui estão alguns detalhes sobre o script. Movemos o cálculo dos objetivos (Ytrain, Ytest, Ytest1) para fora da função de avaliação, pois eles não são alterados durante a busca de parâmetros. Inicializamos as constantes:
n — o número de redes neurais no ensemble;
numEns — o número dos melhores classificadores individuais (numEns*2 + 1), cujas previsões devem ser combinadas.
A função fitnes() possui 4 parâmetros formais, que devem ser otimizados. Mais tarde na função, treine o ensemble, calcule predict e determine bestNN dos melhores, passo a passo. No final, combine as previsões desses melhores usando a média e calcule as métricas. A função retorna uma lista contendo o critério de otimização Score = mean(F1) e a previsão. Nós vamos otimizar o ensemble que usa a combinação pela média. A função de avaliação para otimizar os hiperparâmetros do ensemble com uma votação por maioria simples é semelhante, exceto para a parte final. Você pode realizar a otimização sozinho.
Vamos verificar a operabilidade da função de avaliação e seu tempo de execução:
#---------- evalq( system.time( res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2) ) , env) user system elapsed 8.65 0.19 7.86
Ele demorou cerca de 9 segundos para obter o resultado para todos os cálculos.
> env$res$Score [1] 0.761
Agora nós podemos iniciar a otimização dos hiperparâmetros com 10 pontos de inicialização aleatórios e 20 iterações. Nós estamos procurando o melhor resultado.
#------ evalq( OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 10, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 23 numFeature = 8.0000 r = 3.0000 nh = 3.0000 fact = 7.0000 Value = 0.7770
Ordenamos o histórico de otimização por Value e selecionamos as 10 melhores pontuações:
evalq({
OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init
best.init
}, env)
numFeature r nh fact Value
1 8 3 3 7 0.777
2 8 1 5 7 0.767
3 8 3 2 7 0.760
4 10 7 9 8 0.759
5 8 5 4 7 0.758
6 8 2 7 8 0.756
7 8 6 9 7 0.755
8 8 3 4 8 0.754
9 9 2 13 9 0.752
10 11 2 24 4 0.751
Interpretamos os hiperparâmetros obtidos do melhor resultado. O número de preditores é 8, o tamanho da amostra é 0.3, o número de neurônios na camada oculta é 3, a função de ativação é "radbas". Isso prova mais uma vez que a otimização Bayesiana fornece um amplo espectro de vários modelos, que provavelmente não serão derivados intuitivamente. É necessário repetir a otimização várias vezes e selecionar o melhor resultado.
Assim, os hiperparâmetros ótimos de treinamento foram encontrados. Teste o ensemble com eles.
Treine e teste o ensemble com os parâmetros ótimos
Teste o ensemble, treinado com os parâmetros ótimos obtidos acima, no conjunto de testes. Determine os melhores membros do grupo, combine seus resultados pela média e veja as métricas finais. O script é mostrado abaixo.
Ao treinar o ensemble de redes neurais, crie-o da mesma maneira que durante a otimização.
#--1-Train--optEns-predict--best--test-average------------------------ evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 #--BestParams-------------------------- best.par <- OPT_Res$Best_Par %>% unname numFeature <- best.par[1] # 8L r <- best.par[2] # 3L nh <- best.par[3] # 3L fact <- best.par[4] # 7L bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(OptEns[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(OptEns[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) -> OptScore caret::confusionMatrix(Ytest1, ensPred) -> cm }, env)
Vamos ver os resultados das 7 melhores redes neurais do ensemble:
> env$Score[env$bestNN] [1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981 0.7099502
O resultado depois de calcular a média das melhores redes neurais:
> env$OptScore Accuracy Precision Recall F1 0 0.778 0.751 0.774 0.762 1 0.778 0.803 0.782 0.793 > env$cm Confusion Matrix and Statistics Reference Prediction 0 1 0 178 52 1 59 212 Accuracy : 0.7784 95% CI : (0.7395, 0.8141) No Information Rate : 0.5269 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5549 Mcnemar's Test P-Value : 0.569 Sensitivity : 0.7511 Specificity : 0.8030 Pos Pred Value : 0.7739 Neg Pred Value : 0.7823 Prevalence : 0.4731 Detection Rate : 0.3553 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7770 'Positive' Class : 0
Este resultado é visivelmente melhor que o de qualquer rede neural individual no ensemble e é comparável aos resultados da DNN com os parâmetros ótimos obtidos no artigo anterior desta série.
Conclusão
- Ensembles de classificadores de redes neurais, compostos por redes neurais ELM simples e rápidas, mostram uma qualidade de classificação comparável à dos modelos mais complexos (DNN).
- A otimização de hiperparâmetros de classificadores individuais no ensemble dá um aumento na qualidade de classificação de até = 0.77 (IC 95% = 0.73 - 0.81).
- A qualidade de classificação de um ensemble com média e um conjunto com votação majoritária é aproximadamente a mesma.
- Após o treinamento, o ensemble mantém sua qualidade de classificação a uma profundidade de mais da metade do tamanho do conjunto de treinamento. Nesse caso, a qualidade é retida para até 750 barras, o que é significativamente maior do que o mesmo valor obtido na DNN (250 barras).
- É possível aumentar significativamente a qualidade de classificação do ensemble otimizando o limite de conversão da variável preditiva contínua para uma variável numérica (calibração, otimização de CutOff, busca genética).
- A qualidade de classificação do ensemble também pode ser aumentada usando um modelo treinável (stacking) como um combinador. Ela pode ser uma rede neural ou um ensemble de redes neurais. Na próxima parte do artigo, essas duas variantes de stacking serão testadas. Nós vamos testar os novos recursos fornecidos pelo grupo de bibliotecas TensorFlow para construir uma rede neural.
Anexos
GitHub/PartVI contém:
- FUN_Ensemble.R — funções necessárias para executar todos os cálculos descritos neste artigo.
- RUN_Ensemble.R — scripts para criar, treinar e testar o ensemble.
- Optim_Ensemble.R — scripts para otimizar os hiperparâmetros das redes neurais no ensemble.
- SessionInfo_RunEns.txt — pacotes usados para criar e testar o ensemble.
- SessionInfo_OptEns.txt — pacotes usados para otimizar os hiperparâmetros do ensemble NN.
- ELM.zip — arquivo de artigos sobre redes neurais ELM.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/4227
 Aplicação do método de Monte Carlo para otimizar estratégias de negociação
Aplicação do método de Monte Carlo para otimizar estratégias de negociação
 Construtor de estratégia visual. Criação de robôs de negociação sem programação
Construtor de estratégia visual. Criação de robôs de negociação sem programação
 Como criar uma Especificação de Requisitos para solicitar um robô de negociação
Como criar uma Especificação de Requisitos para solicitar um robô de negociação
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso