確率最適化と最適制御の例

確率モデリングと制御最適化入門

確率モデリングと制御最適化は、不確実性の中で問題を解決するための数学的手法であり、金融、エンジニアリング、人工知能をはじめとする多くの分野で利用されています。

確率モデリングは、株式市場の価格変動やレストランの行列といったランダムな要素を持つシステムを説明するために用いられ、ランダム変数、確率分布、および確率過程に基づいています。モンテカルロ法やマルコフ連鎖といった手法によって、これらのプロセスをモデル化し、その動作を予測することが可能です。

一方、制御最適化は、システムの制御方法を最適化して、より良いソリューションを見つけるために使用されます。これは、自動車の運転から化学プラントの管理に至るまで、幅広いプロセスの自動化や改善に活用されます。代表的な手法には、線形二次コントローラ、モデル予測制御、強化学習があり、これらにより効率的な制御が可能になります。さらに、確率制御最適化は、確率モデリングと制御最適化の両方を組み合わせたもので、投資やサプライチェーン管理など、将来に関する完全な情報がない状況での意思決定に役立ちます。

これらの手法を活用することで、不確実なシステムのモデル化が可能になり、複雑な環境においても情報に基づいた意思決定を行うための重要なツールとなっています。

EA

SMOC (Smart Money Optimal Control) EAは、テクニカル指標、数学モデル、リスク管理手法を組み合わせ、外国為替市場での取引意思決定を行う機能を備えたシステムです。以下に、主要な特徴を示します。

主な特徴

1. 予測管理モデル：予最適化された管理アルゴリズムを用いて価格変動を予測し、取引を判断します。
2. 適応パラメータ：市場のボラティリティやアカウントのドローダウンに応じ、予測期間やロットサイズを動的に調整します。
3. 複数のテクニカル指標：単純移動平均 (SMA)、パラボリックSAR、相対力指数 (RSI)、ATR (Average True Range)などを使用し、トレンドやボラティリティを分析します。
4. 動的ストップロス(SL)とテイクプロフィット(TP)：市場のボラティリティに応じてSL・TPレベルを計算・更新します。
5. リスク管理：口座残高やドローダウンに基づき、ポジションサイズを動的に調整します。

適用分野

• 中長期の取引戦略
• 明確なトレンドを持つ市場
• 高度なリスク管理が求められるポートフォリオ

長所

1. 適応型アプローチ：変動する市場状況に応じてシステムが適応し、安定性が向上する可能性があります。
2. 複合分析：複数の指標や数学モデルを組み合わせることで、市場のさまざまな側面を総合的に分析します。
3. リスク計算：ドローダウン保護機能と、ポジションサイズの動的決定を含みます。
4. 詳細ログ：パフォーマンス分析やデバッグのためのログファイルを生成します。

短所

1. 複雑さ：高度なアルゴリズムのため、システムの理解や最適化が難しくなる場合があります。
2. 計算負荷：最適制御計算が高負荷となる可能性があり、性能の低いシステムでは動作が制限されることがあります。
3. 過剰適合のリスク：多数のパラメータと指標により、過去のデータに過剰適合するリスクがあります。
4. 市場の仮定依存：本戦略は、過去の価格動向が将来の動きの予測に有効であるという前提に基づいていますが、金融市場では必ずしも当てはまるとは限りません。

SMOC EAの主な特徴

モデル予測制御(MPC)：SMOC EAは、最適制御アルゴリズムを使用して将来の価格変動を予測し、取引判断をおこないます。この機能は、OptimalControl()関数により実装されています。

//+------------------------------------------------------------------+
//| Function for optimal control using Model Predictive Control      |
//+------------------------------------------------------------------+
int OptimalControl( double currentPrice)
  {
   int predictionHorizon = CalculateAdaptiveHorizon();
   double mu = EstimateDrift();
   double sigma = EstimateVolatility();
   double baseThreshold = 0.001 ;
   double decisionThreshold = baseThreshold * ( 1 + ( 1 - successRate));
   double dt = 1.0 / 1440.0 ;

   double bestExpectedReturn = - DBL_MAX ;
   int bestDecision = 0 ;
   double bestU1 = 0 , bestU2 = 0 ;

// Optimize the search space
   double u1Start = 0.01 , u1End = 0.99 , u1Step = 0.01 ;
   double u2Start = 0.01 , u2End = 0.99 , u2Step = 0.01 ;

// Calculate historical average price
   int lookbackPeriod = 20 ; // You can adjust this
   double historicalPrices[];
   ArraySetAsSeries (historicalPrices, true );
   CopyClose ( Symbol (), PERIOD_CURRENT , 0 , lookbackPeriod, historicalPrices);
   double avgHistoricalPrice = ArraySum(historicalPrices) / lookbackPeriod;

   for ( double u1 = u1Start; u1 <= u1End; u1 += u1Step)
     {
       for ( double u2 = u2Start; u2 <= u2End; u2 += u2Step)
        {
         double expectedReturn = CalculateExpectedReturn(currentPrice, mu, sigma, dt, predictionHorizon, u1, u2);

         // Compare with historical average
         if (currentPrice > avgHistoricalPrice)
           {
            expectedReturn *= - 1 ; // Invert expected return to favor selling when price is high
           }

         if (expectedReturn > bestExpectedReturn)
           {
            bestExpectedReturn = expectedReturn;
            bestU1 = u1;
            bestU2 = u2;
           }
        }
     }

   LogMessage( StringFormat ( "OptimalControl - Best u1: %f, Best u2: %f, Best Expected Return: %f, Decision Threshold %f" ,
                           bestU1, bestU2, bestExpectedReturn, decisionThreshold));

   if (bestExpectedReturn > decisionThreshold)
       return 1 ; // Buy
   if (bestExpectedReturn < decisionThreshold)
       return - 1 ; // Sell
   return 0 ; // Hold
  }

これは、モデル予測制御(MPC)を用いて最適な取引判断をおこないます。OptimalControl関数はこのアルゴリズムの中核であり、現在の市場状況と予測に基づいて「買う」「売る」「保持する」のいずれかを判断するよう設計されています。

OptimalControl関数は現在の価格を入力として受け取り、取引の決定を表す整数を返します。

• 1：買う
• -1：売る
• 0：保持

主要コンポーネント

1. 適応予測期間：アルゴリズムが市場の状況に応じて予測範囲を調整できるよう、適応予測期間を計算します。
2. 市場パラメーター評価：主要な市場パラメータを評価します。
   • ドリフト(μ)：資産の期待収益を評価します。
   • ボラティリティ(σ)：資産価格の変動率を測定します。
3. 決定しきい値：基本しきい値とアルゴリズムの成功率に基づき動的なしきい値を設定し、市場の変化に対するアルゴリズムの感度を調整します。
4. 最適化プロセス：グリッドサーチを用いて、定義された検索空間内の2つの制御パラメータ（u1とu2）を最適化します。
5. 過去の価格比較：現在の価格を過去の平均と比較し、価格が相対的に高いか低いかに応じて戦略を適応させます。
6. 期待収益の計算：各制御パラメータの組み合わせについて期待収益を計算します（このコードスニペットには別の関数が用いられます）。
7. 意思決定：最高の期待収益と意思決定しきい値を基に、資産を「購入」「売却」「保有」のいずれかに設定します。

詳細なレビュー

1. 初期化とパラメータ計算：関数はまず、変数の初期化と必要なパラメータの計算から開始します。
2. 最適制御パラメータの探索：次にネストされたループに入り、最適な制御パラメータu1とu2の組み合わせを探索します。
3. 各u1とu2の組み合わせに対して、期待収益が計算されます。
4. 現在の価格が過去の平均を上回る場合、期待収益が逆転されます。これにより、価格が高い場合には「売り」、価格が低い場合には「買い」のバイアスがかかります。
5. 計算中、最高の期待収益とその対応するベンチマークが追跡されます。
6. 最適化が完了した後、最適なパラメータと期待される収益性が記録されます。
7. 最後に、最高の期待収益と取引判断に使用するしきい値を比較し、意思決定をおこないます。

主なアイデア

• アルゴリズムは、適応期間と動的しきい値を活用し、市場の状況に応じて柔軟に適応します。
• 短期的な最適化にはMPCアプローチを使用し、長期的な傾向分析には過去の価格比較を用いることで、相互補完的な意思決定を目指します。
• グリッドサーチによりパラメータ空間を徹底的に調査し、安定した決定を促進します。

改善の可能性

1. グリッドサーチをより効率的な最適化アルゴリズムに置き換えることで、パフォーマンスの向上が期待できます。
2. 過去価格の比較に複数の時間枠を取り入れ、傾向分析の精度を高めることが可能です。
3. リスク管理を導入し、リターンの最適化とリスクの最小化をバランスさせることで、全体的な安定性の向上が見込めます。

 /+------------------------------------------------------------------+
//| Calculate expected return for given parameters                   |
//+------------------------------------------------------------------+
double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)
  {
   double tempPrice = currentPrice;
   double totalReturn = 0 ;

   for ( int i = 0 ; i < horizon; i++)
     {
       double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);
       double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);
      totalReturn += nextPrice - tempPrice;
      tempPrice = nextPrice;
     }

   return totalReturn / horizon;
  }

これは、金融モデルやアルゴリズム取引システムの重要なコンポーネントです。この関数は、幾何ブラウン運動(GBM)と呼ばれる確率過程を使用して、指定された期間における資産の期待収益を推定します。

 double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)

パラメータ

1. currentPrice：資産の現在価格
2. mu：ドリフトパラメータ（期待リターン）
3. sigma：ボラティリティパラメータ
4. dt：時間ステップ（通常、1年につき1/ステップ数）
5. Horizon：シミュレーションする時間ステップ数
6. u1、u2：正規分布の確率変数を生成するための乱数

関数の概要

この関数は、金融数学で株価をモデル化するために広く使用されている幾何ブラウン運動モデルを使用して、資産の価格経路をモデル化します。次に、モデル化された経路に沿った平均収益を計算します。

詳細説明

1. 初期化
   • tempPriceは現在の価格に初期化されます。
   • totalReturnは、リターンを累積するために0に設定されます。
2. シミュレーションループ：ループに入り、水平線を何度も走査します。各反復において：a.ランダムな正規変数を生成します

 double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);

この行は、標準正規確率変数を生成するためのボックス＝ミュラー変換を実装しています。これは資産価格のランダムウォークをモデル化する上で重要な要素です。

価格計算

 double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);

この行は幾何学的ブラウン運動の公式を実装しています。

• (mu - 0.5 * sigma * sigma) * dtはドリフト要素
• sigma * MathSqrt(dt) * Zはランダムショック要素

累積リターン

totalReturn += nextPrice - tempPrice;

各ステップのリターンを計算し、累積します。

価格更新

tempPrice = nextPrice;

現在の価格が次の反復のために更新されます。

平均収穫量の計算

 return totalReturn / horizon;

シミュレートされたホライズンにおける平均リターンを返します。

財務モデリングにおける重要性

1. リスク評価：複数の価格経路をシミュレートすることで、資産に関連する潜在的リスクを評価するのに役立ちます。
2. オプション価格：この種のモデリングは、特にモンテカルロ法によるオプション価格設定モデルの基盤となります。
3. ポートフォリオ最適化：期待収益はポートフォリオ最適化アルゴリズムに不可欠な入力です。
4. 取引戦略：アルゴリズム取引戦略では、期待収益をもとに売買の判断を行うことが多く、戦略の根幹を成します。

制限と考慮事項

1. モデルの仮定GBMモデルはリターンが正規分布し独立していると仮定しますが、実際の市場ではこの仮定が成り立たないこともあります。
2. パラメータ推定の精度：モデルの精度は、リターン率(μ)およびボラティリティ(σ)の正確な推定に依存します。
3. 単一シミュレーションの限界：この関数は単一のシミュレーションのみを実行しますが、より信頼性の高い結果を得るためには複数回のシミュレーションが望まれます。
4. 範囲の影響：シミュレーションの範囲と時間ステップ(dt)は結果に大きく影響するため、特定の用途に応じた慎重な選択が求められます。

この関数は、定量金融の基本構成要素であり、現在の市場パラメータをもとに将来の収益を予測します。取引アルゴリズムにこれを実装することで、データに基づいた意思決定が可能となり、複雑な金融環境での活用が期待されます。

適応パラメータ：システムは、市場のボラティリティと口座のドローダウンに基づいて、予測水平線とロットサイズを調整します。これは、CalculateAdaptiveHorizon()やAdjustLotSizeForDrawdown()などの関数を使用して実現されます。

//+------------------------------------------------------------------+
//| Calculate adaptive horizon                                       |
//+------------------------------------------------------------------+
int CalculateAdaptiveHorizon()
  {
   double currentVolatility = EstimateVolatility();
   int baseHorizon = 5 ;
   return MathMax (baseHorizon, MathMin ( 20 , ( int )(baseHorizon * ( 1 + currentVolatility))));
  }

 // Función para ajustar el tamaño del lote basado en drawdown
double AdjustLotSizeForDrawdown()
  {
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   double drawdown = (maxBalance - currentEquity) / maxBalance;

   double baseLotSize = CalculateDynamicLotSize();

   if (drawdown > 0.1 ) // 10% drawdown
     {
       return baseLotSize * 0.5 ; // Reducir el tamaño del lote a la mitad
     }
   else
       if (consecutiveLosses > 3 )
        {
         return baseLotSize * 0.75 ; // Reducir el tamaño del lote en un 25%
        }

   return baseLotSize;
  }

これは取引リスク管理の重要な要素です。この機能は、現在の口座のドローダウンと連続損失の数に基づいて取引ロットのサイズを調整します。

関数の概要

AdjustLotSizeForDrawdown関数は、変動の激しい市場環境でリスクを管理するために、取引ロットサイズを動的に調整するように設計されています。この関数は、次の2つの主要な要素を考慮します：

1. 取引口座の現在のドローダウン
2. 連敗数

主要コンポーネント

1. 静的変数
   • Losses：連続した負け取引の数を追跡します。
   • maxBalance：口座の最大残高を維持します。
2. 口座情報
   • currentBalance：取引口座の現在の残高
   • currentEquity：取引口座の現在のエクイティ（純資産）
3. ドローダウンの計算：ドローダウンは、最大残高から現在のエクイティまでの減少率として計算されます。
4. 基本ロットサイズ：この関数は、CalculateDynamicLotSize() (このスニペットには示されていません) を呼び出して、基本ロットサイズを決定します。
5. ロットサイズの調整以下の2つの条件に基づいてロットサイズを調整します。
• ドローダウンが10%を超える場合
• 3連敗以上の場合

詳細説明

最大残高更新

 if (currentBalance > maxBalance)
   maxBalance = currentBalance;

これにより、ドローダウンを計算する上で極めて重要な、達成した最大残高を追跡することができます。

ドローダウンの計算

 double drawdown = (maxBalance - currentEquity) / maxBalance;

最大残高に対する現在のドローダウンのパーセンテージを計算します。

基本的なロットサイズの取得

 double baseLotSize = CalculateDynamicLotSize();

初期ロットサイズを計算する別の関数を呼び出します。

ドローダウンが大きい場合の調整

 if (drawdown > 0.1 ) // 10% drawdown
  {
   return baseLotSize * 0.5 ; // Reduce lot size by half
  }

ドローダウンが10%を超えると、この機能はロットサイズを半分に減らしてリスクを軽減します。

連続損失の調整

 else if (consecutiveLosses > 3 )
  {
   return baseLotSize * 0.75 ; // Reduce lot size by 25%
  }

3回以上の連続損失があった場合、この機能はロットサイズを25%縮小します。

デフォルトを返す：いずれの条件も満たさない場合、この関数は調整なしで基本ロットサイズを返します。

リスク管理における重要性

1. ドローダウン保護：大幅なドローダウン時にロットサイズを減少させることで、この機能は不利な市場状況でも口座のさらなる損失を防ぎます。
2. 負け越し管理：連続した負けを調整することで、心理的および経済的に壊滅的な影響を与える連敗のダメージを軽減します。
3. 動的リスク調整：市場状況や取引結果に基づいてリスクを動的に管理できるため、柔軟なリスク対応が可能です。

考察と改善の可能性

1. 段階的な調整：機能を改良し、ドローダウンの程度に応じてロットサイズをより段階的に調整することができます。
2. 回復メカニズム：口座がドローダウンから回復する際、ロットサイズを徐々に増加させるための回復メカニズムを追加することが可能です。
3. 最大ロットサイズ：最大ロットサイズを制限することで、リスク管理の強化が図れます。
4. 勝利の追跡：連勝を追跡し、有利な時期にロットサイズを増やす機能を追加することで、利益を最大化することができます。

この機能は、取引システムにおけるリスク管理の重要な側面を担い、困難な市場状況下でも資本を保護し、連敗の影響を最小化するのに役立ちます。

複数のテクニカル指標：EAには分析用の複数のテクニカル指標が組み込まれています。

• 単純移動平均(SMA)
• Parabolic SAR（パラボリックSAR）
• 相対力指数(RSI)
• ATR (Average True Range)

 // Initialize indicator handles
   smaHandle = iMA ( Symbol (), PERIOD_CURRENT , 50 , 0 , MODE_SMA , PRICE_CLOSE );
   psarHandle = iSAR ( Symbol (), PERIOD_CURRENT , 0.02 , 0.2 );
   rsiHandle = iRSI ( Symbol (), PERIOD_CURRENT , 14 , PRICE_CLOSE );
   atrHandle = iATR ( Symbol (), PERIOD_CURRENT , 14 );

動的ストップロス(SL)とテイクプロフィット(TP)：EAは、CalculateDynamicSL()関数とCalculateDynamicTP()関数を使用して、市場のボラティリティに基づいてSLレベルとTPレベルを計算し、更新します。

 double CalculateDynamicSL( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

   return NormalizeDouble (dynamicSL, _Digits );
  }


double CalculateDynamicTP( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

   return NormalizeDouble (dynamicTP, _Digits );
  }

この機能は、現在の市場のボラティリティに基づいて、動的なストップロス(SL)とテイクプロフィット(TP)のレベルを計算し、リスク管理を改善し、取引結果を改善する可能性があります。

機能レビュー

どちらの機能も、ATR (Average True Range)指標を使用して市場のボラティリティを測定し、それに応じてSLとTPのレベルを調整します。取引が買い(1)か売り(-1)かの決定を考慮します。

 double CalculateDynamicSL( double price, int decision)

この関数は、現在の価格、取引の方向性、市場ボラティリティに基づいて、動的なストップロスレベルを計算します。

 double CalculateDynamicTP( double price, int decision)

この関数は、現在の価格、取引の方向性、市場ボラティリティに基づいて、動的テイクプロフィットレベルを計算します。

主要コンポーネント

1. ATR指標：どちらの関数も、市場のボラティリティを測定するためにATR指標を使用します。
2. 価格：資産の現在の市場価格
3. decision：売買の方向を示す整数（買いの場合は1、売りの場合はおそらく-1）。
4. 乗数：グローバル変数multiは、ボラティリティの影響を調整するために使用されます。

詳細説明

CalculateDynamicSL関数

ATR値の取得：

 double atrValue[];
if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
{
   LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
   return 0.0 ;
}
double volatility = atrValue[ 0 ];

このコードは、市場のボラティリティを反映する最新のATR値を取得します。

動的SLの計算：

 double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

買い取引(solution == 1)では、SLを現在価格より下に設定します。

売り取引では、SLは現在価格より上に設定します。

距離はmulti変数と係数（記事では違いを示すために、買いの場合は1.2、売りの場合は0.8に設定）を使用して調整された ATR の倍数として計算されます。

正規化して戻ります。

 return NormalizeDouble (dynamicSL, _Digits );

SL値は、取引される商品の適切な小数点以下の桁数に正規化されます。

CalculateDynamicTP関数

ATR値の取得：この部分はSL機能と同じです。

動的TPの計算：

 double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

買い取引の場合、TPは現在価格より上に設定されます。

売り取引の場合、TPは現在価格より下に設定されます。

距離はmulti変数と係数（記事では違いを示すために、買いの場合は1.8、売りの場合は02.2に設定しましたが、お好きなように設定できます）を使用して調整されたATRの倍数として計算されます。

SL関数同様、正規化して戻ります。

取引における重要性

1. ボラティリティに基づくリスク管理：ATRを利用して、SLおよびTPレベルを現在の市場状況に適応させ、より効果的なリスク管理を実現します。
2. 非対称なリスクと報酬の比率：TPレベルはSLレベルよりもエントリ価格から遠くに設定されるため、有利なリスク/報酬比率を生み出すことができます。
3. 動的調整：市場のボラティリティが変化するたびに、これらの機能は新しい取引のSLおよびTPレベルを自動的に調整します。

検討事項と改善の可能性

1. エラー処理：両方の関数にはATRを取得するための基本的なエラー処理が組み込まれていますが、これをさらに拡張することができます。
2. 設定の簡素化：乗数（例：1.2、0.8、1.8、2.2）をパラメータに変換することで、設定をより簡単にすることができます。
3. 最小距離：SLおよびTPに最小距離を実装することで、ボラティリティが極端に低い状況での問題発生を防げます。
4. 最大距離：同様に、非常に不安定な状況でのリスクを制限するために、最大距離を設定することも可能です。

これらの機能は、市場の状況に適応してSLおよびTPレベルを設定し、リスクを効果的に管理しつつ取引結果を改善するためのアプローチを提供します。

リスク管理：AdjustLotSizeForDrawdown()およびCalculateDynamicLotSize()に実装されている、口座残高とドローダウンに基づいてポジションサイズを調整する関数が含まれています。

 // Function to adjust the lot size based on drawdown
double AdjustLotSizeForDrawdown()
{
   // Static variables to keep track of consecutive losses and maximum balance
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   // Get current account balance and equity
   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   // Update the maximum balance if current balance is higher
   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   // Calculate the current drawdown as a percentage
   double drawdown = (maxBalance - currentEquity) / maxBalance;

   // Calculate the base lot size using a separate function
   double baseLotSize = CalculateDynamicLotSize();

   // If drawdown is greater than 10%, reduce lot size by half
   if (drawdown > 0.1 ) // 10% drawdown
   {
       return baseLotSize * 0.5 ; // Reduce lot size by half
   }
   else if (consecutiveLosses > 3 )
   {
       return baseLotSize * 0.75 ; // Reduce lot size by 25% after 3 consecutive losses
   }

   // Return the base lot size if no adjustments are needed
   return baseLotSize;
}

このAdjustLotSizeForDrawdown()関数は、口座のドローダウンと最近のパフォーマンスに基づいて取引ロットサイズを動的に調整するように設計されています。主な機能は以下の通りです。

1. 静的変数を使用して、連続損失と達成された最大バランスを追跡します。
2. 最大残高と現在のエクイティを比較することで、現在のドローダウンを計算します。
3. 次の2つのリスク管理戦略を実装します。
   • ドローダウンが10%を超えた場合、ロットサイズは半分になる
   • 3連敗以上の場合、ロットサイズは25%縮小される
4. 基本ロットサイズは、CalculateDynamicLotSize()という別の関数を使用して計算されます。
5. いずれのリスク条件も満たさない場合、この関数は調整なしで基本ロットサイズを返します。

このアプローチは、パフォーマンスの低下やボラティリティの上昇の期間に、影響を軽減することで取引口座を保護するのに役立ちます。これは、アルゴリズム取引で適応型ポジションサイズを実装するシンプルかつ効果的な方法です。

 // Function to dynamically calculate the lot size
double CalculateDynamicLotSize()
{
   // Get current account balance and equity
   double accountBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double equity = AccountInfoDouble ( ACCOUNT_EQUITY );
   double riskPercentage = 0.01 ; // 1% risk per trade

   // Use the lower value between balance and equity to be conservative
   double baseAmount = MathMin (accountBalance, equity);

   // Calculate the value of a pip for the current symbol
   double tickSize = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_SIZE );
   double tickValue = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_VALUE );
   double pipValue = (tickValue / tickSize) * 10 ; // Assuming a pip is 10 ticks

   // Calculate lot size based on desired risk
   double riskAmount = baseAmount * riskPercentage;
   double stopLossPips = 50 ; // Adjust according to your strategy

   double lotSize1 = NormalizeDouble (riskAmount / (stopLossPips * pipValue), 2 );

   // Ensure the lotSize is within the allowed limits
   double minLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MIN );
   double maxLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MAX );
   double lotSize2 = MathMax (minLot, MathMin (maxLot, lotSize1));

   return lotSize2;
}

CalculateDynamicLotSize()関数は、口座残高、リスク許容度、現在の市場状況に基づいて、取引に適したロットサイズを計算するように設計されています。主な機能の内訳は次のとおりです。

1. より保守的なアプローチとして、2つの値のうち低い方の値を使用して経常収支残高と資本を抽出します。
2. 取引ごとに固定のリスクパーセンテージを使用します。この場合は1%に設定されています。
3. 1ピップが10ティックに相当すると仮定して、現在の取引銘柄のピップ値を計算します。
4. その後、バッチサイズが次に基づいて計算されます。
   • リスク額（基準額の1%）
   • あらかじめ設定されたストップロス(pips)（この例では50pipsに設定）
   • アイテムの計算値
5. 計算されたロットサイズが取引銘柄に許可されている最小ロットサイズと最大ロットサイズの範囲内であることを保証します。
6. 最終ロットサイズは、小数点以下2桁に正規化されて返されます。

この動的なロットサイズのアプローチは、口座サイズや市場状況に関係なく、取引のリスクを一定レベルに保つために役立ちます。これはリスク管理戦略の重要な要素であり、先に説明したAdjustLotSizeForDrawdown()関数と連動します。

これら2つの関数を組み合わせることで、次のような強力なリスク管理システムが実現します。

1. 口座のパフォーマンスとドローダウンに基づいてポジションサイズを調整します。
2. 取引ごとのリスクの割合を一定に保ちます。
3. 口座残高や市場環境の変化に対応します。

このアプローチは、有利な市場環境でも厳しい市場環境でも、トレーダーが規律を維持し、資本を保護するのに役立ちます。

重要な関数：

1. OptimalControl(double currentPrice)：EAのコア意思決定機能です。モデル予測制御を使用して、買うか、売るか、保持するかを決定します。予測期間の予想収益を計算し、それを決定しきい値と比較します。
2. CalculateExpectedReturn(...)：OptimalControl関数で使用される特定のパラメータ セットの期待収益を計算します。
3. ManageOpenOrder(int decision)：既存の未決済注文を管理し、未決済バーの数に基づいて注文クローズするかどうか、または現在の決定がポジションと競合するかどうかを決定します。
4. ExecuteTrade(int decision)：OptimalControlの決定に基づいて新しい取引を実行し、適切なストップロスとテイクプロフィットのレベルを設定します。
5. UpdateSLTP(ulong ticket, int decision)：現在の市場状況に基づいて、既存のポジションのストップロスとテイクプロフィットのレベルを更新します。
6. EstimateDrift()およびEstimateVolatility()：最適制御計算で使用される価格ドリフトとボラティリティを推定します。
7. IsTrendFavorable(int decision)および IsLongTermTrendFavorable(int decision)：移動平均とRSIを使用して、現在の市場動向が取引決定と一致しているかどうかを確認します。
8. AdjustLotSizeForDrawdown()およびCalculateDynamicLotSize()：現在のドローダウンと口座残高に基づいて取引量を調整し、動的なリスク管理を実装します。
9. LogMessage(string message)：重要なイベントと決定をファイルに記録し、後で分析およびデバッグできるようにします。

結果

1日間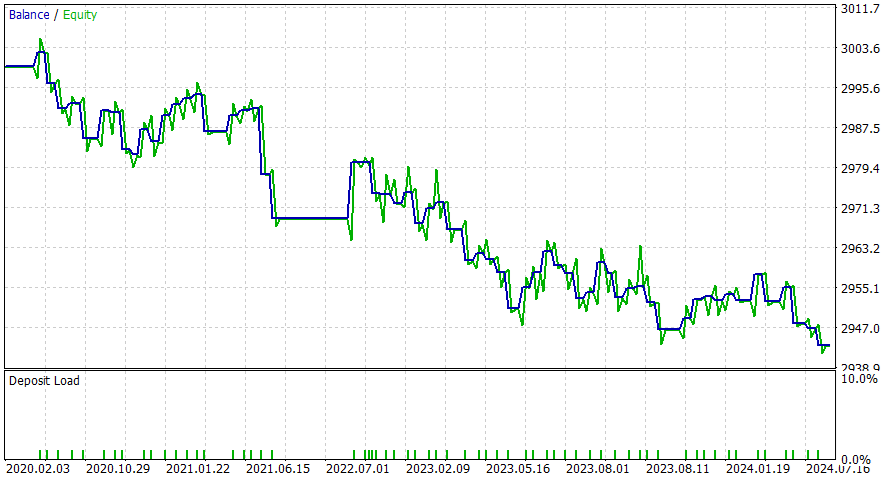

1時間

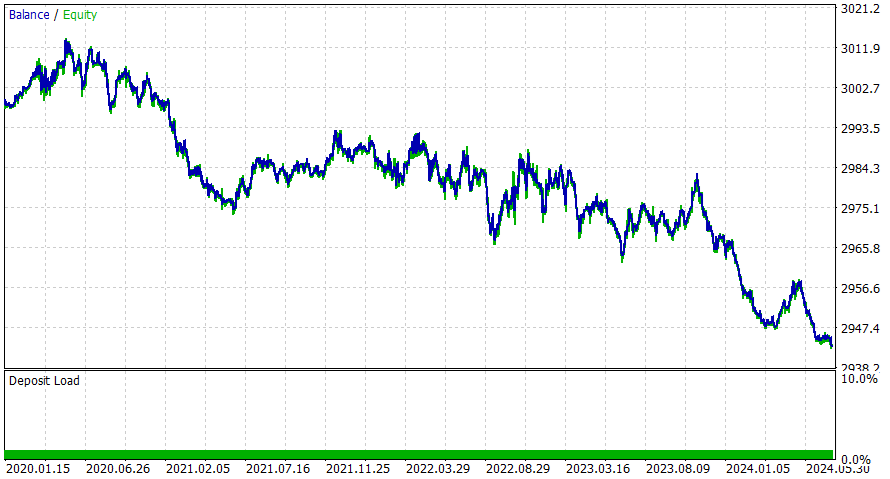
4時間

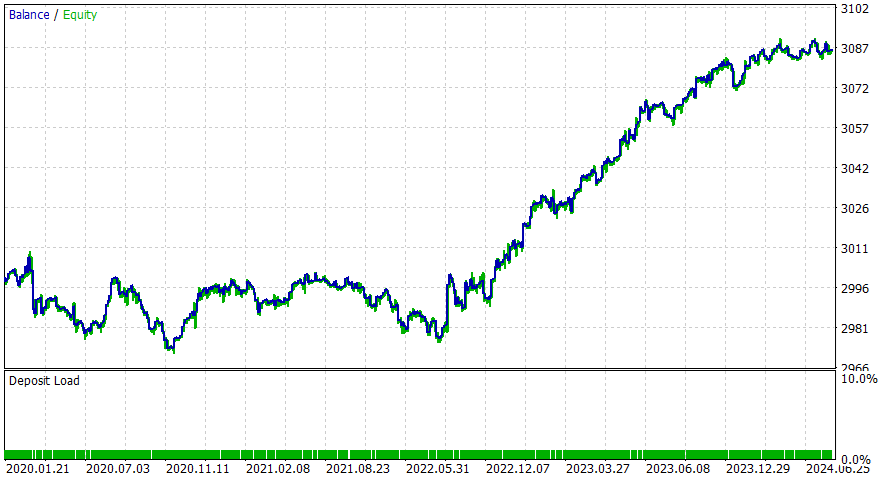
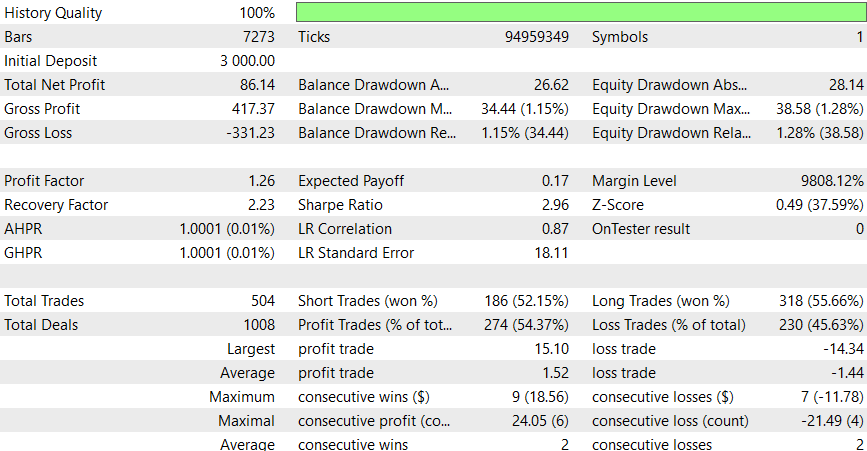
6時間

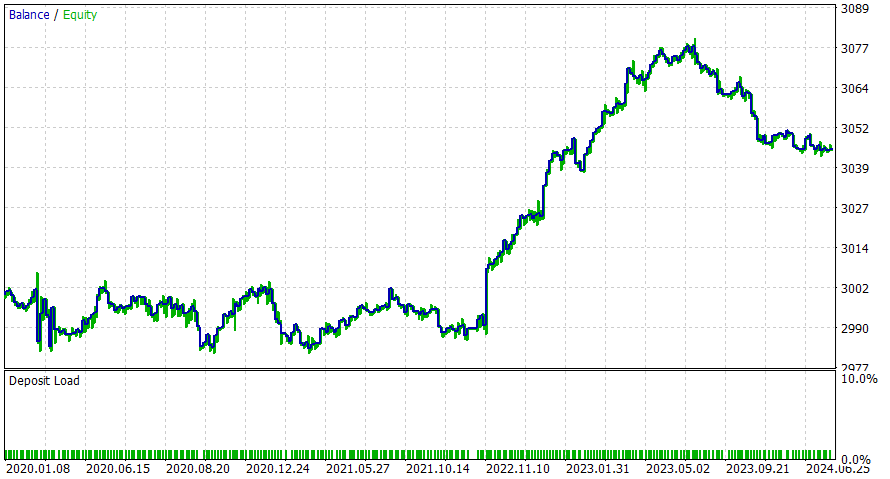
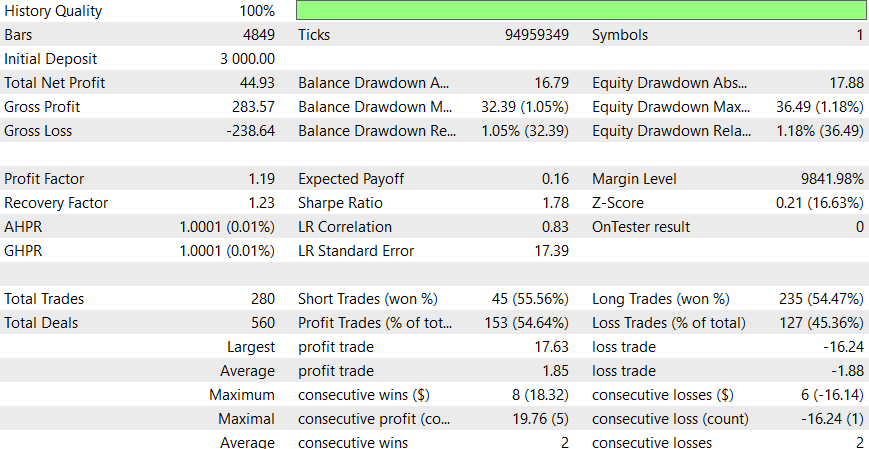
このEAは日中の方がうまく機能するようです。ただし、DL を追加したり、潜在的な改善の考慮を適用したりすることで、より良い結果が得られると確信しています。

結論

SMOC EAは、確率的モデリングと制御の最適化による自動化された取引に対する洗練されたアプローチの簡略版です。移動平均、RSI、ATR、カスタム最適制御アルゴリズムなど、複数の分析方法を組み合わせることで、情報に基づいた取引決定を下すことを目指しています。動的なロットサイズ設定やドローダウンに基づくリスク調整などの機能を備えたこのシステムの適応性は、長期的な持続可能性を重視していることを示しています。ただし、他の取引システムと同様に、実際のパフォーマンスと信頼性を評価するためには、徹底したバックテストとフォワードテストが不可欠です。

以上です。これは高度なEAの単なる簡単な例です。