MetaTrader 5 / Sistemas comerciales
English Русский Deutsch 日本語
preview
Redes neuronales: así de sencillo (Parte 65): Aprendizaje supervisado ponderado por distancia (DWSL)

Redes neuronales: así de sencillo (Parte 65): Aprendizaje supervisado ponderado por distancia (DWSL)

MetaTrader 5 — Sistemas comerciales | 17 abril 2024, 14:01
293 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Introducción

Los métodos de clonación conductual, basados en gran medida en los principios del aprendizaje supervisado, están dando muy buenos resultados. Pero su mayor reto sigue siendo encontrar los modelos perfectos, que a veces resultan muy difíciles de reunir. A su vez, los métodos de aprendizaje por refuerzo son capaces de trabajar con datos de entrada subóptimos. En este caso, encuentra políticas subóptimas para alcanzar el objetivo. No obstante, a la hora de buscar políticas óptimas, a menudo nos enfrentamos a un problema de optimización que resulta más agudo en entornos de alta dimensión y estocásticos.

Para salvar la distancia entre ambos enfoques, se propuso el método Distance Weighted Supervised Learning (DWSL), presentado en el artículo "Distance Weighted Supervised Learning for Offline Interaction Data". Se trata de un algoritmo de aprendizaje offline supervisado para la política dirigida, y, en teoría, converge a una política óptima con un límite de rendimiento mínimo en el nivel de trayectorias de la muestra de entrenamiento. Los ejemplos prácticos de los autores demuestran la superioridad del método propuesto sobre los algoritmos de aprendizaje por imitación y del aprendizaje por refuerzo. Veamos más de cerca este algoritmo DWSL. Evaluaremos de forma práctica sus puntos fuertes y débiles para resolver nuestras tareas.

1. El algoritmo DWSL

Los autores del método Distance Weighted Supervised Learning pretendían obtener un algoritmo capaz de utilizar el mayor conjunto posible de datos para el entrenamiento. Y en este paradigma, se asume que el Agente actúa en un proceso de toma de decisiones determinista de Markov con:

  • el espacio de estados S;
  • el espacio de acciones A;
  • la dinámica determinista de transiciones St+1 = F(St,At), donde St+1 es el nuevo estado del entorno después de ejecutarse la acción At en el estado St;
  • el espacio de objetivos G;
  • la función de recompensa dispersa condicionada a la consecución del objetivo R(S,A,G);
  • el factor de descuento γ.

El espacio de objetivos G es un subespacio del espacio de estados S con una función de dependencia de objetivos G = φ(St), que con frecuencia resulta idéntica a φ(St) = St+n. El objetivo del algoritmo es entrenar una política condicionada al objetivo π(A|S,G), que domina el entorno aprendido y es capaz de alcanzar un objetivo y mantenerse en él después. Para obtener el resultado deseado, maximizaremos el rendimiento descontado de la función de recompensa R(S,A,G) condicionado a la consecución del objetivo G a partir de la distribución de objetivos p(G).

Aunque la formulación de este problema resulta diferente a las anteriores, está estrechamente relacionada con dos formulaciones generales: el problema estocástico del camino más corto y el GCRL.

Los autores del método señalan que el trabajo en el área GCRL supone trayectorias con subobjetivos etiquetados. Estos subobjetivos se especifican mediante la intención política, que proporciona al modelo información sobre la distribución de los objetivos p(G) durante la prueba, lo que limita los datos para la extracción de conocimientos en el aprendizaje offline GCRL. La razón es que muchas fuentes de datos offline no incluyen etiquetas de objetivos (subobjetivos) junto con cada trayectoria. Además, los objetivos pueden ser difíciles de lograr.

Para explorar un conjunto más amplio de datos offline, los autores del método consideran una situación más general, que no implica el acceso a la verdadera dinámica del entorno, las etiquetas de recompensa o la asignación de objetivos durante las fases de prueba y explotación. En la fase de entrenamiento, solo se usa un conjunto de trayectorias de estados y acciones de nivel de optimalidad arbitrario. La distribución p(G) se toma como la distribución de objetivos inducida al aplicar la función de dependencia φ(St) a todos los estados del conjunto de datos. Asumimos que, para la mayoría de los conjuntos de datos prácticos, los objetivos en torno a la distribución de los datos son probablemente cercanos a los objetivos para las tareas de interés. El método DWSL puede usar cualquier función de recompensa dispersa que solo pueda calcularse a partir de las secuencias de estados y acciones disponibles, pero las investigaciones prácticas de los autores del método muestran buenos resultados cuando simplemente se cuenta el número de iteraciones para alcanzar el objetivo.

Intuitivamente, usando la función de recompensa anterior, la mejor estrategia para alcanzar el objetivo G desde el estado actual S consistirá en utilizar el camino con el menor número de pasos de tiempo (camino más corto). No obstante, las trayectorias del conjunto de datos de entrenamiento no siguen necesariamente los caminos más cortos. Como resultado, los métodos de clonación conductual pueden mostrar un comportamiento subóptimo.

Para abordar este problema, el DWSL estima las distancias usando el entrenamiento supervisado y valorando los modelos entrenados dentro de la distribución de datos de la muestra de entrenamiento. El modelo aprende la distribución completa de las distancias entre pares de estados de la muestra de entrenamiento, y utiliza dicha distribución para estimar la distancia mínima al objetivo contenida en el conjunto de datos de cada estado. Luego enseña a la política a seguir dichos caminos. A continuación le mostramos una visualización de autor del método DWSL.

Entre dos estados Si y Sj en la misma trayectoria con i < j, hay al menos un camino de "j - i" pasos de tiempo. Usando esta propiedad generaremos un conjunto de datos etiquetados que contendrá todas las distancias por pares entre estados y objetivos en el conjunto de datos de entrenamiento. Para cada par estado-objetivo seleccionado de la nueva distribución, modelaremos una distribución discreta sobre el número de pasos temporales k desde el estado actual hasta el objetivo, como se muestra en la figura 1, en el extremo izquierdo. Esto nos permitirá obtener una estimación parametrizada de la distribución utilizando el método de máxima verosimilitud en el conjunto de datos etiquetados:

En la práctica, la distribución se modelará como un clasificador discreto sobre las distancias posibles. El camino más corto entre los estados de origen y destino contenidos en el conjunto de datos etiquetados vendrá determinado por el número mínimo de pasos temporales k. Sin embargo, como la distribución se aprende mediante la aproximación de funciones, es probable que la estimación de la distancia mínima explote los errores de modelización. Para minimizar el error anterior, los autores proponen calcular LogSumExp sobre la distribución de distancias para obtener una estimación suave de la distancia mínima:

Tenga en cuenta que, en la fórmula presentada, la distancia se multiplica por "-1" para obtener una estimación del mínimo en lugar del máximo. Aquí α supone un hiperparámetro de la temperatura. Cuando α tiende a "0", el valor de la función d(s, g) se aproximará a la distancia mínima k.

Tras aprender las estimaciones de distancia mínima, queremos usar las trayectorias conocidas que emanan de cada estado. Supongamos que el Agente se encuentra en el estado S y debemos alcanzar el objetivo G. En el estado inicial, el Agente puede realizar una de dos acciones(A1 oA2) que conducirán a los estados S1 y S2, respectivamente. Preferiremos tomar la primera acción si supone el inicio del camino hacia el objetivo con el menor número de pasos (menor distancia estimada al objetivo). Por consiguiente, queremos ponderar las probabilidades de las diferentes acciones por sus estimaciones de la distancia al objetivo (a la derecha de la figura anterior). No obstante, ponderar ingenuamente las acciones de este modo nos dará como resultado una ponderación mayor para todos los puntos de datos cercanos al objetivo, ya que cualquier estado alejado del objetivo tendrá naturalmente una distancia mayor. En su lugar, ponderaremos la probabilidad de las acciones según su reducción en la distancia estimada hasta el objetivo, lo que los autores del método denominaron Ventaja. Esto permite formar un nuevo modelo de entrenamiento del modelo:

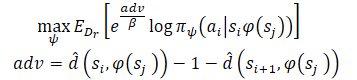
Los autores del método usan la ascensión de grado de Ventajas para garantizar que todas las ponderaciones sean positivas.


2. Implementación con los recursos de MQL5

Después de familiarizarnos con los aspectos teóricos del método Distance Weighted Supervised Learning, pasaremos a la parte práctica de nuestro artículo, donde crearemos nuestra propia variante de implementación utilizando MQL5. Como siempre, trataremos de combinar el algoritmo propuesto con nuestros conocimientos acumulados anteriormente. Y reproduciremos su percepción de los enfoques propuestos. Claro que este enfoque nos aleja en cierta medida del algoritmo del autor y no es una reproducción exacta del mismo, así que las deficiencias que puedan detectarse en el proceso de comprobación solo se aplicarán a esta implementación.

Permítanme decir de entrada que el artículo del autor presenta experimentos sobre el control de robots-manipuladores. En tales circunstancias, fijar objetivos resulta primordial para lograr un resultado positivo. Además, está claro en cada caso. En nuestra aplicación, sin embargo, nos centraremos en maximizar la rentabilidad del robot durante el periodo de entrenamiento. Y para simplificar el modelo, hemos decidido no fijar un subobjetivo en cada paso, lo cual a su vez nos permitirá no entrenar el modelo de fijación de objetivos.

Además, en este documento, entrenaremos el modelo usando enfoques Actor-Crítico. Y usaremos como donante el modelo Actor-Crítico Marginado Estocástico(SMAC). No obstante, lo complementaremos con otros avances. En concreto, añadiremos un mecanismo de ponderación de trayectorias de CWBC. Bien, vayamos por orden. Empezaremos nuestro trabajo describiendo la arquitectura de los modelos.

2.1. Arquitectura de los modelos

Como siempre, la arquitectura de los modelos entrenados se representará en el método CreateDescriptions. En los parámetros del método transmitiremos los punteros a los arrays dinámicos de la descripción de la arquitectura de los 3 modelos:

  • Actor
  • Crítico
  • Codificador aleatorio.

Aquí deberemos recordar que el algoritmo SMAC implica el entrenamiento de un codificador estocástico de estados latentes, que hemos incorporado previamente a la arquitectura del Actor con la capacidad de ser utilizado por el Crítico. En esta aplicación, hemos mantenido esta solución.

En el cuerpo del método comprobaremos los punteros recibidos y, de ser necesario, crearemos nuevos ejemplares del objeto.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
   if(!convolution)
     {
      convolution = new CArrayObj();
      if(!convolution)
         return false;
     }

Suministraremos a la entrada del Actor los datos históricos de los movimientos de precio e indicadores, lo cual se reflejará en el tamaño de su capa de datos de entrada.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Luego suministraremos los datos de origen en la entrada del modelo sin ningún procesamiento previo. Por ello, tras la capa de datos de origen, utilizaremos una capa de normalización de datos por lotes que reunirá los datos de origen obtenidos de diversas fuentes en una forma comparable.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, trataremos de identificar patrones estables en los datos usando capas convolucionales. Y utilizaremos la función SoftMax para obtener una representación probabilística de la atribución de los datos de origen a patrones estables.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = BarDescr;
   int prev_wout = descr.window_out = BarDescr / 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

Tenga en cuenta que estamos buscando patrones estables en el contexto de cada vela individual de los datos históricos.

Los resultados de la búsqueda de patrones se analizarán en 2 capas totalmente conectadas.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A los datos se le añadirá una descripción del estado de la cuenta.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = 2 * LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y generaremos el estado latente estocástico ofrecido por el método SMAC.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación vendrá un bloque de decisión de 2 capas totalmente conectadas.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y en la salida del Actor, pondremos un bloque de autocodificador variacional para hacer la política estocástica. El tamaño de la capa de resultados se corresponderá con la dimensionalidad del vector de acciones del Agente.

//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 13
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

La arquitectura del Crítico se ha trasladado sin cambios. La representación latente del estado del entorno procedente de la capa oculta del Actor se introducirá en la entrada del modelo. Los datos obtenidos no necesitarán convertirse a un formato comparable. Por ello, no usaremos una capa de normalización por lotes en este modelo.

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

A la representación latente le añadiremos las acciones del Actor.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Los datos concatenados se analizarán usando un bloque de decisión de 3 capas totalmente conectadas. El tamaño de la última capa se corresponderá con el tamaño del vector de recompensa descompuesta.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

Al final del método CreateDescriptions, añadiremos una descripción de la arquitectura del codificador aleatorio. Adelantándonos un poco, diremos que el Codificador lo utilizaremos como parte del proceso de determinación de la distancia entre estados del entorno. Usaremos 2 vectores para describir un estado del entorno individual:

  • uno con los datos históricos sobre los movimientos de precio e indicadores;
  • otro con el estado de la cuenta y las posiciones abiertas.

El vector concatenado de estas 2 entidades será lo que suministraremos a la entrada del Codificador.

//--- Convolution
   convolution.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr) + AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

El modelo del codificador no se entrenará. Por consiguiente, el uso de una capa de normalización por lotes no dará el resultado deseado. Por ello, utilizaremos una capa totalmente conectada para llevar los datos a una forma comparable. Después normalizaremos los datos con la capa SoftMax.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = HistoryBars * BarDescr;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = HistoryBars;
   descr.step = BarDescr;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación vendrá un bloque de capas de convolución, que también se cubrirá con una capa SoftMax.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = BarDescr;
   prev_wout = descr.window_out = BarDescr / 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = prev_wout / 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count * prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

En la salida del codificador, utilizaremos una capa completamente conectada que devolverá la incorporación del estado del entorno analizado.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

2.2 Preparación de los métodos auxiliares

Tras describir la arquitectura de los modelos usados, pasaremos a trabajar con la implementación del algoritmo de entrenamiento de los modelos. Pero antes de poner en práctica el propio proceso de aprendizaje, debemos decir unas palabras sobre los métodos que implementarán los bloques individuales del algoritmo general.

En primer lugar, utilizaremos la ponderación y priorización de trayectorias, que ya hemos tratado en el método CWBC. Para ello, moveremos los métodos GetProbTrajectories y SampleTrajectory. Su algoritmo lo describimos detalladamente en el artículo anterior y no nos detendremos en él ahora.

Para el entrenamiento del Actor y el Crítico, utilizaremos recompensas y acciones ponderadas utilizando enfoques del método DWSL. Para evitar operaciones repetitivas, combinaremos el cálculo de los vectores objetivo para ambos modelos en un único método GetTargets, y para poder transferir 2 vectores en una sola operación, crearemos una estructura.

struct STarget
  {
   vector<float>     rewards;
   vector<float>     actions;
  };

Así, el método GetTargets recibirá en sus parámetros:

  • el percentil para determinar el número de estados analizados más próximos de la muestra de entrenamiento;
  • la incorporación del estado analizado;
  • la matriz de incorporaciones de estados en la muestra de entrenamiento;
  • la matriz de recompensas de la muestra de entrenamiento;
  • la matriz de acciones del Agente de la muestra de entrenamiento.

Las 3 últimas matrices se corresponderán entre sí.

El método retornará la estructura de sus 2 vectores objetivo.

STarget GetTargets(int percentile, 
                   vector<float> &embedding, 
                   matrix<float> &state_embedding, 
                   matrix<float> &rewards, 
                   matrix<float> &actions
                  )
  {
   STarget result;

En el cuerpo del método, declararemos la estructura de los resultados y comprobaremos inmediatamente si los tamaños de incorporación del estado analizado se corresponden con los de la matriz de estados de la muestra de entrenamiento.

   if(embedding.Size() != state_embedding.Cols())
     {
      PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__);
      return result;
     }

A continuación, determinaremos la distancia entre el estado analizado y los estados de la muestra de entrenamiento. Utilizaremos LogSumExp, propuesto por los autores del método DWSL, para determinar la distancia suave.

   ulong size = embedding.Size();
   ulong states = state_embedding.Rows();
   ulong k = ulong(states * percentile / 100);
   matrix<float> temp = matrix<float>::Zeros(states, size);
   for(ulong i = 0; i < size; i++)
      temp.Col(MathAbs(state_embedding.Col(i) - embedding[i]), i);
   float alpha=temp.Max();
   vector<float> dist = MathLog(MathExp(temp/(-alpha)).Sum(1))*(-alpha);

A continuación, crearemos matrices locales de recompensa, acción e incorporación, a las que transferiremos los datos de los estados más próximos.

   vector<float> min_dist = vector<float>::Zeros(k);
   matrix<float> k_rewards = matrix<float>::Zeros(k, NRewards);
   matrix<float> k_actions = matrix<float>::Zeros(k, NActions);
   matrix<float> k_embedding = matrix<float>::Zeros(k + 1, size);
   matrix<float> U, V;
   vector<float> S;
   float max = dist.Percentile(percentile);
   float min = dist.Min();
   for(ulong i = 0, cur = 0; (i < states && cur < k); i++)
     {
      if(max < dist[i])
         continue;
      min_dist[cur] = dist[i];
      k_rewards.Row(rewards.Row(i), cur);
      k_actions.Row(actions.Row(i), cur);
      k_embedding.Row(state_embedding.Row(i), cur);
      cur++;
     }
   k_embedding.Row(embedding, k);

Para obtener el vector de recompensas objetivo para el entrenamiento, tendremos que ponderar la matriz de recompensass seleccionadas por la distancia desde el estado analizado. Pero aquí deberemos considerar que la distancia mínima nos ofrecerá el peso mínimo de la recompensa correspondiente. Sin embargo, esto contradice la lógica general: el valor más relevante será el que menos influya en el resultado final. Pero esto tiene fácil arreglo. Bastará con multiplicar el vector de distancia por "-1", mientras que la función SoftMax trasladará los valores obtenidos al plano de las probabilidades. Ahora solo deberemos multiplicar el vector de probabilidades resultante por la matriz de recompensas recogida de los estados más cercanos.   

   vector<float> sf;
   (min_dist*(-1)).Activation(sf, AF_SOFTMAX);
   result.rewards = sf.MatMul(k_rewards);

Aquí añadiremos las normas nucleares para incentivar al Actor a explorar.

   k_embedding.SVD(U, V, S);
   result.rewards[NRewards - 2] = S.Sum() / (MathSqrt(MathPow(k_embedding, 2.0f).Sum() * MathMax(k + 1, size)));
   result.rewards[NRewards - 1] = EntropyLatentState(Actor);

A continuación, tendremos que formar un vector de acción objetivo. Esta vez ponderaremos las acciones según su recompensa preferente. De forma similar al vector distancia, calcularemos el vector de recompensa utilizando la función LogSumExp.

   vector<float> act_sf;
   alpha=MathAbs(k_rewards).Max();   
   dist = MathLog(MathExp(k_rewards/(-alpha)).Sum(1))*(-alpha);

Esta vez la recompensa máxima debería tener el máximo impacto y no necesitaremos invertir los valores. Bastará con trasladar las recompensas a la región de probabilidad usando la función SoftMax. A continuación, multiplicaremos el vector resultante por la matriz de acciones. Escribiremos el resultado obtenido en la estructura. Y retornaremos ambos vectores de valores objetivo al programa de llamada.

Aquí terminaremos el trabajo preparatorio y pasaremos a la implementación del algoritmo principal.

2.3 Asesor de recogida de datos para el entrenamiento

A continuación pasaremos al programa de recogida de datos para el entrenamiento offline del modelo. Al igual que antes, esta tarea se implementará en el asesor "...\DWSL\Research.mq5". No vamos a revisar completamente todo el código de este asesor. La mayoría de sus métodos no han cambiado de un artículo a otro, y los hemos analizado muchas veces en artículos anteriores. Nos centraremos solo en las características clave. Y en primer lugar analizaremos el método OnTick para procesar los ticks, en cuyo cuerpo se implementará el algoritmo principal.

Al principio del método comprobaremos la aparición de un nuevo evento de apertura de una barra y, si es necesario, cargaremos los datos históricos sobre los movimientos de precio y las métricas de los indicadores analizados.

void OnTick()
  {
//---
   if(!IsNewBar())
      return;
//---
   int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates);
   if(!ArraySetAsSeries(Rates, true))
      return;
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();
   Symb.Refresh();
   Symb.RefreshRates();

A partir de los datos obtenidos formaremos un búfer de datos iniciales.

   float atr = 0;
   for(int b = 0; b < (int)HistoryBars; b++)
     {
      float open = (float)Rates[b].open;
      float rsi = (float)RSI.Main(b);
      float cci = (float)CCI.Main(b);
      atr = (float)ATR.Main(b);
      float macd = (float)MACD.Main(b);
      float sign = (float)MACD.Signal(b);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      int shift = b * BarDescr;
      sState.state[shift] = (float)(Rates[b].close - open);
      sState.state[shift + 1] = (float)(Rates[b].high - open);
      sState.state[shift + 2] = (float)(Rates[b].low - open);
      sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f);
      sState.state[shift + 4] = rsi;
      sState.state[shift + 5] = cci;
      sState.state[shift + 6] = atr;
      sState.state[shift + 7] = macd;
      sState.state[shift + 8] = sign;
     }
   bState.AssignArray(sState.state);

Y un búfer de estado de cuenta.

   sState.account[0] = (float)AccountInfoDouble(ACCOUNT_BALANCE);
   sState.account[1] = (float)AccountInfoDouble(ACCOUNT_EQUITY);
//---
   double buy_value = 0, sell_value = 0, buy_profit = 0, sell_profit = 0;
   double position_discount = 0;
   double multiplyer = 1.0 / (60.0 * 60.0 * 10.0);
   int total = PositionsTotal();
   datetime current = TimeCurrent();
   for(int i = 0; i < total; i++)
     {
      if(PositionGetSymbol(i) != Symb.Name())
         continue;
      double profit = PositionGetDouble(POSITION_PROFIT);
      switch((int)PositionGetInteger(POSITION_TYPE))
        {
         case POSITION_TYPE_BUY:
            buy_value += PositionGetDouble(POSITION_VOLUME);
            buy_profit += profit;
            break;
         case POSITION_TYPE_SELL:
            sell_value += PositionGetDouble(POSITION_VOLUME);
            sell_profit += profit;
            break;
        }
      position_discount += profit - (current - PositionGetInteger(POSITION_TIME)) * multiplyer * MathAbs(profit);
     }
   sState.account[2] = (float)buy_value;
   sState.account[3] = (float)sell_value;
   sState.account[4] = (float)buy_profit;
   sState.account[5] = (float)sell_profit;
   sState.account[6] = (float)position_discount;
   sState.account[7] = (float)Rates[0].time;
//---
   bAccount.Clear();
   bAccount.Add((float)((sState.account[0] - PrevBalance) / PrevBalance));
   bAccount.Add((float)(sState.account[1] / PrevBalance));
   bAccount.Add((float)((sState.account[1] - PrevEquity) / PrevEquity));
   bAccount.Add(sState.account[2]);
   bAccount.Add(sState.account[3]);
   bAccount.Add((float)(sState.account[4] / PrevBalance));
   bAccount.Add((float)(sState.account[5] / PrevBalance));
   bAccount.Add((float)(sState.account[6] / PrevBalance));
   double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01');
   bAccount.Add((float)MathSin(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1);
   bAccount.Add((float)MathCos(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1);
   bAccount.Add((float)MathSin(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1);
   bAccount.Add((float)MathSin(2.0 * M_PI * x));

Luego transmitiremos los datos recogidos al modelo del Actor y llamaremos al método de pasada directa. Al mismo tiempo, no nos olvidaremos de controlar el proceso de las operaciones.

   if(bAccount.GetIndex() >= 0)
      if(!bAccount.BufferWrite())
         return;
//---
   if(!Actor.feedForward(GetPointer(bState), 1, false, GetPointer(bAccount)))
      return;

Como resultado de la pasada directa, el modelo del Actor generará un vector de acciones, que decodificaremos. Aquí solo eliminaremos el volumen de operaciones opuestas que no generen beneficios. A diferencia de otros trabajos revisados anteriormente, no añadiremos ruido al vector obtenido para explorar el entorno. La política estocástica del Actor junto con la estocasticidad del estado latente ya generan suficiente variación de acciones para explorar el entorno inmediato del espacio de acciones.

   PrevBalance = sState.account[0];
   PrevEquity = sState.account[1];
//---
   vector<float> temp;
   Actor.getResults(temp);
//---
   double min_lot = Symb.LotsMin();
   double step_lot = Symb.LotsStep();
   double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point();
   if(temp[0] >= temp[3])
     {
      temp[0] -= temp[3];
      temp[3] = 0;
     }
   else
     {
      temp[3] -= temp[0];
      temp[0] = 0;
     }

A continuación, cotejaremos la posición existente con la previsión del Actor y, si es necesario, ejecutaremos operaciones comerciales. Primero para las posiciones largas.

//--- buy control
   if(temp[0] < min_lot || (temp[1] * MaxTP * Symb.Point()) <= stops || (temp[2] * MaxSL * Symb.Point()) <= stops)
     {
      if(buy_value > 0)
         CloseByDirection(POSITION_TYPE_BUY);
     }
   else
     {
      double buy_lot = min_lot + MathRound((double)(temp[0] - min_lot) / step_lot) * step_lot;
      double buy_tp = NormalizeDouble(Symb.Ask() + temp[1] * MaxTP * Symb.Point(), Symb.Digits());
      double buy_sl = NormalizeDouble(Symb.Ask() - temp[2] * MaxSL * Symb.Point(), Symb.Digits());
      if(buy_value > 0)
         TrailPosition(POSITION_TYPE_BUY, buy_sl, buy_tp);
      if(buy_value != buy_lot)
        {
         if(buy_value > buy_lot)
            ClosePartial(POSITION_TYPE_BUY, buy_value - buy_lot);
         else
            Trade.Buy(buy_lot - buy_value, Symb.Name(), Symb.Ask(), buy_sl, buy_tp);
        }
     }

Y luego repetiremos las operaciones para las posiciones cortas.

//--- sell control
   if(temp[3] < min_lot || (temp[4] * MaxTP * Symb.Point()) <= stops || (temp[5] * MaxSL * Symb.Point()) <= stops)
     {
      if(sell_value > 0)
         CloseByDirection(POSITION_TYPE_SELL);
     }
   else
     {
      double sell_lot = min_lot + MathRound((double)(temp[3] - min_lot) / step_lot) * step_lot;;
      double sell_tp = NormalizeDouble(Symb.Bid() - temp[4] * MaxTP * Symb.Point(), Symb.Digits());
      double sell_sl = NormalizeDouble(Symb.Bid() + temp[5] * MaxSL * Symb.Point(), Symb.Digits());
      if(sell_value > 0)
         TrailPosition(POSITION_TYPE_SELL, sell_sl, sell_tp);
      if(sell_value != sell_lot)
        {
         if(sell_value > sell_lot)
            ClosePartial(POSITION_TYPE_SELL, sell_value - sell_lot);
         else
            Trade.Sell(sell_lot - sell_value, Symb.Name(), Symb.Bid(), sell_sl, sell_tp);
        }
     }

Para completar las operaciones del método, todo lo que tendremos que hacer es recoger información del entorno y transferir los datos al búfer de reproducción de experiencias.

   sState.rewards[0] = bAccount[0];
   sState.rewards[1] = 1.0f - bAccount[1];
   if((buy_value + sell_value) == 0)
      sState.rewards[2] -= (float)(atr / PrevBalance);
   else
      sState.rewards[2] = 0;
   for(ulong i = 0; i < NActions; i++)
      sState.action[i] = temp[i];
   sState.rewards[3] = 0;
   sState.rewards[4] = 0;
   if(!Base.Add(sState))
      ExpertRemove();
  }

Llegados a este punto, el proceso de recogida de datos podrá considerarse implementado. Pero no podemos considerar que el trabajo con este asesor esté completo. En el marco de la aplicación del método DWSL, nos gustaría prestar atención a un detalle más. En la parte teórica de este trabajo ya hemos dicho que el método DWSL converge hacia la política óptima con el límite mínimo de rentabilidad a nivel de trayectorias de la muestra de entrenamiento. Y, obviamente, en la búsqueda de una trayectoria óptima, nos gustaría elevar al máximo el listón del límite mínimo de rentabilidad. Para ello, modificaremos el proceso de adición de nuevas trayectorias al búfer de reproducción de experiencias. Tras el rellenado inicial del búfer, iremos sustituyendo gradualmente las pasadas con rendimientos mínimos por otros más rentables. Este proceso se implementará en el método OnTesterPass, que procesará el evento de finalización de la pasada del simulador de estrategias.

En el cuerpo del método, primero inicializaremos las variables locales. E inmediatamente crearemos un ciclo para sondear los frames de las pasadas.  

void OnTesterPass()
  {
//---
   ulong pass;
   string name;
   long id;
   double value;
   STrajectory array[];
   while(FrameNext(pass, name, id, value, array))
     {

En el cuerpo del ciclo, comprobaremos si el frame coincide con el programa actual.

      int total = ArraySize(Buffer);
      if(name != MQLInfoString(MQL_PROGRAM_NAME))
         continue;
      if(id <= 0)
         continue;

Después, el proceso se ramificará según el nivel de rellenado del búfer de reproducción de experiencias. Si el búfer ya está lleno hasta el tamaño máximo especificado, buscaremos en él la pasada con el rendimiento mínimo. Puede tratarse de una pérdida máxima o de un beneficio mínimo.

      if(total >= MaxReplayBuffer)
        {
         for(int a = 0; a < id; a++)
           {
            float min = FLT_MAX;
            int min_tr = 0;
            for(int i = 0; i < total; i++)
              {
               float prof = Buffer[i].States[Buffer[i].Total - 1].account[1];
               if(prof < min)
                 {
                  min = MathMin(prof, min);
                  min_tr = i;
                 }
              }

A continuación, compararemos el valor obtenido con el rendimiento de la última pasada. Y si es superior, simplemente registraremos los datos de la nueva pasada en lugar de la pasada mínima encontrada. Si no, pasaremos a la siguiente pasada.

            float prof = array[a].States[array[a].Total - 1].account[1];
            if(min <= prof)
              {
               Buffer[min_tr] = array[a];
               PrintFormat("Replace %.2f to %.2f -> bars %d", min, prof, array[a].Total);
              }
           }
        }

En el caso de que el búfer aún no esté lleno, simplemente añadiremos una nueva pasada sin operaciones de control innecesarias.

      else
        {
         if(ArrayResize(Buffer, total + (int)id, 10) < 0)
            return;
         ArrayCopy(Buffer, array, total, 0, (int)id);
        }
     }
  }

Aprovecharemos la siguiente prioridad de operaciones:

  1. Rellenado máximo del búfer de reproducción de experiencias para proporcionar a los modelos entrenados la información más completa sobre el entorno.
  2. Tras llenar el búfer de reproducción de experiencias, seleccionaremos las pasadas más rentables para construir la estrategia óptima.

El código completo del asesor y todos sus métodos se presenta en el archivo adjunto. Allí también encontrará el código del asesor de prueba de modelos ".../ DWSL / Test.mq5". Tiene un algoritmo similar al método de procesamiento de ticks, pero está diseñado para una sola ejecución en el simulador de estrategias. Omitiremos su análisis en el marco de este artículo.

2.4 Asesor de entrenamiento de modelos

El proceso de entrenamiento de modelos lo hemos organizado en el asesor "...\DWSL\Study.mq5". Tampoco nos detendremos en un examen detallado de todos sus métodos. Consideraremos únicamente el método Train, en el que se organiza el principal algoritmo de entrenamiento del modelo.

En el cuerpo del método, definiremos el tamaño del búfer de reproducción de experiencias y lo almacenaremos en una variable de estado local del contador de ticks para realizar un seguimiento del tiempo empleado en las operaciones.

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();

A continuación, realizaremos un ciclo a través de todas las trayectorias para contar el número total de estados en el búfer de reproducción de experiencias, lo cual nos permitirá preparar matrices de tamaño suficiente para registrar las incorporaciones de los estados y las correspondientes recompensas y acciones del Agente. Ya hemos visto el uso de estas matrices en el método GetTargets.

   int total_states = Buffer[0].Total;
   for(int i = 1; i < total_tr; i++)
      total_states += Buffer[i].Total;
   vector<float> temp, next;
   Convolution.getResults(temp);
   matrix<float> state_embedding = matrix<float>::Zeros(total_states, temp.Size());
   matrix<float> rewards = matrix<float>::Zeros(total_states, NRewards);
   matrix<float> actions = matrix<float>::Zeros(total_states, NActions);

El siguiente paso consistirá en rellenar los datos de estas matrices. Para ello, organizaremos un sistema de ciclos con una iteración completa de todos los estados del búfer de reproducción de experiencias. En el cuerpo de este sistema de ciclos, recogeremos la descripción de cada estado individual en un único búfer de datos.

   int state = 0;
   for(int tr = 0; tr < total_tr; tr++)
     {
      for(int st = 0; st < Buffer[tr].Total; st++)
        {
         State.AssignArray(Buffer[tr].States[st].state);
         float PrevBalance = Buffer[tr].States[MathMax(st - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(st - 1, 0)].account[1];
         State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance);
         State.Add(Buffer[tr].States[st].account[1] / PrevBalance);
         State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity);
         State.Add(Buffer[tr].States[st].account[2]);
         State.Add(Buffer[tr].States[st].account[3]);
         State.Add(Buffer[tr].States[st].account[4] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[5] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

Y con una pasada directa del codificador generaremos su incorporación.

         if(!Convolution.feedForward(GetPointer(State), 1, false, NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         Convolution.getResults(temp);

Luego almacenaremos el vector resultante en la matriz de incorporación del estado state_embedding.

         if(!state_embedding.Row(temp, state))
            continue;

Mientras que en las matrices de recompensas (rewards) y acciones del Agente (actions) almacenaremos los datos correspondientes del búfer de reproducción de experiencias.

         if(!temp.Assign(Buffer[tr].States[st].rewards) ||
            !next.Assign(Buffer[tr].States[st + 1].rewards) ||
            !rewards.Row(temp - next * DiscFactor, state))
            continue;
         if(!temp.Assign(Buffer[tr].States[st].action) ||
            !actions.Row(temp, state))
            continue;

Nótese que a la matriz de recompensas solo le estamos añadiendo las Ventajas por pasar al siguiente estado. Además, si se produce algún error no finalizaremos el programa por completo, sino que solo pasaremos al siguiente estado. De este modo no completamos todo el proceso de entrenamiento, sino que solo reduciremos ligeramente la base de comparación.

A continuación, incrementaremos el contador de incorporaciones almacenadas. Y antes de pasar a la siguiente iteración de nuestro sistema de ciclos, informaremos al usuario sobre el progreso del proceso de codificación del estado.

         state++;
         if(GetTickCount() - ticks > 500)
           {
            string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states));
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Una vez finalizado el proceso de codificación, reduciremos nuestras matrices al número real de datos completados.

   if(state != total_states)
     {
      rewards.Resize(state, NRewards);
      actions.Resize(state, NActions);
      state_embedding.Reshape(state, state_embedding.Cols());
      total_states = state;
     }

A continuación, prepararemos las variables locales y organizaremos la priorización de las trayectorias. El propio proceso de cálculo de las probabilidades de selección de las trayectorias se situará en un método independiente GetProbTrajectories, cuyo algoritmo presentamos en el artículo anterior.

   vector<float> rewards1, rewards2, target_reward;
   STarget target;
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

Con esto completaremos la fase de preparación de los datos y pasaremos al algoritmo de entrenamiento directo del modelo, que se organizará en un ciclo similar. El número de iteraciones del ciclo de entrenamiento del modelo se especificará en los parámetros externos del asesor.

En el cuerpo del ciclo, primero muestrearemos la trayectoria considerando las probabilidades calculadas anteriormente. El proceso se situará en el método SampleTrajectory, cuyo algoritmo también presentamos en el artículo anterior. Y luego muestrearemos el estado en la trayectoria seleccionada.

   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
   int bar = (HistoryBars - 1) * BarDescr;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i < 0)
        {
         iter--;
         continue;
        }

A continuación, organizaremos el proceso de ramificación según las anteriores iteraciones de aprendizaje. Excluiremos la estimación del estado posterior por los modelos objetivo en la fase inicial, ya que la estimación del estado por parte de los modelos no entrenados resulta completamente aleatoria y puede dirigir el proceso de entrenamiento en la dirección equivocada. A su vez, estimar el estado posterior usando modelos con un nivel de precisión suficiente nos permitirá estimar los rendimientos futuros esperados de la política utilizada en este paso, y así priorizar las acciones pensando en los beneficios subsiguientes.

En este bloque, rellenaremos el búfer de datos de origen con una descripción del estado del entorno posterior. 

         State.AssignArray(Buffer[tr].States[i + 1].state);
         float PrevBalance = Buffer[tr].States[i].account[0];
         float PrevEquity = Buffer[tr].States[i].account[1];
         Account.Clear();
         Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
         Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
         Account.Add(Buffer[tr].States[i + 1].account[2]);
         Account.Add(Buffer[tr].States[i + 1].account[3]);
         Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

Y generaremos las acciones del Agente teniendo en cuenta la política actualizada.

         if(Account.GetIndex() >= 0)
            Account.BufferWrite();
         if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

A continuación, evaluaremos la acción resultante con 2 modelos de críticos objetivo.

         if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

Asimismo, utilizaremos una estimación mínima para calcular la recompensa prevista.

         TargetCritic1.getResults(rewards1);
         TargetCritic2.getResults(rewards2);
         target_reward.Assign(Buffer[tr].States[i + 1].rewards);
         if(rewards1.Sum() <= rewards2.Sum())
            target_reward = rewards1 - target_reward;
         else
            target_reward = rewards2 - target_reward;
         target_reward[NRewards - 1] = EntropyLatentState(Actor);
         target_reward *= DiscFactor;
        }

En el siguiente paso, pasaremos al proceso de entrenamiento de los modelos del Crítico. Estos modelos se entrenarán a partir de los estados y acciones del búfer de reproducción de experiencias.

En primer lugar, copiaremos las descripciones del estado actual del entorno en el búfer de datos de origen.

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);

Y entonces formaremos un búfer de descripción del estado de la cuenta.

      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i].account[2]);
      Account.Add(Buffer[tr].States[i].account[3]);
      Account.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

Los datos recogidos nos permitirán hacer una pasada directa del Actor.

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Tenga en cuenta que realizaremos una pasada directa del Actor antes de entrenar a los Críticos, aunque utilizaremos las acciones del búfer de reproducción de experiencias en el proceso de aprendizaje. Esto se debe al uso del estado latente del Actor como datos de entrada de los Críticos.

Después rellenaremos el búfer de acciones de la base de datos de entrenamiento y llamaremos a los métodos de pasada directa de nuestros Críticos.

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
      //---
      if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) ||
         !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Y aquí usaremos las recompensas ponderadas como valores objetivo para el entrenamiento del modelo. Para obtenerlas, primero añadiremos una descripción del estado de la cuenta al búfer de estado del entorno actual y generaremos una incorporación del estado analizado.

      if(!State.AddArray(GetPointer(Account)) || !Convolution.feedForward(GetPointer(State), 1, false, NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      Convolution.getResults(temp);

El conjunto de datos que tenemos en esta fase será suficiente para llamar al método GetTargets comentado anteriormente, que devolverá los vectores de recompensas y acciones ponderadas.

      target = GetTargets(Percent, temp, state_embedding, rewards, actions);

Con los datos objetivo, podremos realizar una pasada inversa de los modelos del Crítico, pero primero ajustaremos el gradiente de error utilizando el método CAGrad.

      Critic1.getResults(rewards1);
      Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1);
      if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

      Critic2.getResults(rewards2);
      Result.AssignArray(CAGrad(target.rewards + target_reward - rewards2) + rewards2);
      if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

El siguiente paso consistirá en actualizar la política del Actor. Ya hemos realizado antes una pasada directa de modelo. También hemos recibido ya un vector ponderado de acciones específicas. Como consecuencia, dispondremos de todos los datos necesarios para realizar pasadas inversas en la modalidad de aprendizaje supervisado.

      //--- Policy study
      Actor.getResults(rewards1);
      Result.AssignArray(CAGrad(target.actions - rewards1) + rewards1);
      if(!Actor.backProp(Result, GetPointer(Account), GetPointer(Gradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Como podemos ver, al formar el vector de acciones objetivo del Actor, hemos utilizado las Ventajas de acciones extraídas directamente del búfer de reproducción de experiencias. Por consiguiente, no se utilizaban modelos del Crítico entrenados. En este punto, debemos darnos cuenta de que, independientemente de la política del Actor utilizada, su impacto en el movimiento del mercado resulta mínimo. Y sobreestimar la Ventaja utilizando un Crítico aproximado solo podría sesgar los datos según el error de modelización. Y en un paradigma así, entrenar los modelos del Crítico puede parecer una operación superflua. Incluso así, queremos considerar el impacto de la política estudiada en los rendimientos futuros esperados. Para ello, seleccionaremos un Crítico que muestre un error mínimo como resultado del entrenamiento y haremos que evalúe las acciones del Actor generadas por la nueva política. Luego pasaremos el gradiente de desviación de la puntuación obtenida con respecto a la puntuación ponderada al Actor para la optimización de los parámetros.

      CNet *critic = NULL;
      if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError())
         critic = GetPointer(Critic1);
      else
         critic = GetPointer(Critic2);
      if(MathAbs(critic.getRecentAverageError()) <= MaxErrorActorStudy)
        {
         if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         critic.getResults(rewards1);
         Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1);
         critic.TrainMode(false);
         if(!critic.backProp(Result, GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            critic.TrainMode(true);
            break;
           }
         critic.TrainMode(true);
        }

Cabe señalar que las operaciones anteriores solo se realizarán cuando el Crítico esté razonablemente seguro de que la evaluación de las acciones será adecuada. Para regular este proceso, hemos introducido un parámetro externo adicional MaxErrorActorStudy, que definirá el error máximo de estimación del Crítico para permitir el proceso especificado.

Una vez finalizado el proceso de entrenamiento de los modelos, copiaremos los parámetros de los modelos del Crítico entrenados en los modelos objetivo. También debemos señalar aquí que en la fase inicial, antes de incluir el proceso de estimación de estado posterior, transferiremos completamente los parámetros de los modelos entrenados a los modelos objetivo. Y al utilizar el mecanismo de estimación de los estados posteriores, se habilitará el copiado suave de parámetros.

      //--- Update Target Nets
      if(iter >= StartTargetIter)
        {
         TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
         TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
        }
      else
        {
         TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1);
         TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1);
        }

Con esto se completarán las operaciones de una iteración de entrenamiento del modelo. Solo nos quedará informar al usuario sobre el progreso del proceso de entrenamiento del modelo y pasar a la siguiente iteración.

      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), 
                                                                                    Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), 
                                                                                    Critic2.getRecentAverageError());
         str += StringFormat("%-14s %5.2f%% -> Error %15.8f\n", "Actor", iter * 100.0 / (double)(Iterations), 
                                                                                      Actor.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Una vez completadas todas las iteraciones del ciclo de entrenamiento del modelo, borraremos el campo de comentarios en el gráfico del instrumento. Luego informaremos al usuario sobre los resultados del entrenamiento e inicializaremos el proceso de finalización del asesor.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   ExpertRemove();
//---
  }

Con esto, podemos dar por concluida la parte práctica de nuestro artículo. En el archivo adjunto, encontrará el código completo de todos los programas utilizados en este artículo. Procedamos ahora a probar el trabajo realizado.


3. Simulación

Más arriba, hemos trabajado mucho en la implementación de nuestra visión del método DWSL usando MQL5. Debo confesar que ahora tenemos un cierto conglomerado formado por una serie de métodos previamente discutidos, lo cual supone un gran experimento. Y la eficacia de nuestra solución puede comprobarse con datos históricos, que es lo que vamos a hacer.

Como siempre, para el entrenamiento del modelo hemos utilizado los datos históricos de los 7 primeros meses de 2023 del marco temporal EURUSD H1. Los datos para el entrenamiento del modelo se han recopilado en el simulador de estrategias de MetaTrader 5 en el modo de optimización completa de parámetros. En el primer paso, hemos recopilado 500 trayectorias aleatorias. Gracias a nuestra optimización del algoritmo del método OnTesterPass, podemos ejecutar unas cuantas pasadas más. Y los más rentables se seleccionarán en el búfer de reproducción de experiencias.

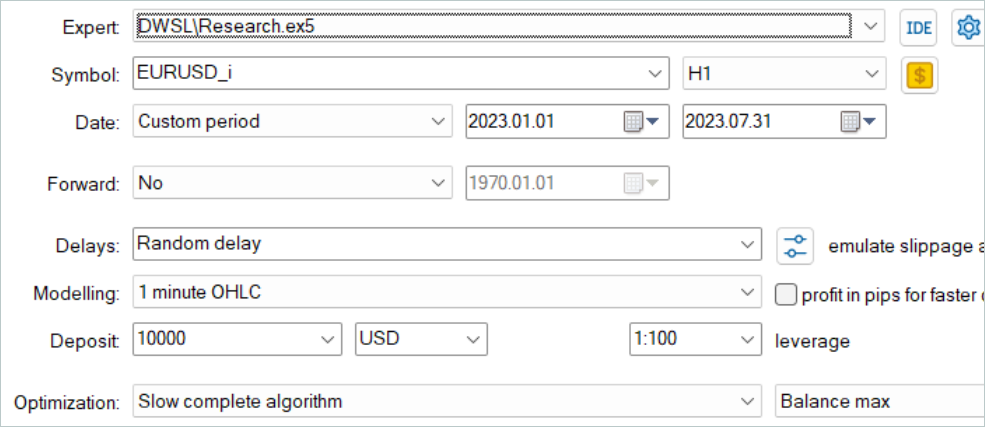
Aquí tenemos que decir de entrada que no debemos aspirar a obtener pasadas lucrativas de políticas aleatorias. En esta fase, se trata de un proceso bastante aleatorio. Y como hemos visto antes, la probabilidad de obtener una pasada totalmente rentable con una política aleatoria en todo el intervalo está cercana a "0". Afortunadamente para nosotros, el método DWSL es capaz de trabajar con datos de origen de cualquier calidad.

Tras recopilar la base de datos de entrenamiento, realizamos la primera ejecución de nuestro asesor de entrenamiento de modelos.

 

Tengo que decir que en este momento no tengo una estrategia totalmente rentable. Y esto se debe en gran medida al bajo rendimiento de las pasadas de la muestra de entrenamiento. No obstante, debemos señalar que el nuevo inicio del asesor de interacción con el entorno ya después del primer ciclo de entrenamiento ha mostrado trayectorias con rendimientos notablemente superiores. Incluso ha aparecido una pasada, posiblemente aleatoria, con beneficio durante todo el periodo de estudio, lo que en general demuestra la eficacia del método y la esperanza de obtener mejores resultados.

Tras varias iteraciones de recopilación de trayectorias y entrenamiento, hemos logrado un modelo que puede generar beneficios de forma sostenible. El modelo resultante se ha probado con datos históricos de agosto de 2023, que no forman parte de la muestra de entrenamiento. Pero como han seguido inmediatamente después al periodo de entrenamiento nos permiten hacer una suposición sobre la comparabilidad de los datos.

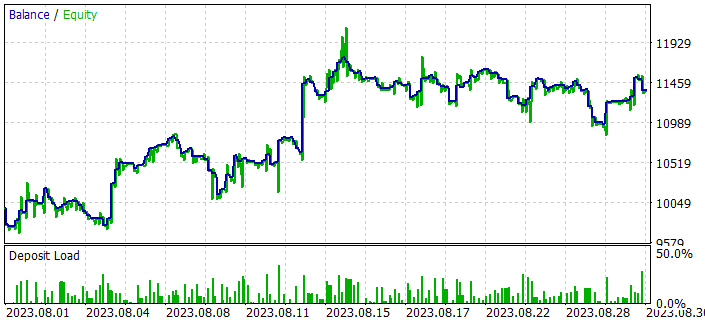
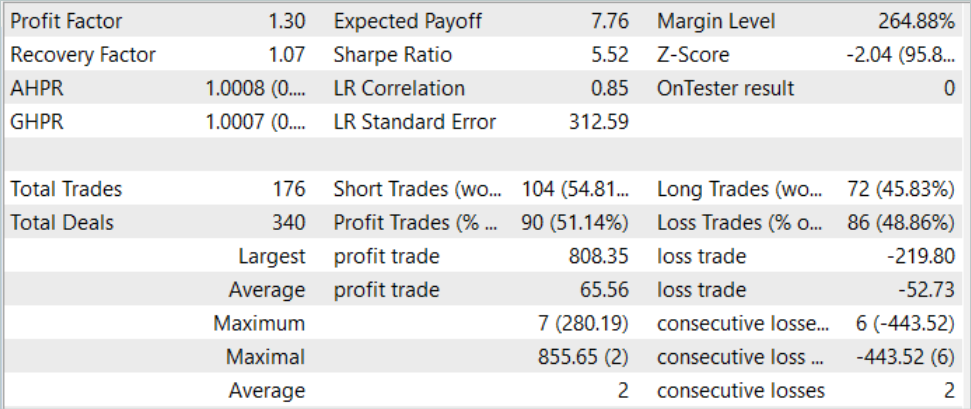
Resultados de las pruebas

Resultados de las pruebas

Según los resultados de las pruebas, el modelo ha sido capaz de obtener beneficios, alcanzando un factor de beneficio de 1,3. El gráfico de balance muestra un crecimiento bastante rápido en la primera mitad del mes. Y además observamos sus fluctuaciones en un rango bastante estrecho. Los resultados positivos incluyen:

  • más del 50% de las posiciones rentables
  • la operación rentable máxima es casi 4 veces superior a la pérdida máxima, mientras que la operación rentable media es casi una cuarta parte superior a la pérdida media
  • Presencia de operaciones en ambos sentidos (60% cortas y 40% largas). Al mismo tiempo, casi el 55% de las posiciones cortas y el 46% de las largas se han cerrado con beneficios.
  • la serie máxima rentable supera a la serie máxima perdedora tanto en número de operaciones como en su suma. 

Los resultados ofrecen una impresión positiva.


Conclusión

En este artículo, hemos introducido otro método interesante para entrenar modelos de Distance Weighted Supervised Learning. El enfoque de estimación ponderada sobre los datos disponibles permite optimizar offline las trayectorias subóptimas recogidas y entrenar políticas bastante interesantes, que posteriormente no muestran malos resultados.

La eficacia del método analizado ha sido confirmada por nuestros resultados prácticos. El entrenamiento ha producido una política capaz de generalizar el material aprendido a nuevos datos, y, en consecuencia, un gráfico de balance rentable durante las pruebas.

No obstante, una vez más me gustaría recordarle que todos los programas presentados en este artículo están destinados únicamente a la demostración de enfoques y no están optimizados para su uso en operaciones reales. 


Enlaces

  • Distance Weighted Supervised Learning for Offline Interaction Data
  • Redes neuronales: así de sencillo (Parte 46): Aprendizaje por refuerzo dirigido a objetivos (GCRL)
  • Redes neuronales: así de sencillo (Parte 53): Descomposición de la recompensa
  • Redes neuronales: así de sencillo (Parte 57): Stochastic Marginal Actor-Critic (SMAC)
  • Redes neuronales: así de sencillo (Parte 62): Uso del transformador de decisiones en modelos jerárquicos

    • Programas utilizados en el artículo:

    # Nombre Tipo Descripción
    1 Research.mq5 Asesor Asesor de recopilación de ejemplos
    2 Study.mq5  Asesor Asesor de entrenamiento de agentes
    3 Test.mq5 Asesor Asesor para la comprobación de modelos
    4 Trayectory.mqh Biblioteca de clases Estructura de descripción del estado del sistema
    5 NeuroNet.mqh Biblioteca de clases Biblioteca de clases para crear una red neuronal
    6 NeuroNet.cl Biblioteca Biblioteca de código de programa OpenCL



    Traducción del ruso hecha por MetaQuotes Ltd.
    Artículo original: https://www.mql5.com/ru/articles/13779

    Archivos adjuntos |
    Descargar ZIP
    MQL5.zip (598.77 KB)
    Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

    Otros artículos del autor

    Pasar a la discusión en el foro de los operadores
    Algoritmos de optimización de la población: Evolución diferencial (Differential Evolution, DE) Algoritmos de optimización de la población: Evolución diferencial (Differential Evolution, DE)
    En este artículo, hablaremos del algoritmo que muestra los resultados más controvertidos entre todos los anteriormente analizados, el algoritmo de Evolución Diferencial (DE).
    Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO) Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO)
    Este artículo presenta un algoritmo de optimización basado en los patrones de las trayectorias en espiral en la naturaleza, como las conchas de los moluscos: el algoritmo de optimización de la dinámica espiral o SDO. El algoritmo propuesto ha sido repensado y modificado a fondo por el autor: en el artículo analizaremos por qué estos cambios han sido necesarios.
    Particularidades del trabajo con números del tipo double en MQL4 Particularidades del trabajo con números del tipo double en MQL4
    En estos apuntes hemos reunido consejos para resolver los errores más frecuentes al trabajar con números del tipo double en los programas en MQL4.
    Creamos un asesor multidivisa sencillo utilizando MQL5 (Parte 4): Media móvil triangular - Señales del indicador Creamos un asesor multidivisa sencillo utilizando MQL5 (Parte 4): Media móvil triangular - Señales del indicador
    Por asesor multidivisa en este artículo entendemos un asesor, o un robot comercial que puede operar (abrir/cerrar órdenes, gestionar órdenes como Trailing Stop Loss y Trailing Profit) con más de un par de símbolos desde un gráfico. Esta vez usaremos un solo indicador, a saber, la media móvil triangular en uno o varios marcos temporales.