MetaTrader 5 / Expert Advisors
Русский Español Deutsch 日本語 Português
preview
Neural networks made easy (Part 41): Hierarchical models

Neural networks made easy (Part 41): Hierarchical models

MetaTrader 5 — Expert Advisors | 24 October 2023, 13:00
1 889 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Introduction

In this article, we will explore the application of hierarchical reinforcement learning in trading. We propose using this approach to create a hierarchical trading model that will be able to make optimal decisions at different levels and adapt to different market conditions.

In this article, we will consider the architecture of the hierarchical model, including various levels of decision making, such as determining entry and exit points for trades. We also present hierarchical model learning methods that combine global-level reinforcement learning and local-level reinforcement learning.

The use of hierarchical learning makes it possible to model complex decision-making structures, as well as effectively use knowledge at different levels. This helps to increase the generalizing ability of the model and its adaptability to changing market conditions.


1. Advantages of hierarchical models

In recent years, the use of hierarchical models in the field of trading has attracted increasing attention and research. Hierarchical learning is a powerful method for modeling complex hierarchical decision-making structures. In trading, this can bring several significant benefits.

The first advantage is the ability of the hierarchical model to adapt to different market conditions. The model can analyze macroeconomic factors at a higher level, such as political events or economic indicators, while at the same time considering microeconomic factors at a lower level, such as technical analysis or asset-specific information. This allows the model to make more informed decisions and adapt to different market situations.

The second benefit relates to more efficient use of available information. Hierarchical models allow you to model and use information at different levels of the hierarchy. High-level strategies can take into account broad trends and tendencies, while low-level strategies can take into account more precise and rapidly changing data. This allows the model to gain a more complete picture of the market and make more informed decisions.

The third advantage of hierarchical models is their ability to allocate computing resources efficiently. High-level strategies can be trained on a larger time scale, while low-level strategies can be more sensitive to rapidly changing data on a small time scale. This allows efficient use of computing resources and speeds up the model training process.

The fourth benefit relates to improved stability and portability of strategies. Hierarchical models have greater generalization power because they are able to model abstract concepts and dependencies at different levels of the hierarchy. This allows building sustainable strategies that can be successfully applied in different conditions and transferred to different markets and assets.

The fifth advantage of using hierarchical models is the ability to break a complex trading problem into simpler subtasks. This reduces the complexity of the task and simplifies the learning process. Each level of the hierarchy may be responsible for certain aspects of trading, such as determining entry and exit points for trades, risk management, or portfolio allocation. This facilitates more efficient model training and improves the quality of its decisions.

Finally, the use of hierarchical models contributes to better interpretability of results and decisions. Because the model has an explicit hierarchical structure, it is easier to understand what factors and variables influence decision making at each level. This allows traders and researchers to better understand the reasons and results of their strategies and make necessary adjustments.

Thus, the use of hierarchical models in trading problems provides a number of advantages, including adaptability to market conditions, efficient use of information, allocation of computing resources, stability and portability of strategies, breaking a complex problem into subproblems, and better interpretability of results. These advantages make hierarchical models a powerful tool for developing successful trading strategies. 

The use of hierarchical models in trading requires special approaches to training. Traditional training methods used in single-level models are not always suitable for hierarchical models due to their complex structure and relationships between levels.

The use of hierarchical learning is one of the specific approaches to training such models. In this case, the model is trained step by step at different levels of the hierarchy, starting from lower levels and successively moving to higher ones. As the model learns at each level, it uses information learned from previous levels, allowing it to capture more abstract dependencies and concepts at higher levels of the hierarchy.

In addition, combining reinforcement learning and supervised learning is important. In this case, the model is trained based on the reward received during the reinforcement task, as well as on the training examples provided at each level of the hierarchy. This approach allows the model to learn from the experiences of other agents and use already acquired knowledge at higher levels of the hierarchy.

An important aspect of training hierarchical models is also their ability to adapt to changing conditions. The model should be flexible and able to quickly adapt to new market conditions and changes in data. For this purpose, dynamic learning can be used, including periodic regularization of the model and updating its parameters based on new data.

One of the striking examples of algorithms for training hierarchical models in trading is Scheduled Auxiliary Control (SAC-X).

The Scheduled Auxiliary Control (SAC-X) algorithm is a reinforcement learning method that uses a hierarchical structure to make decisions. It represents a new approach towards solving problems with sparse rewards. It is based on four main principles:

  1. Each state-action pair is accompanied by a reward vector consisting of (usually sparse) external rewards and (usually sparse) internal auxiliary rewards.
  2. Each reward entry is assigned a policy, called an intent, that learns to maximize the corresponding accumulated reward.
  3. There is a high-level scheduler that selects and executes individual intents with the goal of improving the performance of the external task agent.
  4. Learning occurs outside of policy (asynchronously from policy execution), and experience is exchanged between intentions - for the effective use of information.

The SAC-X algorithm uses these principles to efficiently solve sparse reward problems. Reward vectors allow learning from different aspects of a task and create multiple intentions, each of which maximizes its own reward. The planner manages the execution of intentions by choosing the optimal strategy to achieve external objectives. Learning occurs outside of politics allowing experiences from different intentions to be used for effective learning.

This approach allows the agent to efficiently solve sparse reward problems by learning from external and internal rewards. Using the planner allows coordination of actions. It also involves the exchange of experience between intentions, which promotes the efficient use of information and improves the overall performance of the agent.

SAC-X enables more efficient and flexible agent training in sparse reward environments. A key feature of SAC-X is the use of internal auxiliary rewards, which helps overcome the sparsity problem and facilitate learning on low-reward tasks.

In the SAC-X learning process, each intent has its own policy that maximizes the corresponding auxiliary reward. The scheduler determines which intentions will be selected and executed at any given time. This allows the agent to learn from different aspects of a task and effectively use available information to achieve optimal results.

One of the key advantages of SAC-X is its ability to handle a variety of external applications. The algorithm can be configured to work with different target functions and adapt to different environments and tasks. Thanks to this, SAC-X can be used in a wide range of areas.

In addition, asynchronous exchange of experiences between intentions promotes efficient use of information. The agent can learn from successful intentions and use the acquired knowledge to improve its performance. This allows the agent to quickly and more efficiently find optimal strategies for solving complex problems.

Overall, the Scheduled Auxiliary Control (SAC-X) algorithm is an innovative approach to training agents in sparse reward environments. It combines the use of external and internal auxiliary rewards, a scheduler, and asynchronous learning to achieve high agent performance and adaptability. SAC-X provides new capabilities for solving complex problems and can be applied to a variety of applications where sparse reward is a challenge.

The SAC-X algorithm can be described as follows:

  1. Initialization: Initializing the policies for each intent and their corresponding reward vectors. The scheduler selecting and executing intents is initialized as well.
  2. Training cycle:
    1. Experience collection: The agent interacts with the environment, performing actions based on the selected intent. It collects experience in the form of states, actions, external rewards received and internal auxiliary rewards.
    2. Updating intents: For each intent, the corresponding policy is updated using the collected experience. The policy is adjusted to maximize the cumulative auxiliary reward assigned to this intent.
    3. Planning: The scheduler chooses which intention will be executed in the next step based on the current state and previous executed intentions. The goal of the scheduler is to improve the overall performance of the agent on external tasks.
    4. Asynchronous learning: Updates to policies and the scheduler occur asynchronously, allowing the agent to effectively leverage the information and experience it receives from other intents.
  3. Termination: The algorithm continues the learning loop until it reaches a specified stopping criterion, such as reaching a certain performance or number of iterations.

The SAC-X algorithm allows the agent to effectively use external and internal auxiliary rewards for learning and select the best intentions to achieve optimal results on external tasks. This overcomes the reward sparsity problem and improves agent performance in low reward environments.


2. Implementation using MQL5

The Scheduled Auxiliary Control (SAC-X) algorithm provides for asynchronous training of agents with the possibility of free exchange of experience between different agents. Just like in the previous article, we will divide the entire learning process into 2 stages:

  • Collecting experience
  • Training of policies (strategies of agent behavior)

To collect experience, we will first create 2 structures. We will set a description of a separate state of the system in the first structure SState. It will contain only one static array for storing floating point values.

struct SState
  {
   float             state[HistoryBars * 12 + 9];
   //---
                     SState(void);
   //---
   bool              Save(int file_handle);
   bool              Load(int file_handle);
   //--- overloading
   void              operator=(const SState &obj)   { ArrayCopy(state, obj.state); }
  };

For ease of use, we will create methods for working with Save and Load files in the structure. The method code is quite simple. You can find it in the attachment.

The second STrajectory structure will contain all the information about the accumulated experience of the agent during one pass of the episode. You can see 3 static arrays in it:

  • States - array of states. This is an array of the above created structures, into which all states visited by the agent will be recorded
  • Actions - array of agent actions
  • Revards — array of rewards received from the external environment.

Additionally, we will add 3 variables:

  • Total — number of visited states
  • DiscountFactor — discount factor
  • CumCounted — flag indicating that the cumulative reward is recalculated taking into account the discount factor.

struct STrajectory
  {
   SState            States[Buffer_Size];
   int               Actions[Buffer_Size];
   float             Revards[Buffer_Size];
   int               Total;
   float             DiscountFactor;
   bool              CumCounted;
   //---
                     STrajectory(void);
   //---
   bool              Add(SState &state, int action, float reward);
   void              CumRevards(void);
   //---
   bool              Save(int file_handle);
   bool              Load(int file_handle);
  };

Unlike the above structure for describing a separate state, we will create a constructor for this structure. We will initialize arrays and variables with initial values in it.

STrajectory::STrajectory(void)  :   Total(0),
                                    DiscountFactor(0.99f),
                                    CumCounted(false)
  {
   ArrayInitialize(Actions, -1);
   ArrayInitialize(Revards, 0);
  }

Note that in the constructor we define the total number of states visited to be "0". The flag for calculating the cumulative reward CumCounted is set to 'false'. We will directly calculate the accumulative reward before saving the data to a file. We will need these values when training the model.

Using the Add method, we will add state-action-reward sets to the database.

bool STrajectory::Add(SState &state, int action, float reward)
  {
   if(Total + 1 >= ArraySize(Actions))
      return false;
   States[Total] = state;
   Actions[Total] = action;
   if(Total > 0)
      Revards[Total - 1] = reward;
   Total++;
//---
   return true;
  }

Please note that we save the reward for the previous state since it is received for the transition from the previous state to the current one when performing an action chosen by the agent in the previous state. In this way, we respect the cause-and-effect relationship between action and reward.

The method for calculating CumRevards accumulative rewards is quite simple. But you should pay attention to monitoring the performed calculation flag CumCounted. This is a very important thing. This control prevents repeated calculation of the accumulative reward, which can fundamentally distort the data of the training set, and, as a result, training the model as a whole.

void STrajectory::CumRevards(void)
  {
   if(CumCounted)
      return;
//---
   for(int i = Buffer_Size - 2; i >= 0; i--)
      Revards[i] += Revards[i + 1] * DiscountFactor;
   CumCounted = true;
  }

I suggest you familiarize yourself with the methods of working with files in the attachment. Let's move on to our immediate "workhorses" - our EAs.

We will create the first EA for collecting experience in the Research.mq5 file. We plan to launch the EA in the optimization mode of the strategy tester for parallel collection of experience through several passes of the agent on a training episode of historical data. This is exactly the approach we used in Phase 1 in the previous article. As in the "Fasa1.mql5" EA, we will use the OnTester, OnTesterInit, OnTesterPass and OnTesterDeinit methods to collect and save information from various passes into a single experience accumulation buffer. Now we will use our model to select actions, and not a random value generator, as in the specified EA.

The external EA parameters are copied from the previous ones without changes. In these parameters, we indicate the working timeframe and parameters of the indicators used.

//+------------------------------------------------------------------+
//| Input parameters                                                 |
//+------------------------------------------------------------------+
input ENUM_TIMEFRAMES      TimeFrame   =  PERIOD_H1;
//---
input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod =  9;            //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price
input int                  Agent=1;

Add the Agent parameter to launch the strategy optimizer. It is not used in the EA code and is only needed to regulate the number of agents in the strategy tester optimizer.

In the global variables area, we will declare one element of the SState structure to record the current state of the system. One trajectory structure STrajectory to save the current agent's experience. Declare a static array of trajectories from one element, which we will use to transfer experience between frames.

SState               sState;
STrajectory          Base;
STrajectory          Buffer[];
STrajectory          Frame[1];
CNet                 Actor;
CFQF                 Schedule;
int                  Models = 1;

Here we will also indicate the variables for creating two neural network models: Agent and Scheduler. We will use several agents within one agent model. We will dwell on this issue in more detail when describing the architecture of the models.

There is nothing new in the EA initialization method. We initialize the indicator objects and the trading class, as well as upload pre-trained models. If there are no such models, then we create new ones with random parameters. Find the complete code of the method in the attachment.

I want to dwell on the CreateDescriptions method of describing the architecture of models. We will train our intention agents using the Actor-Critic method. Therefore, we will create a description for three models:

  • Agent (Actor)
  • Critic
  • Scheduler (top-level model of the hierarchy).

Do not be alarmed that global variables were declared for 2 models when creating the architecture description for 3 models. The fact is that we will not train models at the data collection stage. Therefore, the critic functionality is not used. This is why we do not create its model. 

At the same time, in order to create comparable models, we made a common method for declaring the architecture of models. It will be used both at the data collection stage and at the model training stage.

In the method parameters, we receive pointers to 3 objects to transfer the architectures of the created models. In the body of the method, we check the relevance of the received pointers to create new objects if necessary.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *scheduler)
  {
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
//---
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
//---
   if(!scheduler)
     {
      scheduler = new CArrayObj();
      if(!scheduler)
         return false;
     }

First, we create a description of the Actor (agent) architecture. As always, we use the fully connected layer first followed by a data normalization layer.

//--- Actor
   actor.Clear();
   CLayerDescription *descr;
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (int)(HistoryBars * 12 + 9);
   descr.window = 0;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Next, I added another fully connected layer.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 300;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Next, the convolutional layer will try to identify certain patterns in the data.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 100;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

We will process its results with a fully connected layer.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Place another convolutional layer behind it.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 50;
   descr.window = 2;
   descr.step = 2;
   descr.window_out = 4;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

As a result, such a “layer cake” will reduce the data dimension to 100 elements. This architecture will perform data preprocessing.

Next we need to create several intent agents. In order to avoid creating several models, we will use our experience and apply the CNeuronMultiModel class of a multi-model fully connected neural layer. First, we create a fully connected layer of sufficient size.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 1000;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Then we create 2 hidden multi-model fully connected neural layers of 10 models each.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMultiModels;
   descr.count = 200;
   descr.window = 100;
   descr.step = 10;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMultiModels;
   descr.count = 50;
   descr.window = 200;
   descr.step = 10;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

In the final stage of modeling, we create a results output layer, which has its own feature. At the output of our Actor, we should receive a probabilistic distribution of actions. When we considered policy gradient method, we addressed similar issues by normalizing the output with the SoftMax function for a single vector of results. Now we need to normalize the results of 10 models.

By using our fully connected multi-model layer, the results of all 10 models are stored in one matrix. We can use our CNeuronSoftMaxOCL layer to normalize the data. When initializing the layer, we indicate that we need to normalize a matrix consisting of 10 rows.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMultiModels;
   descr.count = 4;
   descr.window = 50;
   descr.step = 10;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = 4;
   descr.step = 10;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

We developed a model with a single data preprocessing unit followed by 10 parallel actors (intention agents). Each actor has a probabilistic distribution of actions at the output.

Similarly, a critic model is created with 10 critics as an output. However, at the output of the critic we expect to receive the value of the 'value' function for each action. Therefore, we do not use the SoftMax layer in the critic model.

The scheduler model in this algorithm is a classic model with one level. However, in the context of this algorithm, the scheduler does not select the agent's action, but selects a specific Actor from our pool to follow its policy in the current situation. The scheduler has the ability to evaluate the current state of the system to select a suitable intent agent. It can also query the states of agents to make a decision.

In this implementation, it is proposed to provide the scheduler with a concatenated vector of the state of the analyzed system and a vector of results from the pool of Actors. This allows the planner to use system state information and Actor outcome evaluations to select a suitable Intent Actor.

In the description of the scheduler model, indicate the source data layer of the appropriate size.

//--- Scheduler
   scheduler.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (int)(HistoryBars * 12 + 9+40);
   descr.window = 0;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }

It is followed by a layer of normalization of the original data.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }

To process the source data, a modular approach similar to that described earlier is used.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 300;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 100;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 50;
   descr.window = 2;
   descr.step = 2;
   descr.window_out = 4;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }

The decision block uses a perceptron with two hidden layers. It is a multi-layer neural network that allows processing and analyzing input data using multiple layers of abstraction and high-level features. Using two hidden layers gives the model greater expressiveness and the ability to capture complex dependencies between input data and output decisions.

At the output of this perceptron, we apply a fully parameterized quantile function. The quantile function allows us to model the conditional distribution of a target variable based on the input data. Instead of predicting a single value, it provides us with information about the probability that the value of the target variable will be within a certain range.

The size of the result layer in the decision block corresponds to the size of our agent pool. This means that each element of the outcome vector represents a probability or score for the corresponding agent in the pool. This allows us to select the best agent or combination of agents based on their scores and probabilities.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFQF;
   descr.count = 10;
   descr.window_out = 32;
   descr.optimization = ADAM;
   if(!scheduler.Add(descr))
     {
      delete descr;
      return false;
     }

The created model architectures provide a wide range of possibilities for assessing the current state of the system and making the optimal decision. Through the use of multi-layer neural networks, models are able to analyze various aspects of input data and extract high-level features that can be associated with effective strategies and decision making.

This allows models to efficiently solve problems with limited data or sparse rewards, and adapt to changing conditions and scenarios.

The OnTick method deserves additional mention. At its beginning, we check whether a new candle is open and collect parameters for the current state of the system. This process is repeated without changes for EAs for several articles in a row, and I will not dwell on it. We then proceed to directly pass through the two models and select an agent action based on their results.

We first perform a forward pass through the pool of Intent Agents.

   State1.AssignArray(sState.state);
   if(!Actor.feedForward(GetPointer(State1), 12, true))
      return;

The obtained results of the direct passage of the agents are concatenated with the current description of the system state and transmitted to the input of the scheduler for evaluation.

   Actor.getResults(Result);
   State1.AddArray(Result);
   if(!Schedule.feedForward(GetPointer(State1),12,true))
      return;

After a forward pass through both models, we use sampling to select a specific intent agent based on their distributions. Then, from the selected agent, we sample a specific action from its probability distribution.

   int act = GetAction(Result, Schedule.getSample(), Models);

It is important to note that we use a model with constant parameters in all passes, without training. Therefore, a greedy choice of agent and action will with a high probability result in a repetition of the same trajectory in each pass. Sampling random values from distributions allows us to explore the environment and obtain different trajectories in each pass. At the same time, the limitation imposed by the distribution makes it possible to conduct research in a given direction.

At the end of the function, we carry out the selected agent action and save the data for later training.

   switch(act)
     {
      case 0:
         if(!Trade.Buy(Symb.LotsMin(), Symb.Name()))
            act = 3;
         break;
      case 1:
         if(!Trade.Sell(Symb.LotsMin(), Symb.Name()))
            act = 3;
         break;
      case 2:
         for(int i = PositionsTotal() - 1; i >= 0; i--)
            if(PositionGetSymbol(i) == Symb.Name())
               if(!Trade.PositionClose(PositionGetInteger(POSITION_IDENTIFIER)))
                 {
                  act = 3;
                  break;
                 }
         break;
     }
//---
   float reward = 0;
   if(Base.Total > 0)
      reward = ((sState.state[240] + sState.state[241]) - 
               (Base.States[Base.Total - 1].state[240] + Base.States[Base.Total - 1].state[241])) / 10;
   if(!Base.Add(sState, act, reward))
      ExpertRemove();
//---
  }

After each pass, information about the actions performed, the system states passed and the reward received is stored in a single buffer for subsequent training of models. These operations are carried out in the OnTester, OnTesterInit, OnTesterPass and OnTesterDeinit methods. Their construction principle was described in detail in the article about the Go-Explore algorithm.

Find the full code of the EA and all its methods in the attachment.

After building the EA to collect experience, we launch it in the optimization mode of the strategy tester and proceed to work on the Study.mq5 model training EA. In the external parameters of this EA, we only indicate the number of training iterations.

//+------------------------------------------------------------------+
//| Input parameters                                                 |
//+------------------------------------------------------------------+
input int                  Iterations     = 100000;

In the block of global variables we already indicate 3 models: Actor, Critic and Scheduler. The architecture of the models was described above.

STrajectory          Buffer[];
CNet                 Actor;
CNet                 Critic;
CFQF                 Scheduler;

In the OnInit function, we first load the training sample that the previous EA creates for us.

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

Load pre-trained or create new models.

//--- load models
   float temp;
   if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) ||
      !Critic.Load(FileName + "Crt.nnw", temp, temp, temp, dtStudied, true) ||
      !Scheduler.Load(FileName + "Sch.nnw", dtStudied, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *critic = new CArrayObj();
      CArrayObj *schedule = new CArrayObj();
      if(!CreateDescriptions(actor, critic, schedule))
        {
         delete actor;
         delete critic;
         delete schedule;
         return INIT_FAILED;
        }
      if(!Actor.Create(actor) || !Critic.Create(critic) || !Scheduler.Create(schedule))
        {
         delete actor;
         delete critic;
         delete schedule;
         return INIT_FAILED;
        }
      delete actor;
      delete critic;
      delete schedule;
     }
   Scheduler.getResults(SchedulerResult);
   Models = (int)SchedulerResult.Size();
   Actor.getResults(ActorResult);
   Scheduler.SetUpdateTarget(Iterations);
   if(ActorResult.Size() % Models != 0)
     {
      PrintFormat("The scope of the scheduler does not match the scope of the Agent (%d <> %d)", 
                                                                     Models, ActorResult.Size());
      return INIT_FAILED;
     }

Initialize the training process start event.

//---
   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

In the Train method, we arrange the direct training process. It is important to note that the training set consists of multiple passes, and in the current implementation we store the states in a sequential trajectory structure rather than combining them all into one common database. This means that to randomly select one state of the system, we need to first select one pass from the array, and then select a state from that pass.

Strictly speaking, we do not associate passages and actions with specific agents of intention. Instead, all agents are trained on a common base of examples. This approach allows us to create interchangeable and consistent agent policies, where each agent can continue executing a policy from any state of the system, regardless of which policy was applied before reaching that state.

At the beginning of the method, we do a little preparatory work: we determine the number of passes in the example database and save the value of the tick counter to control the time of the training process.

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();

After carrying out the preparatory work, we organize a cycle of the model training process.

   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)(((double)MathRand() / 32767.0) * (total_tr - 1));
      int i = 0;
      i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));

Within the training loop, we first select a pass from the training base of examples, as mentioned earlier. We then randomly select a state from the selected pass. This state is passed as input to the forward pass of the Actor and Critic models.

      State1.AssignArray(Buffer[tr].States[i].state);
      if(IsStopped())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         ExpertRemove();
         return;
        }
      if(!Actor.feedForward(GetPointer(State1), 12, true) ||
         !Critic.feedForward(GetPointer(State1), 12, true))
         return;

Upload the obtained results of the direct pass into the corresponding vectors.

      Actor.getResults(ActorResult);
      Critic.getResults(CriticResult);

The resulting vector of results from the Actor's forward pass is concatenated with the system state vector. This combined vector is then fed into the input of the Scheduler model for analysis and evaluation.

      State1.AddArray(ActorResult);
      if(!Scheduler.feedForward(GetPointer(State1), 12, true))
         return;

After performing a forward pass of the scheduler, we apply greedy intent agent selection.

      Scheduler.getResults(SchedulerResult);
      int agent = Scheduler.getAction();
      if(agent < 0)
        {
         iter--;
         continue;
        }

It is important to note that at the beginning of training, sampling can be used to explore the environment as much as possible. However, as the scheduler learns and its strategy improves, we move to greedy agent selection. This is because the planner becomes more experienced and is able to more accurately estimate the states of the system, as well as select the best agent to achieve its goals.

We do not make a decision about choosing an action, since the example database already contains information about the actions performed and the corresponding rewards. From this data, we generate reward vectors for each model and perform the backward pass sequentially for each of them. First we perform a backward pass of the Scheduler.

      int actions = (int)(ActorResult.Size() / SchedulerResult.Size());
      float max_value = CriticResult[agent * actions];
      for(int j = 1; j < actions; j++)
         max_value = MathMax(max_value, CriticResult[agent * actions + j]);
      SchedulerResult[agent] = Buffer[tr].Revards[i];
      Result.AssignArray(SchedulerResult);
      //---
      if(!Scheduler.backProp(GetPointer(Result),0.0f,NULL))
         return;

Then we call the critic's reverse pass method.

      int agent_action = agent * actions + Buffer[tr].Actions[i];
      CriticResult[agent_action] = Buffer[tr].Revards[i];
      Result.AssignArray(CriticResult);
      //---
      if(!Critic.backProp(GetPointer(Result)))
         return;

This is followed by the agent model of intention.

      ActorResult.Fill(0);
      ActorResult[agent_action] = Buffer[tr].Revards[i] - max_value;
      Result.AssignArray(ActorResult);
      //---
      if(!Actor.backProp(GetPointer(Result)))
         return;

At the end of the loop iterations, we check the training time and display information to the user about the training process every 0.5 seconds.

      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("Actor %.2f%% -> Error %.8f\n", 
                                iter * 100.0 / (double)(Iterations), Actor.getRecentAverageError());
         str += StringFormat("Critic %.2f%% -> Error %.8f\n", 
                                iter * 100.0 / (double)(Iterations), Critic.getRecentAverageError());
         str += StringFormat("Scheduler %.2f%% -> Error %.8f\n", 
                                iter * 100.0 / (double)(Iterations), Scheduler.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

After completing the model training process, we log the achieved results and initiate the termination of the EA.

   Comment("");
//---
   PrintFormat("%s -> %d -> %10.7f", __FUNCTION__, __LINE__, Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %10.7f", __FUNCTION__, __LINE__, Critic.getRecentAverageError());
   PrintFormat("%s -> %d -> %10.7f", __FUNCTION__, __LINE__, Scheduler.getRecentAverageError());
   ExpertRemove();
//---
  }

The full Expert Advisor code is available in the attachment. All files of this model are archived in the SAC directory.

The model training process consists of iterations in which we collect examples in optimization mode and run the training process on a real-time chart. If the training result does not meet our expectations, we re-run the example collection operation and re-train the models. These operations are repeated until an optimal result is achieved that meets our learning goals.

Repeated iterations of collecting examples and training models are an integral part of the learning process. They allow us to improve models, adapt them to changing conditions, and strive to achieve optimal results. Each iteration provides us with new data and opportunities to improve our models, allowing us to solve problems more effectively and achieve our goals.

It is important to note that the learning process can be iterative and require several cycles before we achieve the desired result. This is because training models is a complex process that requires constant refinement and improvement. We should be willing to take an iterative approach and be willing to repeat the collection and training operations until we achieve our goals and obtain optimal results.

A system arranged so that the database of examples is constantly updated with each subsequent pass of collecting examples provides us with a significant advantage. This allows us to create the most complete database of examples, which can significantly improve the model’s training and its ability to make optimal decisions.

However, we should keep in mind that increasing the size of the example database has its consequences. First, processing and analyzing larger amounts of data may take longer and require more computing resources. This can lead to longer model training iteration time. Second, increasing the size of the example base can increase training complexity as models should process more data and adapt to more diverse scenarios.


3. Test

The results of training the model on historical EURUSD H1 data for the first 4 months of 2023 showed that the model is capable of generating profit both on the training set and outside it. More than 10 iterations of collecting examples and training the model were conducted, including from 8 to 24 optimization passes in each iteration. In total, more than 200 passes were collected, and the training process included from 100,000 to 10,000,000 iterations.

To check the results of model training, the Test.mq5 EA was created, which used greedy selection of an agent and action instead of sampling. This made it possible to test the operation of the model and eliminate the factor of chance.

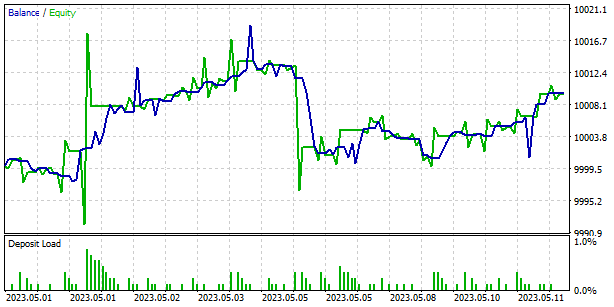
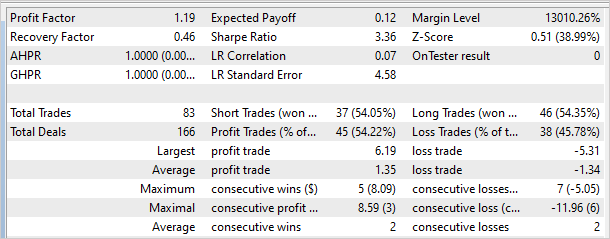
The graph below shows the results of the model outside the training set. Over a short period of time, the model was able to make a small profit. The profit factor was 1.19, and the recovery factor was 0.46.

However, it is worth noting that the balance graph contains unprofitable zones, which may indicate the need for additional iterations of model training. This can help improve its ability to generate profits and reduce the level of risk in trading.

Training results Training results


Conclusion

We can highlight the efficiency of the Scheduled Auxiliary Control (SAC-X) method in training intent agent models for financial markets. SAC-X is an evolution of the classic reinforcement learning approach that takes into account the specifics of financial data and the requirements of trading strategies.

One of the main features of SAC-X is the use of multiple models (Actor, Critic, Planner) to evaluate the state of the system and make decisions. This allows us to take into account various aspects of trading and create a more flexible and adaptive agent policy.

Another important aspect of SAC-X is the use of a scheduler to analyze the state of the system and select the best intent agent. This allows for more efficient and accurate decision making, as well as more consistent trading results.

Testing SAC-X on historical EURUSD data showed its ability to generate profits both on the training set and outside it. However, it should be noted that in some cases unprofitable zones were discovered on the balance chart, which may indicate the need for additional training of the model.

Generally, the Scheduled Auxiliary Control (SAC-X) method is a powerful tool for training intent agent models in the financial industry. It takes into account the specifics of market data, allows you to create adaptive and flexible trading strategies, and demonstrates the potential to achieve stable and profitable trading. Further research and improvement of SAC-X can lead to even better results and expand its application in financial markets.


List of references

  • Learning by Playing – Solving Sparse Reward Tasks from Scratch
  • Neural networks made easy (Part 29): Advantage actor-critic algorithm
  • Neural networks made easy (Part 35): Intrinsic Curiosity Module
  • Neural networks made easy (Part 36): Relational Reinforcement Learning
  • Neural networks made easy (Part 37): Sparse Attention
  • Neural networks made easy (Part 38): Self-Supervised Exploration via Disagreement
  • Neural networks made easy (Part 39): Go-Explore, a different approach to exploration
  • Neural networks made easy (Part 40): Using Go-Explore on large amounts of data



    • Programs used in the article

    # Name Type Description
    1 Research.mq5 Expert Advisor Example collection EA
    2 Study.mql5 Expert Advisor Model training EA
    3 Test.mq5 Expert Advisor Model testing EA
    4 Trajectory.mqh Class library System state description structure
    5 FQF.mqh Class library Class library for arranging the work of a fully parameterized model
    6 NeuroNet.mqh Class library A library of classes for creating a neural network
    7 NeuroNet.cl Code Base OpenCL program code library

    Translated from Russian by MetaQuotes Ltd.
    Original article: https://www.mql5.com/ru/articles/12605

    Attached files |
    Download ZIP
    MQL5.zip (219.34 KB)
    Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

    Other articles by this author

    Go to discussion
    Integrate Your Own LLM into EA (Part 2): Example of Environment Deployment Integrate Your Own LLM into EA (Part 2): Example of Environment Deployment
    With the rapid development of artificial intelligence today, language models (LLMs) are an important part of artificial intelligence, so we should think about how to integrate powerful LLMs into our algorithmic trading. For most people, it is difficult to fine-tune these powerful models according to their needs, deploy them locally, and then apply them to algorithmic trading. This series of articles will take a step-by-step approach to achieve this goal.
    Neural networks made easy (Part 40): Using Go-Explore on large amounts of data Neural networks made easy (Part 40): Using Go-Explore on large amounts of data
    This article discusses the use of the Go-Explore algorithm over a long training period, since the random action selection strategy may not lead to a profitable pass as training time increases.
    Permuting price bars in MQL5 Permuting price bars in MQL5
    In this article we present an algorithm for permuting price bars and detail how permutation tests can be used to recognize instances where strategy performance has been fabricated to deceive potential buyers of Expert Advisors.
    Structures in MQL5 and methods for printing their data Structures in MQL5 and methods for printing their data
    In this article we will look at the MqlDateTime, MqlTick, MqlRates and MqlBookInfo strutures, as well as methods for printing data from them. In order to print all the fields of a structure, there is a standard ArrayPrint() function, which displays the data contained in the array with the type of the handled structure in a convenient tabular format.