
Neural networks made easy (Part 38): Self-Supervised Exploration via Disagreement
Introduction
The exploration problem is a major obstacle in reinforcement learning, especially in cases where the agent receives rare and delayed rewards, which makes it difficult to formulate an effective strategy. One of the possible solutions to this problem is to generate "intrinsic" rewards based on a model of the environment. We have seen a similar algorithm when studying the Intrinsic Curiosity Module. However, most of the created algorithms have only been studied in the context of computer games. But outside of silent simulated environments, training predictive models is challenging due to the stochastic nature of agent-environment interactions. Among the approaches to solving the problem of environmental stochasticity there is the algorithm that Deepak Pathak proposed in his article "Self-Supervised Exploration via Disagreement".
This algorithm is based on a self-learning method, where the agent uses information obtained during interaction with the environment to generate "intrinsic" rewards and update its strategy. The algorithm is based on the use of several agent models that interact with the environment and generate various predictions. If the models disagree, it is considered an "interesting" event and the agent is incentivized to explore that space of the environment. In this way, the algorithm incentivizes the agent to explore new areas of the environment and allows it to make more accurate predictions about future rewards.
1. Algorithm of Exploration via Disagreement
Disagreement-based Exploration is a reinforcement learning method that allows an agent to explore environment without relying on external rewards, but rather by finding new, unexplored areas using an ensemble of models.
In the article "Self-Supervised Exploration via Disagreement", the authors describe this approach and propose a simple method: training an ensemble of forward dynamics models and encouraging the agent to explore the action space where there is maximum inconsistency or variance between the predictions of the models in the ensemble.
Thus, rather than choosing actions that produce the greatest expected reward, the agent chooses actions that maximize disagreement between models in the ensemble. This allows the agent to explore regions of state space where the models in the ensemble disagree and where there are likely to be new and unexplored regions of the environment.
In this case, all models in the ensemble converge to the mean, ultimately reducing the spread of the ensemble and providing the agent with more accurate predictions about the states of the environment and the possible consequences of actions.
In addition, the algorithm of exploration via disagreement allows the agent to successfully cope with the stochasticity of interaction with the environment. The results of experiments conducted by the authors of the article showed that the proposed approach actually improves exploration in stochastic environments and outperforms previously existing methods of intrinsic motivation and uncertainty modeling. In addition, they observed that their approach can be extended to supervised learning, where the value of a sample is determined not based on the ground truth label but based on the state of the ensemble of models.
Thus, the algorithm of exploration via disagreement represents a promising approach to solve the exploration problem in stochastic environments. It allows the agent to explore the environment more efficiently and without having to rely on external rewards, which can be especially useful in real-world applications where external rewards may be limited or costly.
Moreover, the algorithm can be applied in a variety of contexts, including working with high-dimensional data such as images, where measuring and maximizing model uncertainty can be particularly challenging.
The authors of the article demonstrated the effectiveness of the proposed algorithm in several problems, including robot control, Atari games, and maze navigation tasks. As a result of their research, they showed that the algorithm of exploration via disagreement outperforms other exploration methods in terms of speed, convergence, and learning quality.
Thus, this approach to exploration via disagreement represents an important step in the field of reinforcement learning, which can help agents explore the environment better and more efficiently and achieve better results in various tasks.
Let's consider the proposed algorithm.
In the process of interacting with the environment, the agent evaluates the current state Xt and, guided by its internal policy, performs some action At. As a result, the state of the environment changes to a new state Xt+1. A set of such data is stored in an experience replay buffer, which we use to train an ensemble of dynamic models that predict the future environment state.
To maintain independent assessment of the future environment state at the initial stage, all weight matrices of dynamic models in the ensemble are filled with random values. During the training process, each model receives its own random set of training data from the experience replay buffer.
Each model in our ensemble is trained to predict the next state of the real environment. Parts of the state space that have been well explored by the agent have collected enough data to train all models, resulting in consistency between models. As the models are trained, this feature should generalize to unfamiliar but similar parts of the state space. However, regions that are new and unexplored will still have a high prediction error for all models since none of them have been trained on such examples yet. As a result, we have a disagreement in predicting the next state. We therefore use this disagreement as an intrinsic reward for policy direction. Specifically, the intrinsic reward Ri is defined as the variance in the output of different models in the ensemble.
![]()
Please note that in the above formula, the intrinsic reward does not depend on the future state of the system. We will use this property later when implementing this method.
In the case of a stochastic scenario, given a sufficient number of samples, the dynamic prediction model must learn to predict the mean of the stochastic samples. In this way, the dispersion of outputs in the ensemble will decrease, preventing the agent from getting stuck in stochastic local minima of the study. Note that this is different from prediction error-based targets, which will settle to the mean after enough samples. The mean differs from the individual true random states, and the prediction error remains high, which makes the agent always interested in stochastic behavior.
When using the proposed algorithm, each step of the agent's interaction with the environment provides information not only about the reward received from the environment, but also about the information necessary to update the agent's internal model of how the state of the environment changes when performing actions. This allows the agent to extract valuable information about the environment even when there is no explicit external reward.
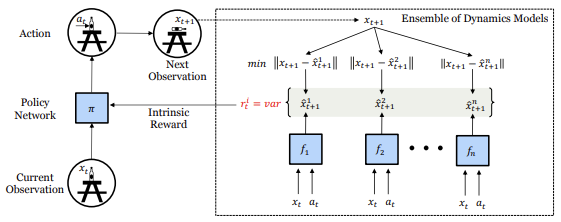
The intrinsic reward iR is used to train the agent's policy, which is calculated as the variance of the outputs of different models in the ensemble. The greater the disagreement between the models' outputs, the higher the value of the intrinsic reward. This allows the agent to explore new areas of state space where the prediction of the next state is uncertain and learn to make better decisions based on this data.
The agent is trained online using data it collects in the process of interacting with the environment. At the same time, the ensemble of models is updated after each interaction of the agent with the environment, which allows the agent to update its internal model about the environment at each step and obtain more accurate predictions of the future environment state.
2. Implementation using MQL5
In our implementation, we will not completely repeat the proposed algorithm, but will only use its main ideas and adjust them to our tasks.
The first thing we will do is ask an ensemble of dynamical models to predict the compressed (hidden) system state, similar to the intrinsic curiosity model. This will allow us to compress the size of the dynamic models and the ensemble as a whole.
The second point is that to determine the intrinsic reward, we do not need to know the true state of the system, but rather the predicted values of dynamic ensemble models. This allows us to use predictive reward not only to stimulate subsequent learning but also to make real-time action decisions. We will not distort external rewards by introducing an intrinsic component when training the agent's policy but will allow it to immediately build a policy for maximizing external rewards. This is our main goal.
However, to maximize learning of the environment during the learning process, when choosing an agent's action, we will add to the predicted reward the variance of the disagreement in dynamic models' predictions for each possible agent's action.
This brings us to another point: to compute predictive states after each action in parallel, we will ask our dynamic models to give us predictions for each possible agent action based on the current state, increasing the size of each model's result layer according to the number of possible actions.
Now that we have defined the main work directions, we can move on to implementing the algorithm. The first question is how to implement an ensemble of dynamic models. All of our previously created models were linear. Parallel computing can be organized using OpenCL tools within one subprocess and one neural layer. Currently it is not possible to implement parallel computing of multiple models. Creating a sequence of calculations for several models leads to a significant increase in the time it takes to train the model.
To solve this issue, I decided to use the method of organizing parallel computing which we used for multi-headed attention. That time we combined the data from all attention heads into single tensors and divided them at the task space level in OpenCL.
We will not now remake our entire library to solve such problems. At this stage, the particular accuracy of the predicted values of the future system state is not important to us. Having the relative synchronous work of the ensemble of models would be enough. Therefore, in dynamic forecasting models we will use fully connected layers.
First, we will create OpenCL program kernels to organize this functionality. The feed forward kernel FeedForwardMultiModels is almost identical with the similar kernel of the base fully connected layer. But there are slight differences.
The kernel parameters remained unchanged. It has three data buffers (weight matrix, source data, and results tensors), as well as two constants: the size of the source data layer and the activation function. But previously, we specified the full size of the previous layer as the size of the source data layer. Now we expect to receive the number of elements of the current model.
__kernel void FeedForwardMultiModels(__global float *matrix_w, __global float *matrix_i, __global float *matrix_o, int inputs, int activation ) { int i = get_global_id(0); int outputs = get_global_size(0); int m = get_global_id(1); int models = get_global_size(1);
In the kernel body, we first identify the current thread. You can notice here the appearance of a second dimension of the problem space, which identifies the current model. The overall dimension of the problems will indicate the size of the ensemble.
Next, we declare the necessary local variables and define the offset in the data buffers, taking into account the neuron being computed and the current model in the ensemble.
float sum = 0; float4 inp, weight; int shift = (inputs + 1) * (i + outputs * m); int shift_in = inputs * m; int shift_out = outputs * m;
The actual mathematical part of calculating the neuron state and the activation function remained unchanged. We have only added offset adjustment in data buffers.
for(int k = 0; k <= inputs; k = k + 4) { switch(inputs - k) { case 0: inp = (float4)(1, 0, 0, 0); weight = (float4)(matrix_w[shift + k], 0, 0, 0); break; case 1: inp = (float4)(matrix_i[shift_in + k], 1, 0, 0); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], 0, 0); break; case 2: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], 1, 0); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], 0); break; case 3: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], matrix_i[shift_in + k + 2], 1); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], matrix_w[shift + k + 3]); break; default: inp = (float4)(matrix_i[shift_in + k], matrix_i[shift_in + k + 1], matrix_i[shift_in + k + 2], matrix_i[shift_in + k + 3]); weight = (float4)(matrix_w[shift + k], matrix_w[shift + k + 1], matrix_w[shift + k + 2], matrix_w[shift + k + 3]); break; } float d = dot(inp, weight); if(isnan(sum + d)) continue; sum += d; }
Once the value of the activation function specified in the parameters is calculated, the result is saved into the matrix_o data buffer.
if(isnan(sum)) sum = 0; switch(activation) { case 0: sum = tanh(sum); break; case 1: sum = 1 / (1 + exp(-sum)); break; case 2: if(sum < 0) sum *= 0.01f; break; default: break; } matrix_o[shift_out + i] = sum; }
This solution allows us to parallelly calculate the value of one layer of all models in the ensemble in one kernel. Of course, it has a limitation: here the architecture of all models in the ensemble is identical, the only differences are in the weighting coefficients.
The situation with the reverse pass is a little different. The algorithm provides for training dynamic models in an ensemble on a different set of training data. We will not create separate training packages for each model. Instead, on each backward pass, we will train only one, randomly selected model from the ensemble. For other models, we will pass the zero gradient to the previous layer. These are the changes we will make to the gradient distribution kernel algorithm inside the CalcHiddenGradientMultiModels layer.
A similar kernel of the base fully connected neural layer receives pointers to four data buffers and two variables in its parameters. This is the tensor of the weight matrix and the tensor of the previous layer results for calculating the derivative of the activation function. There are also 2 gradient buffers: the current and previous neural layers. The first contains the received error gradients, and the second is used to record the results of the kernel and transfer the error gradient to the previous neural layer. In variables, we indicate the number of neurons in the current layer and the activation function of the previous layer. To the specified parameters we add the identifier of the trained model, which we will randomly select on the side of the main program.
__kernel void CalcHiddenGradientMultiModels(__global float *matrix_w, __global float *matrix_g, __global float *matrix_o, __global float *matrix_ig, int outputs, int activation, int model ) {
In the kernel body, we first identify the thread. As in the feed forward kernel, we use a two-dimensional problem space. In the first dimension, we identify the flow within a single model, and the second dimension indicates the model in the ensemble. To collect error gradients, we run a kernel in the context of the neurons of the previous layer. Each thread collects error gradients from all directions on one single neuron.
int i = get_global_id(0); int inputs = get_global_size(0); int m = get_global_id(1); int models = get_global_size(1);
Please note that we will distribute the gradient over only one model, but we will launch threads for the entire ensemble. This is due to the need to reset the error gradient of other models. In the next step, we check whether the gradient needs to be updated for a specific model. If we only need to reset the gradient, then we execute only this function and exit the kernel without performing unnecessary operations.
//--- int shift_in = inputs * m; if(model >= 0 && model != m) { matrix_ig[shift_in + i] = 0; return; }
Here we leave a small loophole for possible future use. If you specify a negative number as the model number to update, the gradient will be calculated for all models in the ensemble.
Next we declare local variables and define offsets in the data buffers.
//--- int shift_out = outputs * m; int shift_w = (inputs + 1) * outputs * m; float sum = 0; float out = matrix_o[shift_in + i]; float4 grad, weight;
This is followed by the mathematical part of the error gradient distribution, which completely repeats the similar functionality of the basic fully connected neuron. Of course, we add the necessary offset in the data buffers. The result of the operations is saved into the gradient buffer of the previous layer.
for(int k = 0; k < outputs; k += 4) { switch(outputs - k) { case 1: weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], 0, 0, 0); grad = (float4)(matrix_g[shift_out + k], 0, 0, 0); break; case 2: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], 0, 0); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], 0, 0); break; case 3: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], matrix_g[shift_out + k + 2], 0); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], matrix_w[shift_w + (k + 2) * (inputs + 1) + i], 0); break; default: grad = (float4)(matrix_g[shift_out + k], matrix_g[shift_out + k + 1], matrix_g[shift_out + k + 2], matrix_g[shift_out + k + 3]); weight = (float4)(matrix_w[shift_w + k * (inputs + 1) + i], matrix_w[shift_w + (k + 1) * (inputs + 1) + i], matrix_w[shift_w + (k + 2) * (inputs + 1) + i], matrix_w[shift_w + (k + 3) * (inputs + 1) + i]); break; } sum += dot(grad, weight); } if(isnan(sum)) sum = 0; switch(activation) { case 0: out = clamp(out, -1.0f, 1.0f); sum = clamp(sum + out, -1.0f, 1.0f) - out; sum = sum * max(1 - pow(out, 2), 1.0e-4f); break; case 1: out = clamp(out, 0.0f, 1.0f); sum = clamp(sum + out, 0.0f, 1.0f) - out; sum = sum * max(out * (1 - out), 1.0e-4f); break; case 2: if(out < 0) sum *= 0.01f; break; default: break; } matrix_ig[shift_in + i] = sum; }
Next, we have to modify the weight matrix update kernel UpdateWeightsAdamMultiModels. As in the error gradient distribution kernel, we will add a model identifier to the existing kernel parameters of the base fully connected layer.
Pay attention that a similar kernel of the base neural layer is already running in a two-dimensional task space. At the same time, we do not need to perform any operations with non-updating models. Therefore, we will call the kernel only for one model, and we will use the model identifier parameter to determine the offset in the data buffers. Otherwise, the kernel algorithm remained unchanged. You can find the entire algorithm in the attachment.
This completes the work on the OpenCL side of the program. Next, we move on to working with the code of our MQL5 library. Here we will create a new class CNeuronMultiModel as a descendant of our base class CNeuronBaseOCL.
The set of class methods is quite standard and includes methods for class initialization, working with files, feed forward and back propagation passes. We also introduce two new variables, in which we will record the number of models in the ensemble and the model identifier to be trained. The latter will change with each return pass.
class CNeuronMultiModel : public CNeuronBaseOCL { protected: int iModels; int iUpdateModel; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronMultiModel(void){}; ~CNeuronMultiModel(void){}; virtual bool Init(uint numInputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, int models); virtual void SetActivationFunction(ENUM_ACTIVATION value) { activation = value; } //--- virtual bool calcHiddenGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronMultiModels; } };
In a class, we do not create new internal objects, so the constructor and destructor of the class remain empty. Let's begin our work on creating methods with the Init class initialization method. The method receives in parameters:
- numInputs — number of neurons in the previous layer for one model
- open_cl — pointer to an OpenCL object
- numNeurons — number of neurons in a layer of one model
- models — number of models in the ensemble.
bool CNeuronMultiModel::Init(uint numInputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, int models) { if(CheckPointer(open_cl) == POINTER_INVALID || numNeurons <= 0 || models <= 0) return false;
In the method body, we immediately check if the pointer to the OpenCL object is relevant and if the dimensions of the layer and ensemble are specified correctly. After that we save the necessary constants into internal variables.
OpenCL = open_cl;
optimization = ADAM;
iBatch = 1;
iModels = models;
Please note that we created the weight matrix update kernel for only the Adam method. Therefore, we will specify this method for optimizing the model regardless of what is obtained in the parameters.
After this, we create buffers to record the results of the neural layer and error gradients. Note that the sizes of all buffers increase in proportion to the number of models in the ensemble. At the initial stage, buffers are initialized with zero values.
//--- if(CheckPointer(Output) == POINTER_INVALID) { Output = new CBufferFloat(); if(CheckPointer(Output) == POINTER_INVALID) return false; } if(!Output.BufferInit(numNeurons * models, 0.0)) return false; if(!Output.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Gradient) == POINTER_INVALID) { Gradient = new CBufferFloat(); if(CheckPointer(Gradient) == POINTER_INVALID) return false; } if(!Gradient.BufferInit((numNeurons + 1)*models, 0.0)) return false; if(!Gradient.BufferCreate(OpenCL)) return false;
Next, we initialize the weight matrix buffer with random values. The buffer size must be large enough to store the weights of all ensemble models within the current neural layer.
//--- if(CheckPointer(Weights) == POINTER_INVALID) { Weights = new CBufferFloat(); if(CheckPointer(Weights) == POINTER_INVALID) return false; } int count = (int)((numInputs + 1) * numNeurons * models); if(!Weights.Reserve(count)) return false; float k = (float)(1 / sqrt(numInputs + 1)); for(int i = 0; i < count; i++) { if(!Weights.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier)) return false; } if(!Weights.BufferCreate(OpenCL)) return false;
Implementation of the Adam optimization method requires the creation of two data buffers to record moments 1 and 2. The size of the specified buffers is similar to the size of the weight matrix. At the initial stage, we initialize these buffers with zero values.
//--- if(CheckPointer(DeltaWeights) != POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum) == POINTER_INVALID) { FirstMomentum = new CBufferFloat(); if(CheckPointer(FirstMomentum) == POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count, 0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum) == POINTER_INVALID) { SecondMomentum = new CBufferFloat(); if(CheckPointer(SecondMomentum) == POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count, 0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; //--- return true; }
Do not forget to monitor the operations processes at every stage. After successful completion of all the above operations, we complete the method.
After initialization, we move on to the feedForward method. In the parameters, this method receives only a pointer to the object of the previous neural layer. And in the method body, we immediately check the relevance of the received pointer.
bool CNeuronMultiModel::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
To perform all feed-forward operations provided by the neural layer algorithm, we have already created a kernel in the OpenCL program. Now we need to transfer the necessary data to the kernel and call its execution.
First we define the problem space. Previously, we decided to use a two-dimensional problem space. In the first dimension, we indicate the number of neurons at the output of one model, and in the second, we specify the number of such models. When initializing the class, we did not save the number of neurons in the layer of one model. Therefore, now, to determine the size of the first dimension of the problem space, we divide the total number of neurons at the output of our layer by the number of models in the ensemble. The second dimension is easier. Here we have a separate variable with the number of models in the ensemble.
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = Output.Total() / iModels; global_work_size[1] = iModels;
After defining the task space, we will pass the necessary initial data to the kernel parameters. Make sure to check the operation execution result.
if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_w, getWeightsIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_i, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FFMultiModels, def_k_ff_matrix_o, Output.GetIndex())) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFMultiModels, def_k_ff_inputs, NeuronOCL.Neurons() / iModels)) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FFMultiModels, def_k_ff_activation, (int)activation)) { printf("Error of set parameter kernel FeedForward: %d; line %d", GetLastError(), __LINE__); return false; }
Note that we use the newly created ID of our new kernel to specify the kernel. To specify the parameters, we use the identifiers of the corresponding kernel of the base fully connected layer. This is possible by saving all kernel parameters and their sequence.
After passing all the parameters, all we have to do is send the kernel to the execution queue.
if(!OpenCL.Execute(def_k_FFMultiModels, 2, global_work_offset, global_work_size)) { printf("Error of execution kernel FeedForward: %d", GetLastError()); return false; } //--- return true; }
We check the results of all operations and exit the method.
Next we move on to working on backpropagation methods. First, let's look at the error gradient distribution method calcHiddenGradients. As with the direct pass, in the method parameters we receive a pointer to the object of the previous neural layer. Immediately, in the body of the method, we check the relevance of the received pointer.
bool CNeuronMultiModel::calcHiddenGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
The next step is to define the problem space. Everything here is similar to the feed forward method.
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = NeuronOCL.Neurons() / iModels; global_work_size[1] = iModels;
Then we pass the initial data to the kernel parameters.
if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_w, getWeightsIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_g, getGradientIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_o, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGMultiModels, def_k_chg_matrix_ig, NeuronOCL.getGradientIndex())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_outputs, Neurons() / iModels)) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_activation, NeuronOCL.Activation())) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; }
As you can see, here is a fairly standard algorithm for organizing the work of the OpenCL program kernel, which we have already implemented more than once. But there is a nuance with passing the model identifier for training. We have to choose a random model number for training. To do this, we will use a pseudorandom number generator. However, do not forget that it is for this model that we must update the weight matrix at the next step. Therefore, we will save the resulting random model identifier into the previously created iUpdateModel variable. We can use its value when updating the weight matrix.
iUpdateModel = (int)MathRound(MathRand() / 32767.0 * (iModels - 1)); if(!OpenCL.SetArgument(def_k_HGMultiModels, def_k_chg_model, iUpdateModel)) { printf("Error of set parameter kernel calcHiddenGradients: %d; line %d", GetLastError(), __LINE__); return false; }
After successfully passing all parameters, we send the kernel to the execution queue and complete the method.
if(!OpenCL.Execute(def_k_HGMultiModels, 2, global_work_offset, global_work_size)) { printf("Error of execution kernel CalcHiddenGradient: %d", GetLastError()); return false; } //--- return true; }
The algorithm for updating the weight matrix completely repeats the steps of preparing and queuing the kernel and does not contain any pitfalls. Therefore, I will not provide the detailed description here. Its full code can be found in the attachment.
To work with files, we use methods Save and Load. Their algorithm is quite straightforward. In the new class, we create only two variables: the number of models in the ensemble and the identifier of the trained model. Only the first variable contains the hyperparameter that we need to save. The process of saving all inherited objects and variables is already organized in the methods of the parent class. This class also provides the necessary controls. Therefore, to save data, we just need to first call a similar method of the parent class, and then save the value of only one hyperparameter.
bool CNeuronMultiModel::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteInteger(file_handle, iModels) <= 0) return false; //--- return true; }
Data loading from a file is organized in a similar way.
This completes our work with the code of the new class. The complete code of all its methods can be found in the attachment.
But before using the class, we need to perform some more actions in our library code. First of all, we need to create constants to identify the kernels and the added parameters.
#define def_k_FFMultiModels 46 ///< Index of the kernel of the multi-models neuron to calculate feed forward #define def_k_HGMultiModels 47 ///< Index of the kernel of the multi-models neuron to calculate hiden gradient #define def_k_chg_model 6 ///< Number of model to calculate #define def_k_UWMultiModels 48 ///< Index of the kernel of the multi-models neuron to update weights #define def_k_uwa_model 9 ///< Number of model to update
Then we add:
- block for creating a new type of neural layer in the CNet::Create method
- new layer type to the CLayer::CreateElement method
- new type in the feed forward dispatch method of the neural network base class
- new type to the backpropagation dispatch method CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject).
We built a class for parallel operation of several independent fully connected layers, which allows us to create ensembles of models. But this is only one part, and not the entire algorithm of research through disagreement. To implement the full algorithm, we will create a new class of CEVD models, similar to the intrinsic curiosity module. There are many similarities in the class structures. This can be seen in the names of methods and variables. We see the experience replay buffer CReplayBuffer. There are two internal models cTargetNet and cForwardNet, but there is no inverse model. As cForwardNet, we will use an ensemble of models. The differences, as always, are in the details.
//+------------------------------------------------------------------+ //| Exploration via Disagreement | //+------------------------------------------------------------------+ class CEVD : protected CNet { protected: uint iMinBufferSize; uint iStateEmbedingLayer; double dPrevBalance; bool bUseTargetNet; bool bTrainMode; //--- CNet cTargetNet; CReplayBuffer cReplay; CNet cForwardNet; virtual bool AddInputData(CArrayFloat *inputVals); public: CEVD(); CEVD(CArrayObj *Description, CArrayObj *Forward); bool Create(CArrayObj *Description, CArrayObj *Forward); ~CEVD(); int feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true); bool backProp(int batch, float discount = 0.999f); int getAction(int state_size = 0); float getRecentAverageError() { return recentAverageError; } bool Save(string file_name, bool common = true); bool Save(string dqn, string forward, bool common = true); virtual bool Load(string file_name, bool common = true); bool Load(string dqn, string forward, uint state_layer, bool common = true); //--- virtual int Type(void) const { return defEVD; } virtual bool TrainMode(bool flag) { bTrainMode = flag; return (CNet::TrainMode(flag) && cForwardNet.TrainMode(flag));} virtual bool GetLayerOutput(uint layer, CBufferFloat *&result) { return CNet::GetLayerOutput(layer, result); } //--- virtual void SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; } virtual void SetBufferSize(uint min, uint max); };
We add the bTrainMode variable to separate the algorithm into operation and training processes. We add the bUseTargetNet flag, since we have eliminated the constant updating of cTargetNet before each model update package. We have also made changes to the method algorithm. But first things first.
The feed forward method and the method of determining the agent action now have the algorithm split into the processes of operation and training. This is because during training we want to force the agent to explore the environment as much as possible. During operation, on the contrary, we want to eliminate unnecessary risks and follow only internal policies. Let's see how this is implemented.
The beginning of the feed forward method repeats that of the corresponding intrinsic curiosity block method. In the parameters, we get the initial state of the system. We supplement it with data on the account state and open positions. Then we call the feed forward method of the trained model.
int CEVD::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { if(!AddInputData(inputVals)) return -1; //--- if(!CNet::feedForward(inputVals, window, tem)) return -1;
But then the action selection algorithm is divided into 2 streams: training and operation. In training mode, we read the hidden (compressed) state of the environment from the trained model and perform a feed forward pass through our ensemble of dynamic models. Let me remind you that, unlike the internal curiosity module, we look at the state forecast not for one specific action, but for the entire range of possible actions at once. And only after a successful Forward pass of the ensemble, we call the method for determining the optimal action. We will get acquainted with this method a little later.
int action = -1; if(bTrainMode) { CBufferFloat *state; //if(!GetLayerOutput(1, state)) // return -1; if(!GetLayerOutput(iStateEmbedingLayer, state)) return -1; if(!cForwardNet.feedForward(state, 1, false)) { delete state; return -1; } double balance = AccountInfoDouble(ACCOUNT_BALANCE); double reward = (dPrevBalance == 0 ? 0 : balance - dPrevBalance); dPrevBalance = balance; action = getAction(state.Total()); delete state; if(action < 0 || action > 3) return -1; if(!cReplay.AddState(inputVals, action, reward)) return -1; }
Once the action is successfully defined, we add the state set to the experience replay buffer.
In operation mode, we do not perform unnecessary actions, but only determine the optimal action based on the agent's intrinsic policy and complete the method.
else action = getAction(); //--- return action; }
The algorithm for determining the optimal action is also divided into 2 branches: training and operation.
int CEVD::getAction(int state_size = 0) { CBufferFloat *temp; //--- get the result of the trained model. CNet::getResults(temp); if(!temp) return -1;
At the beginning of the method, we load the result of the forward pass of the trained model. And then, for model training, we adjust this value by the value of the variance in the forecasts made by the ensemble of dynamic models for each possible action. To do this, we first upload the result of the ensemble into a vector, and then transform the vector into a matrix. In the resulting matrix, each individual row will represent the predicted system state for a separate action. Our matrix contains predictions from all ensemble models. For convenience of processing the results, we will divide the matrix horizontally into several equal matrices of smaller size. The number of such matrices will be equal to the number of models in the ensemble. Each such matrix will have the dimension of rows corresponding to the range of possible actions of our agent.
Now we can use matrix operations and first find a matrix of averages for each individual action of an individual state component. And then we can calculate the variance of deviations of the forecast matrices from the average. We will add the average variance for each action to the predicted reward values of the trained model. At this point, we can use a factor to balance exploration and exploitation. In order to maximize the exploration of the environment, we can use only the variance of the predicted values, without focusing on the expected reward. In this way, we incentivize the model to learn as much as possible from the environment without influencing the agent's policies.
//--- in training mode, make allowances for "curiosity" if(bTrainMode && state_size > 0) { vector<float> model; matrix<float> forward; cForwardNet.getResults(model); forward.Init(1, model.Size()); forward.Row(model, 0); temp.GetData(model); //--- int actions = (int)model.Size(); forward.Reshape(forward.Cols() / state_size, state_size); matrix<float> ensemble[]; if(!forward.Hsplit(forward.Rows() / actions, ensemble)) return -1; matrix<float> means = ensemble[0]; int total = ArraySize(ensemble); for(int i = 1; i < total; i++) means += ensemble[i]; means = means / total; for(int i = 0; i < total; i++) ensemble[i] -= means; means = MathPow(ensemble[0], 2.0); for(int i = 1 ; i < total; i++) means += MathPow(ensemble[i], 2.0); model += means.Sum(1) / total; temp.AssignArray(model); }
During the operation of the model, we do not make any adjustments, but determine the optimal action based on the principle of maximizing the expected reward.
//--- return temp.Argmax(); }
The full code of the method is provided in the attachment.
Let's dwell a little more on the reverse pass method. To eliminate unnecessary iterations during model operation, the backward pass method, in the absence of a model training flag, immediately completes its work. This allows you to quickly switch from model training mode to testing mode without changing the EA code.
bool CEVD::backProp(int batch, float discount = 0.999000f) { //--- if(cReplay.Total() < (int)iMinBufferSize || !bTrainMode) return true;
After passing the control block, we create the necessary local variables.
//--- CBufferFloat *state1, *state2, *targetVals = new CBufferFloat(); vector<float> target, actions, st1, st2, result; matrix<float> forward; double reward; int action;
And after the preparatory work, we organize a model training cycle in the package size that was specified in the method parameters.
//--- training loop in the batch size for(int i = 0; i < batch; i++) { //--- get a random state and the buffer replay if(!cReplay.GetRendomState(state1, action, reward, state2)) return false; //--- feed forward pass of the training model ("current" state) if(!CNet::feedForward(state1, 1, false)) return false;
In the loop body, we first obtain a set of random state from the experience replay buffer, execute the feed forward pass through the training model with the resulting state.
getResults(target); //--- unload state embedding if(!GetLayerOutput(iStateEmbedingLayer, state1)) return false; //--- target net feed forward if(!cTargetNet.feedForward(state2, 1, false)) return false;
After performing a feed forward pass on the training model, we save the result and the hidden state.
Using Target Net, we obtain an embedding of the subsequent system state in a similar way.
//--- reward adjustment if(bUseTargetNet) { cTargetNet.getResults(targetVals); reward += discount * targetVals.Maximum(); } target[action] = (float)reward; if(!targetVals.AssignArray(target)) return false; //--- backpropagation pass of the model being trained CNet::backProp(targetVals);
If necessary, we adjust the external reward of the system to the predicted Target Net value and perform a backpropagation pass of the training model.
At the next step, we train an ensemble of models using the embeddings of the two subsequent states obtained above.
//--- forward net feed forward pass - next state prediction if(!cForwardNet.feedForward(state1, 1, false)) return false; //--- download "future" state embedding if(!cTargetNet.GetLayerOutput(iStateEmbedingLayer, state2)) return false;
First, we perform a feed forward pass through the ensemble of models with the first state embedding.
Then we download the results of the feed forward pass and prepare target values based on them, by replacing the vector of the perfect action with the embedding of the subsequent state obtained using Target Net.
To do this, we translate the results of the direct pass of the ensemble of models into a matrix with the number of columns equal to the embedding of the state. The matrix contains the results of the entire ensemble of models. Therefore, we implement a loop and replace the forecast state with the target state for the perfect action in all ensemble models.
//--- prepare targets for forward net cForwardNet.getResults(result); forward.Init(1, result.Size()); forward.Row(result, 0); forward.Reshape(result.Size() / state2.Total(), state2.Total()); int ensemble = (int)(forward.Rows() / target.Size()); //--- copy the target state to the ensemble goals matrix state2.GetData(st2); for(int r = 0; r < ensemble; r++) forward.Row(st2, r * target.Size() + action);
At first glance, replacing the target state in all models goes against the idea of training ensemble models on different data. But let me remind you that we organized random model selection in the backward pass method of the CNeuronMultiModel class. At this stage, we do not know which model will be trained. Therefore, we prepare target values for all models. The model for training will be chosen later.
//--- backpropagation pass of foward net targetVals.AssignArray(forward); cForwardNet.backProp(targetVals); } //--- delete state1; delete state2; delete targetVals; //--- return true; }
At the end of the iterations in the body of the training cycle, we perform a reverse pass through the ensemble of dynamic Forward models with the prepared data. Please note that when preparing the target values, we only changed the target values of the individual action. We left the rest at the level of forecast values. This allows us, when performing a backpropagation pass, to obtain the error gradient of only a specific action. In other directions we expect to get zero error.
After successful completion of the loop iterations, we remove unnecessary objects and terminate the method.
The remaining methods of the class are constructed similarly to the corresponding methods of the intrinsic curiosity module. Their full code can be found in the attachment.
3. Testing
After creating the necessary classes and their methods, we move on to testing the work done. To test the functionality of the created classes, we will create an Expert Advisor, EVDRL-learning.mq5. As before, we will create an Expert Advisor based on the one from the previous articles. This time we will not make changes to the architecture of the training model. Instead, we will change the class of the model being used. Let's replace the module of intrinsic curiosity with a block of exploration via disagreement.
//+------------------------------------------------------------------+ //| Includes | //+------------------------------------------------------------------+ #include "EVD.mqh" ........... ........... ........... ........... //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CEVD StudyNet;
We will also make changes to the method of describing the architecture of models. We will remove the description of the architecture of the inverse model and make changes to the architecture of the Forward model. The last one is worth dwelling on a bit. Previously, for the forward model, we used a perceptron with one hidden layer. Let's create a similar architecture for ensemble models.
When solving the problem is a straightforward way, we must create a layer of initial data with a buffer size sufficient for all models and two consecutive layers of our new CNeuronMultiModel class of model ensemble. But note that all ensemble models use the same system state. This means that to maintain such an ensemble, we need to repeat one set of data each time in the source data layer as many times as there are models in our ensemble. In my opinion, this is an inefficient use of the memory of our OpenCL context, which incurs additional time spent concatenating a large buffer of source data and at the same time increases the time spent transferring a large amount of data from the device's RAM to the OpenCL context memory.
It would be much more efficient to arrange for all models to access one small data buffer that contains only one copy of the system state. But we did not provide for such an option when creating the feed forward method of our CNeuronMultiModel class.
Let's look at the architecture of our basic fully connected neural layer. In this layer, each neuron has its own weight vector, independent of other neurons in this layer. In practice, this is an ensemble of independent models the size of one neuron. This means we can use one basic fully connected neural layer as a hidden layer for all models in our ensemble. We just need to implement a neural layer of sufficient size to provide all the models in our ensemble with data.
Thus, for our ensemble of Forward models, we create a source data layer of 100 elements. This is the size of the compressed representation of the system state that we receive from the main model. In this case, we do not add an action vector, since we expect to receive predictive states from the model for the entire range of possible actions.
Next we will use an ensemble of 5 models. As a hidden layer, we create one fully connected neural layer of 1000 elements (200 neurons per model).
This is followed by our new model ensemble layer. Here we specify the following description of the neural layer:
- Neural network type (descr.type) defNeuronMultiModels;
- The number of neurons per model (descr.count) 400 (100 elements to describe each of the states of four possible action;
- Number of neurons in the previous layer for 1 model (descr.window ) 200;
- Number of models in the ensemble (descr.step) 5;
- Activation function (descr.activation) TANH (hyperbolic tangent, must correspond to the activation function of the embedding layer in the main model);
- Optimization method (descr.optimization) ADAM (the only one possible for this type of neural layer).
bool CreateDescriptions(CArrayObj *Description, CArrayObj *Forward) { //--- ........... ........... //--- if(!Forward) { Forward = new CArrayObj(); if(!Forward) return false; } //--- Model ........... ........... ........... ........... //--- Forward Forward.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 100; descr.window = 0; descr.activation = None; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 1000; descr.activation = TANH; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMultiModels; descr.count = 400; descr.window = 200; descr.step = 5; descr.activation = TANH; descr.optimization = ADAM; if(!Forward.Add(descr)) { delete descr; return false; } //--- return true; }
We trained and tested the model without changing the conditions: EURUSD pair, H1 timeframe, default indicator parameters.
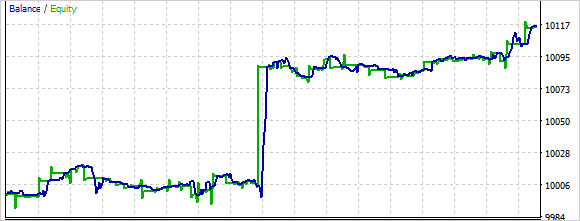
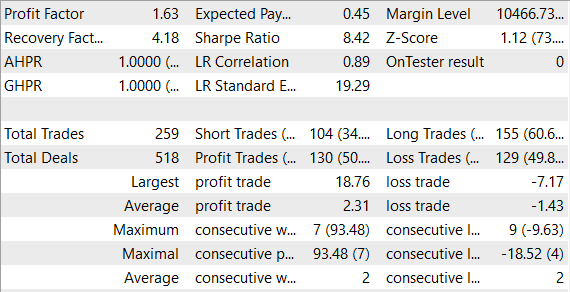
Based on the test training results, I can say that training an ensemble of models requires more time than training a single Forward model. In this case, you can observe how at first the model performs actions rather chaotically. During the learning process, this randomness decreases.
Overall, the model was able to make a profit during testing.
Conclusion
When training reinforcement models, learning from the environment remains an important issue. This article presented another approach to this problem: Exploration via Disagreement. The agent learns online on data that it collects itself in the process of interacting with the environment, using the policy optimization method. At the same time, after each interaction of the agent with the environment, the ensemble of models is updated, which allows the agent to update its internal environment model at each step and obtain more accurate predictions about the future environment states.
We have created a model and tested it using real data in the MetaTrader 5 strategy tester. The mode generated profit during testing. The results suggest that further development in this direction has good prospects. At the same time, the model was trained and tested over a fairly short time period. Additional model training on extended historical data would be required to use the model in real trading.
References
- Self-Supervised Exploration via Disagreement
- Neural networks made easy (Part 35): Intrinsic Curiosity Module
- Neural networks made easy (Part 36): Relational Reinforcement Learning
- Neural networks made easy (Part 37): Sparse Attention
Programs used in the article
| # | Issued to | Type | Description |
|---|---|---|---|
| 1 | EVDRL-learning.mq5 | EA | An Expert Advisor to train the model |
| 2 | EVD.mqh | Class library | Exploration via Disagreement library class |
| 2 | ICM.mqh | Class library | Intrinsic curiosity module library class |
| 3 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library |
…
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/12508
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Sorry, one more amateur question. The Expert Advisor has not made a single trade in the tester. It is just hanging on the chart with no signs of activity. Why?
And one more thing. Are indicator data used only as an additional filter when making a trade?
Thank you very much for this article!
I see that you also offer a zip file with many RL experiments inside. Is there a specific mq5 file, which I can compile, run and evaluate in more detail?
Thank you very much!
Thank you very much for this article!
I see that you also offer a zip file with many RL experiments inside. Is there a specific mq5 file, which I can compile, run and evaluate in more detail?
Thank you very much!
Hi, yes you can. In attachment all files from previous articles.