Neural networks made easy (Part 37): Sparse Attention

Introduction

In the previous article, we discussed relational models which use attention mechanisms in their architecture. We used this model to create an Expert Advisor, and the resulting EA showed good results. However, we noticed that the model's learning rate was lower compared to our earlier experiments. This is due to the fact that the transformer block used in the model is a rather complex architectural solution performing a large number of operations. The number of these operations grows in a quadratic progression as the size of the analyzed sequence increases, leading to an increase in memory consumption and model training time.

However, we recognize the limited resources available to improve the model. Therefore, there is a need to optimize the model with minimal loss of quality.

1. Sparse Attention

When we talk about optimizing a model’s performance, we first need to pay attention to its hyperparameters. The set of such parameters should be optimal, taking into account the resource consumption and the model quality. Increasing the number of neurons in a layer after a certain threshold practically does not lead to an improvement in the model quality. The same can be said about the number of neural layers. However, the set of optimal hyperparameters depends on the specific task and its complexity.

All this applies to the number of attention heads in the multi-head Self-Attention block. Sometimes two heads are enough to get good results, but this is not the optimal value for all problems. All hyperparameters must be selected experimentally for each specific task and model architecture.

This article discusses architectural approaches to reducing the number of operations in the Self-Attention block. However, before moving on to optimizing the algorithm, it is important to remember how the Self-Attention block works.

First, it calculates three entities: Query, Key and Value for each element of the sequence. For this purpose, the vector describing the sequence element is multiplied by the corresponding weights matrix. Then, we multiply the Query matrix by the transposed Key matrix to obtain the dependency coefficients between the elements of the sequence. These coefficients are then normalized using the SoftMax function.

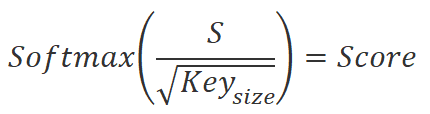
After normalizing the dependency coefficients, we multiply them by the matrix of Value entities to obtain the output values for each element of the sequence. These output values are weighted sums of element values that take into account the importance of each element in the context of the problem.

An increase in the number of sequence elements leads to an increase in the computational complexity of operations in algorithms that use attention mechanisms. This is due to the fact that at each stage the operations of entity calculations, matrix multiplication and normalization of dependency coefficients are performed for each element of the sequence.

If a sequence has too many elements, this can lead to a significant increase in computation time and the cost of computing resources. To optimize the algorithm and to reduce the number of calculations at each stage, we can use various methods, one of which is Sparse Attention. This method was proposed by Rewon Child in the article "Generating Long Sequences with Sparse Transformers", which was published in April 2019.

Sparse Attention is a technique for optimizing the attention mechanism to reduce the amount of computation required to process elements of a sequence.

The idea of the method is to take into account only the most important elements of the sequence when calculating the attention coefficients between them. Thus, instead of calculating attention coefficients for all pairs of elements in a sequence, we select only the most significant pairs.

One of the advantages of the Sparse Attention method is that it can significantly reduce the number of calculations required to process the elements of the sequence. This is especially important when processing large sequences, where the number of calculations can be very large.

In addition, Sparse Attention can help combat the "attention on everything" problem, when the attention mechanism evenly distributes attention to all elements of the sequence, which leads to inefficient use of resources and slows down the algorithm.

Various approaches can be used when implementing Sparse Attention. One is to break the sequence into blocks and calculate attention only between elements within each block and between elements of different blocks. In this case, only the elements that are closest in distance can be taken into account in order to reduce the number of calculations.

Another approach is to select the most important elements in a sequence based on their similarity. This can be done by using different clustering methods.

A third approach is to use some heuristics and algorithms to select the most important elements in a sequence, for example based on their frequency, significance, or context.

The authors note that for Sparse Attention to work effectively, it is necessary to use an algorithm for distributing sequence elements into blocks, which provides a different block structure for each attention head. This approach will allow you to more fully determine the influence of each element of the sequence and improve the efficiency of the algorithm.

Sparse Attention can be applied in various areas of machine learning and natural language processing, including machine translation, text generation, sentiment analysis, and many others. In the article mentioned above, the authors of the method present the algorithm application results for texts, images, and audio recordings.

In addition, Sparse attention can be effectively combined with other attention engine optimization techniques to achieve more accurate results when processing sequences.

Despite its effectiveness, the Sparse Attention method also has its drawbacks. One of them is that the selection of the most important elements in the sequence can be incorrect, which can lead to loss of information. Therefore, it is necessary to choose the appropriate method for each specific task and carefully tune the algorithm parameters.

I believe that the Sparse Attention method can be useful for solving the problems related to financial market analysis. When analyzing the history of financial symbol quotes, we often need to analyze the data in considerable depth, and often only individual elements of this history affect the current situation. Using the Sparse Attention method will reduce the amount of computing resources aimed at selecting significant blocks of data to study. The method will also help eliminate insignificant elements from further operations, which will increase the efficiency of financial market analysis.

However, financial market quotes have a variable structure, due to which we can't work with fixed blocks of elements in the analyzed sequence. To speed up the model learning process, we can use the heuristic of the "80/20" Pareto rule, where we take only 20% of the most significant elements from the total sequence. The significance of elements is determined based on the coefficients of dependence between elements, which are calculated by the first two formulas described earlier. Already after the first iteration, before data normalization, it is possible to accurately identify the most significant elements of the sequence and then exclude the remaining elements from further operations. This reduces the number of operations in the stages of normalization and determining the results of the Self-Attention block.

Since each attention head uses its own unique matrices to determine the Query and Key, it is likely that the elements selected will be different in each attention head.

Now that we have determined the main directions for optimizing the algorithm, we can move on to its implementation using the MQL5 language.

2. Implementation using MQL5

To implement the proposed method, we will create a new neural layer class CNeuronMLMHSparseAttention. Of course, we will not recreate all the class methods anew. Instead, we will inherit from the existing CNeuronMLMHAttentionOCL class. And here, let's analyze which class methods and OpenCL program kernels need to be changed in order to implement the proposed optimization.

As mentioned earlier, our first change to the algorithm concerns the block for determining dependence coefficients. These values are obtained during a direct pass in the MHAttentionScore kernel. For our implementation, we will replace the specified kernel with MHSparseAttentionScore.

In the kernel parameters of the parent class, we passed pointers to 2 data buffers: a concatenated tensor of the Query, Key and Value entities as source data and a buffer for writing the operations results in the form of dependency coefficients. In addition to data buffers, the dimension of internal entities was passed to the kernel. Now we will add the sparse coefficient 'sparse'. We will pass a value in the range from 0 to 1 into it, which will indicate the proportion of selected sequence elements with the maximum influence on the analyzed element.

__kernel void MHSparseAttentionScore(__global float *qkv,    ///<[in] Matrix of Querys, Keys, Values
                                     __global float *score,  ///<[out] Matrix of Scores
                                     int dimension,          ///< Dimension of Key
                                     float sparse            ///< less than 1.0 coefficient of sparse
                                    )
  {
   int q = get_global_id(0);
   int h = get_global_id(1);
   int units = get_global_size(0);
   int heads = get_global_size(1);
//---

The new kernel, like the kernel of the parent class, will rub in a two-dimensional task space. The first dimension will indicate the ordinal number of the sequence element being analyzed, and the second dimension will correspond to the attention head used. In the kernel body, we immediately save the global identifiers of the running thread into local variables.

Next, we will do a little preparatory work, in which we will declare the necessary local variables and determine the offset in the data buffers to the elements being analyzed.

   int shift_q = dimension * (h + 3 * q * heads);
   int shift_s = units * (h + q * heads);
   int active_units = (int)max((float)(units * sparse), min((float)units, 3.0f));
//---
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   float sum = 0.0f;
   float min_s = 0.0f;
   float max_s = 0.0f;

We also determine the absolute value of the selected elements. Please note that when determining the number of significant sequence elements to select, I set a limit: there cannot be less than three elements. This will help us avoid unnecessary disabling of the attention block when using small sequences. We know that the maximum dependence coefficient will almost always be generated by the analyzed elements for its own Key.

Next, we implement a loop in which we will multiply the Query vector of the analyzed element by the Key matrix. In the loop body we will also determine the maximum and minimum values of the resulting vector.

   for(int k = 0; k < units; k++)
     {
      float result = 0;
      int shift_k = dimension * (h + heads * (3 * k + 1));
      for(int i = 0; i < dimension; i++)
        {
         if((dimension - i) > 4)
           {
            result += dot((float4)(qkv[shift_q + i], qkv[shift_q + i + 1], qkv[shift_q + i + 2], qkv[shift_q + i + 3]),
                          (float4)(qkv[shift_k + i], qkv[shift_k + i + 1], qkv[shift_k + i + 2], qkv[shift_k + i + 3]));
            i += 3;
           }
         else
            result += (qkv[shift_q + i] * qkv[shift_k + i]);
        }
      score[shift_s + k] = result;
      if(k == 0)
         min_s = max_s = result;
      else
        {
         max_s = max(max_s, result);
         min_s = min(min_s, result);
        }
     }

In order to preserve the dependencies between the obtained values and the corresponding elements of the sequence, we do not sort the vector to select the most significant elements. Instead, we will iteratively increase the lower bound of the dependence coefficients' significance range until we obtain the required number of "important" elements of the sequence. This functionality will be implemented in the following loop.

   int count = units;
   float temp = max_s;
   while(count > active_units)
     {
      count = 0;
      for(int k = 0; k < units; k++)
        {
         float value = score[shift_s + k];
         if(value < min_s)
            continue;
         count++;
         if(value < temp && value > min_s)
            temp = value;
        }
      if(count > active_units)
         min_s = temp;
     }

After determining the significance range, we move on to the next step, data normalization, which consists of two steps. In the first step, we calculate the exponential values of the dependency levels that we obtained in the previous step. Next, we divide these values by the total. But we should remember about the significance range that we have defined. So, we set the dependence coefficients for elements outside this range to zero and thus exclude them from further operations. This applies to both the exponential calculation and the normalization step.

   if(max_s == 0.0f)
      max_s = 1.0f;
   for(int k = 0; k < units; k++)
     {
      float value = score[shift_s + k];
      if(value < min_s)
        {
         score[shift_s + k] = 0.0f;
         continue;
        }
      value = exp(value / max_s / koef);
      score[shift_s + k] = value;
      sum += value;
     }

   for(int k = 0; (k < units && sum > 1); k++)
     {
      temp = score[shift_s + k];
      if(temp == 0.0f)
         continue;
      score[shift_s + k] = temp / sum;
     }
  }

As a result of the operations of the specified kernel, we obtain only a small number of non-zero dependence coefficients for selected elements of the analyzed sequence, which we will work with further. We also exclude elements of the sequence with zero dependency coefficients from further forward and backward passes.

The next step is to get the attention block output. To do this, according to the Self-Attention algorithm, we need to multiply the 'Score' matrix of normalized dependency coefficients by the 'Value' matrix of entities. This operation is implemented in the MHSparseAttentionOut kernel. In this kernel, we also check for zero dependency coefficients to reduce the number of operations performed.

Pointers to 3 data buffers will be passed in the kernel parameters. The concatenated tensor of the Query, Key and Value entities, together with the 'Score' matrix of dependency coefficients, is the source data for the operations to be performed. The result of the operations will be written to the Out buffer. The dimension of the Key vector of one element of the sequence is also passed in parameters. As we have already seen, we use vectors of the same dimension for the internal entities Query, Key and Value in the multi-headed attention class.

__kernel void MHSparseAttentionOut(__global float *scores, ///<[in] Matrix of Scores
                                   __global float *qkv,    ///<[in] Matrix of Values
                                   __global float *out,    ///<[out] Output tensor
                                   int dimension           ///< Dimension of Value
                                  )
  {
   int u = get_global_id(0);
   int units = get_global_size(0);
   int h = get_global_id(1);
   int heads = get_global_size(1);

This kernel, like the previous one, will be called in a 2-dimensional task space to separate into separate flows of operations according to sequence elements and attention heads. At the beginning of the kernel, we save thread identifiers in local variables.

Next we define offsets in the data buffers.

   int shift_s = units * (h + heads * u);
   int shift_out = dimension * (h + heads * u);

After that, we create a system of nested loops to multiply the vector of dependency coefficients by the Value matrix. This is where we insert a zero dependency factor check to eliminate redundant operations.

   for(int d = 0; d < dimension; d++)
     {
      float result = 0;
      for(int v = 0; v < units; v ++)
        {
         float cur_score = scores[shift_s + v];
         if(cur_score == 0)
            continue;
         int shift_v = dimension * (h + heads * (3 * v + 2)) + d;
         result += cur_score * qkv[shift_v];
        }
      out[shift_out + d] = result;
     }
  }

This concludes our work with the forward pass kernels of our new class. Now let's look at the scope of changes in the backward pass part.

Self-Attention block's feed-backward pass was implemented in the MHAttentionInsideGradients kernel. The algorithm allows you to add the necessary control points along the existing kernel without creating a duplicate of it. I propose to look at the constructed algorithm and the control points added to it.

In the kernel parameters, we will pass pointers to 5 data buffers:

• Concatenated tensor of Query, Key and Value entities (qkv)
• Concatenated tensor for writing error gradients of Query, Key and Value entities (qkv_g)
• Matrix of dependence coefficients (scores)
• Matrix for writing error gradients at the level of the dependency coefficient matrix (scores_g)
• Tensor of error gradients at the output level of the current attention head block.

__kernel void MHAttentionInsideGradients(__global float *qkv, __global float *qkv_g,
                                         __global float *scores, __global float *scores_g,
                                         __global float *gradient, int dimension)
  {
   int u = get_global_id(0);
   int h = get_global_id(1);
   int units = get_global_size(0);
   int heads = get_global_size(1);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

We will call the error gradient distribution kernel in a 2-dimensional space of problems, like both previously considered ones. One dimension will identify the sequence element being analyzed. The second dimension will indicate the current attention head. It is these identifiers that will help us determine the offset in the data buffers to the required elements. Therefore, at the beginning of the kernel, we save these thread identifiers into local variables.

Further, the kernel algorithm is conditionally divided into two blocks. In the first one, we define the error gradient at the level of the dependency coefficient matrix. Here we implement a loop of collecting gradients for the vector of dependence coefficients of the analyzed element of the sequence. Since the unused elements of the sequence with zero dependence coefficients did not influence the final result, the error gradient for them should be zero. Therefore, in the loop body, we first check the current dependency coefficient. When a null value is detected, we simply move on to the next element.

It's important to note that accessing global memory, which stores the elements of all our data buffers, is a relatively expensive operation. In our case, the vector of error gradients at the level of the sequence coefficient matrix is temporary storage and is not used in other kernels. We do not even write the null value to it, since it would be an unnecessary operation without much usefulness.

//--- Calculating score's gradients
   uint shift_s = units * (h + u * heads);
   for(int v = 0; v < units; v++)
     {
      float s = scores[shift_s + v];
      if(s <= 0)
         continue;
      float sg = 0;
      int shift_v = dimension * (h + heads * (3 * v + 2));
      int shift_g = dimension * (h + heads * v);
      for(int d = 0; d < dimension; d++)
         sg += qkv[shift_v + d] * gradient[shift_g + d];
      scores_g[shift_s + v] = sg * (s < 1 ? s * (1 - s) : 1) / koef;
     }
   barrier(CLK_GLOBAL_MEM_FENCE);

In the next step, we distribute the error gradient to the internal Query, Key and Value entities. We first determine the offset in the data buffers, and then create a system of loops to collect error gradients.

Here, inside a nested loop, we check the dependency coefficient and if we find a null value, we simply move on to the next element. This eliminates unnecessary operations.

//--- Calculating gradients for Query, Key and Value
   uint shift_qg = dimension * (h + 3 * u * heads);
   uint shift_kg = dimension * (h + (3 * u + 1) * heads);
   uint shift_vg = dimension * (h + (3 * u + 2) * heads);
   for(int d = 0; d < dimension; d++)
     {
      float vg = 0;
      float qg = 0;
      float kg = 0;
      for(int l = 0; l < units; l++)
        {
         float sg = scores[shift_s + l];
         if(sg <= 0)
            continue;
         uint shift_q = dimension * (h + 3 * l * heads) + d;
         uint shift_k = dimension * (h + (3 * l + 1) * heads) + d;
         uint shift_g = dimension * (h + heads * l) + d;
         //---
         vg += gradient[shift_g] * sg;
         sg = scores_g[shift_s + l];
         kg += sg * qkv[shift_q];
         qg += sg * qkv[shift_k];
        }
      qkv_g[shift_qg + d] = qg;
      qkv_g[shift_kg + d] = kg;
      qkv_g[shift_vg + d] = vg;
     }
  }

After all iterations of this kernel are completed, we get error gradients at the level of the Query, Key and Value entities, which will then be distributed to the corresponding weight matrices and the previous neural layer.

With this we complete the work on the kernels of the OpenCL program and move on to working on the code of the main program. We have added two kernels. Therefore, we need to add the kernel calls in the main program. First, let's create constants for accessing the kernels.

Pay attention that we are creating constants for working with two kernels and only one parameter constant. We have created the kernels based on existing ones and almost completely repeated the structure of the parameters of the basic kernels. Therefore, during the operation of kernels, we can use existing constants. We only create a constant to indicate the sparse parameter.

#define def_k_MHSparseAttentionScore    44 ///< Index of the kernel of the multi-heads sparse attention neuron 
                                           //   to calculate score matrix (#MHSparseAttentionScore)
#define def_k_mhas_sparse                3  ///< less than 1.0 coefficient of sparse
//---
#define def_k_MHSparseAttentionOut      45 ///< Index of the kernel of the multi-heads sparse attention neuron 
                                           //   to calculate multi-heads out matrix (#MHSparseAttentionOut)

Next, we need to implement the creation of kernels in the OpenCL context. We need to increase the total number of active kernels in the context to 46 and call the kernel creation methods.

   opencl.SetKernelsCount(46);

   if(!opencl.KernelCreate(def_k_MHSparseAttentionScore, "MHSparseAttentionScore"))
     {
      PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__);
      return false;
     }
   if(!opencl.KernelCreate(def_k_MHSparseAttentionOut, "MHSparseAttentionOut"))
     {
      PrintFormat("Error of create kernell: %d line %d", GetLastError(), __LINE__);
      return false;
     }

Note that we will have to repeat the above operations for creating kernels in the OpenCL context in three methods of the dispatch class of the CNet neural network. This is not very convenient. So, in the future, I plan to move these operations into a separate method.

   bool              Create(CArrayObj *Description);
   bool              Load(string file_name, float &error, float &undefine, float &forecast, datetime &time, 
                          bool common = true);
   ///< Load method. @param[in] file_name File name to save @param[out] error Average error 
   ///< @param[out] undefine Undefined percent @param[out] Forecast percent 
   ///< @param[out] time Last study time @param[in] common Common flag
   virtual bool      Load(const int file_handle);

In the next step of our work, we move directly to creating methods of our new class. The functionality of our new neural network class CNeuronMLMHSparseAttention largely repeats the functionality of the parent class CNeuronMLMHAttentionOCL. Therefore, we will try to use inherited methods. The main differences are related to the creation of the sparse attention. In this part, we will create a new internal variable m_dSparse to store the sparsity level.

In order not to complicate the work by unnecessary rewriting of methods, I left the class constructor and destructor empty. We do not create new objects in the new class, and to work with the sparsity parameter, we will create overloaded Sparse methods. The ability to overload methods allows you to use methods of the same name for different functionality: with a value in the parameters, passing the value of the parameter to the method; without specifying parameters, the method will return the previously saved value.

class CNeuronMLMHSparseAttention  : public CNeuronMLMHAttentionOCL
  {
protected:
   float             m_dSparse;
   //---
   virtual bool      AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true);
   ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore().
   virtual bool      AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out);
   ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut().

public:
                     CNeuronMLMHSparseAttention(void)   :  m_dSparse(0.3f) {};
                    ~CNeuronMLMHSparseAttention(void) {};
   //---
   void              Sparse(float value)  { m_dSparse = value;}
   float             Sparse(void)         { return m_dSparse; }
   virtual int       Type(void)   const   {  return defNeuronMLMHSparseAttentionOCL;   }
                     ///< Identificatory of class.@return Type of class
   //--- methods for working with files
   virtual bool      Save(int const file_handle);  
                     ///< Save method @param[in] file_handle handle of file @return logical result of operation
   virtual bool      Load(int const file_handle);  
                     ///< Load method @param[in] file_handle handle of file @return logical result of operation
  };

Don't forget to override the virtual identification method of the Type object.

As for the public methods, we also should override the methods for working with files: Save and Load. The algorithm of these methods is quite simple. In these methods, we first call the methods of the same name of the parent class, in which all control points are already defined and algorithms for saving and loading inherited variables and objects are implemented. We just need to check the logical result of executing the called methods. After successful execution of the parent class method, we save or read the value of the sparsity parameter, depending on the functionality of the running method.

bool CNeuronMLMHSparseAttention::Save(const int file_handle)
  {
   if(!CNeuronMLMHAttentionOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, m_dSparse) < sizeof(float))
      return false;
//---
   return true;
  }

We have completed considering the public methods for the operation of the new class. But the main functionality of the class is to create the neural layer algorithm. So, let's get back to the feed forward and backpropagation passes. We have modernized the OpenCL program kernels to enable this functionality.

I will deviate a little from the usual structure which we used to discuss methods when describing the functionality of neural networks. This time I will start not with forward passes but with backward ones. We have not created new kernels for the backpropagation pass. We have only modified the exiting kernel which was used in the parent class. By inheriting the functionality of the parent class, we also inherited algorithms for calling the MHAttentionInsideGradients kernel discussed above. This means that now we can simply use the calcInputGradients backward pass method of the parent class to propagate the error gradients. As for the functionality related to the updating of trained parameters, we did not make any changes and can also use the parent class method updateInputWeights.

Let's move on to feed forward methods. When constructing the feed forward algorithm of the parent class, we did not combine the entire branched algorithm in the body of one method. Instead, we created a structured dispatch method feedForward, in which we sequentially call methods for executing individual functionality in accordance with the Self-Attention algorithm. Thanks to this approach, now we do not need to completely rewrite the feed forward method. We just need to redefine the methods to call two new kernels. The methods are AttentionScore and AttentionOut.

bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
//---
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
      CBufferFloat *qkv = QKV_Tensors.At(i * 2);
      if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)),
                                            inputs, qkv, iWindow, 3 * iWindowKey * iHeads, None))
         return false;
      //--- Score calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      if(IsStopped() || !AttentionScore(qkv, temp, true))
         return false;
      //--- Multi-heads attention calculation
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(qkv, temp, out))
         return false;
      //--- Attention out calculation
      temp = FF_Tensors.At(i * 6);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), 
                                            out, temp, iWindowKey * iHeads, iWindow, None))
         return false;
      //--- Sum and normilize attention
      if(IsStopped() || !SumAndNormilize(temp, inputs, temp))
         return false;
      //--- Feed Forward
      inputs = temp;
      temp = FF_Tensors.At(i * 6 + 1);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), 
                                            inputs, temp, iWindow, 4 * iWindow, LReLU))
         return false;
      out = FF_Tensors.At(i * 6 + 2);
      if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), 
                                            temp, out, 4 * iWindow, iWindow, activation))
         return false;
      //--- Sum and normilize out
      if(IsStopped() || !SumAndNormilize(out, inputs, out))
         return false;
     }
//---
   return true;
  }

To preserve the rules of inheritance, both methods received parameters similar to the methods of the parent class. This is extremely important because changing method parameters would create overloaded methods. But we need to override the methods of the parent class. In method overloading, the system selects one of them according to the parameters specified when the method is called, while in method overriding, the system follows the inheritance hierarchy and uses the last overridden method. Therefore, only if we set to override the methods, when called from the inherited feedForward method, will the system access the overridden methods of our class.

The AttentionScore method in its parameters receives a pointer to objects of two buffers: a concatenated tensor of Query, Key, Value entities and a matrix of dependency coefficients. In addition, the mask flag is passed in the method parameters. We do not use this flag; it is left in the parameters for the reasons stated above.

In the method body, we immediately check if the received pointers are relevant. We also check the relevance of the object working with the OpenCL context. In addition to the object pointers themselves, we check for the presence of created data buffers in the OpenCL context. Only after successfully passing all the specified control points can we proceed to organizing the process of placing the kernel in the execution queue.

All the kernels we created were planned for use in a 2-dimensional problem space. Now we need to create arrays describing the global_work_size task space and the offset in the global_work_offset task space. The size of both arrays must match the problem space. To create a 2-dimensional problem space, we create the two arrays of 2 elements each.

In the elements of the first array, we indicate the total number of elements of the analyzed sequence and the number of attention heads. The position of an element in an array indicates a dimension. Its value indicates the number of threads. Thus, each element of the sequence for each attention head will receive its own separate thread to perform operations. In general, operations on all elements of the sequence will be performed simultaneously (as far as technically possible) in parallel threads.

We will fill the elements of the second array with zero values, since we do not need an offset in the task space.

bool CNeuronMLMHSparseAttention::AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = true)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID ||
      CheckPointer(scores) == POINTER_INVALID)
      return false;
//---
   if(qkv.GetIndex() < 0)
      return false;
   if(scores.GetIndex() < 0)
      return false;
//---
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2];
   global_work_size[0] = iUnits;
   global_work_size[1] = iHeads;
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_qkv, qkv.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionScore, def_k_mhas_score, scores.GetIndex());
   OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_dimension, (int)iWindowKey);
   OpenCL.SetArgument(def_k_MHSparseAttentionScore, def_k_mhas_sparse, (float)m_dSparse);
   if(!OpenCL.Execute(def_k_MHSparseAttentionScore, 2, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

The next step is to pass the parameters to the kernel. We do it by using the SetArgumentBuffer and SetArgument methods. The first one is used to pass pointers to data buffers. The second is used for transmitting discrete values. In the method parameters, we indicate the kernel identifier, the serial number of the parameter being passed (corresponds to the sequence of kernel parameters in the OpenCL program starting with 0) and the passed value.

Here you should be careful about the type of values passed and the specified type of parameter in the kernel. If the types do not match, you may receive a kernel execution error.

Once the preparation work is done, we call the Execute method to send the kernel to the execution queue. In the method parameters we indicate the kernel identifier, the dimension of the task space, and the previously created task space description arrays.

We also check the result of executing the kernel queuing method. If an error occurs when queuing the kernel, request information about the error and display it in the terminal log.

If kernel is successfully added into the execution queue, complete the method with the true result.

Repeat a similar algorithm in the AttentionOut method to call the second kernel.

bool CNeuronMLMHSparseAttention::AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(qkv) == POINTER_INVALID || 
      CheckPointer(scores) == POINTER_INVALID || CheckPointer(out) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2];
   global_work_size[0] = iUnits;
   global_work_size[1] = iHeads;
   if(qkv.GetIndex() < 0)
      return false;
   if(scores.GetIndex() < 0)
      return false;
   if(out.GetIndex() < 0)
      return false;
//---
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_qkv, qkv.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_score, scores.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MHSparseAttentionOut, def_k_mhao_out, out.GetIndex());
   OpenCL.SetArgument(def_k_MHSparseAttentionOut, def_k_mhao_dimension, (int)iWindowKey);
   if(!OpenCL.Execute(def_k_MHSparseAttentionOut, 2, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

This concludes our work with the new neural network class. But there is one more point left. We need to add processing of our new class to the dispatch methods implementing the operation of the model.

First, we add a block for creating a new type of neural layer in the CNet::Create method.

            case defNeuronMLMHSparseAttentionOCL:
               neuron_sparseattention = new CNeuronMLMHSparseAttention();
               if(CheckPointer(neuron_sparseattention) == POINTER_INVALID)
                 {
                  delete temp;
                  return false;
                 }
               if(!neuron_sparseattention.Init(outputs, 0, opencl, desc.window, desc.window_out, desc.step, 
                                                               desc.count, desc.layers, desc.optimization, desc.batch))
                 {
                  delete neuron_sparseattention;
                  delete temp;
                  return false;
                 }
               neuron_sparseattention.SetActivationFunction(desc.activation);
               neuron_sparseattention.Sparse(desc.probability);
               if(!temp.Add(neuron_sparseattention))
                 {
                  delete neuron_mlattention_ocl;
                  delete temp;
                  return false;
                 }
               neuron_sparseattention = NULL;
               break;

Add a new layer type to the CLayer::CreateElement method.

         case  defNeuronMLMHSparseAttentionOCL:
            if(CheckPointer(OpenCL) == POINTER_INVALID)
               return false;
            temp_mlat_ocl = new CNeuronMLMHSparseAttention();
            if(CheckPointer(temp_mlat_ocl) == POINTER_INVALID)
               result = false;
            if(temp_mlat_ocl.Init(iOutputs, index, OpenCL, 1, 1, 1, 1, 0, ADAM, 1))
              {
               m_data[index] = temp_mlat_ocl;
               return true;
              }
            break;

Also, add the new type into the feed forward dispatch method of the neural network's base class.

bool CNeuronBaseOCL::FeedForward(CObject *SourceObject)
  {
   if(CheckPointer(SourceObject) == POINTER_INVALID)
      return false;
//---
   CNeuronBaseOCL *temp = NULL;
   switch(SourceObject.Type())
     {
      case defNeuronBaseOCL:
      case defNeuronProofOCL:
      case defNeuronConvOCL:
      case defNeuronAttentionOCL:
      case defNeuronMHAttentionOCL:
      case defNeuronMLMHAttentionOCL:
      case defNeuronMLMHSparseAttentionOCL:
      case defNeuronDropoutOCL:
      case defNeuronBatchNormOCL:
      case defNeuronVAEOCL:
      case defNeuronLSTMOCL:
      case defNeuronSoftMaxOCL:
         temp = SourceObject;
         return feedForward(temp);
         break;
     }
//---
   return false;
  }

Repeat the operation in he relevant backrpopagation method CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject).

      case defNeuronMLMHAttentionOCL:
      case defNeuronMLMHSparseAttentionOCL:
         mlat = TargetObject;
         if(!bTrain && !mlat.TrainMode())
            return true;
         temp = GetPointer(this);
         return mlat.calcInputGradients(temp);

The full code of all classes and their methods is available in the attachment.

3. Testing

After completing work on the new neural layer class, we can proceed to testing the constructed algorithm in the trading strategy tester of the MetaTrader 5 platform. The trading Strategy Tester allows the testing of trading Expert Advisors and indicators using historical data. To test the operation of the constructed algorithm, we will create a small trading EA that will train the model directly in the process of passing through historical data. We have already created similar EAs when testing previously discussed algorithms. This time, we will use the EA from the previous article as a basis. In this EA, we replace the multi-headed attention neural layer in the EA's model architecture with a newly created sparse attention layer.

In the previous article we tested a relational reinforcement learning model that used a fully parameterized quantile function algorithm using an intrinsic curiosity block. To implement such a model, we created a combination of 3 models: Model, Forward and Inverse. We used the attention block in the first model. So, we will modify this block. The architecture of the other two models remained unchanged.

The architecture of the models is described in the CreateDescriptions function. In order to simplify the model, I decided to remove the use of recursive LSTM blocks. They have been replaced by fully connected layers. So, the training model has the following architecture.

At the model input, we created a layer of initial data with 12 elements to describe each bar of the analyzed history, and 9 elements to describe the current account state.

//--- Model
   Description.Clear();
   CLayerDescription *descr;
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (int)(HistoryBars * 12 + 9);
   descr.window = 0;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

This is followed by a data normalization layer.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

This is followed by 2 consecutive blocks of convolutional and fully connected layers.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count - 2;
   descr.window = 3;
   descr.step = 1;
   descr.window_out = 6;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 50;
   descr.window = 2;
   descr.step = 2;
   descr.window_out = 4;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 100;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

The compressed data is analyzed by the attention block. Here we use the new sparse attention layer. We split the entire sequence of compressed data into 20 blocks of 5 elements. Each block represents one element of the sequence being analyzed. To analyze the data, we will use 4 attention heads, selecting 30% of the most significant sequence elements in each attention head. The analysis will be performed in 2 successive layers with similar parameters. This should be indicated in the 'layers' parameter.  

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHSparseAttentionOCL;
   descr.count = 20;
   descr.window = 5;
   descr.step = 4;
   descr.window_out = 8;
   descr.layers = 2;
   descr.probability = 0.3f;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

The Expert Advisor takes the decision whether to execute a trade in a block of a fully parameterized quantile function. The EA can decide to take one of 4 actions:

• Buy 
• Sell 
• Close all trades
• Not to trade

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFQF;
   descr.count = 4;
   descr.window_out = 32;
   descr.optimization = ADAM;
   if(!Description.Add(descr))
     {
      delete descr;
      return false;
     }

The full EA code is provided in the attachment: SparseRL-learning.mq5.

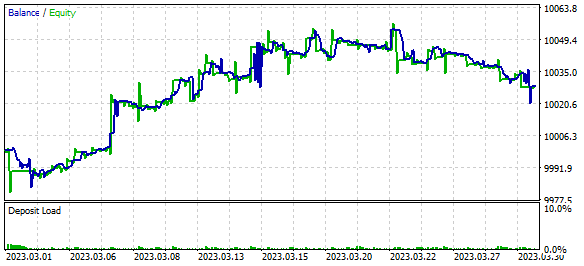
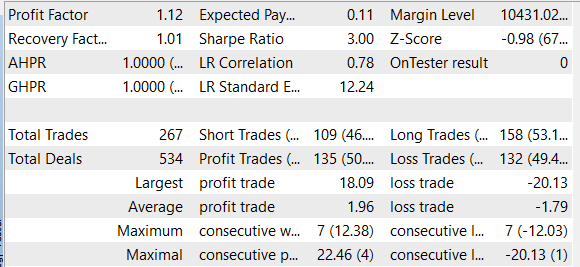
We trained the model and tested the EA using EURUSD H1 historical data for March 2023. During the learning process, the EA showed profit during the testing period. However, the profit was obtained because the size of the average profitable trade was larger than the size of the average losing trade. But the number of winning and losing positions was approximately the same. As a result, the profit factor was 1.12, and the recovery factor was 1.01.

Conclusion

In this article, we studied the Sparse Attention mechanism and added its algorithm to our class library, after which we tested it on historical data. As a result of model testing, we generated some profit, which indicates the potential possibility of using such an architecture to build trading solutions. However, it should be noted that the model presented in the article is intended for informational and testing purposes only.

To use this model in real trading conditions, you must conduct a more detailed analysis of its effectiveness and resistance to market fluctuations. It also requires more careful tuning of the model's hyperparameters to obtain the most optimal results.

You should always remember that using any model for financial market trading always involves the risk of loss. Therefore, before using any model for real trading, you must carefully study its operating principle and assess the possible risks.

Despite this, the Sparse Attention mechanism can be a useful tool for building trading models.

References

1. Generating Long Sequences with Sparse Transformers
2. Attention Is All You Need
3. Neural networks made easy (Part 8): Attention mechanisms
4. Neural networks made easy (Part 10): Multi-Head Attention
5. Neural networks made easy (Part 11): A take on GPT
6. Neural networks made easy (Part 35): Intrinsic Curiosity Module
7. Neural networks made easy (Part 36): Relational Reinforcement Learning

Programs used in the article

#	Issued to	Type	Description
1	SparseRL-learning.mq5	EA	An Expert Advisor to train the model
2	ICM.mqh	Class library	Model organization class library
3	NeuroNet.mqh	Class library	A library of classes for creating a neural network
4	NeuroNet.cl	Code Base	OpenCL program code library