MQL5 Wizard techniques you should know (Part 01): Regression Analysis
1. Introduction
MQL5 wizard allows the rapid construction and deployment of expert advisors by having most of the menial aspects of trading pre-coded in the MQL5 library. This allows traders to focus on their custom aspects of their trading such as special entry and exit conditions. Included in the library are some entry and exit signal classes like signals of 'Accelerator Oscillator' indicator, or signals of 'Adaptive Moving Average' indicator and many others. Besides being based on lagging indicators for most traders they may not be convertible to successful strategies. This is why the ability to create your own custom signal is essential. For this article we will explore how this can be done with regression analysis.
2. Creating the class
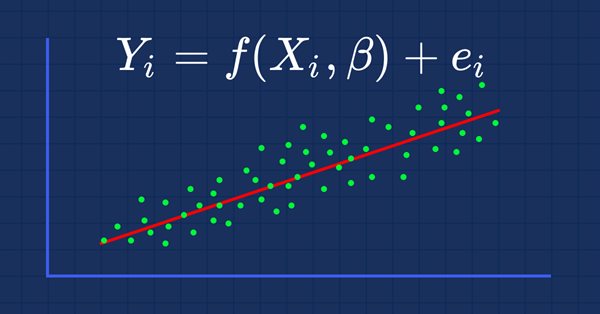
2.1 Regression analysis, per Wikipedia, is a set of statistical processes for estimating the relationships between a dependent variable and one or more independent variables. It can be useful to a trader’s expert signal since price data is a time series. This, therefore, allows one to test for the ability of prior prices and price changes to influence future prices and price changes. Regression analysis can be represented by the equation 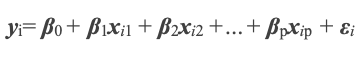
Where y the dependent and therefore predicted variable depends on prior x values each with their own coefficient β, and an error ε. We can think of x values and the y value to be previous and projected price levels respectively. Besides working with price levels, price changes can also be examined in similar fashion. The unknown y is dependent on xs, βs, and ε. Of these though only the xs and β0 (the y-intercept) are known. The y-intercept is known because it is the price immediately before x i 1. We therefore need to find the respective βs for each x and then the ε. Because each x i 1 was a y I at the prior time point of the time series, we can solve for the β values using simultaneous equations. If the next change in price is dependent on only two prior changes, for example, our current equation could be:
And the previous equations would be:
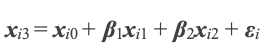
Since we estimate error ε separately, we can solve the two simultaneous equations for the β values. The numbering of the x values in the Wikipedia formula is not in the MQL5 'series' format meaning the highest numbered x is the most recent. I have thus renumbered the x values in the above 2 equations to show how they can be simultaneous. Again we start with the y-intercepts xi1 and xi0 to represent β0 in equation 1. The solving of simultaneous equations is better handled with matrices for efficiency. The tools for this are in the MQL5 Library.
2.2 MQL5 library has an extensive collection of classes on statistics, and common algorithms that clearly negate the need for one to have to code them from scratch. Its code is also open to the public meaning it can be independently checked. For our purposes we’ll use the ‘RMatrixSolve’ function, under class ‘CDenseSolver’ in the 'solvers.mqh' file. At the heart of this function is the use of matrix LU decomposition to quickly and efficiently solve for β values. Articles have been written on this in the MetaQuotes archive and Wikipedia also has an explanation here.
Before we delve into solving for β values it would be helpful to look at how the ‘CExpertSignal’ class is structured as it is the basis for our class. In almost all expert signal classes that can be assembled in the wizard, there is a ‘LongCondition’ function and a ‘ShortCondition’ function. As you would expect, the two return a value that sets whether you should go long or short respectively. This value needs to be an integer in the range of 0 to 100 in order to map with the wizard’s input parameters of ‘Signal_ThresholdOpen’ and ‘Signal_ThresholdClose’. Typically, when trading you want your conditions for closing a position to be less conservative than your conditions for opening. This means the threshold for opening will be higher than the threshold for closing. In developing our signal therefore, we are going to have input parameters for computing the close threshold and separate but similar input parameters for the opening threshold. The selection of inputs to use when computing a condition will be determined by whether or not we have open positions. If we have open positions we will use the close parameters. If no positions are present we will use open parameters. The listing of our expert signal class interface that shows these two sets of parameters is below.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalDUAL_RA : public CExpertSignal { protected: CiMA m_h_ma; // highs MA handle CiMA m_l_ma; // lows MA handle CiATR m_ATR; //--- adjusted parameters int m_size; double m_open_determination,m_close_determination; int m_open_collinearity,m_open_data,m_open_error; int m_close_collinearity,m_close_data,m_close_error; public: CSignalDUAL_RA(); ~CSignalDUAL_RA(); //--- methods of setting adjustable parameters //--- PARAMETER FOR SETTING THE NUMBER OF INDEPENDENT VARIABLES void Size(int value) { m_size=value; } //--- PARAMETERS FOR SETTING THE OPEN 'THRESHOLD' FOR THE EXPERTSIGNAL CLASS void OpenCollinearity(int value) { m_open_collinearity=value; } void OpenDetermination(double value) { m_open_determination=value; } void OpenError(int value) { m_open_error=value; } void OpenData(int value) { m_open_data=value; } //--- PARAMETERS FOR SETTING THE CLOSE 'THRESHOLD' FOR THE EXPERTSIGNAL CLASS void CloseCollinearity(int value) { m_close_collinearity=value; } void CloseDetermination(double value) { m_close_determination=value; } void CloseError(int value) { m_close_error=value; } void CloseData(int value) { m_close_data=value; } //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods for detection of levels of entering the market virtual bool OpenLongParams(double &price,double &sl,double &tp,datetime &expiration); virtual bool OpenShortParams(double &price,double &sl,double &tp,datetime &expiration); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); protected: //--- method of initialization of the oscillator bool InitRA(CIndicators *indicators); //--- methods of getting data int CheckDetermination(int ind,bool close); double CheckCollinearity(int ind,bool close); // double GetY(int ind,bool close); double GetE(int ind,bool close); double Data(int ind,bool close); // };
Also, here is a listing of our ‘LongCondition’ and ‘ShortCondition’ functions.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::LongCondition(void) { int _check=CheckDetermination(0,PositionSelect(m_symbol.Name())); if(_check>0){ return(_check); } return(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::ShortCondition(void) { int _check=CheckDetermination(0,PositionSelect(m_symbol.Name())); if(_check<0){ return((int)fabs(_check)); } return(0); }
To continue though, in order to solve for β values, we will use the ‘GetY’ function. This is listed below.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::GetY(int ind,bool close) { double _y=0.0; CMatrixDouble _a;_a.Resize(m_size,m_size); double _b[];ArrayResize(_b,m_size);ArrayInitialize(_b,0.0); for(int r=0;r<m_size;r++) { _b[r]=Data(r,close); for(int c=0;c<m_size;c++) { _a[r].Set(c,Data(r+c+1, close)); } } int _info=0; CDenseSolver _S; CDenseSolverReport _r; double _x[];ArrayResize(_x,m_size);ArrayInitialize(_x,0.0); _S.RMatrixSolve(_a,m_size,_b,_info,_r,_x); for(int r=0;r<m_size;r++) { _y+=(Data(r,close)*_x[r]); } //--- return(_y); }
The ‘Data’ function referred to will switch between changes in the close price of the symbol being traded or changes in the moving average of the same close price. The option used will be defined by either the ‘m_open_data’ input parameter or the ‘m_close_data’ input parameter depending on whether we are computing the open threshold or the close threshold. The listing for selecting data is shown in the enumeration below.
enum Edata { DATA_TREND=0, // changes in moving average close DATA_RANGE=1 // changes in close };
And the ‘Data’ function that selects this is listed below.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::Data(int ind,bool close) { if(!close) { if(Edata(m_open_data)==DATA_TREND) { m_h_ma.Refresh(-1); return((m_l_ma.Main(StartIndex()+ind)-m_l_ma.Main(StartIndex()+ind+1))-(m_h_ma.Main(StartIndex()+ind)-m_h_ma.Main(StartIndex()+ind+1))); } else if(Edata(m_open_data)==DATA_RANGE) { return((Low(StartIndex()+ind)-Low(StartIndex()+ind+1))-(High(StartIndex()+ind)-High(StartIndex()+ind+1))); } } else if(close) { if(Edata(m_close_data)==DATA_TREND) { m_h_ma.Refresh(-1); return((m_l_ma.Main(StartIndex()+ind)-m_l_ma.Main(StartIndex()+ind+1))-(m_h_ma.Main(StartIndex()+ind)-m_h_ma.Main(StartIndex()+ind+1))); } else if(Edata(m_close_data)==DATA_RANGE) { return((Low(StartIndex()+ind)-Low(StartIndex()+ind+1))-(High(StartIndex()+ind)-High(StartIndex()+ind+1))); } } return(0.0); }
Once we have the β values we can then proceed to estimate the error.
2.3 Standard Error according to Wikipedia can be estimated with the formula below.
![]()
With s as the standard deviation and n the sample size, the error serves as a sobering reminder that not all projections no matter how diligent, will be 100% accurate all the time. We should always factor in and expect some error on our part. The standard deviation, shown in the formula, will be measured between our predicted values and the actual values. For comparison purposes we can also look at a raw error such as the last difference between our forecast and the actual. These two options can be selected from the enumeration below.
enum Eerror { ERROR_LAST=0, // use the last error ERROR_STANDARD=1 // use standard error }
The ’GetE’ function will then return our error estimate depending on the input parameters ‘m_open_error’ or ‘m_close_error’ while using the formula above. This is listed below.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::GetE(int ind,bool close) { if(!close) { if(Eerror(m_open_error)==ERROR_STANDARD) { double _se=0.0; for(int r=0;r<m_size;r++) { _se+=pow(Data(r,close)-GetY(r+1,close),2.0); } _se=sqrt(_se/(m_size-1)); _se=_se/sqrt(m_size); return(_se); } else if(Eerror(m_open_error)==ERROR_LAST){ return(Data(ind,close)-GetY(ind+1,close)); } } else if(close) { if(Eerror(m_close_error)==ERROR_STANDARD) { double _se=0.0; for(int r=0;r<m_size;r++){ _se+=pow(Data(r,close)-GetY(r+1,close),2.0); } _se=sqrt(_se/(m_size-1)); _se=_se/sqrt(m_size); return(_se); } else if(Eerror(m_close_error)==ERROR_LAST){ return(Data(ind,close)-GetY(ind+1,close)); } } //--- return(Data(ind,close)-GetY(ind+1,close)); }
Once again, the use of ‘m_open_error’ or ‘m_close_error’ will be determined by whether or not we have open positions. Once we have our error estimate we should be able to make a ball park prediction for y. Regression analysis however has a number of pitfalls. One such pitfall is the ability of the independent variables to be too similar and therefore over inflate the predicted value. This phenomenon is called collinearity and is worth checking for.
2.4 Collinearity which Wikipedia defines here, can be surmised as the occurrence of high intercorrelations among two or more independent variables in a multiple regression model as per Investopedia. It does not have a formula per se and is detected by the variance inflation factor (VIF). This factor is measured across all the independent variables (x) to help get a sense of how each of these variables is unique in predicting y. It is given by the formula below where R is the regression of each independent variable against the others.
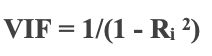
For our purposes though, in taking account of collinearity, we will take the inverse of the spearman correlation between two recent data sets of independent variables and normalise it. Our data sets length will be set by the input parameter ‘m_size’ whose minimum length is 3. By normalization we will simply subtract it from two and invert the result. This normalized weight can then be multiplied either to the error estimate, or the predicted value, or both, or be unused. These options are listed in the enumeration below.
enum Echeck { CHECK_Y=0, // check for y only CHECK_E=1, // check for the error only CHECK_ALL=2, // check for both the y and the error CHECK_NONE=-1 // do not use collinearity checks };
The choice of the applied weight is also set by either input parameter ‘m_open_collinearity’ or ‘m_close_collinearity’. Again, depending on if positions are open. The ‘CheckCollinearity’ listing is given below.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalDUAL_RA::CheckCollinearity(int ind,bool close) { double _check=0.0; double _c=0.0,_array_1[],_array_2[],_r=0.0; ArrayResize(_array_1,m_size);ArrayResize(_array_2,m_size); ArrayInitialize(_array_1,0.0);ArrayInitialize(_array_2,0.0); for(int s=0; s<m_size; s++) { _array_1[s]=Data(ind+s,close); _array_2[s]=Data(m_size+ind+s,close); } _c=1.0/(2.0+fmin(-1.0,MathCorrelationSpearman(_array_1,_array_2,_r))); double _i=Data(m_size+ind,close), //y intercept _y=GetY(ind,close), //product sum of x and its B coefficients _e=GetE(ind,close); //error if(!close) { if(Echeck(m_open_collinearity)==CHECK_Y){ _check=_i+(_c*_y)+_e; } else if(Echeck(m_open_collinearity)==CHECK_E){ _check=_i+_y+(_c*_e); } else if(Echeck(m_open_collinearity)==CHECK_ALL){ _check=_i+(_c*(_y+_e)); } else if(Echeck(m_open_collinearity)==CHECK_NONE){ _check=_i+(_y+_e); } } else if(close) { if(Echeck(m_close_collinearity)==CHECK_Y){ _check=_i+(_c*_y)+_e; } else if(Echeck(m_close_collinearity)==CHECK_E){ _check=_i+_y+(_c*_e); } else if(Echeck(m_close_collinearity)==CHECK_ALL){ _check=_i+(_c*(_y+_e)); } else if(Echeck(m_close_collinearity)==CHECK_NONE){ _check=_i+(_y+_e); } } //--- return(_check); }
Besides checking for collinearity, there are times when regression analysis is not as predictive as it could be due to exogeneous changes in the market. To keep track of this, and measure the ability of our signal’s independent variables to influence our dependent variable (the forecast), we use the coefficient of determination.
2.5 Coefficient of determination is a statistical measurement that examines how differences in one variable can be explained by the difference in a second variable, when predicting the outcome of a given event as per Investopedia. Wikipedia also provides a more exhaustive definition and our formulae shown below are adopted from there.
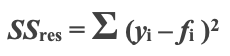
The formula for sum of squares (with y be the actual value and f the forecast value),
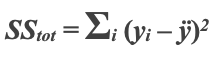
The formula for sum of totals (with y being an actual value and ÿ being the moving average of these values),
And finally, that for the coefficient itself also referred to as R squared.
What this coefficient does is measure the extent to which our xs are influencing the y. This is important because, as mentioned, there are periods when regression ebbs meaning it is safer to stay away from the markets. By monitoring this through a filter we are more likely to trade when the system is dependable. Typically, you want this coefficient to be above 0 with 1 being the ideal. The input parameter used in defining our threshold will be 'm_open_determination’ or ‘m_close_determination’, once again subject to number of open positions. If the coefficient of determination as computed by the 'CheckDetermination' function, listed below, is less than this parameter then the long or short conditions will return zero.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int CSignalDUAL_RA::CheckDetermination(int ind,bool close) { int _check=0; m_h_ma.Refresh(-1);m_l_ma.Refresh(-1); double _det=0.0,_ss_res=0.0,_ss_tot=0.0; for(int r=0;r<m_size;r++) { _ss_res+=pow(Data(r,close)-GetY(r+1,close),2.0); _ss_tot+=pow(Data(r,close)-((m_l_ma.Main(r)-m_l_ma.Main(r+1))-(m_h_ma.Main(r)-m_h_ma.Main(r+1))),2.0); } if(_ss_tot!=0.0) { _det=(1.0-(_ss_res/_ss_tot)); if(_det>=m_open_determination) { double _threshold=0.0; for(int r=0; r<m_size; r++){ _threshold=fmax(_threshold,fabs(Data(r,close))); } double _y=CheckCollinearity(ind,close); _check=int(round(100.0*_y/fmax(fabs(_y),fabs(_threshold)))); } } //--- return(_check); }
Once we can check for the coefficient of determination we would have a workable signal. What follows next would be assembling this signal in the MQL5 wizard into an expert advisor.
3. Assembling with MQL5 Wizard
3.1 Custom ancillary code listing can be used together with the code from the MQL5 wizard in assembling an expert advisor. This is entirely optional and is to the style of the trader. For the purposes of this article we are going to look at custom pending order opening that is based on the symbol’s prevailing ATR, as well as a system of trailing open positions that is based on the same indicator. We will not use take profit targets.
3.1.1 ATR based pending orders can be set by overloading the functions ‘OpenLongParams’ and ‘OpenShortParams’ and customizing them in our signal class as shown below.
//+------------------------------------------------------------------+ //| Detecting the levels for buying | //+------------------------------------------------------------------+ bool CSignalDUAL_RA::OpenLongParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_ATR.Refresh(-1); //--- if a base price is not specified explicitly, take the current market price double base_price=(m_base_price==0.0) ? m_symbol.Ask() : m_base_price; //--- price overload that sets entry price to be based on ATR price =m_symbol.NormalizePrice(base_price-(m_price_level*(m_ATR.Main(0)/m_symbol.Point()))*PriceLevelUnit()); sl =0.0; tp =0.0; expiration+=m_expiration*PeriodSeconds(m_period); return(true); } //--- return(general.OpenLongParams(price,sl,tp,expiration)); } //+------------------------------------------------------------------+ //| Detecting the levels for selling | //+------------------------------------------------------------------+ bool CSignalDUAL_RA::OpenShortParams(double &price,double &sl,double &tp,datetime &expiration) { CExpertSignal *general=(m_general!=-1) ? m_filters.At(m_general) : NULL; //--- if(general==NULL) { m_ATR.Refresh(-1); //--- if a base price is not specified explicitly, take the current market price double base_price=(m_base_price==0.0) ? m_symbol.Bid() : m_base_price; //--- price overload that sets entry price to be based on ATR price =m_symbol.NormalizePrice(base_price+(m_price_level*(m_ATR.Main(0)/m_symbol.Point()))*PriceLevelUnit()); sl =0.0; tp =0.0; expiration+=m_expiration*PeriodSeconds(m_period); return(true); } //--- return(general.OpenShortParams(price,sl,tp,expiration)); }
The MQL5 wizard generated expert advisor has an input parameter ‘Signal_PriceLevel’. By default, it is zero but if assigned a value it represents the distance, in price points of the traded symbol, from the current price at which a market order will be placed. When this input is negative stop orders are placed. When positive limit orders are placed. It is a double data type. For our purposes this input will be a fraction or multiple of the current price points in the ATR.
3.1.2 ATR trailing class is also a customised ‘CExpertTrailing’ class that also uses the ATR to set and move the stop loss. The implementation of its key functions is in the listing below.
//+------------------------------------------------------------------+ //| Checking trailing stop and/or profit for long position. | //+------------------------------------------------------------------+ bool CTrailingATR::CheckTrailingStopLong(CPositionInfo *position,double &sl,double &tp) { //--- check if(position==NULL) return(false); //--- m_ATR.Refresh(-1); double level =NormalizeDouble(m_symbol.Bid()-m_symbol.StopsLevel()*m_symbol.Point(),m_symbol.Digits()); //--- sl adjustment to be based on ATR double new_sl=NormalizeDouble(level-(m_atr_weight*(m_ATR.Main(0)/m_symbol.Point())),m_symbol.Digits()); double pos_sl=position.StopLoss(); double base =(pos_sl==0.0) ? position.PriceOpen() : pos_sl; //--- sl=EMPTY_VALUE; tp=EMPTY_VALUE; if(new_sl>base && new_sl<level) sl=new_sl; //--- return(sl!=EMPTY_VALUE); } //+------------------------------------------------------------------+ //| Checking trailing stop and/or profit for short position. | //+------------------------------------------------------------------+ bool CTrailingATR::CheckTrailingStopShort(CPositionInfo *position,double &sl,double &tp) { //--- check if(position==NULL) return(false); //--- m_ATR.Refresh(-1); double level =NormalizeDouble(m_symbol.Ask()+m_symbol.StopsLevel()*m_symbol.Point(),m_symbol.Digits()); //--- sl adjustment to be based on ATR double new_sl=NormalizeDouble(level+(m_atr_weight*(m_ATR.Main(0)/m_symbol.Point())),m_symbol.Digits()); double pos_sl=position.StopLoss(); double base =(pos_sl==0.0) ? position.PriceOpen() : pos_sl; //--- sl=EMPTY_VALUE; tp=EMPTY_VALUE; if(new_sl<base && new_sl>level) sl=new_sl; //--- return(sl!=EMPTY_VALUE); }
Once again the 'm_atr_weight' will be an optimisable parameter, like with 'm_price_level', that sets how close we can trail open positions.
3.2 Wizard assembly will then be done in straightforward fashion with the only notable stages being the selection of our signal as shown below.

And the addition of our custom trailing method shown below.

4. Testing in Strategy Tester
4.1 Compilation is what would follow assembly in the MQL5 wizard in order to create the expert advisor file and also confirm that there are no errors in our code.
4.2 Default inputs of the expert advisor would also need to be set in the strategy tester inputs tab. The key here is to ensure ‘Signal_TakeLevel’ and ‘Signal_StopLevel’ are set to zero. This is because as mentioned, for the purpose of this article, the exit is defined only by the trailing stop or the ‘Signal_ThresholdClose’ input parameter.
4.3 Optimisation should be performed ideally with the real ticks of the broker you intend to trade with. For this article we will optimize EURUSD on the 4-hour timeframe across its V shaped period of 2018.01.01 to 2021.01.01. For comparison purposes we will run two optimizations: the first one will only use market orders, while the second will be open to pending orders. I use ‘open to’ pending orders because we will still consider the option of using only market orders given that ‘Signal_PriceLevel’ can be zero since optimization is from a negative value to a positive value. Optimization can be set up prior for the option that uses pending orders as shown below. The only difference between this and the option that does not use pending orders is the later will leave 'Signal_PriceLevel' input parameter at 0 not part of the optimised inputs.
4.4 Results from our optimisation are presented below. First is the report and equity curve of the best results from trading only with market orders.
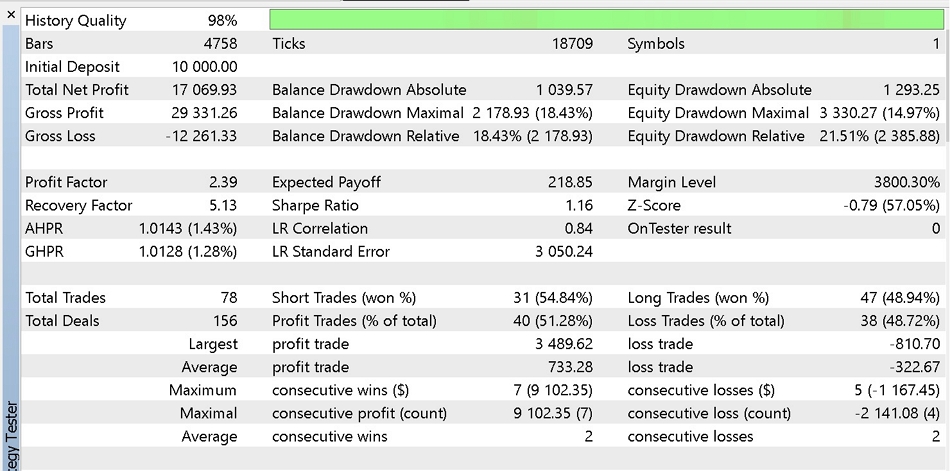
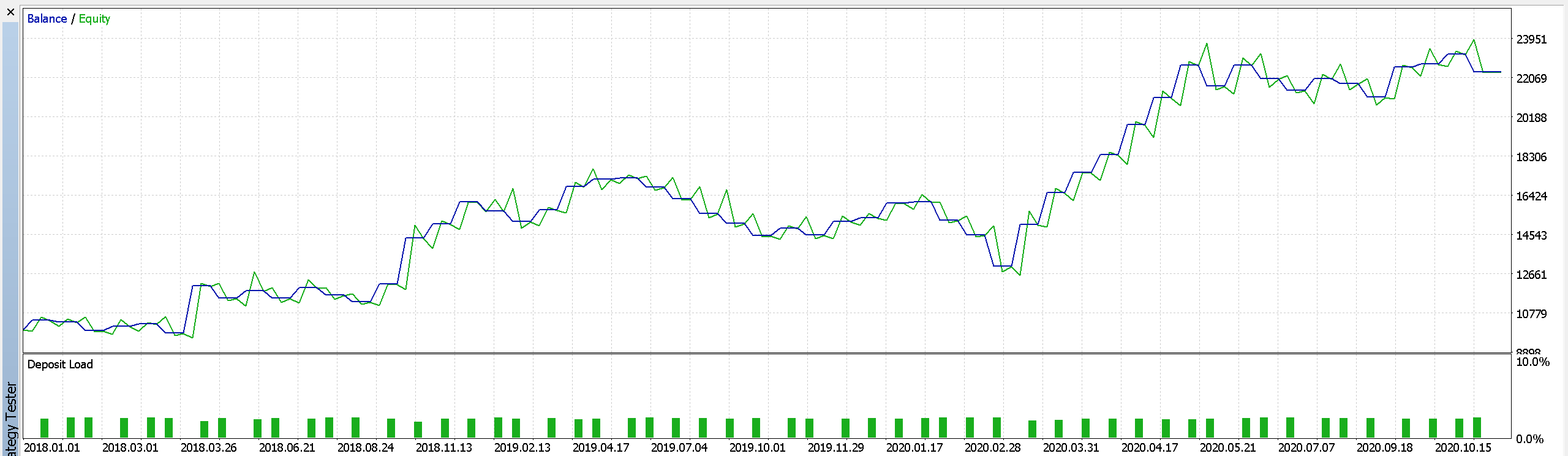
Part of report 1,
Then a likewise report and curve from using pending orders.
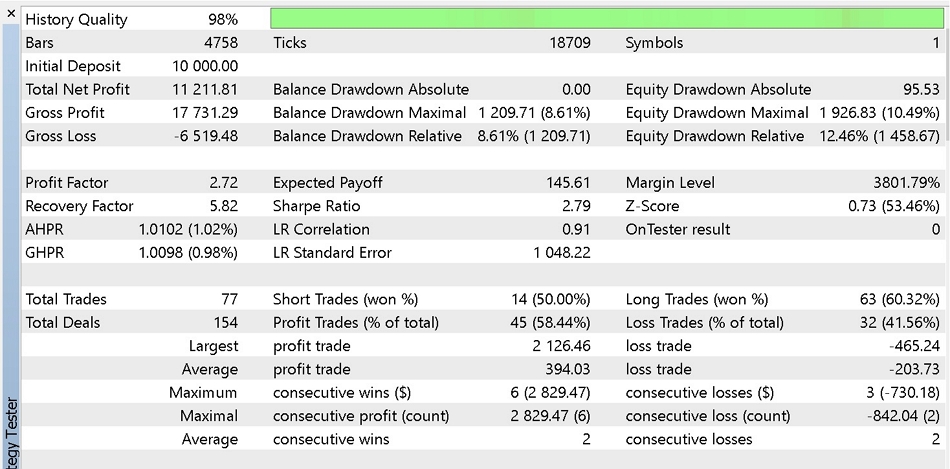
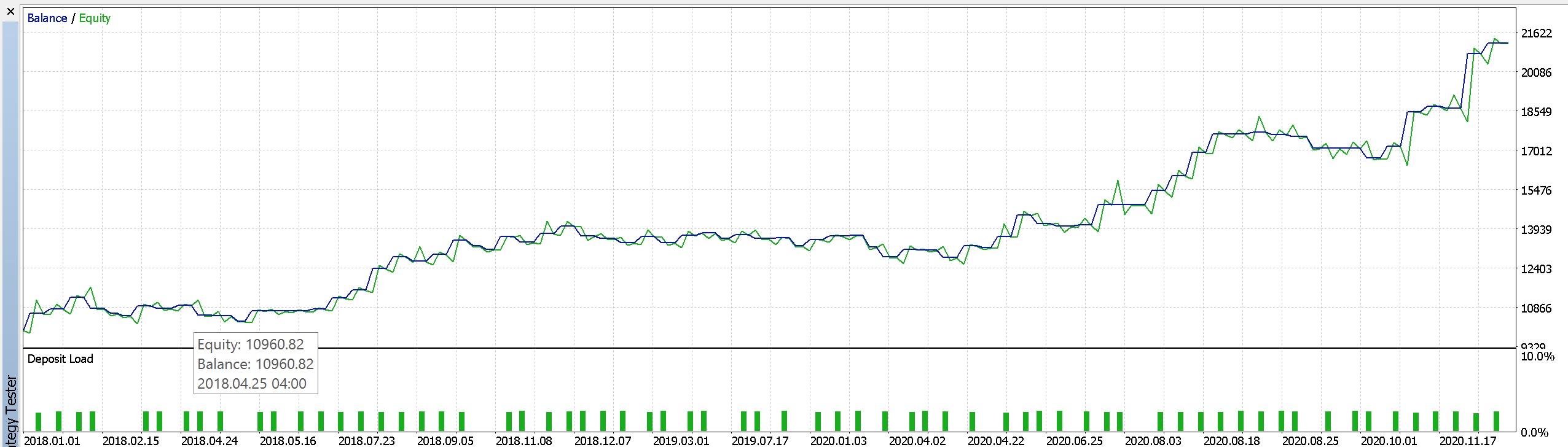
Part of report 2.
It appears our regression analysis signal benefits from using pending orders by having less drawdowns at the sacrifice of some profits. Other modifications could be made as well to enhance this system such as changing the trailing stop class, or the money management type. For our testing purposes we used fixed margin percent and we optimised with our criteria set to 'complex criterion'. It is desirable however to test as extensively as possible on historical tick data and do sufficient forward walks before deploying things which are beyond this article's scope.
5. Conclusion
5.1 MQL5 wizard is clearly a resourceful tool that should be in every trader’s arsenal. What we have considered here is how to take some statistical concepts of regression analysis like collinearity and coefficient of determination, and use them as a foundation to a robust trading system. Next steps would be extensive testing on historical tick data and exploring if this signal can be paired with other unique signals based on a trader's experience or on built-in signals in the MQL5 library in order to come up with a more comprehensive trading system. As will be the case in these series of articles, this article is not meant to provide a grail but rather a process which can be adjusted to better fit a trader's approach to the markets. Thanks for reading!
 How to master Machine Learning
How to master Machine Learning
 Developing a trading Expert Advisor from scratch (Part 8): A conceptual leap
Developing a trading Expert Advisor from scratch (Part 8): A conceptual leap
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
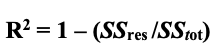
Hi Stephen,
Very good article. I made some tests and it returned good results. Looks like we have an encouraging trade system.
I would like to know how can I use input with non-fixed timeframes for optimization.
I've tried to change these lines, but OnInit "returned non-zero code 1" with no error message.
Can you help me?
Hi Stephen,
Very good article. I made some tests and it returned good results. Looks like we have an encouraging trade system.
I would like to know how can I use input with non-fixed timeframes for optimization.
I've tried to change these lines, but OnInit "returned non-zero code 1" with no error message.
Can you help me?
Hi Stephen,
Very good article. I made some tests and it returned good results. Looks like we have an encouraging trade system.
I would like to know how can I use input with non-fixed timeframes for optimization.
I've tried to change these lines, but OnInit "returned non-zero code 1" with no error message.
Can you help me?
Hello,
Just seeing this. Sorry. This can be a bit tricky because wizard assembled Expert Advisors tend to use and stick to the timeframe of the chart they are attached to. And this is referenced in quite a few different places, not just in the OnInit() function that it seems you're trying to modify. So if your input time frame does not match up with the time frame used and expected in other places (to be the chart time frame), then this is bound to generate errors.
Big picture though, there is a case for reading data and price buffers in more than one time frame so I think in the near future I will look to do an article on how this could be achieved. Thx for your feedback.
I get an error when compiling an expert made using the SignalDUAL_RA. it traces back to the matrix.mqh
The CMatrixDouble is a function call to the MetaEditor built in classes, matrix.mqh, so i presume the error does not lie there.
Can you help me solve this?
Can any one help?
it would not compile for me with the previously mentioned issue (see screenshot). I solved the issue as
_a[r].Set(c,Data(r+c,close)); should be _a.Set(r,c,Data(r+c,close));
with the use of _a[r] we are not editing the r-th row directly but passing it as a reference. This fix worked.