
Eigenvektoren und Eigenwerte: Explorative Datenanalyse in MetaTrader 5
Einführung
Die Hauptkomponentenanalyse (Principal Component Analysis, PCA) ist weithin für ihre Rolle bei der Dimensionenreduzierung während der Datenexploration bekannt. Sein Potenzial geht jedoch weit über die Reduzierung großer Datenmengen hinaus. Das Herzstück der PCA sind Eigenwerte und Eigenvektoren, die eine entscheidende Rolle bei der Aufdeckung verborgener Beziehungen in den Daten spielen. In diesem Artikel werden wir Techniken untersuchen, die die Eigenstruktur nutzen, um diese verborgenen Beziehungen aufzudecken.
Wir beginnen mit der Faktorenanalyse und zeigen, wie die Eigenstruktur zur Identifizierung latenter Variablen beiträgt und ein umfassenderes Verständnis der zugrunde liegenden Datenstruktur ermöglicht. Durch die Identifizierung latenter Variablen können wir Redundanzen zwischen scheinbar unabhängigen Variablen aufdecken und zeigen, dass mehrere Variablen möglicherweise einfach denselben zugrunde liegenden Faktor widerspiegeln. Außerdem werden wir untersuchen, wie Eigenvektoren und Eigenwerte verwendet werden können, um die Beziehungen zwischen den Variablen im Zeitverlauf zu bewerten. Durch die Analyse der Eigenstruktur von Daten, die in verschiedenen Zeitabständen erhoben wurden, können wir wertvolle Erkenntnisse über die dynamischen Beziehungen zwischen den Variablen gewinnen. So können wir Variablen identifizieren, die sich im Laufe der Zeit parallel zueinander bewegen oder ein gegensätzliches Verhalten zeigen.
Latente Variablen in Daten: Hauptfaktorenanalyse
Die Faktorenanalyse ist eine Methodik, die darauf abzielt, verborgene Faktoren aufzudecken, die die Wechselbeziehungen zwischen den beobachteten Variablen in den Daten erklären. Sie stellt gemessene Variablen als Kombinationen latenter Faktoren dar, die für Konstrukte stehen, von denen bekannt ist, dass sie eine Wirkung haben, die aber schwer zu messen oder zu quantifizieren sind. Denken Sie zum Beispiel an die Indikatoren, die ein Händler zur Bewertung des Marktverhaltens verwendet. Die Faktorenanalyse könnte zeigen, dass diese Indikatoren von zugrunde liegenden Faktoren wie der Anlegerstimmung oder der Risikobereitschaft beeinflusst werden. Während die Berechnung technischer Indikatoren einfach sein mag, ist die Quantifizierung der Marktstimmung oder der Risikobereitschaft eine größere Herausforderung. Es ist, als ob man die Wellen auf der Oberfläche eines trüben Gewässers beobachtet. Die Wellen stellen das dar, was wir sehen, während die zugrunde liegende Ursache verborgen bleibt. Die Faktorenanalyse zielt darauf ab, diese verborgenen Ursachen aufzudecken.
Die Faktorenanalyse wird oft fälschlicherweise als Alternative zur Hauptkomponentenanalyse (PCA) angesehen. Beide Techniken reduzieren die Dimensionen der Daten, aber sie unterscheiden sich, wie sich die reduzierten Variablen auf den ursprünglichen Satz beziehen. Die PCA reduziert einen großen Satz von Variablen in einen kleineren Satz unkorrelierter oder orthogonaler Variablen, die als Hauptkomponenten bezeichnet werden. Diese Komponenten erfassen die maximale Varianz der Originaldaten. Stellen Sie sich einen dichten Datensatz mit Hunderten von Variablen vor. Die Durchführung einer PCA könnte ergeben, dass nur drei Variablen mehr als 99 % der Dateninformationen darstellen. Diese drei Hauptkomponenten entsprechen unterschiedlichen Eigenschaften der beobachteten Daten, die durch die Kombination von Bits der Originaldaten erklärt werden. Jede Hauptkomponente wird durch den dichten Satz von Variablen beeinflusst. Im Gegensatz dazu geht die Faktorenanalyse davon aus, dass latente Variablen die beobachteten Variablen beeinflussen. In diesem Text konzentrieren wir uns auf die Berechnung dieser verborgenen Dimensionen und die einzigartigen Perspektiven, die sie auf die beobachteten Variablen bieten, und nicht auf die Dimensionenreduktion.
Eigenwerte und Eigenvektoren sind grundlegende mathematische Konzepte, die für das Verständnis dieses Artikels entscheidend sind. Wenn die Matrix A eine p x p-Matrix ist, x ein Spaltenvektor der Länge p und E ein Skalar ist, dann ist x ein Eigenvektor von A mit dem Eigenwert E, wenn Ax=Ex. Die Richtung des Eigenvektors ist von Bedeutung, nicht seine Länge, und er ist normalerweise auf eine Einheitslänge normiert. Geometrisch gesehen wird ein Vektor durch die Multiplikation mit einer Matrix im Allgemeinen gedreht, aber Eigenvektoren bleiben bei der Multiplikation mit der Matrix in ihrer Richtung unverändert. Diese Richtung ist der Schlüssel zu ihrer Relevanz. Bei einer standardisierten, multivariaten Normalverteilung ist die Kovarianzmatrix die Korrelationsmatrix R. V sei eine p x m-Matrix. Der neue Zufallsvektor y=V“x hat eine Kovarianzmatrix C=V“RV.
Die Matrix V hat wünschenswerte Eigenschaften, die sich auf y übertragen lassen. Für m=1 ist V eine einzelne Spalte, und C ist die Varianz von y. Normalisiert man V so, dass die Summe seiner Komponenten eins ergibt, erhält man den Eigenvektor von R, der dem größten Eigenwert entspricht. Erweitert man dies auf m=2, so ist die zweite Spalte von V, die orthogonal zur ersten steht, der Eigenvektor von R, der dem zweitgrößten Eigenwert entspricht. Dieser Prozess wird für alle p Spalten fortgesetzt, wodurch die Eigenvektoren von R zur Transformationsmatrix für die Zuordnung von x-Variablen zu unabhängigen y-Variablen werden, die die größte Varianz erfassen.
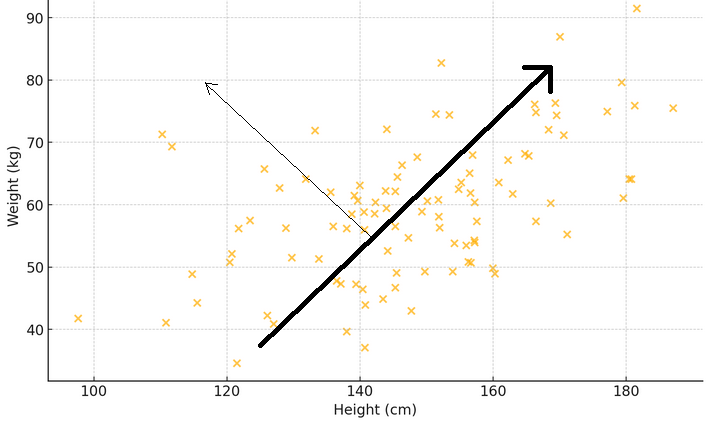
Um zu veranschaulichen, was die beiden vorangegangenen Absätze bedeuten, betrachten Sie ein Streudiagramm, bei dem die x-Achse das Gewicht und die y-Achse die Größe einer Stichprobe von Personen darstellt. Zieht man eine Linie durch die Punkte, die am besten mit der Streuung der Messwerte übereinstimmt, so zeigt diese Linie das Hauptmuster: Größere Menschen sind tendenziell schwerer. Stellen Sie sich einen Eigenvektor als einen Pfeil vor, der in diese Hauptrichtung zeigt und den größten Trend oder das vorherrschende Muster anzeigt. Der entsprechende Eigenwert gibt an, wie stark dieses Phänomen ist. Wenn ein weiterer Pfeil senkrecht zum ersten gezeichnet wird, zeigt er ein sekundäres Muster, wie z. B., dass manche Menschen schwerer oder leichter sind als gewöhnlich für ihre Größe.
Ziel ist es, festzustellen, wie sich jede beobachtete Variable zu den Eigenwerten der Korrelationsmatrix verhält. Dazu müssen die Korrelationen zwischen den Eigenwerten und den beobachteten Variablen berechnet werden. Diese Korrelationen bilden eine spezielle Matrix, die sogenannte Faktorladungsmatrix, die durch Multiplikation jedes Eigenvektors mit der Quadratwurzel des entsprechenden Eigenwerts entsteht. Wenn wir untersuchen, wie die Variablen mit bestimmten Eigenwerten korrelieren, können wir Hypothesen über die Auswirkungen auf die beobachteten Variablen aufstellen. Diese Analyse hilft uns zu verstehen, welche Variablen für die Faktoren am wichtigsten sind, und gibt uns Hinweise auf die angemessene Anzahl von Faktoren, die die beobachteten Variablen beeinflussen.
Beispiel: Hauptfaktorenanalyse für Finanzindikatoren
In diesem Abschnitt wird die Hauptfaktorenanalyse (PFA) anhand eines Datensatzes von Finanzindikatoren demonstriert. Wir werden MQL5 verwenden, um alle Schritte zur Berechnung der Faktorladungsmatrix durchzuführen. Wir beginnen mit der Erfassung der Daten, die uns interessieren. Die in diesem Zusammenhang aus einigen wenigen Indikatoren bestehen, die innerhalb eines bestimmten Bereichs von Fensterlängen abgetastet werden. Zur Veranschaulichung werden wir zwei gängige Indikatoren verwenden: den Indikator des gleitenden Durchschnitts (MA), der Informationen über den Trend liefert, und den Average True Range (ATR), der ein grundlegendes Maß für die Volatilität darstellt. Für diese Indikatoren werden über einen bestimmten Zeitraum hinweg mehrere Zeitfenster erfasst.
Da der größte Teil der Analyse die Untersuchung potenziell großer Matrizen beinhaltet, reicht es aufgrund ihrer Größe nicht aus, sie einfach auf der Registerkarte „Experten“ des Terminals zu drucken. Angesichts des Ziels, alle Analysen innerhalb von MetaTrader 5 durchzuführen, ohne zu anderen Plattformen wie Python oder R zu wechseln, wurde eine grafische Nutzeroberfläche in die Anwendung integriert, die PFA implementiert. Die folgende Grafik zeigt den Datensatz, mit dem wir in diesem Beispiel arbeiten werden. Jede Spalte enthält die Werte für einen Indikator für eine bestimmte Fensterlänge, wie sie in der Spaltenüberschrift angegeben ist. „ATR_2“ bezieht sich auf den ATR-Indikator mit einer Fensterlänge von 2. Der Null-Index zeigt den ältesten Wert in der Zeit, im Zeitraum vom 31.12.2019 bis 31.12.2022, basierend auf den täglichen Preisen von BitCoin (BTCUSD).
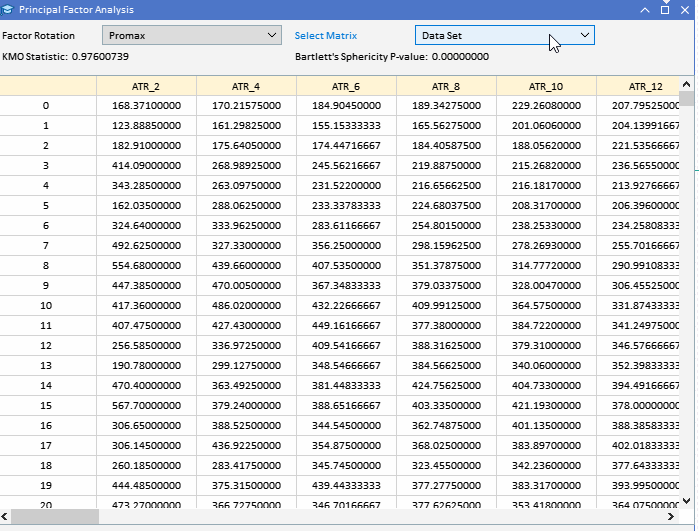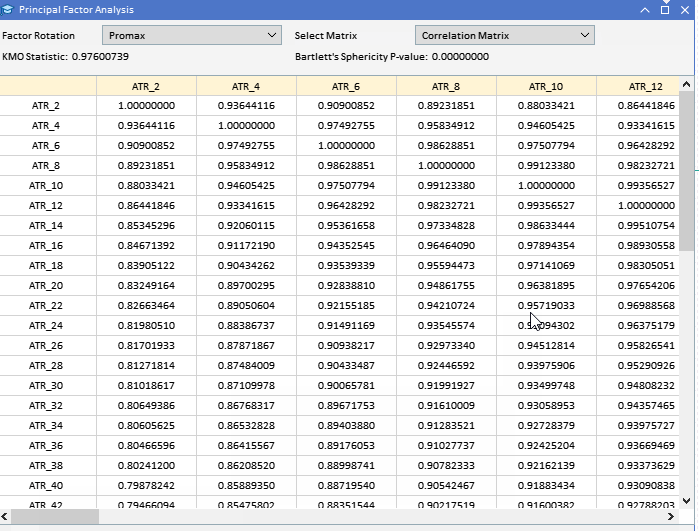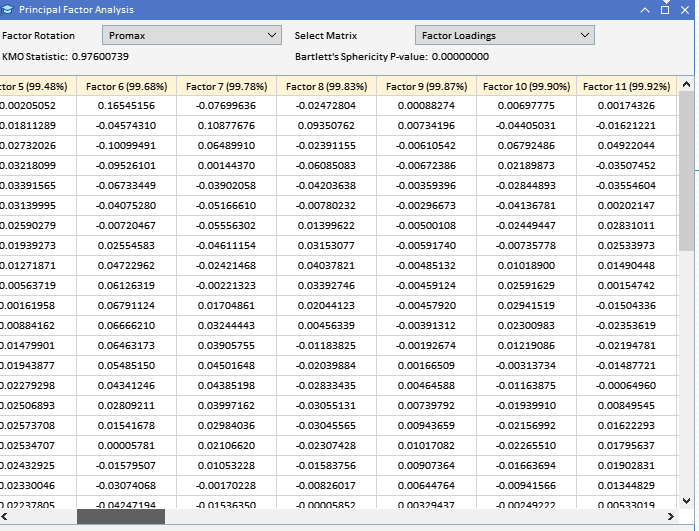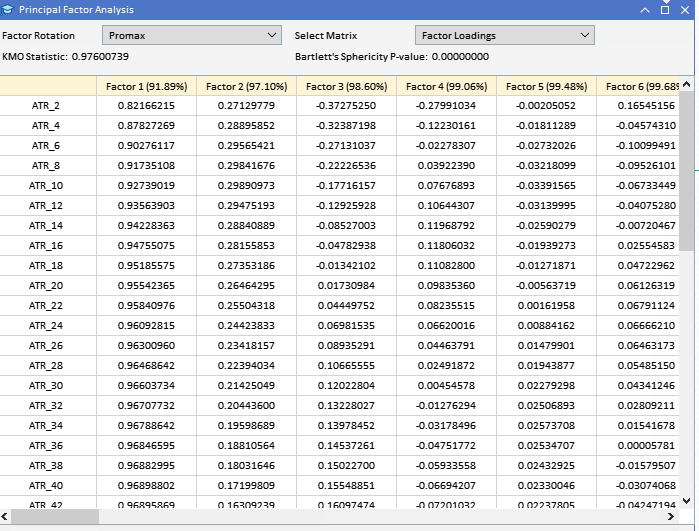
Bevor man versucht, die Hauptfaktoren zu extrahieren, sollte man prüfen, ob ein Datensatz für eine Faktorenanalyse geeignet ist. Es gibt zwei statistische Tests, die mit einem Datensatz durchgeführt werden können, um festzustellen, ob die Variablen wahrscheinlich durch latente Faktoren erklärt werden können. Der erste ist der Kaiser-Meyer-Olkin (KMO)-Test. Das KMO-Kriterium ist eine Statistik, die die Angemessenheit der Stichprobendaten für die Faktorenanalyse misst. Sie quantifiziert den Grad der Korrelation zwischen den Variablen und bewertet den Anteil der Varianz zwischen den Variablen, der gemeinsame Varianz sein könnte, d. h. der den zugrunde liegenden Faktoren zugeschrieben werden kann. Das KMO-Maß vergleicht die Größenordnung der beobachteten Korrelationskoeffizienten mit der Größenordnung der partiellen Korrelationskoeffizienten. Er reicht von 0 bis 1, wobei:
- Werte nahe bei 1 bedeuten, dass die Daten für eine Faktorenanalyse sehr gut geeignet sind.
- Werte unter 0,6 deuten im Allgemeinen darauf hin, dass die Daten für eine Faktorenanalyse nicht geeignet sind.
Mathematisch ist die KMO-Statistik wie folgt definiert:
wobei:
- r(ij) ist der Korrelationskoeffizient zwischen den Variablen i und j.
- p(ij) ist der partielle Korrelationskoeffizient zwischen den Variablen i und j.
Nachstehend finden Sie eine MQL5-Implementierung des KMO-Tests. Die Funktion „kmo()“ benötigt drei Eingabeparameter. Die Matrix „in“ sollte mit dem Datensatz der zu untersuchenden Variablen versehen werden. Die Ergebnisse des Tests werden an den zweiten bzw. dritten Eingabeparameter ausgegeben. Der Vektor „kmo_per_item“ enthält die KMO-Werte für jede Variable (entsprechend jeder Spalte der „in“-Matrix) und „kmo_total“ ist die Gesamt-KMO-Statistik für die kombinierten Variablen.
//+---------------------------------------------------------------------------+ //| Calculate the Kaiser-Meyer-Olkin criterion | //| In general, a KMO < 0.6 is considered inadequate. | //+---------------------------------------------------------------------------+ void kmo(matrix &in, vector &kmo_per_item, double &kmo_total) { matrix partial_corr = partial_correlations(in); matrix x_corr = (stdmat(in)).CorrCoef(false); np::fillDiagonal(x_corr,0.0); np::fillDiagonal(partial_corr,0.0); partial_corr = pow(partial_corr,2.0); x_corr = pow(x_corr,2.0); vector partial_corr_sum = partial_corr.Sum(0); vector corr_sum = x_corr.Sum(0); kmo_per_item = corr_sum/(corr_sum+partial_corr_sum); double corr_sum_total = x_corr.Sum(); double partial_corr_sum_total = partial_corr.Sum(); kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total); return; }
Ein alternativer oder zusätzlicher Test, der zur Beurteilung eines Datensatzes durchgeführt werden kann, ist der Bartletts Test of Sphericity (BTS). Dabei handelt es sich um einen statistischen Test, mit dem untersucht wird, ob eine Korrelationsmatrix eine Identitätsmatrix ist, was darauf hindeuten würde, dass die Variablen nicht miteinander verbunden sind und sich nicht für Strukturerkennungsmethoden wie die Faktorenanalyse eignen. Im Wesentlichen wird getestet, ob die beobachtete Korrelationsmatrix signifikant von der Identitätsmatrix abweicht, bei der alle Diagonalelemente 1 sind, was bedeutet, dass die Variablen perfekt mit sich selbst korrelieren, und die Nicht-Diagonalelemente 0 sind, was bedeutet, dass keine Korrelation zwischen verschiedenen Variablen besteht. Der Test basiert auf dem Chi-Quadrat-Test, dessen Teststatistik nach der folgenden Formel berechnet wird:
wobei :
- n ist die Anzahl der Beobachtungen.
- p ist die Anzahl der Variablen.
-|R| ist die Determinante der Korrelationsmatrix R.
Die Teststatistik folgt einer Chi-Quadrat-Verteilung mit (p(p-1))/2 Freiheitsgraden. Wenn die Bartlett-Teststatistik groß und der zugehörige p-Wert klein ist, typischerweise p-Wert < 0,05, wird die Nullhypothese verworfen. Dies deutet darauf hin, dass sich die Korrelationsmatrix signifikant von einer Identitätsmatrix unterscheidet, was darauf hindeutet, dass die Variablen miteinander in Beziehung stehen und für eine Faktorenanalyse geeignet sind. Andernfalls, wenn der p-Wert groß ist, kann die Nullhypothese nicht zurückgewiesen werden, was darauf hindeutet, dass die Korrelationsmatrix nahe an einer Identitätsmatrix liegt und die Variablen nicht signifikant korreliert sind.
Der folgende Code definiert die Funktion „bartlet_sphericity()“, die BTS implementiert. Die Funktion gibt ihre Ergebnisse an die letzten beiden Eingabeparameter aus. Beides sind skalare Werte. „statistic“ ist die Chi-Quadrat-Statistik und „p_value“ ist der berechnete Wahrscheinlichkeitswert.
//+------------------------------------------------------------------+ //| Compute the Bartlett sphericity test. | //+------------------------------------------------------------------+ void bartlet_sphericity(matrix &in, double &statistic, double &p_value) { long n,p; n = long(in.Rows()); p = long(in.Cols()); matrix x_corr = (stdmat(in)).CorrCoef(false); double corr_det = x_corr.Det(); double neg = -log(corr_det); statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX; double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0; int error; p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error); if(error) Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error); return; }
Wenn einer der Tests oder beide ermutigende Ergebnisse liefern, können wir mit der Extraktion der Hauptfaktoren fortfahren. Anhand des Datensatzes der Indikatoren können wir sehen, dass beide Tests zeigen, dass die Variablen für die Faktorextraktion geeignet sind.
Der nächste Schritt umfasst eine kleine Vorverarbeitung, bei der der Datensatz standardisiert wird. Durch die Standardisierung der Daten wird sichergestellt, dass jeder Indikator unabhängig von seinem Umfang gleichermaßen zur Analyse beiträgt.
//+------------------------------------------------------------------+ //| standardize a matrix | //+------------------------------------------------------------------+ matrix stdmat(matrix &in) { vector mean = in.Mean(0); vector std = in.Std(0); std+=1e-10; matrix out = in; for(ulong row =0; row<out.Rows(); row++) if(!out.Row((in.Row(row)-mean)/std,row)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(in.Rows(), in.Cols()); } return out; }
Die Korrelationsmatrix wird anhand der standardisierten Daten berechnet.
m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false); Anschließend berechnen wir die Eigenwerte und Eigenvektoren der Korrelationsmatrix. Wir haben uns für die Implementierung der Eigenvektor-Dekompostierung in der Aglib-Bibliothek entschieden, da bei der Verwendung der Methode „Eig()“ für native Matrizen ein Problem aufgetreten ist.
CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
Das Problem lässt sich am besten anhand eines Beispiels veranschaulichen. Der folgende Code definiert ein Skript, das die Eigenvektoren und Werte einer symmetrischen Matrix zerlegt.
//+------------------------------------------------------------------+ //| TestEigenDecompostion.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Alglib\linalg.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix dataset = { {1,0.5,-0.2}, {0.5,1,-0.8}, {-0.2,-0.8,1} }; matrix evectors; vector evalues; dataset.Eig(evectors,evalues); Print("Eigen decomposition of \n", dataset); Print(" EVD using built in Eig() \n", evectors); Print(evalues); CMatrixDouble data(dataset); CMatrixDouble vects; CRowDouble vals; CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects); Print(" EVD using Alglib implementation \n", vects.ToMatrix()); Print(vals.ToVector()); } //+------------------------------------------------------------------+
Die Ausgabe des Skripts wird im Folgenden dargestellt.
Sie zeigt den Unterschied in der Darstellung der Eigenvektoren und Werte. Die Alglib-Implementierung sortiert die Vektoren und Werte in aufsteigender Reihenfolge, was bequemer ist. Die systemeigene MQL5-Methode „Eig()“ bietet keine Ordnungsfunktion, aber das ist nicht der Hauptgrund, die Methode als weniger verwendungsfähig anzusehen. Betrachtet man den letzten Eigenvektor (Spalte), so stellt man fest, dass die Vorzeichen der einzelnen Werte genau entgegengesetzt zu denen der entsprechenden Werte sind, die vom Alglib-Code ausgegeben werden. Es ist nicht klar, warum dies der Fall ist. Um zu bestätigen, dass es sich um eine Anomalie handelt, wurde dieselbe Dekompostierung mit Numpy von Python durchgeführt und die Ergebnisse von Alglib wurden wiederholt. Es liegt auf der Hand, dass die Faktorladungen empfindlich auf das Vorzeichen der Eigenvektorgliederwerte reagieren. Da die Ladungen als Korrelationen definiert sind, ist das Vorzeichen des Wertes von großer Bedeutung.
Die Faktorladungsmatrix ergibt sich durch Multiplikation jedes Eigenvektors mit der Quadratwurzel des entsprechenden Eigenwerts. Um zu verhindern, dass wir ungültige Zahlen erhalten, ersetzen wir zunächst alle Eigenwerte kleiner als Null durch 0. Dadurch wird die zugehörige Dimension (Eigenvektor) in der Faktorladungsmatrix effektiv verworfen.
m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
Die Codeschnipsel, die wir bisher gesehen haben, wurden aus der Cpfa-Klasse extrahiert, um die Hauptfaktorenanalyse (PFA) in MetaTrader 5 durchzuführen. Die vollständige Klasse ist unten abgebildet, gefolgt von einer Tabelle, die ihre öffentlichen Methoden dokumentiert.
//+------------------------------------------------------------------+ //| Principal factor extraction | //+------------------------------------------------------------------+ class Cpfa { private: bool m_fitted; //flag showing if principal factors were extracted matrix m_corrmat, //correlation matrix m_data, //standardized data is here m_eigvectors, //matrix of eigen vectors of correlation matrix m_structmat; //factor loading matrix vector m_eigvalues, //vector of eigen values m_cumeigvalues; //eigen values sorted in descending order long m_indices[];//original order of column indices in input data matrix public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Cpfa(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Cpfa(void) { } //+------------------------------------------------------------------+ //| fit() called with input matrix and extracts principal factors | //+------------------------------------------------------------------+ bool fit(matrix &in) { m_fitted = false; m_data = stdmat(in); m_corrmat = m_data.CorrCoef(false); CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_eigvectors = vects.ToMatrix(); m_eigvalues = vals.ToVector(); double sum = 0.0; double total = m_eigvalues.Sum(); if(!np::reverseVector(m_eigvalues) || !np::reverseMatrixCols(m_eigvectors)) return m_fitted; m_cumeigvalues = m_eigvalues; for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++) { sum += m_eigvalues[i] ; m_cumeigvalues[i] = 100.0 * sum/total; } m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_fitted = true; return m_fitted; } //+------------------------------------------------------------------+ //| returns factor loading matrix | //+------------------------------------------------------------------+ matrix get_factor_loadings(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_structmat; } //+------------------------------------------------------------------+ //| get the eigenvector and values of correlation matrix | //+------------------------------------------------------------------+ bool get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return false; } out_eigvalues = m_eigvalues; out_eigvectors = m_eigvectors; return true; } //+------------------------------------------------------------------+ //| returns variance contributions for each factor as a percent | //+------------------------------------------------------------------+ vector get_cum_var_contributions(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return vector::Zeros(1); } return m_cumeigvalues; } //+------------------------------------------------------------------+ //| get the correlation matrix of the dataset | //+------------------------------------------------------------------+ matrix get_correlation_matrix(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_corrmat; } //+------------------------------------------------------------------+ //| returns the rotated factor loadings | //+------------------------------------------------------------------+ matrix rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } CRotator rotator; if(!rotator.fit(m_structmat,factor_rotation_type,4,true)) return matrix::Zeros(1,1); else return rotator.get_transformed_loadings(); } };
| Methode | Beschreibung | Rückgabe Typ |
|---|---|---|
| fit | Extrahiert Hauptfaktoren aus der Eingabematrix „in“. Diese Funktion standardisiert die Eingabedaten, berechnet die Korrelationsmatrix und führt eine Eigenwertzerlegung durch. Außerdem werden die Faktorladungsmatrix und die kumulativen Eigenwerte berechnet. Dies ist die Methode, die nach der Instanziierung des Objekts zuerst aufgerufen werden sollte. | bool |
| get_factor_loadings | Gibt die Faktorladungsmatrix zurück, wenn Hauptfaktoren extrahiert wurden; andernfalls wird eine Nullmatrix zurückgegeben. Die Ladungen werden in absteigender Reihenfolge relativ zum größten Eigenwert sortiert. Nach erfolgreichem Abschluss von „fit()“ können diese und andere Methoden aufgerufen werden, um die Eigenschaften der Analyse abzurufen. | matrix |
| get_eigen_structure | Gibt die Eigenvektoren und Eigenwerte der Korrelationsmatrix zurück. Optional können sie sortiert werden. | matrix, vector |
| get_cum_var_contributions | Gibt die kumulativen Varianzbeiträge jedes Faktors in Prozent zurück, wenn Hauptfaktoren extrahiert wurden; andernfalls wird ein Nullvektor zurückgegeben. | vector |
| get_correlation_matrix | Gibt die Korrelationsmatrix des Datensatzes zurück, wenn Hauptfaktoren extrahiert wurden; andernfalls wird eine Nullmatrix zurückgegeben. | matrix |
| rotate_factorloadings | Gibt die Matrix der rotierten Faktorladungen unter Verwendung des angegebenen Rotationstyps zurück, wenn Hauptfaktoren extrahiert wurden; andernfalls wird eine Nullmatrix zurückgegeben. | matrix |
Da wir nun wissen, wie wir die Faktorladungen erhalten, werden wir im nächsten Abschnitt sehen, was diese Korrelationen aussagen.
Interpretation der Faktorladungen
Faktorladungen stellen die Korrelation zwischen den beobachteten Variablen und den zugrunde liegenden latenten Faktoren dar. Sie geben an, inwieweit eine Variable mit einem Faktor verbunden ist. Um die Interpretation zu erleichtern, sind die Eigenvektoren in absteigender Reihenfolge nach der Größe der entsprechenden Eigenwerte angeordnet. Dadurch wird sichergestellt, dass der erste Eigenvektor dem größten Eigenwert entspricht, der sich auf den latenten Faktor mit dem größten Einfluss auf die beobachteten Variablen bezieht. Die Zeilen der Faktorladungsmatrix folgen der gleichen Reihenfolge wie die Spalten des Originaldatensatzes, d. h. jede Zeile entspricht einer Variablen. Die Spalten stellen die Faktoren in absteigender Reihenfolge der erklärten Varianz dar. Korrelationen über 0,4 oder unter -0,4 werden als signifikant angesehen. Jede Variable mit Werten im Bereich von -0,4 bis 0,4 zeigt an, dass der entsprechende Faktor einen geringen Einfluss auf diese Variable hat.
| Variablen | Faktor 1 | Faktor 2 | Faktor 3 |
|---|---|---|---|
| X1 | 0.8 | 0.3 | 0.1 |
| X2 | -0.3 | -0.93 | 0.00002 |
| X3 | 0.0 | 0.342 | -1 |
| X4 | 0.5 | 0.1 | -0.38 |
| X5 | 0.5 | -0.33 | 0.44 |
Datensätze mit einer einfachen Faktorenstruktur weisen Variablen auf, die auf einem Faktor hoch und auf anderen niedrig laden. Die obige Tabelle zeigt die Faktorladungen eines hypothetischen Datensatzes. Die Variablen X1 bis X4 zeigen, dass sie signifikant auf verschiedene Faktoren geladen werden, während die Variable X5 gemischte Signale liefert, da sie geringfügig auf zwei Faktoren gleichzeitig geladen wird. Merkmale der gemessenen Variablen in Verbindung mit ihren Faktorladungen können Hinweise auf die Art des zugrunde liegenden Faktors liefern. Wenn beispielsweise mehrere Wirtschaftsindikatoren stark auf einem einzigen Faktor lasten, könnte dieser Faktor einen zugrunde liegenden Wirtschaftstrend oder eine Marktstimmung darstellen. Umgekehrt kann eine Variable, die mäßig auf mehreren Faktoren lastet, darauf hindeuten, dass die Variable von mehreren zugrundeliegenden Faktoren beeinflusst wird, von denen jeder zu einem anderen Aspekt des Verhaltens der Variablen beiträgt.
Ein Blick auf die Faktorladungen der zuvor erhobenen ATR-Variablen zeigt, dass die meisten Variablen hohe Ladungen auf Faktor 1 aufweisen, was darauf hindeutet, dass diese Variablen hauptsächlich von diesem Faktor beeinflusst werden. Faktor 1 erklärt einen bedeutenden Teil der Varianz in diesen Variablen, wobei der Prozentsatz der erklärten Varianz durch die Zahl in Klammern angegeben ist (91,89 %). Obwohl Faktor 1 dominant erscheint, weisen einige Variablen auch bemerkenswerte Ladungen auf anderen Faktoren auf. ATR_4, ATR_6, ATR_10, ATR_14 und andere haben moderate Ladungen auf Faktor 2, was auf einen sekundären Einfluss hinweist. ATR_2, ATR_4, ATR_6, ATR_8 haben kleinere, aber signifikante Ladungen auf Faktor 3. Die Faktoren 4 und folgende weisen geringere Ladungen über verschiedene Variablen auf, was darauf hindeutet, dass sie im Vergleich zu den ersten drei Faktoren weniger Varianz im Datensatz erklären.
Wenn die Faktorladungen aufgrund einer komplexen Faktorenstruktur zu schwierig zu interpretieren sind, ist es möglich, die Ladungen zu vereinfachen, indem man sie transformiert, um die Interpretierbarkeit zu verbessern. Diese Art der Transformation wird als Faktorrotation bezeichnet. Es gibt zwei Arten von Rotationen, die auf die Matrix der Faktorladungen angewendet werden können. Orthogonale Rotationen erhalten die Unabhängigkeit der Faktoren. Beispiele hierfür sind Varimax- und Equamax-Rotationen. Orthogonale Rotationen sollten angewendet werden, wenn die Faktoren als unabhängig angesehen werden. Schräge Rotationen ermöglichen eine gewisse Abhängigkeit zwischen den Faktoren. Beispiele sind Promax- und Oblimin-Drehungen. Schräge Rotationen sind angebracht, wenn vermutet wird, dass die Faktoren miteinander zusammenhängen. Durch die Transformation der Korrelationen mittels Rotation werden die Rohkorrelationen der Faktorenstrukturmatrix auf Extremwerte (-1,0,1) gebracht, um die Interpretation der Korrelationen zu erleichtern und die Auswirkungen auf die beobachteten Variablen zu verstärken.
Zur Vereinfachung von Rotationen führen wir die Klasse CRotator ein, die Promax- und Varimax-Rotationen implementiert.
//+------------------------------------------------------------------+ //| class implementing factor rotations | //| implements varimax and promax rotations | //+------------------------------------------------------------------+ class CRotator { private: bool m_normalize, //normalization flag m_done; //rotation flag int m_power, //exponent to which to raise the promax loadings m_maxIter; //maximum number of iterations. Used for 'varimax' double m_tol; //convergence threshold. Used for 'varimax' matrix m_loadings, //the rotated factor loadings m_rotation_mtx, //the rotation matrix m_phi; //factor correlations matrix. ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed //+------------------------------------------------------------------+ //| implements varimax rotation | //+------------------------------------------------------------------+ bool varimax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; vector norm_mat(X.Rows()); if(m_normalize) { for(ulong i = 0; i<X.Rows(); i++) norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum()); X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows()); X = X.Transpose(); } m_rotation_mtx = matrix::Eye(cols,cols); double d = 0,old_d; matrix diag,U,V,transformed,basis; vector S,ones; for(int i =0; i< m_maxIter; i++) { old_d = d; basis = X.MatMul(m_rotation_mtx); ones = vector::Ones(rows); diag.Diag(ones.MatMul(pow(basis,2.0))); transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows)); if(!transformed.SVD(U,V,S)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } m_rotation_mtx = U.Inner(V); d = S.Sum(); if(d<old_d*(1.0+m_tol)) break; } X = X.MatMul(m_rotation_mtx); if(m_normalize) { matrix xx = X.Transpose(); X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows()); } else X = X.Transpose(); m_loadings = X.Transpose(); return true; } //+------------------------------------------------------------------+ //| implements promax rotation | //+------------------------------------------------------------------+ bool promax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; matrix weights,h2; h2.Init(1,1); if(m_normalize) { matrix array = X; matrix m = array.MatMul(array.Transpose()); vector dg = m.Diag(); h2.Resize(dg.Size(),1); h2.Col(dg,0); weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false); } else weights = X; if(!varimax(weights)) return false; X = m_loadings; ResetLastError(); matrix Y = X * pow(MathAbs(X),double(m_power-1)); matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y)); vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag(); if(GetLastError()) { diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag(); ResetLastError(); } matrix D; D.Diag(sqrt(diag_inv)); coef = coef.MatMul(D); matrix z = X.MatMul(coef); if(m_normalize) z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false); m_rotation_mtx = m_rotation_mtx.MatMul(coef); matrix coef_inv = coef.Inv(); m_phi = coef_inv.MatMul(coef_inv.Transpose()); m_loadings = z; return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CRotator(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CRotator(void) { } //+------------------------------------------------------------------+ //| performs rotation on supplied factor loadings passed to /in/ | //+------------------------------------------------------------------+ bool fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05) { m_rotation_type = rot_type; m_power = power; m_maxIter = maxiter; m_tol = tol; m_done=false; if(in.Cols()<2) { m_loadings = in; m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols()); m_phi = matrix::Zeros(in.Rows(),in.Cols()); m_done = true; return true; } switch(m_rotation_type) { case MODE_VARIMX: m_done = varimax(in); break; case MODE_PROMAX: m_done = promax(in); break; default: return m_done; } return m_done; } //+------------------------------------------------------------------+ //| get the rotated loadings | //+------------------------------------------------------------------+ matrix get_transformed_loadings(void) { if(m_done) return m_loadings; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the rotation matrix | //+------------------------------------------------------------------+ matrix get_rotation_matrix(void) { if(m_done) return m_rotation_mtx; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the factor correlation matrix | //+------------------------------------------------------------------+ matrix get_phi(void) { if(m_done && m_rotation_type==MODE_PROMAX) return m_phi; else return matrix::Zeros(1,1); } };
Hier ist ein Überblick über die öffentlichen Methoden:
| Methode | Beschreibung | Parameter | Rückgabe Typ |
|---|---|---|---|
| fit | Führt die angegebene Rotation (Varimax oder Promax) an der angegebenen Faktorladungsmatrix durch. | in: Die zu rotierende Matrix der Faktorladungen | bool |
| get_transformed_loadings | Gibt die Matrix der rotierten Faktorladungen zurück | Keine | matrix |
| get_rotation_matrix | Gibt die in der Transformation verwendete Rotationsmatrix zurück. | Keine | matrix |
| get_phi | Gibt die Faktor-Korrelationsmatrix zurück (nur bei Promax-Rotation). | Keine | matrix |
Anwendung der Rotation auf die Matrix der Faktorladungen.
CRotator rotator; if(!rotator.fit(m_structmat,MODE_PROMAX,4,false)) return; Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());
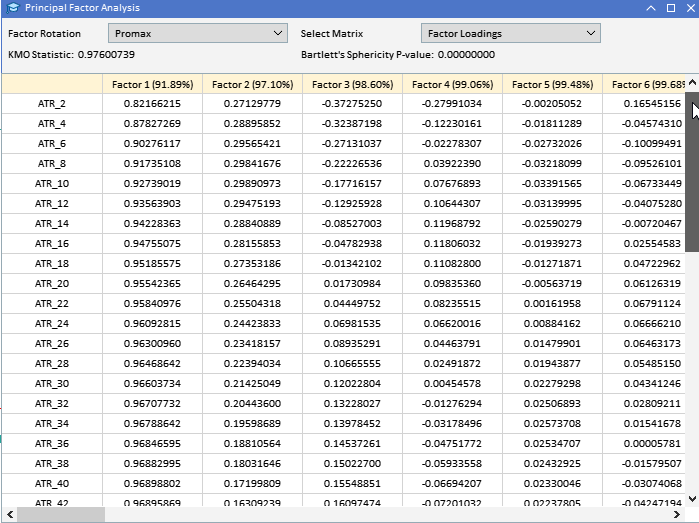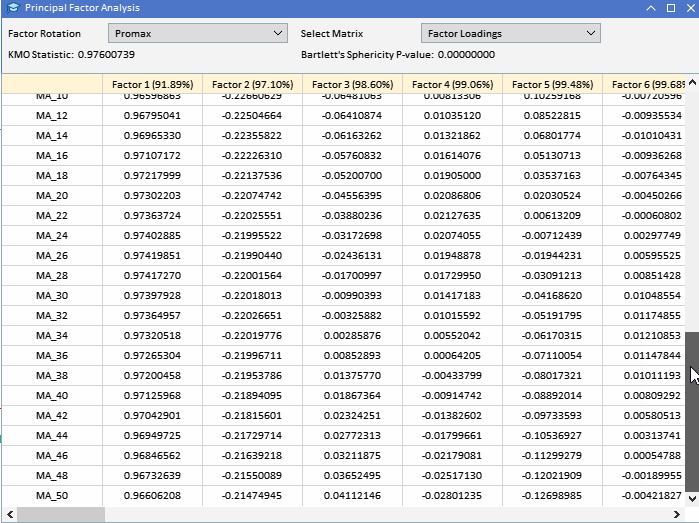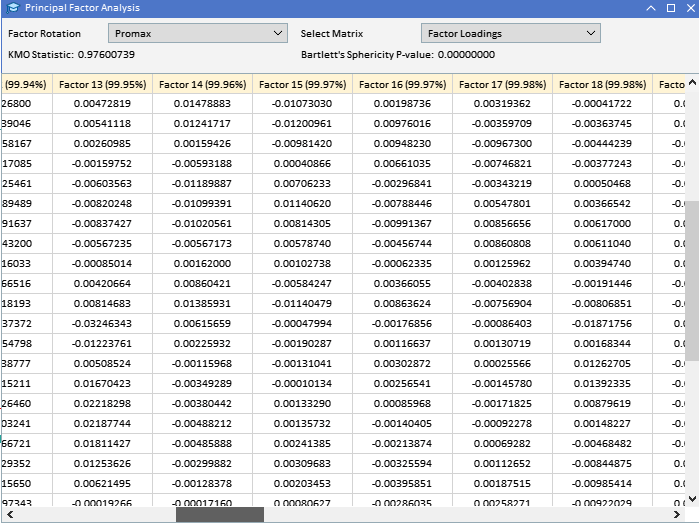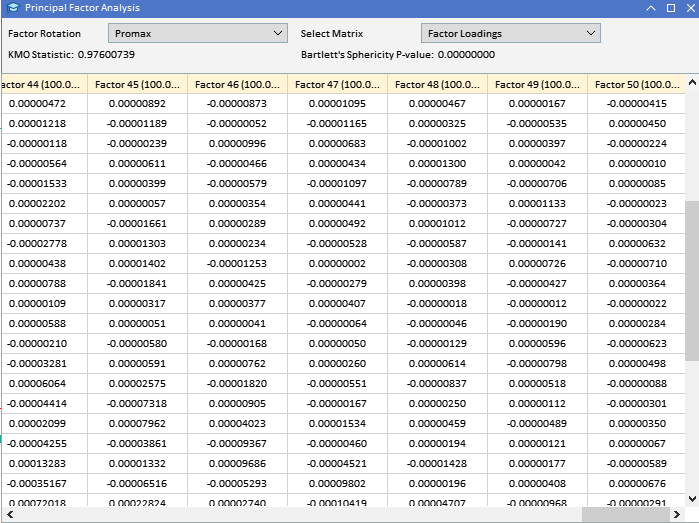
Die promax-rotierten Faktorladungen verdeutlichen die Auswirkungen, die Faktor 1 und Faktor 2 auf die beiden Klassen von Variablen haben. Faktor 1 ist der dominierende Einfluss auf die MA-Variablen.
Faktor 2 erfasst den zusätzlichen Einfluss auf die ATR-Variablen. Der geringe Einfluss anderer Faktoren wird durch die Erfassung weniger signifikanter Muster in den Daten erheblich verstärkt. Diese gedrehte Lösung ermöglicht ein klareres Verständnis der zugrunde liegenden Struktur des Datensatzes und erleichtert die Interpretation. Die Faktorenrotation kann zwar die Interpretierbarkeit der Faktorladungen erheblich verbessern, doch gibt es auch einige Nachteile und Einschränkungen zu beachten:
- Die Rotation könnte die zugrundeliegende Struktur zu stark vereinfachen, indem sie die Variablen dazu zwingt, in hohem Maße auf einen einzigen Faktor zu laden, wodurch möglicherweise komplexere Zusammenhänge überdeckt werden.
- Die Wahl zwischen orthogonalen und schrägen Rotationen hängt von theoretischen Annahmen über die Unabhängigkeit der Faktoren ab, die nicht immer klar oder gerechtfertigt sind.
- In einigen Fällen kann die Rotation zu einem leichten Verlust an erklärter Varianz führen, da das Ziel der Rotation die Interpretierbarkeit und nicht die Maximierung der erklärten Varianz ist.
- Bei einer großen Anzahl von Variablen und Faktoren kann die Interpretation der rotierten Ladungen immer noch schwierig sein, vor allem wenn es keine klare einfache Struktur gibt.
- Rotationen, insbesondere iterative Rotationen wie Varimax, können bei großen Datensätzen rechenintensiv sein, was die Leistung von Echtzeitanwendungen beeinträchtigen kann.
Damit ist unsere Diskussion über die Extraktion der Hauptfaktoren abgeschlossen. Als Nächstes werden wir uns mit der Redundanz in Variablen auf der Grundlage latenter Faktoren befassen und untersuchen, wie latente Faktoren verborgene Beziehungen aufdecken können.
Redundanz in Variablen, die auf latenten Faktoren beruhen
Bei einer großen Anzahl von Variablen ist es sinnvoll, Variablengruppen zu identifizieren, die in hohem Maße redundant sind. Das bedeutet, dass einige Variablen ähnliche Informationen liefern und wir möglicherweise nicht alle berücksichtigen müssen. In der Regel stammt die wichtige Information aus der Redundanz selbst, da sie auf einen gemeinsamen Effekt hinweisen kann, der mehrere Variablen beeinflusst. Durch die Identifizierung von Gruppen stark redundanter Variablen können wir unsere Analyse vereinfachen, indem wir uns auf einige wenige repräsentative Variablen oder einen einzigen Faktor konzentrieren, der gut mit der Gruppe korreliert.
Eine beliebte Methode zur Erkennung redundanter Variablen ist die Verwendung von Streudiagrammen auf Haupt- oder gedrehten orthogonalen Achsen. Variablen, die sich auf dem Diagramm häufen, sind wahrscheinlich redundant. Diese Methode hat jedoch ihre Grenzen. Erstens ist sie subjektiv, und es ist in der Regel praktisch, nur zwei Dimensionen gleichzeitig zu behandeln, um eine effektive Analyse durchzuführen. Eine intuitive Methode zur Erkennung von Redundanz besteht in der Berücksichtigung nicht beobachtbarer zugrunde liegender Faktoren. Wenn wir zum Beispiel drei Faktoren (V1, V2, V3) haben, die zu beobachteten Variablen (X1, X2, X3) führen, und wir feststellen, dass ein Faktor (V3) nur Rauschen ist, dann könnten X1 und X2 redundant sein, wenn V3 ignoriert wird. Mit anderen Worten: Wenn X2 nur eine skalierte Version von X1 ist, sind sie in Bezug auf die wichtigen Faktoren (V1 und V2) redundant.
Um Redundanz rigoros zu messen, betrachten wir die beobachteten Variablen als Vektoren in einem Raum, der durch die zugrunde liegenden Faktoren definiert ist. Wenn wir beobachtete Variablen haben, können wir sie als Vektoren in einem mehrdimensionalen Raum darstellen, wobei jede Dimension einem zugrunde liegenden Faktor entspricht. Diese Vektoren zeigen, wie sich die einzelnen Variablen zu den Faktoren verhalten. Der Winkel zwischen diesen Vektoren gibt an, wie ähnlich sich die Variablen in Bezug auf die Informationen sind, die sie über die zugrunde liegenden Faktoren enthalten. Ein kleinerer Winkel bedeutet, dass die Vektoren fast in die gleiche Richtung zeigen, was auf eine hohe Redundanz hinweist. Mit anderen Worten: Die Variablen liefern ähnliche Informationen.
Um diese Redundanz zu quantifizieren, können wir das Punktprodukt von normalisierten Vektoren (Vektoren mit der Länge 1) verwenden. Dieses Punktprodukt reicht von -1 bis 1, wobei ein Punktprodukt von 1 bedeutet, dass die Vektoren identisch sind, was auf perfekte Redundanz hinweist. Ein Punktprodukt von -1 bedeutet, dass die Vektoren in entgegengesetzte Richtungen verlaufen, was ebenfalls als redundant angesehen werden kann, da die Kenntnis des einen Vektors das Negativ des anderen ergibt. Ein Punktprodukt von 0 bedeutet, dass die Vektoren orthogonal (unabhängig) sind, was bedeutet, dass keine Redundanz vorliegt.
Die Koeffizienten für die Berechnung der beobachteten Variablen aus den zugrundeliegenden Faktoren können mithilfe von Hauptkomponenten ermittelt werden. Dominante Hauptkomponenten (mit großen Eigenwerten) enthalten in der Regel den größten Teil der nützlichen Informationen, während Komponenten mit kleinen Eigenwerten häufig Rauschen darstellen. Die Faktorladungsmatrix, die die Korrelation der Faktoren mit den Variablen zeigt, kann verwendet werden, um standardisierte beobachtete Variablen aus den Hauptkomponenten zu berechnen. In der Praxis nehmen wir oft den absoluten Wert des Punktprodukts, um die Redundanz zu messen, da entgegengesetzte Vektoren ebenfalls Redundanz anzeigen. Durch die Normalisierung der Vektoren wird sichergestellt, dass ihre Länge gleich 1 ist, sodass das Punktprodukt ein direktes Maß für den Kosinus des Winkels zwischen ihnen ist.
Um zu berechnen, inwieweit zwei Variablen durch einen versteckten Faktor miteinander verbunden sind, müssen wir in der Regel zunächst die Anzahl der Hauptkomponenten bestimmen, die wir für wichtig halten. Die Clustering-Berechnungen konzentrieren sich auf die Daten in der ersten dieser Spalten der Faktorladungsmatrix. Jede Zeile in diesen Spalten wird neu skaliert, sodass sie alle den Wert 1 ergeben. Der Grad der Ähnlichkeit zwischen den beiden Variablen ist der absolute Wert des Punktprodukts der beiden entsprechenden Zeilen der transformierten Faktorladungsmatrix.
Der nächste Schritt besteht darin, diese Daten in Gruppen zusammenzufassen, die aus Variablen bestehen, die aufgrund ihrer Beziehung zu einem latenten Faktor sehr ähnlich sind. Einer der besseren Clustering-Algorithmen, der dafür bekannt ist, dass er gute Ergebnisse liefert, ist das hierarchische Clustering. Beim hierarchischen Clustering, auch bekannt als Agglomerative Hierarchische Clusteranalyse (AHC), beginnt die Gruppierung damit, dass jede Variable einer Gruppe mit einem Mitglied zugeordnet wird. Jedes mögliche Paar von Gruppen wird getestet, um die zwei am nächsten liegenden zu finden. Diese Gruppen werden zu einer Gruppe zusammengefasst. Dieser Vorgang wird so lange wiederholt, bis entweder nur noch eine Gruppe übrig ist oder der Grad der Ähnlichkeit zu gering wird.
Die Implementierung von AHC ist in der MQL5-Portierung der Alglib-Bibliothek enthalten. Es ist für unsere Zwecke besonders geeignet, weil es die Möglichkeit bietet, eine nutzerdefinierte Distanzmetrik zu implementieren. Diese Funktionalität wird durch drei Alglib-Klassen bereitgestellt. Um die hierarchische agglomerative Clustering-Implementierung von Alglib zu nutzen, benötigen wir eine Instanz der CAHCReport-Struktur, um die Ergebnisse der Operation zu speichern.CAHCReport m_rep;
Die Klasse CClusterizerState kapselt die Clustering-Engine. Das Clustering kann nicht ohne sie durchgeführt werden.
CClusterizerState m_cs;
Der Prozess beginnt mit der Initialisierung der Clustering-Engine durch einen Aufruf der statischen Methode „ClusterizerCreate()“ der CClustering-Klasse.
CClustering::ClusterizerCreate(m_cs);
Nach der Initialisierung können wir die Parameter des Clustering-Prozesses einstellen, indem wir andere statische Methoden des CClustering verwenden. Alle erfordern eine initialisierte Clusterbildungsmaschine.
CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);
Schließlich löst „ClusterizerRunAHC()“ die eigentliche Operation aus.
CClustering::ClusterizerRunAHC(m_cs,m_rep);
Auf die Ergebnisse kann über die Eigenschaften der CAHCReport-Instanz zugegriffen werden.
Wie bereits erwähnt, werden wir eine nutzerdefinierte Abstandsmetrik für die Operation implementieren. Dies wird erreicht, indem eine Matrix mit den anfänglichen Abständen für jede Variable (Zeile in den Faktorladungen) erstellt wird. Der nachstehende Codeausschnitt zeigt, wie die anfänglichen Entfernungen anhand der angegebenen Belastungen berechnet werden.
for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; }
Zunächst normalisieren wir die Ladungen in Bezug auf die Anzahl der berücksichtigten Dimensionen.
for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } }
Und diese werden zur Berechnung der Entfernungen verwendet. Außerdem sind die normalisierten Ladungen diejenigen, die an den Prozess der Clusterbildung übergeben werden. Nicht die rohen Faktorladungen. Der gesamte Code, der das Clustering implementiert, ist in der Klasse CCluster enthalten.
//+------------------------------------------------------------------+ //| cluster a set of points | //+------------------------------------------------------------------+ class CCluster { private: CClusterizerState m_cs; CAHCReport m_rep; matrix m_pd[]; //+------------------------------------------------------------------+ //| Preprocesses input matrix before clusterization | //+------------------------------------------------------------------+ bool customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true) { int nvars; double dotprod, length; nvars = int(structure.Rows()); int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols()); if(out.Size()<2) if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars))) { Print(__FUNCTION__, " error ", GetLastError()); return false; } if(calculate_custom_distances) { for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; } out[1].Fill(0.0); for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } } } else { out[0] = np::sliceMatrixCols(structure,0,ndim); } return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CCluster(void) { CClustering::ClusterizerCreate(m_cs); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CCluster(void) { } //+------------------------------------------------------------------+ //| cluster a set | //+------------------------------------------------------------------+ bool cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM) { if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM)) return false; CMatrixDouble pp(m_pd[0]); CMatrixDouble pd(m_pd[1]); CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); if(dist==DIST_CUSTOM) CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage); CClustering::ClusterizerRunAHC(m_cs,m_rep); return m_rep.m_terminationtype==1; } //+------------------------------------------------------------------+ //| output clusters to vector array | //+------------------------------------------------------------------+ bool get_clusters(vector &out[]) { if(m_rep.m_terminationtype!=1) { Print(__FUNCTION__, " no cluster information available"); return false; } if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows()) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i = 0; i<m_rep.m_pm.Rows(); i++) { int zz = 0; for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2) { int from = m_rep.m_pm.Get(i,j); int to = m_rep.m_pm.Get(i,j+1); if(!out[i].Resize((to-from)+zz+1)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int k = from; k<=to; k++,zz++) out[i][zz] = m_rep.m_p[k]; } } return true; } };
Die Funktion „cluster()“ führt ein hierarchisches Clustering an einer gegebenen Menge von Eingabepunkten durch. Sie benötigt vier Parameter: einen Verweis auf eine Matrix von Eingabepunkten, die Anzahl der zu berücksichtigenden Faktoren, die zu verwendende Verknüpfungsmethode und das Abstandskriterium. Zunächst wird eine nutzerdefinierte Abstandsmatrix berechnet, wenn das angegebene Abstandskriterium nutzerdefiniert ist. Schlägt die Abstandsberechnung fehl, gibt die Funktion false zurück. Als Nächstes werden zwei Matrizen, pp und pd , aus den berechneten Entfernungsdaten initialisiert. Die Funktion legt dann die Punkte für das Clustering unter Verwendung des Abstandskriteriums fest, das standardmäßig auf euklidisch eingestellt ist, wenn das Kriterium nicht auf die nutzerdefinierte Option gesetzt ist. Wenn das Abstandskriterium nutzerdefiniert ist, werden die Abstände für das Clustering entsprechend festgelegt; nach der Festlegung der Abstände und Punkte konfiguriert die Funktion den hierarchischen Clustering-Algorithmus mit der angegebenen Verknüpfungsmethode. Es führt den agglomerativen hierarchischen Clustering-Algorithmus aus und überprüft die Art der Beendigung des Clustering-Prozesses. Die Funktion gibt true zurück, wenn der Beendigungstyp 1 ist, was eine erfolgreiche Clusterbildung anzeigt, andernfalls gibt sie false zurück.
Die Funktion „get_clusters()“ extrahiert Cluster aus den Ergebnissen eines hierarchischen Clustering-Prozesses und gibt sie aus. Sie benötigt einen Parameter: ein Array von Vektoren out[] , das mit den Clustern gefüllt wird. Die Funktion prüft zunächst, ob der Beendigungstyp des Clustering-Prozesses 1 ist, was eine erfolgreiche Clusterbildung anzeigt. Wenn nicht, wird eine Fehlermeldung ausgegeben und false zurückgegeben. Anschließend iteriert die Funktion durch jede Zeile der Matrix m_rep.m_pm , die die Clustering-Informationen enthält. Für jede Zeile wird eine Variable zz initialisiert, um den Index im Ausgabevektor zu verfolgen. Anschließend werden die Spalten der aktuellen Zeile durchlaufen und dabei Spaltenpaare verarbeitet (die die Start- und Endindizes von Clustern darstellen). Für jedes Paar wird der Bereich der Indizes ( von bis bis ) berechnet und die Größe des aktuellen Ausgabevektors so angepasst, dass er die Clusterelemente aufnimmt. Wenn die Größenänderung fehlschlägt, wird eine Fehlermeldung ausgegeben und false zurückgegeben. Schließlich füllt die Funktion den aktuellen Ausgabevektor mit den Elementen des Clusters auf, wobei sie von bis bis iteriert und zz für jedes Element inkrementiert. Wenn der Prozess erfolgreich abgeschlossen ist, gibt die Funktion true zurück, was bedeutet, dass die Cluster erfolgreich extrahiert und im Array out gespeichert wurden.
Das folgende Codeschnipsel zeigt, wie die CCluster-Klasse verwendet wird.
vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); }In MetaTrader 5 fehlen Werkzeuge, um die Ergebnisse des Agglomerativen Hierarchischen Clustering (AHC) direkt zu visualisieren. Die Konsole des Terminals kann zwar einige Ausgaben anzeigen, ist aber für die Anzeige komplexer Ergebnisse wie die von AHC nicht sehr nutzerfreundlich. AHC-Ergebnisse lassen sich am besten durch Dendrogramme visualisieren, die die hierarchische Struktur der Datengruppierungen zeigen. Ein Dendrogramm veranschaulicht die Bildung von Clustern durch schrittweises Zusammenführen von Datenpunkten oder Clustern. Unten sehen Sie ein manuell erstelltes Dendrogramm, das die Gruppierungen aus unserem Indikatorendatensatz zeigt.
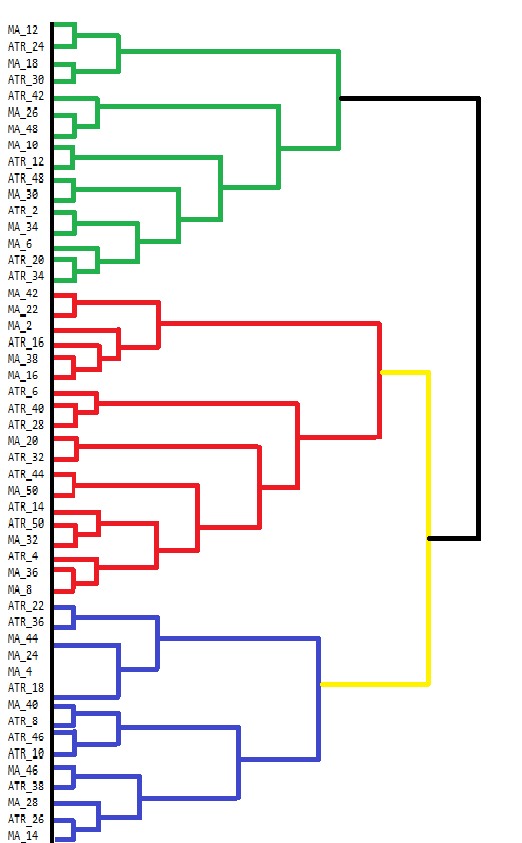
Das Dendrogramm zeigt Cluster von Variablen, die einander am ähnlichsten sind. Variablen, die auf niedrigeren Ebenen verschmelzen (näher am unteren Ende des Dendrogramms), sind einander ähnlicher als solche, die weiter oben verschmelzen. Zum Beispiel sind MA_12 und MA_24 einander ähnlicher als ATR_18. Im Dendrogramm werden verschiedene Farben verwendet, um unterschiedliche Cluster zu kennzeichnen. Die Cluster in Grün, Rot, Blau und Gelb markieren Gruppen von Variablen, die eng miteinander verbunden sind. Jede Farbe steht für eine Gruppe von Variablen, die eine hohe Ähnlichkeit oder Redundanz aufweisen.
Die Höhe, in der zwei Cluster ineinander übergehen, gibt einen Hinweis auf die Unähnlichkeit zwischen ihnen. Je niedriger die Höhe, desto ähnlicher sind die Cluster. Cluster, die auf höheren Ebenen verschmelzen, wie z. B. die schwarze Verschmelzung oben, weisen auf größere Unterschiede zwischen diesen Clustern hin. Dieses hierarchische Clustering kann als Entscheidungsgrundlage für die Variablenauswahl dienen. Durch die Analyse der Cluster kann man sich für die weitere Analyse auf bestimmte repräsentative Variablen innerhalb jedes Clusters konzentrieren und so den Datensatz vereinfachen, ohne dass wesentliche Informationen verloren gehen.
Der MQL5-Code, der zur Erfassung und Analyse des Indikatorendatensatzes verwendet wird, ist im Skript EDA.mq5 enthalten. Es verwendet alle in diesem Artikel beschriebenen Codewerkzeuge, die in pfa.mqh definiert sind.
//+------------------------------------------------------------------+ //| EDA.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\Slope.ex5" #resource "\\Indicators\\CMMA.ex5" #include<pfa.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //+------------------------------------------------------------------+ //|indicator type | //+------------------------------------------------------------------+ enum SELECT_INDICATOR { CMMA=0,//CMMA SLOPE//SLOPE }; //--- input parameters input uint period_inc=2;//lookback increment input uint max_lookback=50; input ENUM_MA_METHOD AppliedMA = MODE_SMA; input datetime SampleStartDate=D'2019.12.31'; input datetime SampleStopDate=D'2022.12.31'; input string SetSymbol="BTCUSD"; input ENUM_TIMEFRAMES SetTF = PERIOD_D1; input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX; input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM; input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE; input ulong Num_Dimensions = 10; //---- string csv_header=""; //csv file header int size_sample, //training set size size_observations, //size of of both training and testing sets combined maxperiod, //maximum lookback indicator_handle=INVALID_HANDLE; //long moving average indicator handle //--- vector indicator[]; //indicator indicator values; //--- matrix feature_matrix; //full matrix of features; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---get relative shift of sample set int samplestart,samplestop,num_features; samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate); samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate); num_features = int((max_lookback/period_inc)*2); //---check for errors from ibarshift calls if(samplestart<0 || samplestop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(samplestart - samplestop) + 1 ; maxperiod=int(max_lookback); //---check for input errors if(size_observations<=0 || maxperiod<=0) { Print("Invalid inputs "); return; } //---allocate memory if(ArrayResize(indicator,num_features)<num_features) { Print(ErrorDescription(GetLastError())); return; } //----get the full collection of indicator values int period_len; int k=0; //--- for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++) { for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++) { period_len=int((iperiod+1) * period_inc); int try=10; while(try) { switch(select_indicator) { case CMMA: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len); break; case SLOPE: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len); break; } if(indicator_handle==INVALID_HANDLE) try--; else break; } if(indicator_handle==INVALID_HANDLE) { Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError()); return; } Comment("copying data to buffer for indicator ",period_len); try = 0; while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10) { try++; Sleep(5000); } if(try<10) ++k; else { Print("error copying to indicator buffers ",GetLastError()); Comment(""); return; } if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle)) indicator_handle=INVALID_HANDLE; } } //---resize matrix if(!feature_matrix.Resize(size_observations,indicator.Size())) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //---copy collected data to matrix for(ulong i = 0; i<feature_matrix.Cols(); i++) if(!feature_matrix.Col(indicator[i],i)) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //--- Comment(""); //---test dataset for principal factor analysis suitability //---kmo test vector kmo_vect; double kmo_stat; kmo(feature_matrix,kmo_vect,kmo_stat); Print("KMO test statistic ", kmo_stat); //---Bartlett sphericity test double bs_stat,bs_pvalue; bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue); Print("Bartlett sphericity test p_value ", bs_pvalue); //---Extract the principal factors Cpfa fa; //--- if(!fa.fit(feature_matrix)) return; //--- matrix fld = fa.get_factor_loadings(); //--- matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation); //--- Print(" factor loading matrix ", fld); //--- Print("\n rotated factor loading matrix ", rotated_fld); //--- matrix egvcts; vector egvals; fa.get_eigen_structure(egvcts,egvals,false); Print("\n vects ", egvcts); Print("\n evals ", egvals); //--- vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); } } //+------------------------------------------------------------------+
Kohärenz in Zeitreihen
Bei der Analyse von Variablen im Zeitverlauf können sich ihre Beziehungen unerwartet ändern. Normalerweise zusammenhängende Variablen können plötzlich voneinander abweichen, was auf ein mögliches Problem hinweist. So können sich beispielsweise Temperaturschwankungen auf die Stromnachfrage auswirken, was wiederum die Erdgaspreise beeinflusst. Wenn sich das übliche Verhaltensmuster ändert, könnte das ein Hinweis darauf sein, dass etwas Ungewöhnliches passiert. Ebenso können sich Variablen, die sich normalerweise unabhängig voneinander verhalten, plötzlich gemeinsam bewegen, z. B. wenn verschiedene Sektoren eines Aktienmarktes aufgrund positiver Wirtschaftsnachrichten gleichzeitig steigen.
Bei der Messung der Kohärenz wird quantifiziert, wie sehr eine Reihe von Zeitreihenvariablen innerhalb eines gleitenden Zeitfensters miteinander verbunden sind. Eine grundlegende Methode besteht darin, zu prüfen, wie viel Varianz durch den größten Eigenwert aufgefangen wird. Diese Methode kann jedoch einschränkend sein, da sie nur eine Dimension berücksichtigt. Ein umfassenderer Ansatz beinhaltet die Summierung der größten Eigenwerte, insbesondere wenn mehrere Beziehungen zwischen den Variablen bestehen. Dieser Ansatz vermittelt ein genaueres Bild der Gesamtkohärenz in einem System mit komplexen Zusammenhängen, setzt aber voraus, dass man vorher weiß, welches die wichtigsten Faktoren sind. Etwas, das vielleicht nicht möglich ist oder einfach zu subjektiv ist.
Für Szenarien, in denen die Anzahl der Beziehungen unbekannt ist oder im Laufe der Zeit schwankt, ist ein allgemeinerer Ansatz erforderlich, insbesondere bei einer großen Anzahl von Variablen. In Szenarien mit unbekannter Dimensionen können wir die sortierten Eigenwerte vom größten zum kleinsten als Mitglieder eines Orchesters darstellen. Der Schlüssel zu einer schönen Musik liegt darin, die verschiedenen Instrumente auf einheitliche Weise zu regulieren. Wenn die einzelnen Orchestermitglieder nicht in der Lage sind, auf dem richtigen Niveau zusammenzuarbeiten, wird die Musik schrecklich sein. Der Zusammenhalt wird schlecht sein. Stellen Sie sich die Klangleistung jedes Orchestermitglieds als einen gewichteten Wert vor, der zur Musik beiträgt, die das Publikum hört. Das Ungleichgewicht dieser Werte stellt die Kohärenz dar. Wir berechnen eine gewichtete Summe, wobei die Gewichte das Volumen angeben, das ein Instrument erzeugen kann.
Wenn jedes Instrument (Variable) unabhängig voneinander seine eigene Melodie spielt, ist der Gesamtklang ungeordnet und chaotisch, d. h. es gibt keine Kohärenz. Wenn die Instrumente jedoch perfekt synchronisiert sind und in Harmonie spielen, entsteht ein zusammenhängendes und wunderschönes Musikstück, das eine vollständige Kohärenz darstellt. Kohärenz ist in dieser Analogie wie die Harmonie eines Orchesters, die anzeigt, wie gut die Instrumente (Variablen) zusammenspielen. Wenn sich die Harmonie plötzlich ändert, deutet dies darauf hin, dass etwas Ungewöhnliches mit den Instrumenten oder der Komposition geschieht.
Betrachten wir zwei Extreme. Wenn die Variablen völlig unabhängig sind. Die Korrelationsmatrix dieser Variablen wird eine Identitätsmatrix sein, und alle Eigenwerte werden gleich sein (1,0). Die gewichtete Summe ist (aufgrund der symmetrischen Gewichte) gleich Null, was eine Nullkohärenz widerspiegelt. Alternativ dazu gibt es bei perfekter Korrelation zwischen den Variablen nur einen Eigenwert ungleich Null, der der Anzahl der Variablen entspricht. Die gewichtete Summe ergibt die Anzahl der Variablen, die nach der Normalisierung (Division durch die Anzahl der Variablen) eine Kohärenz von 1,0 ergibt, was eine perfekte Korrelation widerspiegelt. 0-1 ist ein Maß für die Kohärenz, das auf dem Ungleichgewicht in der Eigenwertverteilung basiert, ohne Annahmen über die Dimensionen zu treffen.
Um die Kohärenz zu veranschaulichen, werden wir einen Indikator erstellen, der die Kohärenz der Schlusskurse verschiedener Symbole innerhalb eines Zeitfensters misst. Dieser Indikator wird den Namen Coherence.mq5 tragen. Die Nutzer können die Kohäsion zwischen zahlreichen Symbolen messen, indem sie sie als kommagetrennte Liste von Instrumentennamen hinzufügen. Der Indikator verwendet einen anderen Ansatz zur Berechnung der Korrelationen zwischen mehreren Variablen. Dieses Mal verwenden wir den nichtparametrischen Korrelationskoeffizienten von Spearman.
covar[0][0] = 1.0 ; for(int i=1 ; i<npred ; i++) { for(int j=0 ; j<i ; j++) { for(int k=0 ; k<lookback ; k++) { nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k); nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k); } if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j])) Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar); } covar[i][i] = 1.0 ; }
Da wir die EVD-Implementierung von Aglib verwenden, brauchen wir nicht die gesamte Matrix der Korrelationen zu definieren, sondern nur das obere oder untere Dreieck zu konstruieren. Wir brauchen die Eigenvektoren nicht, sondern nur die Eigenwerte.
CMatrixDouble cdata(covar); if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects)) { Print(" EVD failed ", GetLastError(), " :", ibar); coherenceBuffer[ibar]=0.0; continue; }
Um die Verteilung der Eigenwerte in der richtigen Orientierung zu erhalten, müssen wir den Vektor umkehren.
vector eval = evals.ToVector(); if(!np::reverseVector(eval)) Print(" failed vecter reversal operation : ", ibar);
Die Kohäsion wird anhand der Eigenwerte berechnet.
double center = 0.5 * (npred - 1) ; double sum = 0.0; for(ulong i=0 ; i<eval.Size() ; i++) { sum += (center - i) * eval[i] / center ; } coherenceBuffer[ibar] = sum / eval.Sum();
Der vollständige Code ist am Ende des Artikels beigefügt. Sehen wir uns an, wie der Indikator bei verschiedenen Fensterlängen aussieht, indem wir die Kohärenz zwischen den Kryptowährungen BTCUSD, DOGUSD und XRPUSD messen.
Bei der Betrachtung des 60-Tage-Plots von Coherence konnten die persönlichen Vorurteile ausgeräumt werden, dass sich diese Symbole mit bemerkenswerter Kohärenz bewegen. Erstaunlich ist, wie stark sie schwankt. Die Werte variieren über das gesamte Spektrum der möglichen Werte.
Wenn wir größere Fensterlängen verwenden, beginnen wir, Perioden der Stabilität der Kohärenz zu sehen, aber auch hier ist die Art dieser Kohärenz unerwartet. Es gibt beträchtliche Zeiträume, in denen fast keine Kohärenz besteht.
Schlussfolgerung
Die Verwendung von Eigenwerten und Eigenvektoren in diesen fortgeschrittenen Techniken unterstreicht ihre Vielseitigkeit und grundlegende Bedeutung in der Datenwissenschaft. Sie bieten einen robusten Rahmen für Dimensionenreduktion, Mustererkennung und die Entdeckung latenter Strukturen in komplexen Datensätzen. Indem wir über die PCA hinausgehen, erschließen wir uns ein reichhaltigeres Instrumentarium, das nuancierte Einblicke bietet. Dieser Text zeigt, dass Eigenvektoren und Eigenwerte weit mehr als nur mathematische Abstraktionen sind; sie sind die Eckpfeiler anspruchsvoller Analysetechniken, die moderne Händler nutzen können, um sich einen Vorteil zu verschaffen. Der gesamte in diesem Artikel gezeigte Code ist in der komprimierten Archivdatei enthalten. In der nachstehenden Tabelle sind die zum Download verfügbaren Dateien aufgeführt.| Datei | Beschreibung |
|---|---|
| Mql5\Include\np.mqh | Include-Datei, die verschiedene Matrix- und Vektorfunktionsprogramme enthält. |
| Mql5\Include\pfa.mqh | pfa.mqh enthält die Definition der Cpfa-Klasse, der CCluster-Klasse und der CRotator-Klasse. Sowie die Funktionsdefinition für die KMO- und BTS-Testimplementierungen. |
| Mql5\Scripts\EDA.mq5 | Das Skript demonstriert die Verwendung aller im Artikel beschriebenen Code-Tools, indem es einen Datensatz mit nutzerdefinierten Indikatoren für die Hauptfaktorenanalyse sammelt. |
| Mql5\Scripts\TestEigenDecomposition.mq5 | Dieses Skript reproduziert die angesprochenen Probleme in Bezug auf die integrierte Matrixmethode „Eig()“. |
| Mql5\Indicators\Coherence.mq5 | Dies ist der Kohärenzindikator, angewandt auf 3 Symbole. |
| Mql5\Experts\PrincipalFactors.mq5 | Dies ist der Quellcode für die Anwendung, die zur Anzeige großer Matrizen verwendet wird. Der Code hängt von der ehrwürdigen Easy and Fast GUI-Bibliothek ab, die in der MQL5-Codebasis gefunden werden kann. |
| Mql5\Experts\PrincipalFactors.ex5 | Dies ist eine kompilierte Version der obigen Auflistung. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15229
 Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 27): Gleitende Durchschnitte und der Anstellwinkel (Angle of Attack)
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 27): Gleitende Durchschnitte und der Anstellwinkel (Angle of Attack)
 Eine alternative Log-datei mit der Verwendung der HTML und CSS
Eine alternative Log-datei mit der Verwendung der HTML und CSS
 Sentiment-Analyse und Deep Learning für den Handel mit EA und Backtesting mit Python
Sentiment-Analyse und Deep Learning für den Handel mit EA und Backtesting mit Python
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.