Die Gruppenmethode der Datenverarbeitung: Implementierung des Kombinatorischen Algorithmus in MQL5

MetaTrader 5 — Beispiele | 7 Juni 2024, 10:24

151

Francis Dube

Einführung

Der Kombinatorische Algorithmus oder GMDH, oft auch als COMBI bezeichnet, ist die Grundform der GMDH und dient als Grundlage für komplexere Algorithmen innerhalb der Familie. Genau wie der Multilayered Iterative Algorithm (MIA) arbeitet er mit einer Eingabedatenprobe, die als Matrix dargestellt wird und Beobachtungen über eine Reihe von Variablen enthält. Die Datenstichprobe wird in zwei Teile unterteilt: eine Trainingsstichprobe und eine Teststichprobe. Die Trainingsstichprobe wird verwendet, um die Koeffizienten des Polynoms zu schätzen, während die Teststichprobe verwendet wird, um die Struktur des optimalen Modells auf der Grundlage des minimalen Wertes des ausgewählten Kriteriums auszuwählen. In diesem Artikel werden wir die Berechnung des COMBI-Algorithmus beschreiben. Außerdem stellen wir seine Implementierung in MQL5 vor, indem wir die im vorherigen Artikel beschriebene Klasse „GmdhModel“ erweitern. Später werden wir auch den eng verwandten Combinatorial Selective Algorithmus und seine MQL5-Implementierung diskutieren. Abschließend wird eine praktische Anwendung der GMDH-Algorithmen vorgestellt, indem Prognosemodelle für den täglichen Bitcoin-Kurs erstellt werden.

Der COMBI-Algorithmus

Der grundlegende Unterschied zwischen MIA und COMBI liegt in der Netzstruktur. Im Gegensatz zu MIA, das aus mehreren Schichten besteht, ist COMBI durch eine einzige Schicht gekennzeichnet.

Netzwerkstruktur der Kombinatorischen Methode

Die Anzahl der Knoten in dieser Schicht richtet sich nach der Anzahl der Eingänge. Dabei steht jeder Knoten für ein Kandidatenmodell, das durch einen oder mehrere der Eingänge definiert ist. Betrachten wir zur Veranschaulichung ein Beispiel für ein System, das wir modellieren wollen und das durch 2 Eingangsvariablen definiert ist. Unter Anwendung des COMBI-Algorithmus werden alle möglichen Kombinationen dieser Variablen verwendet, um ein Kandidatenmodell zu erstellen. Die Anzahl der möglichen Kombinationen ist gegeben durch:

Formel für die maximale Anzahl von Kombinationen

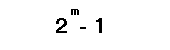
wobei :

m für die Anzahl der Eingangsvariablen steht.

Für jede dieser Kombinationen wird ein Kandidatenmodell erstellt. Die Kandidatenmodelle, die an den Knoten der ersten und einzigen Schicht bewertet werden, sind durch gegeben:

Polynomkandidaten

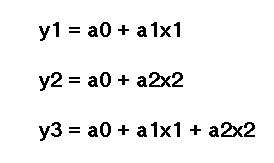
wobei :

„a“ die Koeffizienten sind, mit „a1“ ist der erste Koeffizient und „a2“ ist der zweite Koeffizient.
„x“ die Eingangsvariablen sind, mit „x1“ die erste Eingangsvariable oder den Prädiktor darstellt und „x2“ die zweite.

Dabei wird ein System von linearen Gleichungen gelöst, um Schätzungen für die Koeffizienten eines Kandidatenmodells abzuleiten. Anhand der Leistungskriterien der einzelnen Modelle wird das endgültige Modell ausgewählt, das die Daten am besten beschreibt.

COMBI MQL5 Implementierung

Der Code, der den COMBI-Algorithmus implementiert, stützt sich auf die Basisklasse GmdhModel, die im vorherigen Artikel beschrieben wurde. Sie hängt auch von einer Zwischenklasse LinearModel ab, die in linearmodel.mqh deklariert ist. Damit ist das wichtigste Unterscheidungsmerkmal der COMBI-Methode auf den Punkt gebracht. Die Tatsache, dass COMBI-Modelle ausschließlich linear sind.

//+------------------------------------------------------------------+
//|                                                  linearmodel.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "gmdh.mqh"
//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH linear algorithms   |
//+------------------------------------------------------------------+
class LinearModel:public GmdhModel
  {

protected:
   vector            calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      vector comb = bestCombinations[0][0].combination();
      matrix xx(1,comb.Size());
      for(ulong i = 0; i<xx.Cols(); ++i)
         xx[0][i] = modifiedX[0][ulong(comb[i])];
      vector c,b;
      c = bestCombinations[0][0].bestCoeffs();
      b = xx.MatMul(c);

      return b;
     }



   virtual matrix    xDataForCombination(matrix& x,  vector& comb) override
     {
      matrix out(x.Rows(), comb.Size());

      for(ulong i = 0; i<out.Cols(); i++)
         out.Col(x.Col(int(comb[i])),i);

      return out;
     }

   virtual string    getPolynomialPrefix(int levelIndex, int combIndex) override
     {
      return "y=";
     }

   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber, vector& bestColsIndexes) override
     {
      return ((coeffIndex != coeffsNumber - 1) ? "x" + string(int(bestColsIndexes[coeffIndex]) + 1) : "");
     }



public:
                     LinearModel(void)
     {
     }

   vector            predict(vector& x, int lags) override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;

     }

  };

//+------------------------------------------------------------------+

Die Datei combi.mqh enthält die Definition der Klasse COMBI. Es wird abgeleitet vom LinearModel und definiert die „fit()-Methoden“ zur Anpassung eines Modells.

//+------------------------------------------------------------------+
//|                                                        combi.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "linearmodel.mqh"
//+------------------------------------------------------------------+
//| Class implementing combinatorial COMBI algorithm                 |
//+------------------------------------------------------------------+
class COMBI:public LinearModel
  {
private:
   Combination       getBest(CVector &combinations)
     {
      double proxys[];
      int best[];

      ArrayResize(best,combinations.size());
      ArrayResize(proxys,combinations.size());

      for(int k = 0; k<combinations.size(); k++)
        {
         best[k]=k;
         proxys[k]=combinations[k].evaluation();
        }

      MathQuickSortAscending(proxys,best,0,int(proxys.Size()-1));

      return combinations[best[0]];

     }
protected:

   virtual void      removeExtraCombinations(void) override
     {
      CVector2d realBestCombinations;
      CVector n;
      Combination top;
      for(int i = 0 ; i<bestCombinations.size(); i++)
        {
         top = getBest(bestCombinations[i]);
         n.push_back(top);
        }

      top = getBest(n);

      CVector sorted;

      sorted.push_back(top);

      realBestCombinations.push_back(sorted);

      bestCombinations = realBestCombinations;
     }

   virtual bool      preparations(SplittedData &data, CVector &_bestCombinations) override
     {
      lastLevelEvaluation = DBL_MAX;
      return (bestCombinations.push_back(_bestCombinations) && ulong(level+1) < data.xTrain.Cols());
     }

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,level,out);
      return;
     }

public:
                     COMBI(void):LinearModel()
     {
      modelName = "COMBI";
     }

   bool              fit(vector &time_series,int lags,double testsize=0.5,CriterionType criterion=stab)
     {

      if(lags < 1)
        {
         Print(__FUNCTION__," lags must be >= 1");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      int pAverage = 1;
      double limit  = 0;
      int kBest = pAverage;

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   bool              fit(matrix &vars,vector &targets,double testsize=0.5,CriterionType criterion=stab)
     {

      if(vars.Cols() < 1)
        {
         Print(__FUNCTION__," columns in vars must be >= 1");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      int pAverage = 1;
      double limit  = 0;
      int kBest = pAverage;

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }


  };
//+------------------------------------------------------------------+

Verwendung der COMBI-Klasse

Die Anpassung eines Modells an einen Datensatz mit der COMBI-Klasse ist genau dasselbe wie die Anwendung der MIA-Klasse. Wir erstellen eine Instanz und rufen eine der „fit()-Methoden“ auf. Dies wird in den Skripten COMBI_test.mq5 und COMBI_Multivariable_test.mq5 demonstriert.

//+------------------------------------------------------------------+
//|                                                   COMBI_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\combi.mqh>

input int NumLags = 2;
input int NumPredictions = 6;
input CriterionType critType = stab;
input double DataSplitSize = 0.33;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};

   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }

   COMBI combi;

   if(!combi.fit(tms,NumLags,DataSplitSize,critType))
      return;

   string modelname = combi.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize);

   combi.save(modelname+".json");

   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));

   vector out = combi.predict(in,NumPredictions);

   Print(modelname, " predictions ", out);

   Print(combi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

Beide wenden den COMBI-Algorithmus auf die gleichen Datensätze an, die in den Beispielskripten zur Anwendung des MIA-Algorithmus aus einem früheren Artikel verwendet wurden.

//+------------------------------------------------------------------+
//|                                     COMBI_Multivariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\combi.mqh>

input CriterionType critType = stab;
input double DataSplitSize = 0.33;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};

   COMBI combi;

   if(!combi.fit(independent,dependent,DataSplitSize,critType))
      return;

   string modelname = combi.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_multivars";

   combi.save(modelname+".json");

   matrix unseen = {{8,6,4},{1,5,3},{9,-5,3}};

   for(ulong row = 0; row<unseen.Rows(); row++)
     {
      vector in = unseen.Row(row);
      Print("inputs ", in, " prediction ", combi.predict(in,1));
     }

   Print(combi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

Anhand der Ausgabe von COMBI_test.mq5 können wir die Komplexität des angepassten Polynoms mit der des vom MIA-Algorithmus erzeugten vergleichen. Nachfolgend sind die Polynome für die Zeitreihen bzw. den multivariablen Datensatz aufgeführt.

LR      0       14:54:15.354    COMBI_test (BTCUSD,D1)  COMBI_stab_0.33 predictions [13,14,15,16,17,18.00000000000001]
PN      0       14:54:15.355    COMBI_test (BTCUSD,D1)  y= 1.000000e+00*x1 + 2.000000e+00
CI      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [8,6,4] prediction [18.00000000000001]
QD      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [1,5,3] prediction [9]
QQ      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    inputs [9,-5,3] prediction [7.00000000000001]
MM      0       14:54:29.864    COMBI_Multivariable_test (BTCUSD,D1)    y= 1.000000e+00*x1 + 1.000000e+00*x2 + 1.000000e+00*x3 - 7.330836e-15

Es folgen die Polynome, die durch die MIA-Methode ermittelt wurden.

JQ      0       14:43:07.969    MIA_Test (Step Index 500,M1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
IP      0       14:43:07.969    MIA_Test (Step Index 500,M1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00
II      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [1,2,4] prediction [6.999999999999998]
CF      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [1,5,3] prediction [8.999999999999998]
JR      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      inputs [9,1,3] prediction [13.00000000000001]
NP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
LR      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
ME      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
DJ      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
IP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
ER      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
ES      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
NH      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
CN      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
GP      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
DO      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      
OG      0       14:52:59.698    MIA_Multivariable_test (BTCUSD,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

Das MIA-Modell ist kompliziert, während das COMBI-Modell weniger kompliziert ist, genau wie die Serie selbst. Dies spiegelt den linearen Charakter der Methode wider. Dies wird auch durch die Ausgabe des Skripts COMBI_Multivariable_test.mq5 bestätigt, das einen Versuch darstellt, ein Modell für die Addition von 3 Zahlen zu erstellen, indem es Eingabevariablen und entsprechende Ausgabebeispiele bereitstellt. Hier war der COMBI-Algorithmus in der Lage, die zugrunde liegenden Merkmale des Systems erfolgreich abzuleiten.

Die erschöpfende Suche des COMBI-Algorithmus ist sowohl ein Vorteil als auch ein Nachteil. Positiv ist, dass durch die Auswertung aller Kombinationen der Eingaben sichergestellt wird, dass das optimale Polynom, das die Daten beschreibt, gefunden wird. Bei einer Vielzahl von Eingabevariablen kann diese umfangreiche Suche jedoch sehr rechenintensiv werden. Dies kann zu langen Ausbildungszeiten führen. Es sei daran erinnert, dass die Anzahl der Modellkandidaten durch 2 hoch m minus 1 gegeben ist. Je größer m ist, desto mehr Modellkandidaten müssen bewertet werden. Der Algorithmus Combinatorial Selective (kombinatorische Auswahl) wurde entwickelt, um dieses Problem zu lösen.

Der Algorithmus Combinatorial Selective

Der Algorithmus Combinatorial Selective, den wir als MULTI bezeichnen, wird als eine Verbesserung der COMBI-Methode in Bezug auf die Effizienz angepriesen. Eine erschöpfende Suche wird vermieden, indem ähnliche Verfahren wie bei den mehrschichtigen Algorithmen der GMDH angewandt werden. Daher kann er als mehrschichtiger Ansatz für den ansonsten einschichtigen Charakter des COMBI-Algorithmus betrachtet werden.

Netzwerkstruktur der Methode Combinatorial Selective

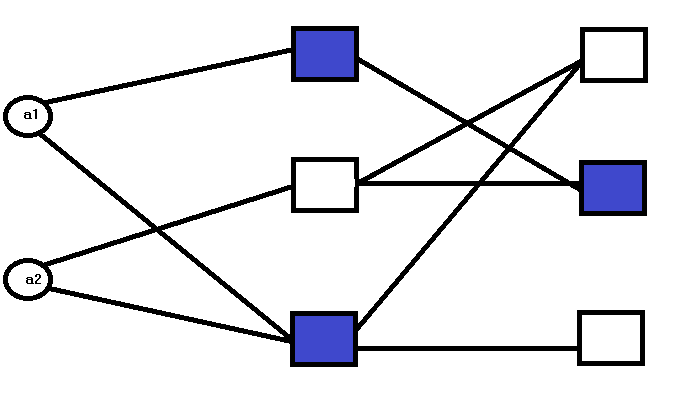
In der ersten Schicht werden alle Modelle, die eine der Eingangsvariablen enthalten, geschätzt, wobei das beste nach den externen Kriterien ausgewählt und an die nächste Schicht weitergegeben wird. In den nachfolgenden Schichten werden verschiedene Eingangsvariablen ausgewählt und zu diesen Kandidatenmodellen hinzugefügt, in der Hoffnung, sie zu verbessern. Neue Schichten werden auf diese Weise hinzugefügt, je nachdem, ob sich die Genauigkeit bei der Schätzung der Outputs erhöht und/oder ob Eingabevariablen verfügbar sind, die noch nicht Teil eines Kandidatenmodells sind. Das bedeutet, dass die maximale Anzahl der möglichen Schichten mit der Gesamtzahl der Eingabevariablen übereinstimmt.

Die Bewertung von Modellkandidaten auf diese Weise führt oft dazu, dass eine erschöpfende Suche vermieden wird, aber sie bringt auch ein Problem mit sich. Es besteht die Möglichkeit, dass der Algorithmus nicht das optimale Polynom findet, das den Datensatz am besten beschreibt. Ein Hinweis darauf, dass in der Trainingsphase mehr Kandidatenmodelle hätten berücksichtigt werden müssen. Die Ableitung des optimalen Polynoms ist eine Frage der sorgfältigen Abstimmung der Hyperparameter. Insbesondere die Anzahl der Kandidatenmodelle, die auf jeder Ebene bewertet werden.

Implementierung des Algorithmus Combinatorial Selective

Die Implementierung des Algorithmus Combinatorial Selective ist in multi.mqh enthalten. Sie enthält die Definition der Klasse MULTI, die von LinearModel erbt.

//+------------------------------------------------------------------+
//|                                                        multi.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "linearmodel.mqh"

//+------------------------------------------------------------------+
//|  Class implementing combinatorial selection MULTI algorithm      |
//+------------------------------------------------------------------+
class MULTI : public LinearModel
  {

protected:

   virtual void      removeExtraCombinations(void) override
     {
      CVector2d realBestCombinations;
      CVector n;
      n.push_back(bestCombinations[0][0]);
      realBestCombinations.push_back(n);
      bestCombinations = realBestCombinations;
     }

   virtual bool      preparations(SplittedData &data, CVector &_bestCombinations) override
     {
      return (bestCombinations.setAt(0,_bestCombinations) && ulong(level+1) < data.xTrain.Cols());
     }

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      if(level == 1)
        {
         nChooseK(n_cols,level,out);
         return;
        }

      for(int i = 0; i<bestCombinations[0].size(); i++)
        {

         for(int z = 0; z<n_cols; z++)
           {
            vector comb = bestCombinations[0][i].combination();
            double array[];
            vecToArray(comb,array);
            int found = ArrayBsearch(array,double(z));
            if(int(array[found])!=z)
              {
               array.Push(double(z));
               ArraySort(array);
               comb.Assign(array);
               ulong dif = 1;
               for(uint row = 0; row<out.Size(); row++)
                 {
                  dif = comb.Compare(out[row],1e0);
                  if(!dif)
                     break;
                 }

               if(dif)
                 {
                  ArrayResize(out,out.Size()+1,100);
                  out[out.Size()-1] = comb;
                 }
              }

           }
        }
     }



public:
                     MULTI(void):LinearModel()
     {
      CVector members;
      bestCombinations.push_back(members);
      modelName = "MULTI";
     }

   bool              fit(vector &time_series,int lags,double testsize=0.5,CriterionType criterion=stab,int kBest = 3,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 1)
        {
         Print(__FUNCTION__," lags must be >= 1");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   bool              fit(matrix &vars,vector &targets,double testsize=0.5,CriterionType criterion=stab,int kBest = 3,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 1)
        {
         Print(__FUNCTION__," columns in vars must be >= 1");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

  };
//+------------------------------------------------------------------+

Die MULTI-Klasse arbeitet ähnlich wie die COMBI-Klasse mit den bekannten „fit()-Methoden“. Im Vergleich zur COMBI-Klasse sollten die Leser auf die zusätzlichen Parameter in den Methoden „fit()“ achten. „kBest“ und „pAverage“ sind zwei Parameter, die bei der Anwendung der MULTI-Klasse möglicherweise sorgfältig angepasst werden müssen. Die Anpassung eines Modells an einen Datensatz wird in den Skripten MULTI_test.mq5 und MULTI_Multivariable_test.mq5 gezeigt. Der Code wird im Folgenden vorgestellt.

//+----------------------------------------------------------------------+
//|                                                   MULTI_test.mq5           |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com     |
//+----------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\multi.mqh>

input int NumLags = 2;
input int NumPredictions = 6;
input CriterionType critType = stab;
input int Average  = 1;
input int NumBest  = 3;
input double DataSplitSize = 0.33;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};

   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }

   MULTI multi;

   if(!multi.fit(tms,NumLags,DataSplitSize,critType,NumBest,Average,critLimit))
      return;

   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));

   vector out = multi.predict(in,NumPredictions);

   Print(" predictions ", out);

   Print(multi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                    MULTI_Mulitivariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\multi.mqh>

input CriterionType critType = stab;
input double DataSplitSize = 0.33;
input int Average  = 1;
input int NumBest  = 3;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};

   MULTI multi;

   if(!multi.fit(independent,dependent,DataSplitSize,critType,NumBest,Average,critLimit))
      return;

   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};

   for(ulong row = 0; row<unseen.Rows(); row++)
     {
      vector in = unseen.Row(row);
      Print("inputs ", in, " prediction ", multi.predict(in,1));
     }

   Print(multi.getBestPolynomial());

  }
//+------------------------------------------------------------------+

Es ist ersichtlich, dass die Polynome, die durch die Ausführung der Skripte aus unseren einfachen Datensätzen abgeleitet werden, genau die gleichen sind wie die, die durch die Anwendung des COMBI-Algorithmus erhalten werden.

IG      0       18:24:28.811    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [1,2,4] prediction [7.000000000000002]
HI      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [1,5,3] prediction [9]
NO      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   inputs [9,1,3] prediction [13.00000000000001]
PP      0       18:24:28.812    MULTI_Mulitivariable_test (BTCUSD,D1)   y= 1.000000e+00*x1 + 1.000000e+00*x2 + 1.000000e+00*x3 - 7.330836e-15
DP      0       18:25:04.454    MULTI_test (BTCUSD,D1)   predictions [13,14,15,16,17,18.00000000000001]
MH      0       18:25:04.454    MULTI_test (BTCUSD,D1)  y= 1.000000e+00*x1 + 2.000000e+00

Ein GMDH-Modell für Bitcoin-Preise

In diesem Abschnitt des Textes werden wir die GMDH-Methode anwenden, um ein Vorhersagemodell der täglichen Bitcoin-Schlusskurse zu erstellen. Dies wird in dem Skript GMDH_Price_Model.mq5 realisiert, das am Ende des Artikels angehängt ist. Obwohl sich unsere Demonstration speziell mit dem Symbol Bitcoin beschäftigt, kann das Skript auf jedes Symbol und jeden Zeitrahmen angewendet werden. Das Skript hat mehrere vom Nutzer veränderbare Parameter, die verschiedene Aspekte des Programms steuern.

//--- input parameters
input string   SetSymbol="";
input ENUM_GMDH_MODEL modelType = Combi;
input datetime TrainingSampleStartDate=D'2019.12.31';
input datetime TrainingSampleStopDate=D'2022.12.31';
input datetime TestSampleStartDate = D'2023.01.01';
input datetime TestSampleStopDate = D'2023.12.31';
input ENUM_TIMEFRAMES tf=PERIOD_D1;    //time frame
input int Numlags = 3;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input int Average  = 10;
input int NumBest  = 10;
input double DataSplitSize = 0.2;
input double critLimit = 0;
input ulong NumTestSamplesPlot = 20;

Sie sind in der folgenden Tabelle aufgeführt und beschrieben.

Namen der Eingabeparameter	Beschreibung
SetSymbol	Legt den Namen des Symbols für die Schlusskurse fest, die als Trainingsdaten verwendet werden. Bleibt das Symbol leer, wird das Symbol des Diagramms angenommen, auf das das Skript angewendet wird.
modeltype	Dies ist eine Enumeration, die die Wahl des GMDH-Algorithmus darstellt.
TrainingSampleStartDate	Anfangsdatum für den Zeitraum der Schlusskurse der Stichproben.
TrainingSampleStopDate	Enddatum für den Zeitraum der Schlusskurse der Stichproben.
TestSampleStartDate	Datum des Beginns des Zeitraums, in dem die Preise außerhalb der Stichprobe liegen.
TestSampleStopDate	Enddatum des Zeitraums, in dem die Preise außerhalb der Stichprobe liegen.
tf	Der verwendete Zeitrahmen.
Numlags	Definiert die Anzahl der verzögerten Werte, die für die Prognose des nächsten Schlusskurses verwendet werden.
critType	Legt die externen Kriterien für den Modellbildungsprozess fest.
polyType	Polynomtyp, der verwendet werden soll, um während des Trainings neue Variablen aus vorhandenen zu konstruieren, gilt nur, wenn der MIA-Algorithmus ausgewählt wurde.
Average	Die Anzahl der besten Teilmodelle, die bei der Berechnung der Abbruchkriterien berücksichtigt werden.
Numbest	Bei MIA-Modellen die Anzahl der besten Teilmodelle, auf deren Grundlage die neuen Eingaben der nachfolgenden Schicht erstellt werden. Bei COMBI-Modellen ist dies die Anzahl der Kandidatenmodelle, die auf jeder Ebene für die nachfolgenden Iterationen ausgewählt werden.
DataSplitSize	Anteil der Eingabedaten, die für die Bewertung von Modellen verwendet werden sollten.
critLimit	Der Mindestwert, um den das externe Kriterium verbessert werden sollte, um die Ausbildung fortzusetzen.
NumTestSamplePlot	Der Wert definiert die Anzahl der Stichproben aus dem Out-of-Sample-Datensatz, die zusammen mit den entsprechenden Vorhersagen visualisiert werden.

Das Skript beginnt mit der Auswahl einer geeigneten Stichprobe von Beobachtungen, die als Trainingsdaten verwendet werden sollen.

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//get relative shift of IS and OOS sets
   int trainstart,trainstop, teststart, teststop;
   trainstart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStartDate);
   trainstop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TrainingSampleStopDate);
   teststart=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestSampleStartDate);
   teststop=iBarShift(SetSymbol!=""?SetSymbol:NULL,tf,TestSampleStopDate);
//check for errors from ibarshift calls
   if(trainstart<0 || trainstop<0 || teststart<0 || teststop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(trainstart - trainstop) + 1 ;
   size_outsample = (teststart - teststop) + 1;
//---check for input errors
   if(size_observations <= 0  || size_outsample<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---download insample prices for training
   int try
         = 10;
   while(!prices.CopyRates(SetSymbol,tf,COPY_RATES_CLOSE,TrainingSampleStartDate,TrainingSampleStopDate) && try)
     {
      try
         --;
      if(!try)
        {
         Print("error copying to prices  ",GetLastError());
         return;
        }
      Sleep(5000);

Eine weitere Stichprobe von Schlusskursen wird heruntergeladen, um die Leistung des Modells anhand eines Diagramms der vorhergesagten und tatsächlichen Schlusskurse zu veranschaulichen.

//---download out of sample prices testing
   try
         = 10;
   while(!testprices.CopyRates(SetSymbol,tf,COPY_RATES_CLOSE|COPY_RATES_TIME|COPY_RATES_VERTICAL,TestSampleStartDate,TestSampleStopDate) && try)
     {
      try
         --;
      if(!try)
        {
         Print("error copying to testprices  ",GetLastError());
         return;
        }
      Sleep(5000);
     }

Die nutzerdefinierten Parameter des Skripts ermöglichen die Anwendung eines der drei GMDH-Modelle, die wir diskutiert und implementiert haben.

//--- train and make predictions
   switch(modelType)
     {
      case Combi:
        {
         COMBI combi;
         if(!combi.fit(prices,Numlags,DataSplitSize,critType))
            return;
         Print("Model ", combi.getBestPolynomial());
         MakePredictions(combi,testprices.Col(0),predictions);
        }
      break;

      case Mia:
        {
         MIA mia;
         if(!mia.fit(prices,Numlags,DataSplitSize,polyType,critType,NumBest,Average,critLimit))
            return;
         Print("Model ", mia.getBestPolynomial());
         MakePredictions(mia,testprices.Col(0),predictions);
        }
      break;

      case Multi:
        {
         MULTI multi;
         if(!multi.fit(prices,Numlags,DataSplitSize,critType,NumBest,Average,critLimit))
            return;
         Print("Model ", multi.getBestPolynomial());
         MakePredictions(multi,testprices.Col(0),predictions);
        }
      break;

      default:
         Print("Invalid GMDH model type ");
         return;
     }
//---

Das Programm endet mit der Anzeige eines Diagramms, das die vorhergesagten Schlusskurse zusammen mit den tatsächlichen Werten aus dem Out-of-Sample-Datensatz darstellt.

//---
   ulong TestSamplesPlot = (NumTestSamplesPlot>0)?NumTestSamplesPlot:20;
//---
   if(NumTestSamplesPlot>=testprices.Rows())
      TestSamplesPlot = testprices.Rows()-Numlags;
//---
   vector testsample(100,slice,testprices.Col(0),Numlags,Numlags+TestSamplesPlot-1);
   vector testpredictions(100,slice,predictions,0,TestSamplesPlot-1);
   vector dates(100,slice,testprices.Col(1),Numlags,Numlags+TestSamplesPlot-1);
//---
//Print(testpredictions.Size(), ":", testsample.Size());
//---
   double y[], y_hat[];
//---
   if(vecToArray(testpredictions,y_hat) && vecToArray(testsample,y) && vecToArray(dates,xaxis))
     {
      PlotPrices(y_hat,y);
     }
//---
   ChartRedraw();
  }

Nachfolgend finden Sie die Charts der Vorhersagen, die mit dem kombinatorischen bzw. dem mehrschichtigen iterativen Algorithmus erstellt wurden.

Kombinatorisches Modell für Bitcoin-Vorhersagen

MIA-Modell Bitcoin-Prognosen

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass der kombinatorische Algorithmus GMDH einen Rahmen für die Modellierung komplexer Systeme bietet, mit besonderen Stärken in Bereichen, in denen datengesteuerte, induktive Ansätze von Vorteil sind. Seine praktische Anwendung ist aufgrund der Ineffizienz des Algorithmus bei der Verarbeitung großer Datenmengen begrenzt. Der kombinatorische selektive Algorithmus mildert dieses Manko nur bis zu einem gewissen Grad. Der Geschwindigkeitsgewinn wird durch die Einführung weiterer Hyperparameter geschmälert, die abgestimmt werden müssen, um das Beste aus dem Algorithmus herauszuholen. Die Anwendung der GMDH-Methode in der Finanzzeitreihenanalyse zeigt, dass sie wertvolle Erkenntnisse liefern kann.

Datei	Beschreibung
Mql5\include\VectorMatrixTools.mqh	Header-Datei mit Funktionsdefinitionen für die Bearbeitung von Vektoren und Matrizen.
Mql5\include\JAson.mqh	Enthält die Definition der nutzerdefinierten Typen, die zum Parsen und Erzeugen von JSON-Objekten verwendet werden.
Mql5\include\GMDH\gmdh_internal.mqh	Header-Datei mit Definitionen der in der gmdh-Bibliothek verwendeten nutzerdefinierten Typen.
Mql5\include\GMDH\gmdh.mqh	Include-Datei mit Definition der Basisklasse GmdhModel.
Mql5\include\GMDH\linearmodel.mqh	Include-Datei mit der Definition der Zwischenklasse LinearModel, die die Grundlage für die Klassen COMBI und MULTI bildet.
Mql5\include\GMDH\combi.mqh	Include-Datei mit Definition der COMBI-Klasse.
Mql5\include\GMDH\multi.mqh	Include-Datei mit der Definition der Klasse MULTI.
Mql5\include\GMDH\mia.mqh	Enthält die Klasse MIA, die den mehrschichtigen iterativen Algorithmus implementiert.
Mql5\script\COMBI_test.mq5	Ein Skript, das die Verwendung der COMBI-Klasse durch die Erstellung eines Modells einer einfachen Zeitreihe demonstriert.
Mql5\script\COMBI_Multivariable_test.mq5	Ein Skript, das die Anwendung der COMBI-Klasse zur Erstellung eines Modells für einen multivariablen Datensatz zeigt.
Mql5\script\MULTI_test.mq5	Ein Skript, das die Verwendung der MULTI-Klasse durch die Erstellung eines Modells einer einfachen Zeitreihe demonstriert.
Mql5\script\MULTI_Multivariable_test.mq5	Ein Skript, das die Anwendung der MULTI-Klasse zur Erstellung eines Modells für einen multivariablen Datensatz zeigt.
Mql5\script\GMDH_Price_Model.mqh	Ein Skript zur Demonstration eines GMDH-Modells für eine Preisreihe.

Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/14804

Beigefügte Dateien |

ZIP herunterladen

VectorMatrixTools.mqh (6.41 KB)

JAson.mqh (33.43 KB)

combi.mqh (4.02 KB)

gmdh.mqh (23.86 KB)

gmdh_internal.mqh (82.09 KB)

linearmodel.mqh (2.84 KB)

mia.mqh (12.1 KB)

multi.mqh (4.05 KB)

COMBI_Multivariable_test.mq5 (1.54 KB)

COMBI_test.mq5 (1.59 KB)

GMDH_Price_Model.mq5 (8.41 KB)

MULTI_Mulitivariable_test.mq5 (1.5 KB)

MULTI_test.mq5 (1.55 KB)

Mql5.zip (31.81 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Neuronale Netze leicht gemacht (Teil 69): Dichte-basierte Unterstützungsbedingung für die Verhaltenspolitik (SPOT)

Beim Offline-Lernen verwenden wir einen festen Datensatz, der die Umweltvielfalt nur begrenzt abdeckt. Während des Lernprozesses kann unser Agent Aktionen generieren, die über diesen Datensatz hinausgehen. Wenn es keine Rückmeldungen aus der Umwelt gibt, wie können wir dann sicher sein, dass die Bewertungen solcher Maßnahmen korrekt sind? Die Beibehaltung der Agentenpolitik innerhalb des Trainingsdatensatzes ist ein wichtiger Aspekt, um die Zuverlässigkeit des Trainings zu gewährleisten. Darüber werden wir in diesem Artikel sprechen.

MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 17): Handel mit mehreren Währungen

Der Handel mit mehreren Währungen ist nicht standardmäßig verfügbar, wenn ein Expertenberater über den Assistenten zusammengestellt wird. Wir untersuchen 2 mögliche Hacks, die Händler machen können, wenn sie ihre Ideen mit mehr als einem Symbol gleichzeitig testen wollen.

MQL5 beherrschen, vom Anfänger zum Profi (Teil II): Grundlegende Datentypen und die Verwendung von Variablen

Dies ist eine Fortsetzung der Serie für Anfänger. In diesem Artikel werden wir uns ansehen, wie man Konstanten und Variablen erstellt, Daten, Farben und andere nützliche Daten schreibt. Wir werden lernen, wie man Enumerationen (Aufzählungen) wie Wochentage oder Linienstile (durchgezogen, gepunktet usw.) erstellt. Variablen und Ausdrücke sind die Grundlage der Programmierung. Sie sind definitiv in 99 % der Programme vorhanden, daher ist es wichtig, sie zu verstehen. Wenn Sie also neu in der Programmierung sind, kann dieser Artikel sehr nützlich für Sie sein. Erforderliche Programmierkenntnisse: sehr einfach, innerhalb der Grenzen meines vorherigen Artikels (siehe den Link am Anfang).

Aufbau eines Modells von Kerzen, Trend und Nebenbedingungen (Teil 2): Zusammenführung integrierter Indikatoren

In diesem Artikel geht es darum, die Vorteile der im MetaTrader 5 integrierten Indikatoren zu nutzen, um Signale abseits eines Trends zu erkennen. In Fortführung des vorherigen Artikels werden wir untersuchen, wie wir unsere Idee mit Hilfe von MQL5-Code in das endgültige Programm übertragen können.