Implementierung des verallgemeinerten Hurst-Exponenten und des Varianz-Verhältnis-Tests in MQL5

Einführung

In dem Artikel „Die Berechnung des Hurst-Exponenten“ wurden wir in das Konzept der Fraktalanalyse eingeführt und erfuhren, wie es auf die Finanzmärkte angewendet werden kann. In diesem Artikel beschrieb der Autor die reskalierte Bereichsmethode (R/S) zur Schätzung des Hurst-Exponenten. In diesem Artikel verfolgen wir einen anderen Ansatz, indem wir die Implementierung des Generalized Hurst Exponet (GHE) zur Klassifizierung der Art einer Reihe demonstrieren. Wir werden uns auf die Verwendung der GHE konzentrieren, um Devisensymbole zu identifizieren, die eine Tendenz zur Mittelwertumkehr aufweisen, in der Hoffnung, dieses Verhalten auszunutzen.

Zu Beginn werden kurz die Grundlagen des GHE erörtert und wie er sich vom ursprünglichen Hurst-Exponenten unterscheidet. In diesem Zusammenhang werden wir einen statistischen Test beschreiben, der zur Bestätigung der Ergebnisse der GHE-Analyse verwendet werden kann, den sogenannten Varianzverhältnis-Test (Variance Ratio Test, VRT). Danach gehen wir zur Anwendung der GHE bei der Identifizierung von Forex-Symbolen über, die für den Mean-Reversion-Handel in Frage kommen. Hier stellen wir einen Indikator für die Generierung von Ein- und Ausstiegssignalen vor. Diese werden wir schließlich in einem einfachen Expert Advisor testen.

Unterbewertung des verallgemeinerten Hurst-Exponenten

Der Hurst-Exponent misst die Skalierungseigenschaften von Zeitreihen. Skalierungseigenschaften sind grundlegende Merkmale, die beschreiben, wie sich ein System verhält, wenn sich seine Größe oder Zeitskala ändert. Im Zusammenhang mit Zeitreihendaten geben die Skalierungseigenschaften Aufschluss über die Beziehung zwischen verschiedenen Zeitskalen und den in den Daten vorhandenen Mustern. Bei einer stationären Reihe treten die Veränderungen der nachfolgenden Werte im Laufe der Zeit allmählicher auf als bei einem geometrischen Random Walk. Um dieses Verhalten mathematisch zu quantifizieren, analysieren wir die Diffusionsrate in der Reihe. Die Varianz dient als Maß für die Rate, mit der andere Werte vom ersten Wert der Reihe abweichen.

In der obigen Formel steht „K“ für eine willkürliche Verzögerung, mit der die Analyse durchgeführt wird. Um ein besseres Bild von der Beschaffenheit der Reihen zu erhalten, müssten wir auch die Varianz bei anderen Verzögerungen bewerten. „K“ kann also ein beliebiger positiver ganzzahliger Wert zugeordnet werden, der kleiner ist als die Länge der Reihe. Die größte Verzögerung ist diskretionär. Es ist wichtig, dies im Auge zu behalten. Die Hurst ist daher mit dem Skalierungsverhalten der Varianz bei verschiedenen Verzögerungen verbunden. Unter Verwendung des Potenzgesetzes wird sie definiert durch:

Die GHE ist eine Verallgemeinerung des Originals, bei der die 2 durch eine Variable ersetzt wird, die normalerweise als „q“ bezeichnet wird. Dadurch ändern sich die obigen Formeln zu:

und

GHE erweitert den eigentlichen Hurst, indem es analysiert, wie verschiedene statistische Merkmale der Veränderungen zwischen aufeinanderfolgenden Punkten in einer Zeitreihe mit verschiedenen Ordnungen von Momenten variieren. In der Mathematik sind Momente statistische Maße, die die Form und die Merkmale einer Verteilung beschreiben. Das Moment q-ter Ordnung ist eine besondere Art von Moment, wobei „q“ ein Parameter ist, der die Ordnung bestimmt. Die GHE hebt für jeden Wert von „q“ unterschiedliche Merkmale einer Zeitreihe hervor. Insbesondere wenn q=1 ist, zeigt das Ergebnis die Skalierungseigenschaften der absoluten Abweichung. Das q=2 ist am wichtigsten, wenn es um die Untersuchung der langfristige Abhängigkeit geht.

Implementierung des GHE in MQL5

In diesem Abschnitt gehen wir auf die Implementierung des GHE in MQL5 ein. Danach werden wir sie durch die Analyse von Stichproben künstlich erzeugter Zeitreihen testen. Unsere Implementierung ist in der Datei GHE.mqh enthalten. Die Datei beginnt mit der Datei VectorMatrixTools.mqh, die Definitionen für verschiedene Funktionen zur Initialisierung gängiger Typen von Vektoren und Matrizen enthält. Der Inhalt dieser Datei wird im Folgenden dargestellt.

//+------------------------------------------------------------------+
//|                                            VectorMatrixTools.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
//+------------------------------------------------------------------+
//|Vector arange initialization                                      |
//+------------------------------------------------------------------+
template<typename T>
void arange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization                                     |
//+------------------------------------------------------------------+
template<typename T>
void slice(vector<T> &vec,const vector<T> &toCopyfrom,ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;
   if(!vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<toCopyfrom.Size() && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization  using array                        |
//+------------------------------------------------------------------+
template<typename T>
void assign(vector<T> &vec,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;

   if(size != vec.Size() &&  !vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<ulong(toCopyfrom.Size()) && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Matrix initialization                                            |
//+------------------------------------------------------------------+
template<typename T>
void rangetrend(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   ulong r = mat.Rows();

   vector col1(r,arange,value,step);

   vector col2 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col1,0) || !mat.Col(col2,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+-------------------------------------------------------------------------------------+
//| ols design Matrix initialization with constant and first column from specified array|
//+-------------------------------------------------------------------------------------+
template<typename T>
void olsdmatrix(matrix<T> &mat,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   vector col0(1,assign,toCopyfrom,start,stop,step);

   ulong r = col0.Size();

   if(!r)
     {
      Print(__FUNCTION__," failed to initialize first column ");
      return;
     }

   vector col1 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col0,0) || !mat.Col(col1,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+------------------------------------------------------------------+
//|vector to array                                                   |
//+------------------------------------------------------------------+
bool vecToArray(const vector &in, double &out[])
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return false;
     }
//---
   if(ulong(out.Size())!=in.Size() && ArrayResize(out,int(in.Size()))!=int(in.Size()))
     {
      Print(__FUNCTION__," resize error ", GetLastError());
      return false;
     }
//---
   for(uint i = 0; i<out.Size(); i++)
      out[i]=in[i];
//---
   return true;
//---
  }
//+------------------------------------------------------------------+
//| difference a vector                                               |
//+------------------------------------------------------------------+
vector difference(const vector &in)
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return vector::Zeros(1);
     }
//---
   vector yy,zz;
//---
   yy.Init(in.Size()-1,slice,in,1,in.Size()-1,1);
//---
   zz.Init(in.Size()-1,slice,in,0,in.Size()-2,1);
//---
   return yy-zz;
  }
//+------------------------------------------------------------------+

 GHE.mqh, enthält die Definition für die Funktion „gen_hurst()“ und ihre Überladung. Die eine liefert die zu analysierenden Daten in einem Vektor, die andere erwartet sie in einem Array. Die Funktion nimmt auch eine ganze Zahl „q“ und die optionalen ganzzahligen Parameter „lower“ und „upper“ mit Standardwerten an. Dies ist dasselbe „q“, das in der Beschreibung der GHE im vorherigen Abschnitt erwähnt wurde. Die letzten beiden Parameter sind fakultativ, „lower“ und „upper“ legen zusammen den Bereich der Verzögerungen fest, für den die Analyse durchgeführt wird, analog zum Bereich der „K“-Werte in den obigen Formeln.  

//+--------------------------------------------------------------------------+
//|overloaded gen_hurst() function that works with series contained in vector|
//+--------------------------------------------------------------------------+
double general_hurst(vector &data, int q, int lower=0,int upper=0)
  {
   double series[];

   if(!vecToArray(data,series))
      return EMPTY_VALUE;
   else
      return general_hurst(series,q,lower,upper);
  }

Wenn ein Fehler auftritt, gibt die Funktion das Äquivalent der eingebauten Konstante EMPTY_VALUE zurück, zusammen mit einer hilfreichen String-Meldung, die auf der Registerkarte Experten des Terminals ausgegeben wird. Innerhalb von „gen_hurst()“ beginnt die Routine mit der Überprüfung der ihr übergebenen Argumente. Es muss sichergestellt werden, dass die folgenden Bedingungen erfüllt sind:

• „q“ darf nicht kleiner als 1 sein.
• „lower“ kann nicht auf einen Wert kleiner als 2 gesetzt werden und kann auch nicht größer oder gleich „upper“ sein. 
• Das Argument „upper“ darf nicht mehr als die Hälfte der Größe der zu analysierenden Datenreihe betragen. Wenn eine dieser Bedingungen nicht erfüllt ist, wird die Funktion sofort einen Fehler anzeigen.

if(data.Size()<100)
     {
      Print("data array is of insufficient length");
      return EMPTY_VALUE;
     }

   if(lower>=upper || lower<2 ||  upper>int(floor(0.5*data.Size())))
     {
      Print("Invalid input for lower and/or upper");
      return EMPTY_VALUE;
     }

   if(q<=0)
     {
      Print("Invalid input for q");
      return EMPTY_VALUE;
     }

   uint len = data.Size();

   int k =0;

   matrix H,mcord,lmcord;
   vector n_vector,dv,vv,Y,ddVd,VVVd,XP,XY,PddVd,PVVVd,Px_vector,Sqx,pt;
   double dv_array[],vv_array[],mx,SSxx,my,SSxy,cc1,cc2,N;

   if(!H.Resize(ulong(upper-lower),1))
     {
      Print(__LINE__," ",__FUNCTION__," ",GetLastError());
      return EMPTY_VALUE;
     }

   for(int i=lower; i<upper; i++)
     {
      vector x_vector(ulong(i),arange,1.0,1.0);

      if(!mcord.Resize(ulong(i),1))
        {
         Print(__LINE__," ",__FUNCTION__," ",GetLastError());
         return EMPTY_VALUE;
        }

      mcord.Fill(0.0);

Das Innenleben der Funktion beginnt mit einer „for“-Schleife von „unten“ nach „oben“, und für jedes „i“ wird mit der Funktion „arange“ ein Vektor „x_vector“ mit „i“ Elementen erstellt. Anschließend wird die Größe der Matrix „mcord“ so geändert, dass sie „i“ Zeilen und eine Spalte hat.

 for(int j=1; j<i+1; j++)
        {
         if(!diff_array(j,data,dv,Y))
            return EMPTY_VALUE;

Die innere Schleife beginnt mit der Hilfsfunktion „diff_array()“, um die Differenzen im Array „data“ zu berechnen und sie in den Vektoren „dv“ und „Y“ zu speichern.

 N = double(Y.Size());

         vector X(ulong(N),arange,1.0,1.0);

         mx = X.Sum()/N;

         XP = MathPow(X,2.0);

         SSxx = XP.Sum() - N*pow(mx,2.0);

         my = Y.Sum()/N;

         XY = X*Y;

         SSxy = XY.Sum() - N*mx*my;

         cc1 = SSxy/SSxx;

         cc2 = my - cc1*mx;

         ddVd = dv - cc1;

         VVVd = Y - cc1*X - cc2;

         PddVd = MathAbs(ddVd);

         PddVd = pow(PddVd,q);

         PVVVd = MathAbs(VVVd);

         PVVVd = pow(PVVVd,q);

         mcord[j-1][0] = PddVd.Mean()/PVVVd.Mean();
        }

Hier wird die Varianz bei einer bestimmten Verzögerung berechnet. Die Ergebnisse werden in der Matrix „mcord“ gespeichert.

 Px_vector = MathLog10(x_vector);

      mx = Px_vector.Mean();

      Sqx = MathPow(Px_vector,2.0);

      SSxx = Sqx.Sum() - i*pow(mx,2.0);

      lmcord = log10(mcord);

      my = lmcord.Mean();

      pt = Px_vector*lmcord.Col(0);

      SSxy = pt.Sum() - i*mx*my;

      H[k][0]= SSxy/SSxx;

      k++;

Außerhalb der inneren Schleife, im letzten Abschnitt der äußeren Schleife, werden die Werte der Haupt-Matrix H aktualisiert. Schließlich gibt die Funktion den Mittelwert der „H“-Matrix geteilt durch „q“ zurück.

 return H.Mean()/double(q);

Um unsere GHE-Funktion zu testen, wurde die Anwendung GHE.ex5 vorbereitet, die als Expert Advisor implementiert wurde. Es ermöglicht die Visualisierung von Zufallsreihen mit vordefinierten Merkmalen und die Beobachtung, wie die GHE funktioniert. Die volle Interaktivität ermöglicht die Einstellung aller Parameter des GHE sowie der Länge der Serie in Grenzen. Ein interessantes Merkmal ist die Möglichkeit, die Reihen vor der Anwendung der GHE logarithmisch zu transformieren, um zu testen, ob die Vorverarbeitung der Daten auf diese Weise von Vorteil ist.

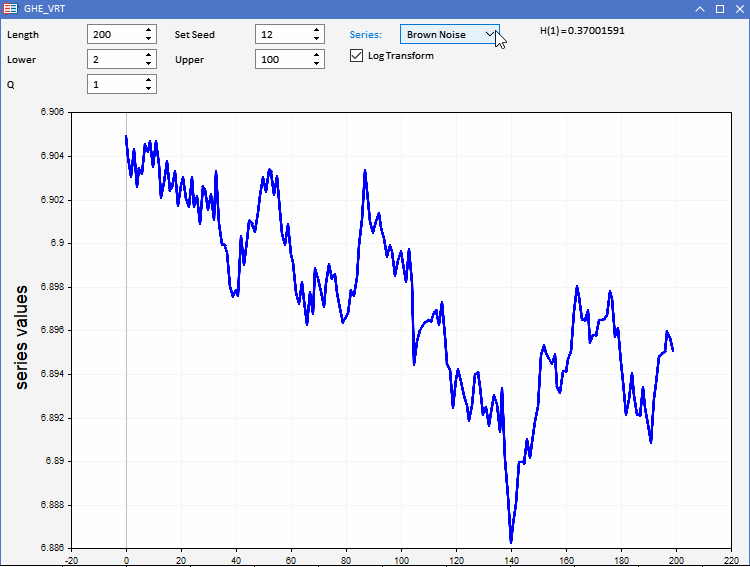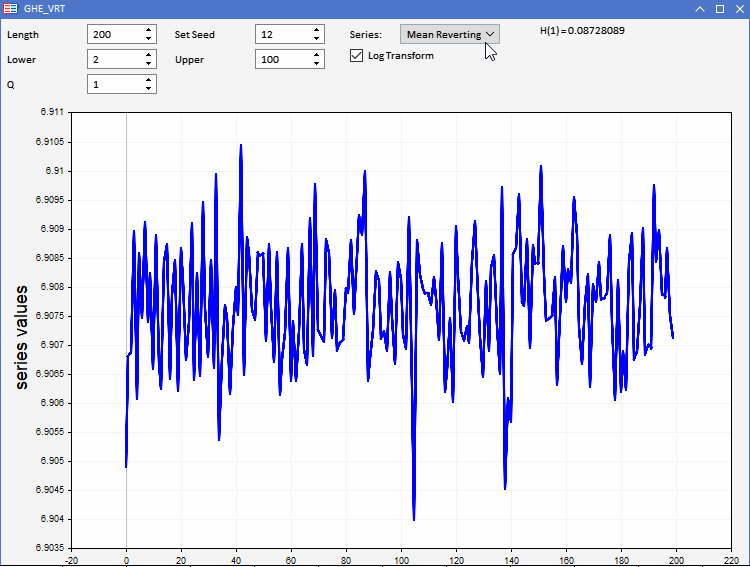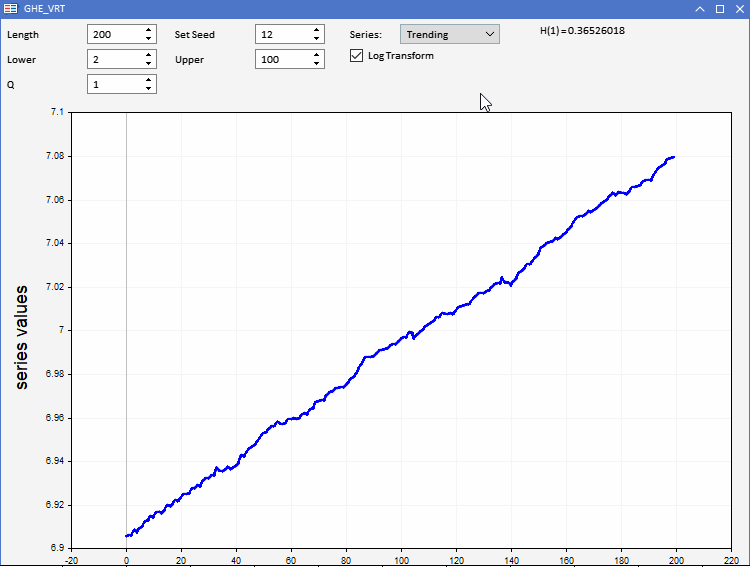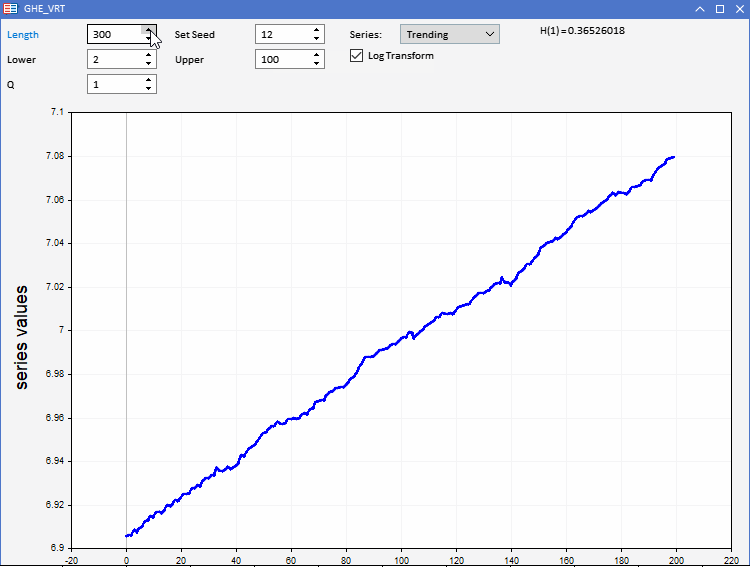
Wir alle wissen, dass Datensätze bei realen Anwendungen mit übermäßigem Rauschen behaftet sind. Da die GHE eine Schätzung liefert, die von der Stichprobengröße abhängt, müssen wir die Signifikanz des Ergebnisses prüfen. Dies kann durch einen Hypothesentest, den so genannten Varianzquotiententest (Variance Ratio Test, VR), erfolgen.

Der Varianzquotiententest

Der Varianzquotiententest ist ein statistischer Test, der zur Beurteilung der Zufälligkeit einer Zeitreihe verwendet wird, indem untersucht wird, ob die Varianz der Reihe proportional mit der Länge des Zeitintervalls zunimmt. Der Test basiert auf der Idee, dass, wenn die zu testende Reihe einem Random Walk folgt, die Varianz der Reihenänderungen über ein bestimmtes Zeitintervall linear mit der Länge des Intervalls zunehmen sollte. Nimmt die Varianz langsamer zu, kann dies auf eine serielle Korrelation in den Reihenänderungen hindeuten, was wiederum bedeutet, dass die Reihen vorhersehbar sind. Der Varianzquotient prüft, ob:

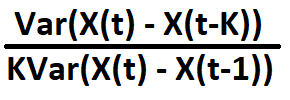
gleich 1 ist, wobei:
- X() ist die Zeitreihe von Interesse.
- K ist eine willkürliche Verzögerung.
- Var() bezeichnet die Varianz.

Die Nullhypothese des Tests lautet, dass die Zeitreihe einem Random Walk folgt und somit das Varianzverhältnis gleich 1 sein sollte. Ein Varianzverhältnis, das signifikant von 1 abweicht, kann dazu führen, dass die Nullhypothese zurückgewiesen wird, was auf das Vorhandensein einer Form von Vorhersagbarkeit oder serieller Korrelation in den Zeitreihen hindeutet.

Durchführung des Varianzquotiententests

Der VR-Test ist als die in VRT.mqh definierte Klasse CVarianceRatio implementiert. Es gibt zwei Methoden, die aufgerufen werden können, um einen VR-Test „Vrt()“ durchzuführen, eine funktioniert mit Vektoren und die andere mit Arrays. Die Parameter der Methode werden im Folgenden beschrieben:

• „lags“ gibt die Anzahl der Perioden oder Lags an, die bei der Varianzberechnung verwendet werden. Im Zusammenhang mit der Verwendung des VR-Tests zur Bewertung der Signifikanz unserer GHE-Schätzung könnten wir „lags“ entweder auf die entsprechenden „unteren“ oder „oberen“ Parameter von „gen_hurst()“ setzen. Dieser Wert kann nicht kleiner als 2 sein. 
• „Trend“ ist eine Enumeration, die es ermöglicht, den Typ des Random Walk zu spezifizieren, auf den wir testen wollen. Nur zwei Optionen haben eine Auswirkung: TREND_CONST_ONLY und TREND_NONE.
• „debiased“ gibt an, ob eine entschärfte Version des Tests verwendet werden soll, die nur anwendbar ist, wenn „overlap“ wahr ist. Wenn die Funktion auf „true“ gesetzt ist, verwendet sie eine Technik zur Korrektur von Verzerrungen, um die Schätzung des Varianzverhältnisses anzupassen, um eine genauere Darstellung der wahren Beziehung zwischen den Varianzen zu erreichen. Dies ist vor allem dann von Vorteil, wenn man mit kleinen Stichprobenreihen arbeitet.
  
• „overlap“ gibt an, ob alle überlappenden Blöcke verwendet werden sollen. Wenn false, muss die Länge der Reihe minus eins ein genaues Vielfaches von „lags“ sein.  Wenn diese Bedingung nicht erfüllt ist, werden einige Werte am Ende der Eingabereihen verworfen.
• „robust“ wählt aus, ob entweder Heteroskedastizität (true) oder nur Homoskedastizität (false) berücksichtigt werden soll. In der statistischen Analyse hat ein heteroskedastischer Prozess eine nicht konstante Varianz, während eine homoskedastische Reihe durch eine konstante Varianz gekennzeichnet ist. 
  

Die Methode „Vrt()“ gibt bei erfolgreicher Ausführung den Wert „true“ zurück, woraufhin eine der Get-Methoden aufgerufen werden kann, um alle Aspekte des Testergebnisses zu erfassen.

//+------------------------------------------------------------------+
//| CVarianceRatio  class                                            |
//| Variance ratio hypthesis test for a random walk                  |
//+------------------------------------------------------------------+
class CVarianceRatio
  {
private:
   double            m_pvalue;     //pvalue
   double            m_statistic;  //test statistic
   double            m_variance;   //variance
   double            m_vr;         //variance ratio
   vector            m_critvalues; //critical values

public:
                     CVarianceRatio(void);
                    ~CVarianceRatio(void);

   bool              Vrt(const double &in_data[], ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);
   bool              Vrt(const vector &in_vect, ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);

   double            Pvalue(void) { return m_pvalue;}
   double            Statistic(void) { return m_statistic;}
   double            Variance(void) { return m_variance;}
   double            VRatio(void) { return m_vr;}
   vector            CritValues(void) { return m_critvalues;}
  };

Innerhalb von „Vrt()“ wird, wenn „overlap“ falsch ist, geprüft, ob die Länge der Eingabereihe durch „lags“ teilbar ist. Ist dies nicht der Fall, wird das Ende der Reihe abgeschnitten und eine Warnung bezüglich der Datenlänge ausgegeben. Anschließend ordnen wir die „nobs“ auf der Grundlage der aktualisierten Länge der Reihe neu zu. Und wir berechnen „mu“, den Trendterm. Hier berechnen wir die Differenzen benachbarter Elemente in der Reihe und speichern sie in „delta_y“. Mit „delta_y“ wird die Varianz berechnet und in der Variablen „sigma2_1“ gespeichert. Wenn es keine Überschneidungen gibt, berechnen wir die Varianz für nicht überlappende Blöcke. Andernfalls berechnen wir die Varianz für sich überschneidende Blöcke. Wenn „debiased“ zusammen mit „overlap“ aktiviert ist, passen wir die Abweichungen an. Hier wird „m_varianced“ in Abhängigkeit von „overlap“ und „robust“ berechnet. Schließlich werden das Varianzverhältnis, die Teststatistik und der p-Wert berechnet.

//+------------------------------------------------------------------+
//| main method for computing Variance ratio test                    |
//+------------------------------------------------------------------+
bool CVarianceRatio::Vrt(const vector &in_vect,ulong lags,ENUM_TREND trend=1,bool debiased=true,bool robust=true,bool overlap=true)
  {
   ulong nobs = in_vect.Size();

   vector y = vector::Zeros(2),delta_y;

   double mu;

   ulong nq = nobs - 1;

   if(in_vect.Size()<1)
     {
      Print(__FUNCTION__, "Invalid input, no data supplied");
      return false;
     }

   if(lags<2 || lags>=in_vect.Size())
     {
      Print(__FUNCTION__," Invalid input for lags");
      return false;
     }

   if(!overlap)
     {
      if(nq % lags != 0)
        {
         ulong extra = nq%lags;
         if(!y.Init(5,slice,in_vect,0,in_vect.Size()-extra-1))
           {
            Print(__FUNCTION__," ",__LINE__);
            return false;
           }
         Print("Warning:Invalid length for input data, size is not exact multiple of lags");
        }
     }
   else
      y.Copy(in_vect);

   nobs = y.Size();

   if(trend == TREND_NONE)
      mu = 0;
   else
      mu = (y[y.Size()-1] - y[0])/double(nobs - 1);

   delta_y = difference(y);

   nq = delta_y.Size();

   vector mudiff = delta_y - mu;

   vector mudiff_sq = MathPow(mudiff,2.0);

   double sigma2_1 = mudiff_sq.Sum()/double(nq);

   double sigma2_q;

   vector delta_y_q;

   if(!overlap)
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1,lags) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1,lags))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq);
     }
   else
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq*lags);
     }


   if(debiased && overlap)
     {
      sigma2_1 *= double(nq)/double(nq-1);
      double mm = (1.0-(double(lags)/double(nq)));
      double m = double(lags*(nq - lags+1));// * (1.0-double(lags/nq));
      sigma2_q *= double(nq*lags)/(m*mm);
     }

   if(!overlap)
      m_variance = 2.0 * (lags-1);
   else
      if(!robust)
         m_variance = double((2 * (2 * lags - 1) * (lags - 1)) / (3 * lags));
      else
        {
         vector z2, o, p;
         z2=MathPow((delta_y-mu),2.0);
         double scale = pow(z2.Sum(),2.0);
         double theta = 0;
         double delta;
         for(ulong k = 1; k<lags; k++)
           {
            if(!o.Init(3,slice,z2,k,z2.Size()-1) ||
               !p.Init(3,slice,z2,0,z2.Size()-k-1))
              {
               Print(__FUNCTION__," ",__LINE__);
               return false;
              }
            o*=double(nq);
            p/=scale;
            delta = o.Dot(p);
            theta+=4.0*pow((1.0-double(k)/double(lags)),2.0)*delta;
           }
         m_variance = theta;
        }
   m_vr = sigma2_q/sigma2_1;

   m_statistic = sqrt(nq) * (m_vr - 1)/sqrt(m_variance);

   double abs_stat = MathAbs(m_statistic);

   m_pvalue = 2 - 2*CNormalDistr::NormalCDF(abs_stat);

   return true;
  }

Um die Klasse zu testen, ändern wir die Anwendung GHE.ex5, die zur Demonstration der Funktion „gen_hurst()“ verwendet wird. Denn die GHE wird durch eine Reihe von Verzögerungen definiert, auf die sich die Analyse konzentriert. Wir können die VRT kalibrieren, um die Signifikanz der GHE-Ergebnisse über denselben Bereich von Verzögerungen zu testen. Wenn wir die VRT mit der minimalen und maximalen Verzögerung durchführen, sollten wir ausreichende Informationen erhalten. In GHE.ex5 wird das Varianzverhältnis bei der „unteren“ Verzögerung zuerst angezeigt, bevor das Varianzverhältnis bei der „oberen“ Verzögerung angezeigt wird.
Denken Sie daran, dass ein Varianzverhältnis, das signifikant abweicht, ein Hinweis auf die Vorhersagbarkeit der Daten ist. Varianzquotienten nahe bei 1 deuten darauf hin, dass die Reihe nicht weit von einem Random Walk entfernt ist. Wenn wir mit der Anwendung herumspielen und verschiedene Parameterkombinationen testen, stellen wir fest, dass sowohl die GHE- als auch die VRT-Ergebnisse von der Stichprobengröße beeinflusst werden.

Bei Serienlängen von weniger als 1000 lieferten beide manchmal unerwartete Ergebnisse.

Außerdem gab es Fälle, in denen die Ergebnisse der GHE signifikant voneinander abwichen, wenn Tests mit Rohwerten und logarithmierten Werten verglichen wurden.

Da wir nun mit der VRT und GHE vertraut sind, können wir sie auf unsere Mean-Reversion-Strategie anwenden. Wenn bekannt ist, dass sich eine Preisreihe im Mittelwert umkehrt, können wir anhand der aktuellen Abweichung vom Mittelwert grob abschätzen, wie sich der Preis entwickeln wird. Die Grundlage unserer Strategie wird auf der Analyse der Merkmale einer Preisreihe über einen bestimmten Zeitraum beruhen. Auf der Grundlage dieser Analyse erstellen wir ein Modell, mit dem wir abschätzen können, an welchen Punkten der Preis nach einer zu großen Abweichung von der Norm wahrscheinlich wieder einbrechen wird. Wir brauchen eine Möglichkeit, diese Ablenkung zu messen und zu quantifizieren, um Einstiegs- und Ausstiegssignale zu erzeugen.

Der z-Score

Der z-Score misst die Anzahl der Standardabweichungen, um die der Kurs von seinem Mittelwert abweicht. Durch die Normalisierung der Preise oszilliert der z-Score um Null. Sehen wir uns an, wie eine Darstellung des z-Scores aussieht, indem wir ihn als Indikator implementieren. Der vollständige Code ist nachstehend aufgeführt.

//+------------------------------------------------------------------+
//|                                                       Zscore.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<VectorMatrixTools.mqh>
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
//--- plot Zscore
#property indicator_label1  "Zscore"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input int      z_period = 10;
//--- indicator buffers
double         ZscoreBuffer[];
vector vct;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,ZscoreBuffer,INDICATOR_DATA);
//----
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0);
//---
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,z_period-1);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(rates_total<z_period)
     {
      Print("Insufficient history");
      return -1;
     }
//---
   int limit;
   if(prev_calculated<=0)
      limit = z_period - 1;
   else
      limit = prev_calculated - 1;
//---
   for(int i = limit; i<rates_total; i++)
     {
      vct.Init(ulong(z_period),assign,close,ulong(i-(z_period-1)),i,1);
      if(vct.Size()==ulong(z_period))
         ZscoreBuffer[i] = (close[i] - vct.Mean())/vct.Std();
      else
         ZscoreBuffer[i]=0.0;
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Aus diesem Chart ist ersichtlich, dass die Indikatorwerte nun normaler verteilt sind.

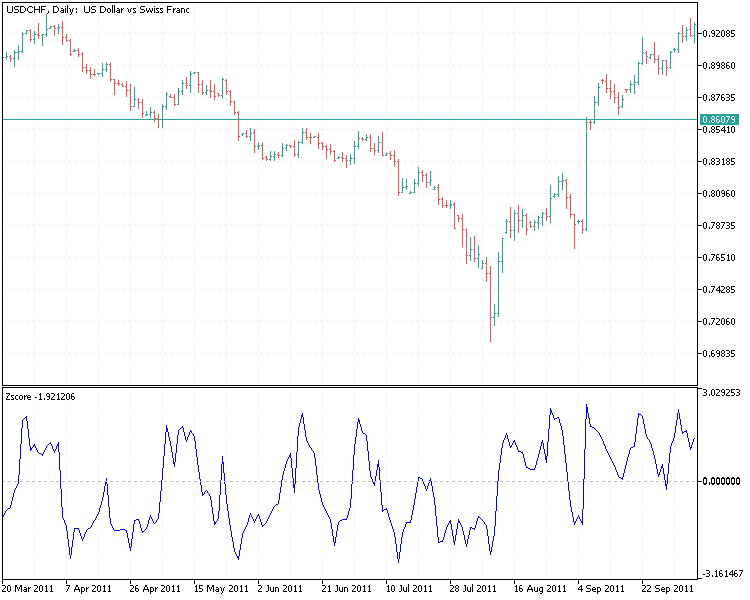
Handelssignale werden generiert, wenn der z-Score signifikant von 0 abweicht und einen historisch abgeleiteten Schwellenwert überschreitet. Ein extrem negativer z-Score signalisiert einen günstigen Zeitpunkt, um zu kaufen, während das Gegenteil ein guter Zeitpunkt ist, um zu verkaufen. Das heißt, wir brauchen zwei Schwellenwerte für Kauf- und Verkaufssignale. Einen Negativen (für Kauf) und einen Positiven (für Verkauf). Nachdem wir unsere Eingaben gemacht haben, gehen wir zur Bestimmung unserer Existenz über. Eine Möglichkeit besteht darin, eine weitere Reihe von Schwellenwerten abzuleiten, die bei einer bestimmten Position (Kauf oder Verkauf) funktionieren. Bei Verkäufen können wir unsere Position schließen, wenn der z-Score wieder gegen 0 tendiert. In ähnlicher Weise schließen wir eine Kaufposition, wenn der Z-Score von dem extremen Niveau, bei dem wir gekauft haben, gegen 0 klettert.

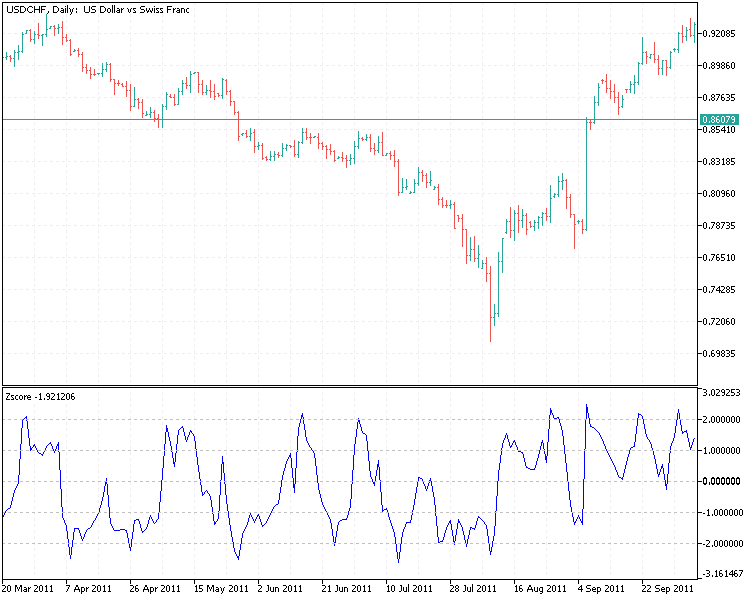
Wir haben nun unsere Ein- und Ausstiege mit dem Indikator Zscore.ex5 definiert. Lassen Sie uns all dies in einem EA zusammenfassen. Der Code ist unten abgebildet.

//+------------------------------------------------------------------+
//|                                                MeanReversion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Zscore.ex5"
#include<ExpertTools.mqh>
//---Input parameters
input int  PeriodLength  = 10;
input double LotsSize = 0.01;
input double  LongOpenLevel = -2.0;
input double  ShortOpenLevel = 2.0;
input double  LongCloseLevel = -0.5;
input double  ShortCloseLevel = 0.5;
input ulong  SlippagePoints = 10;
input ulong  MagicNumber    = 123456;
//---
 int indi_handle;
//---
 double zscore[2];
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(PeriodLength<2)
    {
     Print("Invalid parameter value for PeriodLength");
     return INIT_FAILED;
    }
//---
   if(!InitializeIndicator())
    return INIT_FAILED;
//---        
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---    
      int signal = GetSignal();
//---      
      if(SumMarketOrders(MagicNumber,_Symbol,-1))
       {
        if(signal==0)
         CloseAll(MagicNumber,_Symbol,-1);
        return; 
       }
      else
        OpenPosition(signal);
//---   
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Initialize indicator                                             |
//+------------------------------------------------------------------+
bool InitializeIndicator(void)
{
 indi_handle = INVALID_HANDLE;
//---
 int try = 10;
//---
 while(indi_handle == INVALID_HANDLE && try>0)
  {
   indi_handle = (indi_handle==INVALID_HANDLE)?iCustom(NULL,PERIOD_CURRENT,"::Indicators\\Zscore.ex5",PeriodLength):indi_handle;
   try--;
  }
//---
 if(try<0)
  {
   Print("Failed to initialize Zscore indicator ");
   return false;
  }
//---
 return true;
}
//+------------------------------------------------------------------+
//|Get the signal to trade or close                                  |
//+------------------------------------------------------------------+
int GetSignal(const int sig_shift=1)
{
//---
 if( CopyBuffer(indi_handle,int(0),sig_shift,int(2),zscore)<2)
   {
    Print(__FUNCTION__," Error copying from indicator buffers: ", GetLastError());
    return INT_MIN;
   } 
//---   
 if(zscore[1]<LongOpenLevel && zscore[0]>LongOpenLevel)
     return (1);
//---   
 if(zscore[1]>ShortOpenLevel && zscore[0]<ShortOpenLevel)
     return (-1);          
//---   
 if((zscore[1]>LongCloseLevel && zscore[0]<LongCloseLevel) ||
    (zscore[1]<ShortCloseLevel && zscore[0]>ShortCloseLevel))
     return (0);
//---
 return INT_MIN;
//--- 
}
//+------------------------------------------------------------------+
//|  Go long or short                                                |
//+------------------------------------------------------------------+
bool OpenPosition(const int sig)
{

 long pid;
//--- 
 if(LastOrderOpenTime(pid,NULL,MagicNumber)>=iTime(NULL,0,0))
   return false;
//---   
 if(sig==1)
   return SendOrder(_Symbol,0,ORDER_TYPE_BUY,LotsSize,SlippagePoints,0,0,NULL,MagicNumber);
 else
  if(sig==-1)
    return SendOrder(_Symbol,0,ORDER_TYPE_SELL,LotsSize,SlippagePoints,0,0,NULL,MagicNumber); 
//--- 
  return false;                   
}

Er ist sehr einfach, es sind keine Stop-Loss- oder Take-Profit-Levels definiert. Unser Ziel ist es, zunächst den EA zu optimieren, um den optimalen Zeitraum für den Zscore-Indikator sowie die optimalen Einstiegs- und Ausstiegsschwellen zu ermitteln. Wir werden die Daten über mehrere Jahre hinweg optimieren und die optimalen Parameter außerhalb der Stichprobe testen, aber vorher machen wir einen kurzen Umweg, um ein weiteres interessantes Instrument vorzustellen. In dem Buch „Algorithmic Trading: Winning Strategies And Their Rationale“ beschreibt der Autor Enest Chan ein interessantes Instrument zur Entwicklung von Mean-Reversion-Strategien, die so genannte „Half life of mean reversion“ oder die Halbwertszeit der Rückkehr zum Mittelwert.

Half life of mean reversion

Die „half life of mean reversion“ ist die Zeit, die eine Abweichung vom Mittelwert benötigt, um sich zu halbieren. Im Zusammenhang mit dem Preis eines Vermögenswerts gibt die Halbwertszeit der Mean Reversion an, wie schnell der Preis dazu neigt, zu seinem historischen Mittelwert zurückzukehren, nachdem er von diesem abgewichen ist. Sie ist ein Maß für die Geschwindigkeit, mit der die Rückkehr zum Mittelwert erfolgt. Mathematisch lässt sich die Halbwertszeit mit der Geschwindigkeit der Rückkehr zum Mittelwert durch die Gleichung wie folgt ausdrücken:

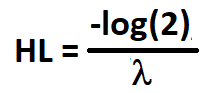
Wobei:
- HL ist die Halbwertszeit.
- log() ist der natürliche Logarithmus.
- lambda ist die Geschwindigkeit der Rückkehr zum Mittelwert.

In der Praxis bedeutet eine kürzere Halbwertszeit eine schnellere Rückkehr zum Mittelwert, während eine längere Halbwertszeit auf eine langsamere Rückkehr zum Mittelwert hindeutet. Das Konzept der Halbwertszeit kann zur Feinabstimmung von Parametern in Mean-Reversion-Handelsstrategien verwendet werden und hilft dabei, Ein- und Ausstiegspunkte auf der Grundlage historischer Daten und der beobachteten Geschwindigkeit der Mean-Reversion zu optimieren. Die Halbwertszeit der Rückkehr zum Mittelwert ergibt sich aus der mathematischen Darstellung eines mittleren Umkehrungsprozesses, der in der Regel als Ornstein-Uhlenbeck-Prozess modelliert wird. Der Ornstein-Uhlenbeck-Prozess ist eine stochastische Differentialgleichung, die eine zeitkontinuierliche Version der Rückkehr zum Mittelwert beschreibt.

Nach Chan lässt sich durch die Berechnung der Halbwertszeit der Rückkehr zum Mittelwert feststellen, ob diese eine geeignete Strategie ist. Erstens: Wenn Lambda positiv ist, sollte die Rückkehr zum Mittelwert überhaupt nicht angewendet werden. Selbst wenn Lambda negativ ist und sehr nahe bei Null liegt, wird von der Anwendung der Rückkehr zum Mittelwert abgeraten, da dies darauf hindeutet, dass die Halbwertszeit lang sein wird. Die mittlere Umkehrung sollte nur verwendet werden, wenn die Halbwertszeit relativ kurz ist.

Die Halbwertszeit der Rückkehr zum Mittelwert ist als Funktion in MeanReversionUtilities.mqh implementiert, der Code ist unten angegeben. Sie wird durch Regression der Preisreihe gegen die Reihe der Differenzen zwischen den nachfolgenden Werten berechnet. Lambda ist gleich dem Beta-Parameter des Regressionsmodells, und die Halbwertszeit wird durch Division von -log(2) durch Lambda berechnet.

//+------------------------------------------------------------------+
//|Calculate Half life of Mean reversion                             |
//+------------------------------------------------------------------+
double mean_reversion_half_life(vector &data, double &lambda)
  {
//---
   vector yy,zz;
   matrix xx;
//---
   OLS ols_reg;
//---
   yy.Init(data.Size()-1,slice,data,1,data.Size()-1,1);
//---
   zz.Init(data.Size()-1,slice,data,0,data.Size()-2,1);
//---
   if(!xx.Init(zz.Size(),2) || !xx.Col(zz,0) || !xx.Col(vector::Ones(zz.Size()),1) || !ols_reg.Fit(yy-zz,xx))
     {
      Print(__FUNCTION__," Error in calculating half life of mean reversion ", GetLastError());
      return 0;
     }
//---
   vector params = ols_reg.ModelParameters();
   lambda = params[0];
//---
   return (-log(2)/lambda);
//---
  }

Wir werden sie in Verbindung mit der GHE und der VRT verwenden, um eine Stichprobe von Preisen über einen ausgewählten Zeitraum von Jahren für einige Devisensymbole zu testen. Wir verwenden die Testergebnisse, um ein geeignetes Symbol auszuwählen, auf das wir den zuvor erstellten EA anwenden werden. Es wird über denselben Zeitraum von Jahren optimiert und schließlich außerhalb der Stichprobe getestet.  Das nachstehende Skript akzeptiert eine Liste von Kandidatensymbolen, die mit Hilfe der GHE, VRT und der Halbwertszeit getestet werden.

//+------------------------------------------------------------------+
//|                                                 SymbolTester.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<MeanReversionUtilities.mqh>
#include<GHE.mqh>
#include<VRT.mqh>

//--- input parameters
input string   Symbols = "EURUSD,GBPUSD,USDCHF,USDJPY";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2020.01.02 00:00:01';
input datetime StopDate=D'2015.01.18 00:00:01';
input int Q_parameter = 2;
input int MinimumLag = 2;
input int MaximumLag = 100;
input bool ApplyLogTransformation = true;
//---
CVarianceRatio vrt;
double ghe,hl,lb,vlower,vupper;
double prices[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(StartDate<=StopDate)
     {
      Print("Invalid input for StartDater or StopDate");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;
//---in case there are less than two symbols specified
   if(num_symbols<1)
     {
      Print("Invalid input. Please list at least one symbol");
      return;
     }
//---loop through all paired combinations from list
   for(uint i=0; i<symbols.Size(); i++)
     {

      //--- get prices for the pair of symbols
      if(CopyClose(symbols[i],TimeFrame,StartDate,StopDate,prices)<1)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //---
      if(ApplyLogTransformation && !MathLog(prices))
        {
         Print("Mathlog error ", GetLastError());
         return;
        }
      //---
      if(!vrt.Vrt(prices,MinimumLag))
         return;
      //---
      vlower = vrt.VRatio();
      //---
      if(!vrt.Vrt(prices,MaximumLag))
         return;
      //---
      vupper = vrt.VRatio();
      //---
      ghe = general_hurst(prices,Q_parameter,MinimumLag,MaximumLag);
      //---
      hl = mean_reversion_half_life(prices,lb);
      //--- output the results
      Print(symbols[i], " GHE:  ", DoubleToString(ghe)," | Vrt: ",DoubleToString(vlower)," ** ",DoubleToString(vupper)," | HalfLife ",DoubleToString(hl)," | Lambda: ",DoubleToString(lb));
     }
  }
//+------------------------------------------------------------------+

Die Ausführung des Skripts führt zu den folgenden Ergebnissen:

19:31:03.143    SymbolTester (USDCHF,D1)        EURUSD GHE:  0.44755644 | Vrt: 0.97454284 ** 0.61945905 | HalfLife 85.60548208 | Lambda: -0.00809700
19:31:03.326    SymbolTester (USDCHF,D1)        GBPUSD GHE:  0.46304381 | Vrt: 1.01218672 ** 0.82086185 | HalfLife 201.38001205 | Lambda: -0.00344199
19:31:03.509    SymbolTester (USDCHF,D1)        USDCHF GHE:  0.42689382 | Vrt: 1.02233286 ** 0.47888803 | HalfLife 28.90550869 | Lambda: -0.02397976
19:31:03.694    SymbolTester (USDCHF,D1)        USDJPY GHE:  0.49198795 | Vrt: 0.99875744 ** 1.06103587 | HalfLife 132.66433924 | Lambda: -0.00522482

Das USDCHF-Symbol hat die vielversprechendsten Testergebnisse über den ausgewählten Zeitraum. Wir werden also die Parameter des EA für den Handel mit dem USDCHF optimieren. Eine interessante Übung wäre es, den Zscore-Zeitraum für die Optimierung auszuwählen und zu sehen, ob er von der berechneten Halbwertszeit abweicht.

Hier sehen wir die optimale Zscore-Periode, sie liegt sehr nahe an der berechneten Halbwertszeit der Mean Reversion. Das ist ermutigend. Natürlich wären umfangreichere Tests erforderlich, um die Nützlichkeit der Halbwertszeit zu bestimmen.

Schließlich testen wir den EA außerhalb der Stichprobe mit den optimalen Parametern.

Die Ergebnisse sehen nicht gut aus. Dies ist wahrscheinlich darauf zurückzuführen, dass der Markt ständig in Bewegung ist, sodass die Merkmale, die während des Zeitraums, in dem der EA optimiert wurde, beobachtet wurden, nicht mehr gelten. Wir brauchen dynamischere Eintritts- und Austrittsschwellen, die den Veränderungen der zugrunde liegenden Marktdynamik Rechnung tragen.

Wir können das, was wir hier gelernt haben, als Grundlage für die weitere Entwicklung nutzen. Ein Weg, den wir erkunden können, ist die Anwendung der hier beschriebenen Instrumente zur Umsetzung einer Paarhandelsstrategie. Anstelle des Zscore-Indikators, der auf einer einzigen Preisreihe basiert, kann er auf der Spanne zweier kointegrierter oder korrelierter Instrumente beruhen.

Schlussfolgerung

In diesem Artikel haben wir die Implementierung des verallgemeinerten Hurst-Exponenten in MQL5 demonstriert und gezeigt, wie er zur Bestimmung der Eigenschaften einer Preisreihe verwendet werden kann.  Wir haben uns auch mit der Anwendung des Varianzverhältnistests sowie mit der Halbwertszeit der mittleren Umkehrung beschäftigt.  Die folgende Tabelle enthält eine Beschreibung aller Dateien, die dem Artikel beigefügt sind.

Datei	Beschreibung
Mql5\include\ExpertTools.mqh	Enthält Funktionsdefinitionen für die Durchführung von Handelsoperationen, die in dem EA MeanReversion verwendet werden
Mql5\include\GHE.mqh	Enthält die Definition einer Funktion zur Implementierung des verallgemeinerten Hurst-Exponenten
Mql5\include\OLS.mqh	Enthält die Definition der OLS-Klasse, die die Regression der kleinsten Quadrate implementiert
Mql5\include\VRT.mqh	Enthält die Definition der Klasse CVarianceRatio, die den Test des Varianzverhältnisses kapselt
Mql5\include\VectorMatrixTools.mqh	Verfügt über verschiedene Funktionsdefinitionen zur schnellen Initialisierung gängiger Vektoren und Matrizen
Mql5\include\TestUtilities.mqh	Hat eine Reihe von Deklarationen, die in der OLS-Klassendefinition verwendet werden
Mql5\include\MeanReversionUtilities.mqh	Enthält verschiedene Funktionsdefinitionen, darunter eine, die die Halbwertszeit der mittleren Umkehrung implementiert
Mql5\Indicators\Zscore.mq5	Indikator, der vom EA MeanReversion verwendet wird
Mql5\scripts\SymbolTester.mq5	Skript, das zum Testen von Symbolen auf die Rückkehr zum Mittelwert verwendet werden kann
Mql5\Experts\GHE.ex5	Expert Advisor App, die zum Erkunden und Experimentieren mit den GHE- und VRT-Tools verwendet werden kann
Mql5\scripts\MeanReversion.mq5	EA demonstriert eine einfache Mean-Reversion-Strategie