MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 26): Gleitende Durchschnitte und der Hurst-Exponent

Einführung

Wir setzen diese Serie über Techniken mit dem MQL5-Assistenten fort, die sich auf alternative Methoden der Finanzzeitreihenanalyse zum Nutzen von Händlern konzentrieren. In diesem Artikel betrachten wir den Hurst Exponenten. Dies ist eine Metrik, die uns sagt, ob eine Zeitreihe eine hohe positive Autokorrelation oder eine negative Autokorrelation über einen langen Zeitraum aufweist. Die Anwendungen dieser Messung können sehr umfangreich sein. Wie würden wir sie nutzen? Zunächst berechnen wir den Hurst-Exponenten, um festzustellen, ob sich der Markt in einem Trend befindet (was in der Regel einen Wert von mehr als 0,5 ergibt) oder ob es sich um einen Seitwärtsmarkt (mean-reverting/whipsaw) handelt (was einen Wert von weniger als 0,5 ergeben würde). Da wir uns aufgrund der letzten beiden Artikel in einer „Saison der gleitenden Durchschnitte“ befinden, werden wir in diesem Artikel die Informationen des Hurst-Exponenten mit der relativen Position des aktuellen Kurses zu einem gleitenden Durchschnitt verbinden. Die relative Position des Preises zu einem gleitenden Durchschnitt kann einen Hinweis auf die nächste Richtung des Preises geben, allerdings mit einem großen Vorbehalt.

Sie müssen wissen, ob sich die Märkte in einem Trend oder in einer Schwankungsbreite (mean-reverting) befinden. Da wir zur Beantwortung dieser Frage den Hurst-Exponenten heranziehen können, müssen wir uns nur ansehen, wo sich der Kurs im Verhältnis zum Durchschnitt befindet, und dann einen Handel platzieren. Aber selbst das kann noch etwas überstürzt sein, da sich schwankende Märkte in der Regel besser über kürzere Zeiträume studieren lassen als trendfolgende Märkte, die bei der Betrachtung längerer Zeiträume deutlicher werden. Aus diesem Grund bräuchten wir zwei separate gleitende Durchschnitte, um die relative Position des Preises abzuwägen, bevor eine definitive Bedingung beurteilt werden kann. Dabei handelt es sich um einen sich schnell bewegenden Durchschnitt für schwankende oder sich um den Mittelwert bewegende Märkte und um einen sich langsam bewegenden Durchschnitt für Märkte, die sich im Trend bewegen, wie durch den Hurst-Exponenten bestimmt. Jeder Markttyp, wie er vom Exponenten festgelegt wird, hätte also seinen eigenen gleitenden Durchschnitt. Dieser Artikel befasst sich daher mit der reskalierten Bereichsanalyse als Mittel zur Schätzung des Hurst-Exponenten. Wir werden den Schätzungsprozess Schritt für Schritt durchgehen und mit einer Expertensignalklasse abschließen, die diesen Exponenten implementiert.

Aufteilung der Zeitreihen

Auf Wikipedia wird die Formel für den Hurst-Exponenten wie folgt dargestellt:

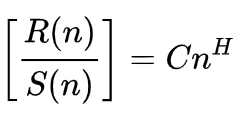
Wobei

• n ist der Umfang der analysierten Stichprobe
• R() ist der neu skalierte Bereich der Stichprobe
• S() ist die Standardabweichung der Stichprobe
• C ist eine Konstante
• H ist der Hurst-Exponent

Bei dieser Formel haben wir es mit zwei Unbekannten zu tun, und um sowohl die Konstante C als auch den gesuchten Exponenten H zu finden, müssen wir mehrere Segmente der Stichprobenmenge regressieren. H ist eine Potenz, was in der Arithmetik bedeutet, dass wir beide Seiten der Gleichung logarithmieren, um H zu lösen, und das ist unser letzter Schritt, wie wir weiter unten sehen werden. Der allererste Schritt besteht also darin, Segmente innerhalb der gesampelten Daten zu identifizieren oder zu definieren.

Die Mindestanzahl von Segmenten, die wir aus einer Stichprobe erhalten können, ist 2. Das Maximum, das wir aus einer Stichprobe erhalten können, hängt vom Stichprobenumfang ab, und die rudimentäre Formel ist der Stichprobenumfang geteilt durch 2. Jetzt suchen wir nach zwei Unbekannten, d. h. wir brauchen mehr als ein Punktepaar, um wie in der Praxis mindestens 2 Gleichungen zu haben. Die Anzahl der Gleichungen oder Punktpaare, die wir aus einer Stichprobe erzeugen können, ist durch die Hälfte des Stichprobenumfangs minus 1 gegeben. Bei einem Stichprobenumfang von 4 Datenpunkten wird also nur ein Punktpaar für die Regression erzeugt, was eindeutig nicht ausreicht, um den Hurst-Exponenten und die C-Konstante zu ermitteln.

Eine Stichprobe mit 6 Datenpunkten kann jedoch mindestens 2 Punktepaare erzeugen, die zur Schätzung des Exponenten und der Konstante verwendet werden können. In der Praxis sollte der Stichprobenumfang so groß wie möglich sein, da der Hurst-Exponent, wie in der Definition erwähnt, eine „langfristige“ Eigenschaft ist. Außerdem gilt die oben genannte Wikipedia-Formel für Stichproben, wenn n gegen unendlich tendiert. Daher ist es wichtig, dass die Stichprobengröße so groß wie möglich ist, um einen repräsentativen Hurst-Exponenten zu schätzen.

Die Aufteilung der Stichprobe in Segmente, wobei jeder Teil/Segmentsatz ein einzelnes Punktepaar erzeugt, ist der „erste Schritt“. Ich verwende den Begriff „erster Schritt“, weil wir bei dem Ansatz, den wir für diesen Artikel verwenden, wie im Quellcode unten gezeigt wird, die Daten nicht einseitig aufteilen und alle Segmente auf einmal definieren, bevor wir zum nächsten Schritt übergehen, sondern für jede Aufteilung das Punktepaar berechnen, das von dieser Probenaufteilung abgebildet wird. Ein Teil des Quellcodes, der diese Aufgabe erfüllt, ist unten angegeben:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   double _std = Data.Std();
   if(_std == 0.0)
   {  printf(__FUNCSIG__ + " uniform sample with no standard deviation! ");
      return;
   }
   int _t = Fraction(Data.Size(), 2);
   if(_t < 3)
   {  printf(__FUNCSIG__ + " too small sample size, cannot generate minimum 2 regression points! ");
      return;
   }
   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      int _rows = Fraction(Data.Size(), t);
      _segments.Init(_rows, t);
      int _r = 0, _c = 0;
      for(int s = 0; s < int(Data.Size()); s++)
      {  _segments[_r][_c] = Data[s];
         _c++;
         if(_c >= t)
         {  _c = 0;
            _r++;
            if(_r >= _rows)
            {  break;
            }
         }
      }
      
      ...

   }
   ...
}

Wir greifen also bei jedem Schritt auf eine Matrix zu, um die sich nicht überschneidenden Segmente aus der Stichprobe der Daten zu protokollieren. In der Gesamtiteration beginnen wir mit der kleinsten Segmentgröße 2 und arbeiten uns dann bis zur halben Größe der Datenstichprobe vor. Deshalb gibt es einen Validierungsschritt für den Umfang der Datenstichprobe, bei dem wir überprüfen, ob die Hälfte des Umfangs mindestens 3 beträgt. Ist er kleiner als drei, dann ist die Berechnung des Hurst-Exponenten sinnlos, da wir im letzten Schritt nicht mindestens zwei Punktepaare für die Regression erhalten.

Der andere Validierungsschritt, den wir an der Datenstichprobe durchführen, besteht darin, sicherzustellen, dass die Daten eine gewisse Variabilität aufweisen, da eine Standardabweichung von Null zu einer Zahl führt, die nicht gültig ist gültig oder eine Null-Division.

Mittlere Anpassung

Nachdem wir eine Reihe von Segmenten in einer bestimmten Iteration haben (wobei die Gesamtzahl der Iterationen durch die Hälfte des Stichprobenumfangs begrenzt ist), müssen wir den Mittelwert jedes Segments ermitteln. Da unsere Segmente zeilenweise in einer Matrix vorliegen, kann jede Zeile als Vektor abgerufen werden. Sobald wir den Vektor jeder Zeile haben, können wir den Mittelwert dank der integrierten Vektorfunktion „mean“ leicht ermitteln, was uns unnötigen Code erspart. Der Mittelwert jedes Segments wird dann von jedem Datenpunkt in seinem jeweiligen Segment subtrahiert. Dies wird als Mittelwertanpassung bezeichnet. Sie ist aus mehreren Gründen wichtig für den Prozess der Entfernungsanalyse und Skalenanalyse.

Erstens werden alle Daten in jedem Segment normalisiert, wodurch sichergestellt wird, dass sich die Analyse auf die Schwankungen um den Mittelwert konzentriert und nicht von den absoluten Werten der einzelnen Datenpunkte in einem Segment beeinflusst wird. Zweitens dient diese Normalisierung dem Zweck, Verzerrungen und Ausreißer zu reduzieren, die das Erreichen einer repräsentativeren Skala erschweren könnten.

Dies gewährleistet außerdem die Konsistenz über alle Segmente hinweg, sodass sie besser vergleichbar sind, als wenn die absoluten Werte ohne diese Normalisierung betrachtet würden. Wir führen diese Anpassung innerhalb von MQL5 über den folgenden Quellcode durch:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
      ...

      vector _means;
      _means.Init(_rows);
      _means.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  vector _row = _segments.Row(r);
         _means[r] = _row.Mean();
      }
      
      ...
   }
   ...
}

Die Matrix- und Vektordatentypen sind wiederum unverzichtbar, um nicht nur den Mittelwert zu finden, sondern auch die Normalisierung zu beschleunigen.

Kumulative Abweichung

Sobald wir über mittelwertbereinigte Segmente verfügen, müssen wir diese Abweichungen vom Mittelwert für jedes Segment aufsummieren, um die kumulativen Abweichungen jedes Segments zu erhalten. Dies kann als eine Form der Dimensionalitätsreduzierung angesehen werden, die als Grundlage für die bereichsskalierte Analyse dient. Wir führen dies in unserem Quellcode wie folgt durch:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      
      ...

      matrix _deviations;
      _deviations.Init(_rows, t);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _deviations[r][c] = _segments[r][c] - _means[r];
         }
      }
      vector _cumulations;
      _cumulations.Init(_rows);
      _cumulations.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _cumulations[r] += _deviations[r][c];
         }
      }

      ...

   }
   ...
}

Um es kurz zu machen: Für jeden „t“-Wert erhalten wir eine Gruppe von Segmenten, die unsere Datenstichprobe unterteilen. Von jeder Stichprobe wird der Mittelwert gebildet und von den Datenpunkten innerhalb des jeweiligen Segments subtrahiert. Diese Subtraktion dient als eine Form der Normalisierung, und sobald sie abgeschlossen ist, haben wir im Wesentlichen eine Matrix von Datenpunkten, bei der jede Zeile ein Segment aus der ursprünglichen Datenprobe ist. Um die Dimensionen der Segmente zu reduzieren, summieren wir die Abweichungen von ihren jeweiligen Mittelwerten, sodass ein mehrdimensionales Segment einen einzigen Wert ergibt. Dies bedeutet, dass wir nach der Durchführung der Abweichungskumulierungen auf der Matrix einen Vektor von Summen erhalten, der in unserem obigen Quelltext mit „_cumulations“ bezeichnet ist.

Skalierter Bereich und Log-Log-Diagramm

Sobald wir die kumulierten Abweichungen über alle Segmente in einem Vektor haben, besteht der nächste Schritt einfach darin, die Spanne zu finden, die die Differenz zwischen der größten Gesamtabweichung und der kleinsten Gesamtabweichung ist. Beachten Sie, dass wir bei der Aufzeichnung der Abweichungen der einzelnen Datenpunkte in den obigen Segmenten nicht den absoluten Wert aufgezeichnet haben. Wir haben einfach den Segmentwert minus den Mittelwert des Segments aufgezeichnet. Das bedeutet, dass sich unsere Kumulationen sehr leicht zu Null summieren. Dies ist in der Tat etwas, das einer Validierungsprüfung unterzogen werden sollte, bevor mit der Berechnung des Hurst-Exponenten fortgefahren wird, da es leicht zu einem ungültigen Ergebnis führen kann. Diese Validierung wird im beigefügten Quellcode nicht durchgeführt, und die Leser können diese Anpassungen selbst vornehmen. Diesen vorletzten Schritt führen wir im folgenden Code aus:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
       ...
       
       ...

      _points[t - 2][0] = log((_cumulations.Max() - _cumulations.Min()) / _std);
      _points[t - 2][1] = log(t);
   }
   LinearRegression(_points, H, C);
}

Wie aus dem obigen Quellcode ersichtlich, erhalten wir die kumulativen Bereiche und auch ihre natürlichen Logarithmen, da wir einen Exponenten (Potenz) suchen und Logarithmen helfen, Exponenten zu lösen. Aus der obigen Gleichung geht hervor, dass sich der Stichprobenumfang auf einer Seite der Gleichung befindet. Daher erhalten wir auch seinen natürlichen Logarithmus, und dieser dient als y-Diagramm, wobei das x-Diagramm den natürlichen Logarithmus des skalierten Bereichs geteilt durch die Standardabweichung der Datenstichprobe darstellt. Diese Punktpaare, x und y, sind für jede Segmentgröße eindeutig. Eine andere Segmentgröße innerhalb der Datenstichprobe stellt ein anderes Paar von x-y-Punkten dar, und je mehr davon vorhanden sind, desto repräsentativer ist unser Hurst-Exponent. Und wie bereits erwähnt, ist die Gesamtzahl der möglichen Paare von x-y-Punkten durch die Hälfte des Umfangs der Datenstichprobe begrenzt.

Unsere Matrix „_points“ stellt also die logarithmische Darstellung dar, die in der reskalierten Bereichsanalyse zu finden ist. Dieses Diagramm dient als Eingabe für die Berechnungen der linearen Regression.

Lineare Regression

Die lineare Regression wird mit einer von der „Hurst“-Methode getrennten Funktion durchgeführt. Der einfache Code ist unten angegeben:

//+------------------------------------------------------------------+
// Function to perform linear regression
//+------------------------------------------------------------------+
void CSignalHurst::LinearRegression(matrix &Points, double &Slope, double &Intercept)
{  double _sum_x = 0.0, _sum_y = 0.0, _sum_xy = 0.0, _sum_xx = 0.0;
   for (int r = 0; r < int(Points.Rows()); r++)
   {  _sum_x += Points[r][0];
      _sum_y += Points[r][1];
      _sum_xy += (Points[r][0] * Points[r][1]);
      _sum_xx += (Points[r][0] * Points[r][0]);
   }
   Slope = ((Points.Rows() * _sum_xy) - (_sum_x * _sum_y)) / ((Points.Rows() * _sum_xx) - (_sum_x * _sum_x));
   Intercept = (_sum_y - (Slope * _sum_x)) / Points.Rows();
}

Die Lineare Regression ist das Verfahren, mit dem wir die Schlüsselkoeffizienten in der Gleichung y = mx + c für eine gegebene Menge von Punkten ermitteln. Die angegebenen Koeffizienten definieren die Gleichung für die beste Anpassungslinie dieser eingegebenen x-y-Punkte. Diese Gleichung ist für uns wichtig, weil die Steigung dieser Best-Fit-Linie der Hurst-Exponent ist, während der y-Achsenabschnitt als Konstante C dient. Zu diesem Zweck nimmt die Funktion „LinearRegression“ als Referenzeingaben zwei „double“-Werte an, die als Platzhalter für den Hurst-Exponenten und die C-Konstante dienen, und gibt genau wie die Funktion „Hurst“ einen leeren Wert zurück.

In diesem Artikel ist unser primäres Ziel die Berechnung des Hurst-Exponenten, aber ein Teil der Ergebnisse, die wir aus diesem Prozess erhalten, ist, wie bereits erwähnt, die C-Konstante. Welchem Zweck dient diese C-Konstante dann? Sie ist eine Metrik für die Variabilität einer Datenstichprobe. Stellen Sie sich ein Szenario vor, in dem die Preisreihen von zwei Aktien denselben Hurst-Exponenten, aber unterschiedliche C-Konstanten haben, wobei eine einen C-Wert von 7 und die andere einen C-Wert von 21 hat.

Ein ähnlicher Exponentenwert deutet darauf hin, dass die beiden Aktien ähnliche „Persistenz“-Merkmale aufweisen, d. h. wenn der Hurst-Exponent für beide unter 0,5 liegt, neigen beide Aktien zu einer starken Mittelwertumkehr, während ein Exponent von mehr als 0,5 bedeutet, dass sie langfristig zu einem starken Trend neigen. Ihre unterschiedlichen C-Konstanten deuten jedoch trotz ähnlicher Kursentwicklung eindeutig auf unterschiedliche Risikoprofile hin. Dies liegt daran, dass die C-Konstante als Proxy für die Volatilität verstanden werden kann; die Aktien mit einer höheren C-Konstante würden im Gegensatz zu den Aktien mit einer geringeren C-Konstante größere Kursschwankungen über ihre Durchschnittswerte aufweisen. Dies könnte bedeuten, dass die Positionsgrößen für die beiden Aktien unterschiedlich sind, wenn alle anderen Faktoren konstant bleiben.

Kompilierung zu einer Signalklasse

Wir verwenden unsere generierten Hurst-Exponent-Werte, um die Kauf- und Verkaufs-Bedingungen des gehandelten Symbols innerhalb einer nutzerdefinierten Signalklasse zu bestimmen. Der Hurst-Exponent ist dazu gedacht, sehr langfristige Trends zu erfassen, weshalb er definitionsgemäß umso genauer ist, je weiter die Stichprobengröße gegen unendlich geht. Für praktische Zwecke müssen wir sie jedoch anhand einer bestimmten Größe der historischen Wertpapierkurse messen. Wir werden einen von zwei verschiedenen gleitenden Durchschnitten bei der Bewertung unserer Kauf-/Verkaufs-Bedingungen berücksichtigen, und daher wird die endgültige Größe der Historie, die zur Berechnung des Hurst-Exponenten verwendet wird, als Summe der beiden Zeiträume angenommen, die zur Berechnung dieser beiden Durchschnitte verwendet werden.

Dies ist möglicherweise nicht ausreichend, denn wie bereits erwähnt, ist der Hurst-Exponent per Definition umso zuverlässiger, je länger der Zeitraum der Datenerhebung ist; daher kann der Leser bei Bedarf Änderungen vornehmen, um eine für seine Perspektive repräsentativere Größe der Vergangenheit zu erhalten. Wie immer ist der vollständige Quellcode beigefügt. Für jede der Bedingungsfunktionen (Kauf und Verkauf) beginnen wir also damit, die Schlusskurse in einen Vektor zu kopieren, der der Größe unserer Datenstichprobe entspricht. Der Umfang unserer Datenstichprobe ergibt sich aus der Summe der langen und kurzen Zeiträume.

Anschließend berechnen wir den Hurst-Exponenten, indem wir die Funktion „Hurst“ aufrufen, und werten den zurückgegebenen Wert aus, um festzustellen, wie er im Vergleich zu 0,5 ist. Variationen dieser Implementierung können vorgenommen werden, indem ein Schwellenwert über und unter dem Wert von 0,5 hinzugefügt wird, um die Einstiegs- oder Entscheidungspunkte einzugrenzen. Wenn unser Hurst-Wert über 0,5 liegt, dann ist Persistenz gegeben, und daher würden wir für die langfristige Bedingung schauen, ob wir über dem gleitenden Durchschnitt der langsamen Periode (langfristig) liegen. Wenn dies der Fall ist, könnte dies auf eine Kauf-Position hindeuten. Ebenso würden wir für die Verkaufs-Bedingung darauf achten, ob wir unter dem gleitenden Durchschnitt der langsamen Periode liegen, und falls ja, würde dies die Eröffnung einer Verkaufs-Position bedeuten.

Sollte der Hurst-Exponent unter 0,5 liegen, würde dies bedeuten, dass wir uns in einem „Rangeing“- oder „Mean Reverting“-Markt befinden. In diesem Fall würden wir den aktuellen Geldkurs mit dem gleitenden Durchschnitt der schnellen Periode vergleichen. Bei einer Kauf-Bedingung, wenn der Preis unter dem schnellen gleitenden Durchschnitt liegt, würde dies auf eine Kauf-Position hindeuten. Umgekehrt, liegt der Kurs in einer Verkaufs-Bedingung über dem schnellen gleitenden Durchschnitt, deutet dies auf die Eröffnung einer Verkaufs-Position hin. Die Umsetzung dieser beiden Bedingungen wird im Folgenden erläutert:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::LongCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::ShortCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}

Strategieprüfung & Berichte

Wir führen Tests auf dem 4-Stunden-Zeitrahmen für das Paar GBPCHF für das Jahr 2023 durch und erhalten die folgenden Ergebnisse:

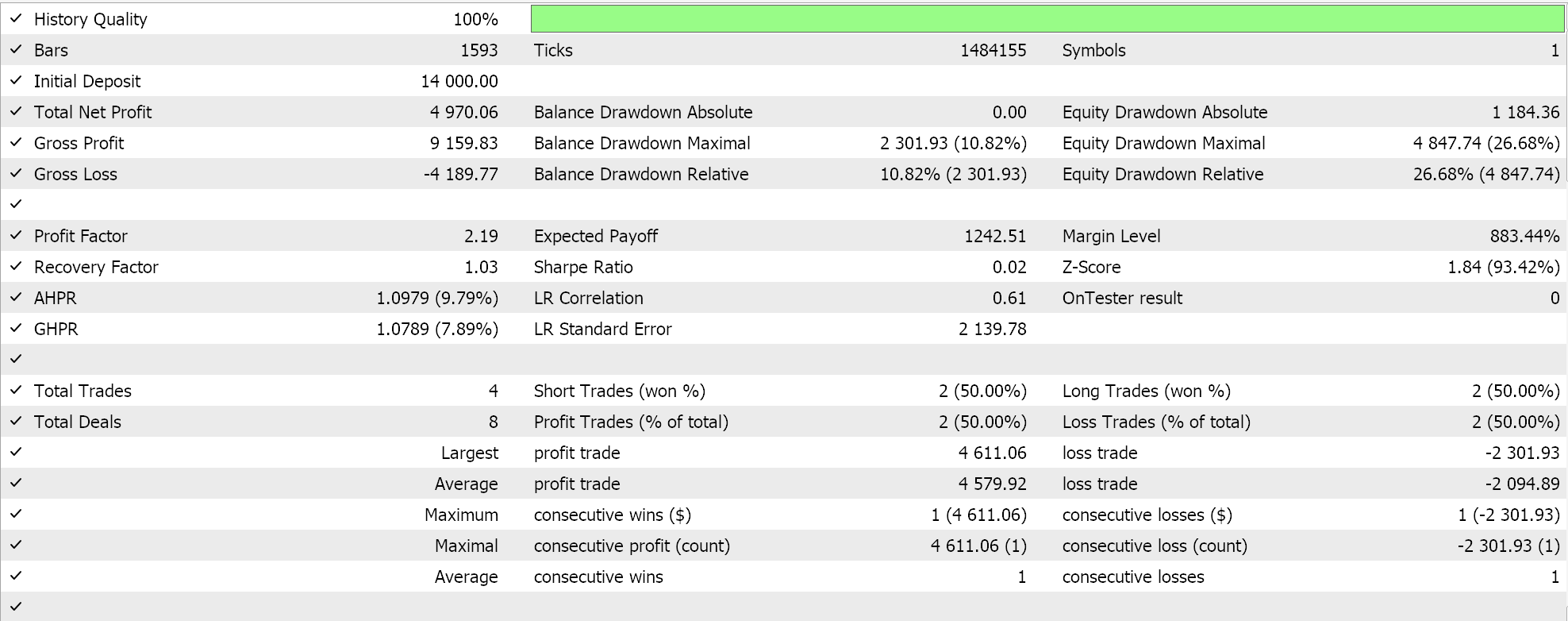
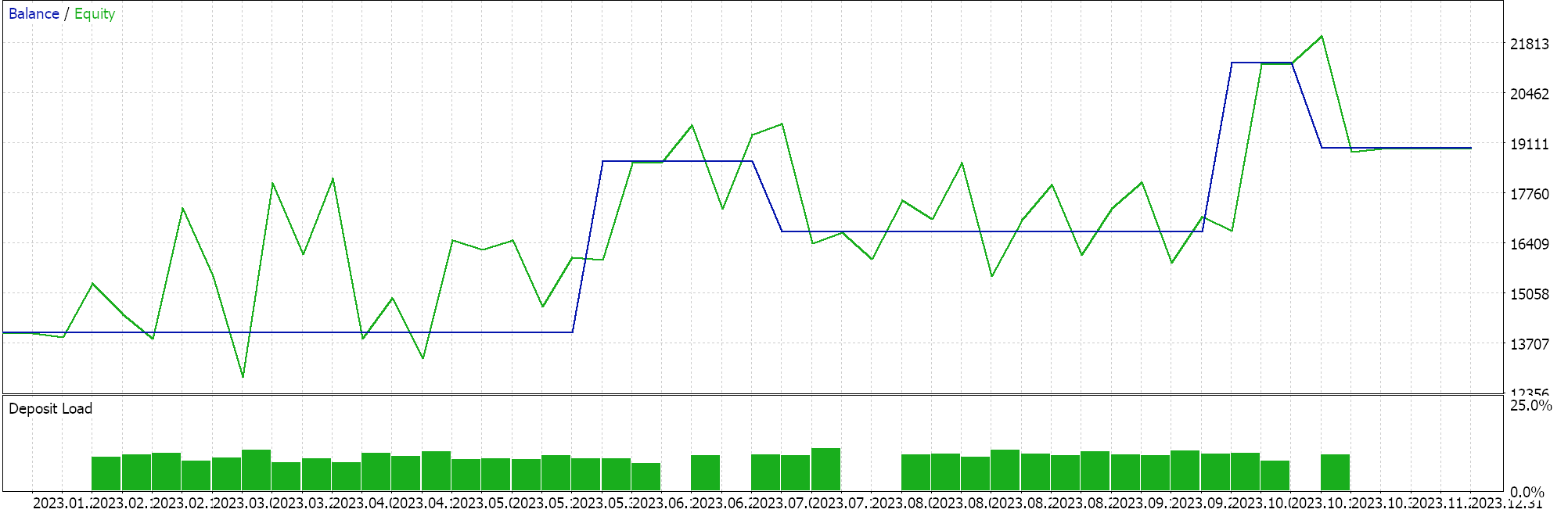
In unserem obigen Testlauf wurden auf dem 4-Stunden-Zeitrahmen nicht viele Handelsgeschäfte gemacht, was ein gutes Zeichen sein könnte, da es auf einen diskriminierenden Expert Advisor hinweist. Wie immer sind jedoch Tests über längere Zeiträume und insbesondere Vorwärtsgänge erforderlich, bevor eine Entscheidung über die Wirksamkeit des Experten getroffen werden kann.

Rohe Autokorrelation als Kontrolle

Der Hurst-Exponent behauptet, beurteilen zu können, ob eine Reihe persistente Merkmale aufweist (Werte über 0,5) oder antipersistent ist (Werte unter 0,5), indem er als Autokorrelationsmetrik fungiert. Aber angenommen, wir würden einfach die Korrelationen der Datenreihen messen, ohne uns die Mühe zu machen, diesen Exponenten zu berechnen, und die Ergebnisse unserer tatsächlichen Messungen der Korrelationen zur Bewertung der Marktbedingungen verwenden, wie anders würde unser Expert Advisor dann abschneiden?

Wir entwickeln eine solche nutzerdefinierte Signalklasse, die erwartungsgemäß weniger Funktionen hat und einfach zuerst nach positiven Korrelationen über den längeren (langsameren) Mittelungszeitraum sucht. Wenn es eine solche positive Korrelation gibt, wird der gleitende Durchschnitt über diesen langsameren Zeitraum verwendet, um trendfolgende Setups zu ermitteln, bei denen Kurse oberhalb dieses Durchschnitts nach oben und Kurse unterhalb nach unten gerichtet sind. Besteht jedoch über die längeren Zeiträume keine positive Korrelation, so wird bei der kürzeren (schnelleren) Mittelungsperiode eine negative Korrelation gesucht. In diesem Fall würden wir nach „Mean Reverting Setups“ Ausschau halten, bei denen ein Kurs unterhalb des sich schnellen Durchschnitts aufwärts deutet und ein Kurs oberhalb nach unten. Der Code für unsere Kauf- und Verkaufs-Bedingung lautet wie folgt:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAC::LongCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() < _ma.Mean())
               {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAC::ShortCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() > _ma.Mean())
               {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}

Wir haben fast ähnliche Testläufe für das gleiche Paar GBPCHF auf dem 4-Stunden-Zeitrahmen für das Jahr 2023 durchgeführt und unsere Ergebnisse aus den besten Läufen sind unten dargestellt:

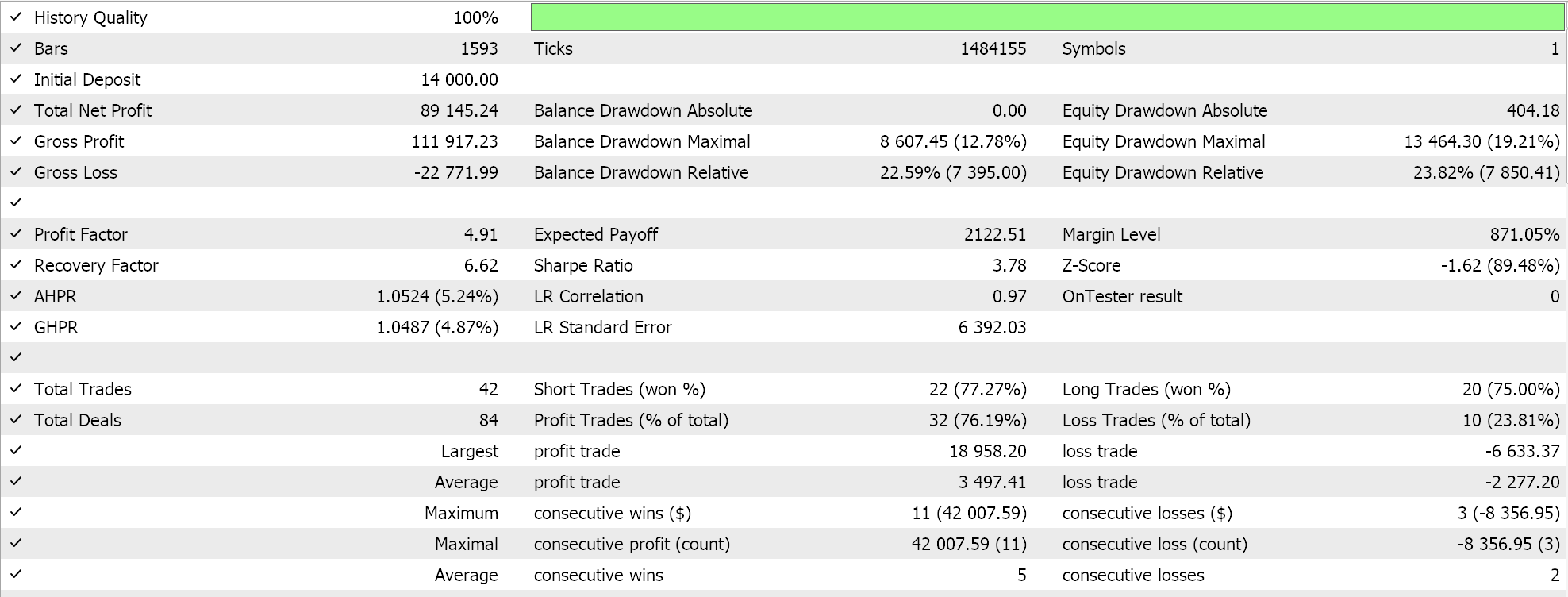
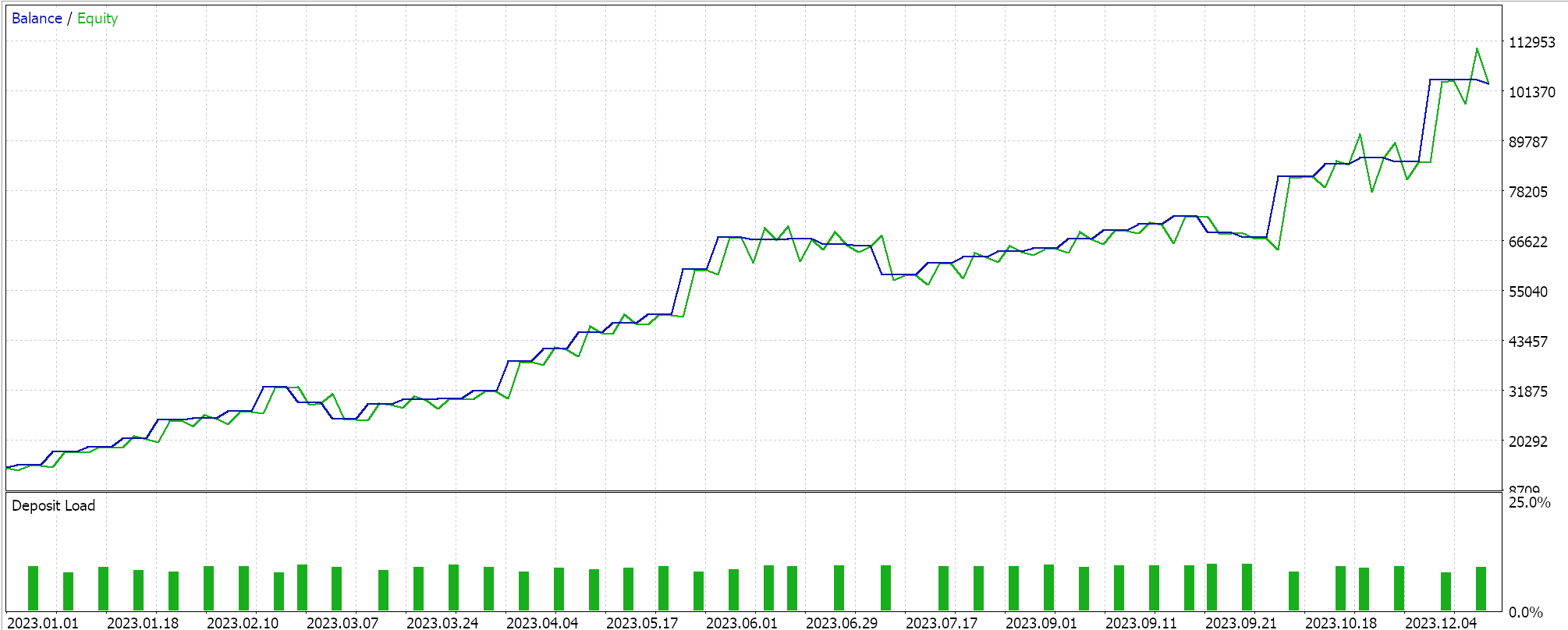
Zwischen diesem und dem Hurst-Exponent-Signal besteht ein deutlicher Leistungssprung oder -unterschied.

Schlussfolgerung

Der Hurst-Exponent wurde zu Beginn des letzten Jahrhunderts in erster Linie als Instrument zur Vorhersage der Ebbe und Flut des Nils entwickelt, sobald ein umfangreicher Datensatz mit Pegelständen des Wassers zur Verfügung stand. Seitdem wurde sie für eine Vielzahl von Anwendungen eingesetzt, darunter auch für die Analyse von Finanzzeitreihen. Für diesen Artikel haben wir seinen Zeitreihenexponenten mit gleitenden Durchschnitten gepaart, um bei der Erstellung einer nutzerdefinierten Signalklasse besser zwischen trendfolgenden Märkten und Märkten mit Mittelwertumkehr zu unterscheiden.

Auch wenn die ersten Testläufe, die wir oben durchgeführt haben, eindeutig ein gewisses Potenzial gezeigt haben, gibt es angesichts der relativen Leistung im Vergleich zu unserem rohen Autokorrelationssignal eindeutig noch Argumente für seine Verwendung. Er ist rechenintensiv, filtert seine Trades zu stark und seine besten Läufe weisen einen zu hohen Drawdown auf, was angesichts des relativ kleinen Testfensters, das für diese Läufe verwendet wird, bedenklich ist. Wie immer könnten unabhängige Testläufe zu anderen und noch vielversprechenderen Ergebnissen führen, und der Leser ist herzlich eingeladen, diese auszuprobieren. Die Zusammenstellung und Kompilierung des beigefügten Quellcodes zu einem Expert Advisor folgt den Richtlinien, die hier und hier dargestellt sind. Es wird empfohlen, dass diese weiteren Tests mit Real-Tick-Daten des Brokers durchgeführt werden und sich über eine gesunde Anzahl von Jahren erstrecken.