Die Basisklasse der Populationsalgorithmen als Rückgrat einer effizienten Optimierung

Inhalt

1. Einleitung. Aussichten und Möglichkeiten der Übernahme von Algorithmen aus der Basisklasse der Population
2. Implementierung der Basisklasse von Populationsalgorithmen
3. Code der abgeleiteten Algorithmen
4. Code der vereinheitlichten Testumgebung für alle Algorithmen
5. Hinzufügen gängiger und bekannter Testfunktionen
6. Aufbau von 3D-Testfunktionen
7. Schlussfolgerungen

1. Einführung, Aussichten und Möglichkeiten der Übernahme von Algorithmen aus der Basisklasse der Population

In der Welt der modernen Informatik und der künstlichen Intelligenz ist die Basisklasse, die dazu dient, Optimierungsalgorithmen in endgültige Softwarelösungen zu integrieren, ein Schlüsselelement, das den Entwicklern unendliche Horizonte an technischen Möglichkeiten eröffnet. Die Vererbung von dieser Basisklasse im Zusammenhang mit Populationsalgorithmen bietet nicht nur Komfort und Effizienz bei der Entwicklung neuer Optimierungsmethoden, sondern erweitert auch die Aussichten für die Entwicklung hybrider Algorithmen, die sich an eine Vielzahl von Problemen anpassen können.

Die Kombination von Optimierungsalgorithmen innerhalb einer Basisklasse eröffnet die Möglichkeit, innovative Lösungen zu schaffen, die die besten Eigenschaften verschiedener Methoden kombinieren. Die hybriden Algorithmen, die aus diesem Ansatz hervorgegangen sind, sind in der Lage, die Beschränkungen einzelner Methoden effektiv zu überwinden und bei der Lösung komplexer Optimierungsprobleme neue Höhen zu erreichen.

Darüber hinaus gewährleistet die Basisklasse für Populationsalgorithmen eine einfache Nutzung und Prüfung der entwickelten Algorithmen mit Standard-Testfunktionen. Dies ermöglicht Forschern und Entwicklern, die Effizienz neuer Optimierungsmethoden schnell zu bewerten, indem sie ihre Leistung mit bestehenden Lösungen vergleichen.

Stellen wir uns vor, die Welt der Optimierung und der Lösungssuche sei wie die erstaunliche kulinarische Welt, in der jede Optimierungsmethode eine einzigartige Zutat ist, die einem Gericht seinen eigenen Geschmack verleiht. Hybridisierung ist in diesem Zusammenhang wie die geschickte Kombination verschiedener Zutaten, um neue, schmackhaftere und interessantere Gerichte zu kreieren.

Es gibt eine breite Palette verschiedener Optimierungsmethoden - genetische Algorithmen, evolutionäre Strategien, Ameisenalgorithmen, Partikelschwarmoptimierung und viele andere. Jede von ihnen hat ihre eigenen Stärken und Fähigkeiten, aber auch ihre Grenzen.

Hier kommt die Hybridisierung ins Spiel! Sie können das Beste aus jeder Methode nehmen und sie wie ein erfahrener Koch zu einzigartigen Kombinationen kombinieren. Auf diese Weise können hybride Optimierungsmethoden die Stärken verschiedener Ansätze kombinieren, ihre Schwächen ausgleichen und effizientere und leistungsfähigere Werkzeuge für die Suche nach optimalen Lösungen schaffen.

Stellen Sie sich die Kombination eines genetischen Algorithmus mit der lokalen Suche wie eine perfekte Kombination aus scharfer Paprika und süßem Honig in einem Gericht vor, die ihm einen tiefen und reichen Geschmack verleiht. Ebenso ermöglicht die Hybridisierung von Populationsalgorithmen die Entwicklung innovativer Methoden, mit denen sich schnell und präzise optimale Lösungen in verschiedenen Bereichen finden lassen, seien es technische Probleme, Finanzanalysen oder künstliche Intelligenz.

Hybridisierung in der Optimierung bedeutet also nicht nur das Mischen von Methoden, sondern ist die Kunst, neue Ansätze zu schaffen, die das Potenzial jeder Methode maximieren und hervorragende Ergebnisse erzielen. Letztendlich können wir durch Hybridisierung effizientere, innovative und leistungsfähige Optimierungsmethoden entwickeln, die die komplexesten Probleme lösen und zu neuen Entdeckungen und Fortschritten in verschiedenen Bereichen führen können.

Darüber hinaus ermöglicht die einheitliche Basisklasse die Integration einzelner Elemente jedes Algorithmus in nutzerdefinierte Lösungen für die Entwicklung neuer, einzigartiger und leistungsstarker Optimierungsmethoden.

2. Implementierung der Basisklasse von Populationsalgorithmen

Im Zusammenhang mit dem Artikel über die Vererbung von einer Basisklasse für Populationsalgorithmen und die Schaffung hybrider Optimierungsmethoden können wir mehrere interessante Kombinationen als Beispiele betrachten:

• Genetischer Algorithmus mit erweiterter lokaler Suche. Bei dieser Kombination wird mit Hilfe eines genetischen Algorithmus global nach einer optimalen Lösung gesucht, und die gefundene Lösung wird mit Hilfe einer lokalen Suche in der Nachbarschaft verfeinert. Auf diese Weise lassen sich die Vorteile der globalen und der lokalen Suche kombinieren, was die Genauigkeit und die Geschwindigkeit der Konvergenz des Algorithmus erhöht.

• Evolutionsstrategie mit dem Ameisenalgorithmus. Hier kann die Evolutionsstrategie zur Änderung der Modellparameter verwendet werden, während der Ameisenalgorithmus dazu dient, den optimalen Pfad im Parameterraum zu finden. Diese Kombination kann bei der Optimierung komplexer Probleme, bei denen die optimale Kombination von Parametern gefunden werden muss, wirksam sein.

• Partikelschwarm mit genetischer Programmierung. In dieser Kombination können die Schwarmteilchen zur Erkundung des Lösungsraums und die genetische Programmierung zur Entwicklung von Programmstrukturen verwendet werden, die das Optimierungsproblem lösen. Dies ermöglicht eine effiziente Erkundung sowohl des Parameterraums als auch der Lösungsstrukturen.

• Simulated Annealing Suche mit genetischem Algorithmus. In diesem Fall kann das simulierte Abkühlen (simulated annealing) verwendet werden, um den Lösungsraum unter Berücksichtigung des Temperaturregimes zu erkunden, und ein genetischer Algorithmus kann verwendet werden, um optimale Lösungen in einem bestimmten Raum zu finden. Diese Kombination kann eine tiefere Erkundung des Lösungsraums ermöglichen und die Konvergenz des Algorithmus verbessern.

Bei der Nutzung der Fähigkeiten von Populationsalgorithmen, die in einer einzigen Basisklasse zusammengefasst sind, können wir auch die folgenden Richtungen in Betracht ziehen:

• Kombinierte metaheuristische Methode. Bei dieser Methode können verschiedene metaheuristische Algorithmen wie genetische Algorithmen, Ameisenalgorithmen, Partikelschwarm-Optimierungsalgorithmen, Simulated Annealing usw. kombiniert werden. Diese Algorithmen können parallel oder sequentiell arbeiten, Informationen austauschen und ihre Stärken kombinieren, um die optimale Lösung effizienter zu finden.

• Hybride Methode mit adaptiver Steuerung der Suchstrategien. Bei diesem Ansatz können adaptive Kontrollmechanismen eingesetzt werden, um verschiedene Optimierungsstrategien in Abhängigkeit von den Problemeigenschaften dynamisch zu kombinieren. So können wir beispielsweise die Gewichte oder Parameter der einzelnen Methoden je nach ihrer Leistung in der aktuellen Optimierungsphase ändern.

• Hybride Methode mit künstlichen neuronalen Netzen. Bei diesem Ansatz können künstliche neuronale Netze zur adaptiven Steuerung der Parameter und Optimierungsstrategien von Populationsalgorithmen eingesetzt werden. Neuronale Netze können im laufenden Betrieb lernen, sich an Veränderungen im Suchraum anpassen und optimale Parameter für jede Optimierungsmethode vorschlagen.

• Gemeinsame Optimierung und die Methode des Verstärkungslernens. Mit diesem Ansatz können Populationsalgorithmen mit Techniken des Verstärkungslernens (reinforcement learning) kombiniert werden, um ein hybrides System zu schaffen, das komplexe Lösungsräume effizient erkunden und optimieren kann. Agenten für das Verstärkungslernen können aus den Ergebnissen von Populationsalgorithmen lernen und umgekehrt, wodurch Wechselwirkungen zwischen verschiedenen Optimierungsmethoden entstehen.

Die unterschiedliche Anzahl von externen Parametern in den einzelnen Optimierungsalgorithmen kann zu Problemen bei der Vererbung und einheitlichen Anwendung führen. Um dieses Problem zu lösen, wurde auf der Grundlage der Ergebnisse umfangreicher Tests beschlossen, die externen Parameter der Standardalgorithmen im Konstruktor anzugeben. Gleichzeitig ist es möglich, diese Parameter vor der Initialisierung der Algorithmen zu ändern. Das Objekt eines jeden Algorithmus stellt also die endgültige Lösung dar, die zur Verwendung bereit ist. Früher waren Algorithmen und ihre Parameter getrennte Einheiten.

Beginnen wir also mit den Parametern des Algorithmus. Es ist zweckmäßig, jeden Parameter mit Hilfe der Struktur S_AlgoParam zu beschreiben, die den Parameternamen und den Wert enthält. Dementsprechend wird das Array von Objekten dieser Struktur eine Reihe von externen Parametern der Algorithmen darstellen.

struct S_AlgoParam
{
    double val;
    string name;
};

Jeder Optimierungsalgorithmus hat einen Suchagenten - eine elementare Einheit und ein unverzichtbarer Teilnehmer an der Suchstrategie - eine Firefly (Glühwürmchen) im Firefly-Algorithmus, eine fleißige Biene im Bienenalgorithmus, eine fleißige Ameise im Ameisenalgorithmus usw. Sie sind einzigartige Künstler im Optimierungslabyrinth, die die Brillanz der Kunst des Suchens und Entdeckens optimaler Wege zum Erfolg offenbaren. Ihre Bemühungen und Bestrebungen verwandeln wie durch Zauberhand das Datenchaos in die Harmonie von Lösungen und erhellen den Weg zu neuen Horizonten der idealen Optimierung.

So stellt jeder Agent eine spezifische Lösung des Optimierungsproblems dar und hat zwei obligatorische Eigenschaften: Koordinaten im Suchraum (optimierte Parameter) und die Lösungsqualität (Fitnessfunktion). Um die Funktionalität und die Möglichkeiten zu erweitern und spezifische Eigenschaften von Algorithmen zu implementieren, werden wir den Agenten in Form der Klasse C_AO_Agent formalisieren, die wir anschließend vererben können.

class C_AO_Agent
{
  public:
  ~C_AO_Agent () { }

  double c []; //coordinates
  double f;    //fitness
};

Die meisten logischen Operationen in Optimierungsalgorithmen wiederholen sich und können separat als eine Reihe von Funktionen der Klasse C_AO_Utilities entworfen werden, deren Objekt wiederum sowohl in Algorithmusklassen als auch in Agenten verwendet werden kann.

Die Klasse C_AO_Utilities enthält die folgenden Methoden:

• Scale: Die Überladene Methode, die den „In“-Eingang vom Bereich [InMIN, InMAX] auf den Bereich [OutMIN, OutMAX] skaliert. Es ist auch möglich, eine umgekehrte Skalierung durchzuführen, wenn der Parameter „revers“ auf „true“ gesetzt wird.
• RNDfromCI: Erzeugt eine zufällige reelle Zahl innerhalb des angegebenen Bereichs [min, max].
• RNDintInRange: Erzeugt eine zufällige Ganzzahl innerhalb des angegebenen Bereichs [min, max].
• RNDbool: Erzeugt einen zufälligen booleschen Wert (true/false).
• RNDprobab: Erzeugt eine Zufallswahrscheinlichkeit (reelle Zahl zwischen 0 und 1).
• SeInDiSp: Berechnet den Wert unter Berücksichtigung des angegebenen „Step“ innerhalb des Bereichs [InMin, InMax].
• Die Methoden „DecimalToGray“, „IntegerToBinary“, „GrayToDecimal“, „BinaryToInteger“ und „GetMaxDecimalFromGray“: Konvertierungen zwischen Dezimalzahlen, Binärzahlen und Gray-Codes durchführen.
• Die Methoden „GaussDistribution“ und „PowerDistribution“: Sie führen die Berechnungen für die Normalverteilung bzw. die Potenzverteilung durch.
• Methode „Sorting“ (Schablonenmethode): Sortiert das Array „p“ vom Typ „T“ in absteigender Reihenfolge.
• Struktur „S_Roulette“: Enthält die Felder „start“ und „end“ zur Darstellung des Bereichs.
• Die Methoden „PreCalcRoulette“ und „SpinRoulette“: „PreCalcRoulette“ berechnet Bereiche für Objekte vom Typ „T“ und speichert sie im Array „roulette“. „SpinRoulette“ führt die Drehung des Roulettes auf der Grundlage der Populationsgröße „aPopSize“ durch.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_Utilities
{
  public: //--------------------------------------------------------------------
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  double RNDfromCI             (double min, double max);
  int    RNDintInRange         (int min, int max);
  bool   RNDbool               ();
  double RNDprobab             ();
  double SeInDiSp              (double In, double InMin, double InMax, double Step);
  void   DecimalToGray         (ulong decimalNumber, char &array []);
  void   IntegerToBinary       (ulong number, char &array []);
  ulong  GrayToDecimal         (const char &grayCode [], int startInd, int endInd);
  ulong  BinaryToInteger       (const char &binaryStr [], const int startInd, const int endInd);
  ulong  GetMaxDecimalFromGray (int digitsInGrayCode);
  double GaussDistribution     (const double In, const double outMin, const double outMax, const double sigma);
  double PowerDistribution     (const double In, const double outMin, const double outMax, const double p);

  //----------------------------------------------------------------------------
  template<typename T>
  void Sorting (T &p [], T &pTemp [], int size)
  {
    int    cnt = 1;
    int    t0  = 0;
    double t1  = 0.0;
    int    ind [];
    double val [];

    ArrayResize (ind, size);
    ArrayResize (val, size);

    for (int i = 0; i < size; i++)
    {
      ind [i] = i;
      val [i] = p [i].f;
    }

    while (cnt > 0)
    {
      cnt = 0;
      for (int i = 0; i < size - 1; i++)
      {
        if (val [i] < val [i + 1])
        {
          t0 = ind [i + 1];
          t1 = val [i + 1];
          ind [i + 1] = ind [i];
          val [i + 1] = val [i];
          ind [i] = t0;
          val [i] = t1;
          cnt++;
        }
      }
    }

    for (int u = 0; u < size; u++) pTemp [u] = p [ind [u]];
    for (int u = 0; u < size; u++) p [u] = pTemp [u];
  }

  //----------------------------------------------------------------------------
  struct S_Roulette
  {
      double start;
      double end;
  };
  S_Roulette roulette [];

  template<typename T>
  void PreCalcRoulette (T &agents [])
  {
    int aPopSize = ArraySize (agents);
    roulette [0].start = agents [0].f;
    roulette [0].end   = roulette [0].start + (agents [0].f - agents [aPopSize - 1].f);

    for (int s = 1; s < aPopSize; s++)
    {
      if (s != aPopSize - 1)
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s].f - agents [aPopSize - 1].f);
      }
      else
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s - 1].f - agents [s].f) * 0.1;
      }
    }
  }
  int  SpinRoulette (int aPopSize);
};
//——————————————————————————————————————————————————————————————————————————————

Da stochastische Optimierungsalgorithmen auf der Generierung von Zufallszahlen beruhen, kann dieser Vorgang hunderte oder sogar tausende Male durchgeführt werden, um jede Lösung zu erhalten. Daher ist es ratsam, die Erzeugung von Zufallszahlen zu optimieren, indem bestimmte Aufgaben getrennt werden. Da der Standardgenerator ganze Zahlen erzeugt, besteht die Möglichkeit, diesen Prozess zu beschleunigen.

Wir haben bereits die Methode „RNDfromCI“ kennen gelernt, die eine zufällige reelle Zahl innerhalb des angegebenen Bereichs [„min“, „max“] erzeugt:

double C_AO_Utilities ::RNDfromCI (double min, double max)
{
  if (min == max) return min;
  if (min > max)
  {
    double temp = min;
    min = max;
    max = temp;
  }
  return min + ((max - min) * rand () / 32767.0);
}

Oft ist es notwendig, eine zufällige ganze Zahl zu generieren, z. B. um einen Agenten in einer Population zufällig auszuwählen. Die Methode „RNDintInRange“ wird uns dabei helfen.

int C_AO_Utilities :: RNDintInRange (int min, int max)
{
  if (min == max) return min;
  if (min > max)
  {
    int temp = min;
    min = max;
    max = temp;
  }
  return min + rand () % (max - min + 1);
}

Eine boolesche Zufallsvariable lässt sich mit der Methode „RNDbool“ im Vergleich zu den beiden obigen Methoden sehr schnell ermitteln, weshalb es sinnvoll ist, die Zufallsvariablen je nach Aufgabe in separate Methoden aufzuteilen.

bool C_AO_Utilities :: RNDbool ()
{
  return rand () % 2 == 0;
}

Es gibt noch eine weitere Methode „RNDprobab“, mit der wir eine reelle Zufallszahl im Bereich [0.0, 1.0] erhalten können. Sie eignet sich hervorragend für die Ermittlung der Wahrscheinlichkeit bestimmter Operationen, z. B. der Wahrscheinlichkeit einer Kreuzung im genetischen Algorithmus. Solche Operationen werden auch recht häufig durchgeführt.

double C_AO_Utilities :: RNDprobab ()
{
  return (double)rand () / 32767;
}

Betrachten wir nun die Basisklasse „C_AO“ der Populationsoptimierungsalgorithmen. Diese Klasse beschreibt die erforderlichen Attribute aller Populationsalgorithmen, wie z. B.:

• Methoden und Eigenschaften der Klasse „C_AO“:

- SetParams: virtuelle Methode zur Einstellung der Algorithmusparameter.
- Init: virtuelle Methode zur Initialisierung des Algorithmus unter Angabe des minimalen und maximalen Suchbereichs, der Schrittweiten und der Anzahl der Epochen.
- Moving: virtuelle Methode zur Ausführung eines Algorithmusschrittes.
- Revision: virtuelle Methode zur Durchführung einer Revision des Algorithmus.
- GetName: Methode zum Abrufen des Algorithmusnamens.
- GetDesc: Methode zum Abrufen der Algorithmusbeschreibung.
- GetParams: Methode zum Abrufen von Algorithmusparametern als String.

• Geschützte Eigenschaften der Klasse „C_AO“:

- ao_name: Name des Algorithmus.
- ao_desc: Algorithmusbeschreibung.
- rangeMin, rangeMax, rangeStep: Arrays zum Speichern des minimalen und maximalen Suchbereichs sowie des Schrittweiten.
- coords: Anzahl der Koordinaten.
- popSize: Größe der Population.
- Revision: Revisionsflag.
- u: Objekt der Klasse „C_AO_Utilities“ zur Ausführung von Hilfsfunktionen.

#include "#C_AO_Utilities.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO
{
  public: //--------------------------------------------------------------------
  C_AO () { }
  ~C_AO () { for (int i = 0; i < ArraySize (a); i++) delete a [i];}

  double      cB     []; //best coordinates
  double      fB;        //FF of the best coordinates
  C_AO_Agent *a      []; //agents
  S_AlgoParam params []; //algorithm parameters

  virtual void SetParams () { }
  virtual bool Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
  { return false;}

  virtual void Moving   () { }
  virtual void Revision () { }

  string GetName   () { return ao_name;}
  string GetDesc   () { return ao_desc;}
  string GetParams ()
  {
    string str = "";
    for (int i = 0; i < ArraySize (params); i++)
    {
      str += (string)params [i].val + "|";
    }
    return str;
  }


  protected: //-----------------------------------------------------------------
  string ao_name;      //ao name;
  string ao_desc;      //ao description

  double rangeMin  []; //minimum search range
  double rangeMax  []; //maximum search range
  double rangeStep []; //step search

  int    coords;       //coordinates number
  int    popSize;      //population size
  bool   revision;

  C_AO_Utilities u;     //auxiliary functions

  bool StandardInit (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP []) //step search
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator
    fB       = -DBL_MAX;
    revision = false;

    coords  = ArraySize (rangeMinP);
    if (coords == 0 || coords != ArraySize (rangeMaxP) || coords != ArraySize (rangeStepP)) return false;

    ArrayResize (rangeMin,  coords);
    ArrayResize (rangeMax,  coords);
    ArrayResize (rangeStep, coords);
    ArrayResize (cB,        coords);

    ArrayCopy (rangeMin,  rangeMinP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeMax,  rangeMaxP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeStep, rangeStepP, 0, 0, WHOLE_ARRAY);

    return true;
  }
};
//——————————————————————————————————————————————————————————————————————————————

In derselben Datei befindet sich neben der Basisklasse auch die Enumeration „E_AO“, die die IDs der Optimierungsalgorithmen enthält, sowie die Funktion SelectAO, mit der wir eine Instanz des entsprechenden Algorithmus erstellen und seinen Zeiger erhalten können.

#include "AO_BGA_Binary_Genetic_Algorithm.mqh"
#include "AO_(P_O)ES_Evolution_Strategies.mqh"
#include "AO_DE_Differential_Evolution.mqh"
#include "AO_SDSm_Stochastic_Diffusion_Search.mqh"
#include "AO_ESG_Evolution_of_Social_Groups.mqh";

//——————————————————————————————————————————————————————————————————————————————
enum E_AO
{
  AO_BGA,
  AO_P_O_ES,
  AO_SDSm,
  AO_ESG,
  AO_DE,
  AO_NONE
};
C_AO *SelectAO (E_AO a)
{
  C_AO *ao;
  switch (a)
  {
    case  AO_BGA:
      ao = new C_AO_BGA (); return (GetPointer (ao));
    case  AO_P_O_ES:
      ao = new C_AO_P_O_ES (); return (GetPointer (ao));
    case  AO_SDSm:
      ao = new C_AO_SDSm (); return (GetPointer (ao));
    case  AO_ESG:
      ao = new C_AO_ESG (); return (GetPointer (ao));
    case  AO_DE:
      ao = new C_AO_DE (); return (GetPointer (ao));

    default:
      ao = NULL; return NULL;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Code der abgeleiteten Algorithmen

Betrachten wir den stochastischen Diffusionssuchalgorithmus (SDSm) als Beispiel für die Vererbung von der Basisklasse. Wir werden den „C_SDS_Agent“ dieses Algorithmus von der Basis „C_AO_Agent“ ableiten. Beachten Sie, dass die Initialisierungsmethode des Agenten die Koordinaten „c“ und die Fitness „f“ enthält, diese aber nicht in der Klasse „C_SDS_Agent“ deklariert sind. Dies ist sinnvoll, da diese Attribute für alle Optimierungsalgorithmus-Agenten erforderlich sind und vom Basisalgorithmus geerbt werden, sodass sie nicht erneut deklariert werden müssen.

//——————————————————————————————————————————————————————————————————————————————
class C_SDS_Agent : public C_AO_Agent
{
  public: //--------------------------------------------------------------------
  ~C_SDS_Agent () { }

  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double cPrev     []; //previous coordinates (dishes)
  double fPrev;        //previous fitness

  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Die Klasse „C_AO_SDSm“ des SDSm-Algorithmus ist von der Klasse „C_AO“ abgeleitet. Bei der Deklaration eines Klassenobjekts im Konstruktor werden die externen Parameter des Algorithmus initialisiert, die anschließend vom Nutzer nach Wunsch geändert werden können. Die Parameter werden in Form eines Arrays zur Verfügung stehen, und wir müssen uns keine Gedanken über die Kompatibilität mit der Testumgebung machen.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDSm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SDSm () { }
  C_AO_SDSm ()
  {
    ao_name = "SDSm";
    ao_desc = "Stochastic Diffusion Search";

    popSize    = 100; //population size

    restNumb   = 100;  //restaurants number
    probabRest = 0.05; //probability restaurant choosing

    ArrayResize (params, 3);

    params [0].name = "popSize";    params [0].val  = popSize;

    params [1].name = "restNumb";   params [1].val  = restNumb;
    params [2].name = "probabRest"; params [2].val  = probabRest;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;

    restNumb   = (int)params [1].val;
    probabRest = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    restNumb;          //restaurants number
  double probabRest;        //probability restaurant choosing

  C_SDS_Agent *agent []; //candidates

  private: //-------------------------------------------------------------------
  struct S_Riverbed //river bed
  {
      double coordOnSector []; //coordinate on the sector (number of cells: number of sectors on the coordinate, cell value: specific coordinate on the sector)
  };

  double restSpace [];      //restaurants space
  S_Riverbed    rb [];      //riverbed

  void Research  (const double  ko,
                  const int     raddr,
                  const double  restSpace,
                  const double  rangeMin,
                  const double  rangeStep,
                  const double  pitOld,
                  double       &pitNew);
};
//——————————————————————————————————————————————————————————————————————————————

Als Nächstes sollten wir insbesondere die Initialisierungsmethode „Init“ der Klasse „C_AO_SDSm“ besprechen. Die Methode geht folgendermaßen vor:

1. Gleich zu Beginn müssen wir die Basisklassenmethode „StandardInit“ aufrufen und ihr „rangeMinP“, „rangeMaxP“, „rangeStepP“ übergeben. Wenn die Methode „false“ zurückgibt, gibt die Funktion „Init“ ebenfalls „false“ zurück, was bedeutet, dass die Initialisierung des Algorithmus fehlgeschlagen ist.
2. Entfernen von Agenten mit „delete“. Dies ist bei der Wiederverwendung eines Algorithmusobjekts erforderlich.
3. Dann ändern wir die Größe der Arrays „agent“ des SDSm-Algorithmus und „a“ der Basisklasse auf „popSize“ und führen einen Typenanpassung (cast) durch.
4. Als Nächstes führen wir Maßnahmen durch, die dem in dem Artikel über SDSm beschriebenen Algorithmus ähneln.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SDSm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  for (int i = 0; i < ArraySize (agent); i++) delete agent [i];

  ArrayResize (agent, popSize);
  ArrayResize (a,     popSize);

  for (int i = 0; i < popSize; i++)
  {
    a     [i] = new C_SDS_Agent ();
    agent [i] = (C_SDS_Agent *)a [i];

    agent [i].Init (coords);
  }

  ArrayResize (restSpace, coords);
  ArrayResize (rb,        coords);
  for (int i = 0; i < coords; i++)
  {
    ArrayResize     (rb [i].coordOnSector, restNumb);
    ArrayInitialize (rb [i].coordOnSector, -DBL_MAX);
  }

  for (int i = 0; i < coords; i++)
  {
    restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

4. Code der vereinheitlichten Testumgebung für alle Algorithmen

Obwohl im Moment keine Notwendigkeit besteht, Testumgebungen zu „vervielfältigen“, werden wir dennoch alle Funktionen der Testumgebung in die Klasse „C_TestStand“ übertragen. So können wir die Funktionalität der Testumgebung bequem kapseln. Da sich bei den Funktionen der Testumgebung keine wesentlichen Änderungen ergeben haben, werde ich sie nicht im Einzelnen beschreiben. Werfen wir einfach einen Blick auf den aktuellen Stand der Dinge:

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>

//——————————————————————————————————————————————————————————————————————————————
class C_TestStand
{
  public: void Init (int width, int height)
  {
    W = width;  //750;
    H = height; //375;

    WscrFunc = H - 2;
    HscrFunc = H - 2;

    //creating a table ---------------------------------------------------------
    string canvasName = "AO_Test_Func_Canvas";

    if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
    {
      Print ("Error creating Canvas: ", GetLastError ());
      return;
    }

    ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
    ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

    ArrayResize (FunctScrin, HscrFunc);

    for (int i = 0; i < HscrFunc; i++) ArrayResize (FunctScrin [i].clr, HscrFunc);

  }

  struct S_CLR
  {
    color clr [];
  };

  //----------------------------------------------------------------------------
  public: void CanvasErase ()
  {
    Canvas.Erase (XRGB (0, 0, 0));
    Canvas.FillRectangle (1,     1, H - 2, H - 2, COLOR2RGB (clrWhite));
    Canvas.FillRectangle (H + 1, 1, W - 2, H - 2, COLOR2RGB (clrWhite));
  }

  //----------------------------------------------------------------------------
  public: void MaxMinDr (C_Function & f)
  {
    //draw Max global-------------------------------------------------------------
    int x = (int)Scale(f.GetMaxFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 1, W/2 - 1, false);
    int y = (int)Scale(f.GetMaxFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 1, H   - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 14, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 15, COLOR2RGB(clrBlack));

    //draw Min global-------------------------------------------------------------
    x = (int)Scale(f.GetMinFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 0, W/2 - 1, false);
    y = (int)Scale(f.GetMinFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 0, H - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
  }

  //----------------------------------------------------------------------------
  public: void PointDr (double &args [], C_Function & f, int shiftX, int shiftY, int count, bool main)
  {
    double x = 0.0;
    double y = 0.0;

    double xAve = 0.0;
    double yAve = 0.0;

    int width  = 0;
    int height = 0;

    color clrF = clrNONE;

    for(int i = 0; i < count; i++)
    {
      xAve += args [i * 2];
      yAve += args [i * 2 + 1];

      x = args [i * 2];
      y = args [i * 2 + 1];

      width  = (int)Scale(x, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
      height = (int)Scale(y, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

      clrF = DoubleToColor(i, 0, count - 1, 0, 270);
      Canvas.FillCircle(width + shiftX, height + shiftY, 1, COLOR2RGB(clrF));
    }

    xAve /=(double)count;
    yAve /=(double)count;

    width  = (int)Scale(xAve, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
    height = (int)Scale(yAve, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

    if(!main)
    {
      Canvas.FillCircle(width + shiftX, height + shiftY, 3, COLOR2RGB(clrBlack));
      Canvas.FillCircle(width + shiftX, height + shiftY, 2, COLOR2RGB(clrWhite));
    }
    else
    {
      Canvas.Circle (width + shiftX, height + shiftY, 5, COLOR2RGB (clrBlack));
      Canvas.Circle (width + shiftX, height + shiftY, 6, COLOR2RGB (clrBlack));
    }
  }

  //----------------------------------------------------------------------------
  public: void SendGraphToCanvas ()
  {
    for (int w = 0; w < HscrFunc; w++)
    {
      for (int h = 0; h < HscrFunc; h++)
      {
        Canvas.PixelSet (w + 1, h + 1, COLOR2RGB (FunctScrin [w].clr [h]));
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void DrawFunctionGraph (C_Function & f)
  {
    double ar [2];
    double fV;

    for (int w = 0; w < HscrFunc; w++)
    {
      ar [0] = Scale (w, 0, H, f.GetMinRangeX (), f.GetMaxRangeX (), false);
      for (int h = 0; h < HscrFunc; h++)
      {
        ar [1] = Scale (h, 0, H, f.GetMinRangeY (), f.GetMaxRangeY (), true);
        fV = f.CalcFunc (ar, 1);
        FunctScrin [w].clr [h] = DoubleToColor (fV, f.GetMinFunValue (), f.GetMaxFunValue (), 0, 270);
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void Update ()
  {
    Canvas.Update ();
  }

  //----------------------------------------------------------------------------
  //Scaling a number from a range to a specified range
  public: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
    else
    {
      if (Revers)
      {
        if (In < InMIN) return (OutMAX);
        if (In > InMAX) return (OutMIN);
        return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
      else
      {
        if (In < InMIN) return (OutMIN);
        if (In > InMAX) return (OutMAX);
        return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
    }
  }

  //----------------------------------------------------------------------------
  private: color DoubleToColor (const double In,    //input value
                                const double inMin, //minimum of input values
                                const double inMax, //maximum of input values
                                const int    loH,   //lower bound of HSL range values
                                const int    upH)   //upper bound of HSL range values
  {
    int h = (int) Scale (In, inMin, inMax, loH, upH, true);
    return HSLtoRGB (h, 1.0, 0.5);
  }

  //----------------------------------------------------------------------------
  private: color HSLtoRGB (const int    h, //0   ... 360
                           const double s, //0.0 ... 1.0
                           const double l) //0.0 ... 1.0
  {
    int r;
    int g;
    int b;
    if (s == 0.0)
    {
      r = g = b = (unsigned char)(l * 255);
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
    else
    {
      double v1, v2;
      double hue = (double) h / 360.0;
      v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
      v1 = 2.0 * l - v2;
      r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
      g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
      b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
  }

  //----------------------------------------------------------------------------
  private: double HueToRGB (double v1, double v2, double vH)
  {
    if (vH < 0) vH += 1;
    if (vH > 1) vH -= 1;
    if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
    if ((2 * vH) < 1) return v2;
    if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
    return v1;
  }

  //----------------------------------------------------------------------------
  public: int W; //monitor screen width
  public: int H; //monitor screen height

  private: int WscrFunc; //test function screen width
  private: int HscrFunc; //test function screen height

  public:  CCanvas Canvas;      //drawing table
  private: S_CLR FunctScrin []; //two-dimensional matrix of colors
};
//——————————————————————————————————————————————————————————————————————————————

Werfen wir nun einen Blick auf den Code der Testumgebung selbst. Bei der Betrachtung der Eingaben derTestumgebung wird deutlich, dass wir nun in der Lage sind, den Optimierungsalgorithmus und die Testfunktionen in den Einstellungen zu wählen. So können wir eindeutige Reihen von Testfunktionen erstellen, um den Algorithmus zu testen. Jetzt können wir Tests nur für glatte oder nur für diskrete Funktionen durchführen. Außerdem ist es jetzt möglich, jede beliebige Kombination von Testfunktionen zu wählen, die den Bedürfnissen des Nutzers am besten entspricht.

#include "PAO\#C_TestStandFunctions.mqh"
#include "PAO\#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
input string AOparam            = "----------------"; //AO parameters-----------
input E_AO   AOexactly_P        = AO_NONE;

input string TestStand_1        = "----------------"; //Test stand--------------
input double ArgumentStep_P     = 0.0;   //Argument Step

input string TestStand_2        = "----------------"; //------------------------
input int    Test1FuncRuns_P    = 5;     //Test #1: Number of functions in the test
input int    Test2FuncRuns_P    = 25;    //Test #2: Number of functions in the test
input int    Test3FuncRuns_P    = 500;   //Test #3: Number of functions in the test

input string TestStand_3        = "----------------"; //------------------------
input EFunc  Function1          = Hilly;
input EFunc  Function2          = Forest;
input EFunc  Function3          = Megacity;

input string TestStand_4        = "----------------"; //------------------------
input int    NumbTestFuncRuns_P = 10000; //Number of test function runs
input int    NumberRepetTest_P  = 10;    //Test repets number

input string TestStand_5        = "----------------"; //------------------------
input bool   Video_P            = true;  //Show video
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_AO *AO = SelectAO (AOexactly_P);
  if (AO == NULL)
  {
    Print ("AO is not selected...");
    return;
  }

  Print (AO.GetName (), "|", AO.GetDesc (), "|", AO.GetParams ());

  //============================================================================
  C_TestStand ST; //stand
  ST.Init (750, 375);

  double allScore = 0.0;
  double allTests = 0.0;

  C_Function *F1 = SelectFunction (Function1);
  C_Function *F2 = SelectFunction (Function2);
  C_Function *F3 = SelectFunction (Function3);

  if (F1 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();

    FuncTests (AO, ST, F1, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F1, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F1, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F1;
  }

  if (F2 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F2, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F2, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F2, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F2;
  }

  if (F3 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F3, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F3, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F3, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F3;
  }

  Print ("=============================");
  if (allTests > 0.0) Print ("All score: ", DoubleToString (allScore, 5), " (", DoubleToString (allScore * 100 / allTests, 2), "%)");
  delete AO;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_AO          &ao,
                C_TestStand   &st,
                C_Function    &f,
                const  int     funcCount,
                const  color   clrConv,
                double        &allScore,
                double        &allTests)
{
  if (funcCount <= 0) return;

  allTests++;

  if (Video_P)
  {
    st.DrawFunctionGraph (f);
    st.SendGraphToCanvas ();
    st.MaxMinDr          (f);
    st.Update            ();
  }

  int    xConv      = 0.0;
  int    yConv      = 0.0;
  double aveResult  = 0.0;
  int    params     = funcCount * 2;
  int    epochCount = NumbTestFuncRuns_P / (int)ao.params [0].val;

  //----------------------------------------------------------------------------
  double rangeMin  [], rangeMax  [], rangeStep [];
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeMax,  params);
  ArrayResize (rangeStep, params);

  for (int i = 0; i < funcCount; i++)
  {
    rangeMax  [i * 2] = f.GetMaxRangeX ();
    rangeMin  [i * 2] = f.GetMinRangeX ();
    rangeStep [i * 2] = ArgumentStep_P;

    rangeMax  [i * 2 + 1] = f.GetMaxRangeY ();
    rangeMin  [i * 2 + 1] = f.GetMinRangeY ();
    rangeStep [i * 2 + 1] = ArgumentStep_P;
  }

  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    //--------------------------------------------------------------------------
    if (!ao.Init (rangeMin, rangeMax, rangeStep)) break;

    // Optimization-------------------------------------------------------------
    for (int epochCNT = 1; epochCNT <= epochCount && !IsStopped (); epochCNT++)
    {
      ao.Moving ();

      for (int set = 0; set < ArraySize (ao.a); set++)
      {
        ao.a [set].f = f.CalcFunc (ao.a [set].c, funcCount);
      }

      ao.Revision  ();

      if (Video_P)
      {
        //drawing a population--------------------------------------------------
        st.SendGraphToCanvas  ();

        for (int i = 0; i < ArraySize (ao.a); i++)
        {
          st.PointDr (ao.a [i].c, f, 1, 1, funcCount, false);
        }
        st.PointDr (ao.cB, f, 1, 1, funcCount, true);

        st.MaxMinDr (f);

        //drawing a convergence graph---------------------------------------------
        xConv = (int)st.Scale (epochCNT, 1, epochCount, st.H + 2, st.W - 3, false);
        yConv = (int)st.Scale (ao.fB, f.GetMinFunValue (), f.GetMaxFunValue (), 2, st.H - 2, true);
        st.Canvas.FillCircle (xConv, yConv, 1, COLOR2RGB (clrConv));

        st.Update ();
      }
    }

    aveResult += ao.fB;
  }

  aveResult /= (double)NumberRepetTest_P;

  double score = aveResult;

  Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", NumbTestFuncRuns_P, "; result: ", aveResult);
  allScore += score;
}
//——————————————————————————————————————————————————————————————————————————————

5. Fügen wir die gängigen Testfunktionen hinzu

Manchmal werde ich gefragt, warum ich solche weithin bekannten und aktiv genutzten Optimierungsalgorithmen nicht in die Forschungs- und Entwicklungsreihe der Testfunktionen aufgenommen habe. Der Grund liegt darin, dass sie nach meiner Klassifizierung alle in die Kategorie der „einfachen“ Testfunktionen fallen. Mehr als die Hälfte ihrer Oberflächen sind in der Nähe der globalen Extremwerte konzentriert, was sie zu „vorhersehbar“ für angemessene Tests macht. Trotzdem sind die Menschen daran gewöhnt, ihnen zu vertrauen, und neigen dazu, ihre Algorithmen an solchen Funktionen zu testen. Deshalb habe ich beschlossen, Ackley, Goldstein-Price und Shaffer #2 in das Set aufzunehmen. Dies wird dazu beitragen, die Auswahl der Testfunktionen für die Nutzer auszubalancieren und umfassendere und zuverlässigere Tests von Optimierungsalgorithmen bereitzustellen, die den Forschern neue Horizonte eröffnen und zu einem besseren Verständnis ihrer Effizienz beitragen.

Ackley-Gleichung:

f(x, y) = -(-20 * exp(-0.2 * sqrt(0.5 * (x^2 + y^2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20)

wobei:
- x, y - Funktionseingänge,
- e - Eulersche Zahl (ungefähr 2,71828),
- π - Zahl Pi (ungefähr 3,14159).

Funktionscode:

double Core (double x, double y)
{
  double res1 = -20.0 * MathExp (-0.2 * MathSqrt (0.5 * (x * x + y * y)));
  double res2 = -MathExp (0.5 * (MathCos (2.0 * M_PI * x) + MathCos (2.0 * M_PI * y)));
  double res3 = -(res1 + res2 + M_E + 20.0);

  return Scale (res3, -14.302667500265278, 0.0, 0.0, 1.0);
}

Goldstein-Price-Gleichung:

f(x, y) = -([1 + (x + y + 1)^2 * (19 - 14x + 3x^2 - 14y + 6xy + 3y^2)] * [30 + (2x - 3y)^2 * (18 - 32x + 12x^2 + 48y - 36xy + 27y^2)])

Funktionscode:

double Core (double x, double y)
{
  double part1 = 1 + MathPow ((x + y + 1), 2) * (19 - 14 * x + 3 * x * x - 14 * y + 6 * x * y + 3 * y * y);
  double part2 = 30 + MathPow ((2 * x - 3 * y), 2) * (18 - 32 * x + 12 * x * x + 48 * y - 36 * x * y + 27 * y * y);

  return Scale (-part1 * part2, -1015690.2717980597, -3.0, 0.0, 1.0);
}

Shaffer #2 Gleichung:

f(x, y) = -(0.5 + ((sin(x^2 - y^2)^2 - 0.5) / (1 + 0.001 * (x^2 + y^2))^2))

Funktionscode:

double Core (double x, double y)
{
  double numerator   = MathPow (MathSin (x * x - y * y), 2) - 0.5;
  double denominator = MathPow (1 + 0.001 * (x * x + y * y), 2);
    
  return Scale (-(0.5 + numerator / denominator), -0.9984331449753265, 0, 0, 1.0);
}

Anmerkung: Die Werte der Testfunktionen sind auf [0,0, 1,0] normiert.

6. Aufbau von 3D-Testfunktionen

Manchmal ist es notwendig, nicht nur von Zahlen und Gleichungen zu abstrahieren, sondern sie visuell zu sehen, um ein tieferes Verständnis der Testfunktionen und ihrer Entlastung zu erlangen. Also beschloss ich, die Möglichkeit zu nutzen, 3D-Szenen mit DirectX in der MetaTrader 5-Plattform zu erstellen. Ich habe mich von der Datei „...\MQL5\Experts\Examples\Math 3D Morpher\Math 3D Morpher.mq5“ inspirieren lassen, die von den Entwicklern in der Standarddistribution enthalten ist und die Funktionen visualisiert, die ich früher entwickelt habe (und die ich der Liste der Funktionen für die Testumgebung hinzufügen möchte). Deshalb habe ich beschlossen, einen Visualizer für Testfunktionen zu erstellen.

Dazu musste ich die Datei Functions.mqh erweitern, in der die Klasse der Testfunktionen gespeichert ist, die beim Testen von Optimierungsalgorithmen verwendet werden. Die zusätzlichen Funktionen, die ich hinzugefügt habe, ermöglichen es Ihnen nicht nur, Änderungen an Funktionen visuell zu studieren, wenn Sie sie bei Bedarf modifizieren, sondern auch ihre Eigenschaften und Merkmale genauer zu erkunden.

So macht die Recherche nicht nur mehr Spaß und ist anschaulicher, sondern hilft mir auch, das Verhalten von Testfunktionen besser zu verstehen. Letztlich hilft mir die 3D-Visualisierung, nicht nur Zahlen auf dem Bildschirm zu sehen, sondern direkt mit der Form und Struktur von Funktionen zu interagieren, was wichtig ist, wenn ich sie modifiziere und Eigenschaften analysiere.

Code für zusätzliche Funktionen zur Erstellung eines Modells für eine 3D-Szene:

//——————————————————————————————————————————————————————————————————————————————
//GenerateFunctionDataFixedSize
bool GenerateFunctionDataFixedSize (int x_size, int y_size, double &data [], double x_min, double x_max, double y_min, double y_max, C_Function &function)
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  double dx = (x_max - x_min) / (x_size - 1);
  double dy = (y_max - y_min) / (y_size - 1);

  ArrayResize (data, x_size * y_size);

  //---
  for (int j = 0; j < y_size; j++)
  {
    for (int i = 0; i < x_size; i++)
    {
      double x = x_min + i * dx;
      double y = y_min + j * dy;

      data [j * x_size + i] = function.Core (x, y);
    }
  }
  return (true);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//GenerateDataFixedSize
bool GenerateDataFixedSize (int x_size, int y_size, C_Function &function, double &data [])
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  return GenerateFunctionDataFixedSize (x_size, y_size, data,
                                        function.GetMinRangeX (),
                                        function.GetMaxRangeX (),
                                        function.GetMinRangeY (),
                                        function.GetMaxRangeY (),
                                        function);
}
//——————————————————————————————————————————————————————————————————————————————

Zusätzlich habe ich diskrete Varianten der bereits bekannten Funktionen SkinDiscrete und HillyDiscrete hinzugefügt.

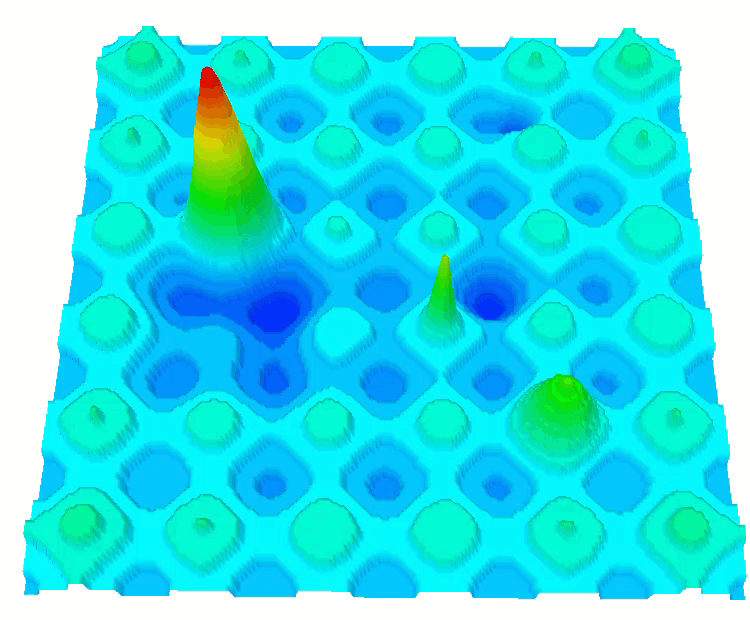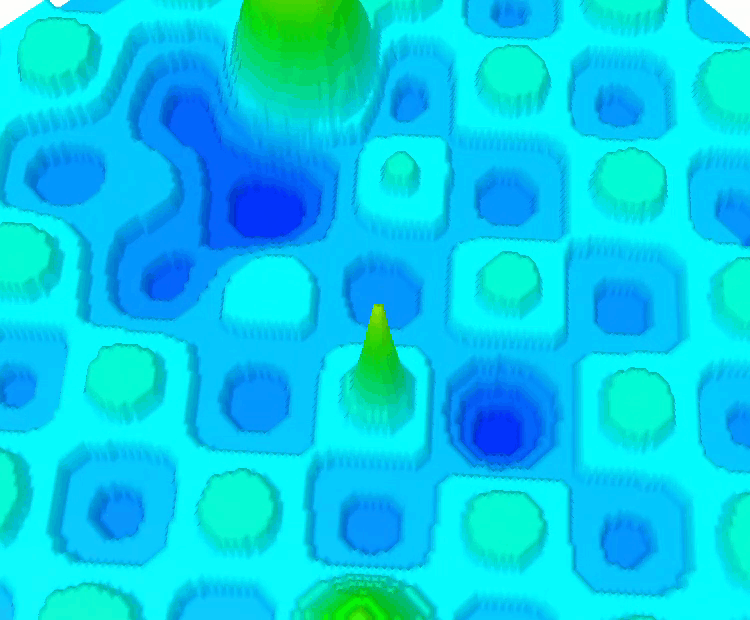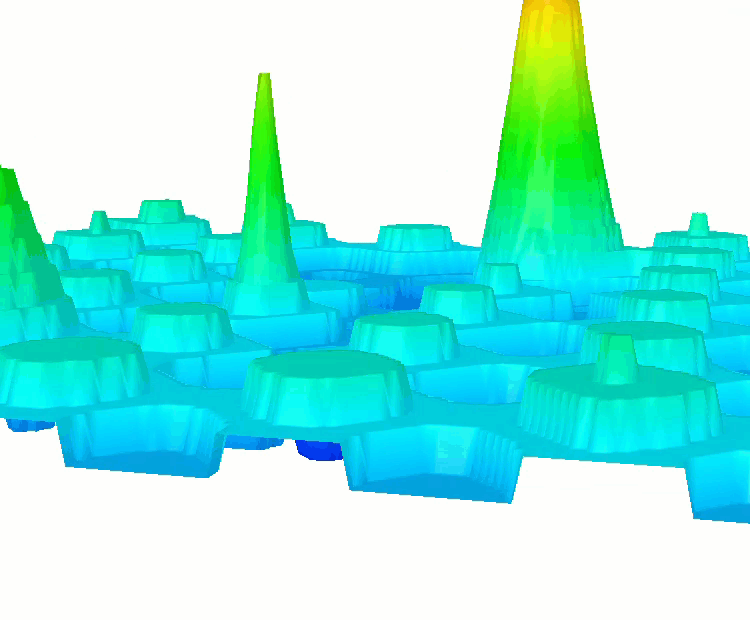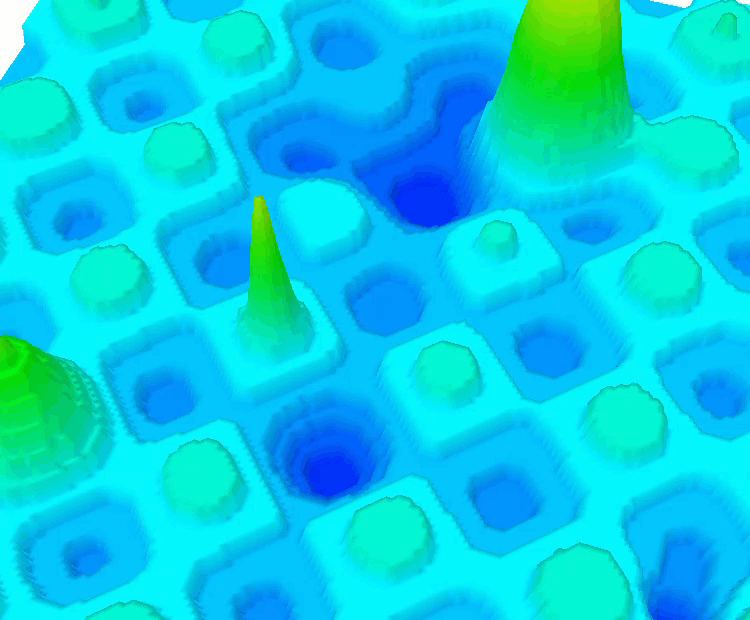
Die Funktion HillyDiscrete

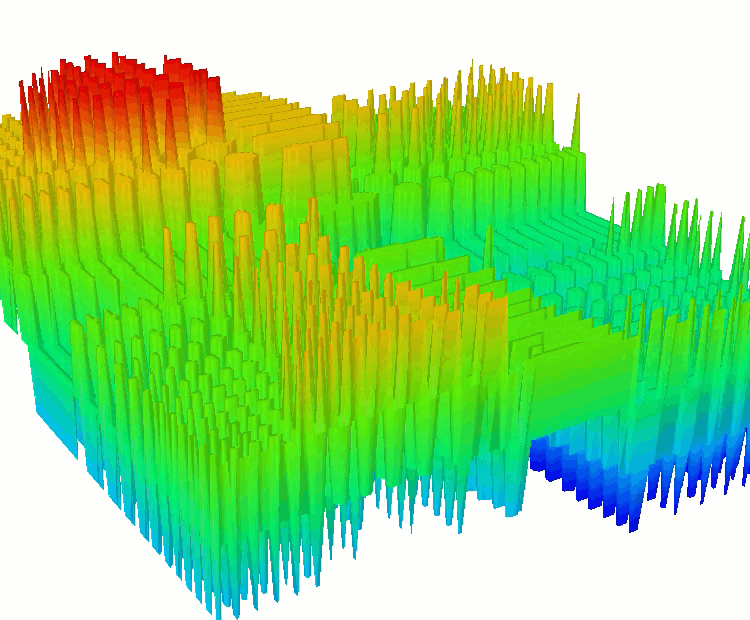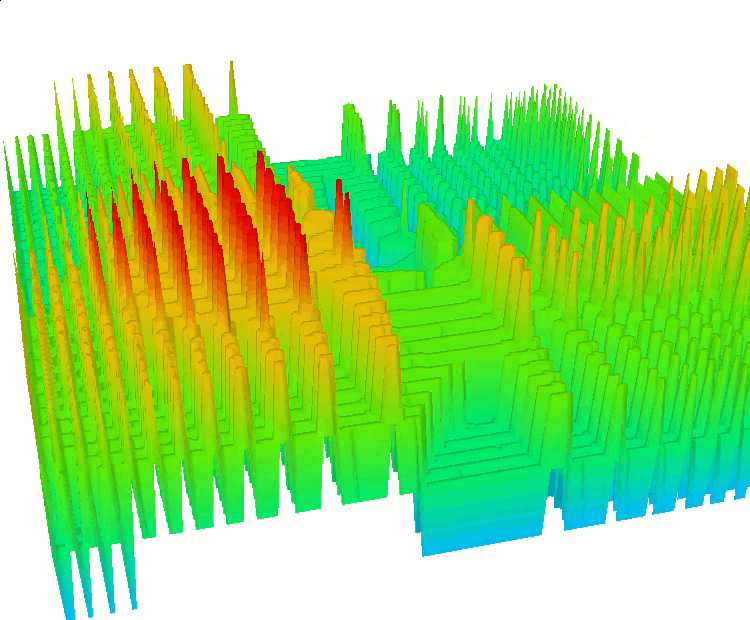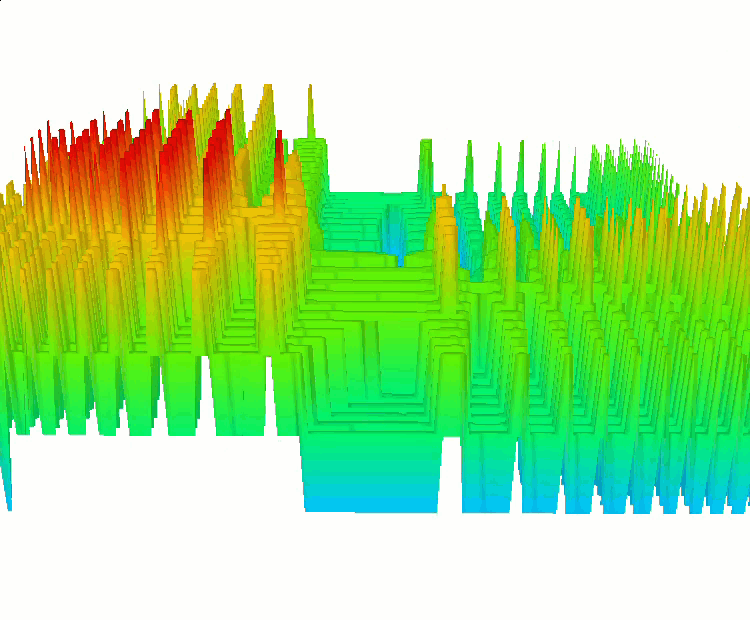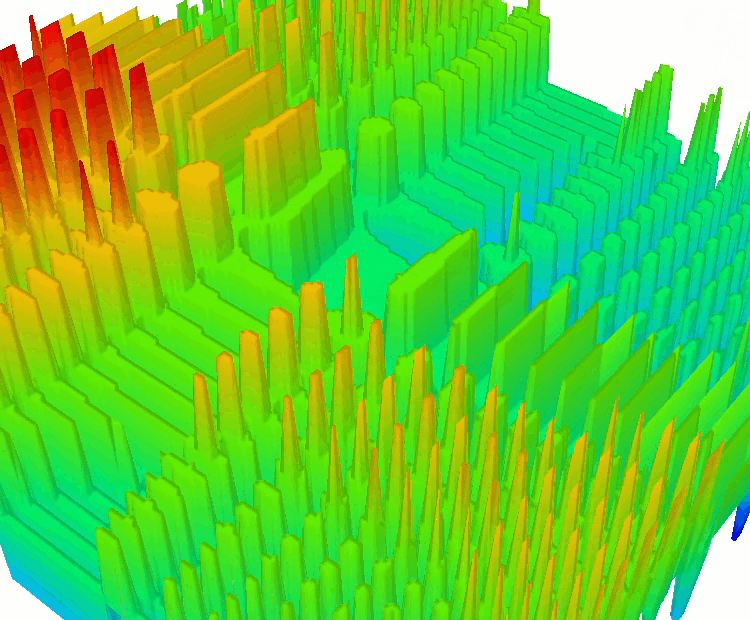
Die Funktion SkinDiscrete

Die Funktion Shaffer #2

7. Zusammenfassung

Wir werden weiterhin die Testfunktionen „Hilly“, „Forest“ und „Megacity“ verwenden, die sich bereits einen Namen als echte Tests für Optimierungsalgorithmen gemacht haben und dazu beitragen, eine zuverlässige Rangliste zu erstellen. Wir sollten uns jedoch nicht nur auf diese Funktionen beschränken - schließlich wurde die Liste der Testfunktionen erfolgreich erweitert! Sie haben also die freie Wahl: Experimentieren Sie, forschen Sie, entdecken Sie neue Horizonte, denn das ist das Schöne an der wissenschaftlichen Forschung.

Am Ende unserer kulinarischen Erkundung hybrider Optimierungsmethoden durch Vererbung von Basisklassen stellen wir fest, dass die Schaffung eines solchen Ausgangspunkts die Tür zu endlosen Forschungsmöglichkeiten öffnet. Die Kombination verschiedener Populationsalgorithmen in einer Klasse ermöglicht es uns nicht nur, die Genauigkeit und Geschwindigkeit der Suche nach optimalen Lösungen zu verbessern, sondern auch ein universelles Werkzeug für die Forschung zu schaffen.

Die Erstellung einer einzigen Testumgebung, der eine Vielzahl von Testfunktionen — diskret, glatt, spitz, nicht differenzierbar — kombiniert, eröffnet neue Möglichkeiten zum Testen und Vergleichen verschiedener Optimierungsmethoden. Dieser Ansatz ermöglicht es den Forschern, nicht nur Standardfunktionen zu verwenden, sondern auch eigene Testumgebungen zu erstellen, die an spezifische Aufgaben und Anforderungen angepasst sind.

Die Kombination von Populationsalgorithmen in einer Klasse und die Schaffung einer universellen Testumgebung eröffnet uns einen spannenden Weg zur Schaffung neuer „gastronomischer“ Kombinationen von Optimierungsmethoden, die es uns ermöglichen, neue Geschmacksnoten in der Welt der Suche nach optimalen Lösungen zu entdecken. Lassen Sie uns dieses kulinarische Experiment fortsetzen und neue Meisterwerke auf dem Weg zu Spitzenleistungen und Innovationen im Bereich der Optimierung schaffen!