Neuronales Netz in der Praxis: Kleinste Quadrate

Einführung

Hallo und herzlich willkommen zu einem neuen Artikel über neuronale Netze.

Im vorherigen Artikel „Neuronales Netzwerk in der Praxis: Die Sekante“, haben wir begonnen, über angewandte Mathematik in der Praxis zu diskutieren. Dies war jedoch nur eine kurze und schnelle Einführung in das Thema. Wir haben gesehen, dass die grundlegende mathematische Operation, die verwendet werden muss, die trigonometrische Funktion ist. Und im Gegensatz zu dem, was viele denken, handelt es sich nicht um eine Tangensfunktion, sondern um eine Sekantenfunktion. Obwohl dies alles zunächst recht verwirrend erscheinen mag, werden Sie bald feststellen, dass alles viel einfacher ist, als es scheint. Im Gegensatz zu vielen Menschen, die in der mathematischen Umgebung nur Verwirrung stiften, entwickelt sich hier alles ganz natürlich.

Etwas Seltsames und Unverständliches

Allerdings gibt es einen kleinen Makel, den ich nicht nachvollziehen konnte. Das ergibt keinen Sinn, zumindest für mich. Da dies für jeden nützlich sein könnte, der dasselbe versucht, habe ich es so gelassen. Wir werden dieses Problem hier lösen, denn wenn wir es nicht lösen, werden wir viele andere Probleme auf der mathematischen Seite haben.

Der oben genannte Artikel enthält den folgenden Code:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+

Dieser Code konstruiert kleine Kreise, deren Position im Array A in Zeile 22 angegeben ist. Noch nichts Besonderes, aber genau so war es gedacht. Wenn man jedoch die Punkte aufträgt, erhält man folgendes Ergebnis:

Diese Punkte befinden sich an den falschen Stellen. Sie sind in Bezug auf die X- und Y-Achse invertiert. Warum? Ehrlich gesagt, weiß ich nicht, wie ich das erklären soll. Dies geschieht, weil wir in Zeile 33 des Codes die Werte im Array erfassen und dann die Position hinzufügen. Auf diese Weise sollte der Compiler verstehen, dass wir auf den nächsten Wert im Array verweisen. Genau so geschieht es, und wenn es anders wäre, würde ein Fehler wegen unerlaubten Speicherzugriffs auftreten. Dies würde als Bereichsfehler behandelt, und die Anwendung würde abgebrochen.

In global.x werden jedoch nur ungerade Indexwerte hinzugefügt, keine geraden. Die zu global.y hinzugefügten Werte stehen also auf einem geraden Index, während sie eigentlich auf einem ungeraden Index stehen müssten.

Das wurde mir erst klar, als ich anfing, die Berechnungen für diesen Artikel zu schreiben, denn die Berechnungen stimmten nicht mit den Ergebnissen der App überein. Also beschloss ich, den Grund dafür zu finden. Sie können dasselbe tun, indem Sie den Code wie unten gezeigt leicht abändern.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         canvas.FillCircle(global.x + (vx = A[c1++]), global.y + (vy = A[c1++]), 5, ColorToARGB(clrRed, 255));
38.         s += StringFormat("[ %d <> %d ] ", vx, vy);
39.     }
40.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
41. }
42. //+------------------------------------------------------------------+

Diese Änderung ermöglicht es uns zu sehen, was passiert. Das Ergebnis ist unten dargestellt:

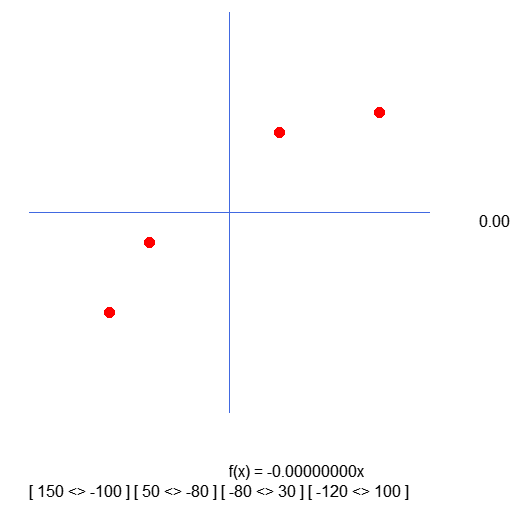
Beachten Sie die Werte innerhalb der Klammern. Sie sind das Ergebnis der in Zeile 37 durchgeführten Erfassung. Das heißt, wir legen die Werte fest, die für die Positionierung der Kreise im Diagramm verwendet werden. Es ist jedoch zu beachten, dass sie im Vergleich zu dem, was im Array deklariert ist, invertiert sind. Und das ist ziemlich seltsam. Daher müssen wir den Code wie unten gezeigt ändern.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         vx = A[c1++];
38.         vy = A[c1++];
39.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
40.         s += StringFormat("[ %d <> %d ] ", vx, vy);
41.     }
42.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
43. }
44. //+------------------------------------------------------------------+

Wenn wir nun diesen neuen Code verwenden, sieht das Ergebnis wie folgt aus:

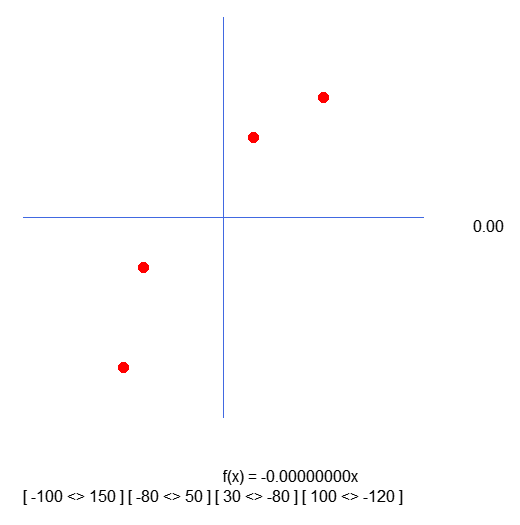
Wie Sie sehen, entsprechen die Werte in den eckigen Klammern dem, was im Array angegeben ist. Ich bitte um Entschuldigung, dass ich diesen Fehler nicht früher bemerkt habe. Doch dies soll all jenen als Warnung dienen, die die Dinge auf ihre eigene Weise regeln wollen. Da ich nicht verstanden habe, warum die Indizes vertauscht wurden, weiß ich nicht, wie ich das erklären soll. Nachdem wir diese wirklich notwendige Korrektur vorgenommen haben, können wir zu weiteren Arbeiten übergehen.

Vorbereitung auf Mathe und noch mehr Mathe

Was wir von diesem Punkt an tun, kann ziemlich verwirrend sein, wenn man nur in den Code eintaucht. Da ich möchte, dass Sie genau verstehen, was wir tun werden und warum, werde ich alles in aller Ruhe erklären. Ich empfehle daher, sorgfältig zu lesen. Ändern Sie den Code, wie er erscheint. Versuchen Sie zu verstehen, was vor sich geht. Erst wenn Sie alles verstanden haben, gehen Sie zum nächsten Schritt über. Versuchen Sie nicht, Schritte zu überspringen, weil Sie vielleicht gar nichts verstehen.

Als erstes werden wir den Code leicht verändern.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31.     double ly;
32. 
33.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
34.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
35. 
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         s += StringFormat("sy%d = %.4f  | ", c0, ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 50, s, ColorToARGB(clrBlack));
46. }
47. //+------------------------------------------------------------------+
48. void NewAngle(const char direct, const double step = 0.2)
49. {
50.     canvas.Erase(ColorToARGB(clrWhite, 255));
51. 
52.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
53.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
54.     canvas.TextOut(global.x, global.y + _SizeLine + 20, StringFormat("f(x) = %.8fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
55.     canvas.Line(
56.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
57.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
58.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
59.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
60.                 ColorToARGB(clrForestGreen)
61.             );
62.        
63.     Func_01();
64. 
65.     canvas.Update(true);
66. }
67. //+------------------------------------------------------------------+

Dies ist zwar nicht der optimalste Weg, aber das in der folgenden Animation gezeigte Ergebnis ist genau das, was wir visualisieren wollen:

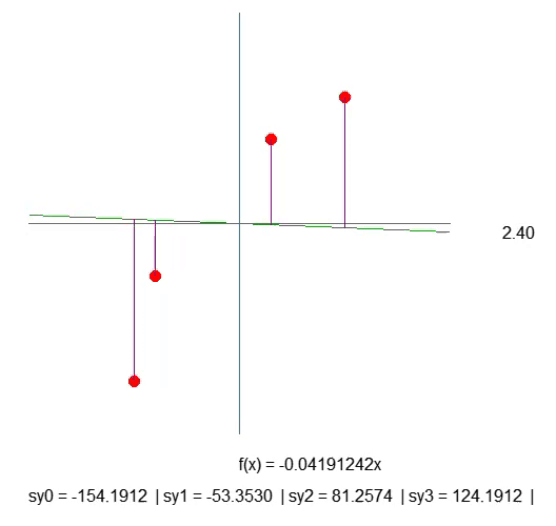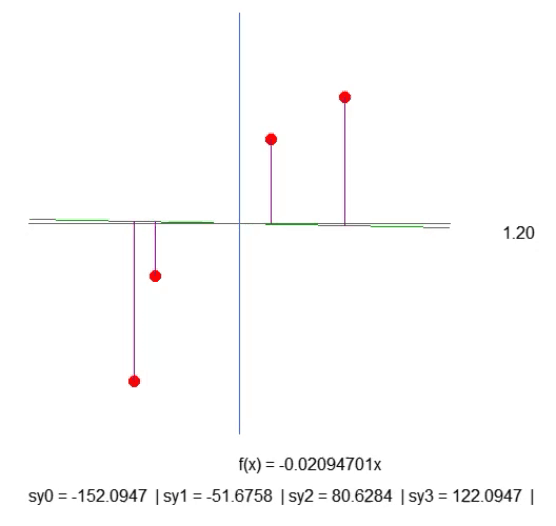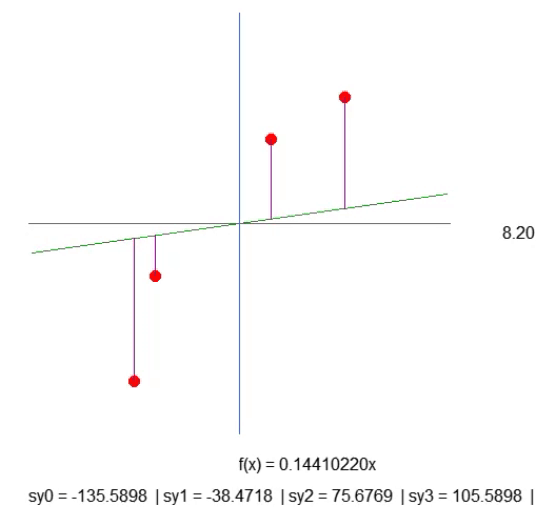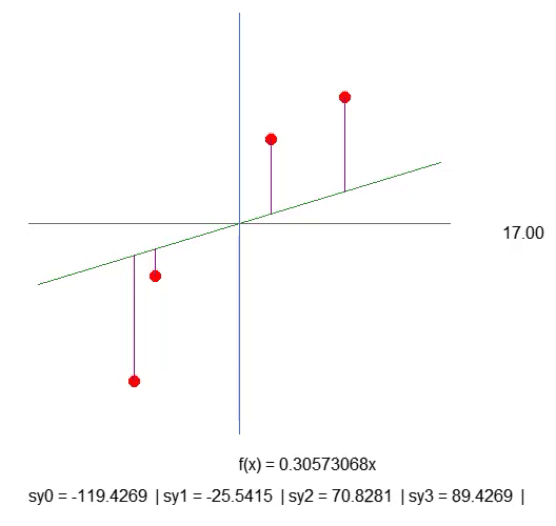
Wir erstellen einfach eine lila Linie. Sie gibt den Abstand zwischen der Linie und dem Punkt an. Bitte beachten Sie dies. Die Länge der Zeile wird durch den Code in Zeile 41 des Fragments bestimmt. Die Berechnung ist nicht ganz so, wie sie sein sollte, aber sie funktioniert. Wir sollten also nichts überstürzen, denn später werden wir diese Berechnung ändern müssen. In Zeile 43 erstellen wir einen Zeichenkette, mit dem wir die Länge der gegebenen lila Linie herausfinden können. Schauen Sie sich die Animation an, und Sie werden sehen, dass es negative Längen gibt, was keinen Sinn macht. Es ist zu früh, sich darüber Gedanken zu machen. Zunächst einmal möchte ich, dass Sie das Wesen unserer Arbeit verstehen.

Jetzt möchte ich, dass Sie, lieber Leser, ein wenig nachdenken. Die Geradenfunktion wird auf der Grundlage des Steigungskoeffizienten berechnet. Dieser Koeffizient lässt sich aus dem Winkel ablesen, den wir durch Klicken auf die Pfeile nach rechts oder links ändern. Und die Geschwindigkeit, mit der sich diese Steigung ändert, wird durch den „Step“-Wert in Zeile 52 angegeben.

Schauen Sie sich dann die Länge jeder der lila Linien an. Mit etwas Geduld können wir die Steigung der Geraden so steil wie möglich machen, sodass die Länge jeder der violetten Linien nicht mehr zunimmt (sie kann abnehmen, aber sie sollte nicht zunehmen). Wenn wir den Punkt erreichen, an dem keine der Längen mehr wächst, haben wir die ideale Steigung gefunden.

Beachten Sie jedoch Folgendes: In diesem Fall müssen wir nur vier Elemente berücksichtigen, was recht einfach ist. Bei Hunderten oder Tausenden von Punkten in der Matrix wäre es jedoch sehr schwierig, die Werte manuell so anzupassen, dass sie nicht ansteigen. Mit einem mathematischen Trick können wir diesen Prozess vereinfachen. Der Trick ist folgender: Wenn wir die Längen der einzelnen violetten Linien addieren, brauchen wir nur einen Wert zu beobachten, und wenn dieser anfängt, anzusteigen, wissen wir, dass wir den optimalen Neigungspunkt überschritten haben. Einfach, nicht wahr? Ändern wir also den Code wie folgt.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

Das Ergebnis ist im nachstehenden Bild zu sehen. Die Anpassung der Werte ist auf diese Weise viel einfacher.

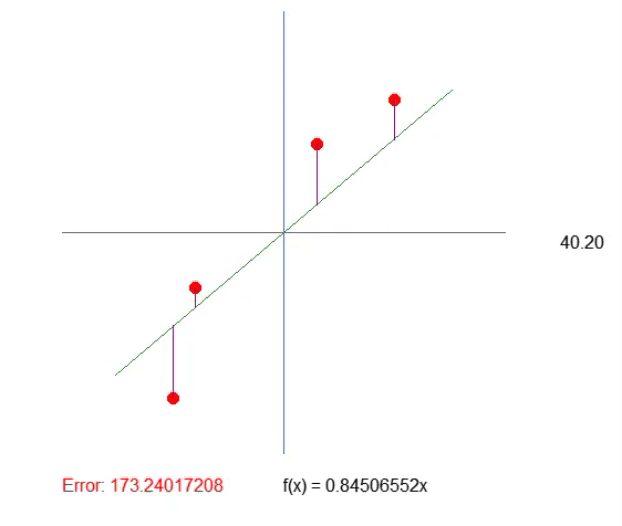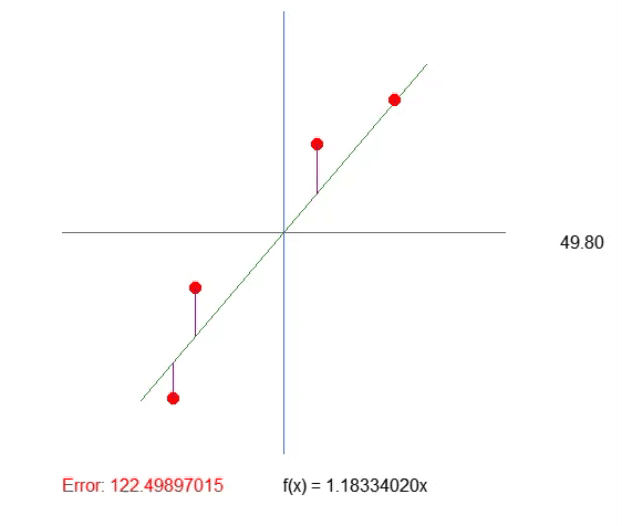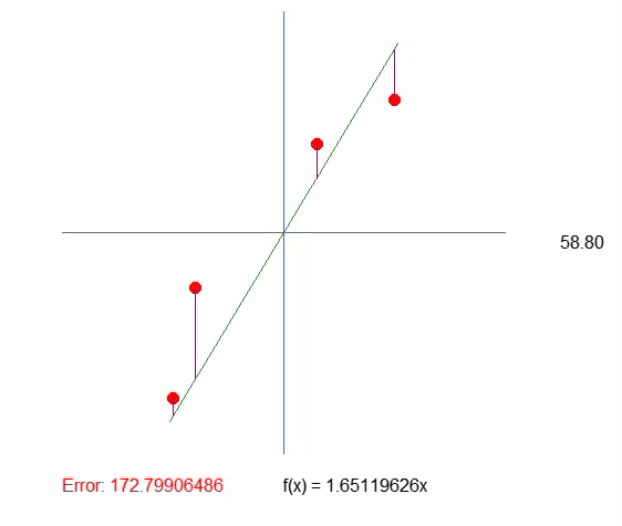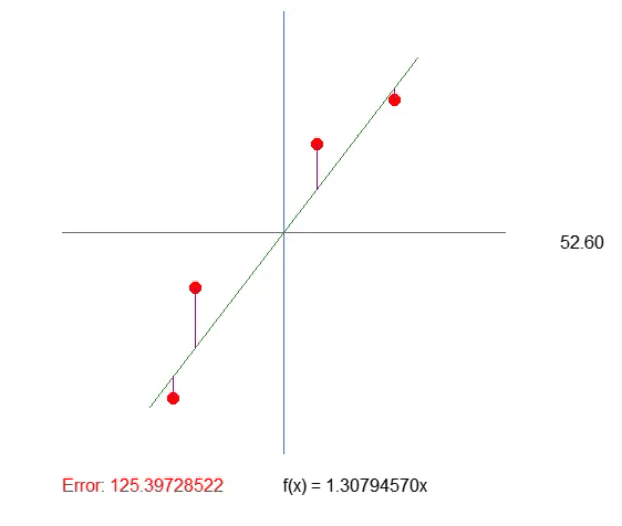
Einstellen des Quadranten

Bevor wir uns ganz auf die mathematische Seite stürzen, müssen wir eine kleine Änderung vornehmen. Das hat zwar keine direkte Auswirkung auf unsere Arbeit, ist aber von Bedeutung, wenn wir das Erklärte in anderen Programmen oder beim manuellen Experimentieren anwenden wollen. Oft beginnen wir damit, alles manuell auszuprobieren und die Berechnungen auf dieselbe Weise durchzuführen. Die folgenden Hinweise sollen Ihnen helfen, den Fehler zu vermeiden, sich blind auf die Berechnungen des Programms zu verlassen.

Auch wenn sie völlig falsch sind. Programmieranfänger machen diesen Fehler oft, und das kann viel Zeit und Mühe kosten. Infolgedessen konzentrieren sie sich darauf, das Problem auf die falsche Weise zu lösen. Jeder gute Programmierer ist auch ein Mensch, der sehr misstrauisch gegenüber den Berechnungen ist, die er anstellt. Der Programmierer versucht immer, verschiedene Dinge auf viele verschiedene Arten zu testen, bevor er dem Ergebnis vertraut.

Ich erzähle Ihnen das, weil wir bei der Erstellung eines grafischen Bildes immer im vierten Quadranten der kartesischen Ebene arbeiten, auch wenn viele Menschen das nicht wissen. Das beeinflusst alles. Nicht für die Berechnungen selbst, sondern für diejenigen, die die gleichen Berechnungen manuell oder in einem anderen Programm durchführen wollen. Zum Beispiel MatLab, SCILab oder sogar das gute alte Excel. In Excel können wir beispielsweise eine grafische Darstellung der Werte und Formeln erstellen, die wir hier verwenden.

Das ist gut, aber was hat das alles mit dem zu tun, was wir tun werden? Nun, liebe Leserin, lieber Leser, wenn Sie sich die Datenmatrix im Programm ansehen, werden Sie feststellen, dass sie im Vergleich zu dem, was in der Grafik dargestellt ist, etwas seltsam aussieht. Wenn wir die gleichen Werte in einem anderen Grafikprogramm aufzeichnen, sehen wir, dass die Y-Achse invertiert ist. Aber ich verstehe immer noch nicht, wie das passiert. Nehmen Sie sich Zeit und sehen Sie sich die folgenden Bilder an, um sie besser zu verstehen.

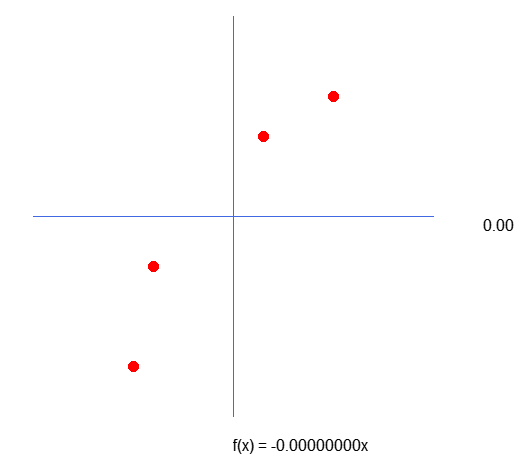
Das obige Bild ist zu sehen, wenn ein Chart in MetaTrader 5 gezeichnet wird. Wenn Sie dieselben Werte jedoch z. B. in Excel grafisch darstellen, sieht das Diagramm wie folgt aus:

Diese Diskrepanz kann dazu führen, dass die meisten der durchzuführenden Tests völlig unverständlich sind. Vor allem, wenn Sie überprüfen müssen, ob die Berechnungen korrekt durchgeführt werden.

Im vorigen Thema haben wir bereits herausgefunden, wie man Daten richtig präsentiert. Jetzt müssen wir dieses Problem lösen. Das Problem ist, dass die Y-Achse invertiert (oder gespiegelt) ist.

Warum versagt die Darstellung?! Der Grund dafür ist einfach, und wir haben ihn bereits zu Beginn des Themas erwähnt. Der Bildschirm, auf dem die Daten dargestellt werden, befindet sich im vierten Quadranten. Das liegt daran, dass der Ursprung, d. h. der Punkt (0, 0), in der oberen linken Ecke liegt. Achten Sie nun auf Folgendes. Selbst wenn wir den Bezugspunkt in die Mitte des Bildschirms verlegen, wird diese Übertragung nur virtuell sein. Das bedeutet, dass wir den physikalischen Bezugspunkt nicht verändern. Wir verschieben lediglich die Darstellung der Berechnung auf einen anderen Ausgangspunkt. Aus diesem Grund addieren wir im Programm die Werte eines Punktes in der Matrix zu einer anderen Menge von Punkten. So können wir den virtuellen Ursprung von der oberen linken Ecke an eine beliebige Stelle auf dem Bildschirm verschieben.

Aber vielleicht haben Sie in der obigen Abbildung bemerkt, dass es ein Problem mit der Art und Weise gibt, wie wir diese Virtualisierung implementieren. Die Y-Achse ist invertiert oder gespiegelt. Um dies zu beheben, müssen wir ein paar Dinge im Code ändern. Es ist einfach, aber es wird alles viel klarer machen.

Im Code werden wir die folgenden Änderungen vornehmen:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
41.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
42.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

Bitte beachten Sie, dass die Änderungen sehr subtil sind. Zunächst ändern wir die Werte in der Matrix. Dann ändern wir die Berechnung in Zeile 40, damit die Punkte richtig positioniert werden. Es ist auch notwendig, die Zeilen 41 und 42 zu ändern, die Berechnungen durchführen, um die lila Linien korrekt mit den Punkten zu verbinden. Diese Art der Festsetzung, auch wenn sie hauptsächlich ästhetischer Natur ist, schafft Vertrauen bei denjenigen, die sich eingehender mit dem Thema befassen wollen. Jetzt können wir die erstellten Diagramme vergleichen, ohne zu denken, dass in dem einen oder anderen Programm etwas schlecht berechnet wurde. Das Verfahren ist viel einfacher geworden.

Dadurch wird auch die Durchführung der Aufgabe wesentlich erleichtert. Denn wenn der Fehlerwert steigt, bedeutet das, dass wir uns in die falsche Richtung bewegen. Wenn sie zurückgeht, dann bewegen wir uns in die richtige Richtung.

Doch nun stellt sich eine weitere Frage, und von diesem Punkt aus werden wir uns mit der Frage befassen, was das Thema der neuronalen Netze antreibt. Die Anpassung der Steigung der Tangente oder des Steigungsfaktors ist recht einfach, wenn man sich den Fehlerwert ansieht. Aber gibt es eine Möglichkeit, dies automatisch einzurichten? Ist es möglich, einen Mechanismus zu schaffen, der es der Maschine ermöglicht, nach dem besten Wert des Koeffizienten zu suchen? Es ist wichtig, sich daran zu erinnern, dass wir jetzt nur noch eine Variable im System verwenden, da die Tangente genau durch den Punkt (0, 0) geht, der der Anfang der kartesischen Ebene ist. Dies ist jedoch nicht immer der Fall. Doch lassen Sie uns zunächst diese einfachere Frage klären. Dies ist der Fall, wenn wir nur eine Variable anpassen müssen.

Wenn Sie den vorigen Artikel verfolgt haben, wissen Sie, dass ich erwähnt habe, wie man eine Sekantenlinie so berechnet, dass sie zu einer Tangente wird. Selbst wenn das funktioniert, sollten wir uns eine andere, etwas einfachere Hypothese überlegen, bei der wir uns nicht so viel Mühe geben müssen, um den Wert der Steigung zu finden. Wir wollen versuchen, eine Formel zu finden, mit der sich der Koeffizient schneller und einfacher berechnen lässt.

Dazu müssen wir einige mathematische Tricks anwenden. Aus Gründen der besseren Übersichtlichkeit werden wir dies in einem neuen Thema behandeln.

Suche nach der kleinstmöglichen Fläche

Wenn Sie sich schon einmal mit dem Thema künstliche Intelligenz befasst haben, ist Ihnen vielleicht aufgefallen, dass es etwas gibt, das immer wieder auftaucht. Aber verwechseln Sie künstliche Intelligenz nicht mit neuronalen Netzen. Obwohl diese beiden Konzepte miteinander verbunden sind, müssen sie unterschiedlich angegangen werden. Dies ist vom Standpunkt der Programmierung aus betrachtet. Es gibt ein paar kleine Unterschiede, aber hier möchte ich ein neuronales Netz erstellen, das eine Gleichung finden kann, die die Werte in der Datenbank am besten darstellt. Diese Art der Berechnung wird von einem neuronalen Netz durchgeführt. Künstliche Intelligenz sucht an der Basis. Das neuronale Netz schafft die Grundlage.

In diesem Fall können wir beginnen, Neuronen dafür zu verwenden, aber meiner Meinung nach ist es noch zu früh. Wir können dafür selbst Berechnungen erstellen, was eine enorme Zeitersparnis bei der Bearbeitung bedeutet.

Um die Steigung zu berechnen oder eine Berechnung zu erstellen, werden wir Ableitungen verwenden. Wir könnten dies auch auf andere Weise umsetzen, aber hier werden wir Ableitungen verwenden, was der schnellste Weg ist. Ich gehe davon aus, dass Sie alles verstanden haben, was im vorherigen Thema erklärt wurde, sodass wir fortfahren können. Kommen wir nun zum mathematischen Teil der Frage.

Um den Fehler zu ermitteln, führen wir die folgende mathematische Berechnung durch.

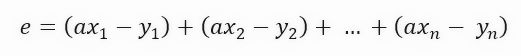
Der Wert der Konstante <a> in der Formel ist genau der Winkelkoeffizient der Geraden, das heißt, es ist der Wert der entstehenden Tangente. Aber diese Formel ist nicht kompakt genug. Wir können dies vereinfachen, indem wir die Formel ein wenig kompakter gestalten, wie unten gezeigt.

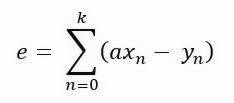
Obwohl sie wie unterschiedliche Formeln aussehen, repräsentieren sie dasselbe, nur die Notation wurde geändert, um kompakter zu sein. Da sie kompakter ist, ist es einfacher, die Formeln zu schreiben, die wir im Folgenden entwickeln werden. Beachten Sie, dass wir bei jedem Schritt eine Summe von Werten haben, die der Länge der violetten Linie im Diagramm entspricht, das im vorherigen Thema gezeigt wurde. Das hindert uns daran, Ableitungen zu verwenden, denn wenn wir versuchen, eine solche Formulierung abzuleiten, kommen wir auf eine Nullkonstante. Wir wollen das in der folgenden Formel dargestellte Ergebnis erhalten.

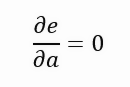
Wir wollen also den Fehler im Verhältnis zur Steigung der Geraden ausgeben, und je mehr sich dieser Wert der Null nähert, desto mehr nähert sich die Steigung dem Idealwert. Das ist die Idee. Aber dieser Wert kann kaum Null sein. Sie kann sich dem Wert Null nähern, und je näher sie diesem Wert kommt, desto besser, aber wie ich schon sagte, können wir keine Funktion ableiten, die die Länge der lila Linie bestimmt. Es gibt jedoch einen Weg. Wir müssen die violette Linie in eine quadratische Figur umwandeln, und in diesem Fall suchen wir nicht nach der minimalen Länge der Linie, sondern nach der kleinstmöglichen Fläche des Quadrats, das von jeder der Linien gebildet wird. Daraus ergibt sich die nachfolgend dargestellte neue Formulierung.

Beachten Sie, dass wir jetzt (auch wenn es nicht so aussieht) denselben Koeffizienten berechnen, nur dass wir dieses Mal die Fläche des Quadrats verwenden, das durch jede der lila Linien im Diagramm gebildet wird. Die Dinge werden jetzt viel interessanter. Wenn wir diese Gleichung weiterentwickeln, erhalten wir das folgende Ergebnis.

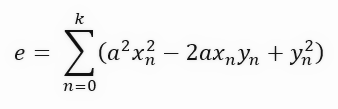
Sie haben vielleicht nicht verstanden, was wir gerade getan haben. Diese Gleichung, die einfach dadurch entstanden ist, dass man die Berechnung von der Länge einer Linie auf die Fläche eines Quadrats umgestellt hat, ist eigentlich eine sehr interessante Gleichung. Sehen Sie das? Können Sie mir sagen, wie diese Gleichung lautet?

Wenn Sie nicht wissen, was diese Gleichung bedeutet, machen Sie sich keine Sorgen. Dies ist nichts anderes als eine quadratische Gleichung. Dies ist dieselbe Gleichung, die die Parabel erzeugt, und daher ist es die Gleichung, mit der wir die Ableitung ersten Grades erstellen können. Wir wollen die Ableitung nach der Steigung ermitteln. Aber vorher füge ich noch einen Schritt hinzu, den wir normalerweise nicht machen. Ich möchte Ihnen zeigen, warum die endgültige Formel so aussieht. In diesem zusätzlichen Schritt werden die Begriffe gruppiert und entsprechend getrennt, wie unten dargestellt.

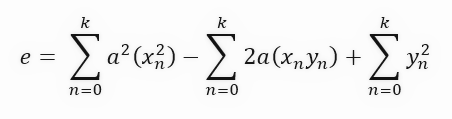
Wir haben die Gleichung vereinfacht, um sie bei der Herleitung besser verstehen zu können. In der Regel wird dieser zusätzliche Schritt nicht durchgeführt; wir gehen direkt zur unten stehenden Endformel über.

Heilige Mutter Gottes! Jetzt ist alles sehr kompliziert geworden. Ich verstehe überhaupt nichts, wie ist das möglich? Was sind das für verrückte Berechnungen? Wie kann ich das alles in Code umsetzen?! Alles ist unter Kontrolle. Ruhe bewahren. Normalerweise zeige ich keine Formeln, um den Leser nicht zu verwirren. Und dabei ist alles ganz einfach: Das ist genau die Ableitung, die wir berechnen müssen. So erhält man einen Näherungswert für den Winkelkoeffizienten der Linie.

Übertragen wir dies nun in das Codeformat und sehen wir, was passiert. Der Code lautet wie folgt.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err, d0, d1;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = d0 = d1 = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         d0 += (vx * vy);
41.         d1 += MathPow(vx, 2);
42.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
43.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
44.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
45.         err += MathAbs(ly);
46.     }
47.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
48.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 40, StringFormat("(de/da) : %.8f", d0 / d1), ColorToARGB(clrForestGreen));
49. }
50. //+------------------------------------------------------------------+

Beachten Sie, dass die eigentlichen Berechnungen im Code im Gegensatz zu dem, was Sie sich bei der Betrachtung all dieser Formeln vorstellen könnten, recht einfach und unkompliziert sind. In Zeile 40 berechnen wir die Summe der Punkte. In Zeile 41 berechnen wir das Quadrat der Punkte in X. Das ist alles sehr einfach. In Zeile 48 drucken wir den Wert des Graphen aus. Hören Sie genau zu, was ich sage: Dieser Wert ist ideal, wenn wir nur eine einzige Variable in die Geradengleichung einsetzen. Schauen Sie sich die Formel der Gleichung der folgenden Linie an.

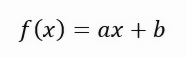
In dieser Gleichung ist der Wert < a > genau der Winkelkoeffizient. Der Wert < b > gibt den Punkt an, an dem sich die Wurzel der Gleichung befindet. Für diejenigen, die es nicht wissen: Die Wurzeln einer Gleichung sind die Punkte, an denen eine Kurve oder gerade Linie (in diesem Fall) die Y-Achse berührt, wenn der X-Wert gleich Null ist. Da der Wert von < b > bei dieser Lösung gleich Null ist, zeigt der als Idealwert zurückgegebene Wert lediglich die Steigung an, die dem Idealwert am nächsten kommt. Das bedeutet aber nicht, dass sie tatsächlich korrekt ist, denn wir sagen, dass die Wurzel der Gleichung genau im Ursprung liegt, was bedeutet, dass X und Y gleich Null sind. In Wirklichkeit geschieht dies nur selten, und zwar so selten, dass wir beim Ausführen dieser Anwendung die unten gezeigte Animation erhalten.

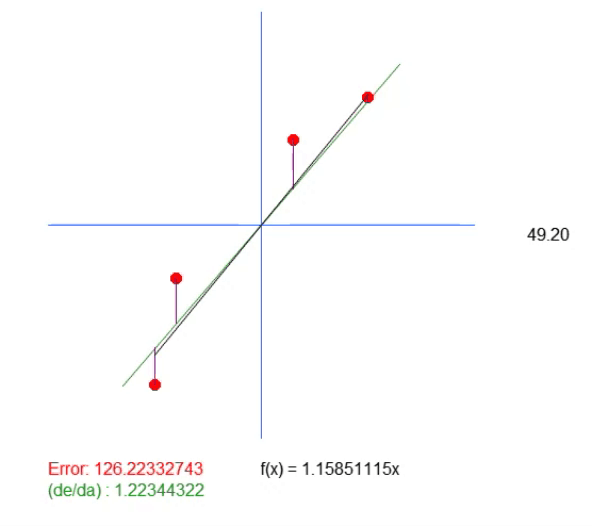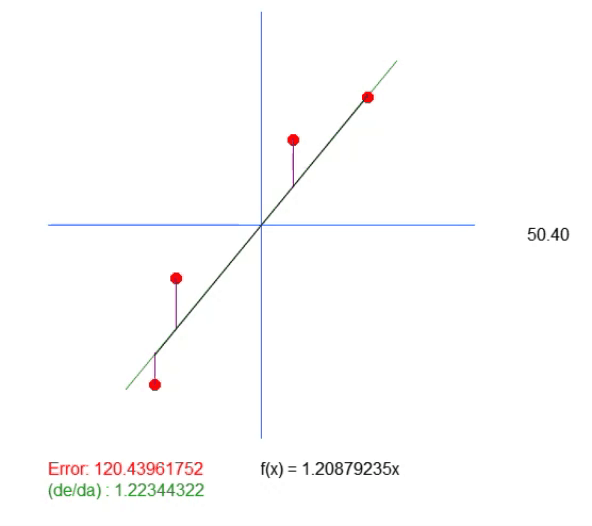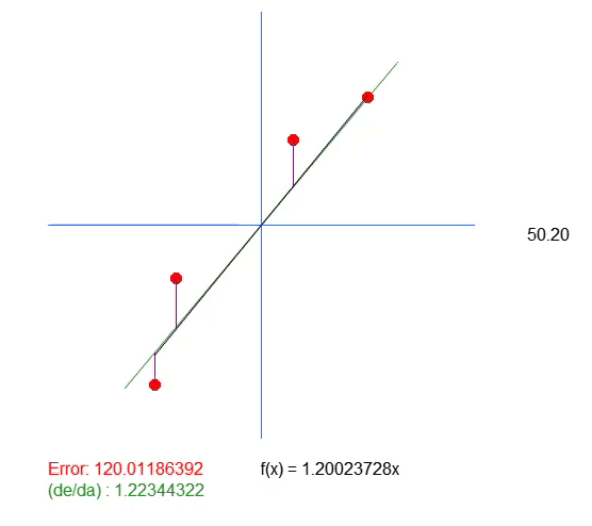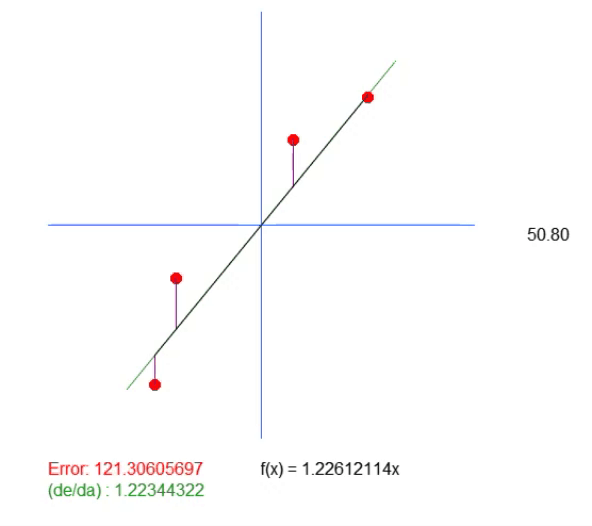
Beachten Sie, dass es eine weitere Zeile in dieser Animation gibt. Sie wird nur benötigt, um zu zeigen, wo der berechnete Idealwert liegen wird. Wenn Sie sich jedoch den Fehlerwert ansehen, können Sie feststellen, dass der Koeffizient in der Gleichung leicht von dem in Grün angezeigten Wert abweicht.

Dieser grüne Wert entspricht genau dem Wert, den wir anhand der Gleichung berechnet haben. Wie man sieht, reicht es hier nicht aus, nur den Wert der Steigung zu berechnen. Wir benötigen die Gleichung der Linie, die wir erstellen, und dazu brauchen wir neben dem Wert < a > auch den Wert < b >. Dies ist notwendig, um eine allgemeinere Lösung zu erhalten und nicht an den Punkt (0, 0) gebunden zu sein.

Dieser Punkt (0, 0), der eigentlich nicht Teil der Datenbank ist, hat einen impliziten Einfluss auf die Ergebnisse der Berechnungen des Winkelkoeffizienten. Um diesen Punkt richtig zu entfernen, müssen wir einige Dinge in der Anwendung ändern, damit Sie sich von diesem Referenzpunkt (0, 0) wegbewegen können.

Verschieben der Wurzel der Linienfunktion

Da wir die Anwendung für weitere Arbeiten vorbereiten müssen (die im nächsten Artikel besprochen werden), werden wir im weiteren Verlauf dieses Artikels einen recht interessanten Mechanismus entwickeln. Dann können wir uns auf die mathematische Seite konzentrieren.

Um diesen Mechanismus hinzuzufügen, sind keine besonderen Änderungen am Code erforderlich. Die Auswirkung ist jedoch beträchtlich, da sie es uns ermöglicht, die Geradengleichung zu finden, die uns in jeder Situation die kleinstmögliche Fläche liefert. Dies wird ein allgemeiner Mechanismus sein, um die am besten geeigneten Konstanten zu finden. Mit diesem Mechanismus wird die lineare Regression, die in das Diagramm eingezeichnet wird, die Datenbank angemessener widerspiegeln.

Die Durchführung dieser Änderungen ist sehr einfach. Alles, was wir tun müssen, ist, die Wurzel der Geradenfunktion zu verschieben. Diese Worte scheinen etwas kompliziert zu sein, aber wenn wir die Änderung in Code umsetzen, wird alles ganz einfach, wie Sie unten sehen können.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define _ToRadians(A) (A * (M_PI / 180.0))
009. #define _SizeLine 200
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y;
017.     double  Angle,
018.             Const_B;
019. }global;
020. //+------------------------------------------------------------------+
021. void PlotText(const uchar line, const string sz0)
022. {
023.     uint w, h;
024. 
025.     TextGetSize(sz0, w, h);
026.     canvas.TextOut(global.x - (w / 2), global.y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
027. }
028. //+------------------------------------------------------------------+
029. void Func_01(void)
030. {
031.     int A[]={
032.                 -100, -150,
033.                  -80,  -50,
034.                   30,   80,
035.                  100,  120
036.             };
037. 
038.     int vx, vy;
039.     double ly, err;
040.     string s0 = "";
041. 
042.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
043.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
044. 
045.     err = 0;
046.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
047.     {
048.         vx = A[c1++];
049.         vy = A[c1++];
050.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
051.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
052.         s0 += StringFormat("%.4f || ", MathAbs(ly));
053.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
054.         err += MathPow(ly, 2);
055.     }
056.     PlotText(3, StringFormat("Error: %.8f", err));
057.     PlotText(4, s0);
058. }
059. //+------------------------------------------------------------------+
060. void NewAngle(const char direct, const char updow, const double step = 0.1)
061. {
062.     canvas.Erase(ColorToARGB(clrWhite, 255));
063. 
064.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
065.     global.Const_B += (step * updow);  
066.     PlotText(1, StringFormat("Angle in graus => %.2f", MathAbs(global.Angle)));
067.     PlotText(2, StringFormat("f(x) = %.4fx %c %.4f", -MathTan(_ToRadians(global.Angle)), (global.Const_B < 0 ? '-' : '+'), MathAbs(global.Const_B)));
068.     canvas.LineAA(
069.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
070.                 (global.y - (int)global.Const_B) - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
071.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
072.                 (global.y - (int)global.Const_B) + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
073.                 ColorToARGB(clrForestGreen)
074.             );
075.        
076.     Func_01();
077. 
078.     canvas.Update(true);
079. }
080. //+------------------------------------------------------------------+
081. int OnInit()
082. {    
083.     global.Angle = 0;
084.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
085.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
086. 
087.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
088.     global.x /= 2;
089.     global.y /= 2;
090.         
091.     NewAngle(0, 0);
092. 
093.     canvas.Update(true);
094.     
095.     return INIT_SUCCEEDED;
096. }
097. //+------------------------------------------------------------------+
098. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
099. {
100.     return rates_total;
101. }
102. //+------------------------------------------------------------------+
103. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
104. {
105.     switch (id)
106.     {
107.         case CHARTEVENT_KEYDOWN:
108.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
109.                 NewAngle(-1, 0);
110.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
111.                 NewAngle(1, 0);
112.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_UP))
113.                 NewAngle(0, 1);
114.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_DOWN))
115.                 NewAngle(0, -1);
116.             break;
117.     }
118. }
119. //+------------------------------------------------------------------+
120. void OnDeinit(const int reason)
121. {
122.     canvas.Destroy();
123. }
124. //+------------------------------------------------------------------+

Hier sind die Ergebnisse:

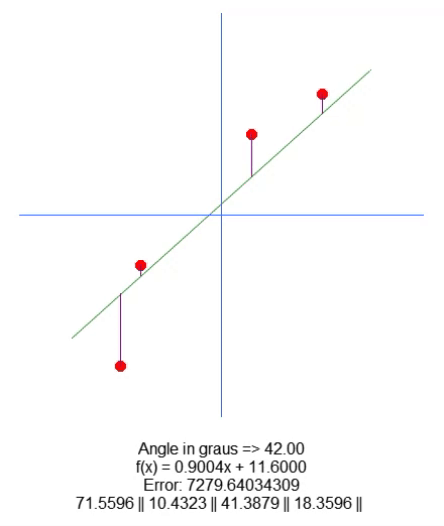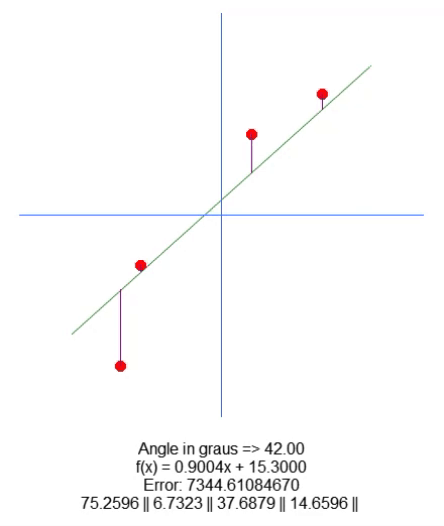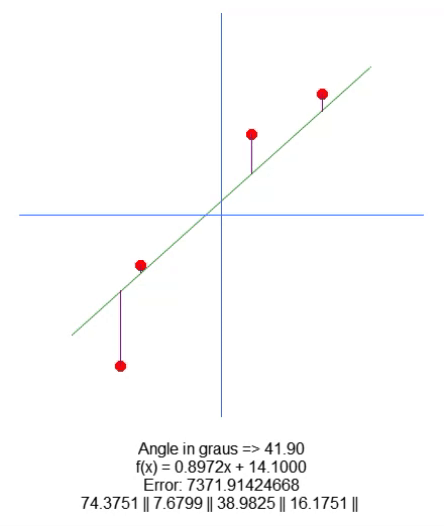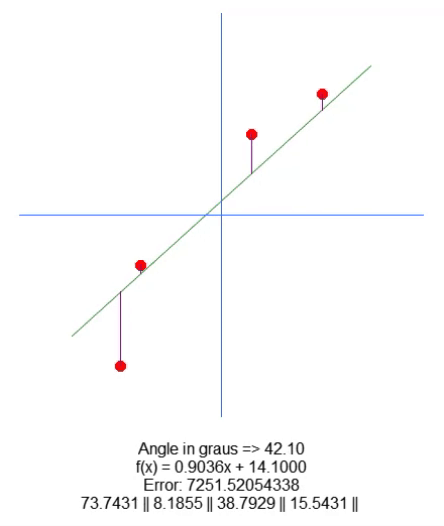
Um die Wurzel zu verschieben, haben wir in Zeile 18 eine Variable hinzugefügt. Mit Hilfe der Auf- und Abwärtspfeile können wir den Wert dieser Variablen in Zeile 65 ändern. Alles andere ist ziemlich einfach. Wir müssen nur den Wert für die violette Linienlänge auf der Grundlage des Wertes dieser neuen Variablen im Code anpassen. Ich bin mir sicher, dass ich nicht erklären muss, wie man das macht, denn es ist ganz einfach.

Abschließende Überlegungen

In diesem Artikel haben wir gesehen, dass mathematische Formeln oft viel komplizierter aussehen als ihre Umsetzung in Code. Viele Leute denken, dass solche Dinge schwierig sind, aber wir haben hier gezeigt, dass alles viel einfacher ist, als es scheint. Aber wir haben noch nicht alle Arbeiten erledigt. Wir haben nur einen Teil davon umgesetzt. Nun müssen wir einen Weg finden, die Gleichung einer Geraden auf eine geeignetere Weise zu schreiben. Dazu werden wir den letzten Code aus diesem Artikel verwenden. Im Gegensatz zu dem, was Sie sich zu Beginn dieses Themas vielleicht vorgestellt haben, ist die Suche nach einer Geraden durch eine Schleife nicht so einfach, wie es scheint. Dies geschieht, weil wir eine weitere Variable hinzufügen, nach der wir suchen. Stellen Sie sich nur vor, wie viel Arbeit es machen würde, eine Gleichung zu finden, wenn wir eine Million Variablen hätten. Dies mit „brute force“ zu tun, wäre völlig unmöglich, aber mit dem richtigen Einsatz von Mathematik ist es viel einfacher, die Gleichung zu finden.

Eine letzte Sache: Bevor Sie mit dem nächsten Artikel weitermachen, versuchen Sie, die Gleichung mit Hilfe des Codes zu finden, der am Ende des Artikels angegeben ist und die obige Abbildung erzeugt. Sie werden sehen, dass dies eine ziemlich schwierige Aufgabe ist. Wir sehen uns also im nächsten Artikel.