Нейронная сеть на практике: Метод наименьших квадратов

Введение

Всем привет и добро пожаловать в новую статью о нейронных сетях.

В предыдущей статье "Нейронная сеть на практике: Секущая прямая", мы начали рассматривать вопрос о прикладной математике на практике. Однако это было лишь краткое и быстрое введение в тему. Мы видели, что основной математической операцией, которая будет использоваться, является тригонометрическая функция. И, вопреки представлениям многих, это не функция тангенса, а функция секанса. Хотя поначалу всё это может показаться довольно запутанным, вскоре вы убедитесь, что всё гораздо проще, чем кажется. И в отличие от многих людей, которые по только создают большую путаницу в математической среде, здесь всё развивается совершенно естественно.

То, что было странно и непонятно

Однако есть один небольшой недостаток, если можно так выразиться, который я не смог понять, так как он не имеет смысла. Но хотя бы не для меня. Поскольку это может послужить предостережением для тех, кто попытается сделать то же самое, я оставил всё как есть. Но здесь мы исправим эту проблему, потому что, если мы ее не исправим, у нас будет много других проблем с математической стороны.

В приведенной выше статье есть следующий отрывок, который показан ниже:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+

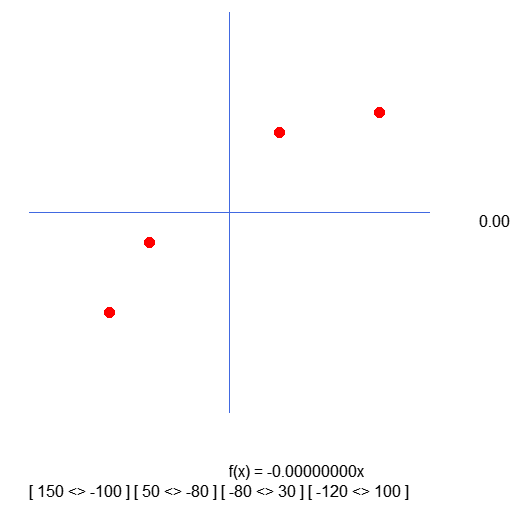
Данный фрагмент предназначен для построения маленьких окружностей, положение которых находится в массиве A, присутствующем в строке 22. Пока ничего особенного, именно так и было задумано. Однако при построении точек мы увидим следующее изображение:

Эти точки расположены в неправильных местах. Они перевернуты по отношению к осям X и Y. Но почему? Честно говоря, не знаю, как это объяснить. Это происходит потому, что в строке 33 фрагмента мы перехватываем значения, которые находятся в массиве, а затем добавляем позицию. Таким образом компилятор должен понять, что мы указываем на следующее значение в массиве. Всё происходит именно так, а если бы всё было по-другому, то была бы сгенерирована ошибка несанкционированного доступа к памяти, что воспринималось бы как ошибка диапазона, и приложение закрылось бы.

Однако в global.x добавляются нечетные значения индекса, а не четные. И значения, добавленные в global.y, относятся к четному индексу, в то время как ожидалось бы, что они относятся к нечетному.

Я понял это только тогда, когда начал писать математическую часть для этой статьи, поскольку расчеты не совпадали с результатами, которые предоставило приложение. Поэтому я решил найти причину. Вы можете сделать то же самое, слегка изменив фрагмент, как показано ниже.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         canvas.FillCircle(global.x + (vx = A[c1++]), global.y + (vy = A[c1++]), 5, ColorToARGB(clrRed, 255));
38.         s += StringFormat("[ %d <> %d ] ", vx, vy);
39.     }
40.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
41. }
42. //+------------------------------------------------------------------+

Данная модификация позволяет нам видеть, что происходит. Результат показан на изображении ниже:

Обратите внимание на значения внутри скобок. Они являются результатом захвата, который выполнился в строке 37. Т.е. мы фиксируем значения, которые используются для расположения кругов на графике. Однако обратите внимание, что они инвертированы по сравнению с тем, что объявлено в массиве. И это довольно странно. Поэтому нам необходимо изменить код, как показано в следующем фрагменте.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         vx = A[c1++];
38.         vy = A[c1++];
39.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
40.         s += StringFormat("[ %d <> %d ] ", vx, vy);
41.     }
42.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
43. }
44. //+------------------------------------------------------------------+

Теперь, когда мы используем этот новый фрагмент кода, результат будет выглядеть так:

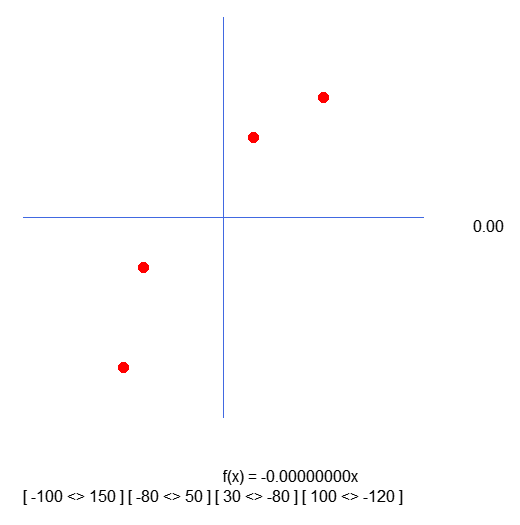
Теперь мы можем заметить, что значения внутри квадратных скобок соответствуют тому, что объявлено в массиве. Я прошу прощения за то, что не заметил эту ошибку раньше. Но пусть это послужит предостережением для всех тех, кто хочет поступать по-своему. Поскольку я не понял, почему индексы были перевернуты, я не знаю, как объяснить, почему происходит сбой. Сделав эту поправку, которая действительно необходима, мы можем перейти к дальнейшей работе.

Готовимся делать расчеты, много расчетов

То, что мы делаем, начиная с этого момента, может быть довольно запутанным, если просто погрузиться в код. Поскольку я хочу, чтобы вы точно поняли, что и почему мы будем делать, я объясню всё спокойно. Поэтому рекомендую читать без спешки. Изменяйте код по мере его отображения. Пробуйте и пытайтесь понять происходящее. Только когда всё поймете, переходите к следующему этапу. Не пытайтесь пропускать шаги, потому что в этом случае вы можете вообще ничего не понять.

Первое, что будет сделано - это легкое изменение кода, как показано во фрагменте ниже.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31.     double ly;
32. 
33.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
34.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
35. 
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         s += StringFormat("sy%d = %.4f  | ", c0, ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 50, s, ColorToARGB(clrBlack));
46. }
47. //+------------------------------------------------------------------+
48. void NewAngle(const char direct, const double step = 0.2)
49. {
50.     canvas.Erase(ColorToARGB(clrWhite, 255));
51. 
52.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
53.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
54.     canvas.TextOut(global.x, global.y + _SizeLine + 20, StringFormat("f(x) = %.8fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
55.     canvas.Line(
56.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
57.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
58.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
59.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
60.                 ColorToARGB(clrForestGreen)
61.             );
62.        
63.     Func_01();
64. 
65.     canvas.Update(true);
66. }
67. //+------------------------------------------------------------------+

Хотя всё происходит не самым оптимальным образом, результат, показанный в анимации ниже, представляет именно то, что мы хотим визуализировать:

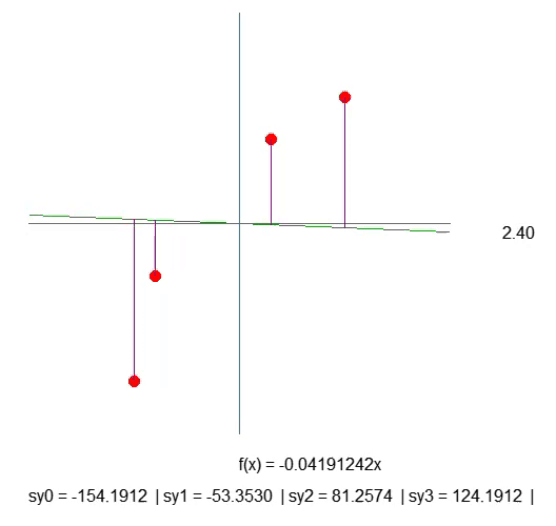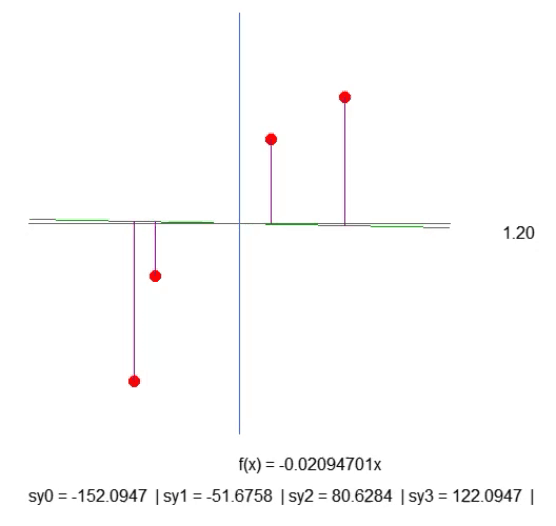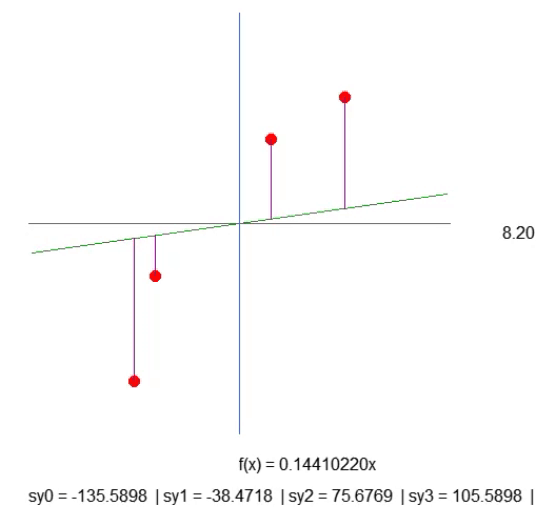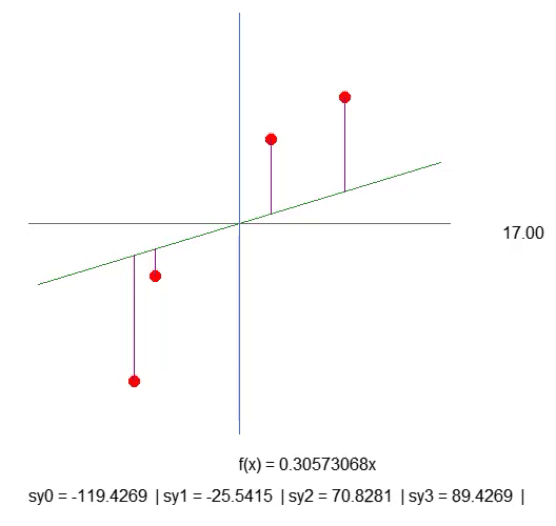
Мы просто создаем фиолетовую линию. Она показывает расстояние между прямой и точкой. Обратите внимание на это. Длина линии определяется по строке 41 фрагмента. Расчет не совсем такой, каким он должен быть, но он работает. Так что давайте не будем спешить, ведь позже нам понадобится изменить этот расчет. В строке 43 мы создаем текстовую строку, которая позволяет нам узнать длину данной фиолетовой линии. Когда мы посмотрим на анимацию, то заметим, что есть отрицательные длины, но это не имеет смысла. Пока рано беспокоиться об этом. Прежде всего я хочу, чтобы вы поняли суть нашей с вами работы.

А теперь я хочу, чтобы вы, дорогой читатель, немного поразмышляли. Функция прямой линии рассчитывается на основе коэффициента наклона. Данный коэффициент можно получить из угла, который мы изменяем, нажимая на стрелки вправо или влево. А скорость, с которой изменяется этот наклон, задается с помощью значения `step`, присутствующего в строке 52.

Тогда посмотрите на длину каждой из фиолетовых линий. Немного терпения, и мы сможем сделать наклон прямой линии как можно более крутым, чтобы длина каждой из фиолетовых линий перестала увеличиваться (она может уменьшаться, но не должна увеличиваться). Когда мы добьемся того, что ни одна из длин не будет расти, мы найдем идеальный коэффициент наклона.

Но обратите внимание на следующее: В данном случае нам надо рассмотреть всего четыре элемента, что довольно просто. Однако если бы в массиве были сотни или тысячи точек, регулировать вручную значения, чтобы они не увеличивались, было бы очень сложно. Мы можем использовать математический трюк, чтобы упростить данный процесс. Хитрость заключается в следующем: Если мы сложим значения длины каждой из фиолетовых линий, нам нужно будет наблюдать только за одним значением, и если оно начнет расти, то мы будем знать, что прошли оптимальную точку коэффициента наклона. Просто, не правда ли? Поэтому мы еще раз изменим фрагмент кода, как показано ниже.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

Результат можно увидеть в прилагаемой анимации. И вы заметите, что настраивать величины таким образом гораздо проще.

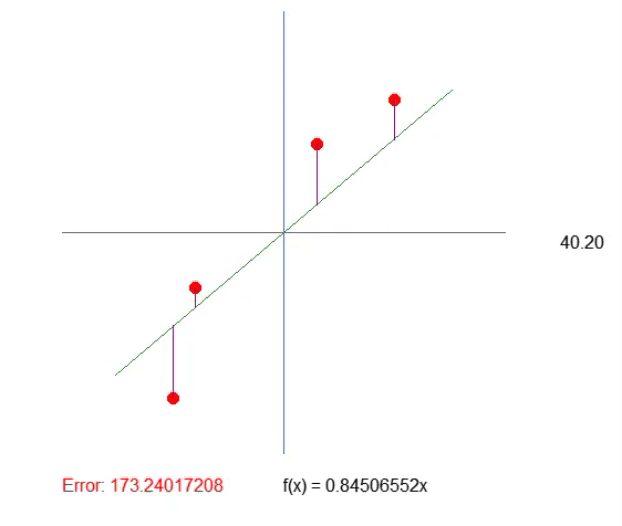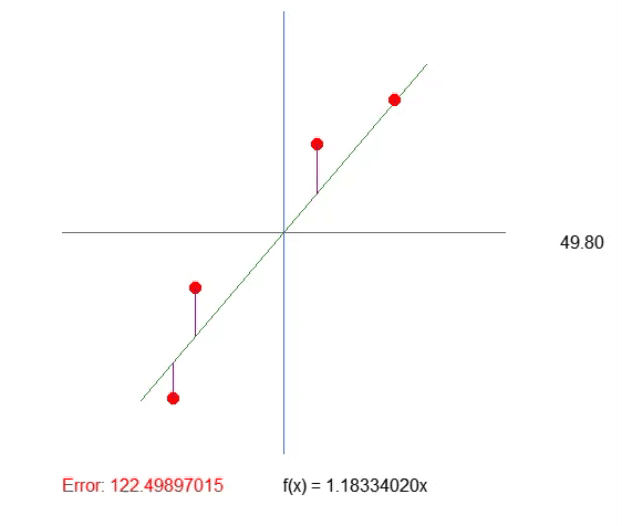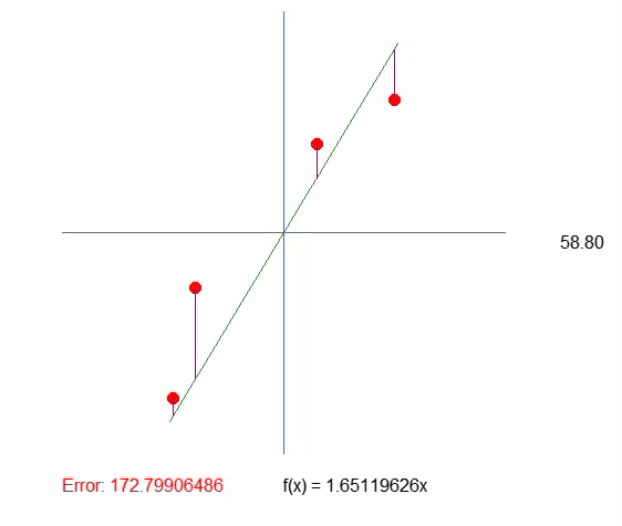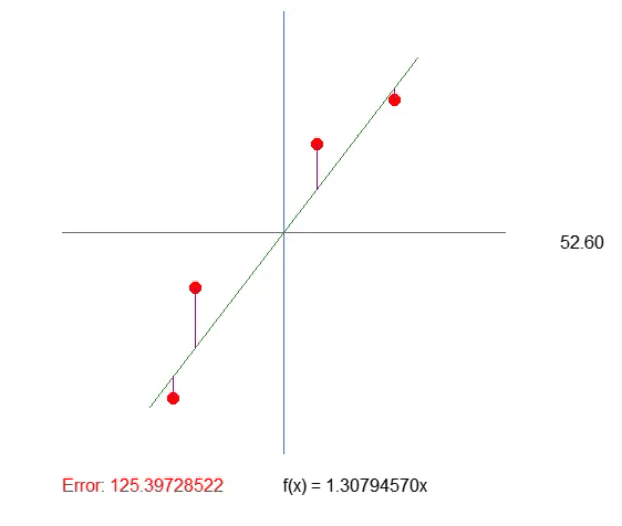
Регулировка квадранта

Прежде чем мы полностью погрузимся в математическую сторону, нам нужно сделать небольшую модификацию. Хотя она не будет напрямую влиять на то, что мы собираемся делать, она будет актуальна, если мы решим применить то, что объяснялось в других программах, или при проведении экспериментов вручную. Часто мы начинаем с того, что пробуем всё вручную, выполняя расчеты таким же образом. Это поможет вам избежать ошибки, когда мы слепо полагаемся на расчеты программы.

Даже если они совершенно неправильны. Начинающие программисты нередко допускают эту ошибку, и она может стоить немало времени и сил. В итоге они сосредотачиваются на решении проблемы неправильным образом. Каждый хороший программист - это еще и человек, который с большим подозрением относится к расчетам, которые он проводит. Всегда нужно пробовать разные способы, прежде чем сделать вывод о том, что мы можем быть уверены в результатах.

Я говорю вам об этом, потому что, хотя многие люди не обращают на это внимания (я сам иногда не обращаю), но когда мы создаем графическое изображение, мы всегда работаем в четвертом квадранте декартовой плоскости. Это влияет на всё. Не на сами вычисления, а на тех, кто хочет выполнить эти же вычисления вручную или в другой программе. Например, MatLab, SCILab или даже старый добрый Excel. В Excel, например, у нас есть возможность создать графическое представление значений и формул, которыми мы здесь пользуемся.

Это хорошо, но какое отношение имеет всё это к тому, что мы собираемся сделать? Что ж, дорогой читатель, если посмотреть на матрицу данных, которая находится в программе, то можно заметить, что она немного странная по сравнению с тем, что представлено на графике. Если мы построим те же значения в другой графической программе, то увидим, что ось Y перевернута. Но как это происходит, я так и не понял. Не торопитесь, посмотрите на изображения ниже, чтобы лучше понять.

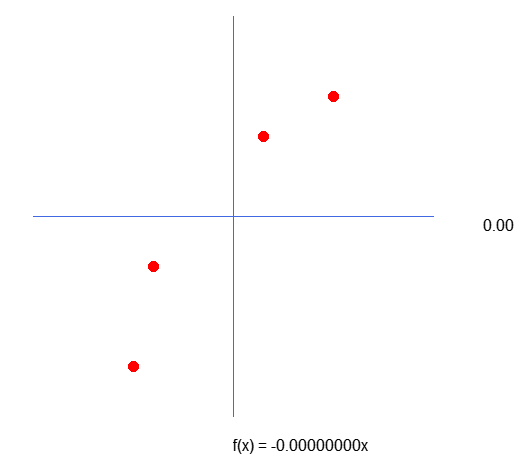
Приведенное выше изображение показано при построении графика в MetaTrader 5. Однако при построении тех же значений, например, в Excel, график будет выглядеть следующим образом:

Подобное несоответствие может привести к тому, что большинство тестов, которые нужно выполнить, окажутся совершенно непонятными. Особенно если понадобится проверить, правильно ли выполняются расчеты.

В предыдущей теме мы уже разобрались с тем, как правильно представлять данные. Теперь нам нужно исправить эту проблему. Дело в том, что ось Y перевернута (или зеркальна).

Почему происходит этот сбой в представлении?! Причина проста, мы о ней упомянули в самом начале темы. Экран, на который мы наносим данные, находится в четвертом квадранте. Это связано с тем, что начало координат, то есть точка (0, 0), находится в левом верхнем углу. Теперь обратите внимание! Даже если мы изменим точку отсчета на центр экрана, этот перенос будет только виртуальным. Это означает, что мы не меняем физическую точку отсчета. Мы просто переносим представление вычислений в другую точку отсчета. По этой причине в программе мы добавляем значения точки в матрице к другому набору точек. Это нам позволяет перенести виртуальное начало координат из левого верхнего угла в любое другое место на экране.

Но вы, возможно, заметили, что на изображении выше есть проблема с тем, как мы реализуем данную виртуализацию. Ось Y перевернута или зеркально отражена. Чтобы исправить это, нам надо изменить несколько моментов в коде. Это просто, но оно сделает всё намного понятнее.

В коде мы внесем следующие изменения, которые можно увидеть во фрагменте ниже:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
41.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
42.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

Обратите внимание, что изменения очень тонкие. Сначала мы изменяем значения в матрице. Затем мы изменим расчет в строке 40, чтобы точки правильно расположились. Также необходимо изменить строки 41 и 42, в которых производятся расчеты для правильного соединения фиолетовых линий с точками. Данный вид коррекций, даже если они носят в основном эстетический характер, дает уверенность тем, кто хочет провести более глубокое изучение вопроса. Ведь теперь мы сможем сравнивать сгенерированные графики, не думая, что в одной или другой программе что-то было плохо рассчитано. Процесс стал намного проще.

И реализация задачи теперь тоже гораздо проще. Поскольку, если значение ошибки увеличивается, значит, мы движемся в неправильном направлении. Если оно уменьшится, значит, мы движемся в правильном направлении.

Хорошо, но теперь возникает другой вопрос, и с этого момента мы начнем вникать в то, что управляет темой нейронных сетей. Корректировка наклона касательной прямой или коэффициента наклона довольно проста, если посмотреть на значение ошибки. Но есть ли способ настроить его автоматически? Или, скорее, создать механизм, позволяющий машине искать наилучшее значение коэффициента. Необходимо помнить, что сейчас мы используем только одну переменную в системе, поскольку касательная прямая проходит точно через точку (0, 0), которая является началом декартовой плоскости. Но это не всегда так. Однако, давайте сначала решим этот более простой вопрос. Именно в этом случае нам нужно регулировать только одну переменную.

Если вы поняли предыдущую статью, то должны были заметить, что я упоминал, как вычислить секущую прямую так, чтобы она стала касательной. Хорошо, но даже если это сработает, давайте подумаем о другой гипотезе, чуть более простой, в которой нам не нужно будет зацикливаться, чтобы найти значение углового коэффициента. Давайте попробуем найти формулу, чтобы коэффициент можно было вычислить быстрее и проще.

Для этого нам нужно применить некоторые математические хитрости. Для большей ясности изложения, мы рассмотрим это в новой теме.

В поисках минимально возможной площади

Если вы изучали тему искусственного интеллекта, то должны были заметить, что в ней постоянно что-то упоминается. Но не нужно путать искусственный интеллект с нейронными сетями. Несмотря на то, что эти два понятия коррелируют, подходить к ним надо по-разному. Это с точки зрения программирования. Есть несколько небольших отличий, но здесь я намерен создать нейронную сеть, которая сможет найти уравнение, наилучшим образом отражающее значения в базе данных. Данный вид вычислений выполняется нейронной сетью. Искусственный интеллект ищет на базовом уровне. Нейронная сеть создает основу.

В этом случае мы уже можем начать использовать для этого нейроны, но, на мой взгляд, пока еще рановато. Мы можем сами создать расчеты для этого, это позволит сэкономить огромное количество времени на обработку.

Для того, чтобы вычислить или создать расчет для нахождения углового коэффициента, мы будем использовать производные. Мы можем реализовать это и другим способом, но здесь мы будем использовать производные, это самый быстрый способ. Я предположу, что вы поняли всё, что объяснялось в предыдущей теме, чтобы можно было продвигаться дальше. Теперь перейдем к математической части вопроса.

Чтобы вычислить погрешность, мы выполним следующий математический расчет.

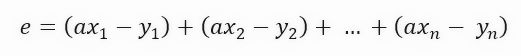
Значение константы < a >, которое можно увидеть в формуле, как раз и является угловым коэффициентом прямой линии, то есть это значение касательной прямой, которая создается. Очень хорошо, но данная формула недостаточно компактна. Мы можем упростить её, сделав так, чтобы формула стала немного более компактной, как показано ниже.

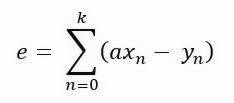
Хотя они выглядят как разные формулы, они представляют одно и то же, только нотация была изменена на более компактную. Поскольку она более компактна, это облегчит написание формул, которые мы разработаем ниже. Обратите внимание, что на каждом шаге мы имеем сумму значений, которая является длиной фиолетовой линии на графике, который был показан в предыдущей теме. Такие вещи не позволяют нам использовать производные, ведь если мы попытаемся вывести такую формулировку, то в результате получим нулевую константу. Но мы хотим получить результат, представленный в формуле ниже.

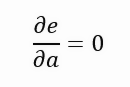
Таким образом, мы хотим вывести погрешность относительно углового коэффициента прямой линии, и по мере того, как это значение стремится к нулю, угловой коэффициент становится всё ближе и ближе к идеальному значению. В принципе, такова наша идея, однако это значение вряд ли будет равно нулю. Он может приближаться к нулю, и чем ближе к нему, тем лучше, но, как я уже говорил, мы не можем вывести функцию, определяющую длину фиолетовой линии. Но, тем не менее, выход есть. Это нужно для того, чтобы превратить фиолетовую линию в квадратную фигуру, и при этом мы ищем не минимальную длину линии, а наименьшую возможную площадь квадрата, который образован каждой из линий. Таким образом, мы получим новую формулировку, представленную ниже.

Обратите внимание, что теперь (хотя это и не похоже на правду) мы вычисляем один и тот же коэффициент, только на этот раз используем площадь квадрата, образованного каждой из фиолетовых линий на графике. Всё становится гораздо интереснее. Если развить это уравнение, то мы получим то, что показано ниже.

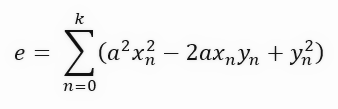
Возможно, вы не поняли, что мы только что сделали. Но это уравнение, которое возникло просто при изменении вычисления от длины линии к площади квадрата, на самом деле очень интересное уравнение. Вы видите это?! Можете ли вы сказать мне, что это за уравнение? Да или нет?

Если вы не можете понять, что это за уравнение, не волнуйтесь, не надо расстраиваться. Это уравнение - ни что иное, как квадратное уравнение. Верно, это то же самое уравнение, которое порождает параболу, и, следовательно, это уравнение, которое позволяет нам создать производную первой степени. Помните, что мы хотим получить производную по отношению к угловому коэффициенту. Но перед этим я добавлю еще один шаг, который мы обычно не совершаем. Я хочу показать вам, почему итоговая формула выглядит именно так. Этот дополнительный шаг заключается в группировке терминов и их соответствующем разделении так, как показано ниже.

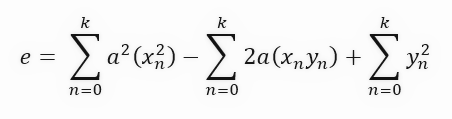
Мы упростили уравнение, чтобы его было легче понять, когда мы будем делать вывод. Обычно этот дополнительный шаг не выполняется; мы сразу переходим к окончательной формуле, которую вы видите ниже.

Матерь Божья! Да помилует нас всех Господь. Теперь всё стало очень сложно; я вообще ничего не понимаю, как это возможно, что это за безумные вычисления, как я смогу реализовать всё это в коде?! Всё под контролем. Сохраняйте спокойствие. Обычно я не люблю показывать формулы, чтобы не запутать читателя. И в то же время, всё очень просто: это вычисление как раз и является той производной, которую нам нужно вычислить. Таким образом, мы получим приблизительное значение углового коэффициента прямой линии.

Давайте теперь переведем это в формат кода и посмотрим, что получится. Это видно по приведенному ниже фрагменту.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err, d0, d1;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = d0 = d1 = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         d0 += (vx * vy);
41.         d1 += MathPow(vx, 2);
42.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
43.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
44.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
45.         err += MathAbs(ly);
46.     }
47.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
48.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 40, StringFormat("(de/da) : %.8f", d0 / d1), ColorToARGB(clrForestGreen));
49. }
50. //+------------------------------------------------------------------+

Обратите внимание: в отличие от того, что можно себе представить, глядя на все эти формулы, выполнение фактических вычислений в коде довольно просто и понятно. В строке 40 мы вычисляем сумму точек. Уже в строке 41 мы вычисляем квадрат точек в X. Это всё очень просто. В строке 48 мы выводим значение графика. Теперь слушайте внимательно: Это найденное значение является идеальным, если в уравнении прямой мы берем только одну переменную. Чтобы вы поняли то, что я пытаюсь донести, посмотрите на формулу уравнения прямой линии. Это можно увидеть чуть ниже.

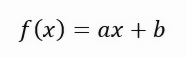
В этом уравнении значение < a > является именно угловым коэффициентом. Значение < b > указывает на точку, в которой находится корень уравнения. Для тех, кто не знает, корни уравнения - это точки, в которых кривая или прямая линия (в данном случае) касается оси Y, когда значение X равно нулю. Тогда, поскольку значение < b > в этом решении равно нулю, то возвращаемое значение в качестве идеального значения показывает всего лишь то, что должно быть угловым коэффициентом, наиболее близким к идеальному. Но это не означает, что он действительно правильный, поскольку мы говорим, что корень уравнения находится точно в начале координат, то есть X и Y равны нулю. А в реальности такое случается редко, настолько редко, что при запуске этого приложения, мы получим в результате анимацию, показанную ниже.

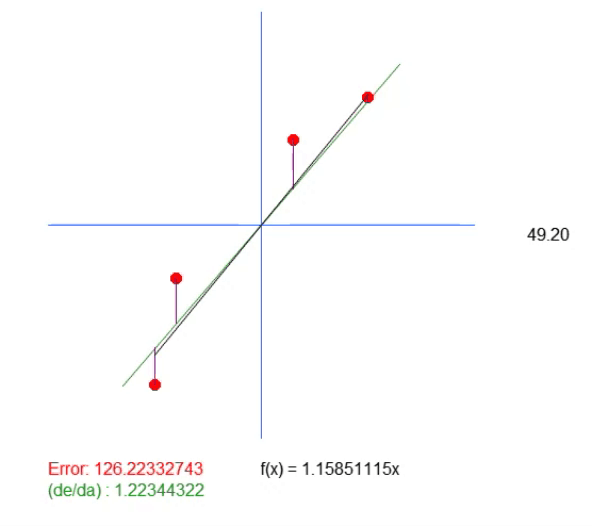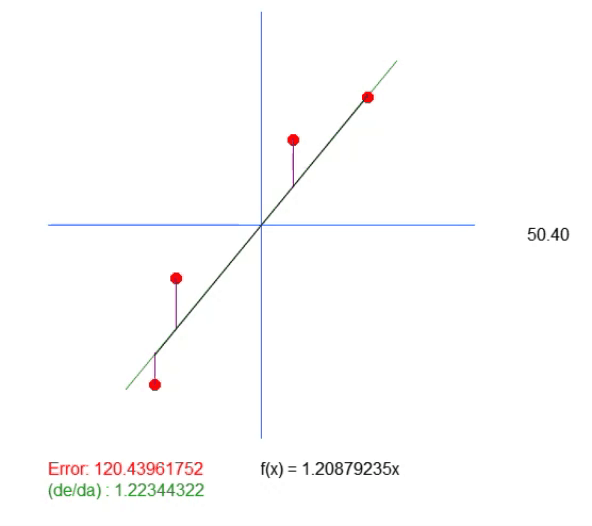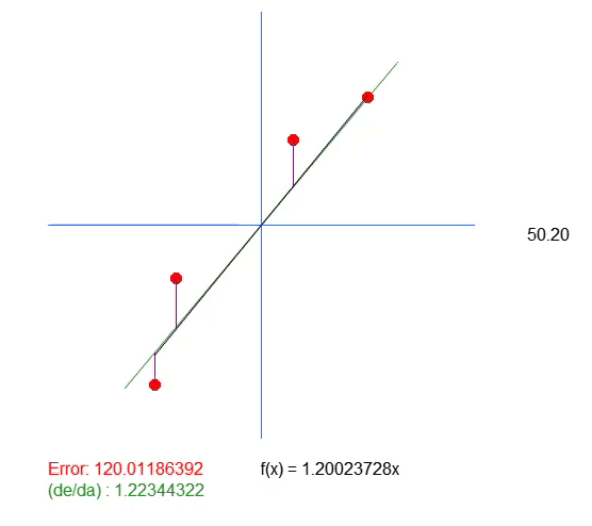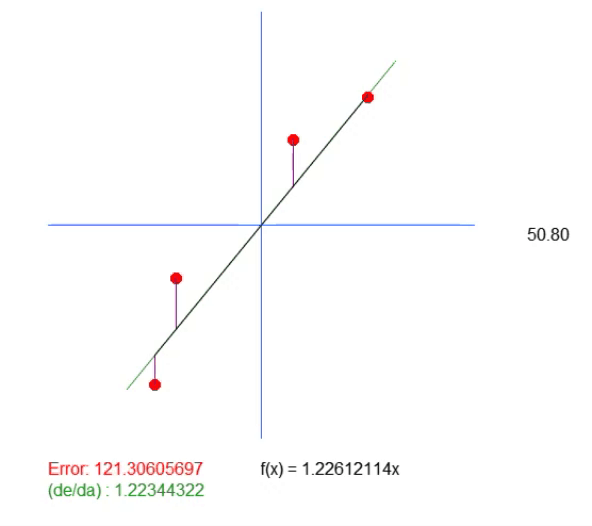
Обратите внимание: в этой анимации есть нижняя линия. Она нужна только для того, чтобы показать, где будет находиться рассчитанное идеальное значение. Но если смотреть на величину ошибки, то можно заметить, что коэффициент в уравнении немного отличается от того, что показано зеленым цветом.

Данное зеленое значение как раз соответствует тому, которое мы рассчитали на основе разработанного уравнения. Можно заметить, что простое вычисление значения углового коэффициента здесь недостаточно. Нам нужно уравнение создаваемой прямой линии, а для этого, помимо значения < a >, мы также должны получить значение < b >. Это нужно для того, чтобы иметь более общее решение и не быть привязанным к точке (0, 0).

Данная точка (0, 0), которая фактически не является частью базы данных, оказывает неявное влияние на результаты расчетов углового коэффициента. Однако, чтобы удалить эту точку должным образом, мы должны изменить несколько моментов в приложении, чтобы вы могли выйти из этой точки отсчета, которая находится точно в (0, 0).

Передвигаем корень функции прямой

Поскольку нам нужно подготовить приложение к дальнейшей работе (о чем пойдет речь в следующей статье), мы создадим довольно любопытный механизм в оставшейся части этой статьи. Позже в следующей части, мы сможем сосредоточиться на математической стороне.

Добавление этого механизма не требует от нас особых изменений в коде. Однако эффект будет весьма значительным, так как позволит нам найти уравнение прямой линии, при котором мы получим наименьшую возможную площадь в любой ситуации. Таким образом, создается общий механизм для поиска наиболее подходящих констант, и это необходимо для того, чтобы линейная регрессия, которая будет построена на графике, более адекватно отражала базу данных.

Внести эти изменения очень просты. Всё, что нам нужно сделать, - это перенести корень функции прямой линии. Эти слова кажутся немного сложными, но когда мы реализуем их в коде, всё становится довольно простым, как можно видеть ниже.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define _ToRadians(A) (A * (M_PI / 180.0))
009. #define _SizeLine 200
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y;
017.     double  Angle,
018.             Const_B;
019. }global;
020. //+------------------------------------------------------------------+
021. void PlotText(const uchar line, const string sz0)
022. {
023.     uint w, h;
024. 
025.     TextGetSize(sz0, w, h);
026.     canvas.TextOut(global.x - (w / 2), global.y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
027. }
028. //+------------------------------------------------------------------+
029. void Func_01(void)
030. {
031.     int A[]={
032.                 -100, -150,
033.                  -80,  -50,
034.                   30,   80,
035.                  100,  120
036.             };
037. 
038.     int vx, vy;
039.     double ly, err;
040.     string s0 = "";
041. 
042.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
043.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
044. 
045.     err = 0;
046.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
047.     {
048.         vx = A[c1++];
049.         vy = A[c1++];
050.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
051.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
052.         s0 += StringFormat("%.4f || ", MathAbs(ly));
053.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
054.         err += MathPow(ly, 2);
055.     }
056.     PlotText(3, StringFormat("Error: %.8f", err));
057.     PlotText(4, s0);
058. }
059. //+------------------------------------------------------------------+
060. void NewAngle(const char direct, const char updow, const double step = 0.1)
061. {
062.     canvas.Erase(ColorToARGB(clrWhite, 255));
063. 
064.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
065.     global.Const_B += (step * updow);  
066.     PlotText(1, StringFormat("Angle in graus => %.2f", MathAbs(global.Angle)));
067.     PlotText(2, StringFormat("f(x) = %.4fx %c %.4f", -MathTan(_ToRadians(global.Angle)), (global.Const_B < 0 ? '-' : '+'), MathAbs(global.Const_B)));
068.     canvas.LineAA(
069.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
070.                 (global.y - (int)global.Const_B) - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
071.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
072.                 (global.y - (int)global.Const_B) + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
073.                 ColorToARGB(clrForestGreen)
074.             );
075.        
076.     Func_01();
077. 
078.     canvas.Update(true);
079. }
080. //+------------------------------------------------------------------+
081. int OnInit()
082. {    
083.     global.Angle = 0;
084.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
085.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
086. 
087.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
088.     global.x /= 2;
089.     global.y /= 2;
090.         
091.     NewAngle(0, 0);
092. 
093.     canvas.Update(true);
094.     
095.     return INIT_SUCCEEDED;
096. }
097. //+------------------------------------------------------------------+
098. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
099. {
100.     return rates_total;
101. }
102. //+------------------------------------------------------------------+
103. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
104. {
105.     switch (id)
106.     {
107.         case CHARTEVENT_KEYDOWN:
108.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
109.                 NewAngle(-1, 0);
110.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
111.                 NewAngle(1, 0);
112.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_UP))
113.                 NewAngle(0, 1);
114.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_DOWN))
115.                 NewAngle(0, -1);
116.             break;
117.     }
118. }
119. //+------------------------------------------------------------------+
120. void OnDeinit(const int reason)
121. {
122.     canvas.Destroy();
123. }
124. //+------------------------------------------------------------------+

Вот результат:

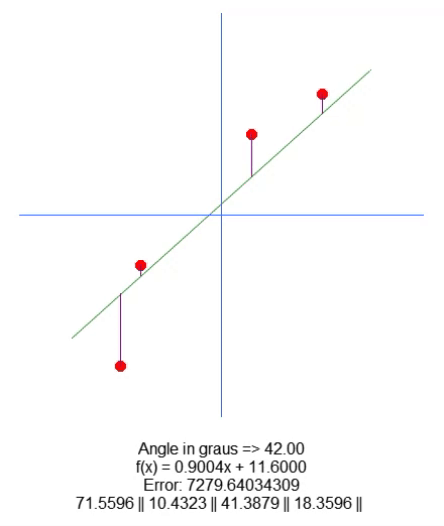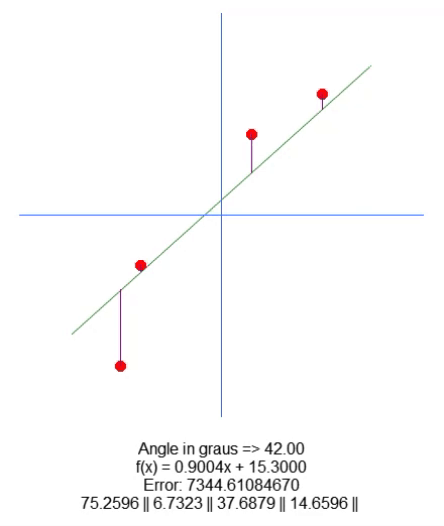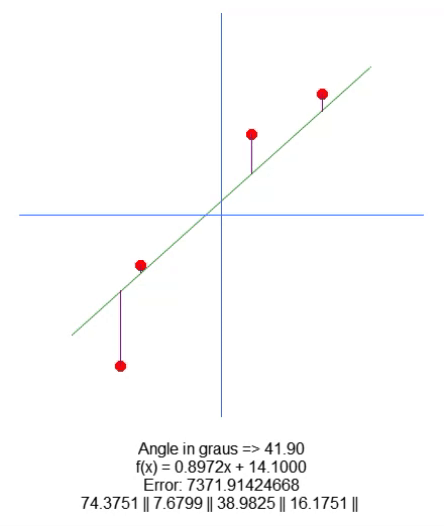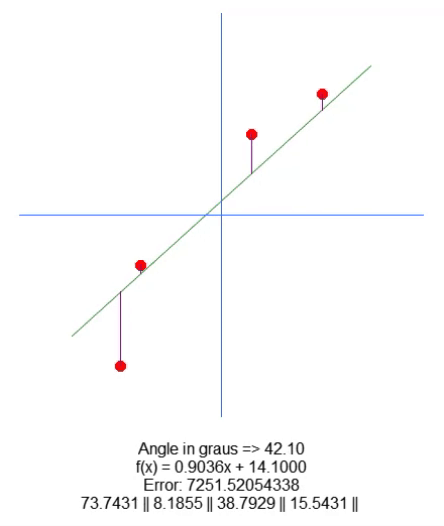
По сути, всё, что требовалось для перемещения корня, - это добавить переменную в строку 18. И с помощью стрелок вверх и вниз мы можем менять значение этой переменной в строке 65. Всё остальное довольно просто. Нам только нужно скорректировать значение длины фиолетовой линии, основываясь на значении этой новой переменной, присутствующей в коде. Я уверен, что мне не нужно объяснять, как это делается, поскольку это очень просто.

Заключительные идеи

В этой статье мы увидели, что математические формулы часто выглядят гораздо сложнее, чем их реализация в коде. Многие считают, что заниматься подобными вещами сложно, но здесь мы показали, что всё гораздо проще, чем кажется. Однако мы еще не выполнили всю работу. Мы реализовали лишь часть. Теперь нам нужно найти способ составить уравнение прямой более подходящим способом. Для этого мы используем последний код из данной статьи. В отличие от того, что вы могли себе представить в начале этой темы, найти функцию прямой линии, проходящей через цикл, не так просто, как казалось. Это происходит, потому что мы добавляем еще одну переменную для поиска. Только подумайте, сколько работы потребовалось бы, чтобы найти уравнение, если бы у нас был миллион переменных. Сделать это грубой силой было бы совершенно невозможно, но при правильном использовании математики найти уравнение гораздо проще.

И последняя деталь: прежде чем перейти к следующей статье, используйте код, приведенный в конце. Он генерирует последнюю анимацию, чтобы попытаться найти уравнение. Вы увидите, что это довольно сложная задача. Так что до встречи в следующей статье.