Schätzung der zukünftigen Leistung mit Konfidenzintervallen

Einführung

Die Entwicklung profitabler automatisierter Handelssysteme ist keine leichte Aufgabe. Selbst wenn man einen profitablen Expert Advisor erstellt, stellt sich die Frage, ob sich das Risiko lohnt. Wir könnten uns damit zufrieden geben, dass unsere Strategie nicht das gesamte ihr zugewiesene Kapital aufbrauchen wird, aber das ist kein Grund, den Live-Handel sofort zu aktivieren. Letztendlich ist der Gewinn das Motiv, und wenn wir später feststellen, dass unsere Strategie zwar profitabel ist, aber nicht profitabel genug, um das Risiko zu rechtfertigen, oder im Vergleich zu anderen Anlagemöglichkeiten schlechte Renditen erzielt, werden wir das zweifellos sehr bedauern.

Daher werden wir in diesem Artikel Techniken aus der Statistik untersuchen, die uns helfen können, die zukünftige Leistung eines automatisierten Handelssystems anhand von Daten zu schätzen, die bei Out-of-Sample-Tests gesammelt wurden.

Ist das gut genug?

Wenn wir ein potenzielles Handelssystem testen, erhalten wir natürlich eine Sammlung von verschiedenen Leistungskennzahlen. Diese Daten geben uns intuitiv einen Hinweis auf das Gewinnpotenzial des Systems, aber diese Intuition ist möglicherweise nicht ausreichend. Eine Strategie, die beim Testen viel Gewinn abgeworfen hat, kann beim Live-Handel weniger sternengleiche Renditen erzielen. Gibt es eine Möglichkeit, eine bessere Vorstellung davon zu bekommen, ob die bei den Tests beobachtete Leistung auf demselben Niveau bleibt? Wenn nicht, wie schlecht wird die Leistung dann sein?

Hier könnten statistische Standardmethoden helfen. Es ist anzumerken, dass die hier erörterten Techniken nicht dazu gedacht sind, genaue Schätzungen vorzunehmen, und dass sie dies auch niemals sein werden. Sie bieten Methoden zur Identifizierung von Strategien, die mit hoher Wahrscheinlichkeit einen signifikanten oder akzeptablen Gewinn erzielen.

Ich habe viele gesehen, die rohe Sharpe-Ratio-Zahlen verwenden, um wahrscheinlichkeitsbasierte Annahmen über die zukünftige Performance zu treffen. Dies ist gefährlich, denn die Ergebnisse der Vergangenheit sind kein Hinweis auf künftige Gewinne. Mit den Finanzmärkten ist nicht zu spaßen. Die Kurscharts drehen sich in die eine oder andere Richtung, oft aus unbekannten Gründen. Wir wollen geeignete wahrscheinlichkeitsbasierte Leistungsprognosen berechnen, die wir bei unseren Entscheidungsprozessen anwenden können.

Konfidenzintervalle

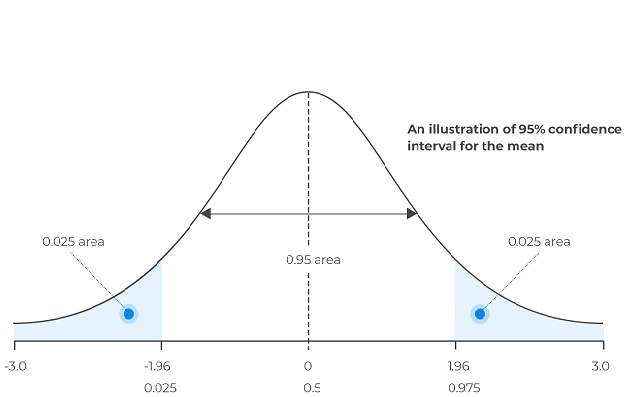
Ein Konfidenzintervall bezieht sich auf die Wahrscheinlichkeit, dass eine bestimmte statistische Größe einer Datensammlung oder einer Population für einen bestimmten Zeitraum innerhalb eines bestimmten Bereichs liegt. Sie messen den Grad der Gewissheit, indem sie die Wahrscheinlichkeit berechnen, dass die berechneten Werte die wahre Statistik enthalten, die geschätzt wird. Statistiker verwenden in der Regel Konfidenzniveaus von 90 % bis 99 %. Diese Intervalle können mit verschiedenen Methoden berechnet werden. In diesem Artikel werden wir uns auf einige gängige Boostrap-Techniken konzentrieren.

Der Bootstrap

Das Bootstrapping-Verfahren ist ein Verfahren, bei dem eine Sammlung von Daten verwendet wird, um zahlreiche weitere neue Datensätze zu erstellen, indem eine zufällige Auswahl aus den Originaldaten getroffen wird. Die neuen Datensätze haben die gleichen Mitglieder wie das Original, aber einige Mitglieder in den neuen Datensätzen sind Duplikate.

Original	Bootstrap1	Bootstrap2	Bootstrap3	Bootstrap4
A	A	A	A	B
B	A	B	B	B
C	B	B	B	C
D	C	D	C	D
E	D	E	C	E

Die obige Tabelle veranschaulicht dies besser. Die Originalspalte enthält den Originaldatensatz, die anderen Spalten stellen aus dem Original konstruierte Datensätze dar. Wie man sieht, haben die Bootstrap-Spalten ein oder mehrere Duplikate. Indem wir dies viele Male tun, können wir viele Daten generieren, die Proben repräsentieren, die wir derzeit nicht beobachten können oder die uns unbekannt wären. In dem Artikel „Anwendung der Monte-Carlo-Methode zur Optimierung von Handelsstrategien“ haben wir bereits Beispiele für die Anwendung des Bootstrap auf den Handel gesehen.

Der Kern der Bootstrapping-Theorie besteht darin, dass der ursprüngliche Datensatz repräsentativ für eine größere Datensammlung, die Grundgesamtheit, sein sollte, die nicht beobachtet werden kann und die man zu modellieren versucht. Wenn wir also diese Bootstraps erstellen, werden sie zu Proxys der unbeobachtbaren Stichprobe. Die statistischen Eigenschaften dieser Bootstraps können zusammen mit der ursprünglichen Stichprobe verwendet werden, um Rückschlüsse auf die unbekannte und/oder nicht beobachtbare Population zu ziehen.

Bootstrapping-Konfidenzintervalle

Es werden drei Methoden zur Verstärkung von Konfidenzintervallen demonstriert. Dabei handelt es sich um die Pivot-Methode, die Perzentil-Methode und schließlich die bias-korrigierte und beschleunigte Methode (bcd).

Die Methode Pivotstatistik umfasst die Erstellung zahlreicher Bootstraps, die zur Berechnung der Teststatistiken verwendet werden. Eine Teststatistik bezieht sich auf ein beliebiges Merkmal der Grundgesamtheit, das wir zu schätzen versuchen, z. B. den Mittelwert oder den Median. Die geschätzten Grenzen werden dann gefunden, indem der Wert der Teststatistik aus dem ursprünglichen Datensatz relativ zu dem Wert angepasst wird, der erforderlich ist, um den Erwartungswert der Bootstrap-Stichproben auf den ursprünglichen Wert zu erhöhen.

Bei der Perzentil-Method wird die Verteilung der berechneten Teststatistiken aus den Bootstrap-Stichproben berücksichtigt, wobei davon ausgegangen wird, dass diese Verteilung derjenigen der unbekannten Grundgesamtheit ähnlich ist. Die Grenzen werden zu dem Intervall zwischen den Perzentilen der Verteilung der berechneten Teststatistiken, die aus den Bootstrap-Stichproben gewonnen wurden.  

Die bias-korrigierte und beschleunigte Methode ist etwas anspruchsvoller. Nach der Erstellung unserer Bootstraps und der Berechnung der Teststatistiken für jeden. Wir berechnen den Bias-Korrekturfaktor, der den Anteil der Bootstrap-Schätzungen angibt, der unter dem des Originaldatensatzes liegt. Dann wird der Beschleunigungsfaktor mit Hilfe einer Methode namens Jackknife-Methode berechnet. Dies ist eine weitere Resampling-Methode zur Schätzung des Ausmaßes, in dem die Varianz der transformierten Teststatistik von ihrem Wert abhängt.

Die Perzentilmethode wird dann zur Berechnung der unteren und oberen Grenzen verwendet, die entsprechend der Verzerrungskorrektur und den Beschleunigungsfaktoren geändert werden. Die endgültigen Konfidenzintervalle ergeben sich aus den geänderten Werten, nachdem sie sortiert wurden.

Sehen wir uns an, wie diese Techniken in Code umgesetzt werden können.

Die Klasse CBoostrap

CBoostrap ist eine Klasse, die die Berechnung von Konfidenzintervallen unter Verwendung der drei soeben beschriebenen Bootstrap-Methoden kapselt. Damit können die Nutzer Konfidenzintervalle für mehrere konfigurierbare Wahrscheinlichkeiten berechnen und auch die Anzahl der zu erzeugenden Bootstraps angeben.

#include<Math\Alglib\specialfunctions.mqh>
#include<Math\Stat\Math.mqh>
#include<UniformRandom.mqh>

Die Definition der Klasse beginnt mit der Aufnahme einiger wesentlicher mathematischer Hilfsprogramme aus der Standardbibliothek.

//+------------------------------------------------------------------+
//|Function pointer                                                  |
//+------------------------------------------------------------------+
typedef double(*BootStrapFunction)(double &in[],int stop=-1);

Der Funktionszeiger BootStrapFunction definiert eine Funktionssignatur zur Berechnung der Teststatistik oder der Populationsparameter.

//+------------------------------------------------------------------+
//|Boot strap types                                                  |
//+------------------------------------------------------------------+
enum ENUM_BOOSTRAP_TYPE
  {
   ENUM_BOOTSTRAP_PIVOT=0,
   ENUM_BOOTSTRAP_PERCENTILE,
   ENUM_BOOTSTRAP_BCA
  };

Die Enumeration ENUM_BOOSTRAP_TYPE erleichtert die Auswahl einer bestimmten Boostrap-Berechnungsmethode: z.B. Pivot, Percentile oder BCA.

//+------------------------------------------------------------------+
//|Constructor                                                       |
//+------------------------------------------------------------------+
CBootstrap::CBootstrap(const ENUM_BOOSTRAP_TYPE boot_type,const uint nboot,const BootStrapFunction function,double &in_samples[])
  {
//--- set the function pointer
   m_function=function;
//--- optimistic initilization of flag
   m_initialized=true;
//--- set method of boostrap to be applied
   m_boot_type=boot_type;
//--- set number of boostrap iterations
   m_replications=nboot;
//---make sure there are at least 5 boostraps
   if(m_replications<5)
      m_initialized=false;
//--- initilize random number generator
   m_unifrand=new CUniFrand();
   if(m_unifrand!=NULL)
      m_unifrand.SetSeed(MathRand());
   else
      m_initialized=false;
//--- copy samples to internal buffer
   if(ArrayCopy(m_data,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- initialize shuffled buffer
   if(ArrayCopy(m_shuffled,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- set memory for bootstrap calculations container
   if(ArrayResize(m_rep_cal,(int)m_replications)!=(int)m_replications)
     {
      Print("Memory allocation error ", GetLastError());
      m_initialized=false;
     }
//--- check function pointer
   if(m_function==NULL)
     {
      Print("Invalid function pointer");
      m_initialized=false;
     }
  }

CBoostrap wird durch einen parametrischen Konstruktor definiert, dessen Eingabeparameter die Art einer Boostrap-Operation bestimmen:

• boot_type - legt die Methode der Boostrap-Berechnung fest.

• nboot - steht für die Anzahl der gewünschten Boostrap-Stichproben, die erzeugt werden sollen. Es wird empfohlen, mindestens 100 zu verwenden, obwohl es idealer ist, Tausende zu erzeugen, um zuverlässige Ergebnisse zu erhalten.

• function - verweist auf eine vom Nutzer bereitgestellte Funktionsdefinition zur Berechnung des zu schätzenden Populationsparameters. Die Parameter dieser Funktion sind ein Array der Datenproben, die zur Berechnung der Teststatistik verwendet werden. Der Standard-Integer-Parameter des Funktionszeigers definiert die Anzahl der Arrayelemente, die für die Berechnung verwendet werden.

• Schließlich ist das Array in_samples der Datencontainer, aus dem die Bootstraps generiert werden. Derselbe Datensatz und Bootstrap-Variationen davon werden an den Funktionszeiger zur Berechnung der Teststatistik übergeben.

//+------------------------------------------------------------------+
//| public method for calculating confidence intervals               |
//+------------------------------------------------------------------+
bool CBootstrap::CalculateConfidenceIntervals(double &in_out_conf[])
  {
//--- safety check
   if(!m_initialized)
     {
      ZeroMemory(in_out_conf);
      return m_initialized;
     }
//--- check input parameter values
   if(ArraySize(in_out_conf)<=0 ||
      in_out_conf[ArrayMaximum(in_out_conf)]>=1 ||
      in_out_conf[ArrayMinimum(in_out_conf)]<=0)
     {
      Print("Invalid input values for function ",__FUNCTION__,"\n All values should be probabilities between 0 and 1");
      return false;
     }
//--- do bootstrap based on chosen method
   switch(m_boot_type)
     {
      case ENUM_BOOTSTRAP_PIVOT:
         return pivot_boot(in_out_conf);
      case ENUM_BOOTSTRAP_PERCENTILE:
         return percentile_boot(in_out_conf);
      case ENUM_BOOTSTRAP_BCA:
         return bca_boot(in_out_conf);
      default:
         return false;
     }
//---
  }

Eine von nur zwei öffentlich verfügbaren Methoden für die Klasse CalculateConfidenceIntervals() nimmt als Eingabe ein Array von Wahrscheinlichkeitswerten. So viele, wie der Nutzer möchte. Diese Werte geben die Wahrscheinlichkeiten an, dass der wahre Parameterwert innerhalb des berechneten Intervalls liegt.

Um beispielsweise Konfidenzintervalle zu berechnen, deren Wahrscheinlichkeit 90 % beträgt, würde der Nutzer ein Array mit dem Wert 0,9 angeben, woraufhin die Methode ein Wertepaar zurückgibt. Die zurückgegebenen Werte werden in das gleiche Array geschrieben, das als Eingabe übergeben wurde. Für jedes einzelne Element der Eingabematrix ersetzt die Methode ein Wertepaar, wobei der erste Wert jedes Paares die untere Grenze des Intervalls und der zweite die obere Grenze darstellt.

Wie bereits erwähnt, ist es möglich, mehr als ein Konfidenzintervall mit unterschiedlichen Wahrscheinlichkeiten anzufordern. Die Ausgabe ordnet die Grenzen in der Reihenfolge der geringsten Wahrscheinlichkeit bis zur höchsten, die als Eingabe angegeben wurde.

Bevor wir die Verwendung der Klasse demonstrieren, müssen wir festlegen, welche Daten wir zur Messung der Leistung einer Handelsstrategie verwenden werden. In der Regel ist es üblich, die Leistung einer Strategie nach der Rendite zu klassifizieren. Um diesen Wert zu berechnen, müssen sowohl die Aktienkurve als auch die Renditereihen untersucht werden.

Anhand der Renditereihen einer Strategie können wir verschiedene Leistungskennzahlen berechnen. Der Einfachheit halber verwenden wir die mittlere annualisierte Rendite als Teststatistik, deren zukünftigen Wert wir mit einer bestimmten Wahrscheinlichkeit schätzen wollen.

Anhand dieser Teststatistik können wir die niedrigsten durchschnittlichen Erträge abschätzen, die wir für eine Strategie erwarten können. Auch das obere Konfidenzniveau gibt eine ungefähre Vorstellung davon, wie gut die Leistung sein wird, wenn alles gut läuft.

Die Klasse CReturns

Um die Renditereihen zu sammeln, die zur Annäherung an die künftige mittlere Rendite benötigt werden, verwenden wir die Klasse CReturns. Der Code der Klasse aus dem Artikel „Mathematik im Handel: Sharpe- und Sortino-Kennzahlen“ wurde angepasst. Ein besonderes Merkmal dieser Version ist die Möglichkeit, die Art der Renditereihen auszuwählen, die für die Leistungsberechnungen verwendet werden sollen.

//+------------------------------------------------------------------+
//| Class for calculating Sharpe Ratio in the tester                 |
//+------------------------------------------------------------------+
class CReturns
  {
private:
   CArrayDouble*     m_all_bars_equity;
   CArrayDouble*     m_open_position_bars_equity;
   CArrayDouble*     m_trade_equity;

   CArrayDouble*     m_all_bars_returns;
   CArrayDouble*     m_open_position_bars_returns;
   CArrayDouble*     m_trade_returns;

   int               ProcessHistory(void);
   void              CalculateReturns(CArrayDouble &r,CArrayDouble &e);

public:
                     CReturns(void);
                    ~CReturns(void);

   void              OnNewTick(void);

   bool              GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[]);
   bool              GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[]);
  };

returns.mqh definiert eine Enumeration, die den Typ der Renditeserie bestimmt. ENUM_RETURNS_ALL_BARS definiert eine Reihe von bar-by-bar Returns für alle Bars einer Testperiode. ENUM_RETURNS_POSITION_OPEN_BARS ist eine Reihe von Rückgaben, die die barweisen Rückgaben für die Bars darstellen, in denen eine Position offen war. ENUM_RETURNS_TRADES definiert nur eine Rückgabeserie von abgeschlossenen Handelsgeschäften, es werden keine Informationen Balken für Balken mit dieser Option gesammelt.

//+------------------------------------------------------------------+
//| Enumeration specifying granularity of return                     |
//+------------------------------------------------------------------+
enum ENUM_RETURNS_TYPE
  {
   ENUM_RETURNS_ALL_BARS=0,//bar-by-bar returns for all bars
   ENUM_RETURNS_POSITION_OPEN_BARS,//bar-by-bar returns for bars with open trades
   ENUM_RETURNS_TRADES//trade returns
  };

Mit Hilfe der Klasse CReturns kann die Reihe der Kapitalwerte, die die Kapitalkurve definieren, über die Methode GetEquityCurve() abgerufen werden.

//+------------------------------------------------------------------+
//| get equity curve                                                 |
//+------------------------------------------------------------------+
bool CReturns::GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[])
  {
   int m_counter=0;
   CArrayDouble *equity;
   ZeroMemory(out_equity);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         m_counter=m_all_bars_equity.Total();
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         m_counter=m_open_position_bars_equity.Total();
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         m_counter=(m_trade_equity.Total()>1)?m_trade_equity.Total():ProcessHistory();
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(m_counter < 2)
      return false;
//---
   if(ArraySize(out_equity)!=m_counter)
      if(ArrayResize(out_equity,equity.Total()) < m_counter)
         return false;
//---
   for(int i=0; i<equity.Total(); i++)
      out_equity[i]=equity[i];
//---
   return(true);
//---
  }

In ähnlicher Weise kann GetReturns() die Reihe der Rückgaben ausgeben. Beide Methoden benötigen als Eingabe die gewünschte spezifische Rückgabeserie sowie ein Array, dem die Werte zugewiesen werden sollen.

//+------------------------------------------------------------------+
//|Gets the returns into array                                       |
//+------------------------------------------------------------------+
bool CReturns::GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[])
  {
//---
   CArrayDouble *returns,*equity;
   ZeroMemory(out_returns);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         returns=m_all_bars_returns;
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         returns=m_open_position_bars_returns;
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         if(m_trade_equity.Total()<2)
            ProcessHistory();
         returns=m_trade_returns;
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(equity.Total() < 2)
      return false;
//--- calculate average returns
   CalculateReturns(returns,equity);
//--- return the mean return
   if(returns.Total()<=0)
      return false;
//---
   if(ArraySize(out_returns)!=returns.Total())
      if(ArrayResize(out_returns,returns.Total()) < returns.Total())
         return false;
//---
   for(int i=0; i<returns.Total(); i++)
      out_returns[i]=returns[i];
//---
   return(true);
//---
  }

Ein Beispiel

Der nachstehende Code des Expert Advisors zeigt, wie CReturns verwendet wird, um die Renditeserien zu sammeln. In unserem Beispiel wird die Rückgabeserie in einer Binärdatei gespeichert. Obwohl es möglich ist, die Konfidenzintervallberechnungen mit CBootstrap innerhalb von OnTester durchzuführen. In unserem Beispiel werden wir diese Reihe stattdessen mit einem separaten Programm analysieren.

//+------------------------------------------------------------------+
//|                                           MovingAverage_Demo.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <Bootstrap.mqh>
#include <Files\FileBin.mqh>
#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
input ENUM_RETURNS_TYPE rtypes  = ENUM_RETURNS_ALL_BARS; // return types to record
input uint BootStrapIterations  = 10000;
input double BootStrapConfidenceLevel = 0.975;
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input bool   SaveReturnsToFile = true;
input string ReturnsFileName = "MovingAverage_Demo";

//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;
CReturns ma_returns;
#define MA_MAGIC 1234501
//+------------------------------------------------------------------+
//| Calculate optimal lot size                                       |
//+------------------------------------------------------------------+
double TradeSizeOptimized(void)
  {
   double price=0.0;
   double margin=0.0;
//--- select lot size
   if(!SymbolInfoDouble(_Symbol,SYMBOL_ASK,price))
      return(0.0);
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,price,margin))
      return(0.0);
   if(margin<=0.0)
      return(0.0);

   double lot=NormalizeDouble(AccountInfoDouble(ACCOUNT_MARGIN_FREE)*MaximumRisk/margin,2);
//--- calculate number of losses orders without a break
   if(DecreaseFactor>0)
     {
      //--- select history for access
      HistorySelect(0,TimeCurrent());
      //---
      int    orders=HistoryDealsTotal();  // total history deals
      int    losses=0;                    // number of losses orders without a break

      for(int i=orders-1; i>=0; i--)
        {
         ulong ticket=HistoryDealGetTicket(i);
         if(ticket==0)
           {
            Print("HistoryDealGetTicket failed, no trade history");
            break;
           }
         //--- check symbol
         if(HistoryDealGetString(ticket,DEAL_SYMBOL)!=_Symbol)
            continue;
         //--- check Expert Magic number
         if(HistoryDealGetInteger(ticket,DEAL_MAGIC)!=MA_MAGIC)
            continue;
         //--- check profit
         double profit=HistoryDealGetDouble(ticket,DEAL_PROFIT);
         if(profit>0.0)
            break;
         if(profit<0.0)
            losses++;
        }
      //---
      if(losses>1)
         lot=NormalizeDouble(lot-lot*losses/DecreaseFactor,1);
     }
//--- normalize and check limits
   double stepvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   lot=stepvol*NormalizeDouble(lot/stepvol,0);

   double minvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   if(lot<minvol)
      lot=minvol;

   double maxvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX);
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);
  }
//+------------------------------------------------------------------+
//| Check for open position conditions                               |
//+------------------------------------------------------------------+
void CheckForOpen(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- check signals
   ENUM_ORDER_TYPE signal=WRONG_VALUE;

   if(rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=ORDER_TYPE_SELL;    // sell conditions
   else
     {
      if(rt[0].open<ma[0] && rt[0].close>ma[0])
         signal=ORDER_TYPE_BUY;  // buy conditions
     }
//--- additional checking
   if(signal!=WRONG_VALUE)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),
                               SymbolInfoDouble(_Symbol,signal==ORDER_TYPE_SELL ? SYMBOL_BID:SYMBOL_ASK),
                               0,0);
     }
//---
  }
//+------------------------------------------------------------------+
//| Check for close position conditions                              |
//+------------------------------------------------------------------+
void CheckForClose(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- positions already selected before
   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])
      signal=true;
//--- additional checking
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);
     }
//---
  }
//+------------------------------------------------------------------+
//| Position select depending on netting or hedging                  |
//+------------------------------------------------------------------+
bool SelectPosition()
  {
   bool res=false;
//--- check position in Hedging mode
   if(ExtHedging)
     {
      uint total=PositionsTotal();
      for(uint i=0; i<total; i++)
        {
         string position_symbol=PositionGetSymbol(i);
         if(_Symbol==position_symbol && MA_MAGIC==PositionGetInteger(POSITION_MAGIC))
           {
            res=true;
            break;
           }
        }
     }
//--- check position in Netting mode
   else
     {
      if(!PositionSelect(_Symbol))
         return(false);
      else
         return(PositionGetInteger(POSITION_MAGIC)==MA_MAGIC); //---check Magic number
     }
//--- result for Hedging mode
   return(res);
  }
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit(void)
  {
//--- prepare trade class to control positions if hedging mode is active
   ExtHedging=((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE)==ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
   ExtTrade.SetExpertMagicNumber(MA_MAGIC);
   ExtTrade.SetMarginMode();
   ExtTrade.SetTypeFillingBySymbol(Symbol());
//--- Moving Average indicator
   ExtHandle=iMA(_Symbol,_Period,MovingPeriod,MovingShift,MODE_SMA,PRICE_CLOSE);
   if(ExtHandle==INVALID_HANDLE)
     {
      printf("Error creating MA indicator");
      return(INIT_FAILED);
     }
//--- ok
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   ma_returns.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
   double returns[],confidence[],params[];
   ArrayResize(confidence,1);
   confidence[0]=BootStrapConfidenceLevel;
//---
   double ret=0.0;
//---
   if(ma_returns.GetReturns(rtypes,returns))
     {
      CBootstrap minreturn(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,returns);

      if(minreturn.CalculateConfidenceIntervals(confidence))
        {
         ret=confidence[0];
         string fname=ReturnsFileName+"_"+_Symbol+".returns";
         CFileBin file;
         if(SaveReturnsToFile && file.Open(fname,FILE_WRITE|FILE_COMMON)!=INVALID_HANDLE)
            file.WriteDoubleArray(returns);

        }

     }
//---
   return(ret);
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }

Ein Skript liest die gespeicherten Daten und übergibt sie an eine Instanz von CBootstrap. Die Teststatistik wird mit der Funktion MeanReturns() berechnet, deren Signatur mit dem Funktionszeiger von BootStrapFunction übereinstimmt. Aufruf von CalculateConfidenceIntervals() mit einem Array mit den Werten 0,9, 0,95, 0,975, was 90%, 95% und 97,5% Konfidenzintervallen entspricht.

//+------------------------------------------------------------------+
//|                                       ApproximateMeanReturns.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Math.mqh>
#include<Files\FileBin.mqh>
#include<Bootstrap.mqh>
//--- input parameters
input string   FileName="MovingAverage_Demo_EURUSD.returns";//returns file name
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input uint BootStrapIterations=10000;
input string BootStrapProbability="0.975,0.95,0.90";
//---
CBootstrap *meanreturns;
double logreturns[],bounds[],bootstraps[];
string sbounds[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int done=StringSplit(BootStrapProbability,StringGetCharacter(",",0),sbounds);
//---
   if(done)
     {
      ArrayResize(bounds,done);
      for(int i=0; i<done; i++)
         bounds[i]=StringToDouble(sbounds[i]);
      if(ArraySort(bounds))
         for(int i=0; i<done; i++)
            sbounds[i]=DoubleToString(bounds[i]);
     }
//---
   if(!done)
     {
      Print("error parsing inputs ", GetLastError());
      return;
     }
//---
   if(!LoadReturns(FileName,logreturns))
      return;
//---
   meanreturns=new CBootstrap(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,logreturns);
//---
   if(meanreturns.CalculateConfidenceIntervals(bounds))
     {
      for(int i=0; i<done; i++)
         Print(EnumToString(AppliedBoostrapMethod)," ",sbounds[i],": ","(",bounds[i*2]," ",bounds[(i*2)+1],")");
     }
//---
   delete meanreturns;
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Load returns from file                                           |
//+------------------------------------------------------------------+
bool LoadReturns(const string fname,double &out_returns[])
  {
   CFileBin file;
//---
   if(file.Open(fname,FILE_READ|FILE_COMMON)==INVALID_HANDLE)
      return false;
//---
   if(!file.ReadDoubleArray(out_returns))
     {
      Print("File read error ",GetLastError());
      return false;
     }
//---
   return true;
  }
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }
//+------------------------------------------------------------------+

Bevor Sie sich die endgültige Ausgabe der berechneten Intervalle ansehen, ist es immer eine gute Idee, einen Blick auf das Verteilungsdiagramm der Bootstrap-Teststatistik zu werfen. Dazu können die Daten, auf die mit GetBootStrapStatistics() zugegriffen wird, grafisch dargestellt werden.

Ein Blick auf die Ergebnisse des Moving Average EA zeigt, dass OnTester eine negative Zahl liefert, was darauf hindeutet, dass sich die zukünftige Performance trotz der positiven Ergebnisse des Einzeltests verschlechtern könnte. -0,12 ist der ungünstigste zu erwartende Durchschnittsertrag.  

Die Ergebnisse für verschiedene Konfidenzintervalle sind unten dargestellt.

ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.90000000: (-0.07040966776550685 0.1134376873958945)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.95000000: (-0.09739322056041048 0.1397669758772337)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.97500000: (-0.12438450770122121 0.1619709975134838)

Dieses Beispiel demonstriert die Berechnung der prognostizierten, wahrscheinlichkeitsbasierten mittleren Renditen für den Moving Average EA. Das gleiche Prinzip lässt sich auch für andere Leistungskennzahlen anwenden. Allerdings ist ein Wort der Warnung angebracht. Leistungskennzahlen auf der Grundlage von Quoten können problematisch sein. Der Grund dafür ist der Nenner bei der Berechnung der Metrik. Wenn sie sehr klein wird, erhalten wir sehr große Zahlen.

Die beste Möglichkeit, die Eignung dieser Methoden zur Schätzung der künftigen Leistung für eine bestimmte Kennzahl zu ermitteln, ist die Untersuchung der Verteilung der Boostrap-Statistiken. Worauf wir achten müssen, sind schwere Schwänze. Ergebnisse, die aus Verteilungen mit starken Ausläufern gewonnen werden, sollten mit Vorsicht verwendet werden.

Ein Beispiel für die Schätzung einer Worst-Case-Sharpe-Ratio für denselben EA wird durch Umschreiben der Funktion erreicht, die dem Funktionszeiger-Parameter des CBootstrap-Konstruktors übergeben wird.

Die Ergebnisse des Tests zeigen wiederum eine weitaus schlechtere Leistung im Vergleich zum Ergebnis des Einzeltests.

Schlussfolgerung

Das Wissen um die Bandbreite der künftig zu erwartenden Wertentwicklung kann uns helfen, bessere Anlageentscheidungen bei der Wahl der Strategie zu treffen. Obwohl die vorgestellte Methode auf statischen Lehrbüchern basiert, sollten sich die Nutzer der damit verbundenen Einschränkungen bewusst sein.

Die berechneten Konfidenzintervalle sind nur so gut wie die Daten, auf denen sie basieren. Wenn die für die Berechnung verwendeten Stichproben unzureichend sind, kommt es zu einem klassischen Szenario Unsinn rein Unsinn raus. Es ist immer wichtig, geeignete Proben auszuwählen, die repräsentativ für die Bedingungen sind, die in der Zukunft auftreten können.

Dateiname	Beschreibung
Mql5files\include\Bootstrap.mqh	enthält die Definition der Klasse CBootstrap
Mql5files\include\Returns.mqh	enthält die Definition der Klasse CReturns
Mql5files\include\UniformRandom.mqh	eine Klasse zur Erzeugung gleichmäßig verteilter Zahlen zwischen 0 und 1
Mql5files\scripts\ApproximateMeanReturns.mq5	Skript, das die vom Strategietester gespeicherte Datei liest und die Konfidenzintervalle der mittleren Erträge des Projekts berechnet
Mql5files\experts\ MovingAverage_Demo.mq5	Ein Expert Advisor zur Demonstration der Anwendung von CBootstrap und CReturns.