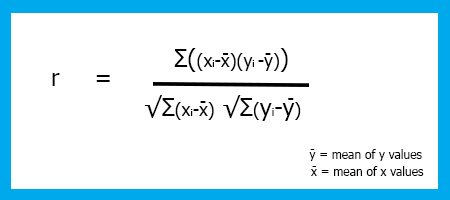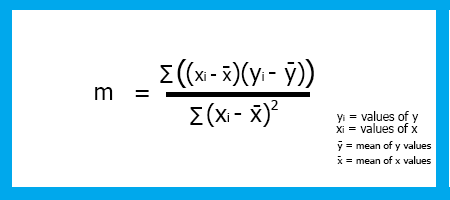
Datenwissenschaft und maschinelles Lernen (Teil 01): Lineare Regression
Einführung
Die Versuchung, auf der Grundlage unzureichender Daten voreilige Theorien aufzustellen, ist der Fluch unseres Berufs.
"Sherlock Holmes"
Datenwissenschaft
Ist ein interdisziplinäres Gebiet, das wissenschaftliche Methoden, Prozesse, Algorithmen und Systeme einsetzt, um Wissen und Erkenntnisse aus verrauschten, strukturierten und unstrukturierten Daten zu extrahieren und dieses Wissen und die Erkenntnisse aus den Daten in einem breiten Spektrum von Anwendungsbereichen anzuwenden.
Ein Datenwissenschaftler ist jemand, der Programmiercode erstellt und diesen mit statistischem Wissen kombiniert, um Erkenntnisse aus Daten zu gewinnen.
Was können Sie von dieser Artikelserie erwarten?
- Theorie (wie bei mathematischen Gleichungen): Die Theorie ist in der Datenwissenschaft am wichtigsten. Man muss die Algorithmen genau kennen und wissen, wie sich ein Modell verhält und warum es sich auf eine bestimmte Weise verhält. Das zu verstehen ist viel schwieriger als den Algorithmus selbst zu programmieren.
- Praktische Beispiele in MQL5 und Python
Lineare Regression
Es ist ein Vorhersagemodell, das verwendet wird, um die lineare Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu finden.
Die lineare Regression ist einer der Kernalgorithmen, der von vielen Algorithmen verwendet wird, wie z.B.;
- Logistische Regression, die ein auf linearer Regression basierendes Modell ist
- Support Vector Machine, dieser berühmte Algorithmus in der Datenwissenschaft ist ein linear basiertes Modell
Was ist ein Modell?
Ein Modell ist nichts anderes als ein Suffix.
Theorie
Jede gerade Linie, die durch den Graphen verläuft, hat eine Gleichung:
Wie kommt man zu dieser Gleichung?
Angenommen, man hat zwei Datensätze mit den gleichen Werten von x und y
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
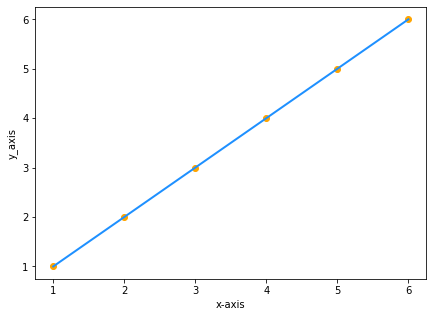
Die grafische Darstellung schaut so aus:
Da y gleich x ist, lautet die Gleichung unserer Linie y=x Richtig? FALSCH
Überlegung,
y = x ist mathematisch dasselbe wie y = 1x, das ist in der Datenwissenschaft ganz anders, die Formel für die Linie wird y=1x sein, wobei 1 der Winkel ist, der zwischen der Linie und der x-Achse auch bekannt als die Steigung der Linie
aber,
Steigung = Änderung von y / Änderung von x = m (bezeichnet als m)
Unsere Formel lautet nun y = mx
Schließlich müssen wir unserer Gleichung eine Konstante hinzufügen, d. h. den Wert von y, wenn x gleich Null war, mit anderen Worten den Wert von y, wenn die Linie die y-Achse kreuzte.
Schlussendlich,
lautet unsere Gleichung y = mx + c (Dies ist nichts anderes als ein Modell in der Datenwissenschaft)
wobei c der y-Achsenabschnitt ist
Einfache lineare Regression
Die einfache lineare Regression hat eine abhängige Variable und eine unabhängige Variable. Hier versuchen wir, die Beziehung zwischen zwei Variablen zu verstehen, z. B. wie sich ein Aktienkurs mit der Veränderung eines einfachen gleitenden Durchschnitts ändert.
Komplexe Daten
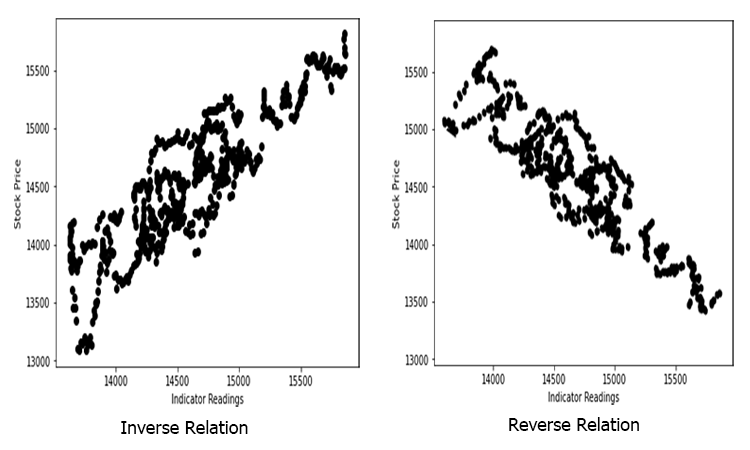
Angenommen, wir haben zufällig gestreute Indikatorwerte, die gegen den Aktienkurs gezogen werden(etwas, das im wirklichen Leben passiert)
In diesem Fall ist unser Indikator/unsere unabhängige Variable möglicherweise kein guter Prädiktor für unseren Aktienkurs/unsere abhängige Variable.
Der erste Filter, den Sie in Ihren Datensätzen anwenden müssen, besteht darin, alle Spalten zu streichen, die nicht stark mit Ihrem Ziel korrelieren, da Sie Ihr lineares Modell nicht mit diesen Spalten erstellen werden.
Die Erstellung eines linearen Modells mit nicht-linear korrelierten Daten ist ein großer grundlegender Fehler; Vorsicht.
Die Beziehung kann invers oder umgekehrt sein, aber sie muss stark sein, und da Sie nach linearen Beziehungen suchen, ist es das, was Sie finden wollen.
Wie messen wir nun die Stärke der Beziehung zwischen der unabhängigen Variablen und dem Ziel? Wir verwenden eine Metrik, die als der Korrelationskoeffizient bekannt ist.
Korrelationskoeffizient
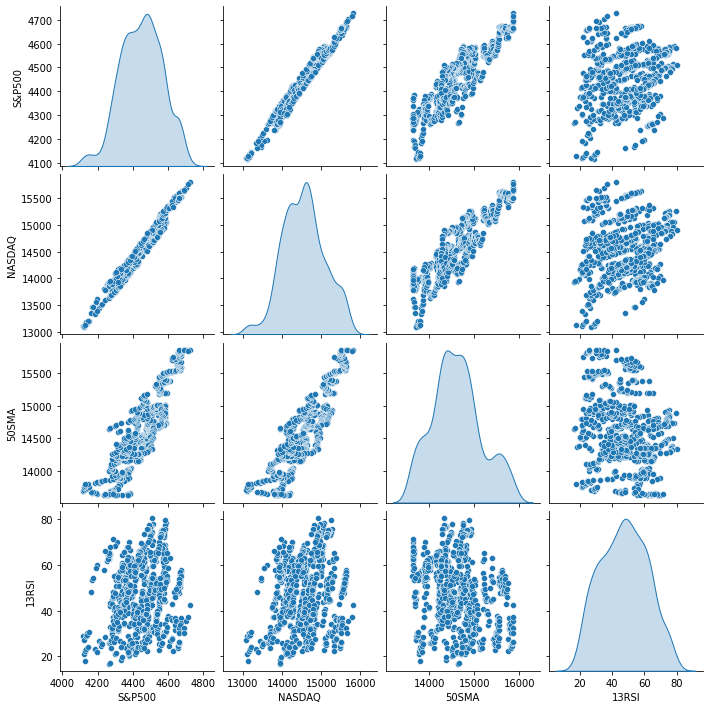
Lassen Sie uns einen Code für ein Skript erstellen, um einen Datensatz zu erstellen, der als Hauptbeispiel für diesen Artikel verwendet werden soll; lassen Sie uns die Prädiktoren des NASDAQ finden.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Im Skript haben wir den NASDAQ-Schlusskurs, die 13-Perioden-RSI-Werte, den S&P 500 und den 50-Perioden-Gleitenden Durchschnitt erfasst. Nach erfolgreicher Kollektion der Daten in einer csv-Datei.
Visualisieren wir die Daten in Python auf dem jupyter notebook von anaconda, für diejenigen, die anaconda nicht auf ihrem Rechner installiert haben, können Sie Ihren Data Science Python Code, der in diesem Artikel verwendet wird, auf google colab ausführen.
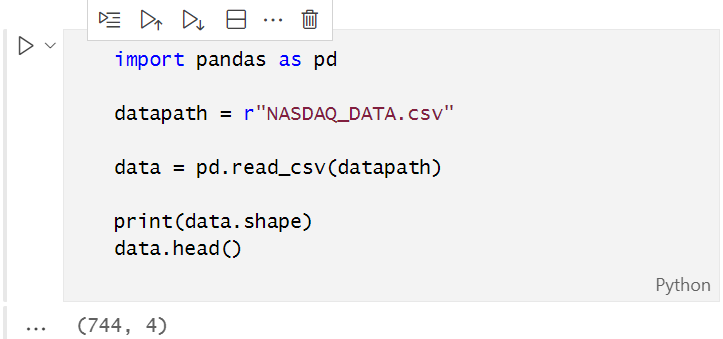
Bevor Sie eine CSV-Datei öffnen können, die von unserem Testskript erstellt wurde, müssen Sie sie in die UTF-8-Kodierung konvertieren, damit sie von Python gelesen werden kann. Öffnen Sie die Csv-Datei mit Notepad und speichern Sie sie dann als UTF-8-Kodierung ab. Es ist ratsam, die Datei in ein externes Verzeichnis zu kopieren, damit sie von Python separat gelesen wird, wenn man auf dieses Verzeichnis verlinkt. Mit pandas lesen wir die Csv-Datei und speichern sie in der Datenvariablen.
Die Ausgabe:
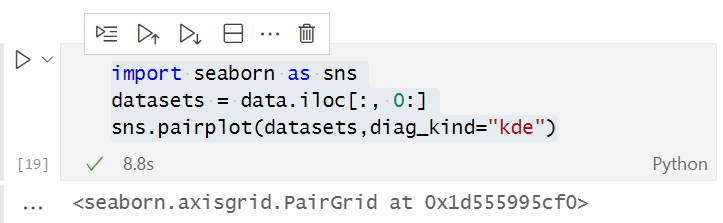
Anhand der visuellen Darstellung der Daten können wir bereits erkennen, dass es eine sehr starke Beziehung zwischen dem NASDAQ und dem S&P 500 sowie eine starke Beziehung zwischen dem NASDAQ und seinem gleitenden 50-Perioden-Durchschnitt gibt. Wie bereits erwähnt, ist die unabhängige Variable, wenn die Daten über das gesamte Diagramm verstreut sind, kein guter Prädiktor für das Ziel, wenn es darum geht, lineare Beziehungen zu finden, aber sehen wir uns an, was die Zahlen über ihre Korrelation aussagen, und ziehen wir eine Schlussfolgerung aus den Zahlen und nicht aus unseren Augen. Um herauszufinden, wie die Variablen miteinander korrelieren, verwenden wir die als Korrelationskoeffizient bekannte Metrik.
Korrelationskoeffizient
Er wird verwendet, um die Stärke zwischen der unabhängigen Variable und dem Zielwert zu messen.
Es gibt verschiedene Arten von Korrelationskoeffizienten, aber wir werden den populärsten für die lineare Regression verwenden, der auch als Pearsons Korrelationskoeffizient( R) bekannt ist und zwischen -1 und +1 liegt.
Eine Korrelation mit den extrem möglichen Werten -1 und +1 bedeutet eine perfekte negative lineare bzw. eine perfekte positive lineare Beziehung zwischen x und y, während eine Korrelation von 0(Null) das Fehlen einer linearen Korrelation anzeigt.
Die Formel für den Korrelationskoeffizienten/Pearson-Koeffizient (R)
Ich habe eine linearRegressionLib.mqh erstellt, innerhalb unserer Hauptbibliothek, kodieren wir die Funktion corrcoef().
Beginnen wir mit der Mittelwertfunktion für die Werte. Mittelwert ist die Summe aller Daten, geteilt durch die Gesamtzahl der Elemente
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }Nun der Code für Pearsons r
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
und die Ergebnisausgabe in unserem TestSript.mq5:
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
schaut so aus:
Correlation Coefficient NASDAQ vs S&P 500 = 0.9807093773142763
Correlation Coefficient NASDAQ vs 50SMA = 0.8746579124626006
Correlation Coefficient NASDAQ Vs rsi = 0.24245225451004537
Wie Sie sehen können, haben NASDAQ und S&P500 eine sehr starke Korrelation mit allen anderen Datenspalten (weil ihr Korrelationskoeffizient sehr nahe bei 1 liegt), so dass wir andere schwache Spalten bei der Erstellung unseres einfachen linearen Regressionsmodells weglassen müssen.
Jetzt haben wir zwei Datenspalten, auf denen wir unser Modell aufbauen wollen.
Der Koeffizient von X
Der Koeffizient von X, auch Steigung (m) genannt, ist per Definition das Verhältnis zwischen der Veränderung von Y und der Veränderung von X oder, mit anderen Worten, die Steilheit der Linie.
Formel:
Steigung = Änderung in Y / Änderung in X
Wenn Sie sich an die Algebra erinnern, die Steigung, das, m in der Formel, ist:
Y = M X + C
Um die Steigung der linearen Regression m zu finden, ist die Formel:
Nachdem wir nun die Formel gesehen haben, wollen wir nun die Steigung unseres Modells berechnen,
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Achten Sie auf die Arrays y_values und x_values. Es sind Arrays, die innerhalb der Init() Funktion innerhalb der Klasse CSimpleLinearRegression initiiert und kopiert wurden.
Hier ist die Funktion CSimpleLinearRegression::Init():
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Wir sind mit der Codierung des Koeffizienten von X fertig und gehen nun zum nächsten Teil über, dem
Y-Abschnitt
Wie bereits erwähnt, ist der Y-Achsenabschnitt der Wert von y, wenn der Wert von x gleich Null ist, oder der Wert von y, wenn die Linie die y-Achse schneidet:

Ermittlung des y-Achsenabschnitts
Aus der Gleichung
Y = M X + C
Wenn man MX auf die linke Seite der Gleichung setzt und die Gleichung auf die linke Seite nach rechts dreht, erhält man die folgende Gleichung für den x-Achsenabschnitt:
C = Y - M X
wobei:
Y = Mittelwert aller y-Werte
x = Mittelwert aller x-Werte
Programmieren wir nun den Code für die Funktion zur Ermittlung des y-Achsenabschnitts ein:
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Wenn wir mit dem y-Abschnitt fertig sind, erstellen wir unser lineares Regressionsmodell, indem wir es in unserer Hauptfunktion LineareRegressionHaupt() ausgeben:
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
Wir verwenden unser Modell auch, um die prognostizierten Werte von y zu erhalten, was in der Zukunft hilfreich sein wird, wenn wir unser Modell weiter aufbauen und seine Genauigkeit analysieren.
Rufen wir die Funktion über die Funktion Onstart() in unserem TestScript.mq5 auf:
lr.LinearRegressionMain(y_nasdaq_predicted);
Sie erzeugt die Ausgabe:
2022.03.03 10:41:35.888 TestScript (#SP500,H1) Das lineare Regressionsmodell ist Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
Innerhalb der void-Funktion fileopen()
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
In unserem TestScript, müssen wir als Erstes zwei Arrays deklarieren:
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
Als Nächstes müssen wir diese Arrays übergeben, um ihre Referenz von unserer Funktion GetDataToArray() zu erhalten
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Achten Sie auf die Spaltennummern, da unsere Funktionsargumente im öffentlichen Teil unserer Klasse wie folgt aussehen:
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Stellen Sie sicher, dass Sie sich auf die richtige Spaltennummer beziehen. Wie Sie sehen können, sind die Spalten in unserer CSV-Datei so angeordnet:
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
Nach dem Aufruf der Funktion GetDataToArray() ist es an der Zeit, die Funktion Init() aufzurufen. Da es keinen Sinn macht, die Bibliothek zu initialisieren, ohne dass die Daten ordnungsgemäß erfasst und in ihren Arrays gespeichert wurden, sieht der Aufruf der Funktion in der richtigen Reihenfolge wie folgt aus:
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
Nachdem wir nun die vorhergesagten Werte im Array y_nasdaq_predicted gespeichert haben, wollen wir die abhängige Variable (NASDAQ), die unabhängige Variable (S&P500) und die Vorhersagen auf derselben Kurve visualisieren.
Führen Sie den folgenden Code in Ihrem Jupyter-Notebook aus:
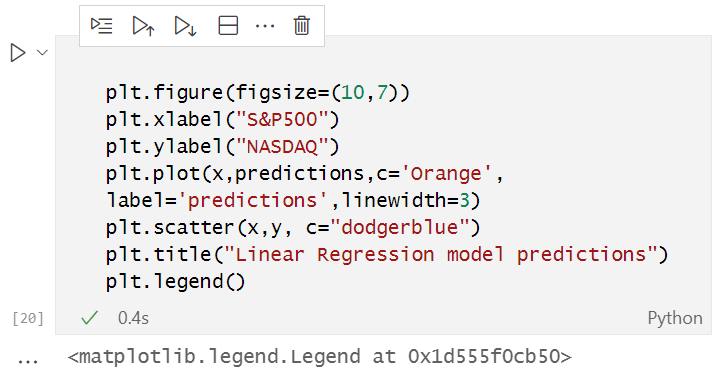
Das Python-Programm ist am Ende des Artikels beigefügt.
Nach erfolgreicher Ausführung des obigen Codeschnipsels erhalten wir die folgende Grafik:
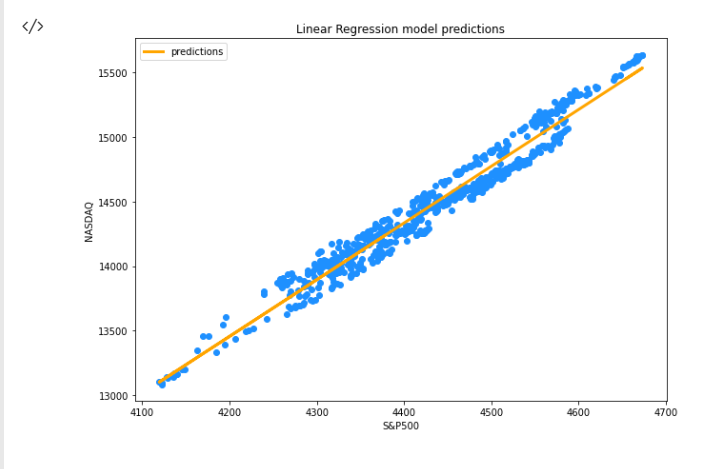
Nun, da wir unser Modell und andere Dinge in unserer Bibliothek haben, wie sieht es mit der Genauigkeit unseres Modells aus? Ist unser Modell gut genug, um irgendetwas zu bedeuten oder um in irgendetwas verwendet zu werden?
Um zu verstehen, wie gut unser Modell die Zielvariable vorhersagt, verwenden wir eine Metrik, die als Koeffizient der Determinante bekannt ist und als R-Quadrat bezeichnet wird.
R-Quadrat
Dies ist der Anteil der Gesamtvarianz von y, der durch das Modell erklärt wurde.
Um das R-Quadrat zu ermitteln, müssen wir den Fehler bei der Vorhersage verstehen. Die Fehler bei der Vorhersage ist die Differenz zwischen dem tatsächlichen/realen Wert von y und dem vorhergesagten Wert von y:
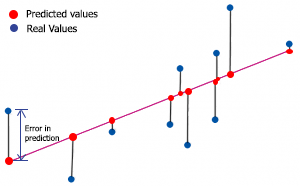
mathematisch:
Fehler = Y tatsächlich - Y prognostiziert
Die Formel für R-Quadrat lautet:
Rsquared = 1 - (Gesamtsumme der quadrierten Fehler / Gesamtsumme der quadrierten Residuen)
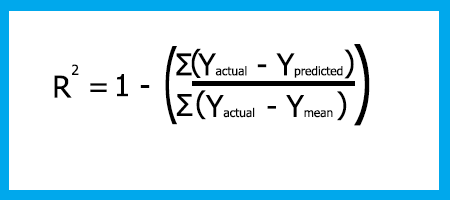
Warum den Fehler quadrieren?
- Fehler können positiv oder negativ sein (über oder unter der Linie), wir quadrieren sie, um sie positiv zu halten.
- Negative Werte könnten den Fehler verringern.
- Wir quadrieren Fehler auch, um große Fehler zu bestrafen, damit wir die bestmögliche Anpassung erhalten.
Null bedeutet, dass das Modell nicht in der Lage ist, die Schwankungen von y zu erklären, was bedeutet, dass das Modell das schlechtestmögliche ist, Eins bedeutet, dass das Modell in der Lage ist, die gesamte Werte von y in Ihrem Datensatz zu erklären (ein solches Modell existiert nicht)
Sie können die Ausgabe von r-squared als Prozentsatz der Genauigkeit Ihres Modells betrachten. Null bedeutet Null Prozent Genauigkeit und Eins bedeutet, dass Ihr Modell zu hundert Prozent genau ist.
Lassen Sie uns nun den Code für das R-Quadrat programmieren:
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
Erinnern Sie sich daran, dass wir innerhalb unserer LinearRegressionMain, wo wir die vorhergesagten Werte in den Abschnitt predicted_y[] gespeichert haben, das per Referenz übergeben wurde, dieses Array in ein globales Variablen-Array kopieren müssen, das im privaten Abschnitt unserer Klasse deklariert wurde.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
Am Ende der Funktion LinearRegressionMain habe ich die Zeile hinzugefügt, die das Array in ein globales Variablen-Array m_ypredicted[] kopiert.
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
Drucken wir nun den R-Quadrat-Wert in unserem TestScript aus:
Print(" R_SQUARED = ",lr.r_squared());
Die Ausgabe ist:
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
Das war's mit der einfachen linearen Regression, nun wollen wir sehen, wie eine mehrfache (multiple) lineare Regression aussehen würde.
Mehrfache lineare Regression
Bei der multiplen linearen Regression gibt es eine unabhängige Variable und mehr als eine abhängige Variable.
Die Formel für das Modell der multiplen linearen Regression lautet:
So sieht unsere Bibliothek aus, nachdem wir die privaten und öffentlichen Abschnitte unserer Klasse hart kodiert haben.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Da wir mit mehreren Werten arbeiten werden, ist dies der Teil, in dem wir mit vielen Referenz-Arrays von Funktionsargumenten spielen werden. Ich konnte keine kürzere Form für die Implementierung finden.
Um ein lineares Regressionsmodell für zwei abhängige Variablen zu erstellen, werden wir diese Funktion verwenden:
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
Der Y-Achsenabschnitt für diese Instanz basiert auf der Anzahl der Datenspalten, die wir gewählt haben. Nach Ableitung der Formel aus der multiplen linearen Regression lautet die endgültige Formel:
C = Y - M1 X1 - M2 X2
So sieht ihr Programmierung aus
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
Im Falle von drei Variablen war es nur eine Frage der harten Kodierung der Funktion wieder und eine weitere Variable hinzufügen.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
Die Konstante/Y-Achsenabschnitt für unsere mehrfache lineare Regression ist, wie bereits erwähnt, folgendermaßen:
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Annahmen der Lineare Regression
Das lineare Regressionsmodell basiert auf einer Reihe von Annahmen. Wenn der zugrunde liegende Datensatz diese Annahmen nicht erfüllt, müssen die Daten möglicherweise transformiert werden, oder ein lineares Modell ist möglicherweise nicht geeignet.
- Linearitätsannahme: Es wird von einer linearen Beziehung zwischen der abhängigen/Zielvariablen und den unabhängigen/Prädiktorvariablen ausgegangen.
- Annahme der Normalität der Fehlerverteilung.
- Die Fehler sollten zusammen mit dem Modell normalverteilt sein.
- Ein Streudiagramm zwischen den tatsächlichen Werten und den vorhergesagten Werten sollte zeigen, dass die Daten gleichmäßig über das Modell verteilt sind.
Vorteile eines linearen Regressionsmodells
Einfache Implementierung und leichtere Interpretation der Ergebnisse und der Koeffizienten.
Nachteile
- Es wird eine lineare Beziehung zwischen abhängigen und unabhängigen Variablen vorausgesetzt, d. h. es wird davon ausgegangen, dass eine geradlinige Beziehung zwischen ihnen besteht.
- Ausreißer haben einen großen Einfluss auf die Regression.
- Lineare Regression geht von der Unabhängigkeit zwischen den Attributen aus.
- Die lineare Regression untersucht die Beziehung zwischen dem Mittelwert der abhängigen Variable und der unabhängigen Variable.
- So wie der Mittelwert keine vollständige Beschreibung einer einzelnen Variablen ist, ist die lineare Regression keine vollständige Beschreibung der Beziehungen zwischen den Variablen.
- Die Grenzen sind linear
Abschließende Überlegungen
Ich denke, dass lineare Regressionsalgorithmen sehr nützlich sein können, wenn man Handelsstrategien erstellt, die auf der Korrelation von Paaren und anderen Dingen wie Indikatoren basieren, obwohl unsere Bibliothek noch lange nicht fertig ist, habe ich das Training und Testen unseres Modells und weitere Verbesserungen der Ergebnisse nicht mit einbezogen, dieser Teil wird im nächsten Artikel zu finden sein, bleiben Sie dran, ich habe den Python-Code auf meinem Github-Repository hier verlinkt, jeder Beitrag zur Bibliothek wird geschätzt, fühlen Sie sich auch frei, Ihre Gedanken im Diskussionsbereich des Artikels zu teilen.
Bis bald
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/10459
 Lernen Sie, wie man ein Handelssystem mit dem RSI entwickelt
Lernen Sie, wie man ein Handelssystem mit dem RSI entwickelt
 Lernen Sie, wie man ein Handelssystem mit Momentum-Indikator entwickelt
Lernen Sie, wie man ein Handelssystem mit Momentum-Indikator entwickelt
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.