从理论到实践 - 页 525 1...518519520521522523524525526527528529530531532...1981 新评论 Igor Makanu 2018.09.03 13:46 #5241 Nikolay Demko:不,你不能用爬虫来评估市场有多大变化。 你只能评估新的预测误差对预测的改变程度与旧的误差相比有多大。 也就是说,SSA并没有说明预测的正确性,SSA的差异只告诉我们误差的不同。市场将走向何方,SSA根本不关心。 如果没有每个SSA的误差估计,你的差异就悬在空中,没有任何依据。我知道这一点已经很久了,但我有希望,所以我在想还能去哪里找:))我想在历史上运行协方差矩阵,分析其中的差异有多大--突然他们在理论上说,价格考虑到了所有等等))))。 马克西姆-德米特里耶夫斯基。我不知道,在我看来,如果亚历山大没有走到最后--没有什么可以挽救这种做法。预测随机游走是很困难的,评估它的一些假想状态:)在这里,除了我上面的帖子之外,特别是轶事部分...说实话,有一些错觉,认为价格图表中的规律性只是不重复其以前的状态。 在SSA中,我将有时间,我会做一组所有可能的协方差矩阵,并尝试分析它们在附近状态下的不重复性,即矩阵应该以不重复的顺序交替出现 也许晚上我会用SSA清理一下代码,然后贴出来,这段代码只是从Matlab移植过来的,我没想到,但Alglib对快速移植这种东西很有帮助,做为一个例子给自己学习,也可能帮助别人理解,这里附上Matlab的SSA 附加的文件: ssa.zip 2 kb Violetta Novak 2018.09.03 13:54 #5242 Smokchi Struck:我将单独强调这个问题。 在什么函数上做回归,使其最后一个点位于价格通道的中心? 我需要一个函数,就像多项式一样,能同时处理人字形和半圆形(从例子中可以看出,多项式不能处理这些主题)。(马克西姆-德米特里耶夫斯基的数字还不能考虑,它不符合价格是遵循一定轨迹的交易通道的理论。这个数字是一个交易通道,最后有一个弹射,它可以以后考虑)。 非线性函数的其他例子有指数函数、对数函数、三角函数、幂函数、高斯函数 和洛伦兹曲线。好吧,Smokchy,你用你的照片让大家都很兴奋!)) Igor Makanu 2018.09.03 15:30 #5243 好吧,还有一点心理学来衡量圣杯 追求的成功程度,喜欢这个视频,显然这个女孩看起来很自然,很有说服力 Maxim Dmitrievsky 2018.09.03 15:38 #5244 Igor Makanu:还有一点心理学来衡量圣杯追求的成功,我喜欢这个视频,显然这个女孩看起来很自然,很有说服力 你可以在晚上用这些眼睛生出一只毛毛虫。 Uladzimir Izerski 2018.09.03 16:18 #5245 Igor Makanu:用一点心理学来衡量圣杯追求的成功,喜欢这个视频,显然这个女孩看起来很自然,很有说服力。 这个女孩很聪明-年轻的她看到了许多人看不见的东西。 Igor Makanu 2018.09.03 16:53 #5246 那么,如果心理学是有趣的,蛋糕上的樱桃... Uladzimir Izerski 2018.09.03 19:04 #5247 Igor Makanu:那么,如果心理学是有趣的,可以说是蛋糕上的樱桃...... 影片的第30分钟是最有趣的),但你必须看完才能理解。 multiplicator 2018.09.03 21:58 #5248 Maxim Dmitrievsky:已经有人告诉你这是一种无用的消遣。直到你花了你的时间,你才会明白。 multiplicator 2018.09.04 01:44 #5249 如何在Excel中做回归。 使用数据/解决方案搜索器功能。 在所附表格中。 第一栏是不适用的号码。 第二列是时间序列。 第三个是一个函数(在本例中是一个多项式)。 第四种是ANC。时间序列的值减去函数的值,并进行平方。 红色单元格中的数据是蓝色列的总和,即偏差的平方之和。 紫色单元格中的是要拟合的系数。 多项式函数是y=ax2+bx+c 其中x是x轴上的坐标值,橙色一栏,从0到201。 y是所选多项式在y轴上的坐标值。 a,b,c是我们要拟合的系数。 在Excel中,该公式看起来像这样=a*A1^2+b*A1+c。也就是说,我们用A栏的值代替X的值(见绿色栏)。 为了找到函数的系数,点击 "数据",然后点击 "查找解决方案"。 在打开的菜单上选择。 设置目标单元格(即我们表格中的红色单元格)。 到一个最小值。 改变单元格(我们表格上的紫色单元格)。 然后单击 "执行"。 也就是说,我们最小化时间序列与函数的偏差的平方。 试着把你自己的功能放在绿色栏里。 指数函数、对数函数、三角函数、幂函数、高斯函数、洛伦兹曲线,其他...问题 仍然是一样的,你必须找到一个函数,其最后一点将在价格通道的中心(对于之字形和半圆形的数字)。 附加的文件: eo4aqs0_1.zip 28 kb 2nr7los_2.zip 25 kb Vladimir 2018.09.04 03:47 #5250 Smokchi Struck:... 也就是说,我们尽量减少时间序列与函数的偏差的平方。试着把你自己的功能放在绿色栏里。 指数函数、对数函数、三角函数、幂函数、高斯函数、洛伦兹曲线,其他...问题 是一样的:你必须找到一个函数,它的最后一点将在价格通道的中心(对于之字形和半圆形的数字)。 有趣的是。首先,这是不准确的,我们不是最小化 "平方",而是 "平方之和"。第二,如果你想给最后一个点更大的价值,那就简单了,在最小化的总和中不只是取平方,而是取加权平方,即乘以一些正的加权系数。它们在数组末尾的值应该更大,而在开始的时候--更小。例如,对于从1到n的点的数量,权重等于q^(n-i),q<1,给偏差乘数的平方,类似于指数移动平均线中课程的权重。如果我们想通过偏差的最小加权平方和的值来比较不同的近似值,往往也会使它们的总和等于1。 而对于一个边界由不同类型的公式描述的曲线型渠道,什么是 "中心"?或者至少对于第一种变体,通过指数函数? 如果它只是从系列中的倒数第二个值到最后一个值这一段的中点,那么它足以使系列中最后两个点的偏差权重变得非常大。或者更简单,找到这个中间,就可以了。 你需要对偏差有一些其他的要求,否则问题就被低估了。 在最后一点计算 "中心 "有什么用? 1...518519520521522523524525526527528529530531532...1981 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
不,你不能用爬虫来评估市场有多大变化。
你只能评估新的预测误差对预测的改变程度与旧的误差相比有多大。
也就是说,SSA并没有说明预测的正确性,SSA的差异只告诉我们误差的不同。市场将走向何方,SSA根本不关心。
如果没有每个SSA的误差估计,你的差异就悬在空中,没有任何依据。
我知道这一点已经很久了,但我有希望,所以我在想还能去哪里找:))我想在历史上运行协方差矩阵,分析其中的差异有多大--突然他们在理论上说,价格考虑到了所有等等))))。
我不知道,在我看来,如果亚历山大没有走到最后--没有什么可以挽救这种做法。预测随机游走是很困难的,评估它的一些假想状态:)
在这里,除了我上面的帖子之外,特别是轶事部分...说实话,有一些错觉,认为价格图表中的规律性只是不重复其以前的状态。 在SSA中,我将有时间,我会做一组所有可能的协方差矩阵,并尝试分析它们在附近状态下的不重复性,即矩阵应该以不重复的顺序交替出现
也许晚上我会用SSA清理一下代码,然后贴出来,这段代码只是从Matlab移植过来的,我没想到,但Alglib对快速移植这种东西很有帮助,做为一个例子给自己学习,也可能帮助别人理解,这里附上Matlab的SSA
我将单独强调这个问题。
在什么函数上做回归,使其最后一个点位于价格通道的中心?
我需要一个函数,就像多项式一样,能同时处理人字形和半圆形(从例子中可以看出,多项式不能处理这些主题)。
(马克西姆-德米特里耶夫斯基的数字还不能考虑,它不符合价格是遵循一定轨迹的交易通道的理论。这个数字是一个交易通道,最后有一个弹射,它可以以后考虑)。
非线性函数的其他例子有指数函数、对数函数、三角函数、幂函数、高斯函数 和洛伦兹曲线。
好吧,Smokchy,你用你的照片让大家都很兴奋!))
好吧,还有一点心理学来衡量圣杯 追求的成功程度,喜欢这个视频,显然这个女孩看起来很自然,很有说服力
还有一点心理学来衡量圣杯追求的成功,我喜欢这个视频,显然这个女孩看起来很自然,很有说服力
你可以在晚上用这些眼睛生出一只毛毛虫。
用一点心理学来衡量圣杯追求的成功,喜欢这个视频,显然这个女孩看起来很自然,很有说服力。
这个女孩很聪明-年轻的她看到了许多人看不见的东西。
那么,如果心理学是有趣的,蛋糕上的樱桃...
那么,如果心理学是有趣的,可以说是蛋糕上的樱桃......
影片的第30分钟是最有趣的),但你必须看完才能理解。
已经有人告诉你这是一种无用的消遣。
直到你花了你的时间,你才会明白。
如何在Excel中做回归。
使用数据/解决方案搜索器功能。
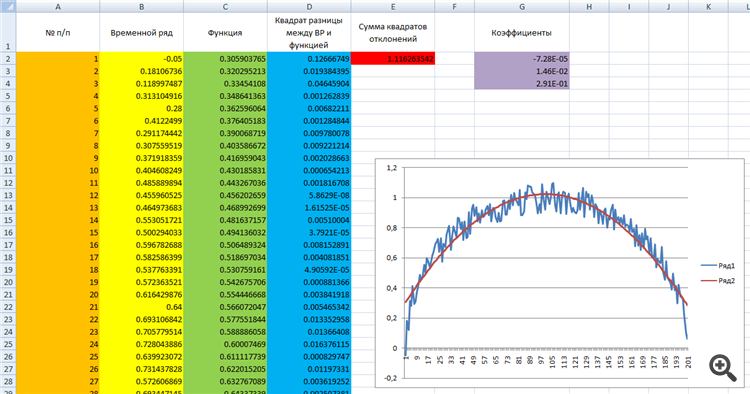
在所附表格中。
第一栏是不适用的号码。
第二列是时间序列。
第三个是一个函数(在本例中是一个多项式)。
第四种是ANC。时间序列的值减去函数的值,并进行平方。
红色单元格中的数据是蓝色列的总和,即偏差的平方之和。
紫色单元格中的是要拟合的系数。
多项式函数是y=ax2+bx+c
其中x是x轴上的坐标值,橙色一栏,从0到201。
y是所选多项式在y轴上的坐标值。
a,b,c是我们要拟合的系数。
在Excel中,该公式看起来像这样=a*A1^2+b*A1+c。也就是说,我们用A栏的值代替X的值(见绿色栏)。
为了找到函数的系数,点击 "数据",然后点击 "查找解决方案"。

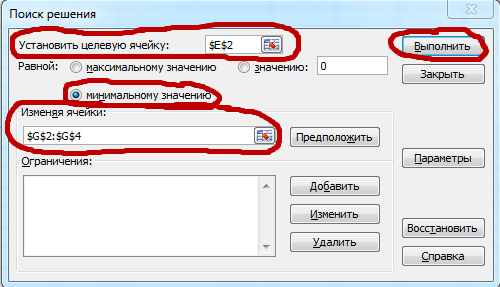
在打开的菜单上选择。
设置目标单元格(即我们表格中的红色单元格)。
到一个最小值。
改变单元格(我们表格上的紫色单元格)。
然后单击 "执行"。
也就是说,我们最小化时间序列与函数的偏差的平方。
试着把你自己的功能放在绿色栏里。
指数函数、对数函数、三角函数、幂函数、高斯函数、洛伦兹曲线,其他...
问题 仍然是一样的,你必须找到一个函数,其最后一点将在价格通道的中心(对于之字形和半圆形的数字)。
...
也就是说,我们尽量减少时间序列与函数的偏差的平方。
试着把你自己的功能放在绿色栏里。
指数函数、对数函数、三角函数、幂函数、高斯函数、洛伦兹曲线,其他...
问题 是一样的:你必须找到一个函数,它的最后一点将在价格通道的中心(对于之字形和半圆形的数字)。
有趣的是。首先,这是不准确的,我们不是最小化 "平方",而是 "平方之和"。第二,如果你想给最后一个点更大的价值,那就简单了,在最小化的总和中不只是取平方,而是取加权平方,即乘以一些正的加权系数。它们在数组末尾的值应该更大,而在开始的时候--更小。例如,对于从1到n的点的数量,权重等于q^(n-i),q<1,给偏差乘数的平方,类似于指数移动平均线中课程的权重。如果我们想通过偏差的最小加权平方和的值来比较不同的近似值,往往也会使它们的总和等于1。
而对于一个边界由不同类型的公式描述的曲线型渠道,什么是 "中心"?或者至少对于第一种变体,通过指数函数?
如果它只是从系列中的倒数第二个值到最后一个值这一段的中点,那么它足以使系列中最后两个点的偏差权重变得非常大。或者更简单,找到这个中间,就可以了。
你需要对偏差有一些其他的要求,否则问题就被低估了。
在最后一点计算 "中心 "有什么用?