MetaTrader 5 / 交易
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
针对交易的组合数学和概率论（第三部分）：第一个数学模型

针对交易的组合数学和概率论（第三部分）：第一个数学模型

MetaTrader 5 — 交易 | 14 十月 2021, 14:15
2 612 0
Evgeniy Ilin
Evgeniy Ilin

内容


概述

在上一篇文章中，我得到了分形的第一个公式。 如此即可假设所有重要的分形相关值都可以用数学模型来描述。 模拟并非旨在描述这类值，而在于它有助于收集第一批数据，从而可对此类结构进行更深入的分析。 在本文中，我决定特别要注意描述第一个数学模型的整个开发过程，直至得到可应用于不同 EA 的数学模型。


新思路

在上一篇文章中研究对称分形时，我们得到了一个通用公式，可计算价格在特定走廊内移动的平均步阶数，该步阶数由相同的较小对称走廊的数量决定。 这个公式如下：

  1. S = K^2 - 新走廊的平均步阶数，基于步阶是另一条走廊的事实
  2. P = K * P0  --> K = P/P0 - 已知走廊比未知走廊大多少倍
  3. P - 平均步阶数未知的走廊宽度（步阶数是原走廊大小的一半）
  4. P0 - 已知走廊的宽度

为了能够描述非对称走廊，我们需要重新定义一些前面提到的概念，令它们更容易理解。 它们当中最重要的是 K。 该值实际上反映了价格在新走廊中的步阶数，前提是这些步阶单边向上或向下。 对于对称走廊，无论我们正在研究（跨越）哪个边界（上边界亦或下边界），步阶数均对等。 这是因为上边界和下边界只是问题的镜像。 至于不对称，经上一篇的代码验证，我们得出在那种情况下平均步阶数确定如下：

  • S = n * m - 走廊有一半不对称的平均步阶数
  • n - 适合走廊上半部分的步阶数
  • m - 适合走廊下半部分的步阶数

因此，对于对称走廊，我们有 “m = n”。 然后，基于以上：

  • S = n * n = m * m = m * n = n^2 = m^2 = K^2
  • K = n = m

这意味着第一个导出公式只是前一个公式的特例，因此不再需要 K。

这个函数的一个有趣的特点是 S(a*k, b*k) = S(a,b) * S(k,k)，这很容易证明：

  • S(n*k ,m*b) = m*k*n*b = n*m * k*b
  • S(n ,m) * S(k ,b) = n*m * k*b

这个属性非常有趣。 通过额外的反射，它可以提供描述整个分形的所有必要公式的推导。 这个属性反映了任意分形的一个非常重要的属性：嵌套的能力。 In other words, any finite fractal of great complexity can be represented as two or more simpler fractals which serve as steps in each other. This property will be used to generalize the formula for more complex cases.

Before proceeding with the fractals, let me remind you that the above defined formulas only work if p=0.5. As soon as the market or fractal parameters begin to deviate from a random walk, this formula begins to change very interestingly, namely:

  • Ss[n,m,p] – a more general formula for the average number of steps (in any direction)
  • S(n ,m)  = Ss[n,m,0,5] – formula for a random walk is a special case of the general formula


平均步阶数的一般公式

换言之，任何具有极大复杂性的有限分形都可由两个或多个更简单的分形来表示，它们相互作为步阶。 如果我们去研究与前一个相关的任意单个分形嵌套层，则无需考虑在特定步阶中发生了哪些步阶。 故此，主要上升和下降步阶发生的频率比率，与相对应的前一层情况准确相同。 换言之，跨越对应嵌套层的边界，即是下一个嵌套层的上升或下降。 但是也知道，当前嵌套层的步阶出现频率比率并不会依赖于当前层的配置。 这意味着分形嵌套原理可经由任何概率 “p” 观察到。 这意味着当 “p” 值发生变化时，公式也应该发生变化，但它应该以某种方式保留其嵌套属性。 一个简单的经验可以帮助我们确定通用公式。 我们知道概率 p 有一个随机游走点，和零与一两个极值点。 我们来看看函数在这三个点上会取什么值。 所以，我们得到以下信息：

  1.  Ss[n,m,1] = Sn[n] = n
  2. Ss[n,m,0] = Sm[m] = m
  3.  Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
  4.  Sn[n,p] – 单一方向到上边界的步阶数
  5. Sn[m,p] – 单一方向到下边界的步阶数

在第一种情况下，我们没有向下步阶 — 所有链都遵循相同的路线。 第二种情况相反，所有步阶都向下，没有向上步阶。 若为极端值，其中一个因子从公式中完全消失。 如果您将其提升为零，则有可能。 任何数的零次方都等于 1。 此外，梯度具有以下形式的不变性：

  • A^X * B^X = (A*B)^X

如果我们用平均步阶代替数字，分形嵌套原则仍将保留。 此外，这将表明幂不取决于 n 和 m。 得到的平均步阶数的通用公式如下：

  • Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

分形嵌套原理可以示意如下：

链

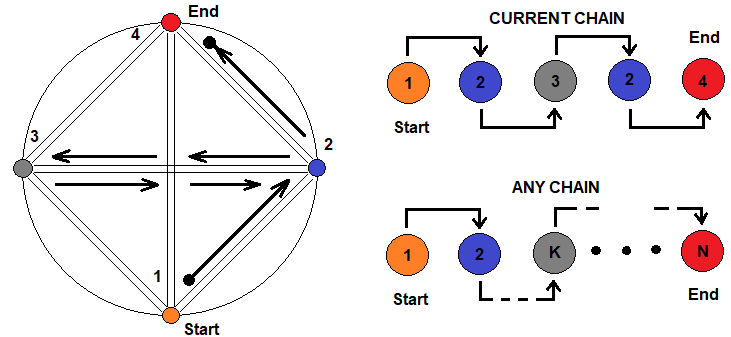
该图显示了四种状态，它们象征着可以相互表达的不同分形。 从一种状态到另一种状态的转换可以经由任何链条进行。 任意选择的链显示在右侧。 下方示意该链可以具有任意长度和复杂度，并且您可以无限次迭代相同状态。 这意味着分形中平均步阶数的公式可以表示为产品链，代表分形嵌套层。


构建幂函数的原型

进一步的思路来自分形嵌套属性，以及来自等幂函数相对于基底的不变性。 所有这些数学原理将有助于推导出更深层次描述分形的公式。 故此，我们另外得到两个函数，其形式我们尚不知道：

  • Pn[p] – 上边界乘数的幂
  • Pm[p] – 下边界乘数的幂

我们知道以下几点：

  • Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
  • Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

通过分析幂函数，可以构建适当的函数原型。 我选择了以下原型：

  1. Pn[p] = 1 , if p >= 0.5
  2. Pn[p] = ( (1 – p)/0.5 ) ^ K
  3. Pm[p] = 1 , if p <= 0.5
  4. Pm[p] = ( p/0.5 ) ^ K
  5. K 是调节函数平坦度的幂

以多项式的形式表示 “2” 和 “4” 会更准确，可以准确地描述给定幂的平滑过渡，但我认为在此这是多余的。 如果您想定义更精确的多项式，这里是原型：

  • Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
  • Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
  • С1 + С2 + … + … СN = 1是相关幂的权重
  • KN 是对应项的幂

我选择的多项式是只有一项的一般多项式的最简单版本。 所有声明的原则都可针对任意分数 “n, m” 进行验证。

我创建了以下程序来验证上述假设：

验证公式

从程序结果中可以看出，一切都正常运行。 为了确定，只需比较两个数字。 如果它们相等，则确定嵌套原理和使用分数n 和m 的能力。


从原型受限族接收最佳函数的一般规划案

现在我们需要判定我们将如何搜索原型所需的系数。 我已选择了最简单的搜索类型 — 在期望范围内生成随机数。 方法规划如下：

逼近规划案

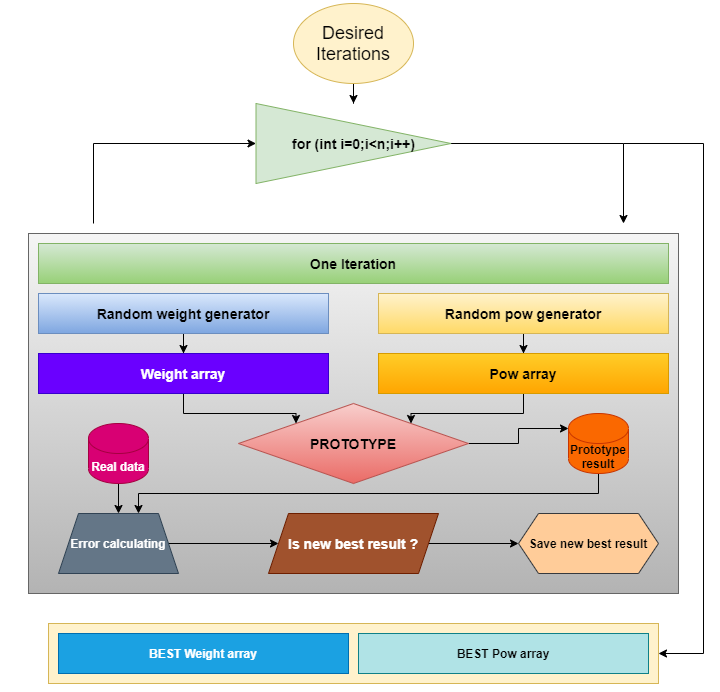
若要它适用于任何函数原型，则我们需要找到真实数据与数学模型最佳匹配的系数。 相同的规划以后会有效，因为在文章的末尾，我们将应用相同的方法来处理另一个原型。


深入分析

现在我们更深入地分析这个公式的结构。 公式的结果是价格在跨越边界其一之前的平均步阶数。 向上和向下的步阶则认定是相等的，但这种相等实际上只有在随机游走的情况下才有可能。 对于非对称分形的完整讲述，有必要额外判定给定值的实际组成。 从逻辑上讲，任何类型的平均步阶数都取决于跨越上边界时的平均步阶数和跨越下边界时的平均步阶数。 我们来找出上边界跨越点的相关值：

  • SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
  • S[U] – 如果步阶链首先到达上边界，则为步阶的平均数
  • S[U,u] – 如果步阶链首先到达上边界，则为平均向上步阶数
  • S[U,d] – 假设步阶链首先到达上边界的平均步阶数
  • P[U] – 价格首先跨越上边界的概率
  • SP[U,ud] – 跨越上边界的平均可能步阶数

下边界的公式类似：

  • SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
  • S[D] – 如果步阶链首先到达下边界，则为任何步阶的平均数
  • S[D,u] – 如果步阶链首先到达下边界，则为平均向上的步阶数
  • S[D,d] – 假设步阶链首先到达下边界的平均步阶数
  • P[D] – 价格首先跨越下边界的概率
  • SP[D,ud] – 跨越下边界的平均可能步阶数

很明显：

  • S = SP[U,ud] + SP[D,ud]

终极情况，我们最终能够获得和使用的所有数值，均取决于五个基础值：

  • S[U,u] = SP[U,u]/P[U] – 如果步阶链首先到达上边界，则为平均向上步阶数
  • S[U,d] = SP[U,d]/P[U] – 假设步阶链首先到达上边界的平均步阶数
  • S[D,u] = SP[D,u]/P[D] – 如果步阶链首先到达下边界，则为平均向上的步阶数
  • S[D,d] = SP[D,d]/P[D] – 假设步阶链首先到达下边界的平均步阶数
  • P[U] – 价格首先跨越上边界的概率

我们将根据不同输入参数的分形运算结果搜索这些值的公式。 在上一篇文章中，我为分形输出选择了以下值：

  • SP[U,u] – 如果步阶链首先到达上边界，则平均向上步阶数
  • SP[U,d] – 假设步阶链首先到达上边界的平均步阶数
  • SP[D,u] – 如果步阶链首先到达下边界，则平均向上的步阶数
  • SP[D,d] – 假设步阶链首先到达下边界的平均步阶数
  • P[U] – 价格首先跨越上边界的概率
  • P[D] – 价格首先跨越下边界的概率
  • S = SP – 任何步阶的平均数

这是一组可由基础值来表示的单独元素：

  • SP[U]
  • S[U,ud] = S[U,u] + S[U,d]
  • S[D,ud] = S[D,u] + S[D,d]
  • P[D] = 1 – P[U]
  • S = SP[U,ud] + SP[D,ud]

在处理分形数学时，我进行了广泛的分析，目标是在一个紧凑的图表中简要显示。 该图例展示的是搜索数学模型过程的结果：

搜索数学模型的顺序

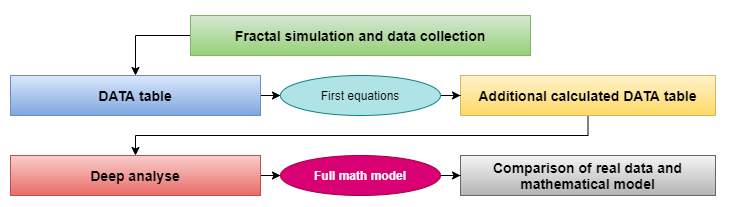
数据集合和结论

针对分形计算结果的更详细研究结果，我注意到最初在构建通用分形概念时确定的六个值是数学相关的。 最初，我在进行对称边界测试时，试图判定这些值之间的依赖关系。 我取得了一些成果。 我针对十种不同的情况做了计算，结果证明这已经足够了：

测试索引

走廊上半部分的步阶 (n)

走廊下半部分的步阶 (n)

( m )

初始步阶的概率

 

( p )

上边界的平均可能向上步阶数

( SP[U,u]  )

上边界的平均可能向下步阶数

( SP[U,d]  )

下边界的平均可能向上步阶数

( SP[D,u]  )

下边界的平均可能向下步阶数

( SP[D,d]  )

上边界的任何步阶的平均可能数

( SP[U,ud]  )

下边界的任何步阶的平均可能数

( SP[D,ud]  )

1

1

1

0.5

0.5

0

0.0

0.5

0.5

0.5

2

2

2

0.5

1.5

0.5

0.5

1.5

2.0

2.0

3

3

3

0.5

3.0

1.5

3.0

1.5

4.5

4.5

4

1

2

0.5

0.888888

0.2222222

0.111111

0.777777

1.11111111

0.8888888

5

2

3

0.5

2.2

1.0

0.8

2.0

3.2

2.8

6

1

2

0.6

1.038781

0.249307

0.066481

0.487534

1.288088

0.554016

7

2

3

0.6

2.811405

1.191072

0.338217

0.906713

4.0024777

1.244931

8

2

3

1.0

2.0

0.0

0.0

0.0

2.0

0.0

9

1

3

0.5

1.25

0.5

0.25

1

1.75

1.25

10

1

4

0.5

1.6

0.8

0.4

1.2

2.4

1.6

 

下面我将示意一个表格，其中包含未显示在分形日志中的计算值。 我们需要它们来评估数值之间的依赖关系：

测试索引

走廊上半部分的步阶 (n)

走廊下半部分的步阶 (n)

( m )

跨越上边界概率

( P(U) )

跨越下边界概率

( P(D) )

跨越上边界时任何步阶的平均数

(S[U,ud]) = SP[U,ud]/P[U]

跨越下边界时任何步阶的平均数

(S[D,ud]) = SP[D,ud]/P[D]

上边界的平均上升步阶数

( S[U,u]  ) = SP[U,u]/P[U]

上边界的平均上降步阶数

( S[U,d]  ) = SP[U,d]/P[U]

下边界的平均上升步阶数

( S[D,u]  ) = SP[D,u]/(P[D])

下边界的平均 
下降步阶数

( S[D,d]  ) = SP[D,d]/(P[D])

平均步阶数

 

( S )

1

1

1

0.5

0.5

1.0

1.0

1.0

0.0

0.0

1.0

1

2

2

2

0.5

0.5

4.0

4.0

3.0

1

1

3

4

3

3

3

0.5

0.5

9.0

9.0

6

3

3

6

9

4

1

2

0.66666

0.3333333

1.6666666

2.6666666

1.3333333

0.33333333

0.33333333

2.33333333

2

5

2

3

0.6

0.4

5.3333333

7

3.6666666

1.66666666

2

5

6

6

1

2

0.789473

0.210526

1.631579

2.631579

1.315790

0.315789

0.315789

2.315789

1.842104

7

2

3

0.810166

0.189498

4.940318

6.569626

3.470159

1.470157

1.784805

4.784

5.2474087

8

2

3

1.0

0.0

2.0

0.0

2.0

0.0

0.0

0.0

2.0

9

1

3

0.75

0.25

2.3333333

5

1.6666666

0.6666666

1

4

3

10

1

4

0.8

0.2

3.0

8.0

2

1

2

6

4

 

从该表格中，您可以找到计算所有四个未知值（由所有其它值组成）所需的前两个方程。 为了得到公式，请注意列 S[U,u]、S[U,d]、S[D,u]、S[D,d]。 非常有趣的是，该列中的数字在 S[U,u], S[U,d] 列和 S[D,u], S[D,d] 列中具有成对相同的小数部分。 此外，您还可以看到 S[U,u] > S[U,d] 及 S[D,d] > S[D,u]。 如果我们成对地减去这些值并与 m、n 进行比较，那么结果是这个差值正好等于到上边界或下边界的相应步阶数：

  • S[U,u] – S[U,d] = n
  • S[D,d] – S[D,u] = m

由此，我们得到两个非常重要的值，它们将有助于判定基础值。 两个方程还不够。 但我们可以得到另外两个方程，这将允许基于略微不同的逻辑来判定相同的值。 如果我们针对分形进行无限长时间的实验，那么上升和下降步阶的出现频率的比率与相应的概率成正比。

若要得到这些比率，我们可做如下假设:

  1. Lim[N0 -- > +infinity] (N0[U]/N0) = p
  2. Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
  3. Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
  4. Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
  5. Lim[N0 -- > +infinity] (N0/N) = S
  6. N0 – 与初始步阶相关的基础实验的数量（组成一个复杂的实验）
  7. N – 由简单实验组成的复杂实验的数量

如果我们将乘数 N0/N0 = 1 引入到 “3” 和 “4” 当中，并在里面正确排列分数，那么我们得到以下结果：

  • Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0)  * Lim[N0 -- > +infinity] (N0/N) =  p*S  = S[UD,u]
  • Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0)  * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S  = S[UD,d]

如果这些极限中的每一个都是有限数，则乘积极限可以表示为极限的乘积。 我们的极限符合此条件。 这就是这些公式是如何推导出来的。 这些公式如下：

  • S[UD,u] = S*p
  • S[UD,d] = S*(1-p)

最好用基础值来表达这些值 — 这提供了两个缺失的方程来判定我们所需的一切：

  • S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
  • S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

结果就是，四个方程有五个未知值。 第五个未知数是形成完整组的概率之一（到达边界之一的概率）。 为了能够找到所有五个未知数，我们需要第五个方程，因为方程组只有在方程数等于未知数时才能有唯一解。 第五个方程式可以直观地得到，因为我们知道它是向上和向下步阶之间的差值。 理想情况下，它就是极限：

  • Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
  • Nt[U] =  – 基准步阶的理想数量，利用基准向上步阶的概率计算
  • Nt[D] – 理想的基准步阶数，利用基准向下步阶的概率计算
  • N0[U] – 向上的实际基准步阶数
  • N0[D] – 向下的实际基准步阶数

在利用跨越边界概率时，我们能够发现类似极限：

  • Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
  • Nb[U] – 基准步阶的理想数量，利用跨越上边界的概率计算
  • Nb[D] – 基准步阶的理想数量，利用跨越下边界的概率计算
  • N0[U] – 向上的实际基准步阶数
  • N0[D] – 向下的实际基准步阶数

利用这两个极限，我们可以组成一个更复杂的极限，例如它们的和、差或商。 我会选择商，这将减少以下表达式，并完全消除 N0 [U] - N0 [D] 的极限。 通过将这两个极限相除并转换方程，我们得到以下结果：

  • P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

这就是第五个方程，从中我们可以找到跨越边界的概率。 结果就是，我们得到了一个由五个方程组成的系统。 它看起来像这样：

  1. S[U,u] – S[U,d] = n
  2. S[D,d] – S[D,u] = m
  3. S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
  4. S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
  5. P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

含有四个未知数的初始方程组也提供相同的结果方程。该系统可通过经典方式依次排除变量求解：

  • -->  S[U,u] = n + S[U,d] – 排除 “S[U,u]”
  • -->  S[D,d] = m + S[D,u] – 排除 “S[D,d]”
  • (n + S[U,d]) * P[U] + S[D,u] * ( 1 – P[U] ) = S*p – 将所有内容替换为等式 3
  • S[U,d] * P[U] + (m + S[D,u]) * ( 1 – P[U] ) = S*(1-p) – 将所有内容替换为等式 4

经过这些变换后，我们只需要从方程 4 里减去方程 3，就可以得到与直观相同的方程。 不幸的是，这个方程组不允许我们求得剩下的四个值。 我希望这个系统能工作，但它并未如愿。 为了理解原因，我不得不用分形数据分析表格。 这令我能够为这四个量值之一创建一个公式。 运用这个额外的公式，我们可以找到所有其余的值。 因此，该系统被证明是有用的。


计算整个数学模型的算法

首先，我们定义逆方程及其使用顺序，从而在知道 S[U,u] 的情况下找到所有其它方程。 我采用这个值是因为我设法找到了计算它的相关公式。 有了这个值，我们可以运用第一个方程立即找到 S[U,d]：

  • S[U,d] = S[U,u] – n

然后，将这两个值代入方程 3 和 4，并找到其余的值 S[D,u] 和 S[D,d]。 S[D,u] 可从第三个方程即刻计算：

  • S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

现在，我们只需要找到最后一个未知值的公式。 将得到的 S[U,d] 表达式代入第四个方程：

  • S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) =  ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

唯一缺失的元素是 P[U] 值，它可以通过求解第五个方程轻松获得。 我们如此来做：

  • P[U] * n – (1 - P[U]) * m = 2*p*S – S
  • --> P[U] * (n + m)  =   2 * p * S – S + m
  • --> P[U] = ( 2 * p * S – S + m ) / (n + m)

这里的已知值如下：

  • n – 到上边界的步阶数
  • m – 到下边界的步阶数
  • p – 初始向上步阶的概率
  • S[U,u] – 如果跨越上边界，则平均上升步阶数
  • P[U] – 跨越上边界的概率

值 4 可如此计算：

  • S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
  • Pn[p] = 1 , if p >= 0.5
  • Pn[p] = ( (1 – p)/0.5 ) ^ K
  • Pm[p] = 1 , if p <= 0.5
  • Pm[p] = ( p/0.5 ) ^ K
  • K 是调节函数平坦度的幂

稍后我们将在一个单独的程序中计算平坦度系数。 现在我们需要判定最重要的值。 通过分析表中的值 S[U,u]，我设法推导出计算对称边界两个值的公式：

  1. S[U,u] = Summ[ i = 0, n] ( i ) ; if n == m
  2. S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

问题是这些公式仅适用于 p = 0.5 和对称边界。 应扩大公式的概念，从而涵盖不对称边界。 之后，我们可以将其推广到不同的 p 值。 在我们进行泛化之前，请注意表格中的测试结果仅适用于 “m > n”。 如果 “m < n”，公式能针对 “S[D,d], S[D,u]” 操作。 在这种情况下，有必要创建算法的镜像模拟，来查找所有其它未知值。

类似地，我们定义逆方程以及它们在 S[D,d] 情况下的使用顺序。 再次，运用第二个方程找到值 S[D,u]：

  • S[D,u] = S[D,d] – m

之后，这两个值都可以代入方程 3 和 4，从而找到 S[U,u] 和 S[U,d]。 S[D,u] 可以从第四个方程即刻计算：

  • S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

现在，我们只需要找到最后一个未知值的公式。 将得到的 S[U,d] 表达式代入第三个方程：

  • S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

结果就是，我们得到了所有必需数据，从而在 “n != m” 的情况下推广公式 S[U,u], S[D,d]。 分析表格数据后得到以下数据：

  1. m > n, p = 0,5
  2. S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

对于相反的情况：

  1. m < n, p = 0,5
  2. S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

对于具有对称边界的标准情况，计算更简单：

  1. m = n, p = 0,5
  2. S[U,u] = Summ[ i = 0 … n] ( i )
  3. S[D,d] = Summ[ i = 0 … m] ( i )


获得终极方程的原型

现在我们来定义一个已修改函数的原型，它将描述所有可能的 p 值的 S[U,u], S[D,d]。 为了构建一个基准工作原型，我们需要 p 轴上的三个点，和一些关于整体结构的假设。 我相信考虑两种类型的通用函数就足够了：

  1. Sp[U,u] = S[U,u] ^ K(p)
  2. Sp[D,d] = S[D,d] ^ K(q)
  3. q = 1-p

第一种类型可以是一个真实的工作原型，或某个标记，表明该结构不同，且需另一种逻辑。 它证明，幂函数能够将所有数据整合在一起。 当然，会有更复杂的原型，也许更准确，但我认为我们的解决方案已相当足够了。 最重要的是理解逻辑。 然而，若您想微调模型，则可以根据文章中提供的数据进行。 我已创建了一个测试程序：

基于原型找到的函数

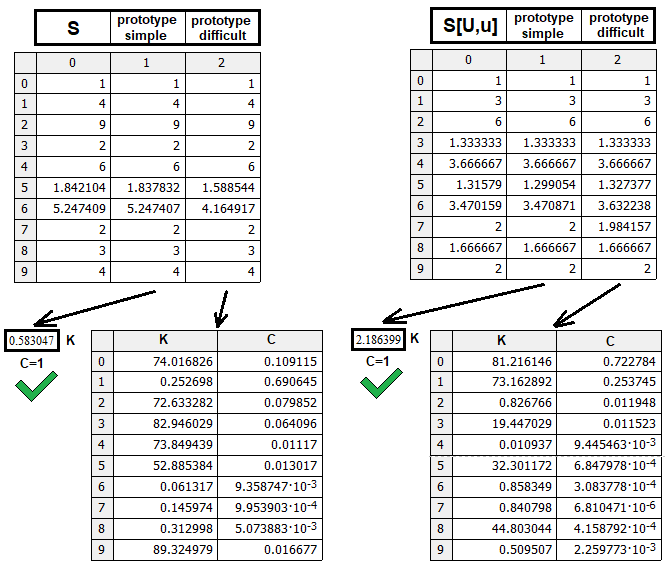
该程序检查两个原型，S(n,m,p) 和 S[U,u](n,m,p)。 S[D,d](n,m,p) 不需要检查，因为这个函数被镜像到 S[U,u](n,m,p)，因此 S[D,d](n, m,p) = S[U,u](m,n,p-1)。 该图例示意已找到的原型在效率方面的比较。 每个原型都在公式中采用相同数量的权重和幂系数的随机组合进行测试。 更简单的原型在搜索周期数相同的情况下显示出更优美的结果。 如有必要，可以进行额外的计算，以了解更复杂原型的功能有哪些。

检查后，我们需要定义嵌套函数 “K(p)”、“K(q)” 的内部结构。 其内部结构必须在点 p=0、p=0.5、p=1、q=0、q=0.5、q=1 处提供强制重合。 我们知道这些点中的函数值，如此可更轻松地选择所需的原型：

  1. p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
  2. p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
  3. p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
  4. q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
  5. q = 1.0 ; Sp[D,d]  = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
  6. q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

第一个和第四个表达式表明在随机游走点的幂应该等于 1。 第二个和第五个表达式表明幂应该是这样的，当把一个值增加时，我们得到 “n” 或 “m”，这可以在上面的结果表格中看到。 第三个和第六个表达式表明幂应该趋于负无穷至零。 这个事实还意味着值 p 和 q 应该在原型的分母当中，因为除以零导致诸如无穷大这样的值。 我们已经有为函数构建幂律原型的经验。 我们能够以此为基础进行修改。 深入分析该问题后，我得到了这个原型：

  • K(p) = 1 + D * Summ(N) (Kn[0] *  | (( p – 0.5 )/(0.5*p)) | ^ A[0]  + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
  • Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
  • D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
  • K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0]  + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
  • Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
  • C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
  • Kn, Km – 相应项的权重
  • A, B - 项式的敏感度

函数看起来很复杂，但它却基于简单的逻辑。 如果 “p=0.5, q=0.5”，累加符号之下的所有内容都变为零，只剩下 1，故而提供条件 “1”、“4”。 如果 “p=1, q=1”，然后累计和中的相关分数，被提升为幂，变成 1：|(( p – 0.5 )/(0.5*p)) |。 这些项用模数符号书写，从而在求幂时排除函数的复数值。 取而代之，相关符号是作为附加因素提供的。 幂不再影响这些项，整个累加和变成 Log[S[U,u]-->n] – 1, Log[S[D,D]-->m] - 1。 通过将此数字与 1 相加，我们得到函数所需的值：Log[S[U,u]-->n], Log[S[D,d]-->m]。

插值多项式是根据类似的逻辑构造的，其中一个例子是众所周知的拉格朗日多项式。 我们的多项式设计用于特定任务，为其所用而存在。 它的优点是对任务的完全适应性。 为了从这组曲线中发现所需的函数，我们只需要找到两个数字数组。


数学模型实现与测试

利用找到的表达式，我们可以轻松实现必要的函数来计算任何分形。 我们只需要一个结构，其可作为容纳主函数所返回全部数据的容器。 其它函数都是辅助。 我们只需要最后一个函数：

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

为了验证数学模型，我在 MathCad15 中实现了此代码的模拟。 如果数学模型组成正确，则表格中的结果应与数学模型返回的结果一致。 程序清单附在文章中，您可以自行查看。 我决定不直接在文章中显示代码，因为它会占用文章的太多空间，但您绝对应该看看结果。 我们比较矩阵，并确保数学模型的可行性：

验证数学模型的准确性

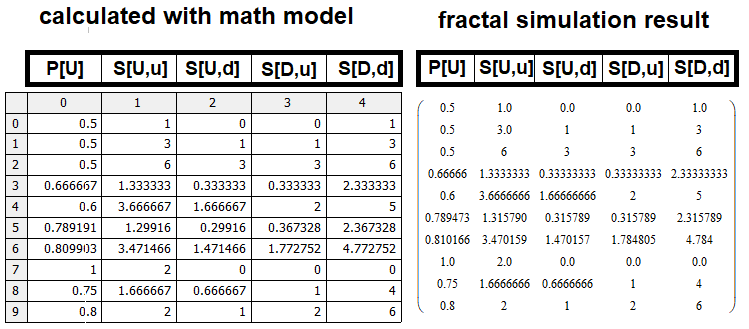
当然，也有一些不准确之处，这是出于我们所找到的原型对应值 S、S[U,u]、S[D,d] 的效率所致。 微小差异的另一个因素可能与模拟的不准确有关，模拟的 n、m 值越大，模拟误差越大，故由于计算能力有限，我们必须限制模拟深度。


结束语

我花了很多时间开发这个数学模型，因为我必须从头开始构思所有的数学内容。 无论如何，结果令我很欣慰。 在后续文章中，我将尝试开发更通用的数学模型，当这些模型组合在一起时，将允许根据其主要特征计算任何交易配置。 甚而，数学模型不仅能适用于描述定价过程，还可以用于描述交易信号和简化复杂的策略，将它们简化为更简单的策略。 这将需要花费一些时间。 


参考


本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/9570

附加的文件 |
下载ZIP
Materials.zip (312.85 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
更好的程序员（第 03 部分）：放弃做这 5 件事成为一名成功的 MQL5 程序员 更好的程序员（第 03 部分）：放弃做这 5 件事成为一名成功的 MQL5 程序员
这是任何想要提高编程职业生涯的从业者必读文章。 本系列文章旨在尽最大可能令您成为最佳程序员，无论您有多少经验。 研讨的思路适用于 MQL5 编程萌新和专业人士。
针对交易的组合数学和概率论（第二部分）：通用分形 针对交易的组合数学和概率论（第二部分）：通用分形
在本文中，我们将继续研究分形，并会特别留意总结所有材料。 为此，我将尝试把所有早期开发归纳为一个紧凑的形式，这对于交易中的实际应用来说将是方便和易于理解的。
更好的程序员（第 04 部分）：如何成为更迅捷的开发人员 更好的程序员（第 04 部分）：如何成为更迅捷的开发人员
每位开发人员都希望能够更快地编写代码，且能够更快、更有效地编写代码并非只是少数人与生俱来的特殊能力。 无论有多少年的敲键盘经验，这项技能每位编码员都可以学习。
更好的程序员（第 02 部分）：停止做这 5 件事变为一名成功的 MQL5 程序员 更好的程序员（第 02 部分）：停止做这 5 件事变为一名成功的 MQL5 程序员
对于任何想要提高编程职业生涯的人来说，这是一篇必读文章。 本系列文章旨在尽最大可能令您成为最佳程序员，无论您有多少经验。 研讨的思路适用于 MQL5 编程萌新和专业人士。