
复购算法:提高效率的数学模型
内容
概述
这种交易方法在各类智能系统中被广泛且积极地运用。 甚至,它还有许多变体和混合体。 此外,从对此类系统的引用数量来看,很明显,该主题不仅在本站点上非常受欢迎,而且在任何其它网络资源上也如此。 所有方法变体都有一个共同的概念,涉及逆市场走势进行交易。 换言之,EA 采用复购来尽可能地低买,并尽可能地高卖。
这是一个古老到自商品出现就有的经典交易形式。 在之前的一篇文章中,我部分谈到了这个话题,同时强调了混合这些方法的可能途径。 在本文中,我们将比论坛用户所做更深入地研究这个概念。 不过,本文将更加通用和广泛,因为复购算法非常适合强调一些非常有趣和有用的功能。
基于均摊算法的细化交易特征的方法
“帮助我摆脱回撤”(来自“我的 EA 赚了很多钱,但有时会令账户爆仓”的作者)
这是许多算法和手动交易者的常见问题。 在撰写这篇文章的时候,我和这样的人有过一次访谈,但他并没有完全领会我的观点。 可悲的是,在我看来,他几乎没有机会理解这种状况的滑稽本质。 毕竟,如果我向更年长、经验更丰富的自己问类似的问题,我也很可能无法理解答案。 我甚至知道,老年自己的真实回答会让我有啥感受。 我会认为自己受到羞辱,或遭劝阻不要进一步从事算法交易。
其实,一切都是如此简单。 我只是有耐心走某条路,获得一些智慧,如果您愿意这么称呼它的话。 这不是理想化和自恋,而是必要的最低限度。 遗憾的是,这条道路花费了数年,而不是数周和数月。
在此,我们有一整个充满梦想和自我欺骗的世界,坦率地讲,我已经开始厌倦一些人的幼稚。 请停止胡说八道,认为您是市场的主宰。 取而代之,请联系有经验的人,并请求他们依据您的预算选择一个 EA。 相信我,这样您会节省很多时间和金钱,更不用说您的理智了。 这些人其一撰写了这篇文章。 下面提供了证明。
关于均摊算法的一般想法
如果我们看一下复购算法或“均摊”,首先似乎这个系统没有亏损的风险。 曾经有一段时间,我对这种技巧一无所知,并对击败任何收益差值的巨大数学期望感到惊讶。 现在很明显,这只是一种错觉,尽管如此,这种方法仍有合理的意义,但更多的在稍后。 一开始,为了能够客观地评估此类系统,我们需要知道一些间接参数,这些参数可以告诉我们的不仅仅是利润增长的简单图像。
策略测试器报告中最相关的参数甚至可有助于理解系统显然在亏损,尽管余额曲线看起来很棒。 正如您可能已经了解,这实际上完全与盈利能力曲线有关。 事实上,交易系统的所有重要指标都是次要的,首先且最基本的是数学特征,当然,这是数学期望及其主要特征。 但值得注意的是,数学期望是一个如此灵活的数值,以至于您总是会陷入一厢情愿的陷阱。
其实,为了正确运用数学期望这样的概念,首先要明白这是概率论的术语,任何这个量化的计算都应该按照概率论的规则进行,即:
- 计算越准确,所分析的样本越大,理想情况下,确切值需从无限个样本中计算得出。
- 如果我们把无穷大分成若干个部分,我们会得到若干个无穷大。
有人可能会想,如果只有有限的真实报价样本可供我们使用,那如何计算特定策略的确切数学期望。 有人会想,为什么我们竟然需要这些无穷大。 问题是,某些均值的所有估算值(例如数学期望)仅在进行这些计算的区域具有权重,而与另外的区域无关。 任何数学特征只有在计算之处才具有权重。 尽管如此,可以区分一些技术来细化特定策略的盈利能力特征,这将令获得的所需参数,越发接近真实值成为可能。
这与我们的任务直接相关。 在意识到我们无法看到无穷长期策略的未来之后,这本身听起来已经完全是胡说八道。 然而,这是一个数学事实,也是计算真实数学特征的必要和充分条件。 我们想到如何在有限样本上计算的数字更接近基于无限样本上计算得出的数字。 精通数学的人都知道,有两个数学概念可以用来计算无限和:
- 积分
- 无穷级数求和
我认为每个人都清楚,为了计算积分以及级数的总和,有必要在所考虑的积分范围内获得函数的所有点,需要计算其积分,或者在所考虑的级数内数字级数的所有元素。 仍然有最完美的选择 — 为我们要积分的函数获取适当的数学表达式,以及用于生成级数元素的表达式。 在许多情况下,如果我们有适当的数学表达式,我们可以得到完成积分或级数之和的精确方程,但在真实交易的情况下,我们就无法应用微积分,一般来说这对我们没有多大帮助,但重要的是理解。
从所有这些得出的结论是,对于任何系统的直接评估,我们只有有限的样本,以及我们在策略测试器中获得的某些参数。 事实上,它们的意义被大大夸张了。 问题是能否用策略测试器参数来判断特定策略的盈利能力,这些参数是否足以给出明确的答案,最重要的是,如何正确运用这些参数,以及我们能否真会正确使用它们。
此外,我们需要明白,对于每种策略,我们若正确评估策略的实际盈利能力和安全性时,任何参数都可能完全不同。 这与利润曲线的评估直接相关。 为了理解这一点,我们首先绘制一个采用复购算法获得的交易曲线的近似视图:
图例. 1
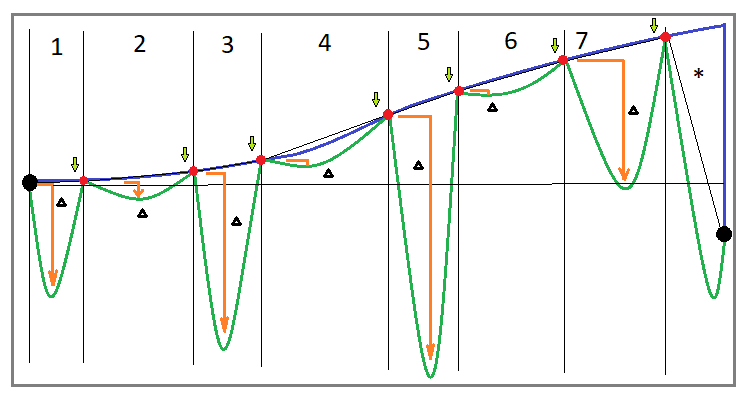
我们从实现一种金融产品的复购开始。 如果您正确实现此算法,那么您的交易在任何情况下都将由轮回组成。 理想情况下,所有轮回都应该为正值。 如果某些轮回负值区域收官,则要么您错误地实现了此算法,要么它不再是纯算法,并且已经对其进行了修改。 但我们会参考经典的复购。 我们定义交易曲线的一些特征参数,来表示经典的复购:
- 余额曲线必须增长,并由 N 次轮回组成
- 所有轮回都有正值利润
- 当交易中断时,我们很可能会发现自己处于最后一个不完整的轮回
- 不完整的轮回具有负值盈利能力
- 轮回在资金方面具有特征性的回撤。
似乎曲线的总体外观乍一看应该清楚地表明这样的系统是有利可图的,但并非一切都那么简单。 如果您看一下最后一个不完整的交易轮回,我特别在起点下方收官,您会发现在某些情况下会很幸运,您应等待轮回的成功收官,而在某些情况下,您可能还未等到最后,就面临巨大的损失,或者令您的资金彻底爆仓。 为什么会发生这事? 事情在于,该图像可能会给人一种错误的印象,即资金的回撤金额在其绝对价值上是有限的,因此,在这种回撤中花费的时间也应该受到限制。
实际上,测试区域越长,平均回撤区域越长。 此处绝对没有限制。 限制仅以您的资金和资金管理品质的形式存在。 不过,基于此原则建立系统的有效方法只能导致您的资金生存期延长,然后再最终爆仓,或者充其量只能赚取很少的利润。
当遇到基于复购(均摊)算法的测试系统时,为了正确评估其生存能力、可靠性和实际盈利能力,应坚持特殊的测试结构。 重点是,这种方法中单次测试的数值会被最小化,原因很简单,当测试任何“正常”策略时,策略测试器中您的整个测试利润非常接近“正态”分布值。 这意味着,测试任何均摊策略时,若持仓时间不长的情况下,您得到的盈利和非盈利测试区域数量大抵相等,这令您很快知道该策略不稳定,或者该策略对市场有正确的理解,并适用于整个历史。
当我们与复购策略打交道时,这种分布可能会强烈畸变,这是由于为了正确测试该系统,您需要设置最大的可能资金。 此外,测试结果高度依赖于测试区段的长度。 事实上,伊这种方式中,所有交易都基于交易轮回,并且该系统的每个独特设置都可以具有完全不同的平均回撤参数,和与之相关的平均回撤持续时间参数。 根据这些指标,太短的测试区段可能会显示过高或过低的测试结果。 原则上,很少进行此类测试,在大多数情况下这可能是导致对这类系统操作信心膨胀的原因。
更准确地评估复购系统的细微之处
现在我们来学习如何使用复购算法正确评估系统的性能,同时应用交易系统的已知参数。 首先,对于这样的评估,我建议使用一个特征 — 恢复因子。 我们来弄清楚如何计算它:
- 恢复因子 = 总利润 / 最大净值回撤
- 总利润 — 每个交易区域的总利润
- 最大净值回撤 — 相对于前一个余额和净值(余额峰值)重合点的最大净值回撤
如我们所见,这是最终利润除以资金的最大回撤。 该指标在经典意义上的数学含义是,根据该思路,它应当展示出系统净值挽回其回撤的能力。 当利用这种特征时,交易系统盈利能力的边界条件是以下事实:
- 恢复因子> 1
如果翻译成可理解的人类语言,这就意味着为了获利,我们可以让资金冒一点不超过相同金额的风险。 在许多情况下,此参数提供了对特定系统交易品质的准确评估。 但用它时,要非常小心,因为关于其数学意义,这是一个相当有争议的参考值。
无论如何,我都不得不向您揭示它的所有缺点,如此您便能了解该参数真的非常随意,其数学释义等级也非常低级。 当然,您也许会说,如果您质疑某事,那就提供另一种备案。 我肯定会这样做,但只会在我们分析这个参数之后。 该参数与最大回撤相关联,而最大回撤又可与交易曲线上的任何点相关联,这意味着如果我们相对于起始余额重新计算此回撤,并将其替换为最大回撤,我们几乎总会得到一个高估的恢复因子。 我们正确地将其全部形式化:
- 恢复因子变化 1 = 总利润 / 按起始本金计算的最大净值回撤
- 按起始本金计算的最大净值回撤 — 按起始余额计算的最大回撤(不是前一个净值最大值)
当然,这不是一个经典的恢复因子,但从本质上讲,相对于普遍接受的边界条件,它实际上更正确地决定了盈利能力。 我们首先直观地讲述计算此指标的两个选项 — 经典选项,和我自己的:
图例. 2
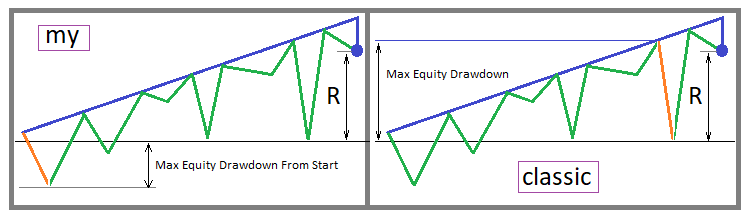
在第一种情况下,可以看出,该参数将取得更高数值,这当然是我们想要的。 但从盈利能力评估的角度来看,有两种方式可以遵循。 经典参数更适合该方式,在其中,最好尽可能延长测试部分的延续时间。 在这种情况下,较高的最大净值回撤值弥补了这种回撤并非始自交易曲线启动处的事实,因此在大多数情况下,这个参数接近真实的估算值。 在多次回测评估当中,我自己的参数更有效。
换言之,您完成的策略测试越多,此参数就越准确。 您的策略测试应在尽可能多的不同区域进行。 这意味着起点和终点的选择应具有最大的可变性。 为了正确评估,有必要选择最不同区域的 “N”,并对其进行测试,然后计算该指标对所有测试区域的算术平均值。 该规则允许我们优化恢复因子的两个版本,包括我自己的和经典版本,唯一的修正是需要执行少量的独立回测来优化经典版本。
尽管如此,说这种为了厘清这些参数而进行的厘清操作较少是不太充分的。 我已演示了我自己的恢复因子版本,以表明任何人都可以提出自己的类似参数,甚至可以将其加入 MetaTrader 中回测的计算特征之一。 但是这些参数中的任何一个都没有任何数学证明,甚至,这些参数中的任何一个都有其自身的误差和适用性限制。 所有这些都意味着,目前没有精确的数学指标来绝对准确地评估使用复购的一种或多种的算法。 不过,随着各种测试数量的增加,我的参数将趋向于绝对准确性。 我将在下一节中提供更多详细信息。
盈利能力的深入和通体理解
通体评估
我相信,每个人都知道盈利的数学期望和盈利因子等参数存在于任何策略测试器报告或交易信号的特征中,但我想没人告诉过您这些特征也可用于计算此类其中没有足够成交分析的交易系统的盈利能力。 故此,您可以通过将 “position” 替换为 “test on the segment” 来使用这些参数。 在计算该指标时,您需要进行多次独立测试,且不考虑任何内部结构。 这种方式将有助于您来评估交易系统的真实前景,且仅用到两个最流行的参数。 此外,它可以向您灌输一个非常有用的习惯 — 多次测试。 为了运用这种方式,您只需要知道以下等式:
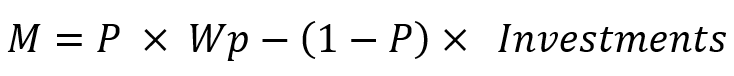
其中:
- M - 预期收益值
- Wp - 期望的利润
- Investments - 您愿意投资多少来达成所期望的盈利
- P - 在达成盈利之前我们将有足够投资的概率
- (1-P) - 在达成盈利之前我们没有足够投资的概率(资金亏损)
下面是类似的盈利因子等式:
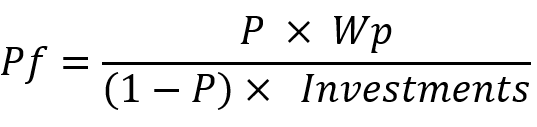
您需要知道的是,对于随机交易并且没有点差、佣金和掉期利率、以及滑点等障碍,这些变量在任何交易系统里将始终取以下值:
若是在预测的时刻,这些特征才能朝着您的方向改变。 故此,我们在不损失资金的情况下获利的概率将取以下值:
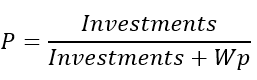
如果您在我们的方程中用这个表达式代替概率,那么您将得到我所提供的恒等式。 如果我们考虑点差、佣金和掉期利率,那么我们会得到以下内容:
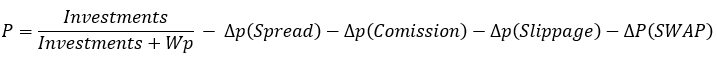
点差、佣金和掉期利率拉低了最终概率,最终导致特征失去有效性。 取而代之,会出现以下不平等式:
- M < 0
- Pf < 1
任何交易系统绝对都是这种情况,这里的复购算法绝对不比任何其它系统更好。 当测试或运营这样的系统时,它能够强烈扭曲信号随机值的分布函数,或回测最终利润,但这种典型场景在短期测试或运营期间会频繁发生。
这是因为如果您在短线区域进行测试,遇到大幅回撤的可能性要小得多。 但是,一旦您开始在更长的区域上进行这些测试,您常常会看到以前从未见过的东西。 但我确信大多数人会自找借口,认为这只是一个意外,且您只需以某种方式绕过这些危险区域。 对于短线区域进行多次测试通常也是如此。
只有一种途径可以克服任何系统的无力盈利。 我们在概率计算方程中添加一个额外的分量:
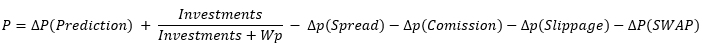
正如我们所看到的,新的分量 “dP(Prediction)” 已经出现在方程当中。 它带有一个加号,我故意这样做是为了表明只有这个分量能够补偿点差、佣金和掉期利率的影响。 这意味着我们首先需要显著的预测品质来克服负面影响,并实现利润:
![]()
只有当我们提供这种特殊的不等式时,我们才能得到我们想要的不等式:
- M > 0
- Pf > 1
厘清方法示例
在本章节中,我想为您提供一些额外的优化操作,令您能够获得更正确的恢复因子值。 我建议回到 “图例 1”,并查看编号片段。 为了优调恢复因子,有必要想象这些片段是独立的测试。 假设我们已经执行了这些测试,以这样的方式,我们就可以不用多次测试。 我们可以这样做是因为这些片段是同时拥有起点和终点的轮回,其就是为回测提供的等效性。
在本节的框架内,考虑到我们正在一次性测试或交易若干金融产品的事实,我认为也值得用其等效图像补充第一张图像。 以下是运用复购算法在多个金融产品上进行并发交易的交易曲线的样子:
图例. 3
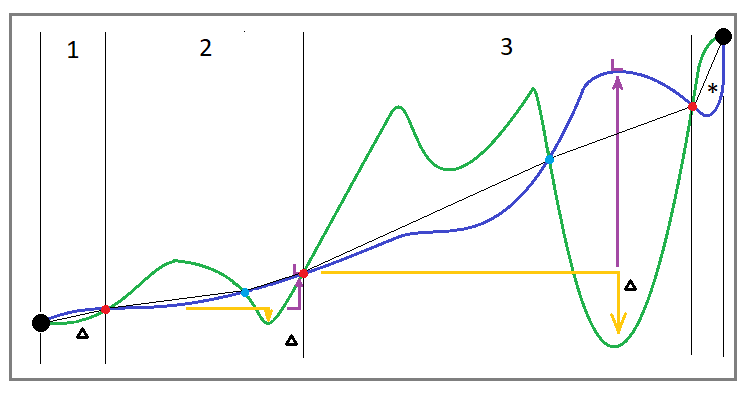
我们可以看到,这条曲线的结构与基于一种金融产品上复购的曲线不同。 我在这里添加了过渡蓝点,这意味着在回撤之前,可能会有“反向回撤”的片段。事实上,我们不能认定这是回撤。 但尽管如此,我们无权在分析之外考虑这些片段。 这就是为什么它们必须成为轮回的一部分。
我认为每次新轮回自前一个轮回的末尾推迟一点更正确。 在这种情况下,上一个轮回的结束应被视为最后一次净值回撤的恢复点。 在图像中,这些轮回由红点隔开。 但事实上,这个轮回的定义是不充分的。 同样重要的是要确定仅仅通过净值固定回撤是不够的,但重点在于是它低于当前轮回的开始。 否则,它是什么样的回撤?
高亮显示这些轮回后,您可以将它们视为分离的独立测试,并计算每次轮回的恢复因子。 这可以通过以下方式完成:
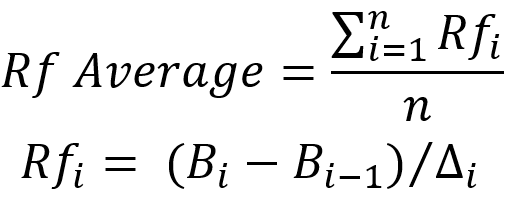
在这个等式中,余额曲线上的相应点(片段余额的最终值和初始值)用作 “B”,而增量表示我们的回撤。 我也希望读者回到最后一张图像。 在其上,由于我上面列出的原因,我从每次轮回的红色起点绘制出增量,而并未像通常那样从蓝色起点绘制出增量。 但如果您需要厘清原始恢复因子,则应从蓝点绘制增量。 在这种情况下,优调参数的方法比参数本身更重要。 按简单的算术平均值采取均摊动作。
无论如何,即使在厘清了一个或另一个自定义或经典参数之后,即便该指标的值超过一个、甚至两个或三个,您也不可理所当然地将其视为该交易系统能赚大钱的标志。
完全相同的方程应该进行多次回测方可应用。 关键点在于这种情况下,任何回测都相当于一次轮回。 我们甚至可以先计算轮回的均值,然后在所有这些之后,再计算相对于回测均值的平均值。 或者,我们可以通过最大化测试片段的持续时间来更轻松地做到这一点。 这种方式至少会为您节省多次测试,因为轮回次数将达到最大值,这意味着将尽可能准确地计算平均恢复因子。
通过多样化提高系统效率
有用的限制
在研究了改进回测某些特征的可能性之后,无疑您的装备更佳,但您仍然不知道主要内容。 根基在于问题的答案 — 为什么必需进行所有这些多重测试或划分成多次轮回? 这个问题真的很复杂,直到您投入如我一样多的付出时间。 可悲的是,这是必要的,但在我的帮助下,您可以大大减少执行此操作所花费的时间。
本章节允许您评估特定参数的客观性。 我将尝试从理论上和方程运用两方面进行解释。 我们从一般等式开始:
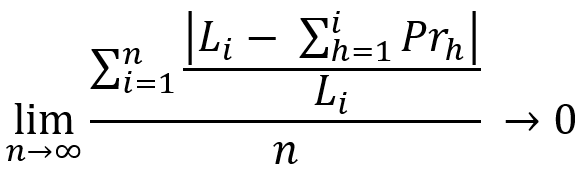
我们研究一个类似的等式,但有一些细微的变化:
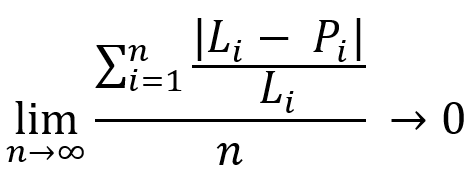
这些方程的本质是相同的。 这些方程表明,在任何可盈利交易系统中,当测试区间的持续时间趋于无穷大时,我们将得到完全融合的余额和当前盈利线,其中某条线代表我们的平均盈利。 在大多数情况下,这条线的性质取决于我们选择的策略。 我们查看下图,以便更深入地理解:
图例. 4
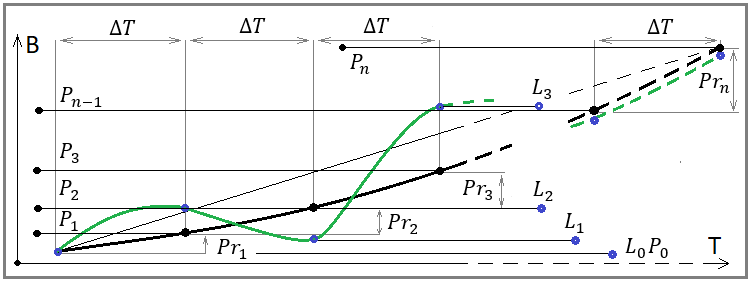
如果您仔细查看这张图片,您会看到我们方程中存在的所有量。 它揭示了我们数学极限的几何意义。 我们的方程中唯一缺少的是 dT 时间间隔。 按照该间隔,我们将余额分步离散化,产生出我们数字序列的所有点,得到这些间隔的余额和盈利,并计算我们在同一点的中线值。 这些方程在数学上等效于以下陈述:
- 我们把多个测试或交易曲线组合在一起的次数越多,它们看起来就越像一条平滑的上升曲线(仅当系统真正有利可图时)
换言之,任何可盈利交易系统在策略测试器或信号的图形部分看起来越优美,我们选择的测试区域越长。 有人也许会说,没有系统可以实现这样的指标,然而,市场里有大量例子,故否定这一点是愚蠢的。 这完全取决于算法的通用性,以及您对市场物性的理解程度。 如果您懂得您正在交易的市场始终固有的数学逻辑,那么实际上您会得到一条无限增长的盈利曲线,并且您无需等待整体无穷大来确认系统的有效性。 当然,很明显这是一项极其艰巨的任务,但无论如何,在许多算法的框架内,这项任务是可实现的。
我们通过如何正确运用学到的技术来终结这个理论介绍。 您也许会问,当我们只有有限的样本,相应地,不可避免的不完整总和时,如何运用这些技术达到无限累加。
- 答案在于将整个历史分成几个片段
- 依据测试持续时间,直到整个历史记录中的一个片段,从中选择若干长度持续增长的片段
- 选择测试方法
- 测试
- 查找得以改善的恢复因子和/或相对回撤
这个棘手的测试规划案的本质是揭示间接迹象,表明我们的极限确实分别趋于无穷大和零。 为了提高测试规划案的效率,我们必须明白,最长的测试区段至少应该比最短的测试区段看起来更优美,理想情况下,每个后续区段都应该更大,看起来更优美。 我用“更优美”这个概念,只是为了让大家清楚,这其实等同于我们的极限。
不过,我们的极限仅在理论考察或准备期间(无论您喜欢什么)时才优秀。 在这方面,问题出现了 — 如何在不求助“眼球分析”的情况下发现这些事实? 我们需要以某种方式把我们的极限与策略测试器报告中的参数进行适配。 换言之,对于策略测试器报告或信号中的参数,我们需要一些替代极限,如此就能换用我们的测试结构。 让我来向您展示一组必要且充分的替代极限:
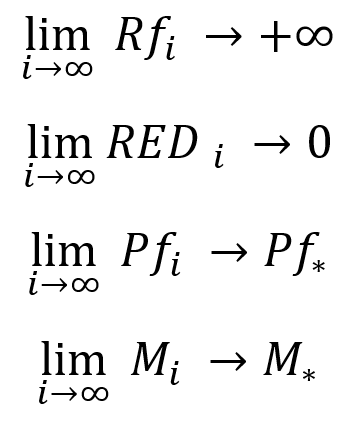
我们应该在此明白什么:
- 在无限测试期间,任何盈利策略的恢复因子趋于无穷大
- 在无限测试期间,(任何盈利策略)净值的相对回撤趋于零
- 在无限测试期间,任何盈利策略的交易盈利因子都趋向其平均值,并且具有有限的真实极限。
- 在无限测试期间,任何盈利策略(未启用自动手数(固定手数))的数学期望趋向其平均值,并且具有有限的真实极限
所有这些都与无限测试有关,不过在继续将它们适应有限样本之前,了解这些极限的数学含义是有用的。 这些表达式与我们方法的适配性应该始自这样一个事实,即我们应当选择若干个测试片段,每个都应比前一个大得多,最好至少两倍。 为了能够明显对比较短和较长测试之间的读数差异,这是必要的。 如果我们以这样的方式对测试进行编号,即随着索引的增加,它的长度随着时间的推移而增加,那么对于有限样本的情况,我们会得到以下适配:
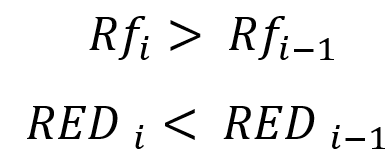
换言之,恢复因子的增加和资金相对回撤的减少是间接证据,最有可能的是,测试片段或信号生存期的进一步增加,令我们的曲线在视觉上变得更加优美。 这意味着我们已确认了我们无限极限的实施。 否则,如果盈利曲线没有变得更直,我们可以宣示这样一个事实,即所获结果非常接近随机,并且未来亏损的可能性非常高。
当然,许多人会说,我们可以更频繁地优化系统,一切都会走向正轨。 在某些极其罕见的情况下,这是可能的,但这种方式需要完全不同的测试方法。 我不建议任何人诉诸这种方式,因为在这种情况下,您得不到任何数学逻辑支持,而于此您能以明确的方式得到一切。
所有这些细微差别理应能说服您,测试复购算法更需要运用这种方式。 特别是,我们甚至可以简化任务,并在最大长度片段上立即测试复购系统。 我们也许逆推这个逻辑。 如果我们不喜欢最长片段的交易表现,那么即使较短片段中更好的表现也表明我们的不等式不再得到满足,系统在这个阶段还没有准备好进行交易。
并发运用于多种金融产品的有用特色
依据有限的历史记录进行测试时,肯定会出现一个问题 — 是否有足够的历史记录可供我们的测试方法正确使用? 问题是,在许多情况下,该策略具有权重,但其品质不足以令人舒心使用。 首先,我们至少应该了解它是否真的具有一个可预测性理论,以及我们是否可以开始进行现代化改造。 在某些情况下,我们实际上没有足够的可用交易历史记录。 我们该怎么做? 正如许多人已经猜到的那样,从小章节的标题来看,为此目的我们应该针对多种金融产品运用。
这似乎是一个显而易见的事实,但不幸的是,一如既往,任何地方都没有数学逻辑。 基于多种金融产品上测试的本质,与增加测试持续时间的本质相当。 唯一的修正是您的系统必须支持多币种。 对于不同的交易工具,系统可能有不同的设置,但希望所有设置都相似。 设置的相似性将表示系统的一个事实:可适用于最大可能数量的交易产品的物性原理。
依据这种方式,及正确实施此类测试,索引 “i” 应该已经理解为固定测试片段上并发测试的金融产品数量。 那么表达式的含义如下:
- 当增加所交易金融产品的数量时,金融产品越多,恢复因子越大
- 当增加所交易金融产品的数量时,金融产品越多,净值的相对回撤越小
事实上,为了简单起见,增加测试数量可以解释为测试总持续时间的增加,就好像我们将针对每个金融产品的每次测试视为一个巨大的整体测试的一部分。 这种抽象只会帮助您理解为什么这种方式也具有相同的动力。 但如果我们更准确地思考这个问题,更深入地理解为什么由几条线组成的曲线会更优美,那么我们应该使用以下概率论的概念:
- 随机值
- 随机变量的方差
- 随机变量的数学期望
- 随机变量的正态分布律
为了充分解释为什么我们需要这一切,我们首先需要一个图像来帮助我们以不同的方式观察回测或交易信号:
图例. 5
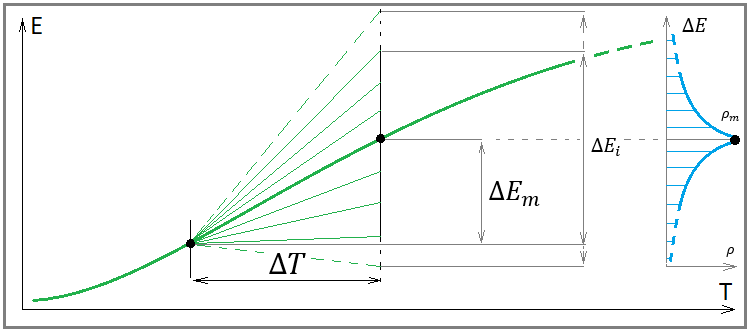
我未在此处绘制一条余额线,因为它在此不能决定任何事情,我们只需要一条盈利线。 该图像的含义是,对于每条盈利线,可以选择无限数量的固定长度的独立片段,其中可以构建盈利线增量的随机变量的分布律。 随机变量的存在意味着将来所选区域中的盈利增量可以在最宽广的范围内具有完全不同的值。
这听起来很复杂,但一切实际上很简单。 我想很多人都听说过正态分布律。 据说它描述了自然界中几乎所有的随机过程。 我想,这无非是萌发的一种幻觉,阻止您“进行思考”。 撇开所有的笑谈,分布律流行的原因在于它是一个人工编译的非常方便的方程,用于描述关于随机变量的数学期望的对称分布。 它将对我们进一步的数学变换和实验有用。
但在开始研究这个定律之前,我们应该定义随机变量的任何分布律的主要属性:
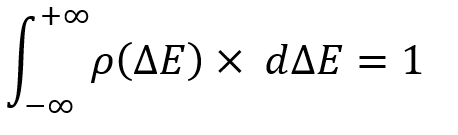
任何随机变量分布律本质上都是非联合事件的完整组的类比。 唯一的区别是,我们没有这些事件的固定数量,我们可以随时选择任何感兴趣的事件,如下所示:
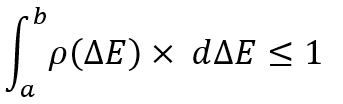
严格来说,这个积分考虑的是在一个随机变量的指示范围内找到一个随机变量的概率,很自然,它不能大于 1。 给定事件空间中的总事件的任何概率都不能大于 1。 不过,这并非最重要的。 于此唯一重要的是,您应当明白在这种情况下,事件仅由一组两个数字来判定。 这些是最小维度随机变量的示例。
这些方程是 “N” 维方程的模仿物,事件可以经由 “N*2” 数字进行判定,甚至更复杂的结构(在多维区域积分的框架内)。 这些是相当复杂的数学部分,但在此它们是多余的。 这里得到的所有定律对于一维变体都是自洽的。
在继续更复杂的结构之前,我们来回顾一下随机值分布律的一些常见参数特征:
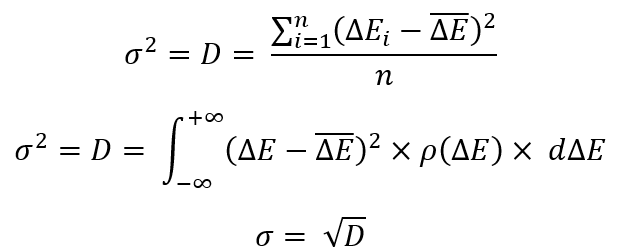
为了定义这些方程中的任何一个,我们需要确定最重要的事情 — 随机变量的数学期望。 在我们的例子中,它看起来如下:
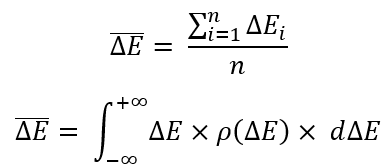
数学期望只是算术平均值。 数学家喜欢给简单的东西起个非常聪明的名字,如此就没有人理解任何事情。 我提供了两个方程。 它们唯一的区别是,第一种适用于有限数量的随机变量(数据量有限);而在第二种情况下,使用“概率密度”上的积分。
积分相当于求总和,唯一的区别是它针对无限数量的随机变量求和。 随机变量分布律,位于积分下,包含整个无穷大的随机变量。 这里有一些差异,但总体来说,本质是相同的。
现在,我们回到前面的方程。 这些只是针对随机变量分布律的一些操作,对大多数数学家来说都很方便。 如同上一个示例,有两种实现 — 其一用于一组有限的随机变量,另一种用于无限随机变量(随机变量分布律)。 它指出 “D” 是所有随机变量和平均随机变量(随机变量的数学期望)之差的平方均值。 此值称为“离散”。 该值的根称为“标准偏差”。
随机变量的正态分布
在随机变量的数学中,这些值被普遍接受。 它们被认为是随机分布律的最重要特征的最便捷描述。 我不赞同这个释义,但无论如何,我都会向您展示它们是如何计算的。 最后,需要这些量化值来理解正态分布律。 您不太可能轻易找到这些信息,但我会告诉您,正态分布律是人为发明的,只有几个目标:
- 判定与数学期望对称的分布规律的简单方式
- 能够设置离散差和标准偏差
- 能够设置数学期望
所有这些选项都允许我们得到一个现成的随机变量分布律方程,称为正态分布律:
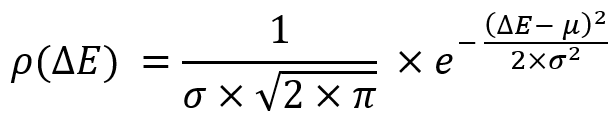
- 可盈利系统并发交易的金融产品越多,我们的盈利图就越优美、越直(多元化的特例)
- 选择测试或交易的区域越长,我们的盈利图就越优美、越直
- 已证明盈利能力的系统进行的并发交易越多,我们的整体盈利能力图就越直,越优美
- 以上所有因素的结合产生了理想的多元化和最优美的图表
所说的一切都仅适用于其盈利能力已在数学和实践中得到证明的交易系统。 我们从定义“更优美的图形”在数学术语中的含义开始。 “标准偏差”,我在上面已经展示了其方程,可以帮助我们解决这个问题。
如果我们有一系列分布密度曲线,拥有相同数学期望的盈利增量随机变量,对于两个几乎相同的图形,象征它们的片段持续时间相同,那么我们更喜欢标准偏差最小的那个。 该系列中的完美曲线可以是标准偏差为零的曲线。 只有当我们知道未来时,这条曲线才能实现,当然这是不可能的,不过,我们必须明白这一点才能比较来自该家族的曲线。
随机值分布规律框架下的利润曲线美化
这个事实是这样理解的,当我们应对一系列曲线时,对于所选时间段内盈利增量的数学期望是相同的,但是当我们应对分布完全任意的曲线时该如何做? 尚不清楚如何比较它们。 有关于此,标准偏差不再完美,我们需要另一个更通用的考虑到缩放的比较值,或者我们必须提出一些算法,将这些分布律简化为某个相对值,其中所有分布率将具有相同的数学期望,故此,经典准则将应用于所有曲线。 我已开发了这样的算法。 其中的技巧之一是以下变换:
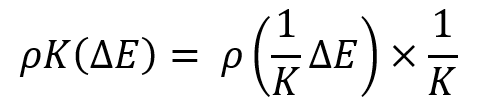
这些曲线的家族将如下所示:
图例. 6
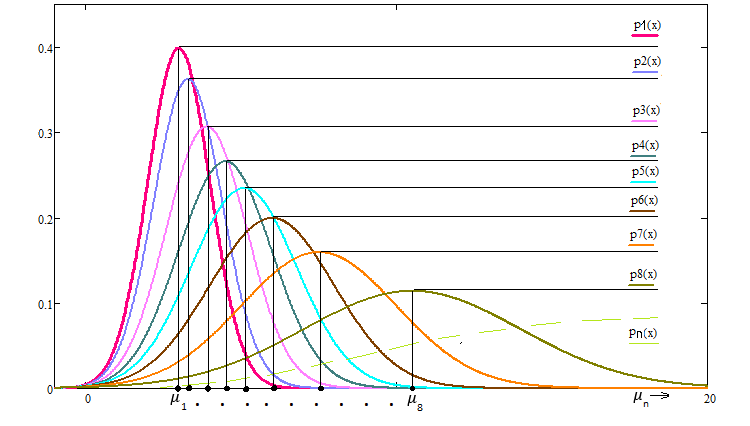
一个非常有趣的事实是,如果我们遵从正态分布律进行这种变换,那么它相对于这种变换是不变的,且看起来像这样:
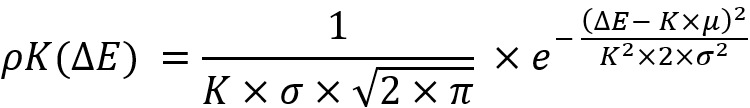
不变性由以下替换构成:
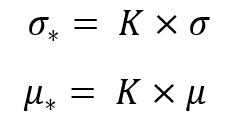
如果我们将这些替换代入前面的方程,那么我们得到相同的分布律,使用带星号的相应值:
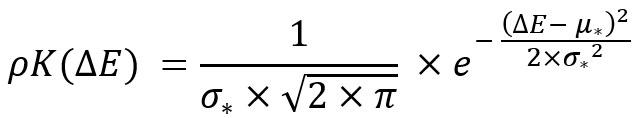
这种变换是必要的,以便不仅确保变换律的不变性,且要确保以下参数的不变性:
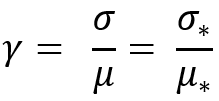
我不得不发明这个参数。 若缺了它,就不可能像任何其它定律一样正确缩放正态分布律。 对于任何其它分布律,此参数也是不变的。 事实上,正态律很容易感知和理解。 其想法是,它可用于具有不同数学期望的任何分布,其本质将与标准偏差相似,只是不需要所有已比较的分布必须具有相同的数学期望。 由此亮明,我们的变换旨在获得一个分布家族,其中给定参数具有相同的值。 似乎很方便,不是吗?
这是定义所谓图形优美的一种方式。 具有最小参数的系统是“最优美的”。 这一切都很好,但是我们需要此参数用于不同的目的。 我们设定的任务是比较两个系统的美感。 想象一下,我们有两个系统,独立进行交易。 如此,我们的目标是合并这些系统,并了解这次合并是否会产生影响,或者更确切地说,我们希望以下内容:
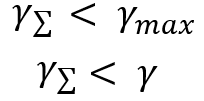
当使用任何分布律时都会观察到这些比率。 这自动意味着,如果我们的并发交易多种金融产品,或系统具有类似的盈利能力,那么多元化是有意义的。 我们将以略微不同的方式证明这一事实。 正如我所说,我想出了一种将所有分布减少到相对随机值的算法。 我们将使用它,但首先我们将在表示两个增量之和的随机变量的分布律框架内分析合并多条曲线的一般过程。 我们将循环逻辑以配对合并。 为此,我们假设我们有 “n+1” 条曲线,每条曲线都有一个定义好的数学期望。 但为了得到随机变量的象征性合并,我们需要了解:
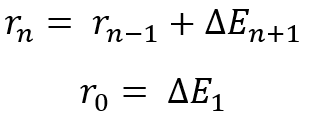
事实上,这是一个循环表达式,并无数学意义,但它展示出合并列表中存在的所有随机变量的逻辑。 简单地说,我们有 “n+1” 条曲线,我们必须使用 “n” 个连续变换来组合它们。 事实上,这意味着我们必须使用某种变换运算符在每个步骤中获得总随机变量的分布律。
我不会深入冗长的解释。 取而代之,我只简单地展示这些变换操作,以便您可自行得出结论。 这些方程实现了所选时间段内两条盈利曲线的合并,并分别计算曲线 “dE1 + dE2” 的两个片段的总盈利,分别低于 “r” 所选值的(Pl)和高于(Pm)的概率:
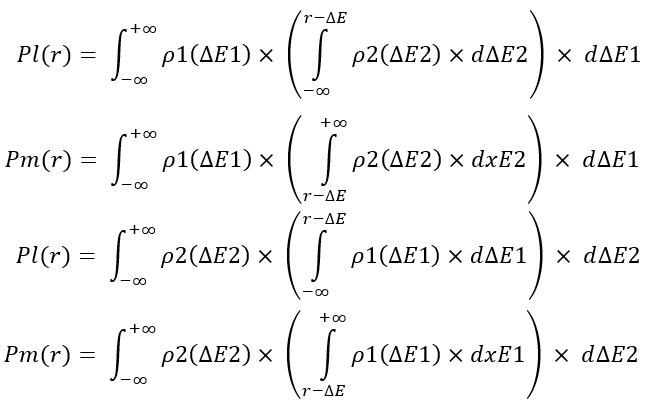
此处有两种实现这些量化值的选项。 两者完全相似。 在计算这些值之后,它们可以用来获得 “r” 随机变量的分布律,这是我们计算出整个循环合并链所需要的。 依据随机变量的定义,我们可以从这些方程中得到相应的分布律,如下所示:
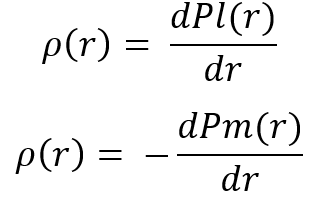
您也许已经猜到了,在获得分布律后,我们就可以在循环变换链中进入下一步。 贯穿整个链条完工后,我们得到了最终的分布,我们已经可以将其与我们用于循环合并链的分布之一进行比较。 我们根据我们得到的分布律创建几个分布,并运行一个合并步骤,作为示例来演示每个合并“比上一个更优美”的事实:
图例. 7
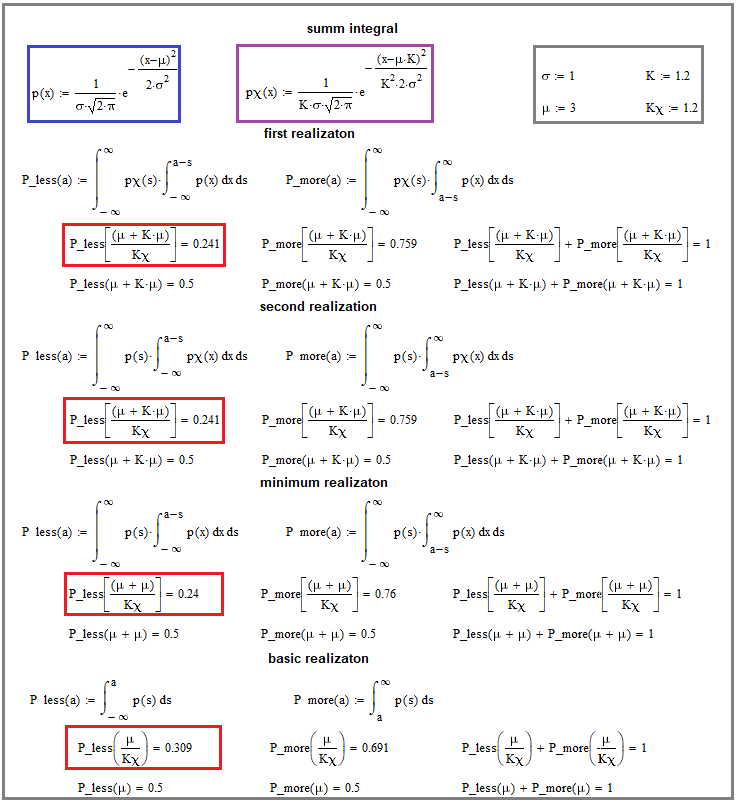
该图像演示了应用我们的合并方程进行的数学合并。 唯一没有显示的是将变换积分重微分为随机合并值分布律。 稍后,我们将看到限定在更常见想法框架内的微分结果,但现在我们先来对付图像中的内容。
注意红色矩形。 它们是这里的基础。 最低积分是说我们根据原始分布律取积分,以此方式计算随机变量的概率,取小于数学期望的值,再除以 “Kx”。 在上面,您将看到两个略有不同的分布合并的类似积分。 在所有情况下,重要的是保持数学期望与所选积分边界值之间的比率(Kx),该值以相应的 “Kx” 表示。
请注意,根据我上面为您给出的方程式,这两个合并选项都显示在那里。 此外,基础分布与自身合并,就好像我们正在合并两条相似的盈利曲线一样。 在图片中相似并不意味着相同,而是对所选时间段内盈利曲线增量的随机变量具有相同的分布律。 证据是我们发现合并随机变量相对于原始变量的相对偏差概率较小。 这意味着对于任何合并中随机利润值的增量,我们有一个更“优美”的分布律。 当然,也有例外需要更深入地研究该主题,但我认为这种方式对于本文来说已经足够了。 您很可能在任何地方都找不到更好的东西,因为这是一种非常特殊的素材。
比较美感的另一种替代方式是变换全部,包括原始分布律和上面研究的循环链的结果。 为了达成这一点,我们只需要使用我们的变换,它允许我们获得一系列可扩展的分布曲线,并执行以下操作:
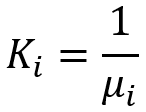
这种变换的诀窍在于,依据这种方式,所有受相应变换影响的分布律都将具有相同的数学期望,且相应地,我们能只用标准偏差来评估它们的“美感”,而不必发明任何奇异的准则。 我已经向您展示了两种方法。 由您来选择最适合您的一种。 您也许已经猜到了,所有这些相对曲线的分布律将如下所示:
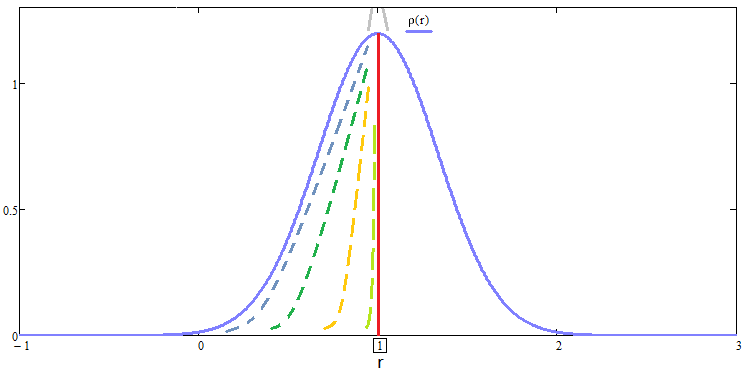
该方法也适用于扩展测试。 此处的扩展测试是指在更长的片段上进行测试。 此应用程序仅适用于确认事实,即测试时间越长,图形越优美。 您必须应用的这个证明的唯一技巧,就是如果我们增加测试的持续时间,那么我们以整数的倍数进行,而在这个数字的倍数中,我们要考虑的不是 1 步而是 “n”,且需应用合并方程。 这样合并将更加简单,因为循环合并链将只包含一个重复的元素,并且只能将结果与此元素进行比较。
结束语
在本文中,我们研究的不是复购算法本身,而是一个更重要的主题,它为您提供了必要的数学方程式和方法,以便更准确、更有效地评估交易系统。 更重要的是,您可以得到数学证明,即什么是有价值的,是什么让它有效,以及如何以自然和健康的方式增加它,知晓您做的一切都是正确的。
我们还证明了,任何盈利系统的图表越优美,我们所用的交易区域越长,还有,在一个账户上更多盈利系统并发交易。 So far, everything is framed in the form of a theory, but in the next article we will consider the applied aspects. To put it simply, we will build a working mathematical model for price simulation and multi-currency trading simulation and confirm all of our theoretical conclusions. You most likely will not find this theory anywhere, so try to delve deeper into this math, or at least understand its essence.
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/12445
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。