트레이딩을 위한 조합론과 확률 이론(3부): 첫 번째 수학적 모델

MetaTrader 5 — 트레이딩 | 20 6월 2024, 16:47

321

Evgeniy Ilin

콘텐츠

소개

우리는 앞의 기사에서 프랙탈의 첫 번째 공식을 얻었습니다. 이를 통해 모든 중요한 프랙탈과 관련된 값을 수학적 모델을 사용하여 설명할 수 있다는 가정이 가능 해졌습니다. 시뮬레이션은 이러한 값을 설명하기 위해 만들어진 것이 아니라 이러한 구조에 대한 심층적인 분석을 가능하게 하는 첫 번째 데이터 수집에 도움이 될 뿐입니다. 저는 이 글에서는 첫 번째 수학적 모델을 개발하는 과정부터 다른 Expert Advisor에 적용할 수 있는 수학적 모델을 얻기까지의 전체 과정을 설명하는 데 특별히 집중을 하기로 결정했습니다.

새로운 아이디어

이전 기사에서 대칭 프랙탈을 고려할 때 우리는 특정 복도 내에서 이동의 결과로 가격의 평균 스텝 수를 계산하는 일반적인 공식을 얻었으며 이는 동일한 대칭의 작은 복도의 수에 의해 결정됩니다. 이 공식은 다음과 같습니다:

S = K^2 - 는 한 스텝이 곧 다른 복도라는 사실에 기반한 새로운 복도의 평균 스텝 수입니다.
P = K * P0 --> K = P/P0 - 알려진 복도가 알려지지 않은 복도보다 몇 배 더 큰지 확인합니다.
P - 평균 스텝 수를 알 수 없는 복도의 폭입니다(스텝 수는 원래 복도 크기의 절반입니다).
P0 - 알려진 복도의 너비

비대칭 복도를 설명하기 위해서 우리는 앞서 살펴본 몇 가지 개념을 보다 이해하기 쉽도록 재정의해야 합니다. 그중 가장 중요한 것은 K입니다. 이 값은 스텝이 위로만 올라가거나 아래로만 내려가는 경우 가격이 새 복도에서 이동해야 하는 스텝 수를 반영합니다. 대칭 복도의 경우 위쪽 또는 아래쪽 중 어느 경계(교차)를 고려하고 있는지에 관계없이 스텝 수는 동일합니다. 이는 위쪽 경계와 아래쪽 경계 모두에 문제가 나타나게 되기 때문입니다. 비대칭성에 관해서는 이전 기사에서 코드를 실험한 한 결과 평균 스텝 수가 다음과 같이 결정된다는 결과를 얻었습니다:

S = n * m - 복도의 비대칭 반쪽의 평균 스텝 수
n - 복도의 위쪽 절반에 해당하는 스텝 수
m - 복도의 아래쪽 절반에 해당하는 스텝 수

따라서 대칭 복도의 경우 "m = n"이 됩니다. 그런 다음 위의 내용을 바탕으로

S = n * n = m * m = m * n = n^2 = m^2 = K^2
K = n = m

즉 첫 번째 파생 공식은 이전 공식의 특수한 경우일 뿐이므로 K는 더 이상 필요하지 않습니다.

이 함수의 흥미로운 특징은 S(a*k, b*k) = S(a,b) * S(k,k)로 증명하기가 매우 쉽다는 점입니다:

S(n*k ,m*b) = m*k*n*b = n*m * k*b
S(n,m) * S(k,b) = n*m * k*b

이 속성은 매우 흥미롭습니다. 좀 더 생각해 보면 이 속성을 통해 전체 프랙탈을 설명하는 데 필요한 모든 공식을 도출할 수 있습니다. 이 속성은 프랙탈의 매우 중요한 특성인 중첩 기능을 반영합니다. 즉 매우 복잡한 유한 프랙탈은 서로 스텝 역할을 하는 두 개 이상의 간단한 프랙탈로 표현될 수 있습니다. 이 속성은 더 복잡한 경우에 사용하는 공식을 일반화하는 데 사용됩니다.

프랙탈을 진행하기 전에 저는 위에서 정의한 공식이 p=0.5일 때만 작동한다는 점을 다시 한번 상기시켜 드립니다. 시장 또는 프랙탈 매개변수가 랜덤워크에서 벗어나기 시작하면 이 공식은 매우 흥미롭게 변화하기 시작합니다:

Ss[n,m,p] - 평균 스텝 수에 대한 보다 일반적인 공식(모든 방향)
S(n,m) = Ss[n,m,0,5] - 랜덤 워크 공식은 일반 공식의 특수한 경우입니다

평균 스텝 수의 일반적인 공식

보다 일반적인 공식의 형태를 결정하기 위해 저는 프랙탈 중첩 원리의 불변성을 사용했습니다. 개별 프랙탈 중첩 수준을 이전 스텝과 비교하면 특정 스텝에서 어떤 스텝이 발생했는지를 생각할 필요가 없습니다. 따라서 기본 업/다운 스텝은 이전 레벨의 상황에 해당했던 주파수의 비율과 정확히 동일한 비율로 발생합니다. 즉 해당 중첩 레벨의 경계를 넘으면 다음 중첩 레벨로 한 스텝 올라가거나 한 스텝 내려갑니다. 그러나 현재 중첩 레벨에 대한 스텝 발생 빈도의 비율은 현재 레벨의 구성에 따르지 않는 것으로 알려져 있습니다. 이는 프랙탈 중첩 원리가 모든 확률 "p"에 대해 관찰된다는 것을 의미합니다. 즉, 'p' 값이 변경되면 수식도 변경되어야 하지만 어떻게든 중첩 속성을 유지해야 합니다. 우리의 경험이 일반적인 공식을 결정하는 데 도움이 될 수 있습니다. 우리는 확률 p에 랜덤 걷기 포인트와 0과 1인 두 극단점이 있다는 것을 알고 있습니다. 이 세 지점에서 함수가 어떤 값을 취할지 살펴봅시다. 다음과 같은 결과를 얻을 수 있습니다:

Ss[n,m,1] = Sn[n] = n
Ss[n,m,0] = Sm[m] = m
Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
Sn[n,p] - 위쪽 경계까지 한 방향으로의 스텝 수
Sn[m,p] - 아래쪽 경계까지 한 방향으로의 스텝 수

첫 번째 경우에는 스텝이 없으며 모든 체인이 동일한 경로를 따릅니다. 두 번째 경우는 그 반대이며 위로 올라가는 스텝이 없이 모든 스텝은 아래로 내려갑니다. 극단적인 값에서는 요소 중 하나가 수식에서 완전히 사라집니다. 0으로 올리면 가능합니다. 0의 거듭제곱에 해당하는 숫자는 모두 1과 같습니다. 또한 정도에는 다음과 같은 형태의 불변성이 있습니다:

A^X * B^X = (A*B)^X

숫자 대신 평균 스텝으로 대체해도 프랙탈 중첩 원리는 그대로 유지됩니다. 또한 이것은 거듭제곱이 n과 m에 의존하지 않는다는 것을 보여줍니다. 평균 스텝 수에 대한 일반적인 공식은 다음과 같습니다:

Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

프랙탈 중첩 원리는 다음과 같이 개략적으로 나타낼 수 있습니다:

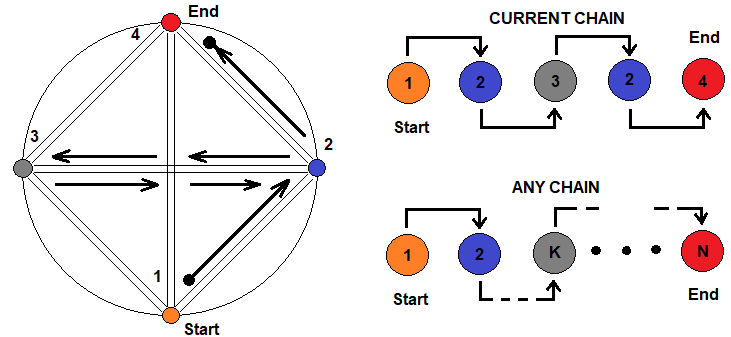
그림은 서로 표현될 수 있는 서로 다른 프랙탈을 상징하는 네 가지 상태를 보여 줍니다. 한 상태에서 다른 상태로 전환하는 것은 모든 체인을 통해 가능합니다. 임의로 선택한 체인이 오른쪽에 표시됩니다. 아래 부분에서 볼 수 있듯이 여러분은 이 체인을 길이와 복잡도에 관계없이 동일한 상태를 무제한으로 반복할 수 있습니다. 즉 프랙탈의 평균 스텝 수에 대한 공식은 프랙탈 중첩 수준을 나타내는 곱의 체인으로 표현될 수 있습니다.

거듭제곱 함수 프로토타입 만들기

프랙탈 중첩 속성과 베이스에 대한 등비곱 함수의 불변성에서 더 많은 아이디어를 얻을 수 있습니다. 이러한 모든 수학적 원리는 우리가 프랙탈에 대한 더 깊은 내용을 알기 위한 추가적인 공식을 도출하는 데 도움이 됩니다. 따라서 우리는 그 형태를 알 수 없는 두 가지 함수를 추가로 얻게 됩니다:

Pn[p] - 위쪽 경계 승수의 거듭제곱
Pm[p] - 아래쪽 경계 승수의 거듭제곱

우리는 다음 사항을 알고 있습니다:

Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

멱함수를 분석하여 적합한 함수의 프로토타입을 만들 수 있습니다. 저는 다음과 같은 프로토타입을 선택했습니다:

Pn[p] = 1 , p >= 0.5
Pn[p] = ( (1 - p)/0.5 ) ^ K
Pm[p] = 1 , p <= 0.5
Pm[p] = (p/0.5) ^ K
K는 함수의 평탄도를 조절하는 거듭제곱입니다.

주어진 거듭제곱의 평탄화적인 전환을 정확하게 설명할 수 있는 다항식의 형태로 '2'와 '4'를 표현하는 것이 더 정확하겠지만 제 생각으로는 여기서는 불필요한 표현이라고 생각됩니다. 여러분이 보다 정확한 다항식을 정의하고 싶다면 여기에 프로토타입이 있습니다:

Pn[p] = C1 * ( (1 - p)/0.5 ) ^ K1 + C2 * ( (1 - p)/0.5 ) ^ K2 ... + ... + CN * ( (1 - p)/0.5 ) *KN
Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 ... + ... + CN * ( p/0.5 ) ^ KN
С1 + С2 + ... + ... СN = 1은 해당 거듭제곱에 대한 가중치입니다.
KN은 해당 용어의 거듭제곱입니다.

제가 선택한 다항식은 항이 하나만 있는 가장 단순한 버전의 일반 다항식입니다. 선언된 모든 원칙은 모든 분수 "n, m"에 대해 확인할 수 있습니다.

저는 위의 가정을 확인하기 위해 다음 프로그램을 만들었습니다:

공식 확인

결과에서 볼 수 있듯이 모두 정상적으로 작동합니다 . 이제 우리는 두 숫자를 비교하면 됩니다. 이 둘이 같으면 중첩 원리와 분수 n과 m을 사용할 수 있다는 것이 확인된 것입니다.

프로토타입이 제한된 제품군에서 최고의 함수를 수신하는 일반적인 계획

이제 우리는 프로토타입에 필요한 계수를 어떻게 검색할지 결정해야 합니다. 저는 가장 간단한 검색 유형인 원하는 범위의 난수를 생성하는 방법을 선택했습니다. 메서드 체계는 다음과 같습니다:

근사 방식

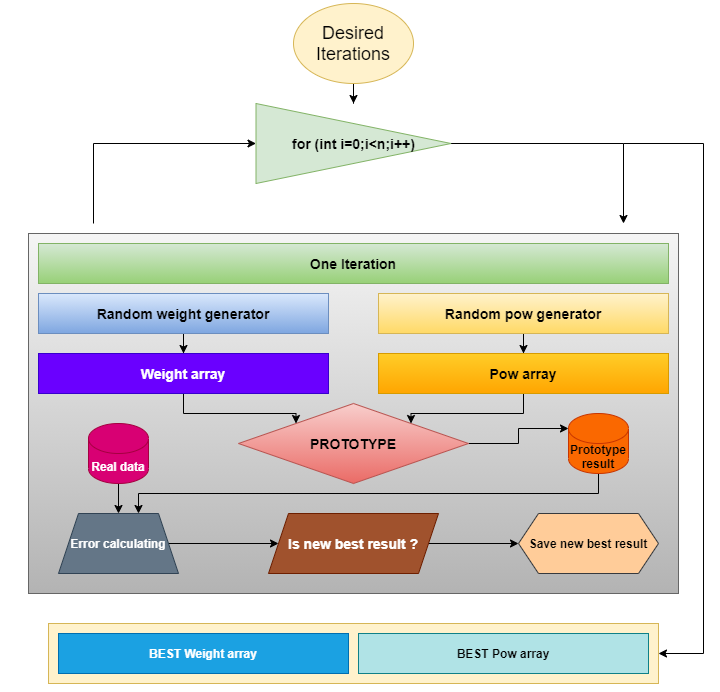
이 체계는 실제 데이터와 수학적 모델을 가장 잘 일치시키는 계수를 찾아야 하는 경우 모든 함수 프로토타입에 적합합니다. 이 글의 마지막 부분에서 우리는 다른 프로토타입을 처리하는 데 동일한 메서드를 적용할 것이므로 이 체계가 앞으로도 유효할 것입니다.

심층 분석

이제 이 공식의 구조를 더 자세히 분석해 보겠습니다. 공식의 결과는 가격이 경계 중 하나를 넘기 전에 이동하는 평균 스텝 수입니다. 위아래 스텝은 동등한 것으로 간주되지만 이러한 동등성은 실제로는 랜덤 워크의 경우에만 가능합니다. 비대칭 프랙탈에 대한 완전한 이해를 위해서 우리는 주어진 값이 실제로 무엇으로 구성되어 있는지 추가로 확인해야 합니다. 논리적으로 모든 유형의 평균 스텝 수는 위쪽 경계를 넘을 때의 평균 스텝 수와 아래쪽 경계를 넘을 때의 평균 스텝 수 모두에 따라 달라집니다. 위쪽 경계 교차점에 대한 관련 값을 찾아보겠습니다:

SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
S[U] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우 모든 스텝의 평균 수입니다.
S[U,u] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
S[U,d] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우의 평균 하향 스텝 수입니다.
P[U] - 가격이 먼저 위쪽 경계를 넘을 확률
SP[U,ud] - 위쪽 경계를 넘을 가능성이 있는 평균 스텝 수입니다.

아래쪽 경계에서도 공식은 비슷합니다:

SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
S[D] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 스텝 수입니다.
S[D,u] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
S[D,d] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 하향 스텝 수입니다.
P[D] - 가격이 먼저 아래쪽 경계를 넘을 확률
SP[D,ud] - 아래쪽 경계를 넘을 수 있는 평균 스텝 수입니다.

이제 분명해집니다:

S = SP[U,ud] + SP[D,ud]

궁극적으로 우리가 얻고 사용할 수 있는 모든 수치는 다섯 가지 기본 수치에 달려 있습니다:

S[U,u] = SP[U,u]/P[U] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
S[U,d] = SP[U,d]/P[U] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우의 평균 하향 스텝 수입니다.
S[D,u] = SP[D,u]/P[D] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
S[D,d] = SP[D,d]/P[D] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 하향 스텝 수입니다.
P[U] - 가격이 먼저 위쪽 경계를 넘을 확률

우리는 다양한 입력 매개변수를 사용한 프랙탈 연산 결과를 바탕으로 이러한 값에 대한 공식을 검색할 것입니다. 이전 글에서 프랙탈 출력과 관련하여 저는 다음 값을 선택했습니다:

SP[U,u] - 스텝 체인이 먼저 위쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
SP[U,d] - 스텝 체인이 먼저 위쪽 경계에 도달할 경우의 평균 하향 스텝 수입니다.
SP[D,u] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 상향 스텝 수입니다.
SP[D,d] - 스텝 체인이 먼저 아래쪽 경계에 도달하는 경우의 평균 하향 스텝 수입니다.
P[U] - 가격이 먼저 위쪽 경계를 넘을 확률
P[D] - 가격이 먼저 아래쪽 경계를 넘을 확률
S = SP - 모든 스텝의 평균 수

다음은 기본값으로 표현될 수 있는 별개의 요소 그룹입니다:

SP[U]
S[U,ud] = S[U,u] + S[U,d]
S[D,ud] = S[D,u] + S[D,d]
P[D] = 1 - P[U]
S = SP[U,ud] + SP[D,ud]

프랙탈의 수학을 다루는 동안 저는 광범위한 분석을 수행했습니다. 이를 간결한 다이어그램으로 간략하게 보여드릴 수 있습니다. 다이어그램은 수학적 모델을 검색하는 결과 프로세스를 보여줍니다:

수학적 모델 검색 순서

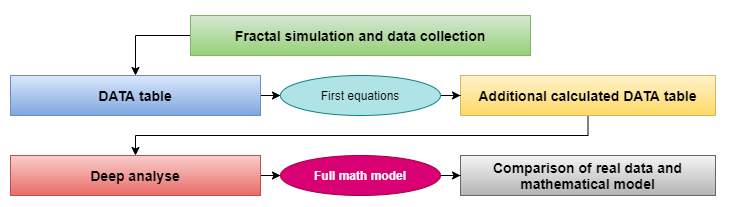
데이터 수집 및 결론

프랙탈 계산 결과를 좀 더 자세히 살펴본 결과 저는 처음 보편적 프랙탈의 개념을 구성할 때 결정했던 여섯 가지의 값이 수학적으로 연관되어 있다는 것을 알게 되었습니다. 처음에는 대칭 경계에 대한 테스트를 수행하여 이러한 값 간의 종속성을 파악하려고 시도 했습니다. 그리고 몇 가지 결과를 얻었습니다. 제가 10가지 경우의 수를 계산해 본 결과 이 정도면 충분하다는 결론이 나왔습니다:

테스트 색인	복도 위쪽 절반의 스텝(n)	복도 아래쪽 절반의 스텝 ( m )	초기 스텝의 확률 ( p )	위쪽 경계의 상향 스텝의 가능한 수의 평균 ( SP[U,u] ) )	위쪽 경계의 하향 스텝의 가능한 수의 평균 ( SP[U,d] )	아래쪽 경계의 상향 스텝의 가능한 수의 평균 ( SP[D,u] ) )	아래쪽 경계의 아래쪽 스텝의 가능한 수의 평균 ( SP[D,d] ) )	위쪽 경계의 모든 스텝의 가능한 수의 평균 ( SP[U,ud] ) )	아래쪽 경계의 모든 스텝의 가능한 수의 평균 ( SP[D,ud] )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

아래에는 프랙탈 로그에는 표시되지 않는 계산된 값이 포함된 표가 나와 있습니다. 이들 값은 우리가 값들 사이의 종속성을 평가하는 데 필요합니다:

테스트 색인	복도 위쪽 절반의 스텝(n)	복도 아래쪽 절반의 스텝 ( m )	위쪽 경계선 통과 확률 ( P(U) )	아래쪽 경계선 통과 확률 ( P(D) )	위쪽 경계를 넘을 때의 평균 스텝 수 (S[U,ud]) = SP[U,ud]/P[U]	아래쪽 경계를 넘을 때의 평균 스텝 수 (S[D,ud]) = SP[D,ud]/P[D]	위쪽 경계의 편균 상향 스텝 수 ( S[U,u] ) = SP[U,u]/P[U]	위쪽 경계의 평균 하향 스텝 수 ( S[U,d] ) = SP[U,d]/P[U]	아래쪽 경계의 평균 상향 스텝 수 ( S[D,u] ) = SP[D,u]/(P[D])	평균 수 아래쪽 경계의 하향 스텝 수의 ( S[D,d] ) = SP[D,d]/(P[D])	평균 스텝 수 ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

이 표에서 여러분은 미지의 값 4개(다른 모든 값을 구성하는)를 모두 계산하는 데 필요한 처음 두 개의 방정식을 찾을 수 있습니다. 공식을 얻으려면 S[U,u], S[U,d], S[D,u], S[D,d] 열에 주의를 기울이세요. 이 열의 숫자가 S[U,u], S[U,d] 열과 S[D,u], S[D,d 열에서 쌍으로 동일한 분수 부분을 갖는다는 점이 매우 흥미롭습니다.] 또한 S[U,u] > S[U,d] 및 S[D,d] > S[D,u]를 확인할 수 있습니다. 이 값을 쌍으로 빼고 m, n과 비교하면 이 차이는 위쪽 또는 아래쪽 경계에 해당하는 스텝 수와 정확히 같다는 것을 알 수 있습니다:

S[U,u] - S[U,d] = n
S[D,d] - S[D,u] = m

따라서 우리는 근간의 값을 결정하는 데 도움이 되는 두 가지 매우 중요한 값을 얻게 됩니다. 두 가지 방정식만으로는 충분하지 않습니다. 그러나 우리는 약간 다른 논리를 기반으로 동일한 값을 결정할 수 있는 두 가지 방정식을 더 얻을 수 있습니다. 만약 우리가 프랙탈을 무한히 오랫동안 실험하면 위아래 스텝의 발생 빈도 비율은 해당 확률에 비례하게 됩니다.

이러한 비율은 다음과 같이 가정하면 얻을 수 있습니다:

Lim[N0 -- > +infinity] (N0[U]/N0) = p
Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
Lim[N0 -- > +infinity] (N0/N) = S
N0 - 초기 스텝와 관련하여 수행된 기본 실험의 수(복잡한 실험을 구성)
N - 간단한 실험으로 구성된 복잡한 실험의 수

승수 N0/N0 = 1을 '3'과 '4'에 도입하고 그 안에 분수를 적절히 배열하면 다음과 같은 결과를 얻을 수 있습니다:

Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0) * Lim[N0 -- > +infinity] (N0/N) = p*S = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0) * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S = S[UD,d]

각 한도가 유한한 수인 경우 곱 한도는 한도의 곱으로 나타낼 수 있습니다. 우리의 한도는 이 조건을 준수합니다. 이러한 공식이 도출되는 방식입니다. 공식은 다음과 같습니다:

S[UD,u] = S*p
S[UD,d] = S*(1-p)

이러한 값을 기본값으로 표현하는 것이 좋습니다 - 이렇게 하면 우리에게 필요한 모든 것을 결정하는 두 가지 누락된 방정식을 얻을 수 있습니다:

S[U,u] * P[U] + S[D,u] * ( 1 - P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 - P[U] ) = S*(1-p)

결과적으로 4개의 방정식에는 5개의 미지수가 있습니다. 다섯 번째 미지수는 전체 그룹을 구성하는 확률 중 하나입니다(경계 중 하나에 도달할 확률). 방정식 시스템은 방정식의 수가 미지수의 수와 같아야만 고유한 해를 가질 수 있습니다. 그러므로 다섯 개의 미지수를 모두 구하려면 우리는 다섯 번째 방정식이 필요합니다. 다섯 번째 방정식이 위쪽과 아래쪽 스텝의 차이라는 것을 우리는 알고 있습니다. 그러므로 직관적으로 구할 수 있습니다. 이상적으로는 이것이 한계입니다:

Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
Nt[U] = - 기본 스텝 업 확률을 사용하여 계산된 이상적인 기본 스텝 업 수입니다.
Nt[D] - 기본 스텝다운 확률을 사용하여 계산된 이상적인 기본 스텝다운 수입니다.
N0[U] - 기본 스텝의 실제 수
N0[D] - 기본 스텝 다운의 실제 수

우리는 경계 통과 확률을 사용하여 비슷한 한계를 찾을 수 있습니다:

Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
Nb[U] - 위쪽 경계를 넘을 확률을 사용하여 계산된 이상적인 기본 스텝 수
Nb[D] - 아래쪽 경계를 넘을 확률을 사용하여 계산된 이상적인 기본 스텝 다운 수입니다.
N0[U] - 기본 스텝의 실제 수
N0[D] - 기본 스텝 다운의 실제 수

우리는 이 두 가지 한계를 사용하여 합계, 차이 또는 몫과 같은 더 복잡한 한계를 구성할 수 있습니다. 저는 다음 식을 줄이고 한계 N0 [U] - N0 [D]를 완전히 제거하는 몫을 선택하겠습니다. 이 두 한계를 나누고 방정식을 변환하면 우리는 다음과 같은 결과를 얻을 수 있습니다:

P[U] * n - (1 - P[U]) * m = p * S - (1 - p) *S

이것이 경계를 넘을 확률을 구할 수 있는 다섯 번째 방정식입니다. 결과적으로 우리는 5개의 방정식으로 이루어진 시스템을 얻게 됩니다. 다음과 같이 표시됩니다:

S[U,u] - S[U,d] = n
S[D,d] - S[D,u] = m
S[U,u] * P[U] + S[D,u] * ( 1 - P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 - P[U] ) = S*(1-p)
P[U] * n - (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

미지수가 4개인 초기 방정식 시스템도 동일한 결과 방정식을 제공합니다. 시스템은 변수를 연속적으로 제외하는 고전적인 방법으로 해결될 수 있습니다:

--> S[U,u] = n + S[U,d] – exclude “S[U,u]”
--> S[D,d] = m + S[D,u] – exclude “S[D,d]”
(n + S[U,d]) * P[U] + S[D,u] * ( 1 - P[U] ) = S*p - 방정식3에 모든 것을 대입합니다.
S[U,d] * P[U] + (m + S[D,u]) * ( 1 - P[U] ) = S*(1-p) - 방정식4에 모든 것을 대입합니다.

이러한 변환 후에는 방정식 3을 4에서 빼기만 하면 우리가 직관적으로 얻은 것과 동일한 방정식을 얻을 수 있습니다. 안타깝게도 이 방정식 체계에서 우리는 나머지 네 개의 값을 찾을 수 없습니다. 저는 이 시스템이 작동하기를 바랐지만 작동하지 않았습니다. 그 이유를 파악하기 위해 저는 프랙탈 데이터로 테이블을 분석해야 했습니다. 이를 통해 저는 이 네 가지 수량 중 하나에 대한 공식을 만들 수 있었습니다. 이 추가 공식을 사용하면 나머지 값을 모두 찾을 수 있습니다. 그래서 이 시스템은 유용한 것입니다.

전체 수학적 모델을 계산하는 알고리즘

먼저 역방정식과 그 사용 순서를 정의하여 모든 S[U,u]를 구해 보겠습니다. 제가 이 값을 사용하는 이유는 계산에 필요한 관련 공식을 찾았기 때문입니다. 이 값을 사용하면 첫 번째 방정식을 사용하여 S[U,d]를 즉시 구할 수 있습니다:

S[U,d] = S[U,u] - n

그런 다음 이 두 값을 방정식 3과 4에 대입하여 나머지 값 S[D,u] 및 S[D,d]를 구합니다. S[D,u]는 세 번째 방정식에서 바로 계산될 수 있습니다:

S[D,u] = ( S*p - S[U,u] * P[U] ) / ( 1 - P[U] )

이제 마지막 미지수에 대한 공식만 찾으면 됩니다. 구한 표현식을 S[U,d] 대신에 네 번째 방정식에 대입합니다:

S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 - P[U] ) = = ( S*(1-p) - ( S[U,u] - n ) * P[U] ) / ( 1 - P[U] )

누락된 유일한 요소는 다섯 번째 방정식을 풀면 쉽게 구할 수 있는 P[U] 값입니다. 이제 해보겠습니다:

P[U] * n - (1 - P[U]) * m = 2*p*S - S
--> P[U] * (n + m) = 2 * p * S - S + m
--> P[U] = (2 * p * S - S + m ) / (n + m)

알려진 값은 다음과 같습니다:

n - 위쪽 경계까지 스텝업 수
m - 아래쪽 경계까지 스텝다운 수
p - 초기 스텝업 확률
S[U,u] - 위쪽 경계를 넘었을 경우의 평균 스텝 수
P[U] - 위쪽 경계를 넘을 확률

값 4가 계산될 수 있습니다:

S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
Pn[p] = 1 , p >= 0.5
Pn[p] = ( (1 - p)/0.5 ) ^ K
Pm[p] = 1 , p <= 0.5
Pm[p] = (p/0.5) ^ K
K는 함수의 평탄도를 조절하는 거듭제곱입니다.

평탄도 계수는 잠시 후 별도의 프로그램에서 계산하겠습니다. 이제 우리는 가장 중요한 값을 결정해야 합니다. 저는 테이블의 값 S[U,u]를 분석하여 대칭 경계에 대한 두 가지 값에 대한 공식을 도출할 수 있었습니다:

S[U,u] = Summ[ i = 0, n] ( i ); if n == m
S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

문제는 이러한 공식이 p = 0.5 및 대칭 경계에만 작동한다는 것입니다. 비대칭 경계가 포함하도록 하기 위해 공식의 개념이 확장되어야 합니다. 그런 다음 우리는 다른 p 값에 대해 공식을 일반화할 수 있습니다. 일반화를 진행하기 전에 표의 테스트 결과는 'm > n'인 경우에만 적용된다는 점에 유의하세요. "m < n"인 경우 공식은 "S[D,d], S[D,u"에 대해 작동합니다. 이 경우 다른 모든 알지 못하는 값을 찾기 위해 알고리즘의 미러 아날로그를 만들어야 합니다.

마찬가지로 역방정식과 S[D,d]의 경우에 사용해야 하는 순서를 정의해 보겠습니다. 다시 두 번째 방정식을 사용하여 값 S[D,u]를 구합니다:

S[D,u] = S[D,d] - m

그런 다음 두 값을 방정식 3과 4에 대입하여 S[U,u] 및 S[U,d]를 구할 수 있습니다. S[D,u]는 네 번째 방정식에서 바로 계산될 수 있습니다:

S[U,d] = (S*(1-p) - S[D,d] * ( 1 - P[U] ) ) / P[U]

이제 마지막 미지수에 대한 공식만 찾으면 됩니다. 구한 식을 S[U,d] 대신 사용하고 세 번째 방정식에 대입합니다:

S[U,u] = (S*p - (S[D,d] - m) * ( 1 - P[U] ) ) / P[U]

그 결과 우리는 "n != m"인 경우에 대해 S[U,u], S[D,d] 공식을 일반화하는 데 필요한 모든 데이터를 얻었습니다. 테이블 데이터를 분석하여 얻은 데이터는 다음과 같습니다:

m > n, p = 0,5
S[U,u] = Summ[ i = 0 ... n] ( i ) + (m-1)/3

반대의 경우:

m < n, p = 0,5
S[D,d] = Summ[ i = 0 ... m] ( i ) + (n-1)/3

대칭 경계가 있는 표준 케이스의 경우에는 계산이 더 간단합니다:

m = n, p = 0,5
S[U,u] = Summ[ i = 0 ... n] ( i )
S[D,d] = Summ[ i = 0 ... m] ( i )

마지막 방정식을 얻기 위한 프로토타입

이제 가능한 모든 p 값에 대해 S[U,u], S[D,d]를 나타내는 수정된 함수의 프로토타입을 정의해 보겠습니다. 기본적인 작업 프로토타입을 만들려면 우리는 P축에 세 개의 점과 전체 구조에 대한 몇 가지 가정이 필요합니다. 저는 이 경우 두 가지 유형의 일반 함수를 고려하는 것으로 충분하다고 생각합니다:

Sp[U,u] = S[U,u] ^ K(p)
Sp[D,d] = S[D,d] ^ K(q)
q = 1-p

첫 번째 유형은 실제 작동하는 프로토타입이거나 혹은 구조가 다르고 다른 로직이 필요하다는 것을 나타내는 특정 마커일 수 있습니다. 이제 거듭 제곱 함수가 모든 데이터를 한데 모을 수 있다는 것이 밝혀졌습니다. 물론 더 복잡한 프로토타입이 있을 수 있고 더 정확할 수도 있지만 우리의 솔루션으로도 충분하다고 생각합니다. 가장 중요한 것은 로직을 이해하는 것입니다. 그러나 만약 여러분이 모델을 미세 조정하려는 경우 이 문서에 제시된 데이터를 기반으로 모델을 조정할 수 있습니다. 제가 테스트 프로그램을 만들어 보았습니다:

프로토타입을 기반으로 함수 찾기

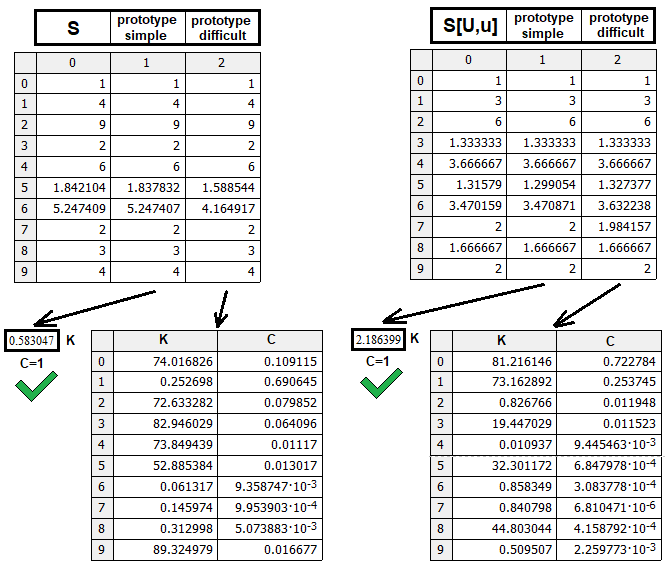
이 프로그램은 프로토타입인 S(n,m,p)와 S[U,u](n,m,p)를 모두 체크합니다. S[D,d]에 대한 확인은 필요하지 않습니다. 왜냐하면 이 함수는 S[U,u](n,m,p)에 미러링 되고 그러므로 S[D,d](n,m,p) = S[U,u](m,n,p-1이 되기 때문입니다. 그림은 찾아낸 프로토타입을 효율성 측면에서 비교한 것입니다. 각 프로토타입은 공식의 가중치와 거듭제곱 계수를 동일한 수의 무작위 조합으로 테스트되었습니다. 더 간단한 프로토타입은 동일한 검색 사이클 횟수로 더 아름다운 결과를 보여줍니다. 필요한 경우 추가적인 계산을 수행하여 더 복잡한 프로토타입이 어떠한지 확인할 수 있습니다.

확인 후 우리는 중첩 함수 "K(p)", "K(q)"의 내부 구조를 정의해야 합니다. 내부 구조는 포인트 p=0, p=0.5, p=1, q=0, q=0.5, q=1에서 의무적으로 우연의 일치를 제공해야 합니다. 우리는 이러한 지점의 함수 값을 알고 있습니다. 이는 우리로 하여금 필요한 프로토타입을 더 쉽게 선택할 수 있게 합니다:

p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
p = 0.0; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
q = 1.0 ; Sp[D,d] = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

첫 번째와 네 번째 표현식은 랜덤워크 지점에서 거듭제곱이 1과 같아야 함을 보여줍니다. 두 번째와 다섯 번째 표현식은 값을 올릴 때 위의 결과 표에서 볼 수 있는 "n" 또는 "m"을 얻을 수 있도록 거듭제곱이 되어야 함을 나타냅니다. 세 번째와 여섯 번째 표현식은 거듭제곱이 0을 제공하기 위해 무한대가 되어야 하는 경향이 있어야 함을 보여줍니다. 이 사실은 프로토타입의 분모에 값 p와 q가 있어야 함을 의미합니다. 왜냐하면 0으로 나누면 그 값들이 무한대와 같이 나오기 때문입니다. 우리는 이미 함수에 대한 거듭제곱 법칙의 프로토타입을 구축한 경험이 있습니다. 이를 기초로 삼아 수정할 수 있습니다. 저는 문제를 심층적으로 분석한 끝에 이 프로토타입을 만들게 되었습니다:

K(p) = 1 + D * Summ(N) (Kn[0] * | (((p - 0.5)/(0.5*p)) | ^ A[0] + Kn[1] * | (((p - 0.5)/(0.5*p)) | ^ A[1] + .... + Kn[N] * | (((p - 0.5)/(0.5*p)) | ^ A[N])
Kn[0] + Kn[1] + .... Kn[N] = Log[S[U,u]-->n] - 1
D = (((p - 0.5)/(0.5*p)) / | (((p - 0.5)/(0.5*p)) |
K(q) = 1 + C * Summ(N) (Km[0] * (((q - 0.5)/(0.5*q)) ^ B[0] + Km[1] * (((q - 0.5 )/(0.5*q)) ^ B[1] + .... + Km[N] * (((q - 0.5 )/(0.5*q)) ^ B[N])
Km[0] + Km[1] + .... Km[N] = Log[S[D,d]-->m] - 1
C = (((q - 0.5)/(0.5*q)) / | (((q - 0.5)/(0.5*q)) |
Kn, Km - 적절한 용어의 가중치
A, B - 용어의 민감도

이 함수는 복잡해 보이지만 기반하는 논리는 간단합니다. "p=0.5, q=0.5"인 경우 합계 기호 이하의 모든 것이 0이 되고 1만 남게 되어 "1", "4"의 조건을 제공합니다. "p=1, q=1"인 경우 합계 내의 관련 분수 중 거듭제곱 된 분수는 1이 됩니다: |(((p - 0.5)/(0.5*p))) |. 이 용어는 거듭제곱이 될 때 함수의 복소수 값을 제외하기 위해 모듈러스 사인을 사용하여 작성됩니다. 대신 관련 사인이 추가적인 요소로 제공됩니다. 거듭제곱은 더 이상 이러한 조건에 영향을 주지 않으며 전체 합계는 Log[S[U,u]-->n] - 1, Log[S[D,D]-->m] - 1로 바뀝니다. 이 숫자를 1에 더하면 함수에 필요한 값을 구할 수 있습니다: Log[S[U,u]-->n], Log[S[D,d]-->m].

보간 다항식은 유사한 논리에 따라 구성되며 그 예로 잘 알려진 라그랑주 다항식이 있습니다. 우리의 다항식은 특정 작업에 적용할 수 있도록 설계되었습니다. 이 도구의 장점은 작업에 완벽하게 적용할 수 있다는 것입니다. 이 커브 제품군에서 원하는 함수를 찾으려면 우리는 두 개의 숫자 배열만 찾으면 됩니다.

수학적 모델 구현 및 테스트

찾은 표현식을 사용하면 프랙탈을 계산하는 데 필요한 기능을 쉽게 구현할 수 있습니다. 우리에게는 메인 함수가 반환할 모든 데이터를 담는 컨테이너가 될 구조는 하나만 필요합니다. 다른 함수들은 보조적인 것들입니다. 우리는 마지막 함수만 있으면 됩니다:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

수학적 모델을 확인하기 위해 저는 이 코드와 동일한 것을 MathCad15에서 구현해 보았습니다. 만약 수학적 모델이 올바르게 구성되었다면 테이블의 결과는 수학적 모델이 반환한 결과와 일치해야 합니다. 프로그램 목록은 글에 첨부되어 있으므로 여러분이 직접 확인하실 수 있습니다. 글의 공간을 너무 많이 차지하기 때문에 저는 이 기사에 코드를 직접 추가하지 않기로 했습니다. 코드가 지면을 너무 많이 차지하기 때문입니다. 그러나 여러분은 결과를 꼭 보셔야 합니다. 이제 행렬을 비교하여 수학적 모델이 실행 가능한지 확인해 보겠습니다:

수학적 모델의 정확성 확인

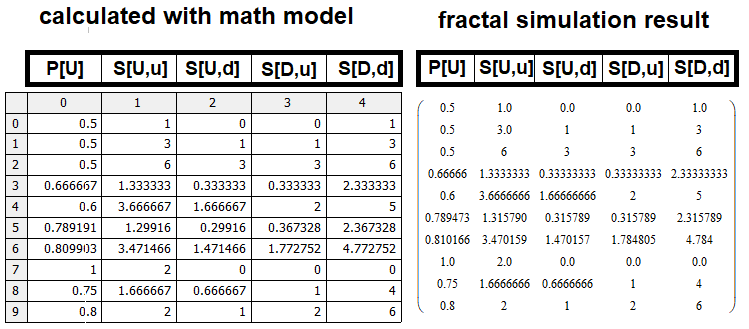
물론 몇 가지 부정확한 부분이 있지만 이는 우리가 찾은 S, S[U,u], S[D,d 값에 대한 프로토타입의 효율성에 기인합니다.] 작은 차이를 발생시키는 다른 요인들은 시뮬레이션 부정확성과 관련이 있을 수 있는데, 이는 제한된 컴퓨팅 성능으로 인해 우리가 시뮬레이션 깊이를 제한해야 하기 때문으로 시뮬레이션 된 n, m 값이 클수록 더 커집니다.

결론

저는 모든 수학을 처음부터 다시 만들어야 했기 때문에 이 수학적 모델을 개발하는 데 많은 시간을 할애했습니다. 어쨌든 저는 그 결과에 만족합니다. 다음 기사에서 저는 모델의 주요 특성 측면에서 모든 거래 구성을 계산할 수 있는 보다 보편적인 수학적 모델을 개발해 볼 것입니다. 또한 수학적 모델은 가격 결정 과정을 설명하는 데 적합할 뿐만 아니라 거래 신호를 설명하고 복잡한 전략을 단순화하여 더 간단한 전략으로 축소하는 데에도 사용될 수 있습니다. 시간이 좀 걸립니다.

참조

트레이딩을 위한 조합론과 확률 이론(1부): 기본 사항

트레이딩을 위한 조합론과 확률 이론(2부): 범용 프랙탈

MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/9570

파일 첨부됨 |

ZIP파일 다운로드

Materials.zip (312.85 KB)

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기

MQL4 및 MQL5 개발 프레임워크 내 OpenAI의 ChatGPT 기능

이 글에서는 Expert Advisors, 지표 및 스크립트를 개발하는 데 드는 시간과 노동 강도를 줄이는 측면에서 OpenAI의 ChatGPT를 살펴보고 그 기능에 대해 알아보겠습니다. 이제부터 ChatGPT를 MQL4 및 MQL5에서 프로그래밍에 올바르게 사용하는 방법을 보여 드리겠습니다.

프리랜스 서비스에서 트레이더의 주문을 처리하여 수익을 창출하는 방법

MQL5 프리랜스는 개발자가 트레이더 고객을 위한 트레이딩 애플리케이션을 만들어 주고 그 대가를 금전적으로 받는 온라인 서비스입니다. 이 서비스는 2010년부터 성공적으로 운영되어 현재까지 100,000개 이상의 총 7백만 달러의 프로젝트가 완료되었습니다. 보시다시피 여기에는 상당한 금액이 관련됩니다.

MQL5의 ALGLIB 수치 해석 라이브러리

이 글에서는 금융 데이터 분석의 효율성을 향상시킬 수 있는 ALGLIB 3.19 수치 분석 라이브러리와 그 응용 프로그램 및 새로운 알고리즘에 대해 간략히 살펴봅니다.

트레이딩을 위한 조합론과 확률 이론(2부): 범용 프랙탈

이 기사에서 우리는 프랙탈에 대해 계속 알아보고 모든 자료를 요약하는 데 집중할 것입니다. 이를 위해 이전의 모든 개발 내용을 간결하게 정리하여 거래에 실제로 적용하기에 편리하고 이해하기 쉬운 형태로 만들 것입니다.

콘텐츠

소개