Применение теории вероятностей на примере торговли на гэпах

Оглавление

• Введение
• Общие рассуждения о советниках
• Торговая стратегия как попытка отвергнуть гипотезу случайного блуждания
• Стратегии торговли на гэпах
• Тестирование стратегии и расчёт оптимального риска в сделке
• Заключение
• Приложенные файлы

Введение

Данная статья продолжает тему применения теории вероятностей и математической статистики в трейдинге, начатую в предыдущих статьях автора. Будет рассмотрено возможное использование методов этих наук в процессе создания и тестирования торговых стратегий.

Для начала рассмотрим такой способ поиска возможностей для торговли, как нахождение отклонений от гипотезы случайного блуждания. Доказано, что если цены ведут себя как случайное блуждание без сноса (отсутствие направленного тренда), то прибыльная торговля невозможна. Это даёт основание для поиска способов опровержения этой гипотезы. Если такое опровержение найдётся, то можно попытаться использовать его для построения торговой стратегии.

Также, в данной статье продолжим изучение темы риска, начатое в ранее опубликованных статьях. Далее, мы будем ссылаться на них, говоря про первую и вторую статьи.

Поскольку основой нашего подхода является теория вероятности, то понимание её основ будет полезным, хотя и не обязательным. Важно понять суть вероятностных методов − чем систематичнее и чаще они применяются, тем заметнее и значимее получаемый от них результат (в силу закона больших чисел). Применения эти должны быть, конечно же, достаточно обоснованными и адекватными.

Общие рассуждения о советниках

При создании торговых советников можно условно выделить три стадии:

1. Генерация идеи.
2. Проверка идеи при всякого рода упрощениях.
3. Адаптация проверенной идеи к реалиям рынка.

Данная статья в основном будет касаться второго этапа. Это позволит более полно сосредоточиться на заявленной теме. К тому же, очевидно, что на форуме эта стадия рассматривается заметно реже, чем остальные.

Опишем сделанные упрощения. Ограничимся советниками торгующими одним активом. Полагаем, что цена актива выражается в валюте капитала счёта. Исключим из рассмотрения неторговые операции (своп, снятие средств с депозита) и не будем выделять различные типы ордеров (считаем, что есть только покупка и продажа по рынку). Будем пренебрегать проскальзыванием при исполнении ордеров, а спред s будем считать фиксированной величиной. Считаем, что советник управляет всем капиталом нашего счёта и нет других советников торгующих на нём.

При подобных упрощениях результат работы советника однозначно определяется как функция v(t) − объём позиции в зависимости от времени. Положительное значение v(t) соответствует покупке, а отрицательное − продаже. Помимо этого известна функция p(t) − цена актива и c0 − начальное количество капитала. На рисунке ниже приведён возможный пример графика позиции v=v(t).

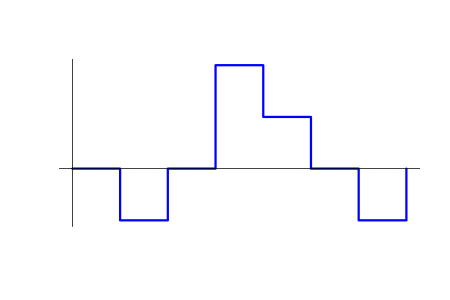
В качестве цены возьмём среднее арифметическое между ценами покупки и продажи.

Отметим, что функции v(t) и p(t) являются кусочно-постоянными (ступенчатыми), поскольку их значения кратны некоторым минимальным шагам приращения. Если нужно более  строгое математическое определение, то можно считать их непрерывными справа и имеющими предел слева в точках разрыва. Считаем, что точки разрыва v(t) никогда не совпадают с таковыми для p(t). То есть в любой момент времени может меняться не более чем одна величина из двух − либо цена, либо объём позиции, либо обе остаются неизменными. Стоит отметить, что моменты времени, в которых могут происходить изменения цены или объёма, также кратны некоторому минимальному шагу.

Исходя из этих данных, мы можем найти функцию c(t) − значение капитала в зависимости от времени. Он определяется как значение баланса для части счёта, отданной советнику под управление, в том случае, если бы мы в момент t закрыли позицию. Поскольку у нас единственный советник на счёте, то эта величина совпадает с эквити счёта, определяемой в MetaTrader 5.

Определим изменение c(t) в момент времени t. Если в этот момент не меняются объём и цена, то оно, естественно, нулевое. Если меняется цена, то приращение капитала равно произведению объёма на приращение цены. Если меняется объём, то возможны два варианта − при уменьшении абсолютного значения объёма позиции капитал не меняется, а при увеличении он уменьшается на величину равную произведению спреда на абсолютную величину изменения объёма. То есть, при частичном закрытии позиции, эквити не меняется, а при наращивании − немного уменьшается. Таким образом, значение капитала c(t) в момент t равно сумме c0=c(0) и всех его изменений, произошедших за время с нулевого момента до t.

Напомним, что в построении нашей теории риска (в двух предыдущих статьях) мы использовали  понятие сделки. Это понятие не совсем совпадает с тем, что называется сделкой в MetaTrader 5 и больше соответствует тому, что называется там трейдом. Если быть, оно соответствует тому, что мы назовём простой позицией. Простая позиция, по нашему определению, задаётся моментами открытия и закрытия, между которыми её объём и направление постоянны. Ниже приведён пример графика v=v(t) для простой позиции.

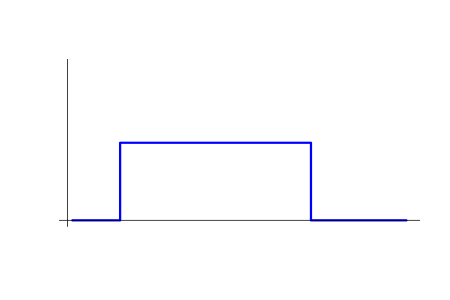
Любую позицию (поскольку она всегда кусочно-постоянна) можно мысленно представить как сумму простых позиций. Такое представление можно сделать бесконечным числом способов. На графике ниже приведён пример того, как одна и та же позиция представляется двумя разными способами в виде суммы простых. Синим цветом изображена исходная позиция, а зелёным и красным − сделки на которые она распадается. При использовании понятия трейдов из MetaTrader 5 мы получим ещё один вариант. Каждый из этих способов может быть вполне осмысленным.

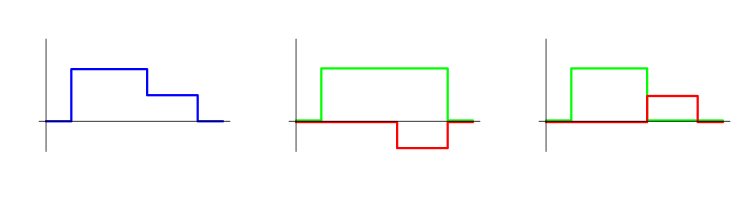
Есть советники, для которых это представление не имеет особого смысла. Например, это могут быть те из них, где позиция то постепенно наращивается, то постепенно сокращается. Но при этом существуют советники, для которых такое представление весьма естественно. Например, позиция может складываться из последовательности не пересекающихся по времени простых позиций. На графике ниже приводятся примеры таких позиций.

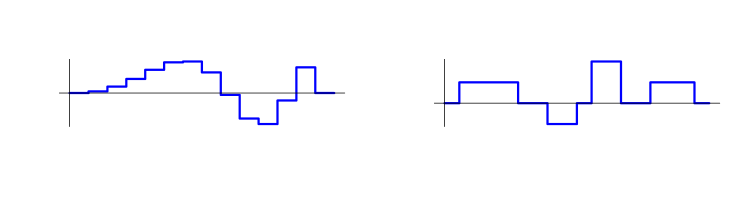
Относительное изменение капитала c1/c0 после каждой сделки (простой позиции) выражается через два числа − доходность a и риск r: c1/c0=1+ra. Доходность равна отношению прироста цены за время сделки к разности цен входа и стоп-лосса, а риск пропорционален объёму сделки и означает долю капитала, которая была бы потеряна при точном срабатывании стоп-лосса.

Таким образом, вместо рассмотрения функций от времени v(t), p(t) и c(t) мы переходим к рассмотрению числовых последовательностей характеризующих последовательность сделок. Это существенно  упрощает дальнейшее изучение. В частности, мы избежим необходимости применения теории случайных процессов, ограничившись конечными совокупностями случайных величин, когда перейдём к рассмотрению вероятностной модели неопределённости.

Общепринятым способом математического моделирования неопределённости поведения цен актива и, соответственно, результатов торговли является теория вероятности. В соответствии с этим подходом мы должны рассматривать функции v(t), p(t) и c(t) как конкретные реализации (траектории) некоторых случайных процессов. В общем виде эта задача практически нерешаема. Основная причина − отсутствие адекватных вероятностных моделей достаточно точно описывающих поведение цен. Поэтому имеет смысл рассматривать частные случаи, где решение возможно. Как уже было указано выше, мы будем рассматривать в этой статье советники, которые формируют позиции, адекватно представимые в виде последовательности простых позиций (сделок).

Стоит коснуться ещё одного вопроса, связанного с советниками. Речь идёт об их параметрах. Полезно рассмотреть их подробнее с целью некоторой формализации (стандартизации) процесса разработки советников. Выделим три основных их вида:

1. Исторические параметры. Параметры, которые могут меняться в процессе работы советника, от сделки к сделке. Это могут быть значения индикаторов, время суток, новостные данные, фазы Луны и т.д. В общем случае, они представляют из себя функции от времени, как и цены или объём позиции. В случае принятого нами упрощения, можно их считать последовательностями чисел, известных в момент входа в сделки. Исходя из значений исторических параметров будут определяться параметры каждой конкретной сделки − направление, объём, стоп-лосс и тейк-профит.
2. Собственно параметры. Будем  для краткости называть их просто параметрами. Фиксируются в момент запуска торговли советником. Могут меняться только в процессе тестирования и оптимизации советника.
3. Мета-параметры. Задают алгоритм оптимизации советника. Например, параметр пользовательского критерия оптимизации. Допустим, мы хотим оптимизировать советник по двум критериям, но сделать это возможно только по одному. Мы формируем новый  из двух исходных, взяв их сумму с некоторыми весами. Эти веса и будут мета-параметрами.

Например, в советнике с гэпами, рассматриваемом далее, минимальный разрыв, считающийся гэпом − параметр советника, а величина каждого конкретного гэпа − исторический параметр. Мета-параметром здесь может быть, например, номер критерия оптимизации (полагаем их пронумерованными в каком-либо порядке, например, оптимизация по прибыли − №1, а по просадке − №2 и т.д.)

Отметим, что в данной статье мы будем пользоваться одним существенным упрощением, связанным с историческими параметрами. Когда мы говорим про распределение доходностей в сделке, то в общем случае оно может зависеть от этих параметров. Мы же предполагаем эту зависимость несущественной. Основная причина в том, что попытка учесть эту зависимость обычно чрезмерно усложняет модель, что в итоге может привести к переподгонке.

Торговая стратегия как попытка отвергнуть гипотезу случайного блуждания

Выше мы писали об отсутствие точных моделей, описывающих поведение цен. Тем не менее, есть приближённые модели, которые могут быть полезны. Например, широко известна модель поведения цен, рассматривающая их как случайное блуждание с нулевым сносом (отсутствие направленного тренда). Обычно эта модель называется гипотезой случайного блуждания. В соответствии с ней, любой советник будет иметь в среднем нулевую прибыль, а с учётом спреда − небольшую отрицательную.

Доказательство невозможности заработать на случайном блуждании довольно непростое, поскольку требует привлечения сложного математического аппарата теории случайных процессов (стохастическое исчисление Ито, марковские моменты времени и т.д.). В целом оно сводится к утверждению того, что при торговле любым способом на случайном блуждании без тренда капитал будет представлять собой мартингал (не нужно путать с мартингейлом). Мартингал − это случайный процесс, у которого среднее значение (математическое ожидание) не меняется со временем. В нашем случае это означает, что математическое ожидание величины капитала в любой момент времени будет равно начальному его значению.

Таким образом, рассмотрение торговой идеи стоит начать с поиска связанных с нею статистически значимых отклонений поведения цены от случайного блуждания. Воспользуемся для этого идеями из теории вероятностей и математической статистики, но сначала сделаем несколько замечаний:

• Любое решение такого рода имеет вероятностный характер − всегда имеется некоторая ненулевая вероятность того, что наши выводы ошибочны.
• Если наш метод не обнаружит отклонений, то это не означает их абсолютное отсутствие − возможно какой-то другой метод их обнаружил бы.
• Наличие статистически значимых отклонений не означает автоматическую возможность получения статистически значимой положительной прибыли − наличие отклонения является необходимым, но недостаточным условием для этого.

Построим метод для поиска отклонения от случайного блуждания. Для этого мы рассмотрим некоторую случайную величину, для которой по выборке, построенной исходя из реальных цен, будем строить эмпирическое распределение вероятностей. С другой стороны, мы построим для неё же теоретическое распределение вероятностей в предположении, что поведение цены в точности является случайным блужданием. Сравнивая эти распределения, мы будем принимать решение об отказе (или невозможности отказа по нашим данным) от гипотезы случайного блуждания.

Построим пример подходящей нам величины. Пусть в начальный момент t0 цена равна p0. Возьмем другое значение цены p1, не равное p0.  Дождёмся момента t1, когда цена достигнет этого значения p(t1)=p1. Найдём цену p2 максимально дальнюю от p1 из цен во временном промежутке между t0 и t1. Введём величину K=(p2-p0)/(p0-p1). Всегда выполняется p1<p0≤p2 или p2≤p0<p1, поэтому всегда K≥0. Ниже приведён график поясняющий данную идею. Синяя черта означает уровень цены p0, а момент её пересечения с графиком цены − момент времени t0. Красная черта означает уровень цены p1, а момент её первого касания графика цены после момента t0 − момент времени t1. Зелёная черта означает уровень цены p2 − максимально удалённой от p1.

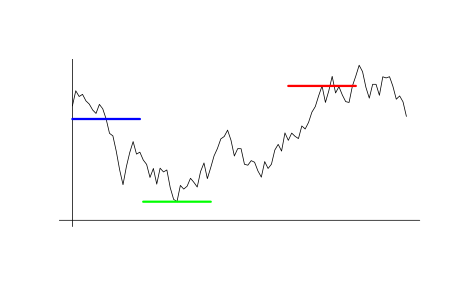
Эта величина имеет простой смысл. Допустим, что в момент t0 мы входим в сделку. Пусть это продажа по цене p0, а цена p1, p1>p0 − стоп-лосс. Цена p2 при этом будет минимально возможной достижимой ценой для тейк-профита, а величина K − максимально возможным достижимой доходностью в сделке. Естественно, в реальности точное значение K на момент входа в сделку нам неизвестно. В рамках вероятностной модели этой неопределённости мы можем говорить лишь о знании закона её вероятностного распределения. Пусть нам известна эта функция распределения вероятности Fk(x), которая определяется как вероятность того, что K<x. Предположим также, что в качестве тейк-профита мы взяли некоторую цену pk такую, что pk-p0=k(p0-p1). Тогда число Fk(k) равно вероятности того, что стоп-лосс будет достигнут раньше, чем тейк-профит. Соответственно, число 1-Fk(k) равно вероятности того, что, наоборот, тейк-профит сработает раньше. Положим на время спред равным нулю. Тогда доходность в случае срабатывания стоп-лосса равна -1 и равна k, если сработает тейк-профит. Матожидание доходности в такой сделке: M=(-1)*Fk(k)+k*(1-Fk(k))=k-(k+1)*Fk(k), которое равно нулю, если Fk(k)=k/(k+1).

Если нам известен вид Fk(x), то мы можем даже проводить предварительную оптимизацию советника. Например, можно искать оптимальное соотношение тейк-профита и стоп-лосса, которое максимизирует матожидание доходности сделки. Затем можно найти оптимальное значение риска в сделке. Таким образом, оптимизацию советника можно проводить даже до того момента, когда советник полностью написан. Это может быть полезно для экономии времени, когда заведомо непригодные идеи отбрасываются на раннем этапе их проверки.

Если предположить, что цены ведут себя как случайное блуждание без тренда, то распределение величины K задаётся функцией распределения Fk(x)=Fk0(x), где Fk0(x)=0, если x≤0 и Fk0(x)=x/(x+1), если x>0. Для определённости, можно считать, что случайное блуждание используемое здесь − это винеровский процесс без сноса (тренд отсутствует). Как видим, при выполнении гипотезы случайного блуждания и при нулевом спреде математическое ожидание доходности сделок равно нулю при любом отношении тейк-профита к стоп-лоссу. При ненулевом спреде оно будет отрицательным.

Вместо величины K можно рассматривать величину Q=K/(K+1)=(p2-p0)/(p2-p1), K=Q/(1-Q). Эту величину можно представлять как отношение тейк-профита к сумме стоп-лосса и тейк-профита. Она оказывается более удобной тем, что она принимает значения на интервале [0;1) и при случайном блуждании имеет более простое распределение чем K − равномерное на этом интервале.

Далее речь будет идти в основном о величине Q. Рассмотрим в общих чертах, как строится и применяется её эмпирическая функция распределения Fq(x). Допустим, у нас есть некоторая идея для торговли, которую мы проверяем на истории цен. У нас есть набор из n точек для входов в сделки, для каждой из которых определены цена входа p0,i и стоп-лосс p1,i, где i=1,...,n. Требуется определить − может ли эта идея принести выгоду. Для каждой сделки найдём максимально удалённую от стоп-лосса до момента его срабатывания цену p2,i. Исходя из этих цен получим n-выборку Qi=(p2,i-p0,i)/(p2,i-p1,i),  i=1,...,n. Эмпирическая функция распределения, строимая по этой выборке, определяется равенством Fq(x)=m(x)/n, где m(x) равна количеству элементов выборки Qi меньших чем x. Если цены ведут себя подобно случайному блужданию без тренда (винеровский процесс без сноса), то функция распределения Fq0(x) величины Q будет иметь простой вид: Fq0(x)=0 при x≤0, Fq0(x)=x при при 0<x≤1, и Fq0(x)=1, при x>1.

Если Fq(x) значимо отличается от теоретической функции распределения при случайном блуждании Fq0(x), то мы должны проверить значимость этого отличия с точки зрения доходности. Если доходность достаточно положительна даже при учёте спреда, то можно переходить к выбору подходящего соотношения профит/стоп-лосс. Это можно сделать максимизируя математическое ожидание доходности. После этого можно подобрать оптимальное значение для величины риска в сделке и переходить к предварительному тестированию идеи. Если результат будет положительный, то имеет смысл переходить к созданию действительно торгующего советника. Далее в статье будет проведена попытка продемонстрировать эту схему на практике.

Возникает вопрос — как проводить подобное сравнение со случайным блужданием для более сложных алгоритмов выхода из сделок. В общем, можно сказать, что также как и для рассмотренного нами случая. Основная проблема в том, что распределение доходностей на случайном блуждании очень редко может быть получено в аналитическом виде. Но всегда есть возможность получить его эмпирическое приближение, используя метод моделирования Монте-Карло.

Стратегии торговли на гэпах

Перед тем как начать анализ идеи сделаем следующее предупреждение. Основная наша задача − демонстрация методов анализа, а не прибыльных стратегий торговли. Слишком большая сосредоточенность на втором привела бы к тому, что мы бы утонули в мелких подробностях, упустив первое. В соответствии с известной поговоркой, мы не будем пытаться раздавать рыбу, а рассмотрим идеи, которые могут оказаться полезными при самостоятельном изготовлении удочки.

Цены актива дискретны и потому всегда меняются скачками. Эти скачки могут отличаться по величине и когда они большие, то их принято называть гэпами. Не существует однозначной границы, отделяющей гэпы от обычных изменений цены − мы вольны задавать её на удобном для нас уровне.

Гэпы хорошо подходят для демонстрации теории, изложенной в предыдущем разделе. Каждый из них задаётся двумя моментами времени и ценами актива в них. Используя ранее введённые обозначения для цен считаем, что p0 − более поздняя цена, а p1 − более ранняя из них. Мы входим в сделку как только происходит гэп. При этом цена p1 может рассматриваться не только как стоп-лосс но и как тейк-профит. Это означает, что мы можем выбрать систему одного из двух типов − надеясь либо на быстрое закрытие гэпа, либо на большое движение цены в направлении разрыва. Под закрытием гэпа понимается, как обычно, возврат цены до уровня p1 или его пробитие.

Поскольку гэпы в классическом виде относительно редки для активов, торгуемых на форексе, то при обсуждении темы данной статьи с администрацией форума автору было предложено обобщить это понятие. Можно в определении гэпа отказаться от требования, что учитывается разрыв только между двумя последующими ценами. Очевидно, количество возможных гэпов в таком случае станет невообразимо огромным и поэтому стоит ограничиться разумными, с торговой точки зрения, вариантами. Например, автору было предложено рассматривать гэпы между ценой закрытия одной американской сессией и ценой открытия следующей.

Поясним как формализуется понятие сессии. Она задается тремя временными промежутками: период, длина и сдвиг. Сессии периодичны и имеют длину не превышающую период. Любой тик либо принадлежит какой-нибудь сессии, либо (это возможно, если её длина строго меньше периода) не принадлежит никакой из них. Сдвиг − время между нулевым моментом времени и началом первой сессии после него и он должен быть меньше периода. Это понятие сессии несколько шире обычного и позволяет рассматривать, например, гэпы между минутными барами. Проиллюстрируем его на схеме ниже. Зелёная стрелка изображает отрезок времени определяющий сдвиг, красная − период и синяя − длину сессии.

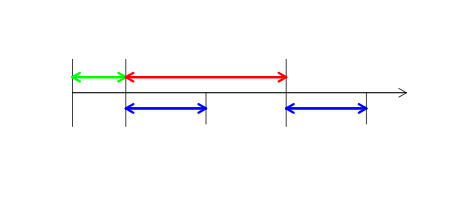
Будем использовать два немного отличающихся советника для сбора статистики связанной с гэпами. Первый − "gaps_reg_stat.mq5" − учитывает гэпы между двумя последующими тиками, а второй − "gaps_ses_stat.mq5" − между сессиями. Эти советники, естественно, не совершают торговли и запускаются только в режиме тестирования. Первый из них имеет смысл запускать только на реальных тиках, а второй − на OHLC минутных баров. Ниже приведены коды этих советников.

// gaps_reg_stat.mq5
#define ND 100

input double gmin=0.1;                 // minimal gap size: USDJPY - 0.1, EURUSD - 0.001
input string fname="gaps\\stat.txt";   // name of file for statistics             

struct SGap
  { double p0;
    double p1;
    double p2;
    double p3;
    double s;
    void set(double p_1,double p,double sprd);
    bool brkn();
    void change(double p);
    double gap();
    double Q();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p,double sprd);
    void change(double p);
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
bool is0=false;

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    if(is0)
      { double p=(tick.bid+tick.ask)*0.5, p0=(tick0.bid+tick0.ask)*0.5;
        gaps.change(p);
        if(MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid);
      }
    else is0=true;
    tick0=tick;
  }

int OnInit()
  { gaps.init();
     return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

void SGap :: set(double p_1,double p,double sprd)
  { p1=p_1; p0=p2=p3=p; s=sprd;
  }

bool SGap :: brkn()
  { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1));
  }

void SGap :: change(double p)
  { if(brkn()) return;
    if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p;
    p3=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { double q=p2-p1;
    if(q==0.0) return 0.0;
    return (p2-p0)/q;
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p,double sprd)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].set(p_1,p,sprd);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

void CGaps :: change(double p)
  { for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        gs[go[i]].change(p);
        if(gs[go[i]].brkn()) go[i]=-1;
      }
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c;
    for(int i=0;i<ngs;++i)
      { if (gs[i].brkn()) c=1; else c=0;
        FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s);
        if(i==ngs-1) break;
        FileWriteString(f,"\n");
      }
    FileClose(f);
  }

// gaps_ses_stat.mq5
#define ND 100

input double gmin=0.001;               // minimal gap size: USDJPY - 0.1, EURUSD - 0.001
input uint   mperiod=1;                // session period in minutes
input uint   mlength=1;                // session length in minutes
input uint   mbias=0;                  // first session bias in minutes
input string fname="gaps\\stat.txt";   // name of file for statistics             

struct SGap
  { double p0;
    double p1;
    double p2;
    double p3;
    double s;
    void set(double p_1,double p,double sprd);
    bool brkn();
    void change(double p);
    double gap();
    double Q();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p,double sprd);
    bool change(double p);
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
int ns0=-1;
ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60;

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    double p=(tick.bid+tick.ask)*0.5;
    gaps.change(p);
    int ns=nsession(tick.time);
    if(ns>=0)
      { double p0=(tick0.bid+tick0.ask)*0.5;
        if(ns0>=0&&ns>ns0&&MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid);
        ns0=ns;
        tick0=tick;
      }
  }

int OnInit()
  { if(speriod==0||slength==0||speriod<slength||speriod<=sbias)
      { Print("wrong session format");
        return(INIT_FAILED);
      }
    gaps.init();
    return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

int nsession(datetime t)
  { ulong t0=(ulong)t;
    if(t0<sbias) return -1;
    t0-=sbias;
    if(t0%speriod>slength) return -1;
    return (int)(t0/speriod);
  }

void SGap :: set(double p_1,double p,double sprd)
  { p1=p_1; p0=p2=p3=p; s=sprd;
  }

bool SGap :: brkn()
  { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1));
  }

void SGap :: change(double p)
  { if(brkn()) return;
    if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p;
    p3=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { double q=p2-p1;
    if(q==0.0) return 0.0;
    return (p2-p0)/q;
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p,double sprd)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].set(p_1,p,sprd);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

bool CGaps :: change(double p)
  { bool chngd=false;
    for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        gs[go[i]].change(p);
        if(gs[go[i]].brkn()) {go[i]=-1; chngd=true;}
      }
    return chngd;
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c;
    for(int i=0;i<ngs;++i)
      { if (gs[i].brkn()) c=1; else c=0;
        FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s);
        if(i==ngs-1) break;
        FileWriteString(f,"\n");
      }
    FileClose(f);
  }

Устроены советники довольно просто. Отметим только массив go[] в классе CGaps, в котором хранятся индексы незакрытых гэпов, что позволяет несколько ускорить работу советников.

В любом случае, для каждого гэпа записывается следующие данные: абсолютная величина разрыва, значение Q, информация о его закрытии и величина спреда в момент возникновения гэпа. Затем проверяется отличие эмпирического распределения величины Q от равномерного и принимается решение о дальнейшем анализе. Для проверки отличия используются графический и вычислительный (подсчёт статистики Колмогорова) методы. Для упрощения, ограничимся приведением значения p-value теста Колмогорова-Смирнова как результата вычислений. Оно принимает значения между нулём и единицей, и чем оно меньше, тем менее вероятно совпадение распределения выборки с теоретическим.

Тест Колмогорова-Смирнова (одновыборочный) выбран нами среди прочих критериев согласия по некоторым соображениям математического характера. Основная причина в том, что нам интересно различение функций распределения в метрике равномерной сходимости, а не в каких-либо интегральных метриках. В библиотеках MQL5 данный тест не был обнаружен, поэтому пришлось пользоваться языком R. Стоит отметить, что при наличии в выборке совпадающих чисел точность данного критерия несколько уменьшается (о чём R выдаёт предупреждение), но остаётся вполне приемлемой.

В случае обнаружения значимого расхождения между теоретическим и эмпирическим распределениями переходим к изучению возможности извлечения прибыли из этого. Если значимого расхождения нет, то либо отказываемся от данной идеи, либо пытаемся её усовершенствовать.

Как мы уже писали выше, имеется две возможности входа в сделку по цене p0 при образовании гэпа − либо в его направлении, либо в противоположном. Подсчитаем матожидание доходностей для обоих этих случаев. Будем при этом учитывать спред, считая его постоянной величиной и обозначая через s. Абсолютную величину гэпа обозначим через g, а минимально допустимое его значение − через g0.

• Вход в направлении гэпа. В этом случае g+s − величина стоп-лосса, а kg-s − величина тейк-профита. Здесь k − отношение профита к лоссу. Величины доходностей: -1 в случае срабатывания стоп-лосса и (kg-s)/(g+s) − в случае срабатывания тейк-профита. Соответствующие вероятности: Fq(q) и 1-Fq(q). Выразим k через q: k=k(q)=q/(1-q). Тогда для матожидания доходности M верно, что M=Fq(q)*(-1)+(1-Fq(q))*(k(q)g-s)/(g+s). Нам подходят только те значения q, для которых M существенно положительно для всех g≥g0. Для этого подойдут такие q, при которых Fq(q) существенно ниже теоретического значения при случайном блуждании Fq(q)<Fq0(q) при g=g0.
• Вход против гэпа. В этом случае g-s − величина тейк-профита, а kg+s − величина стоп-лосса. Здесь k − отношение лосса к профиту. Величины доходностей: -1 в случае срабатывания стоп-лосса и (g-s)/(kg+s) − в случае срабатывания тейк-профита. Соответствующие вероятности: 1-Fq(q) и Fq(q). Выражение для k через q то же самое, что и в предыдущем пункте: k=k(q)=q/(1-q). Для матожидания доходности M получаем формулу M=(1-Fq(q))*(-1)+*Fq(q)(g-s)/(k(q)g+s). Нам подходят только те значения q, для которых M существенно положительно для всех g≥g0. Для этого подойдут такие q, при которых Fq(q) существенно выше теоретического значения Fq(q)>Fq0(q) при g=g0.

Статистика собиралась для двух инструментов:

1. EURUSD
2. USDJPY

Для каждого из них рассматривались следующие типы гэпов:

1. Между последовательными тиками.
2. Между минутными барами.
3. Между торговыми сессиями. Для EURUSD это американская сессия (объединённые вместе Чикагская и Нью-Йоркская), а для USDJPY − Токийская.

Для каждого из этих шести вариантов изучалась статистика для последних по времени:

1. 200 гэпов
2. 50 гэпов

В итоге − 12 вариантов. Для каждого из них приведены следующие результаты:

1. Значение p-value для статистики Колмогорова
2. Среднее значение спреда mean spread в моменты образования гэпа
3. График эмпирической и теоретической (красная линия) функций распределения величины Q
4. График математи ческого ожидания доходности M_cont для торговли в направлении гэпа в зависимости от q в сравнении с теоретической линией M_cont=0 (красная линия). Здесь q означает отношение тейк-профита к сумме тейк-профита и стоп-лосса.
5. График математи ческого ожидания доходности M_rvrs для торговли в направлении противоположном гэпу в зависимости от q в сравнении с теоретической линией M_rvrs=0 (красная линия). Здесь q означает отношение стоп-лосса к сумме тейк-профита и стоп-лосса.

Ниже приводятся все эти варианты результатов.

1. EURUSD, 200 последних гэпов между последовательными тиками. p-value: 3.471654e-07, mean spread: 0.000695

   

   
   

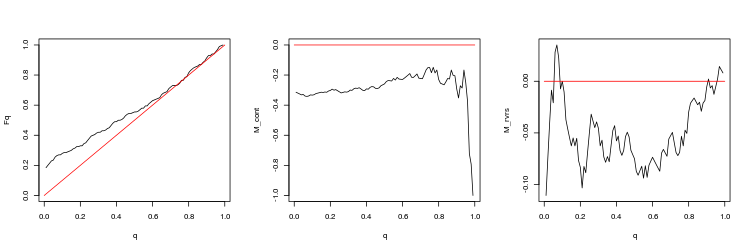
2. EURUSD, 50 последних гэпов между последовательными тиками. p-value: 0.2428457, mean spread: 0.0005724

   
   

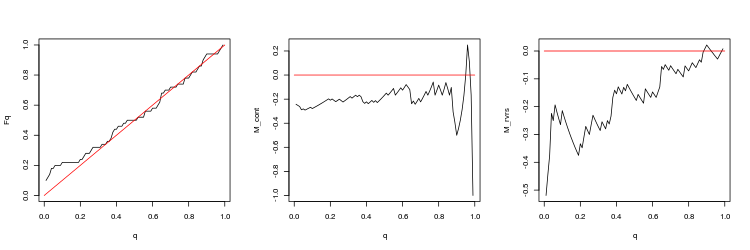
3. EURUSD, 200 последних гэпов между минутными барами. p-value: 8.675995e-06, mean spread: 0.0004352

   
   

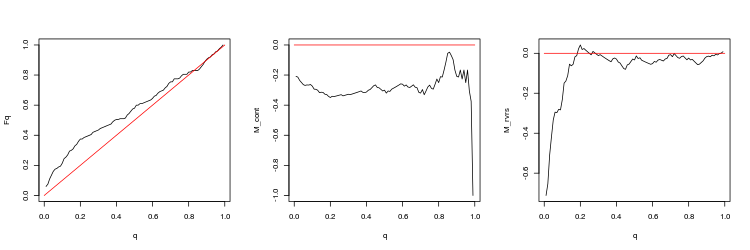
4. EURUSD, 50 последних гэпов между минутными барами. p-value: 0.0125578, mean spread: 0.000404

   
   

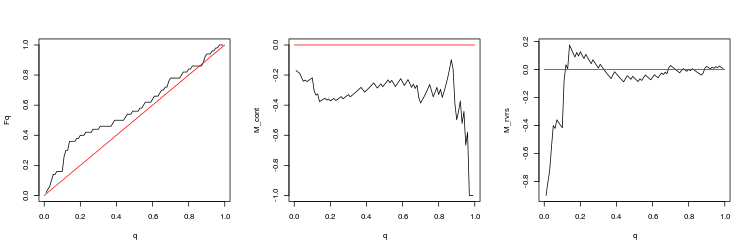
5. EURUSD, 200 последних гэпов между торговыми сессиями. p-value: 0.6659917, mean spread: 0.0001323

   
   

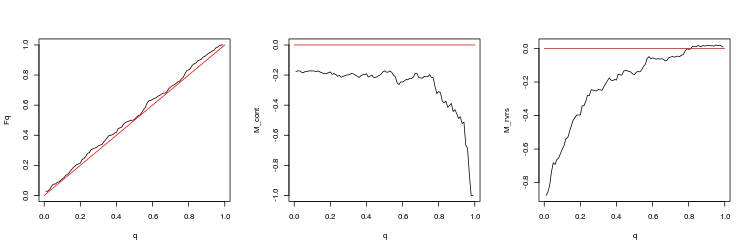
6. EURUSD, 50 последних гэпов между торговыми сессиями. p-value: 0.08915716, mean spread: 0.0001282

   
   

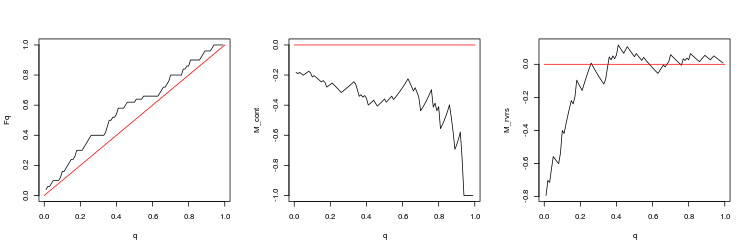
7. USDJPY, 200 последних гэпов между последовательными тиками. p-value: 2.267454e-06, mean spread: 0.09563

   
   

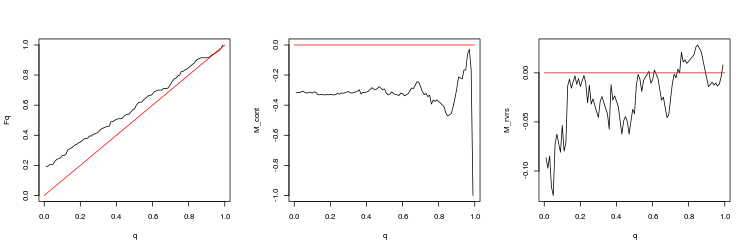
8. USDJPY, 50 последних гэпов между последовательными тиками. p-value: 0.03259067, mean spread: 0.0597

   
   

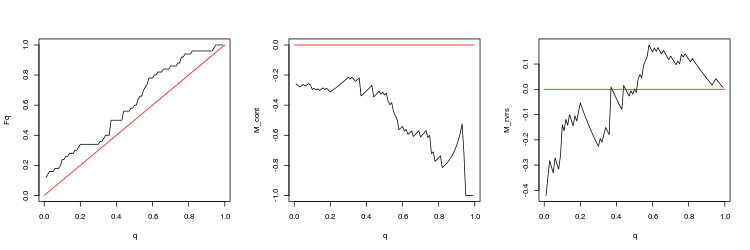
9. USDJPY, 200 последних гэпов между минутными барами. p-value: 0.0003737335, mean spread: 0.05148

   
   

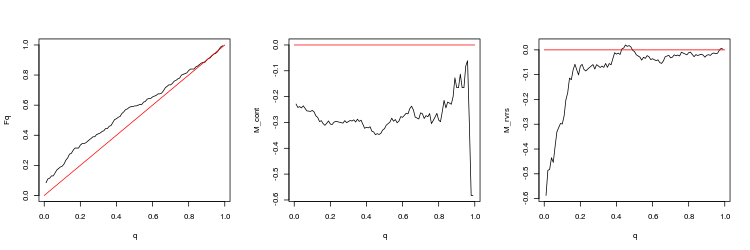
10. USDJPY, 50 последних гэпов между минутными барами. p-value: 0.005747542, mean spread: 0.0474

    
    

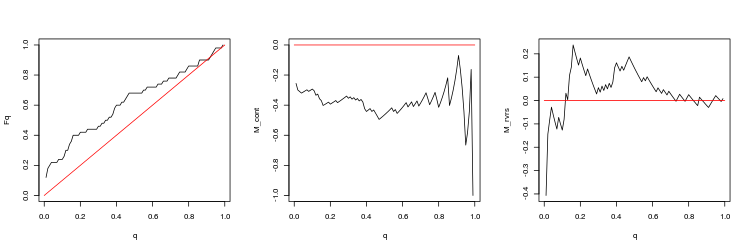
11. USDJPY, 200 последних гэпов между торговыми сессиями. p-value: 0.07743524, mean spread: 0.02023

    
    

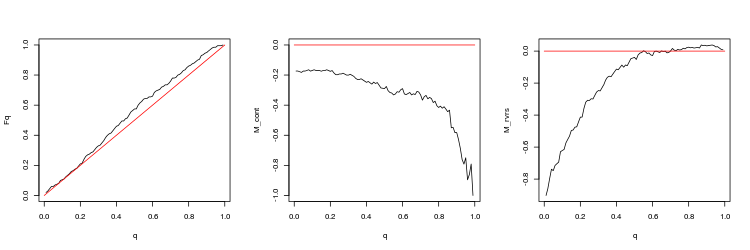
12. USDJPY, 50 последних гэпов между торговыми сессиями. p-value: 0.009191665, mean spread: 0.0185

    
    

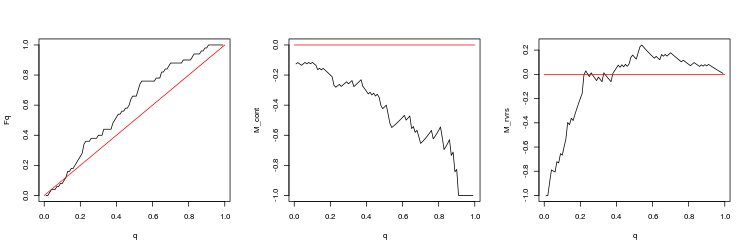
Из этих результатов можно сделать следующие выводы:

• Отклонения от случайного блуждания есть и они достаточно существенны.
• Торговля в направлении гэпов выглядит бесперспективной. Торговля в сторону закрытия гэпов выглядит более предпочтительной, но прибыль невелика (особенно для EURUSD).
• Спреды в момент образования гэпов могут вырастать в несколько раз по сравнению со средним своим значением (верно для гэпов между тиками и минутными барами).
• Гэпы между торговыми сессиями дают отклонение от случайного блуждания только на некоторых промежутках длиной 1-2 месяца, а на промежутках порядка года - отклонение весьма незначительно. На первый взгляд, это определяется тем, какой тренд в это время. Судя по всему, гэпы закрываются лучше при флэте и хуже при наличии тренда вверх или вниз, но необходим более подробный анализ этого варианта. 
• Для дальнейшего анализа выберем вариант гэпов между минутными барами для USDJPY.

Тестирование стратегии и расчёт оптимального риска в сделке

Наиболее перспективным выглядит вариант системы на разрывах между минутными барами USDJPY. Замеченный нами существенный скачок спреда в момент образования гэпа требует от нас более пристального внимания к самому его определению. Уточним его следующим образом. Будем рассматривать гэп не для средней цены, а для бида и аска и будем выбирать ту из них, по которой нам нужно входить в сделку. Это означает, что гэп вверх мы будем определять по биду, а вниз — по аску. То же самое касается и их закрытия.

Построим советник немного изменив тот, что мы использовали для сбора статистики о гэпах между сессиями. Основное изменение коснётся структуры гэпа. Поскольку у нас есть однозначное соответствие между гэпами и сделками, то вся необходимая для торговли информации (объём сделки и условие её закрытия) будет храниться в этой структуре. Для ведения торговли добавлены две функции. Одна из них − pp2v() вычисляет объём для каждой отдельной сделки, а другая − trade() сохраняет соответствие между суммой объёмов сделок и объёмом торговой позиции. Код этого советника − "gaps_ses_test.mq5" приводится ниже.

// gaps_ses_test.mq5
#define ND 100

input uint   mperiod=1;                 // session period in minutes
input uint   mlength=1;                 // session length in minutes
input uint   mbias=0;                   // first session bias in minutes
input double g0=0.1;                    // minimal gap size: USDJPY - 0.1, EURUSD - 0.001
input double q0=0.4;                    // q0=sl/(sl+tp)
input double r=0.01;                    // risk in deal
input double s=0.02;                    // approximate spread
input string fname="gaps\\stat.txt";    // name of file for statistics             

struct SGap
  { double p0;
    double p1;
    double p2;
    double v;
    int brkn();
    bool up();
    void change(double p);
    double gap();
    double Q();
    double a();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p);
    bool change(double pbid,double pask);
    double v();
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
int ns0=-1;
ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60;
double dv=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    bool chngd=gaps.change(tick.bid,tick.ask);
    int ns=nsession(tick.time);
    if(ns>=0)
      { if(ns0>=0&&ns>ns0)
          { if(tick0.ask-tick.ask>=g0) {gaps.add(tick0.ask,tick.ask); chngd=true;}
              else if(tick.bid-tick0.bid>=g0) {gaps.add(tick0.bid,tick.bid); chngd=true;}
          }
        ns0=ns;
        tick0=tick;
      }
    
    if(chngd) trade(gaps.v());
  }

int OnInit()
  {
     gaps.init();
     return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

int nsession(datetime t)
  { ulong t0=(ulong)t;
    if(t0<sbias) return -1;
    t0-=sbias;
    if(t0%speriod>slength) return -1;
    return (int)(t0/speriod);
  }

double pp2v(double psl, double pen)
  { if(psl==pen) return 0.0;
    double dc, dir=1.0;
    double c0=AccountInfoDouble(ACCOUNT_EQUITY);
    bool ner=true;
    if (psl<pen) ner=OrderCalcProfit(ORDER_TYPE_BUY,_Symbol,dv,pen+s,psl,dc);
      else {ner=OrderCalcProfit(ORDER_TYPE_SELL,_Symbol,dv,pen,psl+s,dc); dir=-1.0;}
    if(!ner) return 0.0;
    return -dir*r*dv*c0/dc;
  }

void trade(double vt)
  { double v0=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
    if(-v0<vt<v0) vt=v0*MathRound(vt/v0);
    double vr=0.0;
    if(PositionSelect(_Symbol))
      { vr=PositionGetDouble(POSITION_VOLUME);
        if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL) vr=-vr;
      }
    int vi=(int)((vt-vr)/dv);
    if(vi==0) return;
    MqlTradeRequest request={0};
    MqlTradeResult  result={0};
    request.action=TRADE_ACTION_DEAL;
    request.symbol=_Symbol; 
    if(vi>0)
      { request.volume=vi*dv;
        request.type=ORDER_TYPE_BUY;
      }
      else
        { request.volume=-vi*dv;
          request.type=ORDER_TYPE_SELL;
        }
    if(!OrderSend(request,result)) PrintFormat("OrderSend error %d",GetLastError());
  }

int SGap :: brkn()
  { if(((p0>p1)&&(p2<=p1))||((p0<p1)&&(p2>=p1))) return 1;
    if(Q()>=q0) return -1;
    return 0;
  }

bool SGap :: up()
  { return p0>p1;
  }

void SGap :: change(double p)
  { if(brkn()==0) p2=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { if(p2==p1) return 0.0;
    return (p2-p0)/(p2-p1);
  }

double SGap :: a()
  { double g=gap(), k0=q0/(1-q0);
    return (g-s)/(k0*g+s);
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].p0=gs[ngs-1].p2=p;
    gs[ngs-1].p1=p_1;
    double ps=p+(p-p_1)*q0/(1-q0);
    gs[ngs-1].v=pp2v(ps,p);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

bool CGaps :: change(double pbid,double pask)
  { bool ch=false;
    for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        if(gs[go[i]].up()) gs[go[i]].change(pbid); else gs[go[i]].change(pask);
        if(gs[go[i]].brkn()!=0) {go[i]=-1; ch=true;}
      }
    return ch;
  }

double CGaps :: v(void)
  { double v=0;
    for(int i=0; i<ngo; ++i) if(go[i]>=0) v+=gs[go[i]].v;
    return v;
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT);
    int na=0, np=0, bk;
    double kt=0.0, pk=0.0;
    for(int i=0;i<ngs;++i)
      { bk=gs[i].brkn();
        if(bk==0) continue;
        ++na; if(bk>0) ++np;
        kt+=gs[i].a();
      }
     if(na>0)
       { kt/=na;
         pk=((double)np)/na;
       }
     FileWriteString(f,"na = "+(string)na+"\n");
     FileWriteString(f,"kt = "+(string)kt+"\n");
     FileWriteString(f,"pk = "+(string)pk);
     FileClose(f);
  }

Проведём тестирование этого советника за 2017 год и на основании его результатов определим величину риска для торговли в 2018 году. Ниже приводится график баланса/эквити по результатам теста за 2017 год.

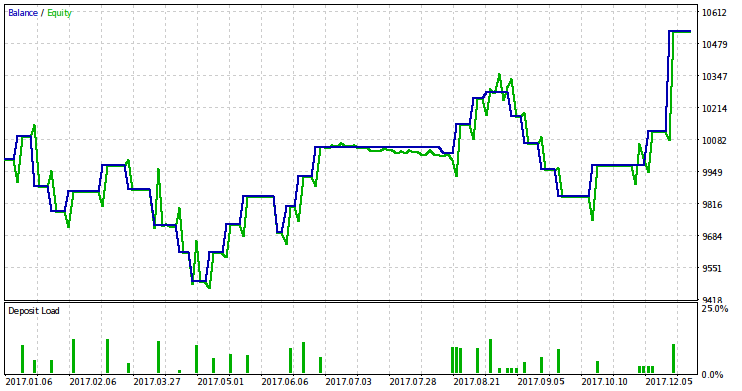
Перед тем, как перейти к объявленной в заголовке теме подсчёта риска, необходимо сделать несколько пояснений. Во-первых, требуется обосновать необходимость определения правильного уровня риска. Во-вторых, необходимо объяснить в чём преимущество применения нашей теории для этой цели.

Спекулятивная торговля всегда связана с неопределённостью. Практически любая торговая система иногда совершает убыточные сделки. По этой причине, риск не должен быть слишком большим − иначе просадка окажется чрезмерной. С другой стороны, рынок в любой момент может измениться настолько, что прибыльная система станет убыточной. Откуда следует вывод, что "время жизни" системы конечно и точно неизвестно. По этой причине, риск не должен быть слишком маленьким − иначе это приведёт к недополучению всей возможной прибыли от торговой системы.

Рассмотрим теперь основные подходы (отличные от нашего) к определению величины риска, сопроводив их краткими характеристиками:

• Определение риска конкретным числовым значением со ссылкой на мнение неких «опытных трейдеров». Обычно называется значение в пределах 0.5-3% от капитала. Этот подход достаточно адекватен несмотря на отсутствие обоснования. Главный его недостаток − отсутствие правила выбора конкретного значения риска для конкретной системы.
• Метод «оптимального f» Ральфа Винса. Он вполне обоснован теоретически, но в результате предлагает, как правило, неадекватно высокое значение для величины риска, что может привести к очень большой просадке.
• Включение величины риска в параметры советника и определения её в процессе тестирования и оптимизации. Здесь сложно сказать что-либо однозначное про обоснованность и адекватность результата − всё очень сильно зависит от устройства советника и того как именно проводится оптимизация. Одной из возможных проблем здесь стоит указать отсутствие учёта неопределённости в результатах дальнейшей торговли. Также возможна переподгонка, что может привести к неоправданному завышению риска (фактически, предыдущий метод − пример тому). В принципе, предлагаемый нами метод − способ разумной оптимизации риска.

Наш метод, в отличие от описанных выше, позволяет получать адекватные и обоснованные значения для риска. Он имеет параметры, варьируя которые можно подогнать его к конкретному стилю торговли.  Опишем суть нашего подхода к вычислению риска. Полагаем, что мы пользуемся торговой системой ровно до тех пор, пока её средняя доходность за заданное нами число сделок не упадёт ниже заданной нами минимальной или же просадка, в этой же последовательности сделок, не станет выше заданной нами максимальной. После этого торговля по данной системе прекращается (например, проводится переоптимизация её параметров). Величина риска выбирается при этом такой, чтобы вероятность того, что система по прежнему прибыльна (а просадка или спад доходности имеют природу естественной случайной флуктуации), была бы не больше заданной.

Более подробное описание нашего метода находится в предыдущих статьях. Во второй из них находится подходящий нам скрипт для подсчёта оптимального значения риска. Этот скрипт применим для случае выхода из сделок с заданными при входе стоп-лоссом и тейк-профитом и при фиксированном их отношении для всех сделок. В той статье он называется "bn.mq5".

Наш советник в результате тестового прохода записывает в текстовый файл данные необходимые в качестве части параметров для скрипта подсчитывающего риск. Оставшаяся часть параметров либо известна заранее, либо подбирается перебором. Если оказывается, что предлагаемое скриптом значение риска нулевое, то следует либо отказаться от данной торговой идеи, либо ослабить свои требования по части просадки/доходности (поменяв параметры), либо использовать данные о сделках на большей истории. Приведём часть скрипта со значениями параметров, которые необходимо задать.

input uint na=26;                     // число сделок в серии
input double kt=1.162698185452029     // соотношение тейкпрофит/стоплосс
input double pk=0.5769230769230769    // вероятность профита

double G0=0.0;                        // наименьшая средняя доходность
double D0=0.9;                        // наименьший минимальный прирост
double dlt=0.17;                      // уровень значимости

Поскольку результаты тестирования за 2017 год показывают не очень хорошее качество торговлии, то и наши требования к ней довольно умеренныt. Мы задаём условие, что на протяжении 26 сделок (na=26) советник неубыточен (G0=0.0) и просадка не более 10% (D0=0.9). Для того, чтобы получить ненулевое значение для риска, уровень значимости приходится выбирать чрезмерно большим (dlt=0.17). В действительности, лучше если он будет не больше одной десятой. То, что нам приходится делать его столь большим, говорит о плохих результатах торговли и что данный советник с данными параметрами лучше не использовать в реальной торговле данным инструментом. При заданных параметрах скрипт выдаст следующий результат для риска: r=0.014. Ниже приведён результат теста советника с этим значением риска за 2018 год.

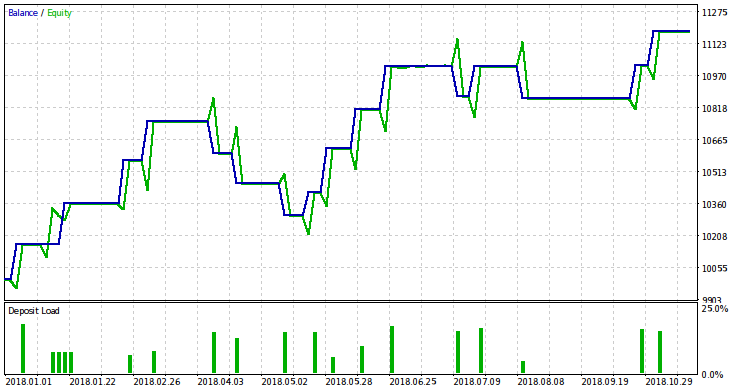
Несмотря на прибыльность, показанную советником при тестировании, вряд ли она сохранится в реальной торговле. Бесперспективность торговли на обычных гэпах для расмотренных инструментов кажется очевидной. Такие гэпы весьма редки (и становятся всё более редкими со временем) и малы по своей величине. Кажется перспективным более углубленное рассмотрение обобщения гэпов − изменений цен между торговыми сессиями. Также, имеет смысл обратить внимание на те инструменты, где обычные гэпы встречаются чаще.

Заключение

Вероятностные способы вполне подходят для создания и настройки торговых советников. При этом, они никоим образом не противоречат другим возможным методам, но зачастую позволяют дополнить их или переосмыслить их по новому.

В данной статье осталась незатронутой тема общей оптимизации советника по его параметрам. Мы коснулись только лишь некоторой части этого вопроса. Имеется существенная связь данной области с вероятностным подходом (с теорией статистических решений). Возможно, со временем получится осветить этот вопрос.

Приложенные файлы

Прилагаются два советника использованных для сбора статистики и третий − для тестовой торговли.

№	Имя	Тип	Описание
1	gaps_reg_stat.mq5	советник	Сбор статистики по гэпам между последующими тиками
2	gaps_ses_stat.mq5	советник	Сбор статистики по гэпам между сессиями
3	gaps_ses_test.mq5	советник	Тестовая торговля по гэпам между сессиями