Теория вероятностей и математическая статистика с примерами (Часть I): Основы и элементарная теория

Оглавление

1. Введение
2. Основания теории
3. Элементарная теория
• 3.1. Комбинаторная вероятность
• 3.2. Схема Бернулли
4. Основы математической статистики
5. Примеры применения математической статистики в рамках элементарной теории
• 5.1. Точечная оценка параметра
• 5.2. Проверка статистических гипотез
6. Заключение
7. Приложенные файлы
   

1.Введение

Трейдинг всегда связан с принятием решений в условиях неопределённости. Это означает, что результаты принятых решений не вполне очевидны в момент принятия этих решений. По этой причине важны теоретические подходы к построению математических моделей, позволяющих содержательно описывать подобные ситуации. Я хотел бы выделить два таких подхода: теория вероятностей и теория игр. Иногда их объединяют вместе, обозначая вероятностные методы, как теорию "игр с природой". Это хорошо показывает существование двух различных видов неопределённости. Первая из них, вероятностная, обычно связана с природными явлениями. Вторая, чисто игровая, связана с деятельностью других субъектов (отдельных людей или их сообществ). Игровая неопределённость гораздо более трудна для теоретического рассмотрения. Иногда даже называют эти неопределённости "плохой" и "хорошей". Зачастую продвижение в понимании исходно игровой неопределённости связано со сведением её к вероятностной форме.

В случае с рынком, очевидно, более важна неопределённость именно игрового характера, поскольку деятельность людей здесь является определяющим фактором. Переход к вероятностным моделям здесь происходит, как правило, на основании соображений о большом количестве игроков, каждый из которых по отдельности мало влияет на изменения цен. Отчасти, это похоже на подход, используемый в статистической физике, что привело к появлению научного подхода, называемого эконофизикой.

В действительности вопрос подобного перехода весьма интересен, нетривиален и заслуживает более подробного рассмотрения. Надеюсь, статьи, посвящённые этому, когда-нибудь появятся и на нашем форуме. В этой же статье мы сосредоточимся на рассмотрении самых основ теории вероятностей и математической статистики.

2. Основания теории

Основой теории вероятностей является формальная система, известная как аксиоматика Колмогорова. Не буду углубляться в разъяснения того, что такое "формальная система" и как правильно понимать математический аксиоматический подход − это всё слишком сложные вопросы из области математической логики. Вместо этого сосредоточимся на базовом объекте теории вероятностей − вероятностном пространстве (probability space). Оно состоит из множества элементарных событий, набора событий и вероятности этих событий. Немного подробнее:

1) Множество элементарных событий (sample space) − множество возможных результатов случайного эксперимента. Обычно обозначается большой греческой буквой "омега" − Ω и на рисунках изображается в виде какой-нибудь фигуры. Элементарные события (elementary event, sample point) обычно обозначаются маленькой греческой буквой "омега" − о, а на рисунках изображаются в виде точки. Стандартный простейший пример, описывающий результат однократного броска монеты: Ω={ω1, ω2}, где ω1=H и ω2=T означают выпадение герба и решки (heads и tails), а фигурные скобки − множество заданное перечислением своих элементов.

На рисунке ниже изображено некое абстрактное Ω в виде прямоугольника и несколько точек − принадлежащих ему элементарных событий:  ω1, ω2 и ω3.

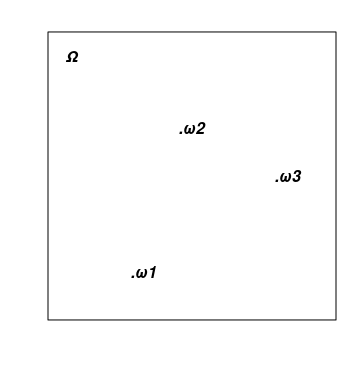
2) Набор случайных событий (event). Каждое такое событие − множество элементарных событий (подмножество всех элементарных событий Ω). В набор событий включаются пустое множество ∅={} (событие, которое никогда не случится) и всё множество Ω (событие, которое случается всегда). Объединение (и пересечение) двух событий из набора должно также принадлежать набору. Подобный набор множеств принято в математике называть алгеброй множеств. В нашем примере с монеткой есть четыре события: {}=∅,  {H}, {T} и {H,T}=Ω. (Вопрос для самопроверки: является ли элементарное событие примером случайного события?)

Обозначаются случайные события обычно большими латинскими буквами: A, B, C, ... и изображаются на рисунках в виде фигур, находящихся внутри фигуры, изображающей Ω. Объединение и пересечение событий обозначается по-разному. Иногда используется запись похожая на сложение и умножение обычных числовых переменных: АВ и А+В, а иногда используются значки ∩ и ∪: А∩В и А∪В.

На рисунке ниже изображено Ω в виде прямоугольника и два пересекающихся события А и В.

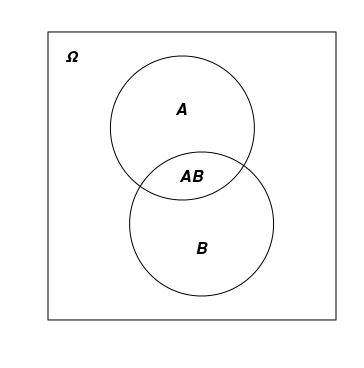
3) Вероятность − числовая функция (probability function) P=P(A), сопоставляющая каждому случайному событию A действительное число на отрезке от 0 до 1. Причём, P(Ω)=1 и P(∅)=0. Помимо этого, выполняется правило называемое аддитивностью: если событие A представляет собой объединение непересекающихся событий B и C, то P(A)=P(B)+P(C). Помимо термина "вероятность", для функции P() используются термины "распределение вероятностей на Ω" или просто "распределение на Ω". Важно не путать это понятие с похожим понятием "функция распределения случайной величины" − они хоть и родственны, но различны. Первая из них − функция, сопоставляющая число множеству, а вторая − обычная числовая функция, сопоставляющая число числу.

Не очень понятно, как изобразить распределение вероятностей посредством рисунка, но интуитивно его можно уподобить распределению единичной массы по объёму Ω. В этой аналогии событие является частью объёма, а вероятность − долей массы оказавшейся в этой части объёма.

Все прочие понятия теории вероятностей являются производными от этих. Выделим здесь очень важное понятие вероятностной зависимости (независимости). Для этого введём понятие условной вероятности события А при условии выполнения события B, P(B)>0. Обозначается она как P(A|B) и по определению P(A|B)=P(AB)/P(B) (напомню, что AB − означает пересечение событий A и B). Событие A, по определению, называется независимым от события B в том случае, когда его условная вероятность при наступлении события B равна его вероятности: P(A|B)=P(A). Используя выражение для условной вероятности, это определение независимости можно переписать в следующем виде: P(A)P(B)=P(AB). Если это равенство не выполняется, то говорят, что событие A зависит от события B.

С интуитивной точки зрения независимость означает, что знание о том, что произошло событие B не меняет неопределённость связанную с событием A. И наоборот, зависимость означает, что выполнение события B несёт информацию о событии A. Точное выражение этого интуитивного понимания даётся в теории информации Клода Шеннона.

Принято выделять элементарную теорию вероятностей. Отличие элементарной теории от неэлементарной заключается в том, что в ней рассматриваются множества элементарных событий, состоящие из конечного числа элементов. Следовательно, оказывается конечным и набор случайных событий (вопрос для самопроверки: почему это верно?). Эта теория развивалась задолго до аксиоматики Колмогорова и не особо нуждалась в ней. Остальная часть статьи будет посвящена этой части теории. Неэлементарная теория будет рассмотрена в следующей статье.

3. Элементарная теория

Поскольку число элементарных исходов конечное число, то можно просто задать вероятность для событий, содержащих ровно по одному элементарному событию (unit set). Надо лишь убедиться, что сумма всех таких вероятностей равна единице. Вероятность любого события будет равна сумме подобных вероятностей. Вовсе не обязательно, что все эти исходные вероятности равны между собой, но мы начнём именно с таких моделей, которые обычно обобщаются под названием "комбинаторная вероятность".

3.1. Комбинаторная вероятность

Пусть Ω состоит ровно из N элементарных исходов, тогда вероятность событий, содержащих их в количестве m, равна m/N. Вычисления вероятности здесь заключается в подсчёте числа вариантов. Как правило, для этого применяются методы комбинаторики, что и стало причиной названия. Приведу несколько примеров:

Пример 1. Пусть имеется n различных предметов. Сколько имеется различных способов их упорядочить (расположить в ряд)? Ответ: n!=1*2*3*....*(n-1)*n способов. Каждый такой способ называется перестановкой, каждая из которых является элементарным событием. Таким образом, N=n! и вероятность события, состоящего из m перестановок, равна m/n! (m/N=m/n!).

Для примера решим несложную задачу: найти вероятность того, что заданный предмет при случайной перестановке окажется на первой позиции. Если первое место занято выбранным предметом, то остальные n-1 предметов можно расставить на оставшихся n-1 местах (n-1)! способами. Таким образом m=(n-1)! и значит искомая вероятность равна m/N=m/n!=(n-1)!/n!=1/n.

Пример 2. Также имеются n различных предметов. Сколько различных наборов по k (k<=n) предметов можно выбрать из них? Здесь возможны два варианта ответа, в зависимости от того считаем ли мы различными два набора, которые отличаются лишь порядком следования предметов. Если различаем их, то ответ: n!/(n-k)! наборов, а если не различаем, то в k! раз меньше: n!/((n-k)!*k!). Набор с учётом порядка называется размещением, а без учёта порядка − сочетанием. Для формулы числа сочетаний, известной ещё и как формула биномиального коэффициента, используются специальные обозначения − есть два варианта, приведённые на следующем рисунке.

Таким образом, если в решаемой задаче неважен порядок элементов набора, то для её решения можно использовать сочетания в качестве множества элементарных событий. Если же порядок важен, то нужно использовать размещения.

Пример 3. Рассмотрим важный пример, приводящий к так называемому гипергеометрическому распределению. Представим теперь, что каждый из наших n предметов помечен одной из двух меток − "хороший" или "плохой". Пусть b, b⋜n предметов "плохие", тогда остальные n-b, наоборот, − "хорошие". Выбираем набор из k элементов без учёта порядка в нём (сочетание). Какова вероятность того события, что в нашем наборе окажется ровно x "плохих" предметов? Задача решается посредством подсчёта числа соответствующих сочетаний. Ответ получается достаточно громоздкий и записывать его лучше через обозначения для числа сочетаний, как показано на следующем рисунке, где искомая вероятность обозначена через p и выражается через x, n, b и k.

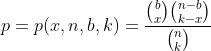
Данный пример хорошо подходит для понимания смысла введения такого понятия, как "случайная величина" (о котором более подробно будет говориться в следующей статье). Вполне может оказаться, что для решения конкретной задачи, связанной с вычислением вероятностей событий, вполне достаточно знания чисел x, n, b и k, а полная информация обо всём исходном наборе событий оказывается излишней. Тогда есть смысл упростить исходную модель, отбросив ненужную информацию. Поступаем следующим образом:

• Числа n, b и k полагаем фиксированными параметрами.
• Вместо пространства элементарных событий Ω, построим на его основе новое Ωх={0, 1, ..., k}, которое состоит из возможных значений для числа х.
• Каждому событию {х} (состоящему из одного элементарного события) сопоставим вероятность, задаваемую приведённой на рисунке выше формулой гипергеометрического распределения.

Получившийся в итоге объект называется "дискретная случайная величина", которая имеет гипергеометрическое распределение для своих возможных значений из Ωх.

3.2. Схема Бернулли

Это другая известная модель из области элементарной теории вероятностей. Обычно говорят про моделирование результата нескольких последовательных бросков монеты, но мы подойдём к её построению немного формальнее.

Пусть заданы целое положительное число n и пара неотрицательных действительных чисел p и q, таких, что p+q=1. Множество элементарных событий Ω состоит из слов длиной ровно n, в которых допускаются только две буквы − H и T (H от heads − герб, а T от tails − решка). Вероятность для события состоящего из одного элементарного события задаётся формулой pu({w})=p^nh*q^nt, где w − слово, а nh и nt, nh+nt=n − количества букв H и T в нём, соответственно.

Несложно увидеть, что, в отличие от комбинаторной вероятности, исходные вероятности в общем случае не равны между собой (они все одинаковы только если p=q=0.5).

Рассмотрим для примера случай n=2. В этом случае Ω={HH, HT, TH, TT}. Количество элементарных событий здесь равно 4, а количество случайных событий − 16. (Вопрос для самопроверки: вывести для схемы Бернулли общий вид формул зависимости числа элементарных событий и числа всех случайных событий от n).

Рассмотрим событие "на первом месте стоит H"={HH, HT}. Его вероятность равна pq+p^2=p. То же самое верно для любого места, что позволяет говорить о параметре p, как о "вероятности выпадения решки в каждом броске". Теперь проверим выполняется ли независимость события А="на втором месте стоит H"={HH, TH} от события В="на первом месте стоит H"={HH, HT}. Воспользуемся определением независимости − пересечение АВ={HH}, P(A)=p, P(B)=p, P(AB)=p^2 и поскольку P(A)P(B)=p*p=p^2=P(AB), то события оказываются независимыми.

Эти утверждения про вероятность результата каждого броска и их независимость оказываются верны и для всех n>2.

Замечу, что мы могли бы задать вероятность совсем по-другому, что вполне могло бы привести как к отсутствию равной вероятности, так и к зависимости результатов бросков. Речь здесь идёт о том, что схема Бернулли не является "единственно правильной" моделью, описывающей последовательность событий, и не стоит ограничиваться только ею.

Теперь посчитаем вероятность события в схеме Бернулли, состоящего из тех слов, в которых буква H встречается ровно k раз, или менее формально − вероятность выпадения монеты гербом ровно k раз в n бросках. Ответ на этот вопрос даёт формула так называемого биномиального распределения, приведённая на следующем рисунке. Через pb обозначена искомая вероятность, зависящая от k, n, p и q.

Рассмотрим ещё один пример, показывающий связь биномиального распределения с рассмотренным выше гипергеометрическим. Он важен как сам по себе, так и в связи с его приложениями в математической статистике (точный тест Фишера). Вопрос достаточно сложный и содержательный с математической точки зрения. Напишем все рассуждения по пунктам.

• На основе пространства элементарных событий схемы Бернулли Ω построим новое − Ω1, куда войдут только те слова, в которых буква H встречается ровно b раз.
• Поскольку любое событие A из Ω1 является событием в Ω, то для него определена вероятность P(A). На её основе введём вероятность P1 в Ω1 по формуле P1(A)=P(A)/Р(Ω1). По сути, при этом используется формула условной вероятности P1(A)=P(A|О1).
• Рассмотрим теперь вероятность P1() события "суффикс слова длиной к содержит ровно х букв H" из Ω1. Оказывается, эта вероятность в точности задаётся формулой гипергеометрического распределения, которая была выписана ранее. Замечательным здесь является тот факт, что в формуле нет зависимости от параметра p.

4. Основы математической статистики

Отличие математической статистики от теории вероятностей обычно описывают как различие в типах решаемых ими задач. В теории вероятностей обычно предполагается, что вероятностная модель полностью известна и на её основе нужно сделать какие-то выводы. В математической статистике знание о модели неполное, но есть дополнительная информация в виде экспериментальных данных, которая помогает уточнить модель. Таким образом, все вопросы, которые разбирались в предыдущей главе − это задачи из области теории вероятностей.

Можно считать только что приведённое определение математической статистики классическим. Есть другой, более современный, подход к определению математической статистики. В нём она определяется как часть теории принятия решений (decision theory). При этом подходе акцент делается на построении оптимальных решающих правил, которые являются оптимальными в смысле минимизации средней цены ошибки. Здесь происходит весьма сильное сближение с методами машинного обучения. Существенное отличие от них заключается в том, что в математической статитистике вид используемой математической модели определяется достаточно чётко (например, с точностью до неизвестного параметра). В МО, как правило, неопределённость распространяется и на вид модели.

Перейдём теперь к примерам задач математической статистики в классическом её понимании.

5. Примеры применения математической статистики в рамках элементарной теории

Можно выделить два типа задач − оценка параметра и проверка гипотез.

Начнём с задачи точечной оценки параметра. Она предполагает наличие в вероятностной модели каких-либо числовых (неслучайных, детерминированных) переменных. Их точное числовое значение неизвестно, но можно посчитать их приблизительное значение, используя данные, полученные в результате случайного эксперимента.

5.1. Точечная оценка параметра

Наиболее общий подход здесь заключается в использовании метода максимального правдоподобия. Если в результате случайного эксперимента реализовалась некое элементарное событие ω, то функцией правдоподобия называется вероятность события {ω} (состоящего только из этого элементарного события). Функцией она называется постольку, поскольку зависит от значения параметра модели. Оценкой максимального правдоподобия (сокращённо ОМП) называется то значение параметра, при котором эта функция достигает своего максимума.

Вообще говоря, различных оценок параметра, помимо ОМП, может быть сделано много разных, но, как доказывается в математической статистике, ОМП является наилучшей в смысле точности. Пояснение того, что здесь подразумевается под словом "точность", оставим до следующей статьи, посвящённой случайным величинам. В любом случае, нужно помнить, что статистическая оценка практически всегда будет отличаться от истинного значения параметра. Поэтому очень важно их различать и не смешивать. Например − вероятность события в схеме Бернулли и её оценка в виде частоты.

Перейдём к вычислению ОМП на примерах.

Пример 1. Оценка параметра b в гипергеометрическом распределении. Имеется партия деталей n=1000 шт. После проверки k=20 из них была обнаружена одна деталь с дефектом: x=1. Оценить число деталей с дефектом во всей партии.

Ниже приведён скрипт hyperg_be.py на Python, решающий эту задачу путём перебора всех возможных вариантов для b. Ответом будет оценка be, в которой значение правдоподобия, определяемое по формуле гипергеометрического распределения, максимально.

from scipy.stats import hypergeom

n = 1000
k = 20
x = 1
lhx = 0.0
be = 0
for b in range(x, n - k + x):
    lh = hypergeom.pmf(x, n, b, k)
    if lh > lhx:
        be = b
        lhx = lh
        
print("be =",be)

Ответ: be = 50, что вполне ожидаемо (каждая 20-я деталь) 

Пример 2 . Оценка параметра n в гипергеометрическом распределении. Требуется оценить количество рыбы в водоёме. Для этого из него выловили сетью b=50 рыб, пометили их и выпустили обратно. После этого ещё раз и таким же образом выловили рыбу в количестве k=55 штук, из которых x=3 оказались помеченными.

Ниже приведён скрипт hyperg_ne.py на Python, решающий эту задачу путём перебора возможных вариантов для n. Ответом будет оценка ne, в которой значение вероятности максимально. Небольшая тонкость заключается в том, что возможные значения для n теоретически лежат в пределах от 50+(55-3)=102 до бесконечности. Это могло бы привести к бесконечному циклу перебора. Но оказывается, что до некоторого значения n функция правдоподобия растёт, а после начинает убывать и стремиться к нулю. Соответственно, ответом будет то первое значение ne, на котором значение функции правдоподобия больше, чем её значение на ne+1.

from scipy.stats import hypergeom

b = 50
k = 55
x = 3
lh0 = 0.0
ne = b + k - x - 1
while True:
    lh = hypergeom.pmf(x, ne+1, b, k)
    if lh < lh0:
        break
    else:
        lh0 = lh
        ne += 1
        
print("ne =",ne)

Ответ: ne = 916, что тоже вполне ожидаемо (ne/b примерно равно k/x, откуда получатся, что ne примерно равно b*k/x).

Все примеры, которые будут приведены далее, связаны со схемой Бернулли или её модификациями. Традиционная для трейдинга интерпретация этой модели заключается в сопоставлении ей дискретизированной версии цены какого-либо актива. Для получения такого представлени используются, например, график ренко или график крестики-нолики.

Не будем отступать от этой традиции. Вместо слов из букв H и T рассмотрим последовательности из чисел 1 и -1, которые, очевидно, соответствуют дискретным шагам цены, соответственно, вверх и вниз. В общем виде шаг цены можно определить как преодоление ею нового уровня на какой-либо сетке цен. Эти сетки уровней обычно определяются так, чтобы либо разница, либо отношение между каждым уровнем и его соседним снизу были одинаковыми − будем использовать второй способ. Недостатком этого способа является невозможность его применения для активов с отрицательными ценами, а достоинством − отсутствие необходимости подбирать величину шага для каждого актива индивидуально. Также есть некоторый произвол в выборе нулевого уровня − в качестве него будем использовать самую первую цену из тех, что подвергаются дискретизации.

Ниже приведён простой скрипт, производящий дискретизацию цену с заданным шагом в процентах, на заданном промежутке.  В файл Discr.mqh вынесена только функция setmv(), в которой собственно и происходит дискретизация цены. Для простоты, в качестве исходной цены берутся только цены открытий минутных баров.

// Построение массива дискретных движений mv[]
// на заданном промежуке времени и с заданным в процентах шагом
void setmv(int& mv[], datetime t1, datetime t2, double dpr)
{
  int ND = 1000;
  ArrayResize(mv, 0, ND);
// Получение истории цен
  double price[];
  int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price);
  if(nprice < 2)
  {
    Print("not enough price history");
    return;
  }
// Построение mv[]
  int lvl = 0, dlvl, nmv = 0, dmv;
  double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr);
  for(int i = 1; i < nprice; ++i)
  {
    dlvl = (int)((log(price[i]) - lp0) / lstep - lvl);
    if(dlvl == 0) continue;
    lvl += dlvl;
    dmv = 1;
    if(dlvl < 0)
    {
      dmv = -1;
      dlvl = -dlvl;
    }
    ArrayResize(mv, nmv + dlvl, ND);
    for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv;
    nmv += dlvl;
  }
}

Скрипт discret_prices.mq5 выводит результат в виде последовательности из 1, -1 и в виде графика дискретного аналога исходной цены.

#include <Discr.mqh>
#include <Graphics\Graphic.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // начало промежутка исследуемого времени
input datetime tstop = D'2020.06.20 00:00';   // конец промежутка исследуемого времени
input double   dprcnt = 0.5;                  // шаг дискретизации цены в процентах
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[], nmv;
  setmv(mv, tstart, tstop, dprcnt);
  nmv = ArraySize(mv);
  if(nmv < 1)
  {
    Print("not enough moves");
    return;
  }
// Вывод mv[] как последовательности 1 и -1
  string res = (string)mv[0];
  for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i];
  Print(res);
// Вывод графика куммулятивной суммы mv[]
  ChartSetInteger(0, CHART_SHOW, false);
  CGraphic graphic;
  graphic.Create(0, "G", 0, 0, 0, 750, 350);
  double x[], y[];
  ArrayResize(x, nmv + 1);
  ArrayResize(y, nmv + 1);
  x[0] = y[0] = 0.0;
  for(int i = 1; i <= nmv; ++i)
  {
    x[i] = i;
    y[i] = y[i-1] + mv[i-1];
  }
  ArrayPrint(x);
  ArrayPrint(y);
  graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices");
  graphic.CurvePlotAll();
  graphic.Update();
  Sleep(30000);
  ChartSetInteger(0, CHART_SHOW, true);
  graphic.Destroy();
}

Во всех дальнейших примерах будут использованы результаты дискретизации цены EURUSD с шагом 0.5% за время с 20 мая до 20 июня 2020 года. В результате получится следующая последовательность дискретных шагов: 1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1. Для наглядности ниже приведены также графики исходной цены и её дискретного аналога.

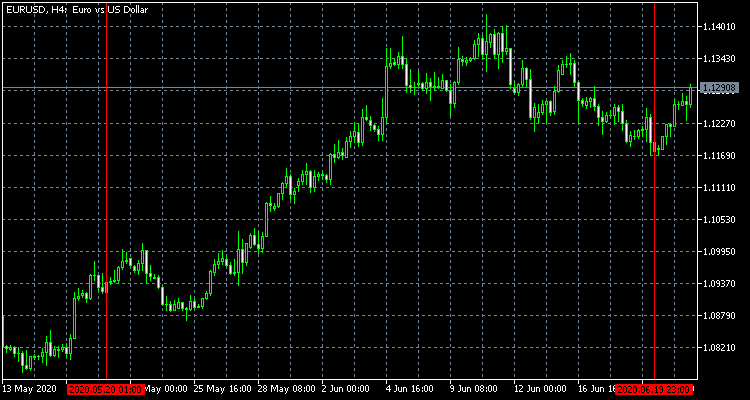
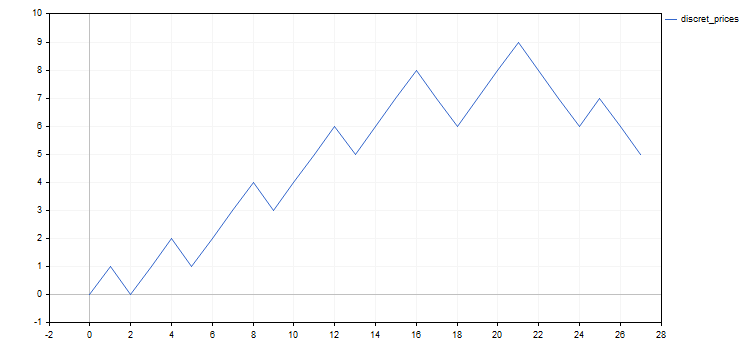
Стоит отметить, что, помимо изучения поведения дискретизированной цены, могут быть и другие способы приложения схемы Бернулли или её модификаций. Укажем на два из них, имеющих отношение к трейдингу.

1. Результаты торговли, при которой совершаются сделки с фиксированными уровнями стоп-лосса, тейк-профита и объёма. Все прибыли в серии сделок будут приблизительно равны между собой и то же самое верно относительно убытков. Поэтому вероятность прибыли будет достаточным параметром для описания результата торговли. Можно, например, поставить вопрос о том, достаточно ли высоко значение вероятности получения прибыли в имеющейся последовательности сделок. 
2. Выбор активов для инвестиций. Пусть в начале периода имеется большой выбор способов для инвестиций. Любой из них, с некоторой вероятностью, может привести в итоге к полной потере инвестированных в него средств. Если имеется некий способ отбора активов, то можно поставить вопрос об отличии вероятности банкротства среди отобранных активов в сравнении с таковой среди отвергнутых.
   

Вернёмся к дальнейшему рассмотрению примеров.

Пример 3. Оценка параметра p в схеме Бернулли. Здесь наблюдается тот редкий случай, когда задачу можно решить на бумаге. Функция правдоподобия имеет вид p^nup*(1-p)^ndn. Берём производную по p и, приравнивая её нулю, получаем вполне ожидаемое значение для оценки р в виде частоты: pe=nup/(nup+ndn)=nup/nmv. Несколько проще искать, как это и делается обычно, максимум не самой функции правдоподобия, а её логарифма. Ответ получится тот же, поскольку логарифм − строго возрастающая функция и максимум будет достигаться при том же значении параметра. Ниже приводится скрипт p_model.mq5 вычисляющий эту оценку.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // начало промежутка исследуемого времени
input datetime tstop = D'2020.06.20 00:00';   // конец промежутка исследуемого времени
input double   dprcnt = 0.5;                  // шаг дискретизации цены в процентах
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 1)
  {
    Print("not enough moves");
    return;
  }
  double pe = calcpe(mv);
  Print("pe=", pe);
}
//+------------------------------------------------------------------+
// Подсчёт оценки вероятности
double calcpe(int& mv[])
{
  int nmv = ArraySize(mv);
  if(nmv < 1) return 0.0;
  int nup = 0;
  for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup;
  return ((double)nup) / nmv;
}

Ответ: pe = 0.59 (число округлено)

Пример 4. Оценка параметра в модифицированной схеме Бернулли. Как я уже писал выше, схема Бернулли вполне может быть изменена, если это потребуется для наших целей моделирования. Рассмотрим возможный вариант такой модификации.

Возможно, самый простой вариант − представить, что последовательность движений разбивается на две меньшие последовательности, следующие одна за другою, и такие, что каждая из них отвечает схеме Бернулли со своими параметрами: n1, p1, n2=n-n1 и p2, где n - длина совокупной последователности.
Таким образом, нужно оценить три параметра − n1, p1 и p2. Максимизируя логарифм функции правдоподобия относительно p1 и p2, можно выразить их аналитически через n1. Оценку для n1 придётся искать уже простым перебором, подставляя выражения для p1 и p2 в формулу для логарифма правдоподобия.
Ниже приведён скрипт p1p2_model.mq5, вычисляющий оценки параметров.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // начало промежутка исследуемого времени
input datetime tstop = D'2020.06.20 00:00';   // конец промежутка исследуемого времени
input double   dprcnt = 0.5;                  // шаг дискретизации цены в процентах
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  int n1e;
  calc_n1e_p1e_p2e(mv, n1e, p1e, p2e);
  Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// Подсчёт оценки вероятности
void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e)
{
  n1e = 0;
  p1e = p2e = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  n1e = 1;
  double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2;
  for(int n1 = 2; n1 < nmv; ++n1)
  {
    llh = llhx_n1(mv, n1, p1, p2);
    if(llh > llhx)
    {
      llhx = llh;
      n1e = n1;
      p1e = p1;
      p2e = p2;
    }
  }
}
//+------------------------------------------------------------------+
// максимум логарифма функции правдоподобия в зависимости от n1
double llhx_n1(int& mv[], int n1, double& p1, double& p2)
{
  p1 = p2 = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0;
  int nu1 = 0, nu2 = 0;
  for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1;
  for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2;
  double l = 0.0;
  if(nu1 > 0)
  {
    p1 = ((double)nu1) / n1;
    l += nu1 * log(p1);
  }
  if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1);
  if(nu2 > 0)
  {
    p2 = ((double)nu2) / (nmv - n1);
    l += nu2 * log(p2);
  }
  if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1));
  return l;
}

Ответ: n1e = 21; p1e = 0.71; p2e = 0.17 (числа округлены). Он кажется достаточно очевидным − наша модель "увидела" смену направления (или коррекцию) движения цены в конце её участка. Это говорит о том, что переход к более сложной модели в данном случае был не напрасен.

Пример 5. В предыдущем примере вероятность движения вверх зависела от его номера (от времени). Рассмотрим другую модификацию схемы Бернулли, в которой эта вероятность зависит от того, каким было предыдущее движение. Построим модель, которая является примером простейшей марковской цепи с двумя состояниями.

Пусть нумерация движений идёт с 0 до n. Для нулевого движения вероятность движения вверх просто положим равной 0.5, поскольку для него нет предыдущего движения. Для остальных позиций вероятность движения вверх будет равна p1, если перед ним было движение вверх и равна p2 если было движение вниз. Вероятности движений вниз в этих двух случаях равны, соответственно, q1=1-p1 и q2=1-p2. Например, вероятность события, в котором ровно одно элементарное событие "вниз-вверх-вверх-вниз" будет равна 0.5*p2*p1*q1.

У нас получилась модель с двумя параметрами, которые можно оценить с помощью ОМП. Здесь опять можно провести все расчёты на бумаге, особенно если максимизировать логарифм функции правдоподобия. Ответ, как и в случае со схемой Бернулли, сведётся к частотам. Обозначим через nud количество того сколько раз после движения вверх происходит движение вниз (u − up, d − down). Аналогичным образом введём обозначения nuu, ndd и ndu. Оценки для p1 и p2 обозначим через p1e и p2e. Тогда эти оценки находятся по формулам p1e=nuu/(nuu+nud) и p2e=ndu/(ndu+ndd).

Ниже приведён скрипт markov_model.mq5, вычисляющий эти оценки.

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // начало промежутка исследуемого времени
input datetime tstop = D'2020.06.20 00:00';   // конец промежутка исследуемого времени
input double   dprcnt = 0.5;                  // шаг дискретизации цены в процентах
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  calcpes(mv, p1e, p2e);
  Print("p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// Подсчёт оценок вероятности
void calcpes(int& mv[], double& p1e, double& p2e)
{
  p1e = p2e = 0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd;
  for(int i = 0; i < nmv - 1; ++i)
    if(mv[i] > 0)
    {
      if(mv[i + 1] > 0) ++nuu;
      else ++nud;
    }
    else
    {
      if(mv[i + 1] > 0) ++ndu;
      else ++ndd;
    }
  nu = nuu + nud;
  nd = ndu + ndd;
  if(nu > 0) p1e = ((double)nuu) / nu;
  if(nd > 0) p2e = ((double)ndu) / nd;
}

Ответ:  p1e = 0.56; p2e = 0.60 (числа округлены). То, что обе вероятности почти равны между собой, говорит об отсутствии зависимости между соседними движениями, а то, что они больше чем 0.5 − о наличии тренда вверх. Также то, что обе оценки вероятностей близки к оценке вероятности для более простой модели (простой схемы Бернулли из третьего примера), говорит о том, что переход к этой усложнённой модели оказался излишним в данном конкретном случае.

5.2. Проверка статистических гипотез

На одном и том же пространстве элементарных событий могут быть заданы различные распределения вероятностей. Гипотезой называют утверждение, конкретизирующее вид распределения. Гипотез должно быть несколько, как минимум две, поскольку решение заключается в предпочтении одной гипотезы остальным. Гипотеза называется простой, если она однозначно определяет вид распределения.

Приведём примеры для схемы Бернулли: гипотеза о равенстве параметра p конкретному числу − простая гипотеза (ровно одно возможное значение параметра, однозначно определяющего распределение), а гипотеза, что этот параметр больше заданного числа − сложная гипотеза (бесконечно много возможных значений параметра).

Далее будем иметь дело с выбором из двух гипотез. Одна из них называется нулевой, а другая − альтернативной. Выбор гипотезы осуществляется с помощью статистического критерия. По сути, это просто функция со значениями 0 и 1 на пространстве элементарных событий, где 0 означает принятие нулевой гипотезы, а 1 − альтернативной.

Таким образом, у нас есть возможность либо принять нулевую гипотезу, либо отвергнуть. При этом альтернативная гипотеза, соответственно, наоборот, либо отвергается, либо принимается. Каждое из этих решений может быть либо правильным, либо ошибочным. Таким образом, получается четыре возможных результата принятия гипотезы, из которых два являются верными и два − ошибочными.

1. Ошибка первого рода − ошибочное отвержение нулевой гипотезы.
2. Ошибка второго рода − ошибочное принятие нулевой гипотезы.

Вероятности ошибок первого и второго рода обозначаются через a1 и a2. Естественно, хотелось бы иметь эти вероятности как можно меньше по значению. Но, к сожалению, это невозможно. Более того, уменьшая вероятность ошибки одного рода, мы закономерно сталкиваемся с ростом вероятности ошибки другого рода. По этой причине обычно прибегают к некоему компромиссу между этими ошибками.

Число 1-a1 называют уровнем значимости критерия, а число 1-a2 − его мощностью. Мощность критерия, особенно для сложной гипотезы, бывает довольно трудно подсчитать. Поэтому зачастую довольствуются только уровнем значимости.

Критерий обычно строится на основе числовой функции (тоже определённой на множестве элементарных событий), которая традиционно называется "статистикой критерия" (test statistic). Множество её значений разбивают на две области, одна из которых соответствует принятию нулевой гипотезы, а другая − её отвержению. Область, в которой нулевая гипотеза отвергается, называется критической.

Важное замечание о "минус первой" гипотезе. Этим термином я обозначил то, что предварительно нужно убедиться, что одна из двух наших гипотез обязательно выполняется. Грубо говоря, если мы отделяем чихуахуа от собак других пород по весу, то мы должны быть уверены, что на весах у нас всегда именно собака, а не слон, мышь или кошка. В противном случае наша проверка гипотез лишена смысла. Особенно часто встречаются примеры нарушения этого принципа в неаккуратных применениях статистических критериев, используемых в эконометрике.

Далее рассмотрены примеры проверки гипотез для схемы Бернулли.

Пример 1. Проверка нулевой гипотезы p=p0 в схеме Бернулли. Эта гипотеза является простой. Альтернативная гипотеза может быть одной из двух следующих вариантов (в обоих случаях − сложная). Статистикой критерия в обоих случаях будет kup − число движений вверх в последовательности, но по-разному будет определена критическая область.

1. p>p0, критическая область справа kup⋝kr
2. p<p0, критическая область слева kup⋜kl

Конкретные значения для kr и kl находятся из условия, что вероятность попадания статистики в критическую область не превосходит выбранную нами вероятность ошибки первого рода. Напомню, что все эти вероятности считаются при условии выполнения нулевой гипотезы, то есть по распределению Бернулли с параметром p=p0.

Проверим эту гипотезу для p0=0.5 на всё той же нашей дискретизированной последовательности цен. Это значение для p0 замечательно тем, что оно соответствует гипотезе "случайного блуждания" или, как иногда говорят, "честной монетке".

Ниже приведён скрипт p0_hypothesis.mq5 делающий проверку этой гипотезы.

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input int    nm = 27;          // общее количество движений в серии
input int    kup = 16;         // количество движений вверх
input double p0 = 0.5;         // проверяемое значение вероятности
input double alpha1 = 0.05;    // вероятность ошибки первого рода
//+------------------------------------------------------------------+
void OnStart()
{
  int kl, kr, er;
  kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er);
  kl=(int)MathQuantileBinomial(alpha1,nm,p0,er);
  Print("kl=", kl, " kup=", kup, " kr=", kr);
  Print("kup<=kl = ", kup<=kl);
  Print("kup>=kr = ", kup>=kr);
}

Ответ:

• kl=9; kup=16; kr=18
• kup<=kl = false
• kup>=kr = false
  

Результат говорит о том, что нулевая гипотеза не может быть отвергнута на данном уровне значимости в пользу ни одной из альтернатив.

Пример 2. Предположим, что у нас имеется две последовательность длины n1 и n2, которые взяты из двух схем Бернулли с параметрами p1 и p2. Нулевая гипотеза здесь заключается в утверждении о выполнении равенства p1=p2, а возможные альтернативы − разные виды их неравенства, которых здесь тоже два. Статистикой критерия во всех этих случаях будет k2 − число движений вверх во второй последовательности из двух, но по-разному будет определена критическая область.

• p2>p1, критическая область справа k2⋝kr
• p2<p1, критическая область слева k2⋜kl

Существенным отличием от предыдущего примера является то, что здесь речь идёт не об утверждениях о точных значениях для p1 и p2, а лишь об их соотношении. Критические области определяются также, как в предыдущем примере, но распределение статистики при выполнении нулевой гипотезы здесь гипергеометрическое, а не биномиальное. В математической статистике этот критерий известен как точный тест Фишера.

Ниже приведён скрипт p1p2_hypothesis.py на Python, решающий эту задачу для разбитой на две части нашей дискретизованной цены. Ради интереса, взято то разбитие, что получилось в четвёртом примере из предыдущего параграфа.

from scipy.stats import hypergeom

n1 = 21; n2 = 6
k1 = 15; k2 = 1
alpha1 = 0.05

kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2))
kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2))

print("kl =", kl, " k2 =", k2, " kr =", kr)
print("k2<=kl =", k2<=kl)
print("k2>=kr =", k2>=kr)

 Ответ:

• kl = 2;  k2 = 2;  kr = 6
• k2<=kl = True
• k2>=kr = False
  

Результат говорит о том, что нулевая гипотеза отвергается на данном уровне значимости в пользу первой альтернативы. Это является дополнительным потверждением того, что наш участок цен может быть разбит на два участка с движением цены в различных направлениях.

6. Заключение

В статье не были освещены такие важные области математической статистики, как описательная статистика, интервальная оценка параметра, асимптотические оценки и байесовский подход в статистике. Основная причина в том, что для их содержательного рассмотрения нужно прояснить понятие случайной величины. Но я решил отложить это до следующей статьи, чтобы эта статья оказалась компактной по объёму и обозримой по содержанию.

7. Приложенные файлы

№	имя	тип	описание
1	hyperg_be.py	Скрипт на Python	Вычисление оценки параметра b гипергеометрического распределения. Пример 5.1.1
2	hyperg_ne.py	Скрипт на Python	Вычисление оценки параметра n гипергеометрического распределения. Пример 5.1.2
3	Discr.mqh	Заголовочный файл MQL5	Файл с функцией setmv(), используемой во всех примерах на MQL5 ниже для дискретизации цены
4	discret_prices.mq5	Скрипт на MQL5	Скрипт проводящий дискретизацию цены и выводящий результат в виде последовательности 1 и -1 и графика
5	p_model.mq5	Скрипт на MQL5	Вычисление оценки параметра p в схеме Бернулли. Пример 5.1.3
6	p1p2_model.mq5	Скрипт на MQL5	Вычисление оценок параметров n1, p1 и p2 в модели из двух схем Бернулли. Пример 5.1.4
7	markov_model.mq5	Скрипт на MQL5	Вычисление оценок параметров p1 и p2 марковской цепи. Пример 5.1.5
8	p0_hypothesis.mq5	Скрипт на MQL5	Проверка гипотезы о равенстве параметра схемы Бернулли заданному числу. Пример 5.2.1
9	p1p2_hypothesis.py	Скрипт на Python	Точный тест Фишера. Пример 5.2.2