Применение метода Монте-Карло для оптимизации торговых стратегий

Оглавление

• Общая теория
• Вероятностная модель советника
• Применение теории
• Устойчивость прибыли к случайному разбросу
• Устойчивость прибыли к просадке
• Устойчивость распределения прибыли сделок к нестационарности цен
• Заключение
• Приложенные файлы
  

Общая теория

Суть метода Монте-Карло можно описать как пример использования аналогии — одного из методов научного познания. Другие примеры аналогии — оптико-механическая аналогия Гамильтона в физике или аналогичные органы в биологии.

Если у нас есть два объекта, которые можно описать одной и той же теорией, то знания, полученные при изучении одного из них, будут применимы и к другому. Этот метод очень полезен, когда изучить один объект гораздо проще, чем другой. Тогда более доступный для изучения объект считается моделью другого, а сам метод называется моделированием. Иногда моделью (или теоретической моделью) называют не один из объектов, а общую для них теорию, но обычно из контекста ясно, о чем именно идёт речь.

Иногда исследователи неверно воспринимают результаты моделирования. Когда речь идет об очевидных примерах — например, про обдув уменьшенной копии самолета в аэродинамической трубе, то всё кажется очевидным. Когда же объекты не связаны и не похожи друг на друга на первый взгляд, то выводы порой кажутся каким-то хитрым трюкачеством или же служат основой для необоснованных, но далеко идущих выводов и обобщений. В действительности дело в том, что общая для объектов теория всегда только приблизительно описывает лишь их некоторые аспекты. Чем меньше требуемая нами точность описания объектов теорией, тем шире множество объектов, которые будут ей подчиняться. Например, оптико-механическая аналогия Гамильтона точно выполняется лишь в пределе, при стремлении длины световой волны к нулю. В реальности только для малой, но всегда конечной длины она выполняется лишь приближённо. Поскольку любая теоретическая модель должна быть достаточно простой, чтобы служить основой для расчётов и выводов, то она всегда будет огрубленной.

Уточним теперь понятие метода Монте-Карло. Это подход к моделированию объектов, теория которых имеет вероятностную (стохастическую) природу. Моделью при этом служит компьютерная программа, алгоритм которой устроен в соответствии с этой теорией. В ней используются генераторы псевдослучайных чисел, чтобы имитировать необходимые случайные величины (случайные процессы) с требуемыми распределениями.

Стоит подчеркнуть (хотя для дальнейшего нашего изложения это и неважно), что природа изучаемого объекта может быть и вероятностной, и детерминированной. Важно лишь, чтобы для него существовала теория, имеющая вероятностный характер. Например, метод Монте-Карло используется для приближенного подсчета обычных интегралов. Это возможно, потому что любой такой интеграл можно рассматривать как математическое ожидание некоторой случайной величины.

Первым примером использования метода Монте-Карло обычно считается решение задачи Бюффона, в котором число Пи определяется посредством случайного  бросания иглы на стол. Название метода появилось гораздо позже, в середине XX века. Ведь все азартные игры — например, рулетка — это генераторы случайных чисел. Плюс ко всему, сознательная отсылка к азартным играм намекает на истоки теории вероятностей, которая начиналась с вычислений, связанных с игрой в кости и карты.

Алгоритм программы для моделирования прост, и это одна из причин распространенности метода. В ней случайным образом, с распределением, соответствующим теории, генерируется множество различных вариантов (сэмплов) состояния изучаемого объекта. Для каждого из них рассчитывается необходимый набор характеристик. В результате получается большая выборка. В то время, как для изучаемого объекта у нас есть только единственный набор характеристик, метод Монте-Карло даёт нам возможность получить их в большом количестве и построить функции их распределения, что дает нам гораздо больше информации.

Общая схема моделирования Монте-Карло, описанная выше, кажется простой. Но при её реализации на практике возникает множество разных, иногда весьма сложных вариаций. Даже если ограничиться применением в области финансов, то можно убедиться, насколько оно обширно — например из этой книги. Мы попробуем применить метод Монте-Карло для изучения устойчивости торговых советников. Для этого нам нужна вероятностная модель, описывающая их работу.

Вероятностная модель советника

Перед тем, как начать реальную торговлю с использованием советника, мы обычно тестируем и оптимизируем его на истории котировок. Возникает резонный вопрос: почему мы полагаем, что результаты торговли в прошлом определяют их в будущем? Естественно, мы не ждем, что все сделки в будущем образуют абсолютно ту же последовательность, что и в прошлом. Но предположение о некоторой их "схожести" у нас, очевидно, имеется. Формализуем это интуитивное представление о "схожести", используя теорию вероятностей. В соответствии с этой формализацией, мы полагаем, что результат каждой сделки — конкретная реализация некоторой случайной величины. "Схожесть" сделок в этом случае определяется через близость соответствующих им функций распределения. В такой формализации сделки, совершенные в прошлом, помогают уточнить вид распределения для будущих сделок и судить об их возможных результатах.

В рамках вероятностной формализации можно строить различные теории. Рассмотрим самую простую и наиболее часто используемую. В ней результат каждой сделки однозначно определяется относительной прибылью k=C1/C0, где C0 и C1 — объем капитала до и после сделки. В дальнейшем относительную прибыль сделки будем называть просто прибылью, а разность C1-C0 — абсолютной прибылью сделки. Предположим, что прибыли всех сделок (как в прошлом, так и в будущем) совместно независимые и одинаково распределенные случайные величины. Их распределение определяется функцией распределения F(x). Таким образом, перед нами стоит задача определить вид этой функции, используя значения прибылей сделок из прошлого. Это стандартная задача математической статистики — восстановление функции распределения по выборке. Любые способы её решения всегда дают приближённые ответы. Представим некоторые из этих способов.

1. В качестве приближения используется эмпирическая (выборочная) функция распределения.

2. Берется простое дискретное распределение, при котором прибыль сделки принимает одно из двух значений. Это либо средний убыток с вероятностью убытка, либо средняя прибыль с вероятностью прибыли.

3. Строится не дискретное, а непрерывное (имеющее плотность) приближение для функции распределения. Для этого используются методы наподобие ядерной оценки плотности.
   

В дальнейшем мы будем использовать первый вариант — он самый простой и универсальный. Трейдеру не очень интересно знать саму функцию. Важно знать, какие величины указывают на возможную прибыль от работы советника, на рискованность его использования или на устойчивость прибыли. И эти величины можно получить, зная функцию распределения.

Конкретизируем алгоритм моделирования в нашем случае. Интересующий нас объект — возможный результат работы советника в будущем. Он однозначно задаётся последовательностью сделок. Каждая сделка задаётся значением прибыли. Прибыли распределены в соответствии с описанным выше эмпирическим распределением. Мы должны сгенерировать большое число таких последовательностей и подсчитать для каждой из них необходимые характеристики. Генерация каждой такой последовательности устроена просто. Обозначим последовательность прибылей сделок, полученных на истории, через k1, k2, ..., kn. Генерируя последовательности длиной N, будем N раз выбирать случайным образом (с равной вероятностью 1/n) одно из ki (выборка с возвращением). Обычно полагают N=n, поскольку при больших N точность приближения F(x) эмпирическим распределением падает. Этот вариант метода Монте-Карло иногда называют методом бутстрапа.

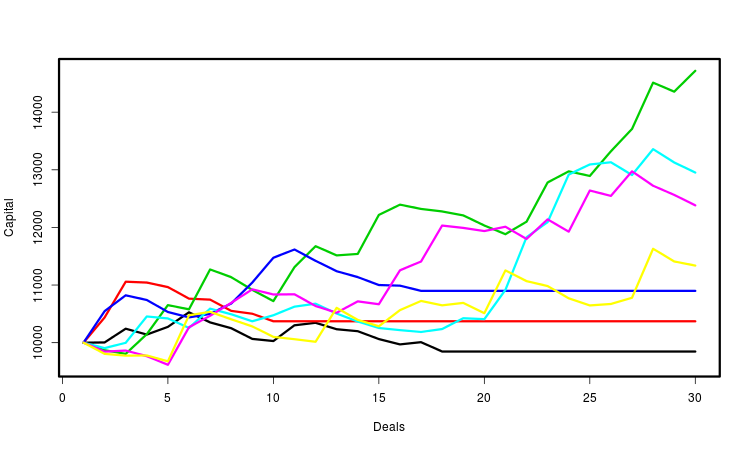
Поясним вышесказанное рисунком. На нём изображено несколько кривых капитала, каждая из которых определяется сгенерированной последовательностью сделок. Для удобства восприятия я обозначил их разными цветами. В действительности их число намного больше — несколько десятков тысяч. Для каждой из них мы вычисляем необходимые характеристики и делаем статистические выводы на основе их совокупности. Очевидно, самая важная из таких характеристик — это конечная прибыль.

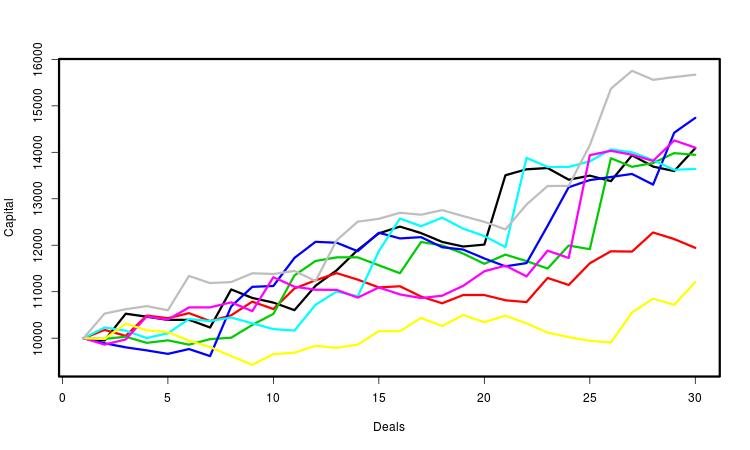
Возможны и другие подходы к вероятностной формализации и дальнейшему моделированию работы советника. Например, вместо последовательностей сделок можно моделировать  последовательности цен и изучать совокупность прибылей, которые советник на них получил. Принцип генерации ценовых рядов можно будет подобрать в зависимости от того, какую задачу требуется решить. Но этот метод потребует гораздо большего количества вычислительных ресурсов. К тому же, в настоящее время в MetaTrader нет регулярных способов использовать его для произвольного советника.

Применение теории

Наша задача — построить конкретные критерии оптимизации. Каждый из них соответствует определенной цели, главная из которых — конечная прибыль, полученная в результате всей серии сделок. Оптимизация по ней встроена в тестер. Но поскольку нам интересна прибыль в будущем, то мы должны как-то оценить возможную степень её отклонения от прибыли в настоящем. Чем меньше это отклонение, тем устойчивее прибыль системы. Рассмотрим три подхода.

1. Получив посредством метода Монте-Карло большую выборку возможных значений прибыли, можем изучить её распределение и связанные с ним величины. Очень важно среднее значение этой прибыли. Важна и дисперсия — чем она меньше, тем устойчивее работа советника и меньше неопределенность в будущих его результатах. Наш критерий будет равен отношению средней прибыли к её среднему разбросу. Он похож на коэффициент Шарпа.
2. Другая важная характеристика — просадка прибыли в серии сделок. Слишком большая просадка может привести к потере депозита, даже если советник прибыльный. По этой причине на просадку обычно накладывается ограничение. Полезно знать, как оно влияет на возможную прибыль. Критерий определен просто как средняя прибыль, но с условием, что моделируется прекращение торговли при превышении допустимого уровня просадки.

3. Построим критерий, измеряющий устойчивость прибыли в плане постоянства распределения прибылей сделок. С точки зрения теории вероятности, это означает стационарность прибылей сделок, которая, в принципе, возможна и в случае нестационарности приращений цены. Для этого мы воспользуемся идеей, похожей на форвард-тестирование. Разобьём исходную выборку сделок на начальную и конечную подвыборки. Для проверки их однородности мы можем применить какой-либо статистический тест. На основании такого теста мы и создадим критерий для оптимизации.
   

Для демонстрации нашей теории воспользуемся советником «Moving Average.mq5», входящим в поставку MetaTrader 5. Внесём в его код небольшие изменения. В начало советника добавим строку кода для включения нашего заголовочного файла:

#include <mcarlo.mqh>

В конец советника добавим код получения и использования нашего оптимизационного параметра:

double OnTester()
  {
   return optpr();         // optimization parameter
  }

Основные вычисления происходят в функциях, которые находятся в заголовочном файле «mcarlo.mqh». Его мы помещаем в папку «MQL5/Include/». Основная функция в этом файле — optpr(). При выполнении необходимых условий она вычисляет заданный параметром noptpr вариант оптимизационного критерия, а иначе возвращает ноль.

double optpr()
  {
   if(noptpr<1||noptpr>NOPTPRMAX) return 0.0;
   double k[];
   if(!setks(k)) return 0.0;
   if(ArraySize(k)<NDEALSMIN) return 0.0;
   MathSrand(GetTickCount());
   switch(noptpr)
     {
      case 1: return mean_sd(k);
      case 2: return med_intq(k);
      case 3: return rmnd_abs(k);
      case 4: return rmnd_rel(k);
      case 5: return frw_wmw(k);
      case 6: return frw_wmw_prf(k);
     }
   return 0.0;
  }

Функция setks() вычисляет массив прибылей сделок, исходя из истории торговли.

bool setks(double &k[])
  {
   if(!HistorySelect(0,TimeCurrent())) return false;
   uint nhd=HistoryDealsTotal();
   int nk=0;
   ulong hdticket;
   double capital=TesterStatistics(STAT_INITIAL_DEPOSIT);
   long hdtype;
   double hdcommission,hdswap,hdprofit,hdprofit_full;
   for(uint n=0;n<nhd;++n)
     {
      hdticket=HistoryDealGetTicket(n);
      if(hdticket==0) continue;

      if(!HistoryDealGetInteger(hdticket,DEAL_TYPE,hdtype)) return false;
      if(hdtype!=DEAL_TYPE_BUY && hdtype!=DEAL_TYPE_SELL) continue;

      hdcommission=HistoryDealGetDouble(hdticket,DEAL_COMMISSION);
      hdswap=HistoryDealGetDouble(hdticket,DEAL_SWAP);
      hdprofit=HistoryDealGetDouble(hdticket,DEAL_PROFIT);
      if(hdcommission==0.0 && hdswap==0.0 && hdprofit==0.0) continue;

      ++nk;
      ArrayResize(k,nk,NADD);
      hdprofit_full=hdcommission+hdswap+hdprofit;
      k[nk-1]=1.0+hdprofit_full/capital;
      capital+=hdprofit_full;
     }
   return true;
  }

Функция sample() генерирует случайную последовательность b[] из исходной последовательности a[].

void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   int na=ArraySize(a);
   for(int i=0; i<na;++i)
     {
      dnc=MathRandomUniform(0,na,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==na) nc=na-1;
      b[i]=a[nc];
     }
  }

Далее мы подробно рассмотрим каждый из трёх вышеуказанных видов оптимизационных критериев. Во всех случаях оптимизировать будем на одном и том же временном интервале — весна/лето 2017 года для EURUSD. Таймфрейм всегда будет 1 час, а режим тестирования — OHLC с минутного графика. Всегда будет использоваться генетический алгоритм по кастомному критерию оптимизации. Поскольку наша задача — демонстрация теории, а не подготовка советника к реальной торговле, то такой упрощённый подход кажется вполне естественным.

Устойчивость прибыли к случайному разбросу

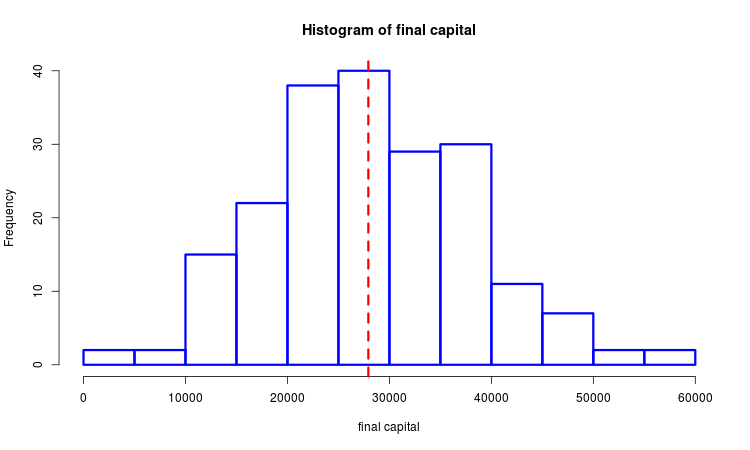
Допустим, что у нас есть выборка из сгенерированных конечных прибылей. Мы можем изучать её с помощью методов математической статистики. На рисунке ниже построена гистограмма и пунктирной линией указана выборочная медиана.

Построим два схожих варианта оптимизационного критерия. Они вычисляются в функциях mean_sd() и med_intq(). Общее в  этих вариантах — то, что они представляют собой отношение среднего к мере разброса. Отличие — в том, как определены среднее и мера разброса. В первом случае это среднее арифметическое и среднеквадратическое отклонение, а во втором — выборочные медиана и интерквартильный размах. Оба они тем больше, чем больше прибыль и чем меньше её разброс. Есть очевидная схожесть с коэффициентом Шарпа, только здесь речь идёт о прибыли во всей серии сделок, а не в одной сделке. Второй вариант критерия более устойчив к выбросам, по сравнению с первым.

double mean_sd(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   return MathMean(cn)/MathStandardDeviation(cn);
  }

double med_intq(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   ArraySort(cn);
   return cn[(int)(0.5*NSAMPLES)]/(cn[(int)(0.75*NSAMPLES)]-cn[(int)(0.25*NSAMPLES)]);
  }

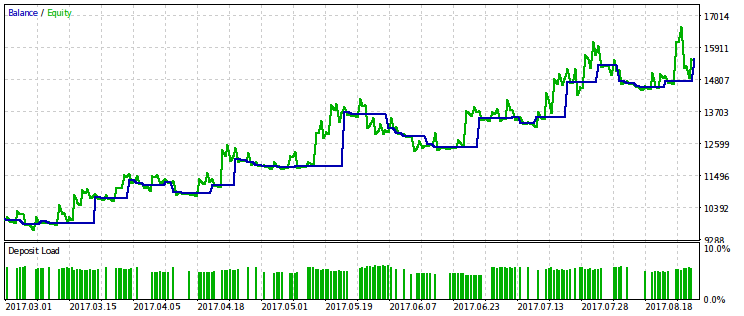
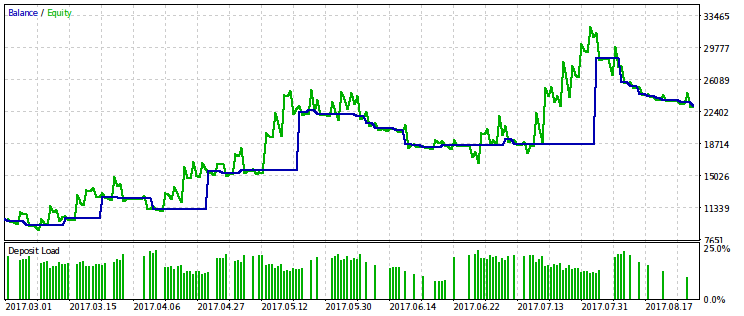
Ниже показаны две пары результатов тестирования советников, оптимизированных по этому критерию. На первой паре — результат оптимизации по первому варианту и, для сравнения,  результат с максимальной прибылью. Очевидно, что первый из них предпочтительнее, поскольку даёт более гладкую кривую капитала. Конечную прибыль при желании можно увеличить, увеличив объём сделок.

Такая же пара результатов приведена для второго варианта оптимизационного критерия. По ней можно сделать такие же выводы.

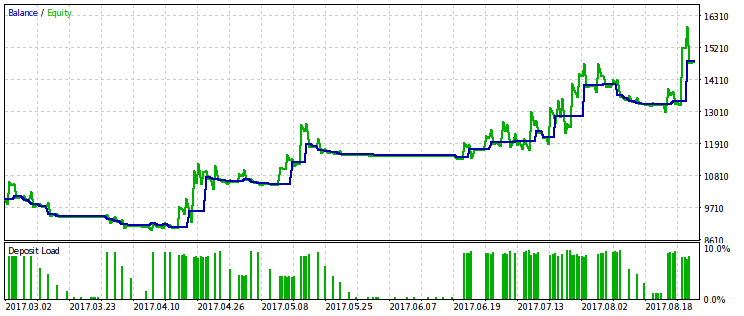
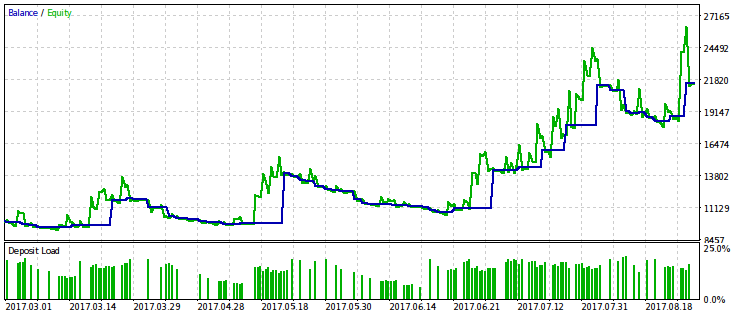
Устойчивость прибыли к просадке

В каждой сгенерированной последовательности сделок мы следим за величиной просадки. Если  остаток капитала после начальной части серии сделок составляет меньшую долю, чем задано параметром rmndmin, то оставшиеся сделки отбрасываются. На рисунке ниже можно увидеть, что в случае превышения уровня относительной просадки капитал перестает меняться, и конечный участок линии капитала становится горизонтальным.

У нас есть два варианта расчета критерия — для абсолютной и относительной просадки. В случае абсолютной просадки доля капитала считается от его начального значения, а в случае относительного — от максимального. Функции, вычисляющие эти варианты параметров, называются, соответственно, rmnd_abs() и rmnd_rel(). В обоих случаях значение критерия — это среднее сгенерированных прибылей.

double rmnd_abs(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

double rmnd_rel(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES],x;
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      x=cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]>x) x=cn[n];
         else if(cn[n]/x<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

Мы можем проводить оптимизацию либо с подходящим фиксированным параметром rmndmin, либо искать его оптимальное значение.

Приведем результаты только для критерия, связанного с относительной просадкой, поскольку её ограничение даёт более выраженный эффект. Проведем оптимизацию с несколькими вариантами фиксированного значения rmndmin: 0.95, 0.75 и 0.2.

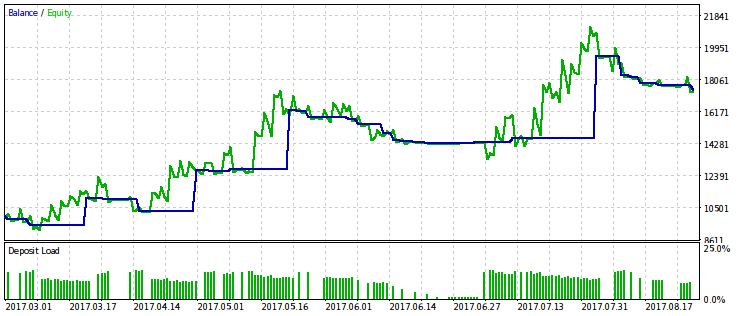
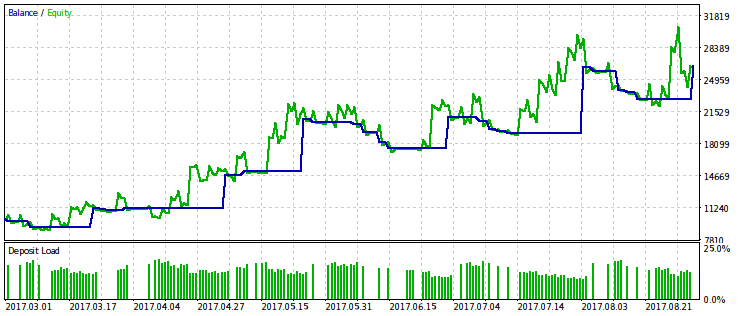
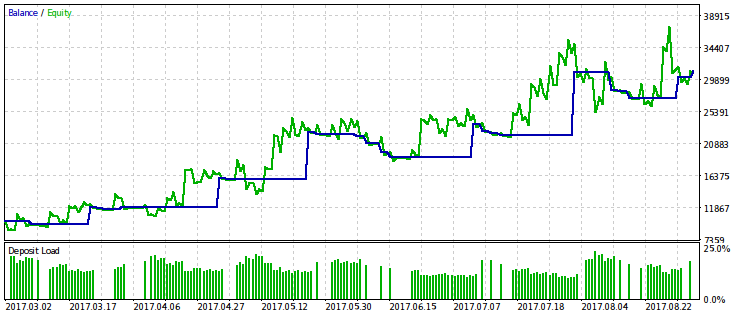
Чем меньше значение rmndmin, тем менее заметно ограничение по просадке, и результаты оптимизации все более похожи на таковые при обычной максимизации прибыли. Это можно считать следствием закона больших чисел – принципа теории вероятностей. На рисунках этот эффект не сразу заметен, поскольку на них разный масштаб по вертикальной оси (из-за подгонки  всех рисунков к одинаковым размерам) и не сразу очевиден рост просадки при уменьшении rmndmin.

Теперь включим параметр rmndmin в число оптимизируемых и продолжим оптимизацию по тому же критерию.

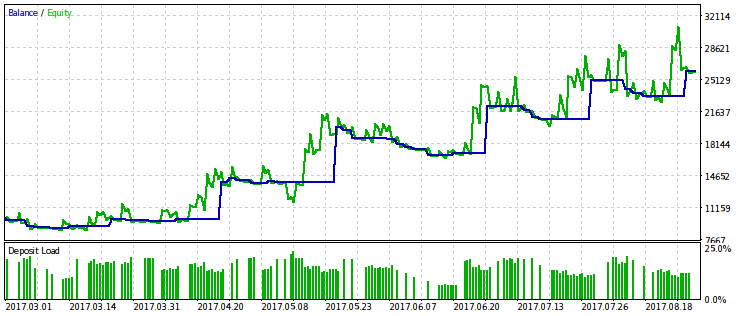
Получим оптимальное значение rmndmin=0.55. При таком его значении мы готовы к просадке почти на половину счета, что выглядит малоприемлемым. Поэтому вряд ли стоит использовать его в реальной торговле. Польза здесь в другом — видно, что "пересиживание" ещё больших просадок, скорее всего, не имеет никакого смысла. Это соответствует второй половине поговорки: "Позволяй прибыли расти, обрезай убытки".

Устойчивость распределения прибыли сделок к нестационарности цен

Поведение цен может меняться. При этом хотелось бы, чтобы результаты работы советника были стабильными. С точки зрения нашей вероятностной модели советника это означает, что нам нужна стационарность прибылей сделок даже  в случае нестационарности приращений цены.

Наш критерий оптимизации сравнивает начальную часть последовательности сделок с конечной, и чем они ближе, тем его значение больше. Близость определяется на основе критерия Уилкоксона-Манна-Уитни. Поясним его суть. Пусть у нас есть две выборки из сделок. Критерий определяет, насколько сильно сдвинута одна относительно другой. Чем меньше сдвиг, тем выше значение критерия. Поясним это рисунком: на нем каждая выборка представлена соответствующей ей гистограммой. Наибольшее значения критерия наблюдается на среднем рисунке.

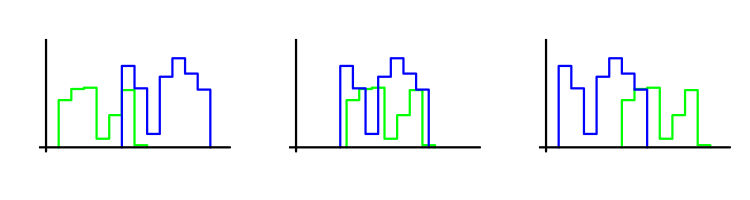
В этом случае сам по себе метод Монте-Карло не используется. Однако большая величина WMW-критерия служит обоснованием для его применения, поскольку подтверждает предположение о том, что вид распределения прибылей сделок сохраняется.

В нашем файле есть и другой вариант критерия — произведения WMW-критерия на прибыль.

double frw_wmw(double &k[])
  {
   if (fwdsh<=0.0||fwdsh>=1.0) return 0.0;
   int nk=ArraySize(k), nkf=(int)(fwdsh*nk), nkp=nk-nkf;
   if(nkf<NDEALSMIN||nkp<NDEALSMIN) return 0.0;
   double u=0.0;
   for (int i=0; i<nkp; ++i)
     for (int j=0; j<nkf; ++j)
       if(k[i]>k[nkp+j]) ++u;
   return 1.0-MathAbs(1.0-2.0*u/(nkf*nkp));
  }

double frw_wmw_prf(double &k[])
  {
   int nk=ArraySize(k);
   double prf=1.0;
   for(int n=0; n<nk; ++n) prf*=k[n];
   prf-=1.0;
   if(prf>0.0) prf*=frw_wmw(k);
   return prf;
  }

WMW-критерий напрямую использовать проблематично, потому что он может принять убыточный вариант за оптимальный. Лучше было бы оптимизировать советник по прибыли и отбрасывать варианты с небольшим значением этого параметра, но пока непонятно, как это сделать. Можно выбирать какое-то количество наилучших с точки зрения WMW-критерия вариантов, а потом выбирать из них тот, который дает максимальную прибыль.

Приведем примеры двух из десяти наилучших проходов. Один будет прибыльным, а другой — убыточным.

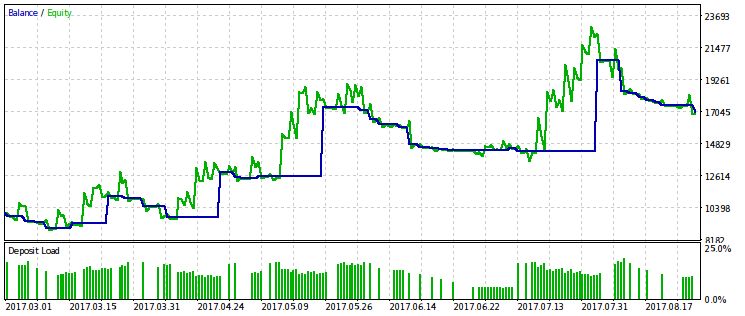
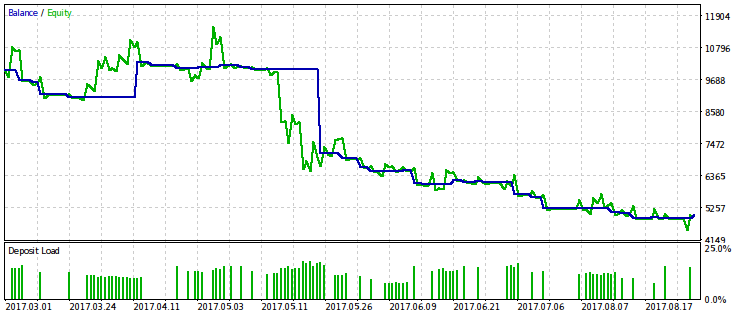
Создаётся впечатление, что WMW-критерий был бы более полезен при сравнении двух различных советников на одном и том же временном промежутке или одного и того же советника на разных. Но пока непонятно, как сделать такое сравнение регулярным.

Также приведем пример оптимизации по критерию, равному произведению WMW-критерия на прибыль. Судя по всему, она очень похожа на простую оптимизацию по прибыли, а значит, ее применять будет избыточно.

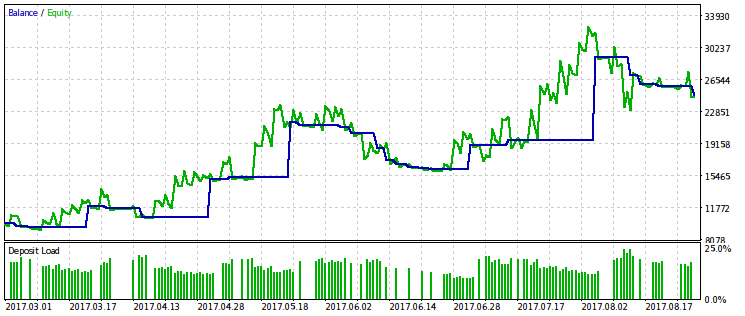
Заключение

В данной статье мы лишь немного лишь коснулись некоторых аспектов обозначенной темы. Завершим её краткими замечаниями.

• Построенные в статье критерии оптимизации могут быть полезны при формализации интуитивных представлений о том, какая последовательность сделок лучше. Это полезно при выборе из большого числа вариантов.
  
• Есть известные меры для риска, наподобие VaR (Value At Risk) или вероятности разорения. Если их использовать напрямую в качестве критерия для оптимизации, то результат будет неважным. Объемы торговли и количество сделок будут заниженными. Поэтому нужен компромиссный критерий, который зависит от двух переменных — и от риска, и от прибыли. Проблема в том, какой именно вариант этого критерия выбрать, поскольку функций от двух переменных  бесконечно много. Выбор критерия, к примеру, может определяться уровнем "агрессивности" торговой стратегии, которая очень сильно варьируется.
  
• Для разных классов советников могут быть полезны различные варианты критериев оптимизации, измеряющие устойчивость. Например, трендовые советники будут отличаться от торгующих в диапазоне, а системы с фиксированным тейк-профитом будут отличаться от закрывающих сделки по трейлинг-стопу. Распределения прибылей таких советников тоже будут принадлежать разным классам, и в зависимости от этого будет более подходящим тот или иной критерий.
• Некоторые критерии полезны не столько для сравнения поведения одного и того же советника на фиксированном промежутке времени при различных наборах параметров, сколько для сравнения двух различных советников. С помощью таких критериев можно сравнивать и работу одного советника на разных временных промежутках.
  
• Моделирование методом Монте-Карло было бы более полным, если бы имелась возможность подавать на вход советника не только имеющуюся историю цен, но и её копии, изменённые случайным образом. Это позволило бы изучать устойчивость советников более основательно, хотя и ценой увеличения объёма вычислений.
  

Приложенные файлы

№	имя	тип	описание
1	Moving Average_mcarlo.mq5	Скрипт	Модифицированный стандартный Moving Average.mq5
2	mcarlo.mqh	Заголовочный файл	Основной файл с функциями, выполняющими все необходимые вычисления