Нейросети в трейдинге: Использование языковых моделей для прогнозирования временных рядов

Введение

В рамках данной серии статей мы познакомились с множеством различных архитектурных решений для моделирования временных рядов. Многие из них достигают приличных результатов. Но можно заметить, что они не полностью используют преимущества сложных паттернов во временных рядах, таких как сезонность и тренд. Эти компоненты являются ключевыми отличительными факторами временных рядов. Как следствие, недавние исследования показывают, что архитектуры, основанные на глубоком обучении, могут быть не такими устойчивыми, как считалось ранее, и даже неглубокие нейронные сети или линейные модели могут их превосходить на некоторых бенчмарках.

Между тем, появление базовых моделей в обработке естественного языка (NLP) и компьютерном зрении (CV), ознаменовало важные вехи в эффективном обучении представлений. Предварительное обучение базовых моделей временных рядов с использованием огромных объемов данных способствует улучшению производительности в последующих задачах. Кроме того, большие языковые модели предоставляют способ использовать существующие представления модели, полученные во время предварительного обучения вместо того, чтобы требовать обучения с нуля. Однако существующие базовые структуры и методы в языковых моделях не полностью улавливают эволюцию временных паттернов, которые являются основополагающими для моделирования временных рядов.

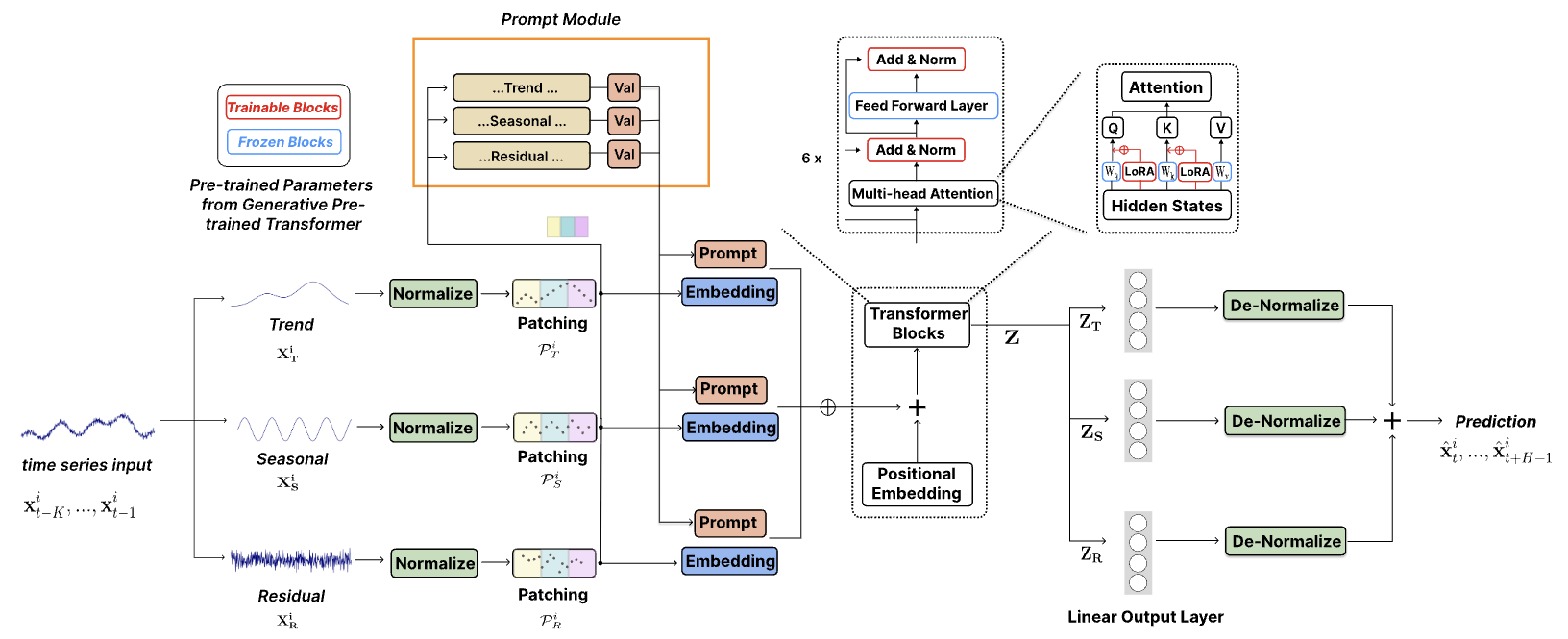
Авторы статьи "TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting" решают актуальные задачи адаптации больших предварительно обученных моделей для задач прогнозирования временных рядов и предлагают комплексную модель на основе GPT, которая получила название TEMPO. Она состоит из двух ключевых аналитических компонентов для эффективного обучения представлений временных рядов. Один фокусируется на моделировании специфических паттернов временных рядов, таких как тренды и сезонность. А другой сосредотачивается на получении более универсальных и передаваемых инсайтов из внутренних свойств данных с помощью подхода на основе подсказок. В частности, TEMPO сначала декомпозирует исходные данные мультимодального временных рядов на три компоненты: тренд, сезонность и остатки. Каждая из этих компонент затем отображается в соответствующее скрытое пространство для построения исходного эмбединга временного ряда для GPT.

Авторы метода проводят формальный анализ, связывая домен временных рядов с частотным доменом, чтобы подчеркнуть необходимость декомпозиции таких компонентов для анализа временных рядов. Кроме того, они теоретически показываем, что механизм внимания с трудом может автоматически выполнять такую декомпозицию.

В TEMPO используются подсказки, которые кодируют временные знания о тренде и сезонности. Это позволяет эффективно настроить GPT на решение задач прогнозирования. Кроме того, тренд, сезонность и остатки используются для предоставления интерпретируемой структуры понимания взаимодействий между исходными компонентами.

1. Алгоритм TEMPO

В своей работе авторы метода TEMPO применяют гибридный подход, который сочетает в себе надежность статистического анализа временных рядов с адаптируемостью методов, основанных на данных. Они предлагают новую интеграцию сезонной и трендовой декомпозиции в предварительно обученные языковые модели, построенные на архитектуре Transformer. Эта стратегия позволяет использовать уникальные преимущества как статистических, так и машинных методов обучения. Тем самым повышая способность модели эффективно обрабатывать данные временных рядов.

Кроме того, вводится полумягкий подход с подсказками, который повышает адаптируемость предварительно обученных моделей для обработки данных временных рядов. Этот инновационный подход позволяет моделям объединить свои обширные знания, полученные при предварительном обучении, с уникальными требованиями, присущими анализу временных рядов.

В случаях использования мультимодальных данных временных рядов представление сложных исходных данных путем их декомпозиции на значимые компоненты, такие как тренды и сезонность, может помочь оптимально извлечь информацию.

Трендовая составляющая XT фиксирует основные долгосрочные закономерности в данных. Сезонная составляющая XS инкапсулирует повторяющиеся краткосрочные циклы, которые можно оценить после удаления трендовой составляющей. Остаточный компонент XR представляет собой оставшуюся часть исходных данных после извлечения тренда и сезонности.

Обратите внимание, что на практике рекомендуется использовать как можно больше информации для достижения более точной декомпозиции. Однако, учитывая вычислительную эффективность, авторы метода предпочитают не использовать декомпозицию для максимально возможного окна данных в каждом экземпляре. Вместо этого они выполняют локальную декомпозицию в каждом экземпляре с использованием фиксированного размера окна. И добавляют обучаемые параметры для оценки различных компонентов локального разложения. Этот принцип распространяется и на другие компоненты модели.

Проведенные авторами метода эксперименты показывают, что декомпозиция значительно упрощает процесс прогнозирования.

Предложенная декомпозиция исходных данных имеет большое значение в современных методах на основе архитектуры Transformer, поскольку механизмы внимания, теоретически, не могут автоматически распутать однонаправленные сигналы тренда и сезона. Если тренд и сезонные компоненты временного ряда не ортогональны, они не могут быть полностью распутаны и разделены каким-либо набором ортогональных оснований. Слой Self-Attention естественным образом преобразуется в ортогональное преобразование, аналогично методу главных компонент. Таким образом, непосредственное внимание к необработанному временному ряду было бы неэффективно для распутывания не ортогональных трендовых и сезонных компонентов.

Сначала авторы метода TEMPO применяют обратимую нормализацию данных по каждому глобальному компоненту для облегчения передачи информации и минимизации потерь, вызванных сдвигами в распределении.

Кроме того, реализуется функцию потерь при реконструкции на основе среднеквадратичной ошибки (MSE). Это позволяет гарантировать, что локальное разложение на компоненты соответствует глобальному разложению, наблюдаемому в обучающей выборке.

Затем осуществляется сегментация исходных данных временных рядов с добавлением позиционного кодирования для извлечения локальной семантики путем агрегирования смежных временных шагов в токены. Это значительно увеличивает исторический горизонт при одновременном снижении избыточности.

Полученные таким образом токены временных рядов передаются на слой эмбединга. Обученные эмбединги представления временного ряда позволяют архитектуре языковой модели эффективно переносить свои возможности в новую последовательную модальность временного ряда.

Методы подсказок продемонстрировали замечательную эффективность в широком спектре приложений, используя возможности априорных знаний о конкретных задачах, закодированных в тщательно разработанных подсказках. Этот успех можно объяснить способностью подсказок обеспечить структурированность, которая согласовывает результаты работы модели с желаемыми целями. Что приводит к повышению точности, согласованности и общего качества генерируемого контента. В стремлении использовать богатую семантическую информацию, заключенную в различных компонентах временных рядов, в своем исследовании авторы метода представили смягченную стратегию подсказок. Этот подход включает в себя генерацию отдельных подсказок, соответствующих каждому основному компоненту временного ряда: тренду, сезонности и остаткам. Подсказки объединяются с соответствующими компонентами исходных данных, что позволяет использовать более совершенный подход к моделированию последовательности, учитывающий многогранный характер данных временных рядов.

Такая структура позволяет ассоциировать экземпляр исходных данных с конкретными подсказками в качестве индуктивного смещения, совместно кодируя критически важную информацию, относящуюся к задаче прогнозирования. Следует отметить, что предложенная авторами метода оперативная конструкция сохраняет высокую степень адаптивности, обеспечивая совместимость с широким спектром анализов временных рядов. Эта адаптивность подчеркивает потенциал стратегии подсказок, которая может развиваться в соответствии со сложностями, представленными различными наборами данных временных рядов.

В своей работе авторы метода TEMPO используют GPT на основе декодера в качестве базовой модели для построения основы представлений временных рядов. Для эффективного использования декомпозированной семантической информацию, подсказки и различные компоненты объединяются вместе и передаются в блок GPT.

В качестве альтернативного варианта возможно создание отдельных блоков GPT для работы с различными типами компонентов временных рядов.

Общий результат прогнозирования должен быть комбинацией прогнозов отдельных компонентов. Каждая компонента после GPT блока подается в полносвязный слой для создания прогнозных значений. Полученные прогнозы проецируются в подпространство исходных данных путем добавления соответствующих статистических показателей, изъятых на шаге нормализации. Сумма прогнозов отдельных компонент позволит реконструировать полную временную траекторию.

Авторская визуализация метода TEMPO представлена ниже.

2. Реализация средствами MQL5

После рассмотрения теоретических аспектов предложенного метода TEMPO мы переходим к практической части нашей статьи, в которой реализуем свое видение изложенных подходов средствами MQL5.

Сразу надо отметить, что, к сожалению, у нас нет предварительно обученной языковой модели. Поэтому мы не можем в полной мере оценить эффективность переноса информации языковых моделей в область прогнозирования временных рядов. Но мы можем воссоздать подобие предложенного архитектурного решения и оценить её эффективность в решении задач прогнозирования временных рядов ценового движения на реальных исторических данных.

И прежде, чем перейти к рассмотрению кода программы, следует немного внимания уделить используемым архитектурным решениям.

Поступающие на вход модели исходные данные проходят деление на компоненты: тренд, сезонность и остаток. Для извлечения тренда авторы метода использовали подсчет среднего значения исходных данных с помощью скользящего окна. Что в целом напоминает стандартный индикатор Moving Average. В своей реализации я предпочел использование ранее рассмотренного метода PLR. На мой взгляд это более информативный метод, способный идентифицировать тенденции различной длины. Однако результаты работы данного метода нельзя напрямую вычесть из исходного ряда. Здесь необходима доработка алгоритма, о которой мы поговорим более детально в процессе реализации.

Второй момент — извлечение сезонности. Думаю, здесь очевидное решение использования частотного спектра. Но как вы знаете, DFT способен полностью представить исходный временной ряд в частотной области. И обратное преобразование iDFT вернет исходный временной ряд без искажений. Для отделения сезонной составляющей исходного временного ряда от шума и выбросов нам необходимо отсечь некоторые частоты спектра. Тут становится вопрос об объеме и списке обнуляемых частот. На этот вопрос нет однозначного ответа. Мы уже обсуждали подобные вопросы при прогнозировании временных рядов в частотной области. Но на этот раз я подошел к решению вопроса несколько с иной стороны. В анализе данных мы используем мультимодальный временной ряд, который относится к одному финансовому инструменту. И вполне ожидаемо, что циклы отдельных компонент будут согласованы между собой. Так почему бы нам не воспользоваться механизмом Self-Attention для выявления согласованных частот в спектрах отдельных унитарных временных рядов. Мы ожидаем, что согласованные частоты спектра выделят сезонную составляющую.

Таким образом мы можем разделить исходные данные на отдельные компоненты, предусмотренные методом TEMPO. Работа выстраиваемой модели частично проясняется. Для разбиения унитарных моделей на отдельные сегменты и их эмбединга у нас уже есть готовое решение. То же можно сказать и об архитектурных решениях на базе Transformer. Но есть вопрос о "подсказках". Авторы метода предлагают использовать подсказки, способные подтолкнуть модель GPT к генерации последовательности в ожидаемом контексте. И в данной работе я решил в качестве "подсказок" использовать результаты работы PLR.

И, наверное, последний глобальный вопрос о количестве используемых моделей внимания: общей или по каждой компоненте. Я выбрал использование общей модели, так как это позволит организовать весь процесс обработки данных одновременно в параллельных потоках. В то время, как при использовании отдельной модели для каждой компоненты приведет к их последовательной обработке. Что, в свою очередь, увеличит как время на обучение моделей, так и в последующем на принятия решения.

Мы обсудили основные моменты выстраиваемой модели и теперь можем переходить к практической работе.

2.1 Дополнение OpenCL программы

А начнем мы свою работу с создания новых кернелов на стороне OpenCL программы. Как было сказано выше, для выделения основных тенденций из мультимодального временного ряда исходных данных мы будем использовать метод кусочно-линейного представления (PLR), который предполагает представление каждого сегмента в виде 3 значений: угол наклона линии, смещение и размер сегмента. Очевидно, что, имея такое представление временного ряда, довольно сложно вычесть тенденции из исходных данных. Тем не менее это возможно. Для реализации такого функционала мы создадим кернел CutTrendAndOther. В параметрах данный кернел получает 4 указателя на буфера данных. 2 из них содержат исходные данные в виде тензора исходного временного ряда (inputs) и тензора кусочно-линейного представления данных (plr). Результаты операций мы сохраним в 2 других буфера:

• trend — тенденции в виде обычного временного ряда;
• other — разница значений между исходными данными и линией тренда.

__kernel void CutTrendAndOther(__global const float *inputs,
                               __global const float *plr,
                               __global float *trend,
                               __global float *other
                              )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Данный кернел мы планируем вызывать в 2 мерном пространстве задач. Первое измерение представляет размер последовательности исходных данных, а второе — количество анализируемых переменных (унитарных последовательностей). В теле кернела мы идентифицируем текущий поток во всех измерениях пространства задач.

После чего определим необходимые константы.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

Следующим шагом нам предстоит найти сегмент кусочно-линейного представления, к которому относится текущий элемент последовательности. Для этого мы организуем цикл с перебором сегментов.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

На основании параметров найденного сегмента мы определим значение линии тенденции в текущей точке и её отклонение от значения исходного временного ряда.

//--- calc trend
   float sloat = plr[shift_plr + pos * step_plr];
   float intercept = plr[shift_plr + pos * step_plr + step_in];
   pos = i - prev_in;
   float trend_i = sloat * pos + intercept;
   float other_i = inputs[shift_in] - trend_i;

И теперь нам остается лишь сохранить полученные значения в соответствующие элементы глобальных буферов результатов.

//--- save result
   trend[shift_in] = trend_i;
   other[shift_in] = other_i;
  }

Аналогичным образом мы построим кернел распределения градиентов ошибки через представленные выше операции для целей обратного прохода CutTrendAndOtherGradient. Легко заметить, что данный кернел в параметрах получает указатели на аналогичные буфера данных с градиентами ошибок.

__kernel void CutTrendAndOtherGradient(__global float *inputs_gr,
                                       __global const float *plr,
                                       __global float *plr_gr,
                                       __global const float *trend_gr,
                                       __global const float *other_gr
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Здесь мы используем то же самое 2 мерное пространство задач, в котором идентифицируем текущий поток. После чего определяем значения констант.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

Далее мы повторяем алгоритм поиска необходимого сегмента.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Но на этот раз, мы рассчитываем градиенты ошибок параметров сегмента.

//--- get gradient
   float other_i_gr = other_gr[shift_in];
   float trend_i_gr = trend_gr[shift_in] - other_i_gr;
//--- calc plr gradient
   pos = i - prev_in;
   float sloat_gr = trend_i_gr * pos;
   float intercept_gr = trend_i_gr;

И сохраняем результаты в буфера данных.

//--- save result
   plr_gr[shift_plr + pos * step_plr] += sloat_gr;
   plr_gr[shift_plr + pos * step_plr + step_in] += intercept_gr;
   inputs_gr[shift_in] = other_i_gr;
  }

Обратите внимание, что мы не перезаписываем, а добавляем градиент ошибки к имеющимся данным в буфере градиентов кусочно-линейного представления. Это связано с тем, что результаты кусочно-линейного представления временного ряда мы планируем использовать в 2 направлениях:

• выделение тенденций, как реализовано в выше представленном кернеле;
• в качестве "подсказок" модели внимания, о чем упоминалось выше.

Следовательно, нам предстоит собрать градиент ошибки из 2 направлений. И чтобы исключить использование дополнительного буфера и излишнюю операцию суммирования значений 2 буферов, мы реализовали суммирования в данном кернеле.

Кроме того, мы создали кернелы CutOneFromAnother и CutOneFromAnotherGradient для разделения сезонной составляющей и прочих данных. Алгоритм данных кернелов очень прост и состоит буквально из 2-3 строк кода. Я думаю, что Вам не составит труда разобраться с ним самостоятельно. А полный код всех программ, используемых при подготовке данной статьи, представлен во вложении.

На этом мы завершаем работу с OpenCL программой и переходим к работе с нашей основной библиотекой.

2.2 Создание класса метода TEMPO

На стороне основной программы нам предстоит выстроить довольно сложный и комплексный алгоритм рассмотренного метода TEMPO. Как Вы уже заметили, предложенный подход имеет сложную и разветвленную структуру потока данных. И, наверное, это тот случай, когда реализация всего подхода в рамках 1 класса значительно повысит эффективность эксплуатации предложенных подходов.

Для реализации предложенных подходов мы создадим класс CNeuronTEMPOOCL, который унаследует основной функционал от базового класса полносвязного слоя CNeuronBaseOCL. Ниже представлена насыщенная структура нового класса. В ней можно найти как уже знакомые нам по прошлым работам элементы, так и абсолютно новые. Подробнее с функционалом каждого элемента в структуре нового класса мы познакомимся в процессе реализации его методов.

class CNeuronTEMPOOCL   :  public CNeuronBaseOCL
  {
protected:
   //--- constants
   uint              iVariables;
   uint              iSequence;
   uint              iForecast;
   uint              iFFT;
   //--- Trend
   CNeuronPLROCL     cPLR;
   CNeuronBaseOCL    cTrend;
   //--- Seasons
   CNeuronBaseOCL    cInputSeasons;
   CNeuronTransposeOCL cTranspose[2];
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CNeuronBaseOCL    cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cZero;
   //--- Noise
   CNeuronBaseOCL    cResidual;
   //--- Forecast
   CNeuronBaseOCL    cConcatInput;
   CNeuronBatchNormOCL cNormalize;
   CNeuronPatching   cPatching;
   CNeuronBatchNormOCL cNormalizePLR;
   CNeuronPatching   cPatchingPLR;
   CNeuronPositionEncoder acPE[2];
   CNeuronMLCrossAttentionMLKV cAttention;
   CNeuronTransposeOCL  cTransposeAtt;
   CNeuronConvOCL    acForecast[2];
   CNeuronTransposeOCL  cTransposeFrc;
   CNeuronRevINDenormOCL cRevIn;
   CNeuronConvOCL    cSum;
   //--- Complex functions
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                         CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   //---
   bool              CutTrendAndOther(CBufferFloat *inputs);
   bool              CutTrendAndOtherGradient(CBufferFloat *inputs_gr);
   bool              CutOneFromAnother(void);
   bool              CutOneFromAnotherGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronTEMPOOCL(void)   {};
                    ~CNeuronTEMPOOCL(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronTEMPOOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual CBufferFloat   *getWeights(void)  override;
  };

Обратите внимание, что несмотря на большое разнообразие вложенных объектов, все они объявлены статично. Это позволяет нам оставить пустыми конструктор и деструктор класса. А всю работу по очистке памяти после удаления объекта класса переложить на систему.

Непосредственная инициализация вложенных переменных и объектов класса реализована в методе Init. Как обычно, в параметрах метода мы получаем основные параметры, позволяющие однозначно определить архитектуру создаваемого слоя. Здесь мы видим уже знакомые нам параметры:

• sequence — размер анализируемой последовательности мультимодального временного ряда;
• variables — количество анализируемых переменных (унитарных последовательностей);
• forecast — глубина планирования прогнозных значений;
• heads — количество голов внимания в используемых механизмах Self-Attention;
• layers — количество слоев в блоках внимания.

bool CNeuronTEMPOOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- base
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                                                          optimization_type, batch))
      return false;

В теле метода для инициализации унаследованных объектов мы, как обычно, вызываем одноименный метод родительского класса. Помимо инициализации унаследованных объектов, в рамках метода родительского класса выполняется минимально-необходимый контроль полученных параметров.

После успешного выполнения операций метода родительского класса мы сохраним полученные параметры во вложенные переменные.

//--- constants
   iVariables = variables;
   iForecast = forecast;
   iSequence = MathMax(sequence, 1);

И тут же определим размер буферов данных для операций частотного разложения сигнала.

//--- Calculate FFTsize
   uint size = iSequence;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

Для выделения тенденций анализируемой последовательности исходных данных мы инициализируем объект кусочно-линейного разложения последовательности.

//--- trend
   if(!cPLR.Init(0, 0, OpenCL, iVariables, iSequence, true, optimization, iBatch))
      return false;

И тут же инициализируем объект для записи определенных тенденций в виде обычного временного ряда.

   if(!cTrend.Init(0, 1, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Отклонение временного ряда тенденций от исходных значений мы запишем в отдельный объект, который будет выполнять роль исходных данных для блока выделения сезонных колебаний.

//--- seasons
   if(!cInputSeasons.Init(0, 2, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Здесь стоит обратить внимание, что полученные исходные данные представляют собой последовательность мультимодальных данных описания отдельных временных шагов. Для выделения же частотного спектра унитарных временных рядов нам необходимо транспонировать тензор исходных данных. А на выходе блока мы выполним обратную операцию. С целью выполнения данного функционала мы инициализируем 2 слоя транспонирования данных.

   if(!cTranspose[0].Init(0, 3, OpenCL, iSequence, iVariables, optimization, iBatch))
      return false;
   if(!cTranspose[1].Init(0, 4, OpenCL, iVariables, iSequence, optimization, iBatch))
      return false;

Результаты частотного разложения сигнала мы будем сохранять в 2 буфера данных. Один для вещественной, а второй для мнимой части сигнала.

   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

А вот для работы блока внимания в частотном домене нам потребуется конкатенировать 2 буфера данных в один объект.

   if(!cInputFreqComplex.Init(0, 5, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

И не забываем, что модели показывают более стабильные результаты при работе с нормализованными данными. Создадим объекты для записи нормализованных данных и изымаемых параметров исходного распределения.

   if(!cNormFreqComplex.Init(0, 6, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;
   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

И вот мы дошли до инициализации объекта внимания в частотном домене. Напомню, что по нашей логике его задача выделить согласованные частотные характеристики в мультимодальных данных, которые помогут нам выделить сезонные колебания в исходных данных.

   if(!cFreqAtteention.Init(0, 7, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

В данном случаем мы используем количество голов внимание и количество слоев в блоке внимания в соответствии со значениями внешних параметров.

После выделения ключевых частотных характеристик мы выполняем обратные операции. Сначала вернем частоты в исходное распределение.

   if(!cUnNormFreqComplex.Init(0, 8, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Затем выделим вещественную и мнимую часть сигнала в отдельные буферы данных.

   if(!cOutputFreqRe.BufferInit(iFFT * iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT * iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

И преобразуем их во временную область.

   if(!cOutputTimeSeriasRe.Init(0, 9, OpenCL, iFFT * iVariables, optimization, iBatch))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT * iVariables, 0) || 
      !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

Тут же мы создадим вспомогательный буфер с нулевыми значениями, который будет использоваться для заполнения недостающих данных (пустых значений).

   if(!cZero.BufferInit(iFFT * iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;

На этом мы завершаем работу с блоком выделения сезонной компоненты. И разницу сигналов выделим в отдельный объект 3 компоненты сигнала.

//--- Noise
   if(!cResidual.Init(0, 10, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

После разделения сигнала исходных данных на 3 компоненты мы переходим к следующему этапу алгоритма TEMPO — прогнозированию последующих значений. Здесь мы сначала конкатенируем данные 3-х компонент в единый тензор.

//--- Forecast
   if(!cConcatInput.Init(0, 11, OpenCL, 3 * iSequence * iVariables, optimization, iBatch))
      return false;

После чего приведем данные в сопоставимый вид.

   if(!cNormalize.Init(0, 12, OpenCL, 3 * iSequence * iVariables, iBatch, optimization))
      return false;

Теперь нам предстоит сегментировать унитарные последовательности, которых стало в 3 раза больше благодаря разложению каждой унитарной последовательности на 3 компоненты.

   int window = MathMin(5, (int)iSequence - 1);
   int patches = (int)iSequence - window + 1;
   if(!cPatching.Init(0, 13, OpenCL, window, 1, 8, patches, 3 * iVariables, optimization, iBatch))
      return false;
   if(!acPE[0].Init(0, 14, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

И добавим к полученным сегментам позиционное кодирование.

Аналогичные операции мы выполним для кусочно-линейного представления исходного временного ряда.

   int plr = cPLR.Neurons();
   if(!cNormalizePLR.Init(0, 15, OpenCL, plr, iBatch, optimization))
      return false;
   plr = MathMax(plr/(3 * (int)iVariables),1);
   if(!cPatchingPLR.Init(0, 16, OpenCL, 3, 3, 8, plr, iVariables, optimization, iBatch))
      return false;
   if(!acPE[1].Init(0, 17, OpenCL, plr, 8 * iVariables, optimization, iBatch))
      return false;

И инициализируем слой кросс-внимания, который проанализирует разложенный нами сигнал на 3 компоненты в контексте кусочно-линейного представления исходного временного ряда.

   if(!cAttention.Init(0, 18, OpenCL, 3 * 8 * iVariables, 3 * iVariables, MathMax(heads, 1), 
                       8 * iVariables, MathMax(heads / 2, 1), patches, plr, MathMax(layers, 1), 
                       2, optimization, iBatch))
      return false;

После обработки мы переходим к прогнозированию последующих данных. И здесь мы понимаем, что, как и в случае частотного разложения, нам необходимо прогнозирования данных унитарных последовательностей. А для этого сначала нужно транспонировать данные.

   if(!cTransposeAtt.Init(0, 19, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

Далее мы используем блок из 2 последовательных сверточных слоя, который будут выполнять роль прогнозирования данных в отдельных унитарных последовательностях. Первый слой спрогнозирует унитарные последовательности для каждого элемента эмбединга.

   if(!acForecast[0].Init(0, 20, OpenCL, patches, patches, iForecast, 3 * 8 * iVariables, 
                                                                      optimization, iBatch))
      return false;
   acForecast[0].SetActivationFunction(LReLU);

А второй свернет последовательности эмбедингов до унитарных рядов анализируемых компонент исходных данных.

   if(!acForecast[1].Init(0, 21, OpenCL, 8 * iForecast, 8 * iForecast, iForecast, 3 * iVariables, 
                                                                            optimization, iBatch))
      return false;
   acForecast[1].SetActivationFunction(TANH);

После чего мы вернем тензор прогнозных значений в размерность ожидаемых результатов.

   if(!cTransposeFrc.Init(0, 22, OpenCL, 3 * iVariables, iForecast, optimization, iBatch))
      return false;

И спроецируем полученные значение в исходное распределение анализируемых компонент. Для этого бы добавим статистические параметры, изъятые при нормализации данных.

   if(!cRevIn.Init(0, 23, OpenCL, 3 * iVariables * iForecast, 11, GetPointer(cNormalize)))
      return false;

Для получения прогнозного значения целевых переменных нам предстоит сложить прогнозные значения отдельных компонентов. Операцию простого суммирования я решил заменить на взвешенную сумму с обучаемыми параметрами в рамках сверточного слоя.

   if(!cSum.Init(0, 24, OpenCL, 3, 3, 1, iVariables, iForecast, optimization, iBatch))
      return false;
   cSum.SetActivationFunction(None);

И для исключения излишнего копирования данных мы осуществим подмену указателей на соответствующие буфера.

   SetActivationFunction(None);
   SetOutput(cSum.getOutput(), true);
   SetGradient(cSum.getGradient(), true);
//---
   return true;
  }

На этом мы завершаем описание метода инициализации нового класса. Не забываем на каждом этапе контролировать процесс выполнения операций. А в завершении метода возвращаем логическое значение выполнения операций вызывающей программе.

После инициализации объекта мы переходим к следующему этапу — построению алгоритма прямого прохода. Должен сказать, что для реализации прямого прохода были построены ряд методов постановки в очередь выполнения выше описанных кернелов. Алгоритм подобных методов Вам уже знаком. И новые методы не используют каких-либо конструктивных особенностей. Поэтому подобные методы мы оставим для самостоятельного изучения. Как Вы помните, полный код данного класса и всех его методов представлен во вложении. А я предлагаю посмотреть на реализацию основного алгоритма прямого прохода в методе CNeuronTEMPOOCL::feedForward.

bool CNeuronTEMPOOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- trend
   if(!cPLR.FeedForward(NeuronOCL))
      return false;

В параметрах метода мы получаем указатель на объект предшествующего слоя, который нам передает исходные данные. И мы сразу передаем полученный указатель в метод прямого прохода вложенного слоя извлечения тенденций по методу кусочно-линейного представления.

Обратите внимание, что на данном этапе мы не осуществляем проверку актуальности полученного указателя. Так как данная проверка уже реализована в вызываемом нами методе вложенного объекта. И организация ещё одной точки контроля будет избыточной.

После определения тенденций мы вычтем их влияние из исходных данных.

   if(!CutTrendAndOther(NeuronOCL.getOutput()))
      return false;

Следующим этапом нашей работы является извлечение сезонной составляющей. Здесь мы сначала транспонируем данные, полученные после вычитания тенденций.

   if(!cTranspose[0].FeedForward(cInputSeasons.AsObject()))
      return false;

Далее мы воспользуемся быстрым преобразованием Фурье для получения спектра частотных характеристик анализируемого сигнала.

   if(!FFT(cTranspose[0].getOutput(), NULL,GetPointer(cInputFreqRe),GetPointer(cInputFreqIm),false))
      return false;

Конкатенируем вещественную и мнимую часть частотных характеристик в единый тензор.

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(),
                                                                           1, 1, iFFT * iVariables))
      return false;

И нормализуем полученные значения.

   if(!ComplexNormalize())
      return false;

Затем в блоке внимания мы выделим значимую часть спектра частотных характеристик.

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

И путем выполнения обратных операций мы получим сезонную составляющую в виде временного ряда.

   if(!ComplexUnNormalize())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;
   if(!DeConcat(cOutputTimeSeriasRe.getOutput(), cOutputTimeSeriasRe.getGradient(), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cTranspose[1].FeedForward(cOutputTimeSeriasRe.AsObject()))
      return false;

После чего выделим значение 3 компоненты.

//--- Noise
   if(!CutOneFromAnother())
      return false;

Выделив 3 компоненты из временного ряда, мы конкатенируем их в единый тензор.

//--- Forecast
   if(!Concat(cTrend.getOutput(), cTranspose[1].getOutput(), cResidual.getOutput(),
              cConcatInput.getOutput(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

Обратите внимание, что при конкатенации данных мы последовательно берем по 1 элементу каждой отдельной компоненты. Это позволяет нам расположить рядом элементы разных компонент, относящиеся к одному временному шагу одного унитарного ряда. Именно такая последовательность данных нам позволит использовать сверточный слой для взвешенного суммирования прогнозных значений отдельных компонент для получения целевой прогнозной последовательности на выходе слоя.

Далее мы нормализуем значения тензора конкатенированных компонент, что позволит нам привести в сопоставимый вид показатели отдельных компонент и анализируемых переменных.

   if(!cNormalize.FeedForward(cConcatInput.AsObject()))
      return false;

Нормализованные данные мы разделим на сегменты и создадим к ним эмбединги.

   if(!cPatching.FeedForward(cNormalize.AsObject()))
      return false;

После чего добавим позиционное кодирование для однозначной идентификации позиции каждого элемента в тензоре.

   if(!acPE[0].FeedForward(cPatching.AsObject()))
      return false;

Аналогичным образом подготовим данные кусочно-линейного представления временного ряда. Сначала нормализуем их.

   if(!cNormalizePLR.FeedForward(cPLR.AsObject()))
      return false;

А затем разобьем на сегменты и добавим позиционное кодирование.

   if(!cPatchingPLR.FeedForward(cPatchingPLR.AsObject()))
      return false;
   if(!acPE[1].FeedForward(cPatchingPLR.AsObject()))
      return false;

Теперь, когда мы подготовили представление компонент и "подсказки", можно воспользоваться блоком внимания, который должен выделить главные особенности представления анализируемого временного ряда.

   if(!cAttention.FeedForward(acPE[0].AsObject(), acPE[1].getOutput()))
      return false;

Затем мы транспонируем данные.

   if(!cTransposeAtt.FeedForward(cAttention.AsObject()))
      return false;

И прогнозируем последующие значения с помощью двухслойного MLP, функции которого выполняют два сверточных слоя.

   if(!acForecast[0].FeedForward(cTransposeAtt.AsObject()))
      return false;
   if(!acForecast[1].FeedForward(acForecast[0].AsObject()))
      return false;

Использование сверточных слоев позволяет нам организовать независимое прогнозирование последовательностей в разрезе отдельных унитарных последовательностей.

Вернем прогнозные данные в исходное представление.

   if(!cTransposeFrc.FeedForward(acForecast[1].AsObject()))
      return false;

И добавим параметры статистического распределения исходных данных, которые были изъяты при нормализации конкатенированного тензора компонент.

   if(!cRevIn.FeedForward(cTransposeFrc.AsObject()))
      return false;

В завершении метода мы суммируем прогнозные значения отдельных компонент для получения желаемого ряда последующих значений.

   if(!cSum.FeedForward(cRevIn.AsObject()))
      return false;
//---
   return true;
  }

Здесь я хочу напомнить, что, благодаря подмене указателей на буферы результатов и градиентов ошибки, мы исключили излишнюю операцию копирования данных из буфера результатов слоя суммирования компонент в буфер результатов нашего слоя. Кроме того, это позволяет нам избежать и обратной операции — копирования градиентов ошибки при построении методов обратного прохода.

Как Вы знаете, в нашей реализации обратный проход, обычно, строится из 2 методов:

• calcInputGradients — распределения градиента ошибки до всех элементов в соответствии с их влиянием на общий результат;
• updateInputWeights — корректировка параметров модели с целью минимизации ошибки.

Сначала мы выполняем операции распределения градиента ошибки, чтобы определить влияние каждого параметра модели на общий результат. Данные операции полностью повторяют поток данных прямого прохода, только в обратном направлении.

bool CNeuronTEMPOOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//--- Devide to Trend, Seasons and Noise
   if(!cRevIn.calcHiddenGradients(cSum.AsObject()))
      return false;

Сначала мы распределим полученный градиент ошибки между отдельными компонентами и скорректируем на параметры нормализации данных.

//--- Forecast gradient
   if(!cTransposeFrc.calcHiddenGradients(cRevIn.AsObject()))
      return false;

Затем пропустим градиент ошибки через MLP прогнозирования последовательности.

   if(!acForecast[1].calcHiddenGradients(cTransposeFrc.AsObject()))
      return false;
   if(acForecast[1].Activation() != None &&
      !DeActivation(acForecast[1].getOutput(), acForecast[1].getGradient(),
                    acForecast[1].getGradient(), acForecast[1].Activation())
     )
      return false;
   if(!acForecast[0].calcHiddenGradients(acForecast[1].AsObject()))
      return false;

И блок кросс-внимания.

//--- Attention gradient
   if(!cTransposeAtt.calcHiddenGradients(acForecast[0].AsObject()))
      return false;
   if(!cAttention.calcHiddenGradients(cTransposeAtt.AsObject()))
      return false;
   if(!acPE[0].calcHiddenGradients(cAttention.AsObject(), acPE[1].getOutput(), 
                                   acPE[1].getGradient(), (ENUM_ACTIVATION)acPE[1].Activation()))
      return false;

Блок кросс-внимания при прямом проходе получает данные из 2 потоков информации:

• конкатенированные компоненты;
• кусочно-линейное представление исходных данных.

Мы последовательно распределим градиент ошибки по обоим направлениям. Сначала по направлению PLR.

//--- Gradient to PLR
   if(!cPatchingPLR.calcHiddenGradients(acPE[1].AsObject()))
      return false;
   if(!cNormalizePLR.calcHiddenGradients(cPatchingPLR.AsObject()))
      return false;
   if(!cPLR.calcHiddenGradients(cNormalizePLR.AsObject()))
      return false;

А затем на конкатенированный тензор компонент.

//--- Gradient to Concatenate buffer of Trend, Season and Noise
   if(!cPatching.calcHiddenGradients(acPE[0].AsObject()))
      return false;
   if(!cNormalize.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cConcatInput.calcHiddenGradients(cNormalize.AsObject()))
      return false;

Далее мы распределим градиент ошибки на буферы отдельных компонент.

//--- DeConcatenate
   if(!DeConcat(cTrend.getGradient(), cOutputTimeSeriasRe.getGradient(), cResidual.getGradient(),
                cConcatInput.getGradient(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

И тут надо понимать, что при разделении конкатенированного тензора на отдельные части каждая из компонент получила свою долю градиента ошибки. Но есть и другой поток информации. При определении остаточной составляющей шума мы из общего значения вычитали сезонную составляющую. Следовательно, сезонная составляющая оказывает влияние на значения шума и должна получить градиент ошибки шума. Скорректируем значения градиентов.

//--- Seasons
   if(!CutOneFromAnotherGradient())
      return false;
   if(!SumAndNormilize(cOutputTimeSeriasRe.getGradient(), cTranspose[1].getGradient(), 
                       cTranspose[1].getGradient(), 1, false, 0, 0, 0, 1))
      return false;

Далее нам предстоит подготовить градиент ошибки для временного ряда сезонной составляющей. Напомню, что при формировании сезонной составляющей из частотного спектра методом обратного преобразования Фурье мы получаем вещественную и мнимую часть временного ряда. Градиент ошибки вещественной части мы определяем по значению, полученному от шума и из конкатенированного тензора компонент. Недостающие элементы дополним нулевыми значениями.

   if(!cOutputTimeSeriasRe.calcHiddenGradients(cTranspose[1].AsObject()))
      return false;
   if(!Concat(cOutputTimeSeriasRe.getGradient(), GetPointer(cZero), GetPointer(cInputFreqRe), 
                                                 iSequence, iFFT - iSequence, iVariables))
      return false;

Для мнимой части мы ожидаем нулевые значения. Поэтому в градиент ошибки запишем сами значения мнимой части с обратным знаком.

   if(!SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm),

                       GetPointer(cOutputTimeSeriasIm), 1, false, 0, 0, 0, -0.5f))
      return false;

Полученные градиенты ошибки переведем в частотную область.

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe),

           GetPointer(cOutputFreqIm), false))
      return false;

И проведем через слой частотного внимания до исходных данных.

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
              cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!ComplexUnNormalizeGradient())
      return false;
   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;
   if(!ComplexNormalizeGradient())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), true))
      return false;
   if(!DeConcat(cTranspose[0].getGradient(), GetPointer(cInputFreqIm), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cInputSeasons.calcHiddenGradients(cTranspose[0].AsObject()))
      return false;

И добавим градиент ошибки шума к полученному градиенту исходных данных.

   if(!SumAndNormilize(cInputSeasons.getGradient(), cResidual.getGradient(),
                       cInputSeasons.getGradient(), 1, 1, false, 0, 0, 1))
      return false;

Теперь нам остается провести градиент ошибки через слой PLR и передать его на уровень предыдущего слоя.

//--- trend
   if(!CutTrendAndOtherGradient(NeuronOCL.getGradient()))
      return false;
//---  input gradient
   if(!NeuronOCL.calcHiddenGradients(cPLR.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), cInputSeasons.getGradient(), 
                       NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Алгоритм метода обновления параметров модели особо не выделяется. В нем лишь последовательно вызываются одноименные методы вложенных объектов, которые содержат обучаемые параметры. Поэтому мы не будем сейчас останавливаться на подробном рассмотрении данного метода. Оставим его для самостоятельного изучения. То же относится и к вспомогательным методам, обслуживающих наш новый класс. Напомню, что полный код класса и всех его методов Вы можете найти во вложении.

Заключение

В данной статье мы познакомились с новым комплексным методом прогнозирования временных рядов TEMPO, авторы которого предложили использовать предварительно обученные языковые модели для прогнозирования временных рядов. Кроме того, авторы метода предложили новый подход в декомпозиции временных рядов, что повышает эффективность обучения представления исходных данных.

В практической части данной статьи мы реализовали свое видение предложенных подходов средствами MQL5. И здесь мы провели довольно большую работу. И, к сожалению, формат статьи не позволяет вместить весь объем проделанной работы. Поэтому результаты работы модели на реальных исторических данных будут представлены в следующей статье.

Ссылки

• TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	StudyEncoder.mq5	Советник	Советник обучения Энкодера
5	Test.mq5	Советник	Советник для тестирования модели
6	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
7	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
8	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL