Эконометрические инструменты для прогнозирования волатильности: Модель GARCH

Введение

Волатильность является важным показателем для оценки изменчивости цен финансовых активов. При анализе котировок уже давно было подмечено, что большие изменения цен очень часто влекут за собой еще большие изменения, особенно это актуально во времена финансовых кризисов. В свою очередь, за малыми изменениями как правило следуют малые изменения цен. Таким образом, спокойные периоды волатильности сменяются периодами относительной нестабильности.

Первой моделью, которая попыталась объяснить данный феномен, была модель ARCH, разработанная Энглем (Engle), — Авторегрессионная условная гетероскедастичность (неоднородность). Помимо эффекта кластерности (группирования доходностей в пачки больших и малых значений), эта модель также объясняла появление тяжелых хвостов и положительный эксцесс, что свойственно всем распределениям приращений цен. Успех условно-гауссовской модели ARCH привел к появлению целого ряда ее обобщений, целью которых было дать объяснения ряду других феноменов, наблюдаемых при анализе финансовых временных рядов. Исторически одним из первых обобщений ARCH модели является GARCH модель (Generalized ARCH).

Основным преимуществом GARCH по сравнению с ARCH моделью является то, что она более экономна и не требует длиннолаговой структуры при подгонке выборочных данных. В данной статье я хочу дать описание того, что из себя представляет GARCH модель, а самое главное предложить готовый инструмент прогнозирования волатильности на ее основе, ведь прогноз — это одна из главных целей при анализе финансовых данных.

Непараметрический подход к оценке волатильности

Использование волатильности для оценки рисков — это довольно популярная тема среди трейдеров. Самый распространенный способ оценить волатильность — просто посчитать показатель стандартного отклонения за определенный период времени.

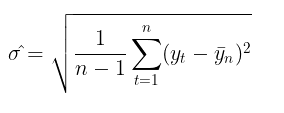
Это так называемый непараметрический подход к оценке волатильности. Рассчитанная так волатильность, называется исторической или эмпирической волатильностью. В гауссовской модели случайного блуждания это основная мера неопределенности и изменчивости, так как там предполагается, что волатильность постоянна во времени.

Параметрический подход к оценке волатильности

В модели GARCH, в свою очередь предполагается, что волатильность является случайной величиной (волатильность сама является волатильной). Это уже ближе к реальному положению дел. Процесс GARCH задается следующими уравнениями:

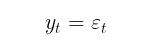
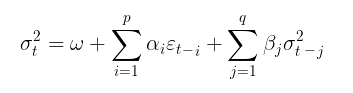
где,

• Yt – логарифмические приращения цен,
• ε t - остатки модели
• σt ² - условная дисперсия
• zt = i.i.d. N(0,1) – стандартное гауссовское распределение
• zt = i.i.d. t-Student(v) – стандартное распределение Стьюдента с v степенями свободы
• (omega,alpha,beta,v) – параметры модели, которые следует оценить по выборке данных

На параметры модели накладываются следующие ограничения:

• omega >0, условие положительности дисперсии,
• alpha≥0,
• beta≥0,
• ∑alphai + ∑betaj <1 , условие стационарности,
• v>2

Если beta = 0, тогда модель GARCH превращается в ARCH модель.

Обычно модель GARCH дополняют какой-либо моделью условного или безусловного математического ожидания. В качестве модели условного математического ожидания можно взять, например, авторегрессионный процесс первого порядка AR(1):

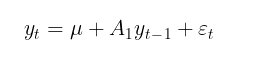
где,

• u – параметр сноса,
• A 1 – параметр модели авторегрессии

Цель моделирования условной средней состоит в том, чтобы определить ряд квадратов остатков (εt²), с помощью которых мы будем находить условную дисперсию. Если автокорреляции в рядах доходностей не наблюдается, что как правило и случается, тогда можно перейти к модели безусловного математического ожидания:

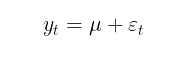
В данной статье для простоты расчетов я буду использовать модель без оценки автокорреляции доходностей. Таким образом, задача оценки волатильности в GARCH модели сводится к параметрической задаче нахождения коэффициентов модели (μ, ω, alpha, beta, v).

Оценка параметров модели GARCH с помощью метода максимального правдоподобия

Для нахождения неизвестных параметров обычно используют метод максимального правдоподобия. В предположении гауссовского распределения остатков et логарифмическая функция правдоподобия принимает вид:

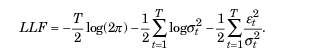
В том случае, если обнаруживают отклонения от нормальности, в качестве подходящего распределения может выступить стандартизированное распределение Стьюдента. Для малых значений параметра v (степени свободы) оно демонстрирует положительность эксцесса и более тяжелые хвосты, чем нормальное распределение. В таком случае функция правдоподобия принимает вид:

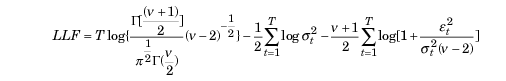
гдe,

• Г — гамма-функция
• T – объем выборки данных

Оптимизатор ALGLIB MinBLEIC

Для того, что бы найти значения параметров модели GARCH, нам нужно максимизировать функцию правдоподобия. Для этой цели необходимо использовать методы оптимизации. С этим может помочь библиотека численного анализа ALGLIB. Для максимизации целевой функции я выбрал алгоритм MinBLEIC(Bound Linear Equality Inequality Constraints).

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

В функции GARCH, которая непосредственно обращается к целевой функции и находит оптимальные значения параметров, необходимо:

• указать стартовые значения параметров,
• задать масштаб данных (очень важный момент, от которого зависит успех оптимизации),
• указать границы, в пределах которых могут изменяться параметры,
• прописать линейные ограничения-неравенства (у нас только одно на стационарность alpha + beta <1),
• указать условия остановки алгоритма оптимизации,
• указать шаг дифференцирования.

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("мат ожидание условного ст отклонения = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

Прогноз волатильности с помощью модели GARCH(1,1)

Точечный прогноз волатильности

После того как параметры модели найдены, можно переходить к основной задаче — прогнозу волатильности. Прогноз волатильности для модели GARCH(1,1) на m шагов вперед рассчитывается по формуле:

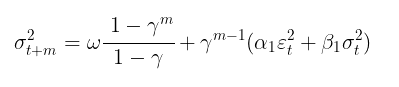
где,

• γ = α1 + β 1.

Данный прогноз при m →∞ сходится к теоретической безусловной дисперсии GARCH (при выполнении условия стационарности модели α1+ β1 < 1).

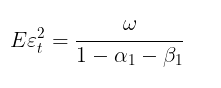
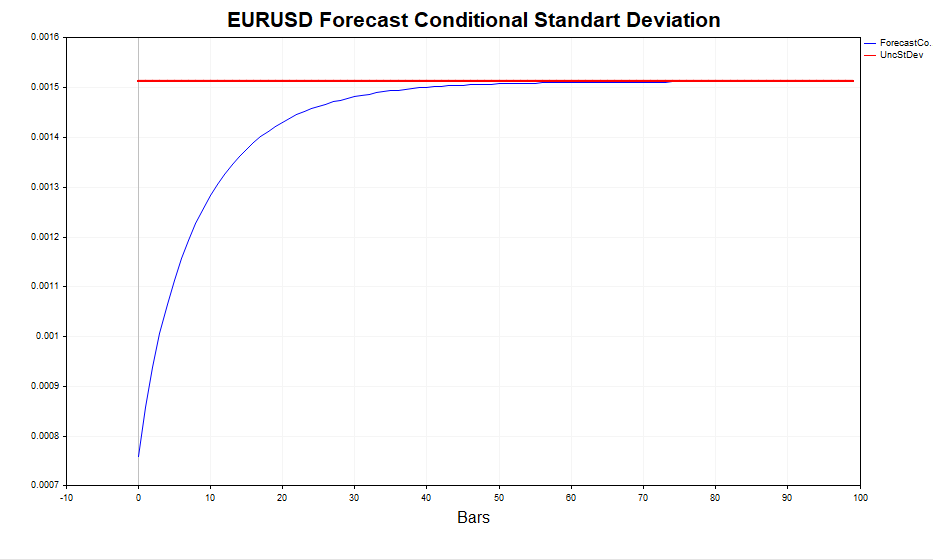
Другими словами, чем отдаленнее прогноз — тем ближе его значения к стационарному значению безусловной дисперсии. Скрипт GARCH дает возможность посчитать прогноз волатильности на m шагов вперед и сравнить эти значения с величиной Eεt ², подтверждая, что так оно и есть на самом деле.

Интервальный прогноз

Точечный прогноз волатильности это хорошо, но более важно получить вероятностную оценку того, в каких границах будут находиться будущие приращения цен, то есть получить доверительные интервалы с определенным уровнем значимости.

В предположении нормальности z t= i.i.d. N(0,1) доверительные интервалы рассчитываются по формуле:

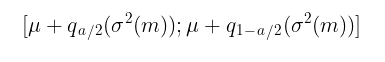
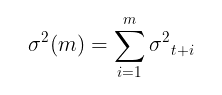
где,

• q – квантиль стандартного нормального распределения

Например, для доверительного интервала с уровнем надежности 90% (а = 1-0,9) это будет интервал:

[ u – 1,65σ ; u + 1,65σ ]

Гораздо сложнее дело обстоит, когда предполагают, что zt = i.i.d. t-Student(v). В таком случае аналитической формулы для обратной функции распределения нет. Поэтому, чтобы построить доверительные интервалы, приходится использовать моделирование по методу Монте-Карло.

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |                              |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

Понятно, что чем больше задано число симуляций (по умолчанию стоит 10000), тем точнее прогноз, но вместе с тем увеличивается и время, необходимое для расчетов. Наиболее приемлемой является цифра в 100000, тогда доверительные интервалы выглядят более симметричными.

Проверка адекватности условно-гауссовской модели GARCH

Для проверки того, насколько хорошо модель GARCH смогла уловить гетероскедастичность волатильности, необходимо проверить стандартизованные остатки на наличие автокорреляции и на соответствие стандартному нормальному распределению. Стандартизированные остатки  — это просто приращения цен за минусом условного (или безусловного) математического ожидания, разделенные на условное стандартное отклонение, рассчитанное по модели GARCH.

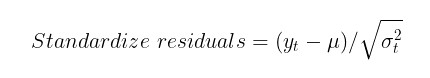
Если модель GARCH адекватна реальным данным, то стандартизованные остатки будут независимыми и одинаково распределенными стандартными нормальными величинами.

В качестве примера анализа остатков, возьмем дневные данные по EURUSD за последние четыре года и рассчитаем параметры модели.

Проверим на автокорреляцию квадраты остатков.

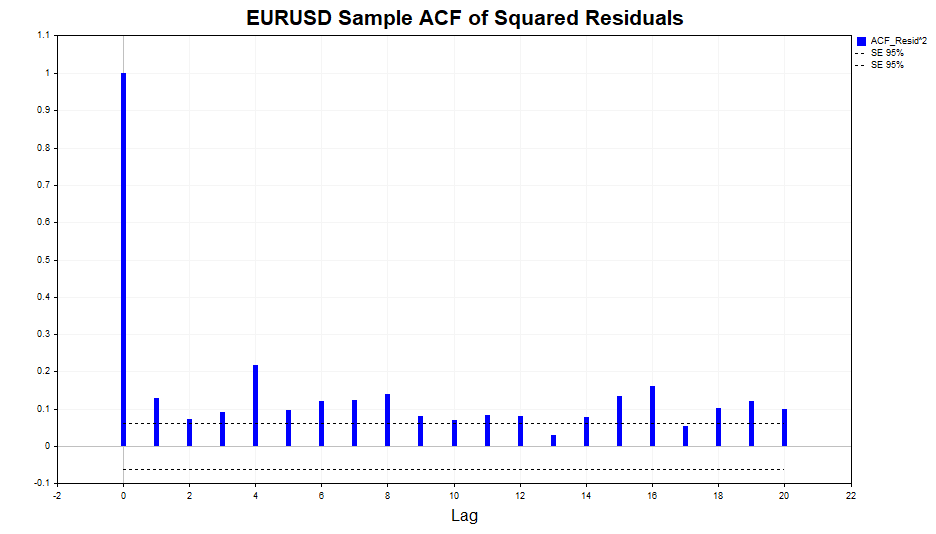
Как видим, небольшая зависимость в данных присутствует, причем до 20 лага включительно. Теперь проверим на автокорреляцию квадраты стандартизированных остатков и посмотрим, смогла ли модель GARCH(1,1) адекватно описать данную зависимость.

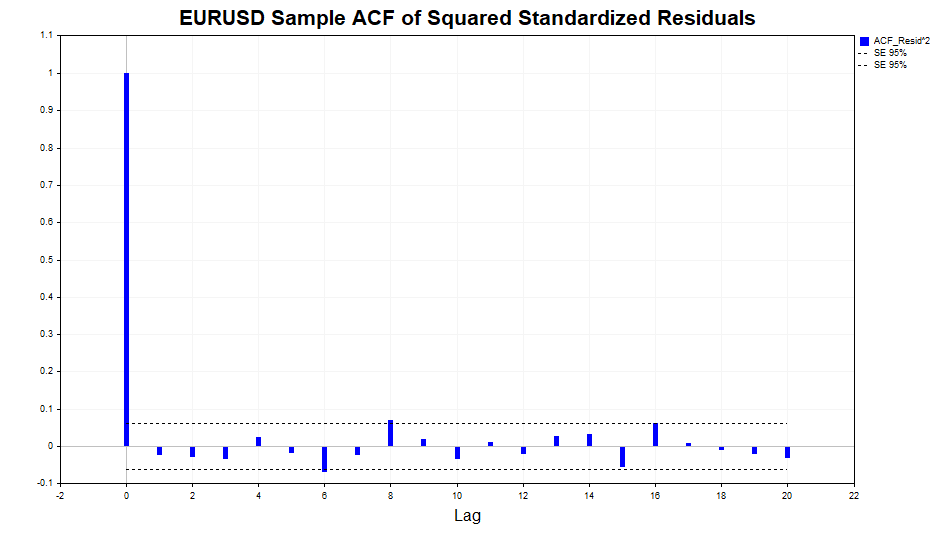
Как видим, модель прекрасно справилась, значимая корреляция в данных отсутствует.

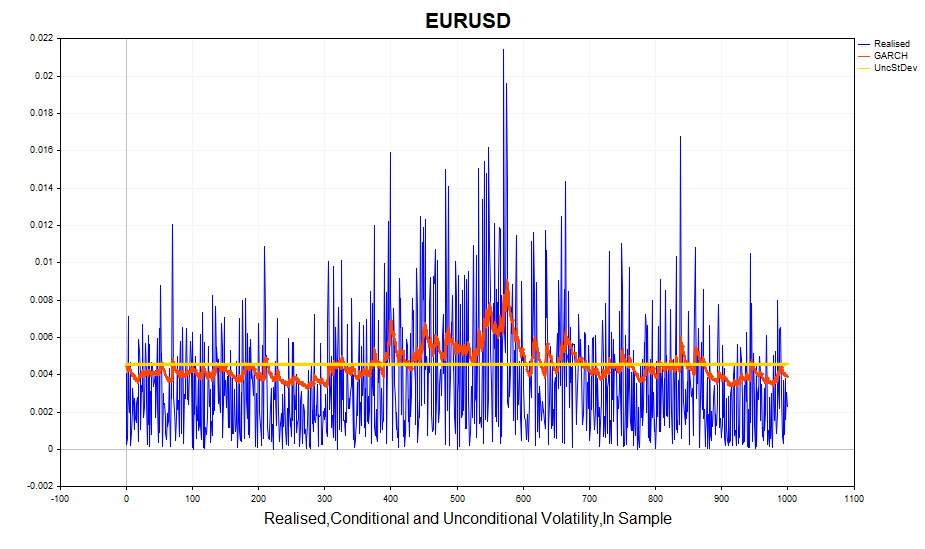
Посмотрим на рассчитанную реализованную волатильность (квадрат логарифмических приращений цен) и условное стандартное отклонение(GARCH). Модель довольно успешно реагирует на изменения волатильности. Безусловное стандартное отклонение выступает в роли среднего значения, вокруг которого колеблется GARCH-волатильность.

Проверим, как обстоит дело с нормальностью стандартизированных остатков.

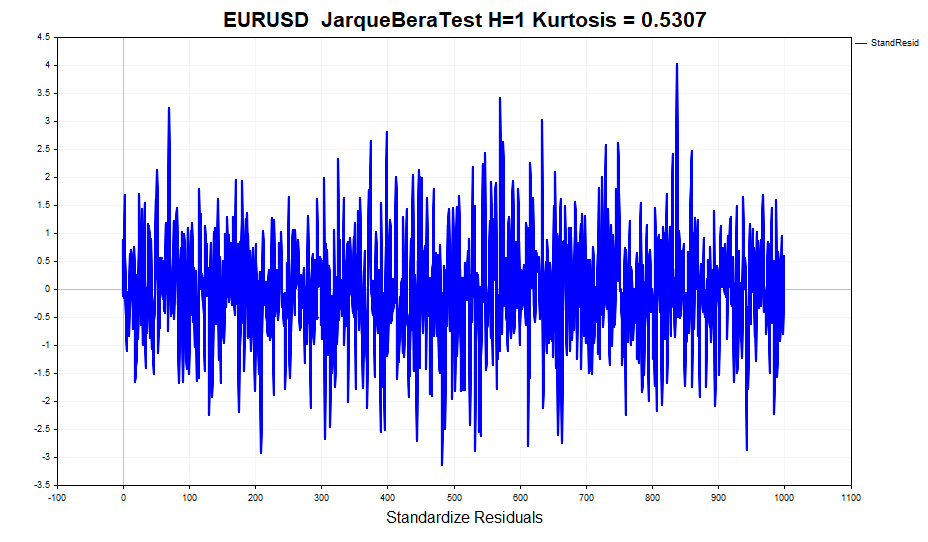
На первый взгляд, данные вполне выглядят нормальными, тяжелых хвостов можно сказать что и нет. Но формальные тесты на проверку нормальности, такие например как JarqueBeraTest, отклоняют нулевую гипотезу. Всему виной эксцесс (0,5307), немного отличающийся от нормального. В то же время значение эксцесса для доходностей равно 1,2904. То есть, модель GARCH частично учла этот эффект островершинности распределения, хотя и не полностью. Напомню, что безусловное распределение GARCH-процесса имеет толстые хвосты. Связано это с тем, что смесь гауссовских распределений с различной дисперсией приводит к распределению с тяжелыми хвостами и положительным эксцессом.

Следовательно, одно из предположений GARCH модели о том, что стандартизированные остатки имеют условное нормальное распределение,  нарушено. Как следствие, оценки параметров модели, полученные по методу максимального правдоподобия, теряют некоторые полезные свойства, а именно — они перестают быть асимптотически эффективными (другими словами, при больших выборках можно найти более точные оценки параметров).

В таком случае, в качестве альтернативы нормальному распределению можно взять распределение Стьюдента, так как при малых степенях свободы оно имеет положительный эксцесс и тяжелые хвосты. При этом количество степеней свободы становится дополнительным неизвестным параметром, который необходимо оценить по выборке.

Все действия, связанные с визуальным отображением разнообразной статистики, которую мы только что вкратце обсудили, для удобства анализа вынесены в скрипт GARCH.

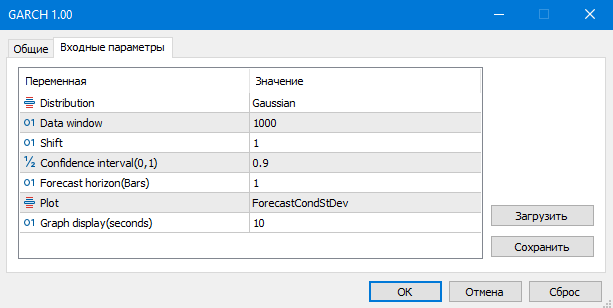
• Distribution – стандартное нормальное распределение или стандартное распределение Стьюдента
• Data window - окно данных для расчета параметров модели
• Shift – смещение окна данных (1- предпоследний бар на графике)
• Confidence interval – уровень значимости доверительного интервала (чем больше уровень значимости, тем шире доверительный интервал)
• Forecast horizon – прогноз волатильности на заданное количество баров вперед
• Plot – отображает на графике: прогноз волатильности, стандартизированные остатки, сравнение реализованной и GARCH-волатильности, автокорреляционную функцию квадратов остатков, автокорреляционную функцию стандартизированных квадратов остатков.

Индикатор iGARCH

Чтобы получить первое представление о модели и данных, для которых мы хотим эту модель применить, вполне подойдет скрипт GARCH. Но для оценки и прогноза волатильности в реальном времени, хотелось бы иметь алгоритм который будет пересчитывать параметры модели на каждом новом баре, оперативно подстраиваясь под постоянно меняющийся рынок. Адаптивный индикатор iGARCH является решением данной задачи.

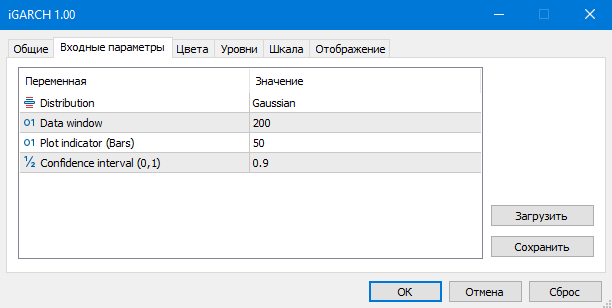
• Plot indicator – количество баров, для которых будет произведен расчет индикатора

Индикатор прогнозирует волатильность (условное стандартное отклонение) и доверительные интервалы для будущих приращений цен с определенным уровнем надежности на один шаг вперед. Прогноз отображается на нулевом баре, данные для расчета параметров (Data window) берутся начиная с первого бара. В связи с тем, что параметры модели оптимизируются на каждом баре, не рекомендуется задавать слишком большие значения Plot indicator(Bars), так как расчет может занять довольно продолжительное время (особенно для модели с распределением Стьюдента).

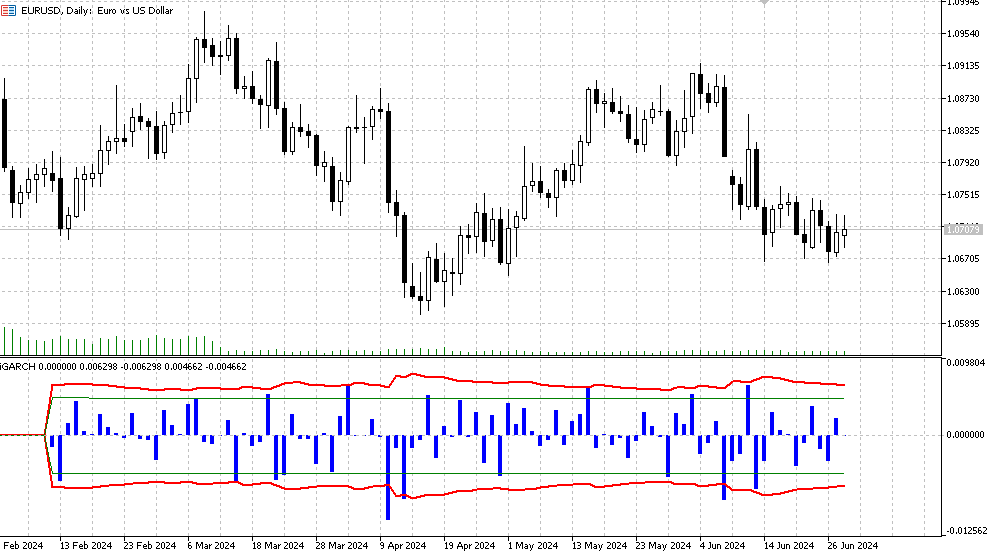
• Гистограмма — значения логарифмической доходности LN(Yt/Yt-1),
• Красная линия — верхняя и нижняя граница прогноза условного стандартного отклонения, определенная для уровня значимости confidence interval (по умолчанию 90%). Это означает, что приблизительно в 90% случаев логарифмические приращения цен будут находиться в этих границах,
• Зеленые линии отображают обычную историческую волатильность, нижнюю и верхнюю границы соответственно.

Дополнительно в журнал выводится следующая информация, которая обновляется на каждом новом баре:

• последние значения оптимизированных параметров (mu, omega, alpha, beta, v),
• значения функции правдоподобия (LLF),
• прогнозные уровни цен для выбранного уровня значимости,
• отчет об успешном завершении оптимизации,
• значения спрогнозированного условного стандартного отклонения,
• значения теоретического безусловного стандартного отклонения GARCH,
• значения исторического стандартного отклонения.

Заключение

В данной работе была рассмотрена одна из самых популярных моделей условной гетероскедастичности — модель GARCH. Мы отметили, что стандартные методы оценки волатильности, предполагающие её постоянство во времени, не отражают реальную ситуацию. В отличие от них, модель GARCH учитывает изменчивость волатильности во времени, что делает её более адекватной для анализа рыночных условий.

На примере модели GARCH(1,1) был разработан адаптивный индикатор, который позволяет прогнозировать волатильность и доверительные интервалы для логарифмов приростов цен на один шаг вперёд по времени. Это предоставляет возможность получить вероятностную оценку будущих изменений цен, и таким образом более эффективно управлять рисками по открытым позициям.

Этот индикатор даёт возможность выбирать не только классическую гауссовскую модель остатков, но и модель, предполагающую, что остатки следуют распределению Стьюдента. При этом оптимизация параметров модели осуществляется на каждом новом баре, что позволяет быстро реагировать на текущую рыночную ситуацию.

Для оценки параметров модели с использованием метода максимального правдоподобия применялся алгоритм оптимизации MinBLEIC из библиотеки численного анализа ALGLIB. Скрипт GARCH рассчитывает всю необходимую статистику, связанную с моделью, и предоставляет визуальные средства для оценки зависимостей в данных.

Таким образом, применение модели GARCH в эконометрических исследованиях и финансовом анализе позволяет получать более точные прогнозы волатильности, что значительно улучшает управление рисками и принятие инвестиционных решений.